
Algoritmo de cerradura de código (Сode Lock Algorithm, CLA)
Contenido:
1.Introducción
2.Implementación del algoritmo
3.Resultados de las pruebas
1. Introducción
Las cerraduras de código, también conocidas como cerraduras digitales o cerraduras de combinación, son mecanismos de seguridad que se usan para controlar el acceso a habitaciones, cajas fuertes, armarios y otros objetos. Se diferencian de las cerraduras convencionales en que, en lugar de utilizar una llave, se debe introducir una combinación numérica determinada para abrirlas.
Las cerraduras de código suelen estar equipadas con un teclado, cilindros especiales u otros mecanismos giratorios en los que hay que especificar una secuencia de números en combinación para abrir la cerradura. Una vez introducida la combinación correcta, la cerradura de código activa un mecanismo que desbloqueará la cerradura, permitiéndonos abrir la puerta o acceder al contenido de la caja fuerte. El usuario puede establecer su propio código o usar el código proporcionado para abrir la cerradura.
Ventajas de las cerraduras de código:
- Seguridad. Las cerraduras de código pueden proporcionar un alto nivel de seguridad, sobre todo si los códigos se cambian con regularidad.
- Comodidad. No tiene que llevar llaves encima, por lo que las cerraduras de código son muy cómodas de usar.
- Posibilidad de establecer varios códigos. Algunos modelos permiten establecer varios códigos distintos para diferentes usuarios o para distintos intervalos de tiempo.
Las cerraduras de código se utilizan en una amplia variedad de aplicaciones: seguridad doméstica, edificios comerciales, hoteles, escuelas, oficinas y otros establecimientos en los que se requiere control de acceso. El uso de cerraduras de código en el contexto de los algoritmos de optimización puede ser una idea interesante. Una posible aplicación de las cerraduras de código en algoritmos de optimización podría ser la creación de un sistema que utilice los principios de las cerraduras de código para resolver problemas de optimización, por ejemplo, para encontrar los valores óptimos de los parámetros en problemas de aprendizaje automático, o para resolver otros problemas de optimización.
El principio de funcionamiento de las cerraduras de código basado en la introducción de la combinación numérica correcta para desbloquear puede ser análogo a los mecanismos de los algoritmos de optimización que intentan encontrar una solución óptima cambiando iterativamente los parámetros y evaluando su eficacia.
Por ejemplo, podemos imaginar un algoritmo de optimización que use la analogía de la cerradura de código de la siguiente manera:
- Combinación como parámetros. Los parámetros que debemos optimizar pueden representarse como una "combinación" de valores de entrada.
- Comprobación de la combinación correcta. El algoritmo puede cambiar los valores de los parámetros y evaluar su eficacia, de manera similar a como un usuario introduce distintas combinaciones en una cerradura de código para verificar su corrección.
- Solución óptima como desbloqueo. Cuando el algoritmo encuentra los valores óptimos de los parámetros, se puede considerar que "desbloquea" la solución óptima.
Así, las cerraduras de código me han inspirado para desarrollar un algoritmo de optimización que utiliza sus principios de funcionamiento y que puede emplearse para encontrar soluciones óptimas en diversas tareas, como el aprendizaje automático y el diseño de sistemas comerciales.
2. Aplicación del algoritmo
Vamos a representar la población de agentes como una población de cerraduras donde cada cerradura representa una solución a un problema. A continuación, podemos esbozar un pseudocódigo aproximado del algoritmo de cerradura de código:
1. Inicialización:
Crearemos un array de cerraduras de tamaño "popSize", cada una con un conjuntos de discos "coords"; cada conjunto tendrá una cantidad de discos "lockDiscs".
2. Selección de la combinación de cerraduras:
Si este es el primer paso, inicializaremos cada unidad de cada conjunto de cada cerradura con un número aleatorio entre 0 y 9.
En caso contrario, para cada cerradura:
- Si el número aleatorio es menor que "copyProb", copiaremos un conjunto de discos de una cerradura seleccionada al azar.
- En caso contrario, para cada conjunto de discos:
- Si el número aleatorio es menor que "rotateProb", ajustaremos el disco a un número aleatorio entre 0 y 9.
- De lo contrario, copiaremos el disco desde una cerradura seleccionada al azar.
3. Evaluación de la calidad de las combinaciones de cerraduras:
Actualizamos la calidad de la combinación de cada cerradura.
Encontramos la cerradura con la combinación de mejor calidad y actualizamos la mejor solución global si es necesario.
Copiamos todas las cerraduras a la papelera general de cerraduras.
Clasificamos la cesta de cerraduras según la adaptabilidad.
4. Repetimos los pasos 2 y 3 durante un número determinado de épocas o hasta que se alcance el criterio de parada.
El concepto es muy emocionante, pero todavía existen algunos aspectos que plantean dudas. En concreto, no está claro cómo una combinación de códigos en una cerradura puede representar la solución a un problema. Resultaría útil disponer de una ilustración que ayude al lector a comprender mejor la cuestión.
Así, vamos a imaginar que estamos representando la solución a un problema en el que tenemos que optimizar uno o varios parámetros como un cerradura de código. En este caso, cada parámetro podrá representarse como una combinación de dígitos, donde cada dígito se encuentra en un disco independiente. El número de discos puede ser cualquiera y se establecerá como parámetro externo del algoritmo. Así, cada parámetro estará representado por un conjunto de discos etiquetados digitalmente.
Si, por ejemplo, un parámetro de tarea tiene un conjunto de 9 discos, cada uno con dígitos del 0 al 9, la combinación podría ser de 000000000 a 999999999. Luego escalaremos el número resultante en la combinación al rango de "min" a "max" del parámetro correspondiente. Así, si tenemos, por ejemplo, tres parámetros optimizables, nuestra cerradura de código tendrá 3 x 9 = 27 discos digitales. La figura 1 ilustra el mecanismo de codificación de un único parámetro.
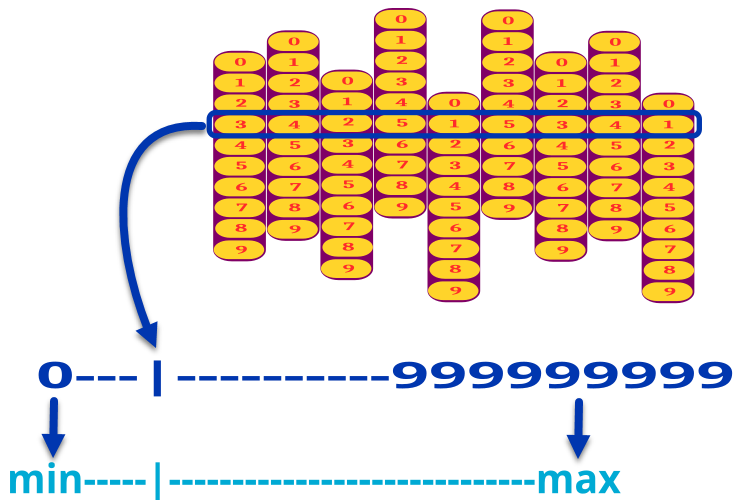
Figura 1. Descodificación de un parámetro de la tarea de un código digital a un valor real
Vamos a integrar ahora los operadores de los algoritmos de optimización, como el cruce y la mutación, en el algoritmo de optimización CLA usando la idea de cerradura de código.
1. Cruce. El cruce en los algoritmos genéticos está diseñado para combinar el material genético de dos progenitores para crear descendencia.
- En el contexto de las cerraduras de código, podemos pensar en el cruce como una combinación de valores de disco de diferentes cerraduras para crear una nueva combinación de parámetros de tarea codificados.
- Este proceso ofrece oportunidades combinatorias para que el algoritmo explore nuevas combinaciones de parámetros, de manera similar a como un usuario puede probar distintas combinaciones en una cerradura de código, al tiempo que utiliza las combinaciones de dígitos más exitosas en distintas cerraduras.
2. Mutación (Mutation). En los algoritmos genéticos, una mutación es un cambio aleatorio en el material genético para crear diversidad en una población.
- En el contexto de las cerraduras de código, la mutación puede interpretarse como la rotación aleatoria de los discos a una posición con cualquier dígito para modificar la combinación en la cerradura de código.
- Este proceso ayuda al algoritmo a explorar nuevas combinaciones de parámetros en todo el espacio de soluciones y a evitar que se quede atascado en óptimos locales.
En general, integrar el cruce y la mutación en el algoritmo de optimización puede ampliar la diversidad de soluciones, acelerar la convergencia hacia la solución óptima y ayudar a evitar la convergencia prematura. Este enfoque puede resultar útil en problemas de optimización con un gran espacio de búsqueda y funciones objetivo complejas. Sin embargo, no nos queda más remedio que hilar fino usando la analogía de los operadores genéticos.
Para resolver el problema, tendremos que encontrar la combinación correcta de números en la cerradura de código. Para ello, deberemos girar los discos para encontrar la combinación de código correcta para abrir la cerradura. A diferencia de los algoritmos genéticos, en los que "girar" un valor de código binario en los genes tiene una probabilidad de 50/50 de arrojar un valor (ya sea 0 o 1), en el algoritmo de cerradura de código podremos utilizar distribuciones de probabilidad en una estrategia de giro de disco. Veamos algunas opciones.
Podemos usar la distribución gaussiana cuando se mutan los parámetros de la combinación: cada parámetro se cambiará por un valor aleatorio que se elegirá de una distribución normal (gaussiana). Esto permitirá realizar algún cambio aleatorio en los parámetros manteniendo hasta cierto punto su valor actual.
Aplicar una distribución gaussiana a una mutación puede resultar útil porque permite controlar el grado de variación de los parámetros. Los parámetros pueden cambiarse a valores pequeños cercanos a los actuales, lo cual ayudará a conservar las buenas propiedades de la solución actual, mientras que la naturaleza aleatoria de la mutación permitirá al algoritmo explorar nuevas regiones del espacio de búsqueda.
Así, el uso de la distribución gaussiana para la mutación puede ayudar a equilibrar la exploración de nuevas soluciones conservando al mismo tiempo las buenas propiedades de las soluciones actuales, lo cual contribuirá a la búsqueda eficiente de la solución óptima en espacios de parámetros complejos.
Del mismo modo, podemos usar la distribución de potencia para el proceso de mutación. A diferencia de la distribución gaussiana, la distribución de potencia tiene colas más pesadas, lo cual significa que pueden ocurrir con mayor probabilidad grandes cambios de parámetros, lo cual puede ser útil cuando necesitamos una exploración más radical del espacio de parámetros. La distribución escalonada puede ayudar al algoritmo a "saltar" fuera de las trampas locales.
También podemos intentar usar una tercera opción, la distribución uniforme, que crea una probabilidad igual de elegir cualquier dígito del disco de la cerradura.
Ahora podemos pasar de la parte teórica a la escritura de código y la investigación práctica.
En el algoritmo CLA del agente que representa la solución del problema, describiremos una cerradura con la estructura "S_CLA_Agent". Aquí tenemos sus principales componentes:
- f - esta variable almacenará el valor de adaptación del agente. Se inicializa como -DBL_MAX, lo que supone el valor más pequeño posible para el tipo double.
- struct S_Lock - tiene una estructura anidada y contiene el array "lock". Este array se utiliza para almacenar la combinación de códigos del parámetro de tarea individual que estamos optimizando.
- S_Lock code [] - array de estructuras "S_Lock". Todo este conjunto representa una "cerradura".
- void Init (int coords, int lockDiscs) - función de inicialización. Toma dos parámetros: "coords", que define el número de conjuntos de parámetros, y "lockDiscs", que define el número de discos en cada conjunto. Dentro de esta función, se inicializará el array "code".
En general, esta estructura representa el agente del algoritmo de optimización CLA. Cada agente posee su propia adaptabilidad y descripción de la combinación de "cerradura" que se optimizará durante la ejecución del algoritmo.
//—————————————————————————————————————————————————————————————————————————————— struct S_CLA_Agent { double f; //fitness struct S_Lock { int lock []; }; S_Lock code []; void Init (int coords, int lockDiscs) { f = -DBL_MAX; ArrayResize (code, coords); for (int i = 0; i < coords; i++) { ArrayResize (code [i].lock, lockDiscs); } } }; //——————————————————————————————————————————————————————————————————————————————
Ahora vamos a describir la clase "C_AO_CLA", derivada de la clase "C_AO". Los principales componentes de la clase son:
- C_AO_CLA () - constructor de clase que inicializa un objeto de la clase. Dentro de este constructor se inicializarán parámetros como "popSize", "lockDiscs", "copyProb", "rotateProb" y "params".
- SetParams () - función que establece los parámetros del algoritmo basándose en los valores del array "params".
- Init () - función de inicialización, admite como parámetros tanto rangos de búsqueda como números de épocas.
- Moving (), Revision () son funciones que se utilizan para ejecutar la lógica básica en el algoritmo.
- lockDiscs, copyProb, rotateProb - variables usadas para almacenar los parámetros del algoritmo.
- S_CLA_Agent agent [] - array de agentes, cada uno de los cuales representa un objeto de la estructura "S_CLA_Agent".
- maxLockNumber, S_CLA_Agent parents [], S_CLA_Agent parTemp [] - variables privadas y arrays que se usan dentro de la clase.
- ArrayToNumber (), LockToDouble () - métodos privados que se utilizan para convertir un array de combinación de códigos en un número, y una cerradura en un número de coma flotante, respectivamente.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_CLA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_CLA () { } C_AO_CLA () { ao_name = "CLA"; ao_desc = "Code Lock Algorithm"; ao_link = "https://www.mql5.com/es/articles/14878"; popSize = 100; //population size lockDiscs = 8; //lock discs copyProb = 0.8; //copying probability rotateProb = 0.03; //rotate disc probability ArrayResize (params, 4); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "lockDiscs"; params [1].val = lockDiscs; params [2].name = "copyProb"; params [2].val = copyProb; params [3].name = "rotateProb"; params [3].val = rotateProb; } void SetParams () { popSize = (int)params [0].val; lockDiscs = (int)params [1].val; copyProb = params [2].val; rotateProb = params [3].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); void Injection (const int popPos, const int coordPos, const double value); //---------------------------------------------------------------------------- int lockDiscs; //lock discs double copyProb; //copying probability double rotateProb; //rotate disc probability S_CLA_Agent agent []; private: //------------------------------------------------------------------- int maxLockNumber; //max lock number S_CLA_Agent parents []; S_CLA_Agent parTemp []; int ArrayToNumber (int &arr []); double LockToDouble (int lockNum, int coordPos); }; //——————————————————————————————————————————————————————————————————————————————
Ahora definiremos el método "Init" en la clase "C_AO_CLA". Este método inicializará el algoritmo con los rangos de búsqueda y el número de épocas dados. Descripción de cada paso:
1. if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; - llamada a la función StandardInit con los rangos de búsqueda especificados. Si la inicialización falla, la función retornará "false".
2. ArrayResize (agent, popSize); - la cadena redimensiona el array de agentes al tamaño de población "popSize".
3. for (int i = 0; i < popSize; i++) agent [i].Init (coords, lockDiscs); - el ciclo inicializa cada agente de la población con el número dado de coordenadas "coords" y discos de cerradura "lockDiscs".
4. ArrayResize (parents, popSize * 2); ArrayResize (parTemp, popSize * 2); - las cadenas redimensionan los arrays "parents" y "parTemp" a dos tamaños de población.
5. for (int i = 0; i < popSize * 2; i++) { parents [i].Init (coords, lockDiscs); parTemp [i].Init (coords, lockDiscs); } - el ciclo inicializa cada padre y padre temporal en los arrays "parents" y "parTemp".
6. maxLockNumber = 0; for (int i = 0; i < lockDiscs; i++) { maxLockNumber += 9 * (int)pow (10, i); } - el ciclo calcula el número máximo en la combinación de cerradura "maxLockNumber" utilizando el número de discos de cerradura "lockDiscs".
7. return true; - si todas las operaciones anteriores se han realizado correctamente, la función retornará "true".
Esta función inicializa los agentes y los padres en un algoritmo de optimización que utiliza cerraduras de código CLA, y establece el número máximo de combinaciones de cerraduras en función del número de discos de cerradura.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_CLA::Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0) //number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (agent, popSize); for (int i = 0; i < popSize; i++) agent [i].Init (coords, lockDiscs); ArrayResize (parents, popSize * 2); ArrayResize (parTemp, popSize * 2); for (int i = 0; i < popSize * 2; i++) { parents [i].Init (coords, lockDiscs); parTemp [i].Init (coords, lockDiscs); } maxLockNumber = 0; for (int i = 0; i < lockDiscs; i++) { maxLockNumber += 9 * (int)pow (10, i); } return true; } //——————————————————————————————————————————————————————————————————————————————
El proceso de iteración de combinaciones digitales en las cerraduras lo describiremos ene l método "Moving" en la clase "C_AO_CLA". El proceso será el siguiente:
- val = 0.0; code = 0; pos = 0; - inicialización de las variables que se usarán en el método.
- if (!revision) {...} - el bloque de código se ejecutará si "revision" es igual a "false". Dentro de este bloque de código, los agentes y los progenitores se inicializarán utilizando valores aleatorios.
- A continuación, se calcularán los valores "code" y "val" para cada agente y cada progenitor, y se utilizarán para actualizar las coordenadas del agente. A continuación, "revision" se establecerá en "true" y la función finalizará.
- for (int i = 0; i < popSize; i++) {...} - el bloque de código se ejecutará si "revision" es igual a "true". Dentro de este bloque de código es donde se actualizarán los agentes. Si el número aleatorio es menor que "copyProb", el código de cerradura de uno de los progenitores se copiará en el agente. En caso contrario, el código de cerradura del agente se actualizará con un valor aleatorio o con el código de cerradura de uno de los progenitores.
- Los valores "code" y "val" se calcularán para cada agente y se utilizarán para actualizar sus coordenadas.
La función se utilizará para actualizar los agentes en el algoritmo de optimización CLA.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CLA::Moving () { double val = 0.0; int code = 0; int pos = 0; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { for (int l = 0; l < lockDiscs; l++) { agent [i].code [c].lock [l] = u.RNDminusOne (10); } code = ArrayToNumber (agent [i].code [c].lock); val = LockToDouble (code, c); a [i].c [c] = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); } } for (int i = 0; i < popSize * 2; i++) { for (int c = 0; c < coords; c++) { for (int l = 0; l < lockDiscs; l++) { parents [i].code [c].lock [l] = u.RNDminusOne (10); } } } revision = true; return; } //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { if (u.RNDprobab () < copyProb) { int pos = u.RNDminusOne (popSize); ArrayCopy (agent [i].code [c].lock, parents [pos].code [c].lock, 0, 0, WHOLE_ARRAY); } else { for (int l = 0; l < lockDiscs; l++) { if (u.RNDprobab () < rotateProb) { //pos = u.RNDminusOne (popSize); //agent [i].code [c].lock [l] = (int)round (u.GaussDistribution (agent [i].codePrev [c].lock [l], 0, 9, 8)); //agent [i].code [c].lock [l] = (int)round (u.PowerDistribution (agent [i].codePrev [c].lock [l], 0, 9, 20)); agent [i].code [c].lock [l] = u.RNDminusOne (10); } else { pos = u.RNDminusOne (popSize); agent [i].code [c].lock [l] = parents [pos].code [c].lock [l]; } } } code = ArrayToNumber (agent [i].code [c].lock); val = LockToDouble (code, c); a [i].c [c] = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————El método "Revision" de la clase "C_AO_CLA " en general está destinado a actualizar la solución global. El método efectuará las siguientes acciones:
- ind = -1; - inicialización de la variable "ind", que se usará para rastrear el índice del agente con el mejor ajuste.
- for (int i = 0; i < popSize; i++) {...} - el ciclo itera cada agente de la población y comprueba si la adaptabilidad del agente es mayor que el valor actual de mejor adaptabilidad "fB". Si es así, "fB" se actualizará y "ind" se establecerá en el índice actual.
- if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); - si se ha encontrado un agente con mejor adaptabilidad, sus coordenadas se copiarán a "cB".
- for (int i = 0; i < popSize; i++) { agente [i].f = a [i].f; } - el ciclo actualiza la adaptabilidad de cada agente en función de los valores actuales de la array "a".
- for (int i = 0; i < popSize; i++) { padres [i + popSize] = agente [i]; } - el ciclo copia cada agente en el array "parents" empezando por la posición "popSize", es decir, en la segunda mitad de la población parental.
- u.Sorting (parents, parTemp, popSize * 2); - esta cadena clasificará el array "parents" utilizando el array "parTemp" como almacenamiento temporal.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CLA::Revision () { //---------------------------------------------------------------------------- int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { agent [i].f = a [i].f; } for (int i = 0; i < popSize; i++) { parents [i + popSize] = agent [i]; } u.Sorting (parents, parTemp, popSize * 2); } //——————————————————————————————————————————————————————————————————————————————
El método "ArrayToNumber" se usa para convertir los caracteres de la combinación de códigos en un número. Acciones del método:
- result = 0; - inicialización de la variable que se utilizará para almacenar el resultado.
- for (int i = 0; i < ArraySize (arr); i++) {...} - el ciclo itera por cada elemento del array "arr". Para cada elemento "arr [i]", multiplica el valor actual "result" por 10 y añade el valor "arr [i]".
- return result; - la cadena retorna el valor "result" final.
En general, este método convierte un array de números enteros en un único número entero interpretando cada elemento del array como un dígito de la representación decimal del número.
Por ejemplo, los valores del array de entrada "arr" (combinación de códigos) son: |0|3|1|5|7|0|. Tendremos que descartar todos los ceros del lado izquierdo de la combinación y empezar a formar el número con el valor 3. El resultado será el número 31570. Si la combinación contiene ceros en todas las celdas del array, el número resultante será 0.
//—————————————————————————————————————————————————————————————————————————————— int C_AO_CLA::ArrayToNumber (int &arr []) { int result = 0; for (int i = 0; i < ArraySize (arr); i++) { result = result * 10 + arr [i]; } return result; } //——————————————————————————————————————————————————————————————————————————————
Para convertir el número de la combinación de códigos en la escala del parámetro a optimizar, se utiliza el método "LockToDouble" en la clase "C_AO_CLA". Esto es lo que hace esta función:
- LockToDouble (int lockNum, int coordPos) - el método admite dos parámetros: "lockNum" que es el número de cerradura "coordPos", y representa la posición de la coordenada en un array de coordenadas (el parámetro a optimizar).
- return u.Scale (lockNum, 0, maxLockNumber, rangeMin [coordPos], rangeMax [coordPos]); - la cadena retorna un valor que se obtiene usando el escalado "lockNum" del rango [0, maxLockNumber] al rango [rangeMin [coordPos], rangeMax [coordPos]].
En general, este método se usa para convertir un número de cerradura en un número de coma flotante basado en un rango determinado, es decir, los números de cerradura se convierten en los valores de los parámetros optimizados del problema.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CLA::LockToDouble (int lockNum, int coordPos) { return u.Scale (lockNum, 0, maxLockNumber, rangeMin [coordPos], rangeMax [coordPos]); } //——————————————————————————————————————————————————————————————————————————————
3. Resultados de las pruebas
Los resultados del algoritmo de optimización CLA en las funciones de prueba son fenomenales. Un 67,86% del valor máximo posible es un resultado excelente. Esto indica el alto rendimiento del algoritmo CLA en la optimización de funciones complejas.
Estos resultados demuestran que el algoritmo CLA resulta bastante eficiente y puede aplicarse con éxito a diversos problemas en los que se requiere la optimización de funciones multidimensionales. Su escalabilidad y capacidad para tratar problemas complejos hacen de él una herramienta prometedora para resolver una amplia gama de problemas de optimización.
CLA|Code Lock Algorithm|100.0|8.0|0.8|0.03|
=============================
5 Hilly's; Func runs: 10000; result: 0.9534490932631814
25 Hilly's; Func runs: 10000; result: 0.8710742215971827
500 Hilly's; Func runs: 10000; result: 0.375900385878165
=============================
5 Forest's; Func runs: 10000; result: 0.9894215656296362
25 Forest's; Func runs: 10000; result: 0.917091907561472
500 Forest's; Func runs: 10000; result: 0.3164221021938828
=============================
5 Megacity's; Func runs: 10000; result: 0.7969230769230768
25 Megacity's; Func runs: 10000; result: 0.693846153846154
500 Megacity's; Func runs: 10000; result: 0.19303076923077062
=============================
All score: 6.10716 (67.86%)
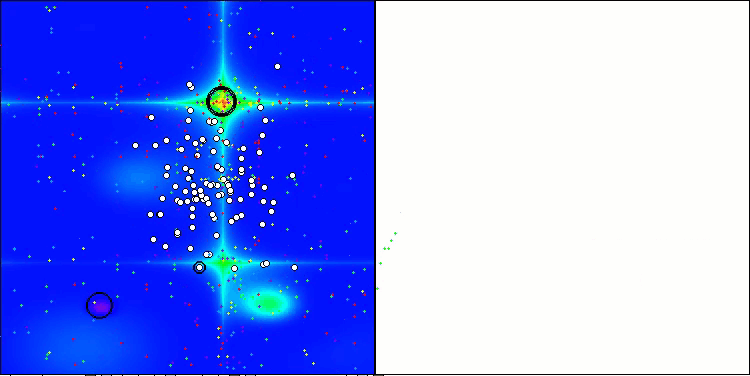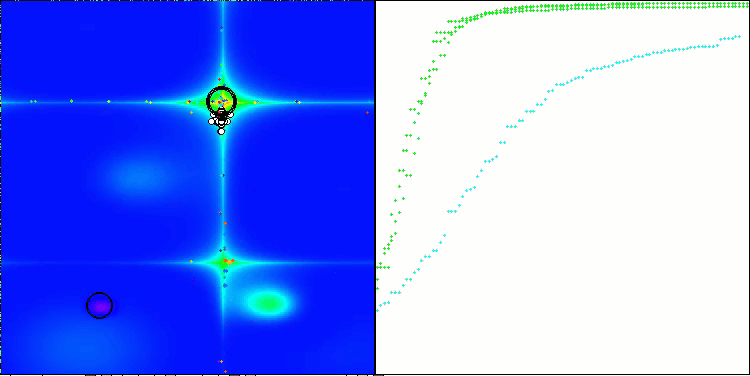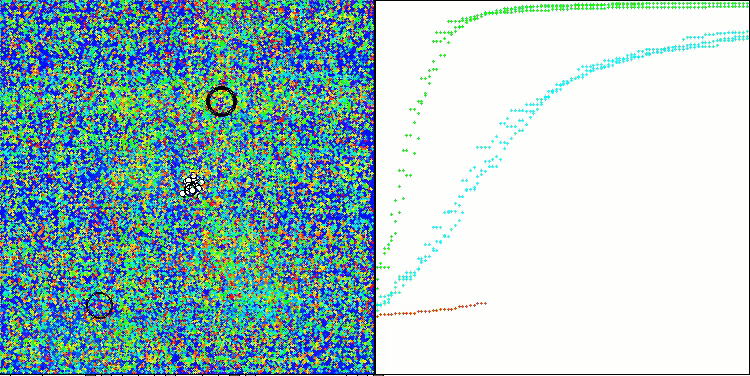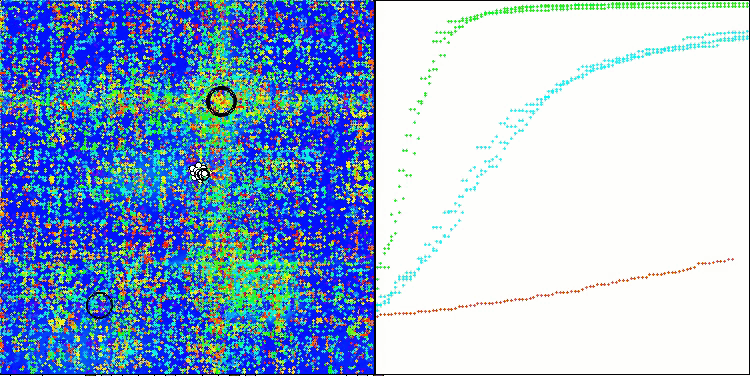
En la representación del funcionamiento del algoritmo en las funciones de prueba, la dispersión de los resultados en las funciones de pequeña dimensionalidad es notable, pero a medida que aumenta el número de parámetros del problema, la dispersión de los resultados desaparece. Además, el potencial del algoritmo en problemas de gran dimensionalidad (1000 parámetros) resulta apreciable por la forma de la curva de convergencia (línea roja): la línea crece con la aceleración. Si eliminamos la restricción del número de ejecuciones de la función de aptitud (nuestras reglas de prueba), el algoritmo seguirá acercándose al óptimo global.
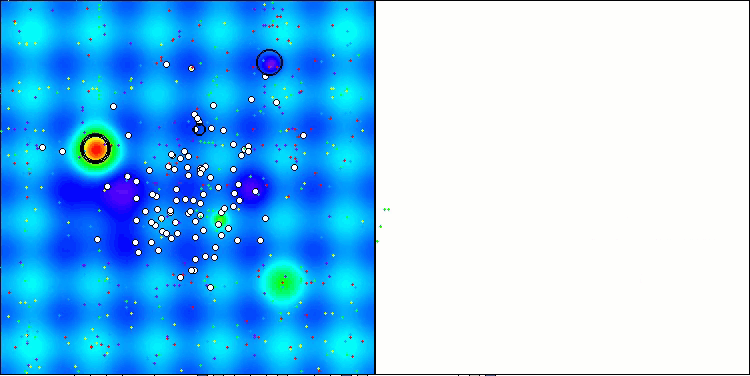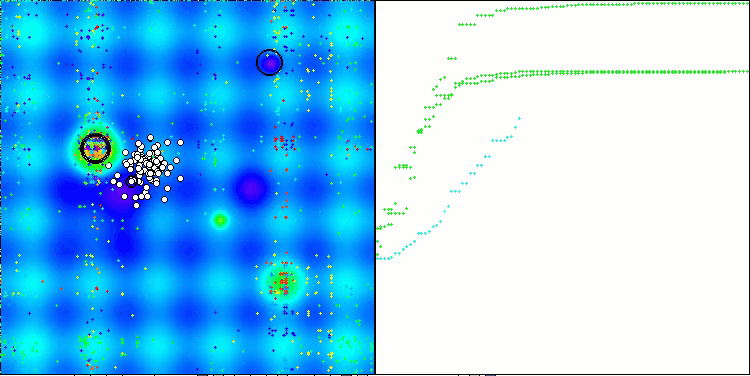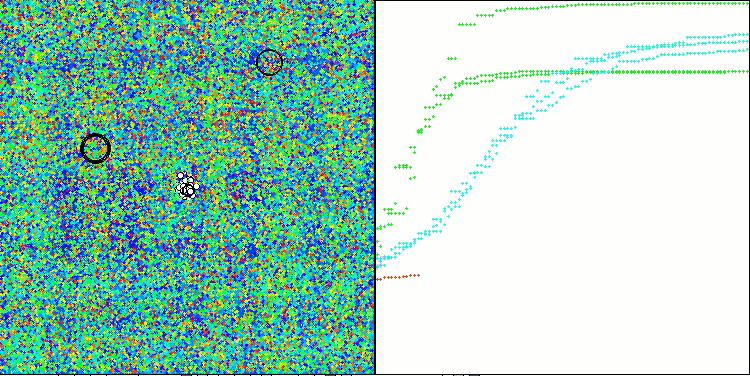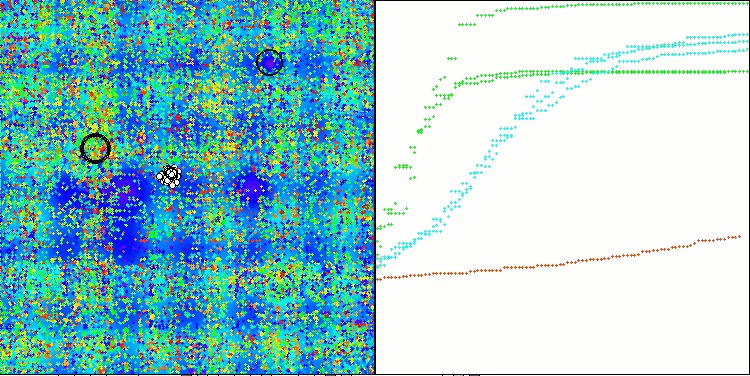
CLA en la función de prueba Hilly.
CLA en la función de prueba de Forest.
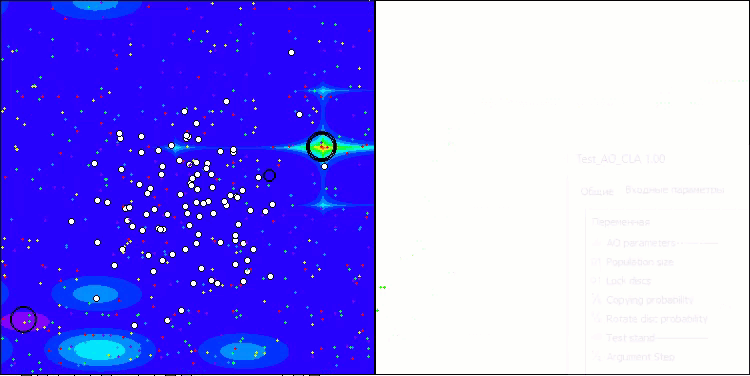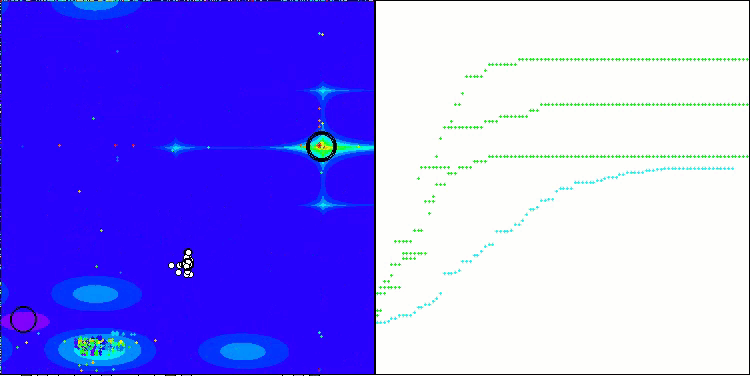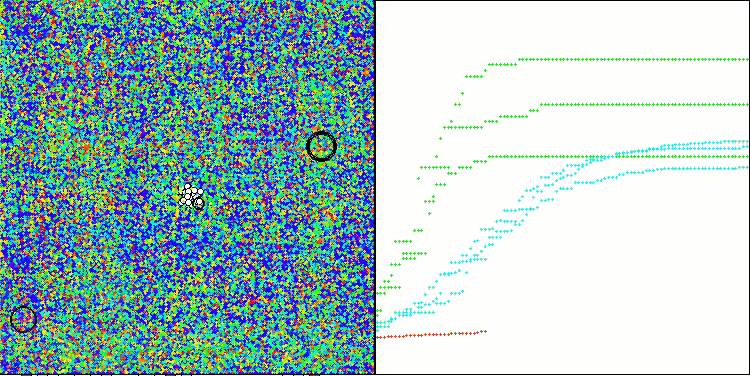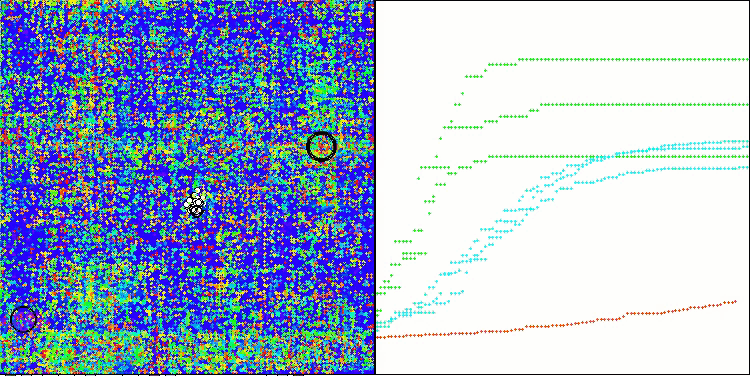
CLA en la función de prueba Megacity.
El algoritmo de cerradura de código ha ocupado el segundo puesto en la tabla de clasificación. En la función aguda de 10 parámetros Forest c, el CLA incluso ha conseguido adelantar al líder de la tabla, el BGA. El color de las celdas de resultados en todas las funciones de prueba es verde (en comparación con todos los algoritmos presentes en la tabla), lo que indica un rendimiento muy uniforme en los distintos tipos de tareas, sin fallos apreciables en pruebas individuales.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | BGA | binary genetic algorithm | 0,99989 | 0,99518 | 0,42835 | 2,42341 | 0,96153 | 0,96181 | 0,32027 | 2,24360 | 0,91385 | 0,95908 | 0,24220 | 2,11512 | 6,782 | 75,36 |
| 2 | CLA | code lock algorithm | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 4 | CTA | comet tail algorithm | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 5 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 6 | ESG | evolution of social groups | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 7 | SIA | simulated isotropic annealing | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 8 | TSEA | turtle shell evolution algorithm | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 9 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 10 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 11 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 12 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 13 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 14 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 15 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 16 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 17 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 18 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 19 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 20 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 21 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 22 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 23 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 24 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 25 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 26 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 27 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 28 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 29 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
| 30 | IWDm | intelligent water drops M | 0,54501 | 0,37897 | 0,30124 | 1,22522 | 0,46104 | 0,14704 | 0,04369 | 0,65177 | 0,25833 | 0,09700 | 0,02308 | 0,37842 | 2,255 | 25,06 |
| 31 | PSO | particle swarm Optimization | 0,59726 | 0,36923 | 0,29928 | 1,26577 | 0,37237 | 0,16324 | 0,07010 | 0,60572 | 0,25667 | 0,08000 | 0,02157 | 0,35823 | 2,230 | 24,77 |
| 32 | Boids | boids algorithm | 0,43340 | 0,30581 | 0,25425 | 0,99346 | 0,35718 | 0,20160 | 0,15708 | 0,71586 | 0,27846 | 0,14277 | 0,09834 | 0,51957 | 2,229 | 24,77 |
| 33 | MA | monkey algorithm | 0,59107 | 0,42681 | 0,31816 | 1,33604 | 0,31138 | 0,14069 | 0,06612 | 0,51819 | 0,22833 | 0,08567 | 0,02790 | 0,34190 | 2,196 | 24,40 |
| 34 | SFL | shuffled frog-leaping | 0,53925 | 0,35816 | 0,29809 | 1,19551 | 0,37141 | 0,11427 | 0,04051 | 0,52618 | 0,27167 | 0,08667 | 0,02402 | 0,38235 | 2,104 | 23,38 |
| 35 | FSS | fish school search | 0,55669 | 0,39992 | 0,31172 | 1,26833 | 0,31009 | 0,11889 | 0,04569 | 0,47467 | 0,21167 | 0,07633 | 0,02488 | 0,31288 | 2,056 | 22,84 |
| 36 | RND | random | 0,52033 | 0,36068 | 0,30133 | 1,18234 | 0,31335 | 0,11787 | 0,04354 | 0,47476 | 0,25333 | 0,07933 | 0,02382 | 0,35648 | 2,014 | 22,37 |
| 37 | GWO | grey wolf optimizer | 0,59169 | 0,36561 | 0,29595 | 1,25326 | 0,24499 | 0,09047 | 0,03612 | 0,37158 | 0,27667 | 0,08567 | 0,02170 | 0,38403 | 2,009 | 22,32 |
| 38 | CSS | charged system search | 0,44252 | 0,35454 | 0,35201 | 1,14907 | 0,24140 | 0,11345 | 0,06814 | 0,42299 | 0,18333 | 0,06300 | 0,02322 | 0,26955 | 1,842 | 20,46 |
| 39 | EM | electroMagnetism-like algorithm | 0,46250 | 0,34594 | 0,32285 | 1,13129 | 0,21245 | 0,09783 | 0,10057 | 0,41085 | 0,15667 | 0,06033 | 0,02712 | 0,24412 | 1,786 | 19,85 |
Conclusiones
El Algoritmo Genético Binario BGA ha desempeñado un cierto papel en la idea del algoritmo CLA. Mi objetivo era desarrollar un algoritmo más rápido. Entonces se me ocurrió la idea de sustituir la codificación binaria por la decimal, y el prototipo para crear el algoritmo fue el mecanismo de cerradura de código, que resultó ser una solución exitosa. El CLA es más rápido que el BGA y compite con él en eficiencia. Además, la codificación decimal permite aplicar distintos tipos de distribuciones al generar una combinación numérica, lo cual puede resultar útil para algunas tareas (en el código, las distribuciones de potencia y normal están comentadas y pueden utilizarse en caso necesario). Los experimentos han demostrado que utilizar una distribución uniforme simple es más eficaz en este caso.
En resumen: el algoritmo de cerradura de código CLA ha mostrado excelentes resultados, estabilidad y eficacia en todas las funciones de prueba. Esto indica la alta escalabilidad del algoritmo y su capacidad para manejar problemas complejos, y pone de relieve la flexibilidad y el carácter prometedor del algoritmo CLA en diversos escenarios de optimización.
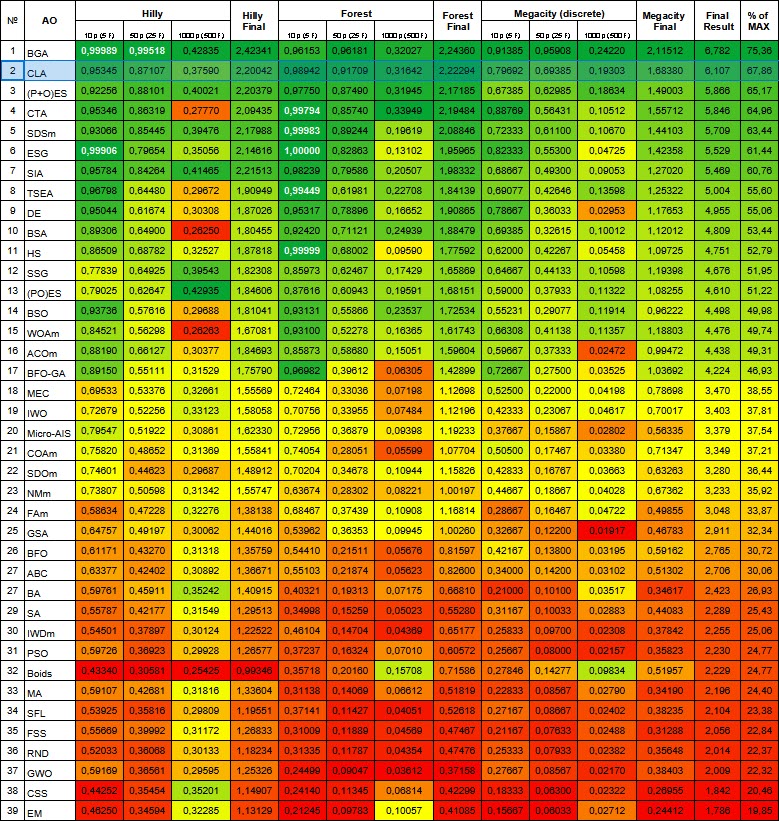
Figura 2. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados superiores o iguales a 0,99 aparecen resaltados en blanco.
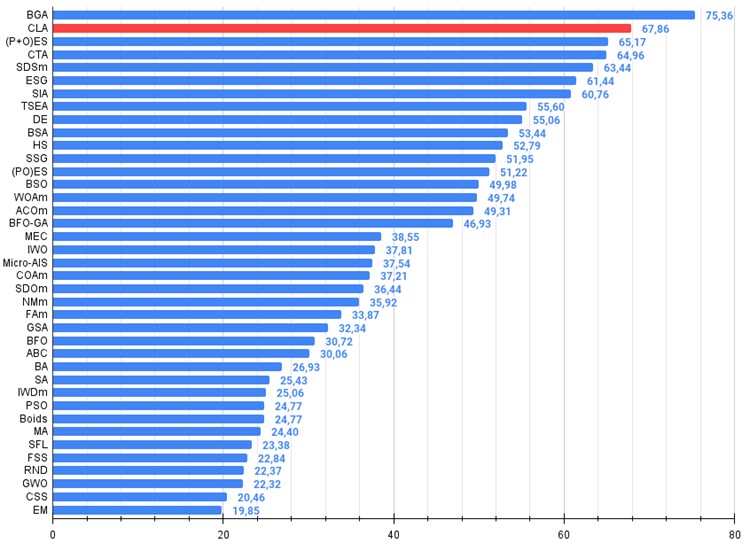
Figura 3. Histograma de los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor),
donde 100 es el máximo resultado teórico posible; el script para calcular la tabla de clasificación está en el archivo)
Ventajas e inconvenientes del algoritmo de cerradura de código (CLA):
Ventajas:
- Fabulosa convergencia en varios tipos de funciones.
- Implementación sencilla.
Desventajas:
- Dispersión de resultados en funciones de dimensionalidad pequeña.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/14878
 Creación de un EA limitador de reducción diaria en MQL5
Creación de un EA limitador de reducción diaria en MQL5
 Cómo usar la API de datos JSON en sus proyectos MQL
Cómo usar la API de datos JSON en sus proyectos MQL
 Redes neuronales: así de sencillo (Parte 91): Previsión en el dominio de la frecuencia (FreDF)
Redes neuronales: así de sencillo (Parte 91): Previsión en el dominio de la frecuencia (FreDF)
 Desarrollamos un asesor experto multidivisa (Parte 11): Comenzamos a automatizar el proceso de optimización
Desarrollamos un asesor experto multidivisa (Parte 11): Comenzamos a automatizar el proceso de optimización
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso