MetaTrader 5 / Ejemplos
English Русский 中文 Deutsch 日本語 Português
preview
Algoritmos de optimización de la población: Evolución diferencial (Differential Evolution, DE)

Algoritmos de optimización de la población: Evolución diferencial (Differential Evolution, DE)

MetaTrader 5 — Ejemplos | 17 abril 2024, 17:13
1 050 0
Andrey Dik
Andrey Dik

Contenido:

1. Introducción
2. Descripción del algoritmo
3. Resultados de las pruebas


1. Introducción

Los métodos de optimización metaheurísticos son una clase de algoritmos que usan enfoques heurísticos para resolver problemas de optimización complejos. Se diferencian de los métodos de optimización numérica, que suelen basarse en el análisis matemático y requieren conocer el gradiente o la derivada de la función objetivo. La principal diferencia entre los métodos metaheurísticos es su capacidad de explorar grandes espacios de búsqueda y encontrar óptimos globales, incluso cuando la función tiene muchos óptimos locales o no es continuamente diferenciable. La ventaja de los métodos metaheurísticos es que pueden trabajar con una "caja negra", es decir, con una función para la que no existe una solución analítica. Se basan en principios probabilísticos estocásticos y ofrecen una buena calidad de solución.

Los algoritmos evolutivos (EA) suponen una clase distinta de métodos de optimización metaheurísticos que simulan el proceso de evolución natural para resolver problemas de optimización complejos. Se basan en los principios de la herencia, mutación, cruce y selección natural. El proceso de evolución en los algoritmos evolutivos sigue el modelo de la selección natural, en el que las soluciones mejor adaptadas tienen más probabilidades de sobrevivir y transmitir sus características a la siguiente generación. De esta forma, la población converge gradualmente hacia la solución óptima. Algunos de los algoritmos evolutivos más populares son: los algoritmos genéticos (AG), la programación evolutiva (PE), las estrategias evolutivas (EE) y la programación genética (GP). Cada uno de estos algoritmos posee sus propias características y se aplica en distintos ámbitos.

En general, los algoritmos evolutivos son herramientas potentes que sirven para resolver problemas de optimización complejos, especialmente en los casos en los que no tenemos acceso a una expresión analítica de la función o al gradiente. Permiten explorar el espacio de búsqueda y encontrar soluciones óptimas combinando información de distintas soluciones individuales.

La evolución diferencial (DE) es uno de los métodos metaheurísticos de optimización, y se diferencia de otros métodos por su sencillez y eficacia. La DE usa una población de vectores que mutan y se entrecruzan para crear nuevas soluciones. No requiere conocer el gradiente y es capaz de encontrar óptimos globales.

El algoritmo DE fue desarrollado en los años 90 por Storn y Price (publicado en "Differential Evolution - A Simple and Efficient Heuristic for global Optimization over Continuous Spaces"), y desde entonces se ha convertido en uno de los métodos de optimización más populares, que utiliza una población de vectores de parámetros para encontrar la solución óptima.


2. Descripción del algoritmo

La idea de la evolución diferencial es una combinación de sencillez y eficacia. El algoritmo de evolución diferencial usa una población de vectores que representan soluciones potenciales. Cada vector está formado por componentes que representan los valores de las variables del problema de optimización.

En la DE, el papel del agente de búsqueda lo desempeña el vector. El algoritmo comienza creando una población aleatoria de vectores; a continuación se produce un proceso iterativo en el que cada vector muta y se cruza con otros vectores de la población. La mutación se realiza añadiendo la diferencia entre dos vectores elegidos al azar entre la población a un tercer vector. Esto crea un nuevo vector que representa una posible solución a la tarea.

Tras la mutación, el vector mutado se cruza con el vector original. El cruce permite combinar la información de los dos vectores y crear nuevas soluciones. El resultado obtenido se compara con la mejor solución actual de la población: si el nuevo vector es mejor, sustituirá al antiguo y pasará a formar parte de la población. La mutación nos permite explorar el espacio de búsqueda, mientras que el cruce nos permite combinar la información de distintos vectores y crear nuevas soluciones.

Este proceso de mutación, cruce y reemplazo se repite durante varias iteraciones hasta que se alcanza una condición de parada, como un número determinado de iteraciones o alcanzar la precisión de solución requerida, en nuestro caso alcanzar 10 000 ejecuciones de la función de aptitud.

La DE es uno de los algoritmos evolutivos más usados para resolver problemas de optimización. El algoritmo diferencial utiliza un operador de diferenciación para crear nuevos candidatos partiendo de la población actual. Estas son las fórmulas básicas usadas en el algoritmo diferencial:

1. Fórmula para crear un nuevo candidato (diferenciación):

r = r1 + F * (r2 - r3)

donde:

  • v - componente del nuevo vector
  • r1, r2 y r3 - componentes de vectores elegidos al azar (soluciones individuales de la población)
  • F - coeficiente de diferenciación, que controla el grado de variabilidad de la solución (dispersión de los valores obtenidos), por defecto, se toma en el rango (0.0;1.0]

2. Fórmula de cruce (crossover):

u = crossover (x, v)

Esta fórmula describe el proceso de cruce entre la solución actual x y un nuevo candidato v. El operador de cruce determinará qué componentes de la solución se tomarán del nuevo candidato. Es la probabilidad de usar el nuevo componente vectorial, en caso contrario el componente permanecerá inalterado, se utilizarán los valores (0,0;1,0].

Vamos a crear el pseudocódigo del algoritmo DE, que es simple y claro debido a la simplicidad del propio algoritmo (de hecho, el código resultará no ser mucho más complicado que su pseudocódigo):

  1. Creamos una población aleatoria de vectores
  2. Calculamos la función de aptitud
  3. Cambiamos a una solución mejor
  4. Mejoramos la población (sustituimos los vectores por mutantes mejores)
  5. Creamos un componente vectorial mutante o dejamos el mismo, lo que sea mejor.
  6. Repetimos desde el paso 2.


Para describir un vector en el algoritmo DE, escribiremos una estructura (así la llamaremos, S_Vector), que representará un vector en un espacio n-dimensional. La estructura tendrá los siguientes campos:

  •  Init (int coords): la función inicializa un vector de coordenadas de longitud dada. Crea dos matrices: "c" y "cPrev", que representan las coordenadas del vector y sus coordenadas anteriores, respectivamente. También establece los valores iniciales f y fPrev como iguales a DBL_MAX. 
  • c []: array que contiene las coordenadas del vector
  • cPrev []: array que contiene las coordenadas del vector en la iteración anterior 
  • f: valor de la función de aptitud para el vector actual 
  • fPrev: valor de la función de aptitud vectorial en la iteración anterior 
//——————————————————————————————————————————————————————————————————————————————
struct S_Vector
{
  void Init (int coords)
  {
    ArrayResize (c,     coords);
    ArrayResize (cPrev, coords);
    f        = -DBL_MAX;
    fPrev    = -DBL_MAX;
  }

  double c     []; //coordinates
  double cPrev []; //previous coordinates
  double f;        //fitness
  double fPrev;    //previous fitness
};
//——————————————————————————————————————————————————————————————————————————————

Un algoritmo tan elemental como DE tiene una descripción de clase igualmente simple; declararemos la clase C_AO_DE. Los campos de la clase C_AO_DE contienen información sobre el estado actual del algoritmo y sus parámetros, mientras que los métodos realizarán diversas operaciones relacionadas con la optimización de la función.

La clase contiene los siguientes campos y métodos:

  • cB []: array que contiene las mejores coordenadas encontradas por el algoritmo
  • fB: valor de la función de aptitud para las mejores coordenadas
  • v []: array de estructuras S_Vector que representan una población de vectores
  • rangeMax[]: array que contiene los valores máximos de cada coordenada del vector
  • rangeMin[]: array que contiene los valores mínimos de cada coordenada del vector
  • rangeStep[]: array que contiene los valores de paso para cada coordenada vectorial
  • Init (int coordsP, int popSizeP, double diffWeightP, double crossProbabP): la función inicializa los parámetros del algoritmo. Toma el número de coordenadas "coordsP", el tamaño de la población "popSizeP", el peso diferencial "diffWeightP" y la probabilidad de cruce "crossProbabP".
  • Moving (): la función ejecuta un paso del algoritmo de evolución diferencial
  • Revision (): la función realiza una revisión de la población del vector
  • SeInDiSp (double In, double InMin, double InMax, double Step): el método calcula un nuevo valor de coordenadas en un rango específico con un paso dado.
  • RNDfromCI (double min, double max): la función genera un número aleatorio en el intervalo [min, max].

//——————————————————————————————————————————————————————————————————————————————
class C_AO_DE
{
  //----------------------------------------------------------------------------
  public: double cB  []; //best coordinates
  public: double fB;     //FF of the best coordinates
  public: S_Vector v []; //vector

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,       //coordinates number
                     const int    popSizeP,      //population size
                     const double diffWeightP,   //differential weight
                     const double crossProbabP); //crossover robability

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;       //coordinates number
  private: int    popSize;      //population size

  private: double diffWeight;   //differential weight
  private: double crossProbab;  //crossover robability

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

El método Init de la clase C_AO_DE inicializará los parámetros del algoritmo de evolución diferencial. El método admite cuatro parámetros:

  • "coordsP" - número de coordenadas,
  • "popSizeP" - tamaño de la población,
  • "diffWeightP" - peso diferencial
  • "crossProbabP" - probabilidad de cruce.

El método usará primero la función MathSrand para reiniciar el generador de números aleatorios. Esto garantizará que cada vez que se ejecute el algoritmo, utilizará una nueva secuencia de números aleatorios.

A continuación, el método inicializará las variables "fB" y "revisión". La variable "fB" contendrá el mejor valor de la función de aptitud encontrado por el algoritmo. Inicialmente se establece en "-DBL_MAX", que es un número muy pequeño. La variable "revision" tendrá el valor "false", lo que significa que la población de vectores aún no ha sido revisada.

A continuación, el método inicializará las variables "coords", "popSize", "diffWeight" y "crossProbab" con los valores transmitidos como parámetros.

A continuación, el método creará un array "v" de tamaño "popSize" que contendrá la población de vectores.

Después, el método creará tres arrays: "rangeMax", "rangeMin" y "rangeStep", cada una de tamaño coords (número de coordenadas).

Por último, el método creará un array "cB" del tamaño coords que contendrá las mejores coordenadas encontradas por el algoritmo.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_DE::Init  (const int    coordsP,      //coordinates number
                     const int    popSizeP,     //population size
                     const double diffWeightP,  //differential weight
                     const double crossProbabP) //crossover robability
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords  = coordsP;
  popSize = popSizeP;

  diffWeight  = diffWeightP;
  crossProbab = crossProbabP;

  ArrayResize (v, popSize);
  for (int i = 0; i < popSize; i++) v [i].Init (coords);

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//——————————————————————————————————————————————————————————————————————————————

Para cambiar los vectores solución en el espacio de búsqueda, escribiremos el método "Moving" de la clase C_AO_DE. El método aplicará operadores de mutación y cruce para generar nuevos vectores candidatos y seleccionará la mejor solución basándose en la función de aptitud.

El primer bloque de código, que comienza con la condición "if (!revision)", se ejecutará solo cuando el método "Moving" se ejecute por primera vez o después de llamar al método "Init". Inicializará la población inicial de vectores con valores aleatorios dentro del rango dado y con un paso especificado en el array "rangeStep".

A continuación, el método utilizará un ciclo "for" para actualizar cada vector de la población. Para cada vector, el método seleccionará tres vectores aleatorios diferentes de la población (r1, r2, r3) que no coincidirán con el vector actual (i) y aplicará los operadores de mutación y cruce para obtener un nuevo vector candidato. El operador de mutación calculará la diferencia entre los vectores "r2" y "r3" multiplicada por el peso diferencial "diffWeight" y añadirá el resultado al vector "r1". El operador de cruce seleccionará la coordenada de un vector y la sustituirá por la coordenada correspondiente del nuevo vector candidato con la probabilidad crossProbab. Si no se cumple la probabilidad de cruce, la coordenada vectorial actual permanecerá invariable.

El lector atento, analizando el código a continuación, comprobará que el método "Moving" para cambiar vectores no implica la creación de coordenadas en el espacio distintas de las que pueden derivarse de las existentes. Así pues, la estocasticidad del algoritmo consistirá únicamente en seleccionar los vectores para el cruce, pero no en crear otros nuevos y originales. Esta característica determinará consecuencias de gran alcance que analizaremos a continuación.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_DE::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        v [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        v [i].c [c] = SeInDiSp (v [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double rnd = 0.0;
  int    r   = 0;
  int    r1  = 0;
  int    r2  = 0;
  int    r3  = 0;

  for (int i = 0; i < popSize; i++)
  {
    do
    {
      r = (int)RNDfromCI (0, popSize);
      if (r >= popSize) r = popSize - 1;

      r1 = r;
    }
    while (r1 == i);

    do
    {
      r = (int)RNDfromCI (0, popSize);
      if (r >= popSize) r = popSize - 1;

      r2 = r;
    }
    while (r2 == i || r2 == r1);

    do
    {
      r = (int)RNDfromCI (0, popSize);
      if (r >= popSize) r = popSize - 1;

      r3 = r;
    }
    while (r3 == i || r3 == r1 || r3 == r2);

    for (int c = 0; c < coords; c++)
    {
      rnd = RNDfromCI (0, 1.0);

      if (rnd < crossProbab)
      {
        v [i].c [c] = v [r1].cPrev [c] + diffWeight * (v [r2].cPrev [c] - v [r3].cPrev [c]);
        v [i].c [c] = SeInDiSp (v [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
      else
      {
        v [i].c [c] = v [i].cPrev [c];
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Por último, necesitaremos el método "Revision", cuya clase C_AO_DE actualizará la mejor solución de la población y almacenará los valores anteriores de la función aptitud y las coordenadas del vector.

En primer lugar, el método inicializará la variable "ind" con el valor "-1". A continuación, utilizará un ciclo "for" para iterar todos los vectores de la población y comprobar si la función de aptitud del vector actual es mayor que "fB" (la mejor función de aptitud encontrada hasta el momento), entonces almacenará el índice de ese vector en la variable "ind".

Si "ind" no es igual a "-1", el método actualizará el valor de "fB" al valor de la función de aptitud del vector con el índice "ind" y almacenará sus coordenadas en el array "cB".

A continuación, el método utilizará otro ciclo "for" para iterar todos los vectores de la población y comprobará si la función de aptitud del vector actual es mayor que su valor anterior; el método almacenará el valor actual de la función de aptitud y las coordenadas del vector en los campos correspondientes v[i].fPrev y v[i].cPrev.

Este método permitirá a la clase C_AO_DE almacenar la mejor solución de la población y los valores anteriores de la función de aptitud y las coordenadas del vector para su uso posterior en la optimización de la función de aptitud.

Podemos ver que la población no se moverá más en el espacio de búsqueda hasta que se encuentre un vector que sea mejor que su versión original (padre). Este punto se añadirá al anterior.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_DE::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (v [i].f > fB) ind = i;
  }

  if (ind != -1)
  {
    fB = v [ind].f;
    ArrayCopy (cB, v [ind].c, 0, 0, WHOLE_ARRAY);
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (v [i].f > v [i].fPrev)
    {
      v [i].fPrev = v [i].f;
      ArrayCopy (v [i].cPrev, v [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————


    3. Resultados de las pruebas

    Impresión del funcionamiento del algoritmo de evolución diferencial en un banco de pruebas:

    C_AO_DE:50;0.2;0.8
    =============================
    5 Rastrigin's; Func runs 10000 result: 80.30183306326985
    Score: 0.99498
    25 Rastrigin's; Func runs 10000 result: 76.15178282331799
    Score: 0.94356
    500 Rastrigin's; Func runs 10000 result: 52.17316317703311
    Score: 0.64645
    =============================
    5 Forest's; Func runs 10000 result: 1.7348423083855402
    Score: 0.98131
    25 Forest's; Func runs 10000 result: 1.28572746338484
    Score: 0.72727
    500 Forest's; Func runs 10000 result: 0.20833645141168078
    Score: 0.11785
    =============================
    5 Megacity's; Func runs 10000 result: 9.640000000000002
    Score: 0.80333
    25 Megacity's; Func runs 10000 result: 3.9199999999999995
    Score: 0.32667
    500 Megacity's; Func runs 10000 result: 0.3548
    Score: 0.02957
    =============================
    All score: 5.57100

    A partir de los valores de salida del algoritmo, vemos excelentes resultados en las pruebas.

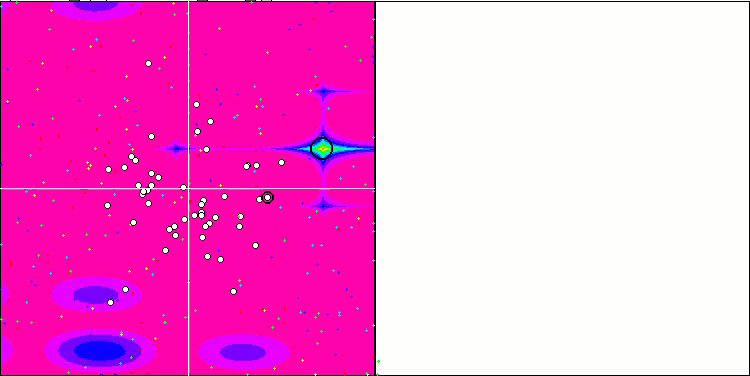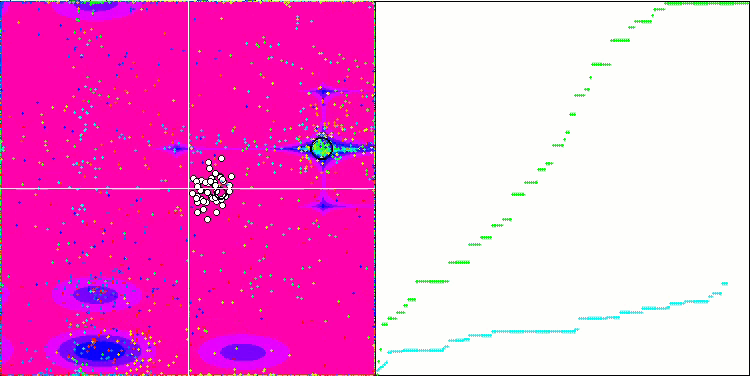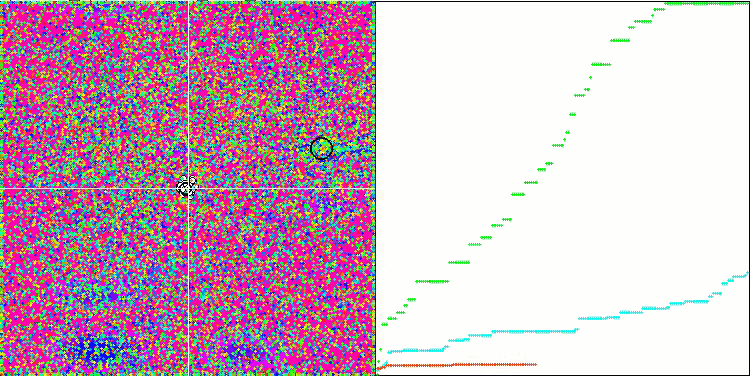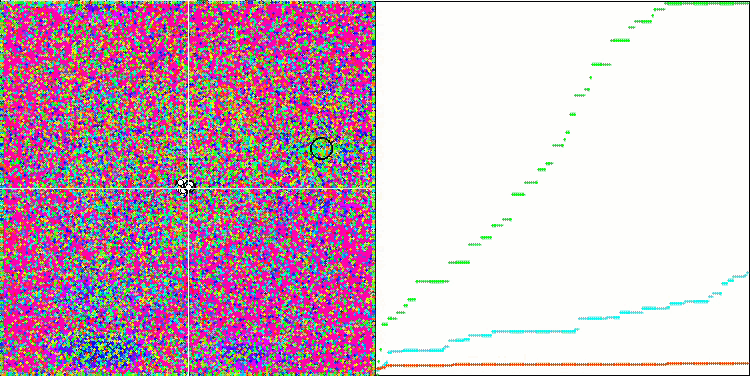
    En la visualización podemos ver la fenomenal convergencia del algoritmo, pero también podemos notar la peculiaridad anteriormente mencionada en la descripción de los métodos "Moving" y "Revision". Al crear la visualización, tras varios intentos, hemos elegido a propósito los más acertados, de hecho los resultados distan mucho de ser siempre tan buenos. Esto se debe a la degeneración de la población, cuando toda la población (hasta el último de los vectores) converge hacia un único extremo. Pero puede que no sea el óptimo global. Como ya hemos comentado, el algoritmo carece de mecanismos para seguir explorando el espacio de búsqueda creando nuevos vectores únicos. El algoritmo DE no crea nuevos vectores, sino que solo genera combinaciones a partir de vectores existentes. Esto explica la completa degeneración de la población, no se crea "sangre nueva" para diversificar la "reserva genética" de la población.

    rastrigin

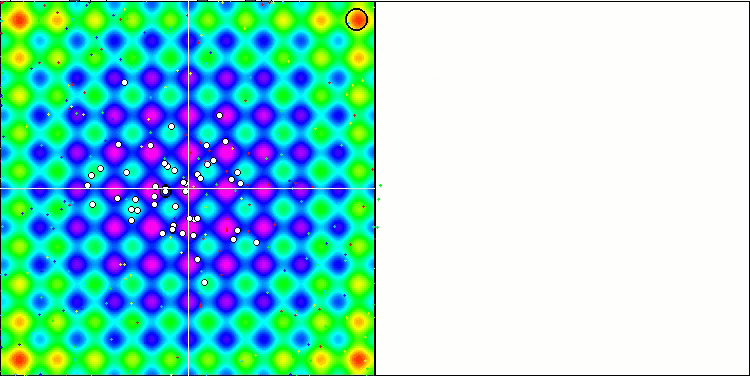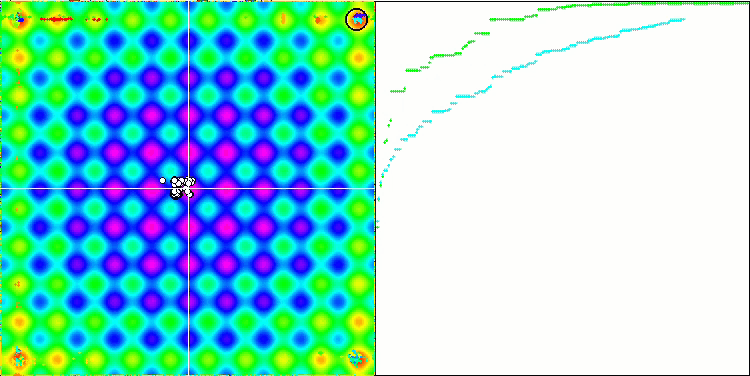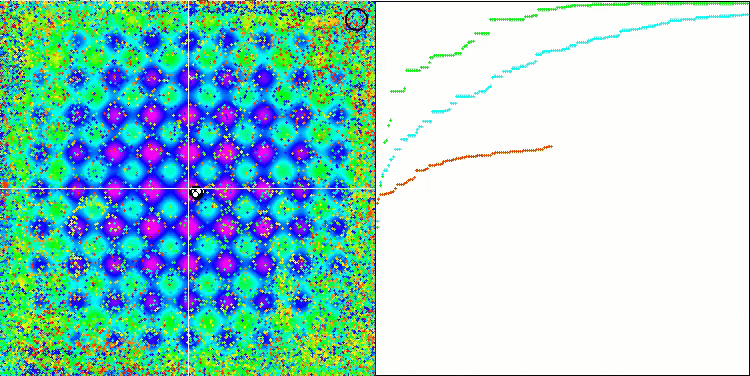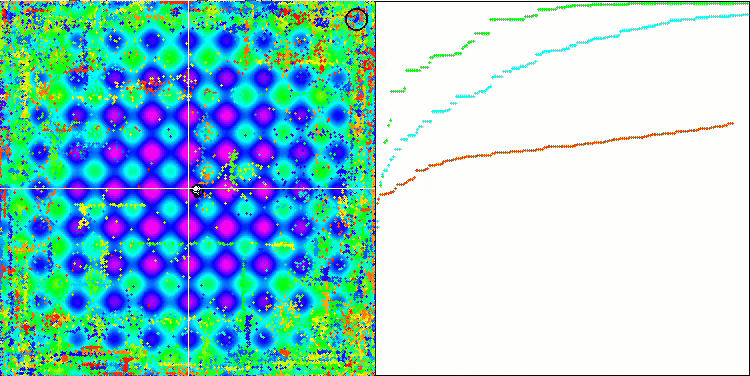
      DE en la función de prueba Rastrigin.

    forest

      DE en la función de prueba Forest.

    megacity

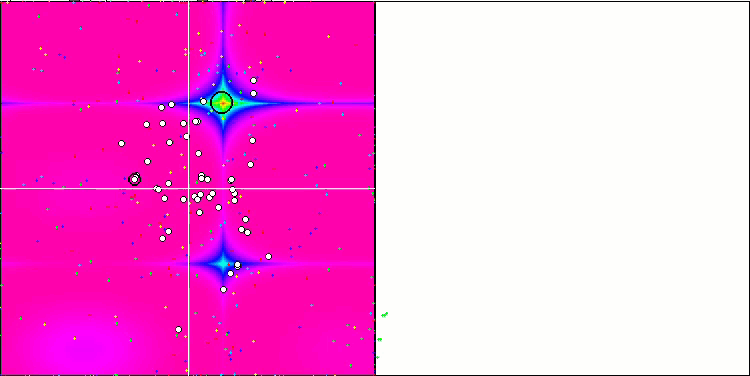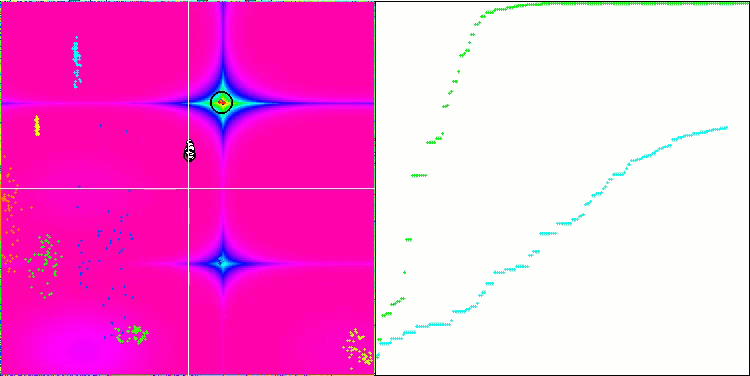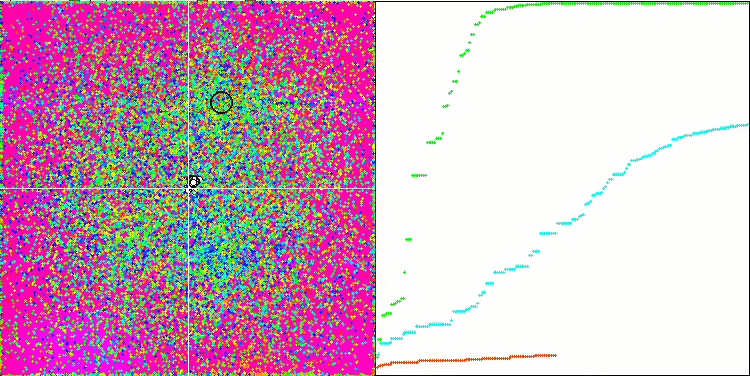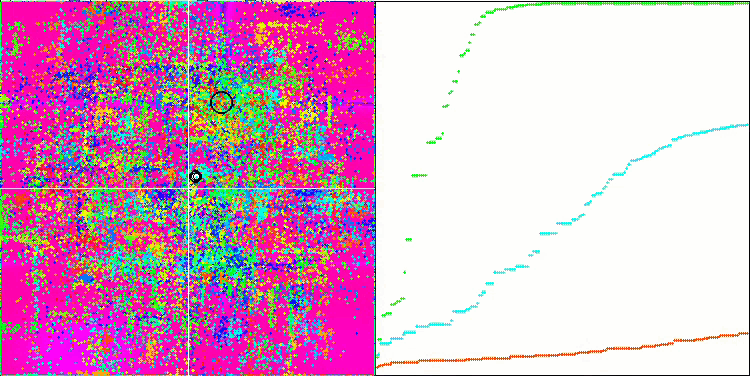
      DE en la función de prueba Megacity.

    differences

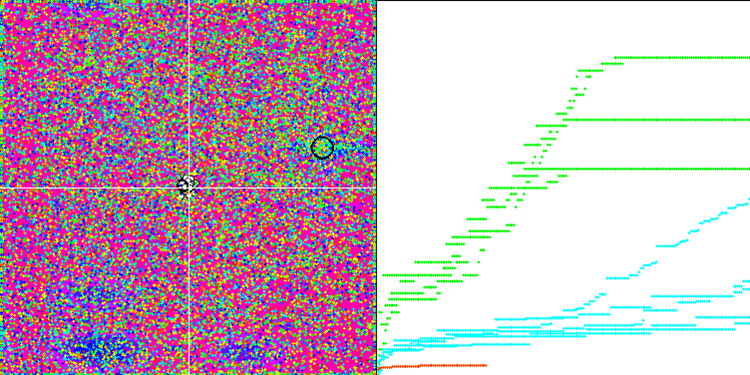
    Un ejemplo de la gran dispersión de la convergencia. Resulta especialmente pronunciado en las funciones Forest y Megacity.


    Vamos a ver la tabla de clasificación final con el nuevo participante, la DE. El algoritmo ha sido capaz de arrebatar el segundo puesto al actual líder SDSm en la prueba Forest con 10 variables. Los resultados del resto de las pruebas también son muy buenos, la DE se ha hecho con el cuarto puesto tras SSG. Cabe señalar que, en lugar de realizar la prueba habitual de 5 veces para cada una de las funciones de prueba, hemos tenido que realizar pruebas de 10 veces debido a la enorme variación de los resultados en las funciones Forest y Megacity. En la función Rastrigin suave, la dispersión de los resultados ha resultado menos pronunciada. 

    №

    AO

    Description

    Rastrigin

    Rastrigin final

    Forest

    Forest final

    Megacity (discrete)

    Megacity final

    Final result

    10 p (5 F)

    50 p (25 F)

    1000 p (500 F)

    10 p (5 F)

    50 p (25 F)

    1000 p (500 F)

    10 p (5 F)

    50 p (25 F)

    1000 p (500 F)

    1

    SDSm

    stochastic diffusion search M

    0,99809

    1,00000

    0,69149

    2,68958

    0,99265

    1,00000

    1,00000

    2,99265

    1,00000

    1,00000

    1,00000

    3,00000

    100,000

    2

    SDS

    stochastic Diffusion Search

    0,99737

    0,97322

    0,58904

    2,55963

    0,96067

    0,93572

    0,79649

    2,69288

    0,78696

    0,93815

    0,71804

    2,44315

    88,201

    3

    SSG

    saplings sowing and growing

    1,00000

    0,92761

    0,51630

    2,44391

    0,72120

    0,65201

    0,83760

    2,21081

    0,54782

    0,61841

    0,99522

    2,16146

    77,683

    4

    DE

    differential evolution

    0,98295

    0,89236

    0,51375

    2,38906

    1,00000

    0,84602

    0,65510

    2,50112

    0,90000

    0,52237

    0,12031

    1,54268

    73,099

    5

    HS

    harmony search

    0,99676

    0,88385

    0,44686

    2,32747

    0,99148

    0,68242

    0,37529

    2,04919

    0,71739

    0,71842

    0,41338

    1,84919

    70,623

    6

    IWO

    invasive weed optimization

    0,95828

    0,62227

    0,27647

    1,85703

    0,70170

    0,31972

    0,26613

    1,28755

    0,57391

    0,30527

    0,33130

    1,21048

    48,250

    7

    ACOm

    ant colony optimization M

    0,34611

    0,16683

    0,15808

    0,67103

    0,86147

    0,68980

    0,64798

    2,19925

    0,71739

    0,63947

    0,05579

    1,41265

    47,387

    8

    MEC

    mind evolutionary computation

    0,99270

    0,47345

    0,21148

    1,67763

    0,60244

    0,28046

    0,21324

    1,09615

    0,66957

    0,30000

    0,26045

    1,23002

    44,049

    9

    SDOm

    spiral dynamics optimization M

    0,69840

    0,52988

    0,33168

    1,55996

    0,59818

    0,38766

    0,37600

    1,36183

    0,35653

    0,15262

    0,25842

    0,76758

    40,289

    10

    COAm

    cuckoo optimization algorithm M

    0,92400

    0,43407

    0,24120

    1,59927

    0,57881

    0,23477

    0,13842

    0,95200

    0,52174

    0,24079

    0,17001

    0,93254

    37,830

    11

    FAm

    firefly algorithm M

    0,59825

    0,31520

    0,15893

    1,07239

    0,50637

    0,29178

    0,41704

    1,21519

    0,24783

    0,20526

    0,35090

    0,80398

    33,139

    12

    ABC

    artificial bee colony

    0,78170

    0,30347

    0,19313

    1,27829

    0,53379

    0,14799

    0,11177

    0,79355

    0,40435

    0,19474

    0,13859

    0,73768

    29,766

    13

    BA

    bat algorithm

    0,40526

    0,59145

    0,78330

    1,78002

    0,20664

    0,12056

    0,21769

    0,54488

    0,21305

    0,07632

    0,17288

    0,46225

    29,499

    14

    CSS

    charged system search

    0,56605

    0,68683

    1,00000

    2,25289

    0,13961

    0,01853

    0,13638

    0,29452

    0,07392

    0,00000

    0,03465

    0,10856

    27,930

    15

    GSA

    gravitational search algorithm

    0,70167

    0,41944

    0,00000

    1,12111

    0,31390

    0,25120

    0,27812

    0,84322

    0,42609

    0,25525

    0,00000

    0,68134

    27,807

    16

    BFO

    bacterial foraging optimization

    0,67203

    0,28721

    0,10957

    1,06881

    0,39364

    0,18364

    0,17298

    0,75026

    0,37392

    0,24211

    0,18841

    0,80444

    27,542

    17

    EM

    electroMagnetism-like algorithm

    0,12235

    0,42928

    0,92752

    1,47915

    0,00000

    0,02413

    0,29215

    0,31628

    0,00000

    0,00527

    0,10872

    0,11399

    19,002

    18

    SFL

    shuffled frog-leaping

    0,40072

    0,22021

    0,24624

    0,86717

    0,19981

    0,02861

    0,02221

    0,25063

    0,19565

    0,04474

    0,06607

    0,30646

    13,200

    19

    MA

    monkey algorithm

    0,33192

    0,31029

    0,13582

    0,77804

    0,09927

    0,05443

    0,07482

    0,22852

    0,15652

    0,03553

    0,10669

    0,29874

    11,777

    20

    SFS

    fish school search

    0,46812

    0,23502

    0,10483

    0,80798

    0,12730

    0,03458

    0,05458

    0,21647

    0,12175

    0,03947

    0,08244

    0,24366

    11,332

    21

    IWDm

    intelligent water drops M

    0,26459

    0,13013

    0,07500

    0,46972

    0,28358

    0,05445

    0,05112

    0,38916

    0,22609

    0,05659

    0,05054

    0,33322

    10,423

    22

    PSO

    particle swarm optimisation

    0,20449

    0,07607

    0,06641

    0,34696

    0,18734

    0,07233

    0,18207

    0,44175

    0,16956

    0,04737

    0,01947

    0,23641

    8,426

    23

    RND

    random

    0,16826

    0,09038

    0,07438

    0,33302

    0,13381

    0,03318

    0,03949

    0,20648

    0,12175

    0,03290

    0,04898

    0,20363

    5,054

    24

    GWO

    grey wolf optimizer

    0,00000

    0,00000

    0,02093

    0,02093

    0,06514

    0,00000

    0,00000

    0,06514

    0,23478

    0,05789

    0,02545

    0,31812

    1,000


    Conclusiones

    El algoritmo de evolución diferencial es capaz de encontrar óptimos globales muy rápidamente y tiene una convergencia excelente, si consideramos los resultados muy mediocres en pruebas individuales. La DE se utiliza ampliamente en diversos campos, como la optimización de parámetros de modelos, el ajuste de redes neuronales, la optimización de funciones en física y economía, y muchos otros. Yo recomendaría hacer múltiples ejecuciones de optimización con este algoritmo, ya que los resultados dependerán mucho de la población inicial en la primera iteración. Aumentar el tamaño de la población mientras se incrementa el número de iteraciones puede resultar útil.

    Con su simplicidad y rapidez de funcionamiento, el algoritmo de evolución diferencial posee desventajas obvias, como la degeneración de la población (y como consecuencia el atasco en los extremos locales); debemos tener en cuenta esto a la hora de elegir la DE para nuestros problemas de optimización.

    El algoritmo de DE analizado en este artículo es una especie de patrón a partir del cual se han creado varias modificaciones. Mis sugerencias para mejorar el algoritmo de evolución diferencial (DE) serían las siguientes:

    1. La utilización de métodos adaptativos de control de parámetros: La DE tiene varios parámetros que deben ajustarse debido a su gran influencia en los resultados.

    El parámetro de peso diferencial recomendado por los autores es "0,2": este es el valor por defecto que hemos adoptado en el script para las pruebas de DE. Este parámetro tiene un impacto significativo en la diversidad de la población; si elegimos un valor inferior a "0,2", podemos conseguir que la convergencia del algoritmo sea aún mejor, pero obtendremos aún más variación en los resultados. Por el contrario, si aumentamos el valor de este parámetro, el algoritmo se volverá robusto frente a la degeneración de la población y el estancamiento en extremos locales, pero al mismo tiempo la calidad de la convergencia disminuirá rápidamente para un número limitado de iteraciones, propiamente, el tiempo de búsqueda aumentará de forma inevitable.

    El parámetro de probabilidad de cruce también afectará a la calidad de la optimización. Los autores recomiendan un valor de "0,9", pero mis experimentos han mostrado un valor mejor, en mi opinión, de "0,8". 

    Considerando lo anterior, parece razonable utilizar métodos adaptativos para controlar y cambiar dinámicamente los parámetros, de modo que el algoritmo pueda ajustarse automáticamente según la tarea.

    2. La utilización de diferentes estrategias de mutación y cruce.

    3. La utilización de métodos híbridos: es posible combinar la DE con otros métodos de optimización, como algoritmos genéticos, métodos de optimización basados en gradientes, métodos de optimización basados en enjambres de partículas, etcétera. Esto puede mejorar el rendimiento del algoritmo y ayudarnos a mejorar la eficiencia del algoritmo en su conjunto.

    4. La mejora de la convergencia: aplicar la creación de vectores aleatorios adicionales para aumentar la diversidad en la población.

    5. La utilización de diferentes estrategias de selección de individuos para la mutación: este algoritmo considerará un método completamente aleatorio de selección de individuos para el cruce, pero también será posible complementar o sustituir completamente este método utilizando otras estrategias diferentes de la selección de individuos para el cruce/mutación, como la estrategia de selección de individuos basada en la aptitud. Esto puede ayudarnos a mejorar la diversidad de la población y mejorar significativamente la robustez del algoritmo frente a las interferencias.

    En general, el algoritmo DE deja una muy buena impresión de su rendimiento, pero siempre debemos tener presentes las características de este interesante algoritmo o hacer algunos intentos de mejorar la evolución diferencial aplicando una combinación de diferentes estrategias y métodos. La DE ha demostrado con creces que los algoritmos pueden ser muy eficientes y seguir resultando increíblemente sencillos y rápidos. El algoritmo de evolución diferencial puede recomendarse para resolver problemas de optimización complejos con alta dimensionalidad, ya que el efecto de la caída de la diversidad durante la evolución resulta menos pronunciado cuando el número de parámetros optimizados es grande.


    rating table

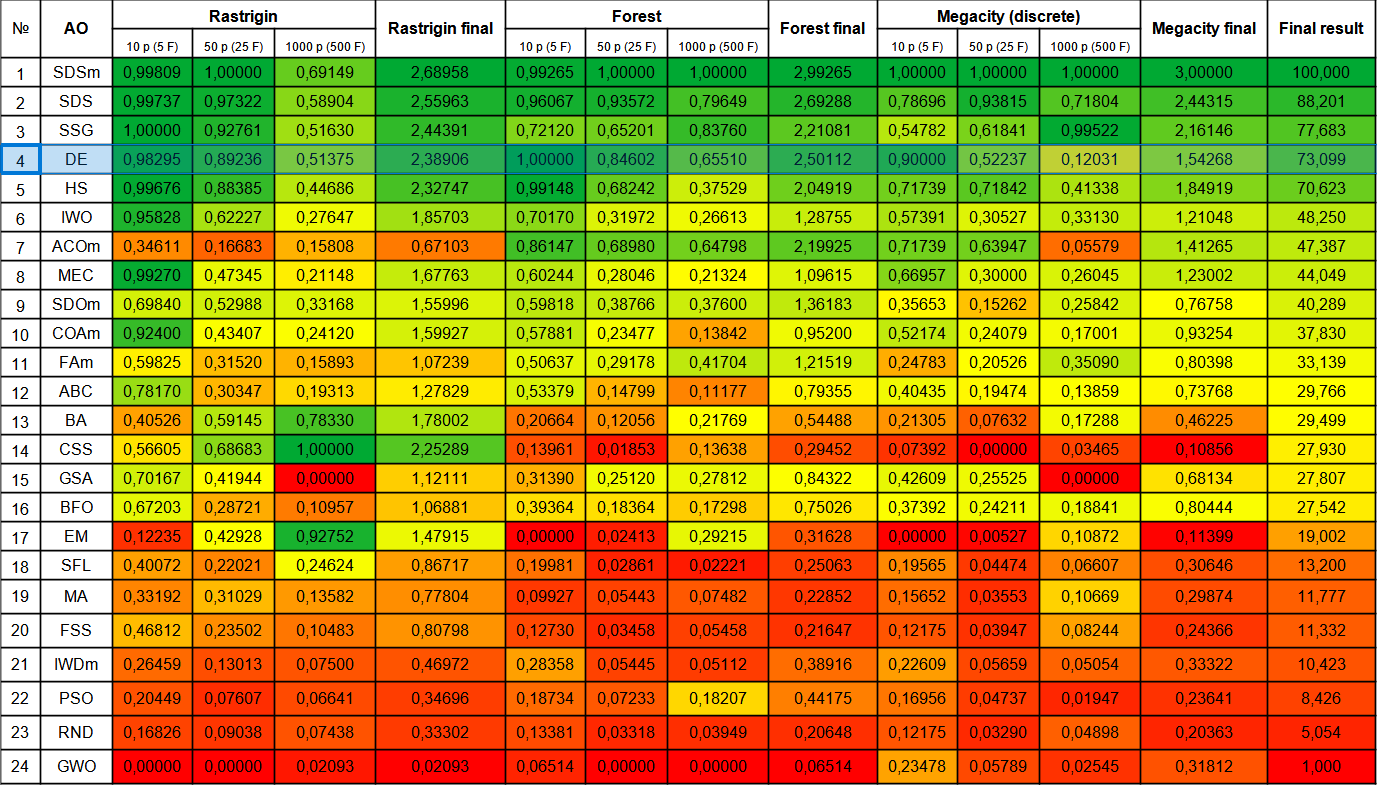
    Figura 1. Clasificación por colores de los algoritmos según sus respectivas pruebas.

    chart

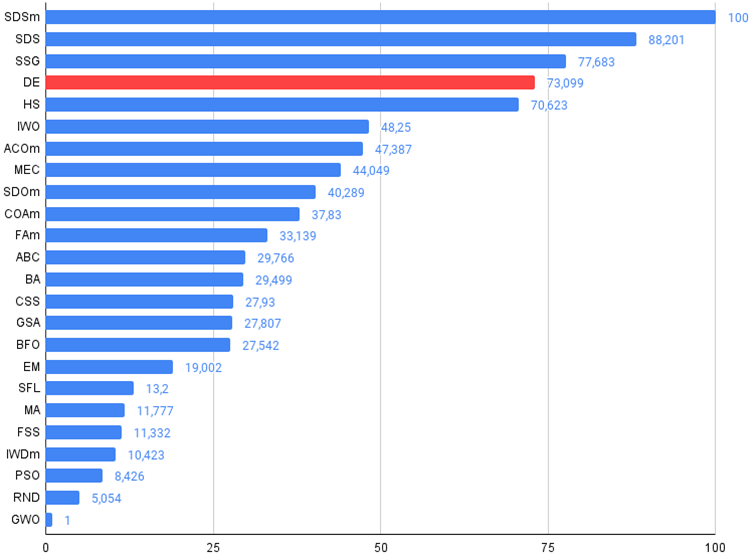
    Figura 2. Histograma de los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor),

    en el archivo hay un script para calcular la tabla de clasificación según la metodología de este artículo).


    Ventajas e inconvenientes del algoritmo de evolución diferencial (DE)

    Ventajas:

    1. Número reducido de parámetros externos.
    2. Aplicación sencilla.
    3. Velocidad de funcionamiento.
    4. Buena escalabilidad.
    5. Excelente rendimiento en diferentes tipos de funciones (teniendo en cuenta los puntos negativos).


    Desventajas:

    1. Alta variación de los resultados.
    2. Tendencia a estancarse en los extremos locales.

    Adjunto al artículo hay un archivo con las versiones reales actualizadas de los códigos de los algoritmos descritos en los artículos anteriores. El autor del presente artículo no se responsabiliza de la exactitud absoluta en la descripción de los algoritmos canónicos; muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos efectuados.

    Traducción del ruso hecha por MetaQuotes Ltd.
    Artículo original: https://www.mql5.com/ru/articles/13781

    Archivos adjuntos |
    Descargar ZIP
    23_The_world_of_AO_DE.zip (412.14 KB)
    Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

    Otros artículos del autor

    Pasar a la discusión en el foro de los operadores
    Cómo crear un panel informativo para mostrar datos en indicadores y asesores Cómo crear un panel informativo para mostrar datos en indicadores y asesores
    En el presente artículo consideraremos la creación de una clase de panel informativo para utilizarla en indicadores y asesores. Este será el artículo introductorio de una pequeña serie de artículos con plantillas para la conexión y el uso de indicadores estándar en asesores. Empezaremos creando un panel, un análogo de la ventana de datos de MetaTrader 5.
    Redes neuronales: así de sencillo (Parte 65): Aprendizaje supervisado ponderado por distancia (DWSL) Redes neuronales: así de sencillo (Parte 65): Aprendizaje supervisado ponderado por distancia (DWSL)
    En este artículo, le presentaremos un interesante algoritmo que se basa en la intersección de los métodos de aprendizaje supervisado y por refuerzo.
    Plantillas listas para conectar indicadores en asesores (Parte 1): Osciladores Plantillas listas para conectar indicadores en asesores (Parte 1): Osciladores
    En este artículo analizaremos los indicadores estándar de la categoría de osciladores. Asimismo, crearemos plantillas listas para su uso en asesores: declaración y configuración de parámetros, inicialización y desinicialización de indicadores, y también obtención de datos y señales de los búferes de indicador en asesores.
    Algoritmos de optimización de la población: Algoritmo de optimización de la dinámica espiral (Spiral Dynamics Optimization, SDO) Algoritmos de optimización de la población: Algoritmo de optimización de la dinámica espiral (Spiral Dynamics Optimization, SDO)
    Este artículo presenta un algoritmo de optimización basado en los patrones de las trayectorias en espiral en la naturaleza, como las conchas de los moluscos: el algoritmo de optimización de la dinámica espiral o SDO. El algoritmo propuesto ha sido repensado y modificado a fondo por el autor: en el artículo analizaremos por qué estos cambios han sido necesarios.