Algoritmo de optimización Brain Storm - Brain Storm Optimization (Parte I): Clusterización

Contenido:

1. Introducción
2. Descripción del algoritmo
3. K-Means

1. Introducción

La BSO (Brain Storm Optimization) es uno de los emocionantes e innovadores algoritmos de optimización populares inspirado en el fenómeno natural de la "tormenta de ideas". Este método de optimización supone un enfoque eficaz para resolver problemas complejos utilizando los principios de la inteligencia y el comportamiento colectivos. La BSO simula el proceso de generación de nuevas ideas y soluciones, de forma similar a como ocurre en las discusiones de grupo, lo cual la convierte en una herramienta única y prometedora para encontrar soluciones óptimas en diversos campos. En este artículo veremos los principios básicos de la BSO, sus ventajas y aplicaciones.

Los métodos basados en poblaciones representan una herramienta importante para resolver problemas de optimización complejos. Sin embargo, en el contexto de los problemas multimodales en los que se requieren múltiples soluciones óptimas, los enfoques existentes se enfrentan a ciertas limitaciones. En este artículo veremos un nuevo método de optimización denominado método de optimización por tormenta de ideas o Brain Storm.

Los enfoques existentes, como los métodos de nichos y clusterización, suelen dividir la población en subpoblaciones para encontrar múltiples soluciones. No obstante, estos métodos adolecen de la necesidad de predeterminar el número de subpoblaciones, lo cual puede suponer un reto, especialmente cuando no se conoce de antemano el número de soluciones óptimas. La BSO compensa esta deficiencia trasladando el espacio objetivo a un espacio en el que los individuos se clusterizan y actualizan según sus coordenadas. A diferencia de los métodos existentes que buscan un único óptimo global, el método BSO propuesto guía el proceso de búsqueda hacia múltiples soluciones "significativas".

Veamos con detalle el método BSO y su aplicabilidad a los problemas de optimización multimodal. El algoritmo basado en tormenta de ideas (BSO) fue desarrollado por Shi y otros en 2015 y se inspira en el proceso natural del brainstorming, en el que las personas se reúnen para generar e intercambiar ideas para resolver un problema.

Existen diversas variantes del algoritmo, como la Hypo Variance Brain Storm Optimization, en la que la estimación de la función objetivo se basa en la hipovarianza o subvarianza en lugar de en la varianza gaussiana. Existen otras opciones, como la Global-best Brain Storm Optimization, en la que el mejor global implica un esquema de reinicialización que se activa según el estado actual de la población, combinado con actualizaciones en las variables y la clusterización basada en la adaptabilidad.

Debemos señalar que cada individuo del algoritmo BSO representa no solo una solución al problema que hay que optimizar, sino también un punto de datos que revela el paisaje del problema. La inteligencia colectiva y las técnicas de análisis de datos pueden combinarse para producir beneficios más allá de lo que cada método podría lograr por sí mismo.

2. Descripción del algoritmo

El algoritmo BSO funciona modelizando este proceso, en el que una población de soluciones candidatas (llamadas "individuos" o "ideas") se actualiza de forma iterativa para converger a una solución óptima. El algoritmo consta de los siguientes pasos principales:

1.Inicialización :

- El algoritmo comienza generando una población inicial de individuos, en la que cada individuo representa una solución potencial al problema de optimización.
- Cada individuo está representado por un conjunto de variables de decisión que definen las características de la misma.

2. Tormenta de ideas:

- En este paso, el algoritmo modela un proceso de tormenta de ideas en el que los individuos generan nuevas ideas (es decir, nuevas soluciones candidatas) combinando y modificando sus propias ideas y las ideas de otros individuos.
- El proceso de tormenta de ideas se rige por una serie de reglas que determinan cómo se generan las nuevas ideas. Estas reglas se inspiran en el proceso humano de tormenta de ideas:

• Generación aleatoria de nuevas ideas
• Combinación de ideas de diferentes individuos
• Modificación de ideas existentes

3.Evaluación :

- Las nuevas ideas generadas (es decir, las nuevas soluciones candidatas) se evalúan usando la función objetivo del problema de optimización.
- La función objetivo mide la calidad o aptitud de cada solución candidata, y el algoritmo trata de encontrar una solución que minimice (o maximice) dicha función.

4. Selección:

- Tras el paso de evaluación, el algoritmo selecciona los mejores individuos de la población para guardarlos para la siguiente iteración.
- El proceso de selección se basa en los valores de aptitud de los individuos, teniendo los más idóneos una mayor probabilidad de ser seleccionados.

5. Finalización:

- El algoritmo continúa iterando a través de las etapas de tormenta de ideas, evaluación y selección hasta que se cumple un criterio de finalización, como el número máximo de iteraciones o el logro de una cierta calidad de solución objetivo.

Vamos a enumerar algunos métodos BSO característicos, las peculiaridades del algoritmo que lo distinguen de otros métodos de optimización basados en poblaciones:

1. Clusterización. Los individuos se agrupan en clústeres según su semejanza de ubicación en el espacio de búsqueda. Para ello se utilizará el algoritmo de clusterización K-means o de K-medias.
2. Convergencia. En esta fase, los individuos de cada clúster se agrupan en torno al centroide del clúster. Esto imita la fase de brainstorming en la que los participantes se reúnen para debatir ideas.
3. Divergencia (Divergence). En esta fase, se generan nuevos individuos. Se pueden generar nuevos individuos partiendo de uno o dos individuos de un clúster. Este proceso imita la fase de tormenta de ideas, en la que los participantes empiezan a pensar con originalidad y a proponer nuevas ideas.
4.Selección (Selection) . Una vez generados los nuevos individuos, se colocarán en el grupo padre principal y, a continuación, el grupo será clasificado. Como consecuencia, en la próxima iteración se trabajará con ideas mejoradas y actualizadas.
5. Mutación. Tras combinar ideas y crear otras nuevas, todas las ideas recién creadas mutarán para añadir diversidad adicional a la población y evitar una convergencia prematura.

Vamos a representar la lógica del algoritmo BSO en forma de pseudocódigo:

1. Inicialización de los parámetros y generación de la población inicial
2. Cálculo de la adaptabilidad de cada individuo de una población
3. Hasta que se cumplan los criterios de parada:
    4. Cálculo de la adaptabilidad de cada individuo de una población
    5. Identificación del mejor individuo de la población
    6. División de la población en clústeres, estableciendo la mejor solución del clúster como centro del clúster.
    7. Para cada nuevo individuo de la población:
        |7.1. Si se cumple la probabilidad pReplace:
        |    |Se genera un nuevo centro desplazado de un clúster seleccionado aleatoriamente (el centro del clúster se desplaza)
        |7.2. Si se cumple la probabilidad pOne:
        |    |Se selecciona un clúster al azar
        |    |Si se cumple la probabilidad pUne_center:
        |    |    |7.2.a se selecciona un centro de clúster
        |    |De lo contrario:
        |         |7.2.b se selecciona un individuo al azar de este clúster
        |7.3 De lo contrario:
        |         |Se seleccionan dos clústeres
        |         |Si se cumple la probabilidad pTwo_center:
        |             |7.3.a Un nuevo individuo se forma mediante la fusión de dos centros de clústeres
        |         |De lo contrario:
        |             |7.3.b Se crea un nuevo individuo fusionando las posiciones de los dos individuos seleccionados de cada clúster seleccionado (los clústeres deben ser diferentes)
        |7.4 Mutación: Añade una desviación gaussiana aleatoria a la posición del nuevo individuo
        |7.5 Si un nuevo individuo queda fuera del espacio de búsqueda, se refleja de nuevo en el espacio de búsqueda
    8. Actualizamos la población actual con nuevos individuos
    9. Volvemos al paso 4 hasta que se cumpla el criterio de parada
10. Traemos de vuelta al mejor individuo de la población como solución
11. Fin del funcionamiento de BSO

Vamos a desglosar las operaciones del paso 7 en pseudocódigo.

La primera operación 7.1, de hecho, no crea un nuevo individuo, sino que desplaza el centro del clúster a partir del cual se pueden crear nuevos individuos posteriormente en otras operaciones del algoritmo. El desplazamiento se produce aleatoriamente en cada coordenada con una distribución normal en la distancia establecida respecto a la posición original en los parámetros externos.

La operación 7.2 selecciona el centro del clúster o un individuo del clúster seleccionado que se mutará en el paso 7.4 para crear un nuevo individuo.

La operación 7.3 está diseñada para crear un nuevo individuo mediante la fusión de los centros de dos clústeres seleccionados aleatoriamente o de dos individuos de estos clústeres seleccionados. Los clústeres deben ser diferentes, pero si solo haya un clúster no vacío disponible (los clústeres pueden estar vacíos), entonces la operación de fusión se realizará en los dos individuos seleccionados en ese único clúster no vacío. Esta operación se concibe como un intercambio de ideas entre grupos de ideas.

La operación de fusión será la siguiente:

donde:
Xf - nuevo individuo tras la fusión,
v - número aleatorio de 0 a 1,
X1 y X2 - individuos aleatorios (o dos centros de clústeres) que deben combinarse.

El significado de la fórmula de fusión consiste en crear una idea en un lugar aleatorio entre otras dos ideas.

La operación de mutación puede describirse usando la fórmula siguiente:

donde:
Xm - nuevo individuo tras la mutación,
Xs - individuo seleccionado para ser mutado,
n(µ, σ) - número aleatorio gaussiano con media µ y varianza σ,
ξ - coeficiente de mutación expresado mediante una expresión matemática.

Calcularemos el coeficiente de mutación usando la fórmula:

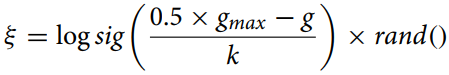
donde:
gmax - número máximo de iteraciones,
g - número de la iteración actual,
k - factor de corrección.

Esta fórmula (coeficiente de mutación) se usa para calcular la distancia de estrechamiento entre individuos en el algoritmo de optimización para cambiar de forma adaptativa el parámetro de mutación. La función "logsig()" ofrece una reducción suave no lineal del valor, mientras que la multiplicación por "rand" añade un elemento estocástico que puede resultar útil para evitar una convergencia prematura y mantener la diversidad de la población.

El factor de corrección "k" del algoritmo BSO (Brain Storm Optimization) desempeña un papel importante en el control de la tasa de cambio del coeficiente "ξ" a lo largo del tiempo. El valor de "k" puede variar según la tarea y los datos específicos y se calcula empíricamente o mediante técnicas de ajuste de hiperparámetros.

En general, "k" debe elegirse para ofrecer un equilibrio entre exploración (exploration) y explotación (exploitation) en el algoritmo. Si "k" es demasiado grande, "ξ" cambiará muy lentamente, lo cual puede provocar una convergencia prematura del algoritmo. Si "k" es demasiado pequeño, "ξ" cambiará muy rápidamente, lo que puede provocar una sobreexploración del espacio de búsqueda y una convergencia lenta.

La función logarítmica sigmoidea, también conocida como función logística, se suele denotar como σ(x) o sig(x). Se calcula mediante la siguiente fórmula:

donde:
exp(-x) - denota un exponente en grado -x.
1 / (1 + exp(-x)) - ofrece un valor de salida entre 0 y 1.

La gráfica de la función sigmoidea se muestra en la siguiente figura. La reducción de funciones desiguales posibilita la exploración en las primeras iteraciones y la mejora en iteraciones posteriores.

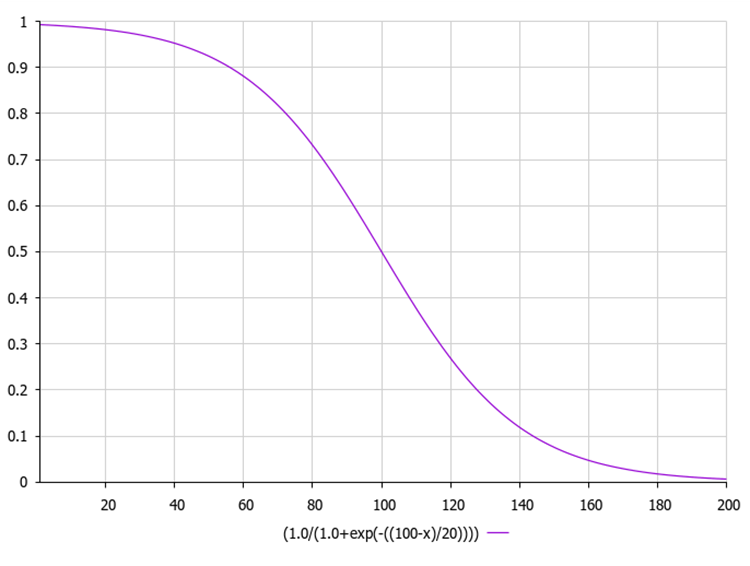
A continuación le mostramos un código de ejemplo para calcular el factor de mutación junto con la función sigmoidea calculada usando el exponente.

En este código, la función "sigmoid" calcula el valor sigmoide del número de entrada "x", mientras que la función "xi" calcula el valor "ξ" según la fórmula anterior. Aquí "gmax" es el número máximo de iteraciones, "g" es el número de iteración actual y "k" es el factor de corrección. La función "MathRand" genera un número aleatorio entre 0 y 32767, así que lo dividimos por 32767.0 para obtener un número aleatorio entre 0 y 1. Después calculamos el valor sigmoidal de este número aleatorio. Este valor lo retornará la función "xi".

double sigmoid(double x) 
{
    return 1.0 / (1.0 + MathExp(-x));
}

double xi(int gmax, int g, double k) 
{
    double randNum = MathRand() / 32767.0; // Generate a random number from 0 to 1
    return sigmoid (0.5 * (gmax - g) / k) * randNum;
}

3. Método de clusterización K-Means

En el algoritmo BSO, se usa un método de análisis de clústeres con la ayuda de K-medias (K-Means) para separar las ideas en grupos distintos. El conjunto actual de "n" soluciones que entran en iteración se divide en "m" categorías para imitar el comportamiento de los participantes en el grupo de discusión y mejorar la eficacia de la búsqueda.

Ahora describiremos un clúster independiente usando la estructura "S_Cluster", que implementa el algoritmo K-means, y supone un método de clustering muy popular.

Vamos a desglosar la estructura:

• centroid[] - array que representa el centroide del clúster.
• f - valor de adaptación del centroide.
• count - número de puntos en el clúster.
• ideasList[] - lista de ideas.

La función "Init" inicializa la estructura cambiando el tamaño de los arrays "centroid" e "ideasList" y estableciendo el valor inicial "f".

//——————————————————————————————————————————————————————————————————————————————
struct S_Cluster
{
    double centroid [];  //cluster centroid
    double f;            //centroid fitness
    int    count;        //number of points in the cluster
    int    ideasList []; //list of ideas

    void Init (int coords)
    {
      ArrayResize (centroid, coords);
      f = -DBL_MAX;
      ArrayResize (ideasList, 0, 100);
    }
};
//——————————————————————————————————————————————————————————————————————————————

La clase C_BSO_KMeans supone una implementación del algoritmo K-means para clusterizar agentes en el algoritmo de optimización BSO. Esto es lo que hace cada método:

1. KMeansInit - el método inicializa los centroides de los clústeres seleccionando agentes aleatorios de los datos. Para cada clúster, se selecciona un agente al azar y sus coordenadas se copian en el centroide del clúster.
2. VectorDistance- el método calcula la distancia euclidiana entre dos vectores. Toma dos vectores como argumentos y retorna su distancia euclídea.
3. KMeans - el método ejecuta la lógica básica del algoritmo k-means para clusterizar los datos. Toma como argumentos un array de datos y un array de clústeres.

El método KMeans ejecuta los siguientes pasos en el proceso:

• Asigna puntos de datos al centroide más cercano.
• Actualiza los centroides basándose en la media de los puntos asignados a cada clúster.
• Repite estos dos pasos hasta que los centroides ya no cambian o se alcanza el número máximo de iteraciones.

El centroide en el método de clusterización K-means es el punto central del clúster. En el contexto del método K-means, el centroide supone la media aritmética de todos los puntos de datos pertenecientes a un clúster determinado.
En cada iteración del algoritmo K-means, se recalculan los centroides, tras lo cual los puntos de datos se agrupan de nuevo en clústeres según el nuevo centroide que resulte más próximo de acuerdo con la métrica elegida.
Así, los centroides desempeñan un papel clave en el método K-means al determinar la forma y la posición de los clústeres.

Esta clase representa una parte clave del algoritmo de optimización BSO, posibilitando la clusterización de agentes para mejorar el proceso de búsqueda. El algoritmo K-means asigna iterativamente los puntos a los clústeres y recalcula los centroides hasta que no suceden más cambios o se alcanza el número máximo de iteraciones.

//——————————————————————————————————————————————————————————————————————————————
class C_BSO_KMeans
{
  public: //--------------------------------------------------------------------

  void KMeansInit (S_BSO_Agent &data [], int dataSizeClust, S_Clusters &clust [])
  {
    for (int i = 0; i < ArraySize (clust); i++)
    {
      int ind = MathRand () % dataSizeClust;
      ArrayCopy (clust [i].centroid, data [ind].c, 0, 0, WHOLE_ARRAY);
    }
  }

  double VectorDistance (double &v1 [], double &v2 [])
  {
    double distance = 0.0;
    for (int i = 0; i < ArraySize (v1); i++)
    {
      distance += (v1 [i] - v2 [i]) * (v1 [i] - v2 [i]);
    }
    return MathSqrt (distance);
  }

  void KMeans (S_BSO_Agent &data [], int dataSizeClust, S_Clusters &clust [])
  {
    bool changed   = true;
    int  nClusters = ArraySize (clust);
    int  cnt       = 0;

    while (changed && cnt < 100)
    {
      cnt++;
      changed = false;

      //Assigning data points to the nearest centroid
      for (int d = 0; d < dataSizeClust; d++)
      {
        int    closest_centroid = -1;
        double closest_distance = DBL_MAX;

        if (data [d].f != -DBL_MAX)
        {
          for (int cl = 0; cl < nClusters; cl++)
          {
            double distance = VectorDistance (data [d].c, clust [cl].centroid);

            if (distance < closest_distance)
            {
              closest_distance = distance;
              closest_centroid = cl;
            }
          }

          if (data [d].label != closest_centroid)
          {
            data [d].label = closest_centroid;
            changed = true;
          }
        }
        else
        {
          data [d].label = -1;
        }
      }


      //Updating centroids
      double sum_c [];
      ArrayResize (sum_c, ArraySize (data [0].c));

      for (int cl = 0; cl < nClusters; cl++)
      {
        ArrayInitialize (sum_c, 0.0);

        clust [cl].count = 0;
        ArrayResize (clust [cl].ideasList, 0);

        for (int d = 0; d < dataSizeClust; d++)
        {
          if (data [d].label == cl)
          {
            for (int k = 0; k < ArraySize (data [d].c); k++)
            {
              sum_c [k] += data [d].c [k];
            }

            clust [cl].count++;
            ArrayResize (clust [cl].ideasList, clust [cl].count);
            clust [cl].ideasList [clust [cl].count - 1] = d;
          }
        }

        if (clust [cl].count > 0)
        {
          for (int k = 0; k < ArraySize (sum_c); k++)
          {
            clust [cl].centroid [k] = sum_c [k] / clust [cl].count;
          }
        }
      }
    }
  }
};
//——————————————————————————————————————————————————————————————————————————————

En el algoritmo BSO (Brain Storm Optimization), la adaptabilidad de un individuo se define como la calidad de la solución que representa y, en un problema de optimización, la adaptabilidad puede resultar igual al valor de la función que hay que optimizar.

El método específico de clusterización puede variar. Un enfoque habitual es usar el método k-means, en el que los centroides de los clústeres se inicializan aleatoriamente y luego se actualizan de forma iterativa para minimizar la suma de cuadrados de las distancias de cada punto al centroide de su clúster.

Debemos señalar que, aunque la adaptabilidad desempeña un papel clave en el proceso de clusterización, no es el único factor que influye en la formación de clústeres. Otros aspectos, como la distancia entre individuos en el espacio de decisión, también pueden desempeñar un papel sustancial. Esto ayuda al algoritmo a mantener la diversidad en la población y evitar una convergencia prematura hacia soluciones inadecuadas.

El número de iteraciones necesarias para la convergencia del algoritmo K-means dependerá en gran medida de varios factores, como el estado inicial de los centroides, la distribución de los datos y el número de clústeres. Sin embargo, en el caso general, K-means suele converger tras un número de iteraciones que va de unas pocas decenas a unos pocos cientos.

También debemos considerar que K-means minimiza la suma de cuadrados de las distancias de los puntos a sus centroides más cercanos, lo cual puede no resultar siempre óptimo dependiendo del problema específico y de la forma de los clústeres en los datos. En algunos casos, otros algoritmos de clusterización pueden resultar más apropiados.

K-means++ supone una versión mejorada del algoritmo K-means propuesto en 2007 por David Arthur y Sergey Vasilvitsky. La principal diferencia entre K-means++ y el K-means estándar es la forma en que se inicializan los centroides. En lugar de seleccionar aleatoriamente los centroides iniciales, K-means++ los selecciona de forma que se maximice la distancia entre ellos. Esto ayuda a mejorar la calidad de la clusterización y acelera la convergencia del algoritmo.

A título informativo, aquí podemos ver los principales pasos de la inicialización en K-means++:

1. Seleccionamos aleatoriamente el primer centroide de los puntos de datos.
2. Para cada punto de datos, calculamos su distancia al centroide más cercano, previamente seleccionado.
3. Seleccionamos el siguiente centroide a partir de los puntos de datos de forma que la probabilidad de que un punto sea seleccionado como centroide resulte directamente proporcional a su distancia hasta el centroide más cercano previamente seleccionado (es decir, el punto que tiene la máxima distancia hasta el centroide más cercano tendrá más probabilidades de ser seleccionado como el siguiente centroide).
4. Repetimos los pasos 2 y 3 hasta seleccionar k centroides.

Una vez inicializados los centroides, K-means++ seguirá funcionando del mismo modo que el algoritmo K-means estándar. Este método de inicialización ayuda a mejorar la calidad de la clusterización y acelera la convergencia del algoritmo. No obstante, este método resulta costoso desde el punto de vista informático.

Si tenemos 1000 coordenadas para cada punto, esto provocará una sobrecarga computacional adicional para el algoritmo K-means++ porque deberá calcular distancias en un espacio de alta dimensionalidad. Sin embargo, K-means++ puede seguir resultando eficaz (es necesario realizar experimentos para confirmar la hipótesis), ya que suele conducir a una convergencia más rápida y a clústeres de mejor calidad.

Cabe señalar que, al trabajar con datos de alta dimensionalidad (como 1 000 coordenadas), pueden surgir problemas adicionales debido a la "maldición de la dimensionalidad". Esto puede hacer que las distancias entre puntos sean menos significativas y dificultar la clusterización. En estos casos, podría resultar útil usar técnicas de reducción de la dimensionalidad como el PCA (análisis de componentes principales) antes de aplicar K-means o K-means++. Esto puede ayudar a reducir la dimensionalidad de los datos y hacer que la clusterización sea más eficaz.

Reducir la dimensionalidad de los datos es un paso importante en el procesamiento de los mismos, especialmente al trabajar con un gran número de coordenadas o características. Esto ayuda a simplificar los datos, reducir el coste computacional y mejorar el rendimiento de los algoritmos de clusterización. Aquí tenemos algunas técnicas de reducción de la dimensionalidad que se utilizan a menudo en la clusterización:

1. Método de componentes principales (PCA). Este método convierte un conjunto de datos con un gran número de variables en un conjunto de datos con menos variables, conservando la máxima cantidad de información posible.
2. Escala multidimensional (MDS). El método intenta encontrar una estructura de baja dimensionalidad que preserve las distancias entre puntos como en el espacio original de alta dimensionalidad.
3. Distribución t del vecino estocástico (t-SNE). Se trata de un método no lineal de reducción de la dimensionalidad que resulta especialmente adecuado para visualizar datos de alta dimensionalidad.
4. Autocodificadores. Se trata de redes neuronales que se usan para reducir la dimensionalidad de los datos. Funcionan aprendiendo a codificar los datos de entrada en una representación compacta y, a continuación, descodifican dicha representación en los datos originales.
5. Método de componentes independientes (ICA). Se trata de una técnica estadística que transforma un conjunto de datos en componentes independientes que pueden resultar más informativos (pueden reflejar mejor la estructura o aspectos importantes de los datos, por ejemplo, pueden hacer visibles algunos factores ocultos o permitir una mejor separación de clases en una tarea de clasificación) que los datos originales.
6. Análisis lineal discriminante (LDA). El método se usa para encontrar combinaciones lineales de características que separen bien dos o más clases.

Por tanto, aunque K-means++ pueda ser más costoso desde el punto de vista informático en la fase de inicialización, especialmente para datos de alta dimensionalidad, aún puede justificarse en algunos casos. Pero siempre merece la pena experimentar y comparar distintos enfoques para determinar cuál funciona mejor para nuestra tarea y nuestro conjunto de datos concretos.

Para aquellos que quieran experimentar adicionalmente con el método K-means++, mostraremos el método de inicialización de este algoritmo (el resto del código no difiere del código de K-means simple).

El siguiente código supone una implementación de la inicialización del algoritmo K-means++. La función admite un array de puntos de datos representado por la estructura S_BSO_Agent, un tamaño de datos (dataSizeClust) y un array de clústeres representado por la estructura S_Cluster. El método inicializa el primer centroide de forma aleatoria a partir de los puntos de datos. A continuación, para cada centroide posterior, el algoritmo calcula la distancia de cada punto de datos hasta el centroide más cercano y selecciona el siguiente centroide con una probabilidad proporcional a la distancia. Para ello, se genera un número aleatorio "r" que va de 0 a la suma de todas las distancias y, a continuación, se iteran todos los puntos de datos, disminuyendo "r" en la distancia de cada punto hasta que "r" sea menor o igual que la distancia del punto actual. En este caso, el punto actual se selecciona como próximo centroide. Este proceso se repetirá hasta que se inicialicen todos los centroides.

En general, se aplica la inicialización K-Means++, que supone una versión mejorada de la inicialización del algoritmo K-means estándar. Los centroides se seleccionan para minimizar la suma potencial de los cuadrados de las distancias entre los centroides y los puntos de datos, lo cual conduce a una clusterización más eficaz y estable.

void KMeansPlusPlusInit (S_BSO_Agent &data [], int dataSizeClust, S_Cluster &clust [])
{
  // Choose the first centroid randomly
  int ind = MathRand () % dataSizeClust;
  ArrayCopy (clust [0].centroid, data [ind].c, 0, 0, WHOLE_ARRAY);

  for (int i = 1; i < ArraySize (clust); i++)
  {
    double sum = 0;
      
    // Compute the distance from each data point to the nearest centroid
    for (int j = 0; j < dataSizeClust; j++)
    {
      double minDist = DBL_MAX;
       
      for (int k = 0; k < i; k++)
      {
        double dist = VectorDistance (data [j].c, clust [k].centroid);
          
        if (dist < minDist)
        {
            minDist = dist;
        }
      }
        
      data [j].minDist = minDist;
      sum += minDist;
    }

    // Choose the next centroid with a probability proportional to the distance
    double r = MathRand () * sum;
      
    for (int j = 0; j < dataSizeClust; j++)
    {
      if (r <= data [j].minDist)
      {
        ArrayCopy (clust [i].centroid, data [j].c, 0, 0, WHOLE_ARRAY);
        break;
      }
      r -= data [j].minDist;
    }
  }
}

Continuará...

En este artículo, hemos analizado la estructura lógica del algoritmo BSO, así como las técnicas de clusterización y las formas de reducir la dimensionalidad del problema de optimización. En el próximo artículo, concluiremos nuestro análisis del algoritmo BSO y resumiremos su rendimiento.