MetaTrader 5 / Ejemplos
English Русский 中文 Deutsch 日本語 Português
preview
Algoritmos de optimización de la población: Método de Nelder-Mead

Algoritmos de optimización de la población: Método de Nelder-Mead

MetaTrader 5 — Ejemplos | 27 mayo 2024, 14:59
206 0
Andrey Dik
Andrey Dik

Contenido:

1. Introducción
2. Descripción del algoritmo
3. Resultados de las pruebas


1. Introducción

El método de Nelder-Mead fue desarrollado en 1965 por John Nelder y Roger Mead. Ambos buscaban un método de optimización que pudiera tratar funciones sin derivadas o sin fórmulas analíticas para las derivadas. Asimismo, querían desarrollar un método fácil de aplicar y eficiente en las máquinas informáticas de la época. Sus investigaciones les llevaron a la idea de usar un símplex, un poliedro en el espacio de parámetros de una función.

La historia del método comenzó con los trabajos de John Nelder y sus colegas del Computer Science Laboratory de Oxford. El equipo se enfrentaba al problema de optimizar funciones que no tenían derivadas analíticas o eran demasiado complejas para calcularlas. Las técnicas de optimización tradicionales, como los métodos de gradiente, no podían aplicarse en estos casos. En su lugar, Nelder y Mead propusieron un nuevo método basado en la búsqueda iterativa de la solución óptima en el espacio de parámetros de la función.

El método de Nelder-Mead se denominó método de símplex y se publicó en el artículo "A Simplex Method for Function Minimisation" en The Computer Journal en 1965. Este método ha sido adoptado por la comunidad científica y se ha generalizado en diversos campos que requieren la optimización de funciones.

Un símplex es un conjunto de puntos que forman un poliedro, donde cada punto es un conjunto de valores de los parámetros de la función a optimizar. La idea consiste en modificar y desplazar el símplex en el espacio de parámetros para encontrar el valor óptimo de la función.

El método de Nelder-Mead pertenece a la clase de algoritmos de optimización incondicional. Es un algoritmo determinista que no requiere el uso de derivadas de funciones y puede trabajar con funciones que tienen múltiples mínimos locales.


2. Descripción del algoritmo

El método de Nelder-Mead no es un método poblacional porque usa un único agente de optimización que representa un símplex, que a su vez consiste en un conjunto de puntos en el espacio de búsqueda, que en sí mismo puede considerarse una población. Sin embargo, usaremos múltiples agentes, cada uno con su propio símplex, por lo que esta implementación bien puede clasificarse como un algoritmo de población.

Así, para simplificar la comprensión de la operación símplex, supongamos que necesitamos optimizar funciones de dos variables, es decir, la dimensionalidad del espacio z = 2, entonces el simplex constará de z + 1 = 3 vértices. El cambio de símplex es una operación sobre el peor punto de estos tres. Denotaremos estos puntos como Best, Good, Worst, siendo Good el segundo punto después de Worst (en caso de que la dimensionalidad sea mayor que dos, Good siempre será el segundo después de Worst de la lista ordenada de vértices).

Entonces con estos tres vértices deberemos realizar cálculos y correcciones de Worst respecto a los otros vértices. Así, desplazaremos Worst respecto al centro geométrico de los vértices salvo el suyo propio, es decir, calcularemos el centroide y desplazaremos Worst respecto al mismo.

En cada iteración del método de Nedler-Mead, realizaremos los siguientes pasos:

1. Clasificación de los vértices del símplex según los valores de la función objetivo, es decir 

f(P0) ⩾ f(P1) ⩾ ... ⩾ f(P(n-1))

donde:

  • P0, P1 ... P(n-1) - puntos del símplex
  • n - número de vértices del símplex

2. Cálculo del centroide: para ello, calcularemos la media de las coordenadas correspondientes de todos los vértices del símplex excepto el peor vértice. Digamos que el vector Xo es el centro de gravedad de todos los vértices salvo X(n-1), entonces: 

Xo = (X0 + X1 + ... + X(n-2)) / (n-1)

donde:

  • X0, X1 ... X(n-2) - vectores correspondientes de las coordenadas de todos los vértices excepto el peor

3. La reflexión (reflection) es la operación de reflexión del peor vértice respecto al centroide. El vector Xr del nuevo vértice reflejado se calculará mediante la siguiente fórmula:

Xr = Xo + α (Xo - Xw)

donde:

  • Xw - vector del peor vértice, se corresponde con el vértice P(n-1)
  • α - coeficiente de reflexión, normalmente igual a 1

4. Estimación de un nuevo vértice; para ello, calcularemos el valor de la función objetivo en este punto. Si el nuevo vértice tiene un valor de función objetivo mejor que el del peor vértice del símplex, podremos sustituirlo, es decir, la reflexión sustituirá al original. La operación de reflexión nos permite explorar una nueva región del espacio de parámetros usando la reflexión desde el centroide del símplex.

5. Expansión: se utiliza para seguir explorando el espacio de parámetros cuando una operación de reflexión ha producido un vértice mejor que el mejor de todos, suponiendo que un movimiento posterior en la dirección de la reflexión mejorará aún más su posición. La operación de expansión nos permite explorar una región aún mayor del espacio de parámetros que la operación de reflexión. Aumenta la distancia entre el centroide y el punto reflejado, lo cual puede ayudar a encontrar nuevos mínimos locales de la función objetivo. Podemos calcular el vector de extensión Xe de la forma siguiente:

Xe = Xo + γ(Xr - Xo)

donde:

  • γ - coeficiente de expansión, normalmente mayor que 1, por defecto 2

5.1. Si se ha realizado una operación de ampliación: calcularemos la función de aptitud del vértice Xe y, si es mejor que el vértice Xr, podrá sustituir al peor vértice Xw del símplex. Una vez realizada la ampliación, continuaremos con el paso 1.

Es importante señalar que el coeficiente de expansión γ debe seleccionarse con cuidado. Si se selecciona demasiado grande, esto podría provocar que el símplex se expanda por una gran región del espacio de parámetros, lo cual puede ralentizar la convergencia o provocar la pérdida de información sobre los extremos locales. Si lo elegimos demasiado pequeño, puede que no explore suficientemente nuevas regiones del espacio de parámetros.

6. Contracción (contraction): se utiliza para calcular un vértice Xc cuando la operación de reflexión ha producido un vértice peor o igual que un punto bueno Xb (segundo peor), es decir, se realiza con la esperanza de encontrar una posición mejor dentro del símplex. Se realiza de la forma siguiente:

Xc = Xo + β(Xw - Xo)

donde:

  • β - factor de contracción, normalmente entre 0 y 1, por defecto 0,5.

6.1.  Si hemos realizado la operación de contracción: se calculará el valor de la función objetivo para el vértice Xc. Si el nuevo vértice tiene un valor de función objetivo inferior al peor vértice del símplex, podrá sustituir al peor vértice. Una vez realizada la ampliación, continuaremos con el paso 1.

La operación de contracción desplazará el símplex más cerca del peor punto, lo cual puede ayudar a explorar la proximidad de ese punto. Al igual que en la operación de expansión, es importante elegir cuidadosamente la relación de contracción β. Si elegimos uno demasiado grande, puede hacer que el símplex se comprima demasiado, con la consiguiente pérdida de información sobre los mínimos locales. Si seleccionamos uno demasiado pequeño, la contracción podría no resultar suficiente para explorar la proximidad del peor punto.

7. Encogimiento (shrinkage): la última operación del método de Nelder-Mead se realizará cuando ninguna de las operaciones anteriores (reflexión, expansión, contracción) provoque una mejora del valor de la función objetivo. La operación de encogimiento reducirá el tamaño del símplex para acotar la zona de búsqueda y centrarla en torno al mejor punto.


Como vemos, los autores tienen cuatro operaciones de símplex. Al trabajar con símplexes, debemos considerar que para iniciar la optimización será necesario calcular la función de aptitud para todos los puntos del símplex. El número de puntos de símplex es "z+1", donde z será la dimensionalidad del espacio de búsqueda. Por ejemplo, si tenemos una dimensionalidad de búsqueda de 1000, deberemos calcular la función de aptitud 1001 veces para iniciar las operaciones con el símplex. Mientras que con un algoritmo de población convencional con una población de 50 agentes podríamos realizar 20 épocas, para este algoritmo solo se realizará una época y se agotará la mayor parte del número limitado de iteraciones.

La operación de encogimiento consiste en desplazar todos los puntos al mejor punto, después de lo cual deberemos calcular la función de aptitud 1000 veces, lo que significa que la operación de encogimiento es muy laboriosa. Según la idea de los autores, esta operación debe invocarse cuando el algoritmo se atasque, cuando desplazar el peor punto del símplex no aporte una mejora de la solución. No obstante, mis experimentos han demostrado que esta operación implica muchísimos recursos computacionales y, además, carece de sentido y supone un suicidio para el algoritmo de optimización, ya que la convergencia de todos los puntos del agente símplex a un único extremo local significaría quedarse atascado y detener la exploración del espacio de búsqueda. Por ello, hemos decidido abandonar la operación de "Shrinkage" para la aplicación práctica del algoritmo.

Así, utilizaremos las 3 primeras operaciones con el símplex; podemos visualizarlas en la figura 1 para mayor claridad:

NMrefl

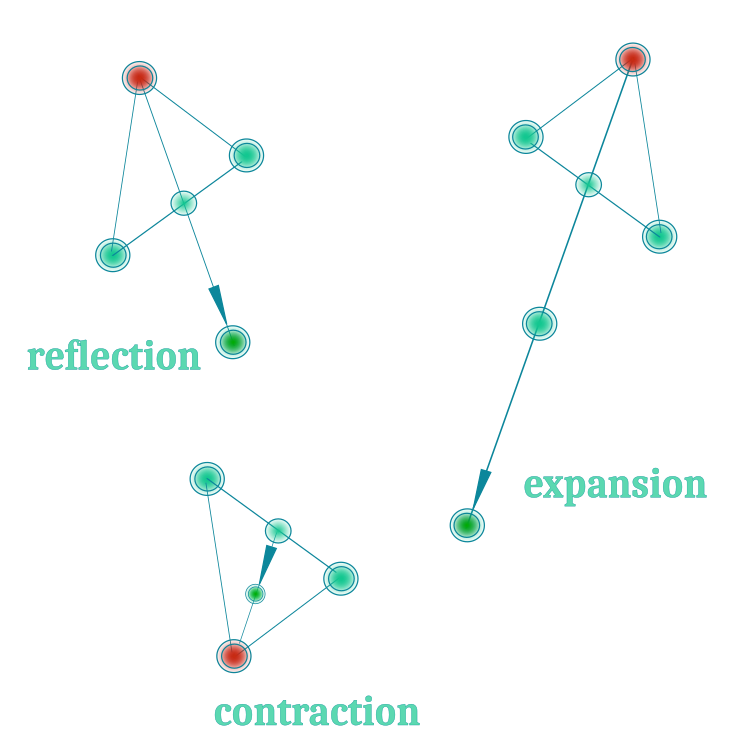
Figura 1. Las tres operaciones básicas del método Nelder-Mead.


Como el método de búsqueda de símplex puede fallar en la elección de los vértices iniciales por ser determinista, su resultado de optimización podría no ser satisfactorio. Los experimentos con este algoritmo no ha hecho sino confirmar los temores: solo funciona aceptablemente en un espacio de coordenadas limitado.

Debido a problemas de convergencia, los vértices del símplex se desplazan simplemente un valor fijo. Imagínese que está de pie sobre unos zancos e intenta sentarse en un banco, pero este es demasiado bajo para hacerlo. Exactamente la misma situación se produce con un símplex cambiante. Para que el algoritmo funcione a la perfección, necesitaremos mucha suerte para que los vértices iniciales del símplex estén en el lugar correcto. Esto es similar a lo que sucede con los zancos: necesitamos un banco alto para sentarnos con seguridad. El algoritmo converge relativamente bien en funciones suaves de un solo extremo, como la parábola. No obstante, nuestros problemas prácticos son mucho más complejos y suelen estar llenos de "trampas" locales, sobre todo en los problemas comerciales, que son intrínsecamente discretos.

Entonces nos surge la pregunta: ¿qué hacer cuando un símplex se queda atascado "para siempre" en un extremo local? La lógica del algoritmo de Nelder-Mead no permite escapar de esta "trampa". Tras cada operación, ya sea de contracción o de expansión, el algoritmo vuelve a la reflexión, intentando superar el peor punto. Visualmente, se parece a un "parpadeo". Para resolver este problema, hemos intentado que el símplex salga de la "trampa" local y siga buscando en nuevas regiones del espacio. Para ello, hemos recurrido al vuelo de Levy, que en algunos casos ayudan a "revitalizar" la población, tal y como se describe en artículos anteriores. Sin embargo, debemos señalar que el vuelo de Levy no siempre es útil y su aplicación depende de la lógica del algoritmo de optimización. En nuestro caso, nos encontramos ante un experimento y los resultados de la mejora no estaban garantizados.

Vamos a pasar a la parte más interesante: la escritura del código.

Después de cada iteración, necesitaremos saber qué operación se ha realizado en el peor vértice del símplex. Para ello resultará cómodo utilizar un enumerador. Además de las tres operaciones básicas con el vértice del símplex, hemos añadido una más, "ninguna", por si se nos ocurre alguna idea para complementar el algoritmo de alguna forma. Llamaremos al enumerador E_SimplexOperation, y sus campos serán:

  • none: no hay operaciones previstas
  • reflection: operación de "reflexión"
  • expansion: operación de "expansión"
  • contraction: una operación de "contracción" 
//——————————————————————————————————————————————————————————————————————————————
enum E_SimplexOperation
{
  none        = 0,
  reflection  = 1,
  expansion   = 2,
  contraction = 3
};
//——————————————————————————————————————————————————————————————————————————————
Para describir un vértice de símplex necesitaremos una estructura S_Point que contenga los siguientes campos:
  • Init(int coords): inicialización del punto, toma el argumento "coords"
  • c []: array de coordenadas de un punto en un espacio multidimensional, el tamaño del array se definirá en el método "Init".
  • f: valor de la función de aptitud del vértice
//——————————————————————————————————————————————————————————————————————————————
struct S_Point
{
  void Init (int coords)
  {
    ArrayResize (c, coords);
    f = -DBL_MAX;
  }
  double c [];
  double f;
};
//——————————————————————————————————————————————————————————————————————————————

Para el símplex utilizaremos la estructura S_Simplex, que supone un símplex para cada agente y contiene los siguientes campos:

  • Init(int coords): inicialización del símplex, tomaremos el argumento "coords", el número de coordenadas
  • S_Point p []: array de vértices de símplex, el tamaño del array se definirá en el método "Init".
  • c []: array de coordenadas del centroide del símplex, el tamaño del array se definirá en el método "Init".
  • S_Point Xr: punto de reflexión
  • S_Point Xe: punto de expansión
  • S_Point Xc: punto de contracción
  • indG: índice del punto bueno (Good) en el símplex
  • indW: índice del punto peor (Worst) en el símplex
  • E_SimplexOperation: tipo de operación del símplex
//——————————————————————————————————————————————————————————————————————————————
struct S_Simplex
{
  void Init (int coords)
  {
    ArrayResize (p, coords + 1);

    for (int i = 0; i <= coords; i++)
    {
      p [i].Init (coords);
    }

    ArrayResize (c, coords);

    Xr.Init (coords);
    Xe.Init (coords);
    Xc.Init (coords);

    operation = none;
  }

  S_Point p [];
  double c  []; //centroid

  S_Point Xr;  //reflection point
  S_Point Xe;  //expansion point
  S_Point Xc;  //expansion point

  int indG;    //index of good point
  int indW;    //index of worst point

  E_SimplexOperation operation; //type of simplex operation
};
//——————————————————————————————————————————————————————————————————————————————

Para el agente de optimización definiremos la estructura S_Agent, que contendrá los siguientes campos:

  • Init (int coords): método de inicialización del agente, tomará un argumento "coords" que especificará el número de coordenadas. El método redimensionará el array "c" a "coords" utilizando la función ArrayResize. A continuación, el campo "f" se establecerá en -DBL_MAX, que es el valor inicial de la función de evaluación del agente. Después se llamará al método "Init" para el campo "s", que representará el agente de símplex
  • c []: array de coordenadas del agente en el espacio multidimensional que se intercambiará con un programa externo. El tamaño del array se definirá en el método "Init".
  • f: valor de la función de aptitud del agente
  • s: agente de símplex representado por la estructura S_Simplex. El símplex se inicializará llamando al método "Init" para el campo "s"
//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (int coords)
  {
    ArrayResize (c, coords);
    f = -DBL_MAX;

    s.Init (coords);
  }

  double c  []; //coordinates
  double f;     //fitness
  S_Simplex s;  //agent simplex
};
//——————————————————————————————————————————————————————————————————————————————

Definiremos el algoritmo del método de búsqueda del símplex de la clase C_AO_NMm, que contendrá los siguientes campos:

  • cB []: array de las mejores coordenadas
  • fB: valor de la función de aptitud de las mejores coordenadas
  • a []: array de los agentes representados por la estructura S_Agent
  • rangeMax []: array de valores máximos del rango de búsqueda para cada coordenada
  • rangeMin []: array de valores mínimos del rango de búsqueda para cada coordenada
  • rangeStep []: array de pasos de búsqueda para cada coordenada
  • Init (const int coordsP, const int popSizeP, const double reflectionCoeffP, const double expansionCoeffP, const double contractionCoeffP): método para inicializar el algoritmo, toma los argumentos que definen el número de coordenadas, el tamaño de la población y los coeficientes para las operaciones de reflexión, expansión y contracción, el método inicializa todos los campos de la clase
  • Moving (): el método realiza el movimiento de los agentes en el algoritmo
  • Revision(): método que realiza una revisión de los agentes del algoritmo.
  • Sorting, CalcCentroid, Reflection, Expansion, Contraction, Flying: realizan operaciones sobre símplexes. Mientras que los métodos 
  • SeInDiSp, RNDfromCI, Scale: se ejecutan para generar y convertir valores en rangos válidos con un tamaño de paso especificado.
//——————————————————————————————————————————————————————————————————————————————
class C_AO_NMm
{
  //----------------------------------------------------------------------------
  public: double cB [];  //best coordinates
  public: double fB;     //FF of the best coordinates
  public: S_Agent a [];  //agent

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,            //coordinates number
                     const int    popSizeP,           //population size
                     const double reflectionCoeffP,   //Reflection coefficient
                     const double expansionCoeffP,    //Expansion coefficient
                     const double contractionCoeffP); //Contraction coefficient

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;        //coordinates number
  private: int    popSize;       //population size
  private: int    simplexPoints; //simplex points


  private: double reflectionCoeff;  //Reflection coefficient
  private: double expansionCoeff;   //Expansion coefficient
  private: double contractionCoeff; //Contraction coefficient

  private: bool   revision;

  private: S_Point pTemp [];
  private: int     ind   [];
  private: double  val   [];

  private: void   Sorting      (S_Point &p []);
  private: void   CalcCentroid (S_Simplex &s, int indW);
  private: void   Reflection   (S_Agent &agent, int indW);
  private: void   Expansion    (S_Agent &agent);
  private: void   Contraction  (S_Agent &agent, int indW);
  private: void   Flying       (S_Agent &agent, int indW);

  private: double SeInDiSp     (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI    (double min, double max);
  private: double Scale        (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Para inicializar el algoritmo usaremos el método "Init" de la clase C_AO_NMm, que inicializa todos los campos de la clase y crea los arrays necesarios para que funcione el algoritmo de optimización.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Init (const int    coordsP,            //coordinates number
                     const int    popSizeP,           //population size
                     const double reflectionCoeffP,   //reflection coefficient
                     const double expansionCoeffP,    //expansion coefficient
                     const double contractionCoeffP)  //contraction coefficient
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords        = coordsP;
  popSize       = popSizeP;
  simplexPoints = coords + 1;

  reflectionCoeff  = reflectionCoeffP;
  expansionCoeff   = expansionCoeffP;
  contractionCoeff = contractionCoeffP;

  ArrayResize (pTemp, simplexPoints);
  ArrayResize (ind,   simplexPoints);
  ArrayResize (val,   simplexPoints);

  ArrayResize (a, popSize);
  for (int i = 0; i < popSize; i++)
  {
    a [i].Init (coords);
  }

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//——————————————————————————————————————————————————————————————————————————————

Normalmente usamos el método Moving para desplazar los agentes en el espacio de búsqueda, pero para el algoritmo NM, dejaremos solo la función de colocación aleatoria inicial de los vértices del símplex del agente en el espacio de búsqueda.
Para crear un vértice de símplex aleatorio, utilizaremos RNDfromCI y lo llevaremos al rango deseado con el paso deseado utilizando el método SeInDiSp. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Moving ()
{
  if (!revision)
  {
    int cnt = 0;

    for (int i = 0; i < popSize; i++)
    {
      for (int p = 0; p < simplexPoints; p++)
      {
        cnt++;
        for (int c = 0; c < coords; c++)
        {
          a [i].s.p [p].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
          a [i].s.p [p].c [c] = SeInDiSp  (a [i].s.p [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

La lógica básica de desplazamiento de los vértices de los símplexes de los agentes se implementará en el método "Revision".

Si aún no se ha realizado la revisión "if (!revision)", entonces deberemos clasificar los vértices en el símplex, construir un centroide y realizar una operación de reflexión para los peores vértices de los agentes de símplex. Es la primera operación de vértice y siempre será una "reflexión". Aquí es donde podremos actualizar la solución global, ya que en este punto tendremos conocimiento del valor de aptitud para cada vértice. Luego estableceremos la variable "revision" en "true" y saldremos del método.

A partir de la siguiente iteración, conoceremos la función de aptitud no para los vértices de símplex, sino para agentes de optimización específicos, y en función de las operaciones realizadas sobre los símplexes, asignaremos las soluciones conocidas de los agentes a sus correspondientes vértices de símplex. Luego deberemos actualizar la solución global con los mejores valores de adaptabilidad del agente.

A continuación, comprobaremos qué operación se ha realizado en los vértices en la iteración anterior. Nos referimos a que los vértices de los símplexes son vectores.

Si hemos realizado una operación de "reflexión":

  • asignaremos el valor de aptitud del agente al vector Xr
  • compararemos la adaptabilidad del vector Xr con Xw, y si el valor es mejor, actualizaremos el vector Xw
  • compararemos la adaptabilidad del vector Xr con Xb, y si el valor es mejor, realizar una "expansión".
  • compararemos la adaptabilidad del vector Xr con Xg (el segundo después del peor vértice), y si el valor es peor, realizar la "contracción".
  • si ha habido una mejora de vértices, realizaremos la "Reflexión", con la clasificación preliminar y la construcción de centroides, de lo contrario ejecutaremos el "Flying" .

Si se ha realizado una operación de "expansión":

  • asignaremos el valor de aptitud del agente al vector Xe
  • compararemos la adaptabilidad del vector Xe con Xw, y si el valor es mejor, actualizaremos el vector Xw
  • realizaremos una "reflexión", con clasificación preliminar y construcción de centroides

Si se ha realizado una operación de "encogimiento":

  • asignaremos el valor de aptitud del agente al vector Xc
  • compararemos la adaptabilidad del vector Xc con Xw, y si el valor es mejor, entonces actualizaremos el vector Xw, de lo contrario efectuaremos el "Flying"
  • si ha habido una mejora de vértices, entonces realizaremos una "reflexión", con clasificación preliminar y construcción de centroides 
//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Revision ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    //sort agent simplex points by FF value and assign BGW
    for (int i = 0; i < popSize; i++)
    {
      Sorting (a [i].s.p);
    }

    //calculate the simplex centroid
    for (int i = 0; i < popSize; i++)
    {
      a [i].s.indG = simplexPoints - 2;
      a [i].s.indW = simplexPoints - 1;

      CalcCentroid (a [i].s, a [i].s.indW);
    }

    //assign the next type of operation - reflection
    for (int i = 0; i < popSize; i++)
    {
      Reflection (a [i], a [i].s.indW);
      a [i].s.operation = reflection;
    }

    //save the best point of the agents’ simplexes as a global solution 
    for (int i = 0; i < popSize; i++)
    {
      if (a [i].s.p [0].f > fB)
      {
        fB = a [i].s.p [0].f;
        ArrayCopy (cB, a [i].s.p [0].c, 0, 0, WHOLE_ARRAY);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  if (revision)
  {
    int pos = -1;

    for (int i = 0; i < popSize; i++)
    {
      if (a [i].f > fB) pos = i;
    }

    if (pos != -1)
    {
      fB = a [pos].f;
      ArrayCopy (cB, a [pos].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    //++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
    //if there was reflection ++++++++++++++++++++++++++++++++++++++++++++
    if (a [i].s.operation == reflection)
    {
      a [i].s.Xr.f = a [i].f;
      bool needUpd = false;

      //------------------------------------------------------------------------
      if (a [i].s.Xr.f > a [i].s.p [a [i].s.indW].f)  //Xr > Xw                 |---w--Xr--g----------b---|
      {
        a [i].s.p [a [i].s.indW] = a [i].s.Xr;        //replace Xw with Xr
        needUpd = true;
      }
      
      //------------------------------------------------------------------------
      if (a [i].s.Xr.f > a [i].s.p [0].f)             //if Xr > Xb            |---w----g----------b---Xr|
      {
        Expansion (a [i]);                            //perform expansion
        continue;
      }

      //------------------------------------------------------------------------
      if (a [i].s.Xr.f <= a [i].s.p [a [i].s.indG].f) //if Xr < Xg            |---w---Xr--g----------b--|
      {
        Contraction (a [i], a [i].s.indG);            //perform contraction
        continue;
      }
      
      if (needUpd)
      {
        Sorting (a [i].s.p);
        a [i].s.indG = simplexPoints - 2;
        a [i].s.indW = simplexPoints - 1;
        CalcCentroid (a [i].s, a [i].s.indW);
        Reflection   (a [i],   a [i].s.indW);
      }
      else Flying (a [i], a [i].s.indW);

      continue;
    }

    //++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
    //if there was expansion +++++++++++++++++++++++++++++++++++++++++++++
    if (a [i].s.operation == expansion)
    {
      a [i].s.Xe.f = a [i].f;

      if (a [i].s.Xe.f > a [i].s.Xr.f) a [i].s.p [a [i].s.indW] = a [i].s.Xe;
      else                             a [i].s.p [a [i].s.indW] = a [i].s.Xr;

      Sorting (a [i].s.p);
      a [i].s.indG = simplexPoints - 2;
      a [i].s.indW = simplexPoints - 1;
      CalcCentroid (a [i].s, a [i].s.indW);
      Reflection   (a [i],   a [i].s.indW);

      continue;
    }

    //++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
    //if there was contraction +++++++++++++++++++++++++++++++++++++++++++
    if (a [i].s.operation == contraction)
    {
      a [i].s.Xc.f = a [i].f;

      if (a [i].s.Xc.f > a [i].s.p [a [i].s.indW].f)
      {
        a [i].s.p [a [i].s.indW] = a [i].s.Xc;

        Sorting (a [i].s.p);
        a [i].s.indG = simplexPoints - 2;
        a [i].s.indW = simplexPoints - 1;
        CalcCentroid (a [i].s, a [i].s.indW);
        Reflection   (a [i],   a [i].s.indW);
      }
      else Flying (a [i], a [i].s.indW);

      continue;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Para calcular el centroide escribiremos el método CalcCentroid; este calculará la media de las coordenadas en el símplex dado "s" hasta el índice especificado indW.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::CalcCentroid (S_Simplex &s, int indW)
{
  double summ = 0.0;

  for (int c = 0; c < coords; c++)
  {
    summ = 0.0;

    for (int p = 0; p < simplexPoints; p++)
    {
      if (p != indW) summ += s.p [p].c [c];
    }

    s.c [c] = summ / coords;
  }
}
//——————————————————————————————————————————————————————————————————————————————

La operación de "reflexión" será realizada por el método "Reflection" para el vértice de índice "indW" del agente de símplex "agent".

Dentro del ciclo, calcularemos el valor reflejado Xr utilizando la fórmula Xr = Xo + reflectionCoeff * (Xo - Xw). Aquí reflectionCoeff será el coeficiente de reflexión que definirá el grado de desviación del vértice reflejado con respecto al vértice inicial.
A continuación, aplicaremos la función SeInDiSp al valor Xr para asegurarnos de que se encuentra dentro del rango válido rangeMin[c] y rangeMax[c], en incrementos de rangeStep[c]. El resultado se almacenará en agent.s.Xr.c[c].
Luego estableceremos la operación "reflection" para el agente agent.s.operation indicando que se ha realizado una operación de reflexión para este agente.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Reflection (S_Agent &agent, int indW)
{
  double Xo;
  double Xr;
  double Xw;

  for (int c = 0; c < coords; c++)
  {
    Xo = agent.s.c [c];
    Xw = agent.s.p [indW].c [c];

    //Xr = Xo + RNDfromCI (0.0, reflectionCoeff) * (Xo - Xw);
    Xr = Xo + reflectionCoeff * (Xo - Xw);

    agent.s.Xr.c [c] = SeInDiSp  (Xr, rangeMin [c], rangeMax [c], rangeStep [c]);
    agent.c      [c] = agent.s.Xr.c [c];
  }

  agent.s.operation = reflection;
}
//——————————————————————————————————————————————————————————————————————————————

La operación de "expansión" se realizará mediante el método "Expansion" para el agente "agent".

Dentro del ciclo, calcularemos el valor expandido de Xe mediante la fórmula Xe = Xo + expansionCoeff * (Xr - Xo) . Aquí expansionCoeff será el coeficiente de expansión que definirá el grado de aumento de la desviación del vértice expandido con respecto al vértice inicial.
A continuación, aplicaremos la función SeInDiSp al valor de Xe para asegurarnos de que se encuentra dentro del rango válido rangeMin[c] y rangeMax[c], en incrementos de rangeStep[c]. El resultado se almacenará en agent.s.Xe.c[c].
Después estableceremos la operación "expansion" para el agente agent.s.operation, indicando que se ha realizado una operación de "expansión" para este agente.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Expansion (S_Agent &agent)
{
  double Xo;
  double Xr;
  double Xe;

  for (int c = 0; c < coords; c++)
  {
    Xo = agent.s.c    [c];
    Xr = agent.s.Xr.c [c];

    //Xe = Xo + RNDfromCI (0.0, expansionCoeff) * (Xr - Xo);
    Xe = Xo + expansionCoeff * (Xr - Xo);

    agent.s.Xe.c [c] = SeInDiSp  (Xe, rangeMin [c], rangeMax [c], rangeStep [c]);
    agent.c      [c] = agent.s.Xe.c [c];
  }

  agent.s.operation = expansion;
}
//——————————————————————————————————————————————————————————————————————————————

La operación de "contracción" se realizará mediante el método "Contraction" para el vértice índice "indW" del agente simplex "agent".

Dentro del ciclo, el valor comprimido Xc se calculará mediante la fórmula Xc = Xo + contractionCoeff * (Xw - Xo) . Aquí contractionCoeff será el coeficiente de contracción que definirá el grado de reducción de la desviación del vértice comprimido con respecto al vértice inicial.
A continuación, aplicaremos la función SeInDiSp al valor de Xc para asegurarnos de que se encuentra dentro del rango válido rangeMin[c] y rangeMax[c], en incrementos de rangeStep[c]. El resultado se almacenará en agent.s.Xc.c[c].
Luego estableceremos la operación de "contracción" para el agente agent.s.operation indicando que se ha realizado una operación de "contracción" para este agente.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Contraction (S_Agent &agent, int indW)
{
  double Xo;
  double Xw;
  double Xc;

  for (int c = 0; c < coords; c++)
  {
    Xo = agent.s.c    [c];
    Xw = agent.s.p [indW].c [c];

    //Xc = Xo + RNDfromCI (0.0, contractionCoeff) * (Xw - Xo);
    Xc = Xo + contractionCoeff * (Xw - Xo);

    agent.s.Xc.c [c] = SeInDiSp  (Xc, rangeMin [c], rangeMax [c], rangeStep [c]);
    agent.c      [c] = agent.s.Xc.c [c];
  }

  agent.s.operation = contraction;
}
//——————————————————————————————————————————————————————————————————————————————

Para el vuelo de Levy, aplicaremos el método "Flying", que realizará una operación de "vuelo" para que el agente empuje el vértice de símplex a nuevas ubicaciones en el espacio de búsqueda con una distribución aleatoria que concentrará la probabilidad más próxima de la mejor solución global con una probabilidad decreciente hasta 0 hacia los límites del espacio de búsqueda.

Después de aplicar el método "Flying", estableceremos la operación "reflection" para el agente agent.s.operation para realizar la lógica del algoritmo en iteraciones posteriores como si se hubiera realizado la operación de reflexión.
Luego aplicaremos la función SeInDiSp al valor de Xr para asegurarnos que está dentro del rango válido de rangeMin[c] y rangeMax[c], en incrementos de rangeStep[c]. El resultado se almacenará en agent.s.Xr.c[c].

Así, el método "Flying" realizará una operación de "vuelo" para el agente, cambiando sus coordenadas en función de las coordenadas actuales de la mejor solución global y de los valores generados aleatoriamente. Esto permitirá al agente explorar nuevas regiones del espacio de soluciones y encontrar potencialmente más soluciones óptimas.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Flying (S_Agent &agent, int indW)
{
  for (int c = 0; c < coords; c++)
  {
    double r1 = RNDfromCI (-1.0, 1.0);
    r1 = r1 > 0.5 ? 1.0 : -1.0;
    double r2 = RNDfromCI (1.0, 20.0);
    r2 = pow (r2, -2.0);

    if (r1 > 0.0) Xr = cB [c] + Scale (r2, 0.0, 1.0, 0.0, rangeMax [c] - cB [c], false);
    else          Xr = cB [c] - Scale (r2, 0.0, 1.0, 0.0, cB [c] - rangeMin [c], false);

    //Xr = RNDfromCI (rangeMin [c], rangeMax [c]);

    agent.s.Xr.c [c] = SeInDiSp  (Xr, rangeMin [c], rangeMax [c], rangeStep [c]);
    agent.c      [c] = agent.s.Xr.c [c];
  }

  agent.s.operation = reflection;
}
//——————————————————————————————————————————————————————————————————————————————


3. Resultados de las pruebas

Impresión del algoritmo de Nelder-Mead en el banco de pruebas:

C_AO_NMm:5;1.0;2.0;0.5
=============================
5 Rastrigin's; Func runs 10000 result: 77.96849465506082
Score: 0.96607
25 Rastrigin's; Func runs 10000 result: 61.68192953373487
Score: 0.76427
500 Rastrigin's; Func runs 10000 result: 50.62713783555849
Score: 0.62730
=============================
5 Forest's; Func runs 10000 result: 0.9552378700292385
Score: 0.54033
25 Forest's; Func runs 10000 result: 0.45877475613538293
Score: 0.25951
500 Forest's; Func runs 10000 result: 0.09902427974784639
Score: 0.05601
=============================
5 Megacity's; Func runs 10000 result: 5.6
Score: 0.46667
25 Megacity's; Func runs 10000 result: 2.304
Score: 0.19200
500 Megacity's; Func runs 10000 result: 0.40280000000000005
Score: 0.03357
=============================
All score: 3.90573

Según los resultados del algoritmo, podemos notar una ola de resultados bastante buenos en la función Rastrigin suave.

En la visualización podemos ver signos de degeneración de la población y concentración de agentes en un solo lugar. La situación se salva un poco con el uso del vuelo de Levy, lo cual resulta evidente en los puntos individuales de las coordenadas correspondientes. Las gráficas de convergencia no son muy estables, solo hemos mostrado visualizaciones de las dos primeras pruebas para cada función porque la ejecución de la tercera prueba con 1 000 variables tarda tanto que no es posible grabarla en un GIF.

rastrigin

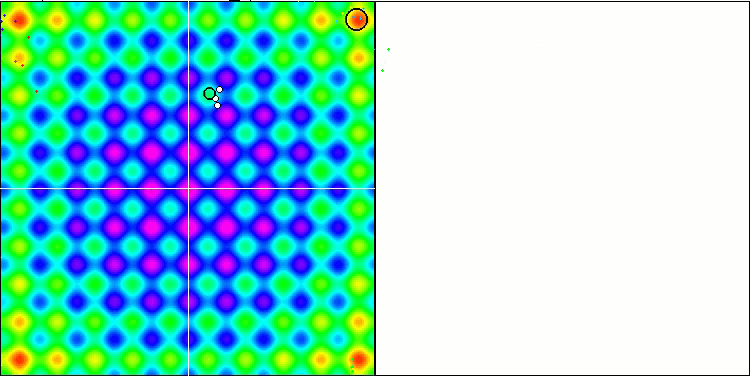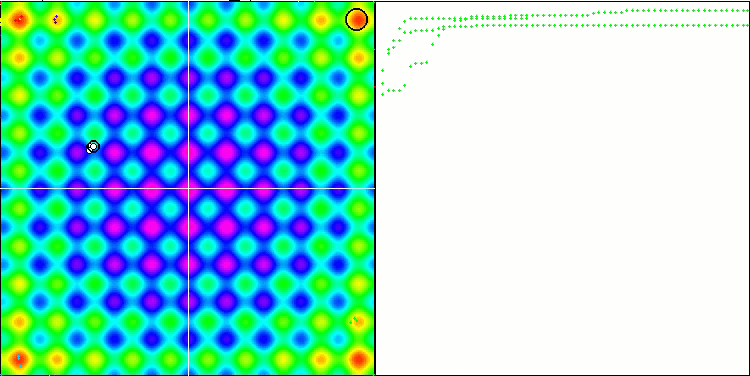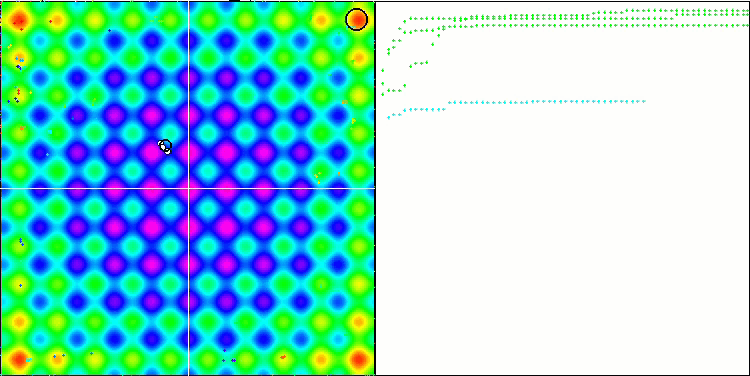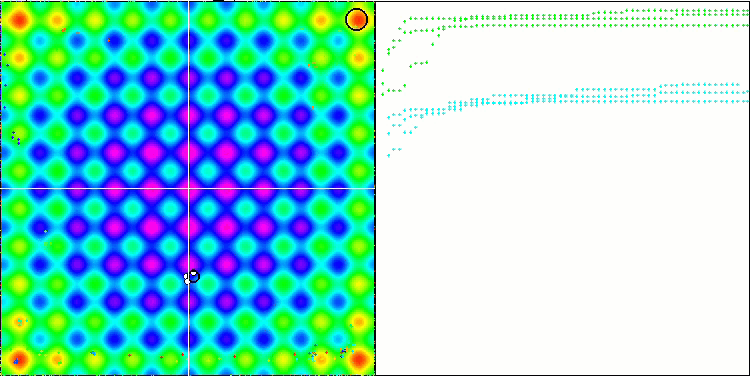
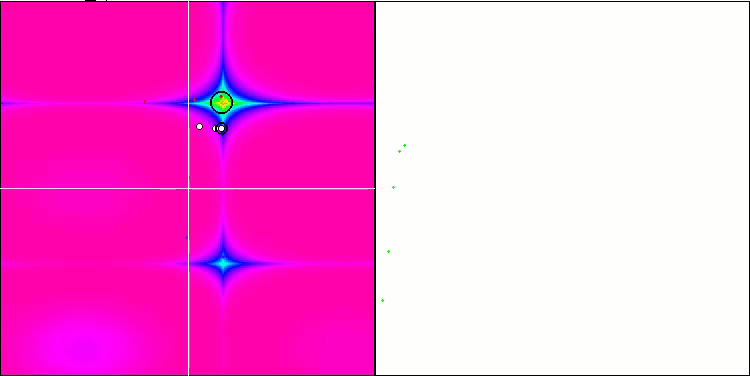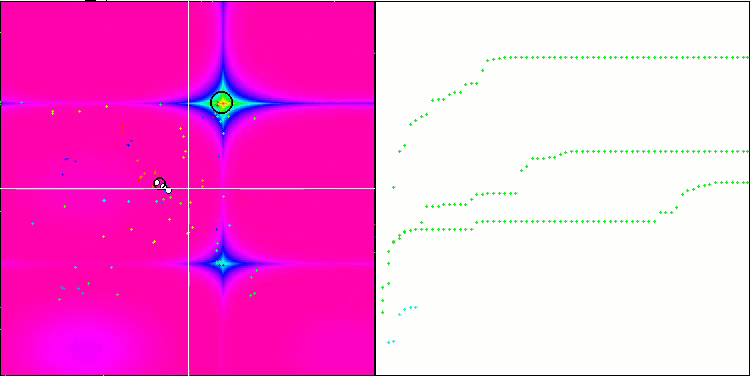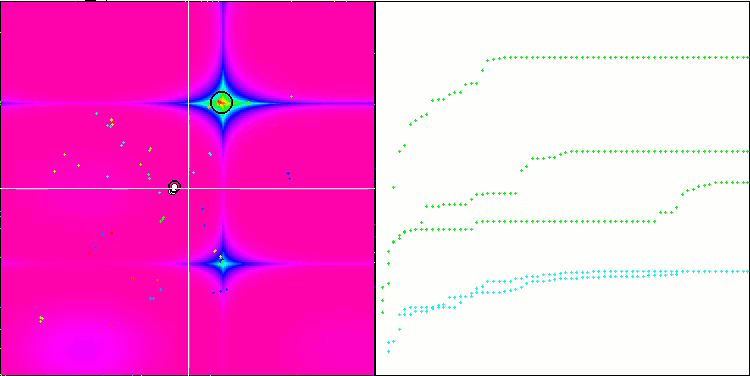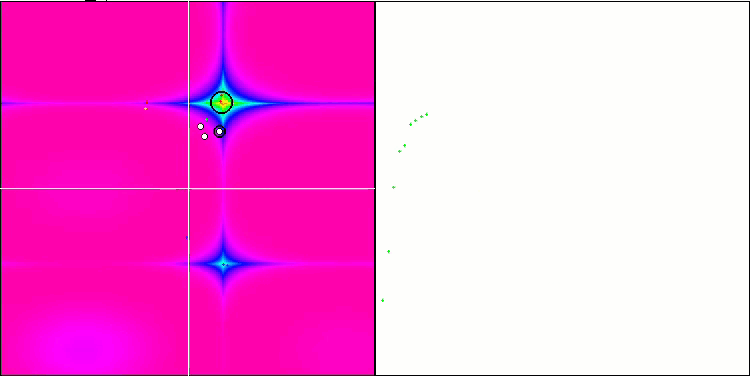
  NMm en la función de prueba Rastrigin.

forest

  NMm en la función de prueba Forest.

megacity

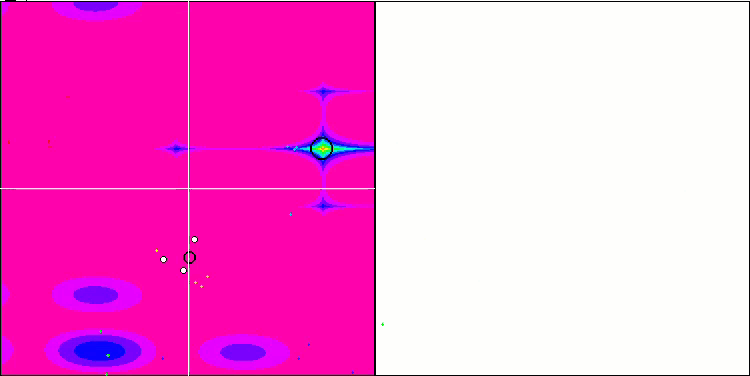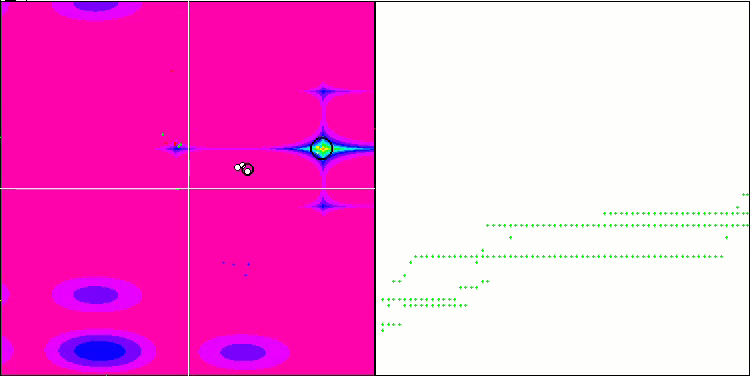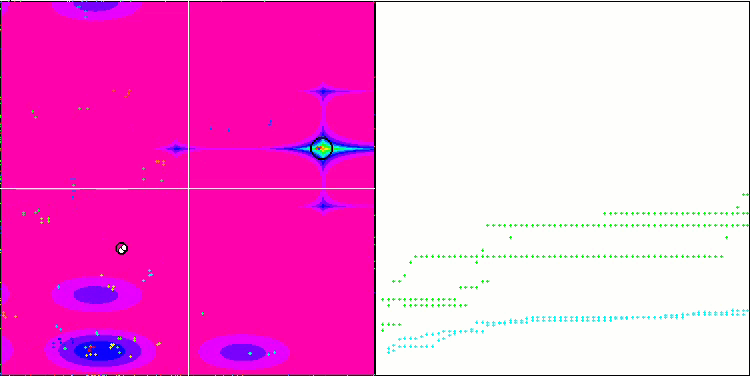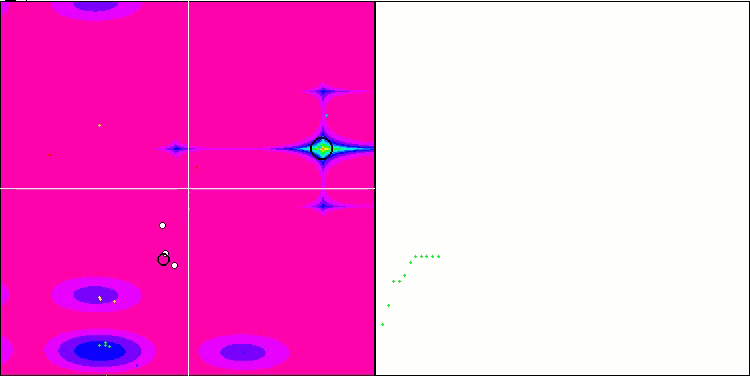
  NMm en la función de prueba Megacity.


El algoritmo del método Nelder-Mead, a pesar de sus numerosos inconvenientes, ha obtenido un honroso 9º puesto.

#

AO

Description

Rastrigin

Rastrigin final

Forest

Forest final

Megacity (discrete)

Megacity final

Final result

10 p (5 F)

50 p (25 F)

1000 p (500 F)

10 p (5 F)

50 p (25 F)

1000 p (500 F)

10 p (5 F)

50 p (25 F)

1000 p (500 F)

1

SDSm

stochastic diffusion search M

0.99809

1.00000

0.69149

2.68958

0.99265

1.00000

1.00000

2.99265

1.00000

1.00000

1.00000

3.00000

100.000

2

SSG

saplings sowing and growing

1.00000

0.92761

0.51630

2.44391

0.72120

0.65201

0.83760

2.21081

0.54782

0.61841

0.99522

2.16146

77.683

3

DE

differential evolution

0.98295

0.89236

0.51375

2.38906

1.00000

0.84602

0.65510

2.50112

0.90000

0.52237

0.12031

1.54268

73.099

4

HS

harmony search

0.99676

0.88385

0.44686

2.32747

0.99148

0.68242

0.37529

2.04919

0.71739

0.71842

0.41338

1.84919

70.623

5

IWO

invasive weed optimization

0.95828

0.62227

0.27647

1.85703

0.70170

0.31972

0.26613

1.28755

0.57391

0.30527

0.33130

1.21048

48.250

6

ACOm

ant colony optimization M

0.34611

0.16683

0.15808

0.67103

0.86147

0.68980

0.64798

2.19925

0.71739

0.63947

0.05579

1.41265

47.387

7

MEC

mind evolutionary computation

0.99270

0.47345

0.21148

1.67763

0.60244

0.28046

0.21324

1.09615

0.66957

0.30000

0.26045

1.23002

44.049

8

SDOm

spiral dynamics optimization M

0.69840

0.52988

0.33168

1.55996

0.59818

0.38766

0.37600

1.36183

0.35653

0.15262

0.25842

0.76758

40.289

9

NMm

Nelder-Mead method M

0.88433

0.48306

0.45945

1.82685

0.46155

0.24379

0.21903

0.92437

0.46088

0.25658

0.16810

0.88555

39.660

10

COAm

cuckoo optimization algorithm M

0.92400

0.43407

0.24120

1.59927

0.57881

0.23477

0.13842

0.95200

0.52174

0.24079

0.17001

0.93254

37.830

11

FAm

firefly algorithm M

0.59825

0.31520

0.15893

1.07239

0.50637

0.29178

0.41704

1.21519

0.24783

0.20526

0.35090

0.80398

33.139

12

ABC

artificial bee colony

0.78170

0.30347

0.19313

1.27829

0.53379

0.14799

0.11177

0.79355

0.40435

0.19474

0.13859

0.73768

29.766

13

BA

bat algorithm

0.40526

0.59145

0.78330

1.78002

0.20664

0.12056

0.21769

0.54488

0.21305

0.07632

0.17288

0.46225

29.499

14

CSS

charged system search

0.56605

0.68683

1.00000

2.25289

0.13961

0.01853

0.13638

0.29452

0.07392

0.00000

0.03465

0.10856

27.930

15

GSA

gravitational search algorithm

0.70167

0.41944

0.00000

1.12111

0.31390

0.25120

0.27812

0.84322

0.42609

0.25525

0.00000

0.68134

27.807

16

BFO

bacterial foraging optimization

0.67203

0.28721

0.10957

1.06881

0.39364

0.18364

0.17298

0.75026

0.37392

0.24211

0.18841

0.80444

27.542

17

EM

electroMagnetism-like algorithm

0.12235

0.42928

0.92752

1.47915

0.00000

0.02413

0.29215

0.31628

0.00000

0.00527

0.10872

0.11399

19.002

18

SFL

shuffled frog-leaping

0.40072

0.22021

0.24624

0.86717

0.19981

0.02861

0.02221

0.25063

0.19565

0.04474

0.06607

0.30646

13.200

19

MA

monkey algorithm

0.33192

0.31029

0.13582

0.77804

0.09927

0.05443

0.07482

0.22852

0.15652

0.03553

0.10669

0.29874

11.777

20

FSS

fish school search

0.46812

0.23502

0.10483

0.80798

0.12730

0.03458

0.05458

0.21647

0.12175

0.03947

0.08244

0.24366

11.332

21

IWDm

intelligent water drops M

0.26459

0.13013

0.07500

0.46972

0.28358

0.05445

0.05112

0.38916

0.22609

0.05659

0.05054

0.33322

10.423

22

PSO

particle swarm optimisation

0.20449

0.07607

0.06641

0.34696

0.18734

0.07233

0.18207

0.44175

0.16956

0.04737

0.01947

0.23641

8.426

23

RND

random

0.16826

0.09038

0.07438

0.33302

0.13381

0.03318

0.03949

0.20648

0.12175

0.03290

0.04898

0.20363

5.054

24

GWO

grey wolf optimizer

0.00000

0.00000

0.02093

0.02093

0.06514

0.00000

0.00000

0.06514

0.23478

0.05789

0.02545

0.31812

1.000


Conclusiones

Si consideramos el peso de los problemas actuales, el algoritmo de Nelder-Mead resulta poco útil, ya que requiere calcular una función de aptitud para cada vértice de símplex en la etapa inicial, lo cual anula su aplicabilidad a los espacios de búsqueda multidimensionales; así, a pesar de los resultados relativamente buenos y su lugar en la tabla de clasificación, no podemos recomendar el uso del algoritmo.

El algoritmo SDS ha sido eliminado de la tabla y solo queda su versión modificada.

rating table

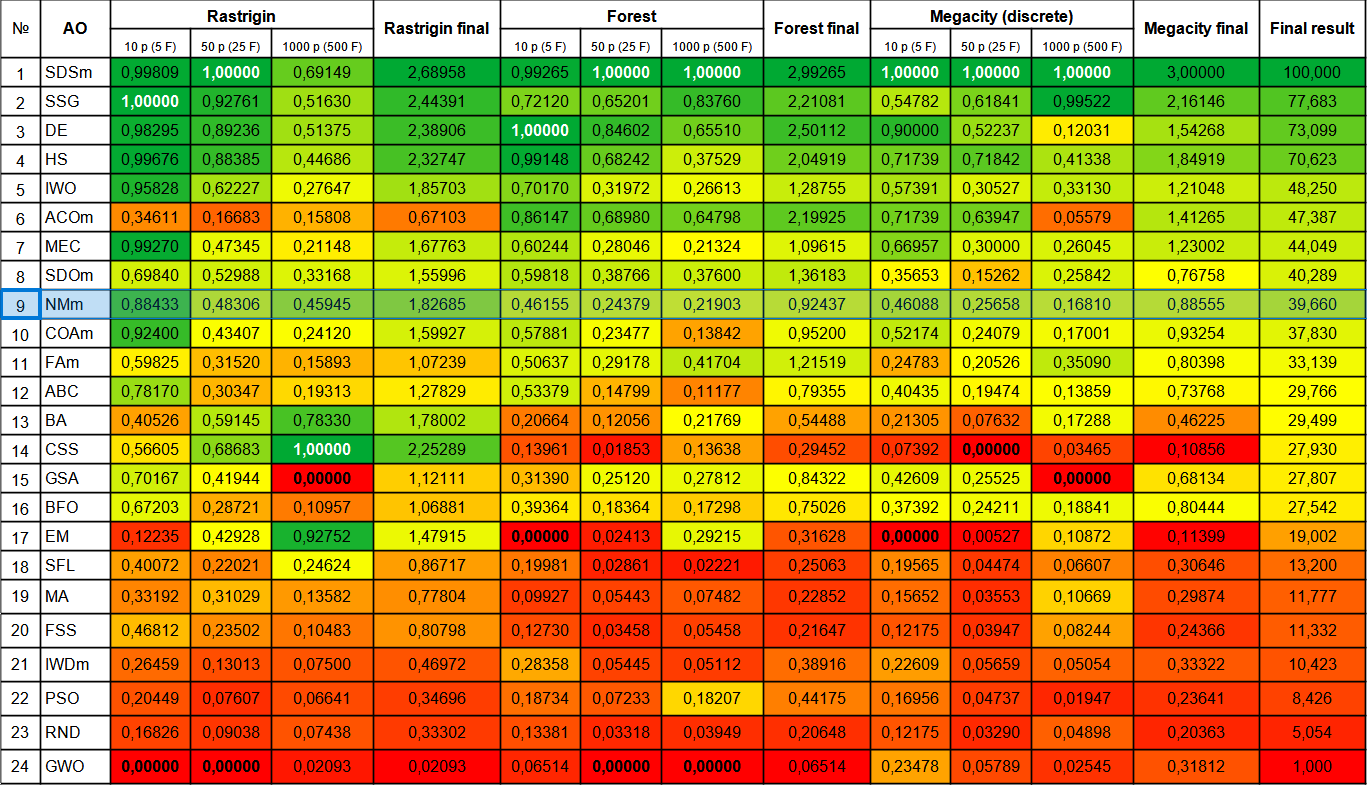
Figura 2. Gradación por colores de los algoritmos según sus respectivas pruebas.

chart

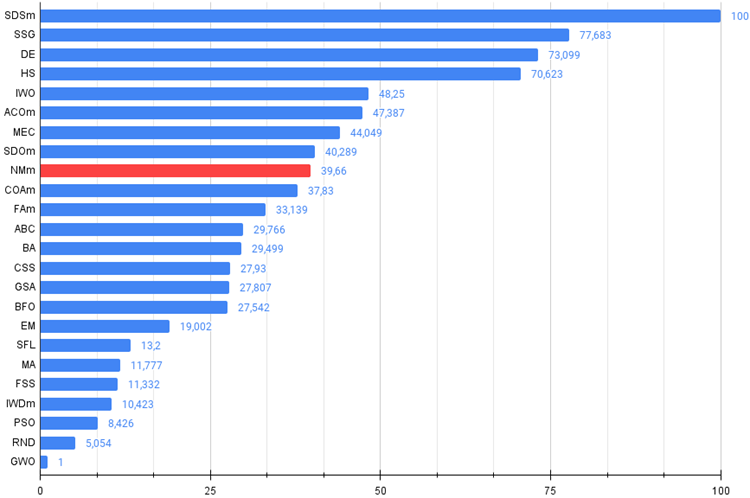
Figura 3. Histograma de los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor,

en el archivo encontrará un script para calcular la tabla de clasificación según la metodología de este artículo).

Ventajas e inconvenientes del algoritmo Nelder-Meade modificado (NMm):

Ventajas:

  1. Posee un número reducido de parámetros externos.
  2. No muestra malos resultados en funciones suaves con pocas variables.

Desventajas:

  1. Difícil implementación.
  2. Difícil de usar con aplicaciones de terceros debido a la necesidad de calcular previamente el ajuste para todos los vértices de símplex.
  3. Baja velocidad de funcionamiento.
  4. Escalabilidad sumamente escasa.
  5. Gran variación en los resultados.
  6. Tendencia a estancarse en los extremos locales.

Tenga en cuenta que los pros y los contras se refieren específicamente a la versión modificada de la búsqueda de símplex, y que la inclusión de la versión normal de NM ni siquiera tiene sentido, debido a sus pésimos resultados.

Adjuntamos al artículo un archivo con las versiones reales actualizadas de los códigos de los algoritmos descritos en los artículos anteriores. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/13805

Archivos adjuntos |
Descargar ZIP
24_The_world_of_AO_NM.zip (421.03 KB)
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores
Características del Wizard MQL5 que debe conocer (Parte 08): Perceptrones Características del Wizard MQL5 que debe conocer (Parte 08): Perceptrones
Los perceptrones, o redes con una sola capa oculta, pueden ser una buena opción para quienes estén familiarizados con los fundamentos del comercio automatizado y quieran sumergirse en las redes neuronales. Paso a paso veremos como se pueden implementar en el ensamblado de clases de señales que forma parte de las clases del Wizard MQL5 para asesores expertos.
Redes neuronales: así de sencillo (Parte 66): Problemática de la exploración en el entrenamiento offline Redes neuronales: así de sencillo (Parte 66): Problemática de la exploración en el entrenamiento offline
El entrenamiento offline del modelo se realiza sobre los datos de una muestra de entrenamiento previamente preparada. Esto nos ofrecerá una serie de ventajas, pero la información sobre el entorno estará muy comprimida con respecto al tamaño de la muestra de entrenamiento, lo que, a su vez, limitará el alcance del estudio. En este artículo, querríamos familiarizarnos con un método que permite llenar la muestra de entrenamiento con los datos más diversos posibles.
Interpretación de modelos: Una comprensión más profunda de los modelos de aprendizaje automático Interpretación de modelos: Una comprensión más profunda de los modelos de aprendizaje automático
El aprendizaje automático es un campo desafiante y gratificante para cualquiera, independientemente de la experiencia que tenga. En este artículo, nos sumergiremos en el funcionamiento interno de los modelos creados, exploraremos el complejo mundo de las funciones, las predicciones y las soluciones eficientes, y comprenderemos claramente la interpretación de los modelos. Asimismo, aprenderemos el arte de hacer concesiones, mejorar las predicciones, clasificar la importancia de los parámetros y tomar decisiones sólidas. Este artículo le ayudará a mejorar el rendimiento de los modelos de aprendizaje automático y a sacar más partido de sus metodologías.
Introducción a MQL5 (Parte 1): Guía del trading algorítmico para principiantes Introducción a MQL5 (Parte 1): Guía del trading algorítmico para principiantes
El presente artículo supone una guía de programación en MQL5 para principiantes que le abrirá la puerta al fascinante mundo del trading algorítmico. Aquí aprenderá los fundamentos de MQL5, el lenguaje de programación para estrategias comerciales en MetaTrader 5, que le guiará en el mundo del trading automatizado. Desde la comprensión de los conceptos básicos hasta los primeros pasos en la programación, este artículo está diseñado para liberar el potencial del trading algorítmico para todos los lectores, incluso para aquellos que no tienen absolutamente ninguna experiencia en programación. Espero que disfrute de este viaje al mundo del trading con MQL5.