Algoritmos de optimización de la población: Algoritmo de búsqueda de sistema cargado (Charged System Search, CSS)

Contenido:

1. Introducción
2. Descripción del algoritmo
3. Resultados de las pruebas

1. Introducción

En física, el espacio que rodea a una carga eléctrica tiene una propiedad conocida como campo eléctrico. Dicho campo ejerce un efecto de fuerza sobre otros objetos cargados eléctricamente. El campo eléctrico que rodea a una carga puntual viene definido por la ley de Coulomb. Coulomb demostró que la fuerza eléctrica entre dos pequeñas esferas cargadas cualesquiera es inversamente proporcional al cuadrado de la distancia entre las partículas, dirigida a lo largo de la línea que las une, y proporcional al producto de las cargas de las dos partículas. Además, la magnitud del campo eléctrico en un punto dentro de una esfera cargada puede obtenerse utilizando la ley de Gauss, que establece que es proporcional a la distancia entre partículas. Usando estos principios, el CSS define una serie de posibles soluciones, que se denominan partículas cargadas. Cada partícula se trata como una esfera cargada (en contraste con el algoritmo electromagnético, o EM, donde la partícula es un punto unidimensional) y puede ejercer efectos eléctricos sobre otros agentes (partículas cargadas).

Por otra parte, la segunda ley de Newton explica que la aceleración de un objeto es directamente proporcional a la fuerza total que actúa sobre dicho objeto. De esta forma, la fuerza eléctrica resultante que actúa sobre la partícula provoca su aceleración. Según la mecánica newtoniana, la posición de una partícula, considerada como una masa puntual de tamaño infinitesimal, resulta completamente conocida en cualquier instante de tiempo si su posición, velocidad y aceleración en el espacio son conocidas en el instante de tiempo anterior. El CSS utiliza las leyes del movimiento de la mecánica newtoniana para determinar la posición de las partículas. La aplicación de estas leyes en teoría debería ofrecer un buen equilibrio entre la exploración y la explotación del algoritmo.

El algoritmo Charged System Search (CSS) fue presentado por primera vez por A. Kaveh y S. Talatahari en 2010.

La optimización supone una parte importante e integral de la resolución de problemas de modelización matemática y el aprendizaje automático. Los algoritmos metaheurísticos son una clase eficiente y popular de métodos de optimización. Una metaheurística puede entenderse como un algoritmo que realiza una búsqueda estocástica de posibles soluciones a un problema, aproximándose a las óptimas, hasta que se cumpla una determinada condición o se alcance un determinado número de iteraciones.

En la literatura científica, se considera que las metaheurísticas combinan heurísticas básicas en esquemas algorítmicos de nivel superior que permiten una exploración más eficaz de los espacios de búsqueda y la toma de decisiones. Esto suele necesitar menos trabajo que desarrollar nuevas heurísticas especializadas. El reto consiste en adaptar esquemas metaheurísticos generales para resolver problemas de optimización difíciles. Además, una aplicación eficaz de la metaheurística puede garantizar que se encuentre una solución casi óptima en un tiempo aceptable. Diversos enfoques para comprender las metaheurísticas nos permiten formular algunas propiedades fundamentales que las caracterizan. En los últimos años, ha aumentado el uso de metaheurísticas y se han realizado esfuerzos para aumentar la potencia de los algoritmos y reducir el tiempo de optimización.

2. Descripción del algoritmo

El algoritmo de búsqueda de sistema cargado (CSS) funciona con partículas cargadas en forma de esfera; el tamaño mínimo de la esfera viene determinado por un parámetro externo (es una fracción de la distancia euclidiana máxima posible a lo largo de todas las coordenadas del espacio de búsqueda), cuando las partículas se acercan a una distancia inferior al radio de la esfera, actúan sobre ellas fuerzas repulsivas, mientras que la dirección de las fuerzas entre las partículas está influida por su diferencia de carga mutua. El algoritmo considera los valores de las coordenadas de la iteración anterior, y esto modela la velocidad de las partículas. La aceleración, un componente del movimiento de las partículas, está influida por las cargas y su distancia mutua.

Teniendo en cuenta lo anterior, vamos a escribir los pasos del pseudocódigo del algoritmo:

1. Inicializamos las partículas con una posición inicial aleatoria en el espacio de búsqueda, y establecemos una posición aleatoria en el espacio para la iteración anterior (suponiendo que haya habido una iteración anterior).

2. Calculamos el valor de la función de aptitud.

3. Calculamos la siguiente posición de las partículas usando las fórmulas.

4. Determinamos el mejor y el peor valor de la función de aptitud entre todas las partículas.

5. Repita los pasos desde el paso número 2 hasta que se cumpla la condición de parada.

Vamos a desglosar las fórmulas para calcular el movimiento mutuo de las partículas. La característica básica de una partícula cargada es su carga:

q = (φp - φw) / (φb - φw)

donde:

• q - carga actual de la partícula
• φp - valor de la función de aptitud de la partícula
• φb - mejor valor de la función de aptitud entre todas las partículas
• φw - peor valor de la función de aptitud entre todas las partículas

Para determinar la distancia entre las partículas usaremos la fórmula:

r(i,j) = (|Xi - Xj|) / (|(Xi - Xj) * 0.5 - Xb|)

donde:

• || - distancia euclidiana
• r(i,j) - distancia entre las partículas i y j
• Xi y Xj - coordenadas correspondientes de las partículas i y j
• Xb - coordenada correspondiente a la mejor posición encontrada para todas las iteraciones.

Aquí, aparentemente, la idea de los autores era tener en cuenta la posición de las partículas en relación con las mejores coordenadas globales. Esto podría haber sido una buena idea, pero mis experimentos sugieren que la mejor solución para este algoritmo sería utilizar solo el cálculo del numerador en la fórmula.

Al igual que en el algoritmo EM, las fuerzas de interacción de EM pueden ser atractivas o repulsivas. Vamos a denotar el signo de la dirección de la variable c. Para tener en cuenta la dirección de las fuerzas, aplicaremos la expresión de la condición que vemos a continuación:

c = -1 si φi < φj, en caso contrario c = 1

donde:

• c - signo de la dirección de las fuerzas de interacción
• φi y φj - valores de la función de aptitud de las partículas i y j

El signo de la dirección de la fuerza puede interpretarse de forma que una partícula con un valor menor de la función de aptitud repele, mientras que una partícula con un valor mayor atrae.

Puesto que hemos acordado que, a diferencia del algoritmo EM, la partícula es una esfera cuyo radio es superior a 0 (el parámetro externo del algoritmo), podemos representar la fuerza sobre la partícula usando la coordenada colineal correspondiente (en nuestro algoritmo, la fuerza total sobre la partícula será un conjunto de vectores) como una fórmula:

F = qi * Q * c * (Xj - Xi)

donde:

• F - fuerza ejercida sobre la partícula
• qi - partícula para la que consideramos la fuerza de influencia sobre ella
• Q - componente que considera la posición mutua de las dos partículas consideradas según la penetración de sus esferas entre sí, la fórmula de Q:

Q = ((qj * r(i,j) * b1) / a^3) + (qj * b2) / r(i,j)^2

donde:

• qj - carga de la partícula que actúa sobre la considerada
• b1 y b2 para "activar/desactivar" el término correspondiente de la expresión, con b1 = 0 y b2 = 1 cuando r >= el radio de la partícula, y b1 = 1 y b2 = 0 si es menor.

Por último, podemos calcular la nueva coordenada de movimiento de la partícula usando la fórmula:

Xn = X + λ1 * U * V + λ2 * U * coordinatesNumber * (F / qi)

donde:

• Xn - nueva coordenada
• λ1 - coeficiente de peso (parámetro externo), determina el grado de influencia del segundo término - velocidad
• λ2 - coeficiente de peso (parámetro externo), determina el grado de influencia del tercer término - aceleración
• U - número aleatorio en el intervalo [0;1].
• V - diferencia entre la coordenada en la iteración actual y en la anterior
• coordinatesNumber - número de coordenadas, en la fórmula original este "coeficiente" no existe, lo introduje porque, con el aumento de la dimensionalidad del espacio de búsqueda, se hace necesario aumentar el coeficiente λ2 (por eso se ha introducido, para evitar el efecto de "congelación" de las partículas).

Los valores relativos de λ1 y λ2 determinan el equilibrio entre diversificación e intensificación de la búsqueda. Aumentar los valores del parámetro λ1 aumenta la influencia de la posición previa de la partícula, potenciando las propiedades exploratorias del algoritmo. Valores grandes de λ2 provocan una fuerte influencia de las fuerzas atractivas y pueden causar una convergencia prematura del algoritmo. Por el contrario, valores pequeños de esta magnitud ralentizan la velocidad de convergencia del algoritmo, ofreciendo una exploración más amplia de la zona de búsqueda.

Vamos a comenzar a analizar el código del algoritmo CSS. El agente de búsqueda del algoritmo es una partícula, que se representa cómodamente como una estructura S_Particle.

La estructura de la partícula incluye los siguientes campos:

• -c: array de coordenadas de las partículas. Este array contiene las coordenadas actuales de la partícula en el espacio.
• -cPrev: array de coordenadas anteriores de la partícula. Este array contiene las coordenadas anteriores de la partícula en el espacio.
• -cNew: array de las nuevas coordenadas de la partícula. Este array contiene las nuevas coordenadas de la partícula que se utilizarán en la siguiente iteración del algoritmo.
• -q: carga de la partícula. Este valor representa la carga asignada a la partícula dada. La carga solo puede tomar valores positivos distintos de 0.
• -f: valor de la función de aptitud de la partícula.

La presencia de una serie de nuevas coordenadas en la estructura de la partícula y su carga ha permitido simplificar el algoritmo a la vista de sus peculiaridades, aunque estas magnitudes podrían ser (y lógicamente a primera vista) mantenidas como variables de uso común por todas las partículas. 

//——————————————————————————————————————————————————————————————————————————————
struct S_Particle
{
  double c     [];  //coordinates
  double cPrev [];  //coordinates
  double cNew  [];  //coordinates
  double q;         //particle charge
  double f;         //fitness
};
//——————————————————————————————————————————————————————————————————————————————

Ahora declararemos la clase C_AO_CSS, que incluye:

Propiedades de clase:

• - p: array de partículas
• - rangeMax: array con los valores máximos del rango de búsqueda para cada coordenada
• - rangeMin: array con los valores mínimos del rango de búsqueda para cada coordenada
• - rangeStep: array con el tamaño de los pasos de búsqueda para cada coordenada
• - cB: array con las mejores coordenadas encontradas
• - fB: valor de la función de aptitud para las mejores coordenadas
• - fW: valor de la función de aptitud para las peores coordenadas

Métodos de clase:

• - Init: inicializa los parámetros del algoritmo (número de coordenadas, número de partículas, tamaño del radio, coeficientes de velocidad y aceleración).
• - Moving: ejecuta el movimiento de partículas
• - Revision: actualiza las mejores coordenadas

Propiedades privadas de la clase:

• - coordinatesNumber: número de coordenadas
• - particlesNumber: número de partículas
• - radius: tamaño del radio
• - speedCo: coeficiente de velocidad
• - accelCo: coeficiente de aceleración
• - F: vector de fuerza
• - revision: bandera sobre la necesidad de revisión

Métodos privados de clase:

• - SeInDiSp: calcula un nuevo valor de coordenadas en un intervalo especificado con un tamaño de paso dado.
• - RNDfromCI: genera un número aleatorio dentro de un intervalo dado

//——————————————————————————————————————————————————————————————————————————————
class C_AO_CSS
{
  //----------------------------------------------------------------------------
  public: S_Particle p     []; //particles
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates
  public: double fW;           //FF of the worst coordinates

  public: void Init (const int    coordinatesNumberP, //coordinates number
                     const int    particlesNumberP,   //particles number
                     const double radiusSizeP,        //radius size
                     const double speedCoP,           //speed coefficient
                     const double accelCoP);          //acceleration coefficient

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber; //coordinates number
  private: int    particlesNumber;   //particles number
  private: double radius;            //radius size
  private: double speedCo;           //speed coefficient
  private: double accelCo;           //acceleration coefficient
  private: double F       [];        //force vector
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

El método C_AO_CSS inicializa los parámetros del objeto de clase. Toma como argumentos los valores del número de coordenadas, el número de partículas, el tamaño del radio, el coeficiente de velocidad y el coeficiente de aceleración.

Dentro del método tiene lugar el reinicio del generador de números aleatorios, el establecimiento de valores iniciales para las variables fB y la revisión. A continuación, los valores de los argumentos son asignados a las variables correspondientes del objeto.
A continuación, los arrays rangeMax, rangeMin, rangeStep, F, p y cB se redimensionan según el número de coordenadas y partículas.
A continuación, el ciclo redimensiona los arrays para cada partícula y establece el valor inicial de la variable f para cada partícula.
Al final del método, el array cB se redimensiona en función del número de coordenadas.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CSS::Init (const int    coordinatesNumberP, //coordinates number
                     const int    particlesNumberP,   //particles number
                     const double radiusSizeP,        //radius size
                     const double speedCoP,           //speed coefficient
                     const double accelCoP)           //acceleration coefficient
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber = coordinatesNumberP;
  particlesNumber   = particlesNumberP;
  radius            = radiusSizeP;
  speedCo           = speedCoP;
  accelCo           = accelCoP;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);
  ArrayResize (F,         coordinatesNumber);

  ArrayResize (p,  particlesNumber);

  for (int i = 0; i < particlesNumber; i++)
  {
    ArrayResize (p [i].c,     coordinatesNumber);
    ArrayResize (p [i].cPrev, coordinatesNumber);
    ArrayResize (p [i].cNew,  coordinatesNumber);
    p [i].f  = -DBL_MAX;
  }

  ArrayResize (cB, coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

La lógica básica del movimiento de partículas (agentes de búsqueda) se implementa en el método Moving ().

En la primera iteración deberemos inicializar los valores iniciales de las coordenadas de las partículas con un número aleatorio en el rango comprendido entre rangeMin y rangeMax, y tomar el valor de la adaptabilidad de las partículas como igual al valor `-DBL_MAX`.

El parámetro externo RadiusSize_P define el tamaño de la partícula en partes de la distancia euclidiana máxima posible sobre todas las coordenadas, que será la raíz de la suma de cuadrados de las diferencias entre los valores máximo y mínimo permitidos para cada coordenada.
Al final del código, estableceremos la variable `revision` en `true`.

//----------------------------------------------------------------------------
if (!revision)
{
  fB = -DBL_MAX;

  for (int obj = 0; obj < particlesNumber; obj++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      p [obj].c     [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      p [obj].cPrev [c] = RNDfromCI (rangeMin [c], rangeMax [c]);

      p [obj].c     [c] = SeInDiSp (p [obj].c     [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      p [obj].cPrev [c] = SeInDiSp (p [obj].cPrev [c], rangeMin [c], rangeMax [c], rangeStep [c]);

      p [obj].f         = -DBL_MAX;
    }
  }

  double r = 0.0;
  double t = 0.0;

  for (int c = 0; c < coordinatesNumber; c++)
  {
    t = rangeMax [c] - rangeMin [c];
    r += t * t;
  }

  radius *= sqrt (r);
  revision = true;
}

El resto del código del método Moving () se ejecuta en la segunda iteración y siguientes y se encarga de desplazar las partículas en el espacio de búsqueda.

En primer lugar, se calcula la diferencia entre los valores de la función de aptitud fB y fW (para las mejores coordenadas encontradas en todas las iteraciones y las peores coordenadas entre las partículas de la iteración actual) y se guarda en la variable de diferencia. Si la diferencia es 0,0, se le asignará un valor de 1,0.

A continuación se ejecuta un ciclo en el que se calcula un nuevo valor para cada partícula. Para cada partícula i se calculará un nuevo valor de carga q.

A continuación, se declaran e inicializan las variables summ1, summ2, q, e, c, b1, b2, X, Q, U, V, t1, t2 para utilizarse en las fórmulas anteriores.

En el ciclo, para cada partícula se calcula la fuerza total F que actúa desde las demás partículas de la población. Para cada partícula i, se ejecuta un ciclo en el que se calculan el sumatorio1 y el sumatorio2. Después se calcula la distancia r entre las partículas i y j. Si r es 0,0, se le asignará un valor de 0,01 para evitar la división por 0. A continuación se calculan los valores de b1 y b2 según el valor de r y radius. Luego se calcula el valor de la dirección de la fuerza c en función de los valores de adaptación de las dos partículas consideradas. Después se calcula el valor de Q. A continuación, para cada coordenada k se calcula el valor de la fuerza F[k].

Teniendo los valores del vector de fuerzas que actúan sobre la partícula, podremos calcular los valores de las nuevas coordenadas para su movimiento. Acto seguido, se ejecuta un ciclo en el que se actualizan los valores de las coordenadas anteriores y las coordenadas actuales de la partícula i.

El código conserva partes de las fórmulas originales como elementos comentados para mostrar cómo era para los autores del CSS.

double difference = fB - fW;
if (difference == 0.0) difference = 1.0;

for (int i = 0; i < particlesNumber; i++)
{
  p [i].q = ((p [i].f - fW) / difference) + 0.1;
}

double summ1 = 0.0;
double summ2 = 0.0;
double q     = 0.1;
double e     = 0.001;
double c     = 0.0;
double b1    = 0.0;
double b2    = 0.0;
double X     = 0.0;
double Q     = 0.0;
double U     = 0.0;
double V     = 0.0;
double t1    = 0.0;
double t2    = 0.0;

for (int i = 0; i < particlesNumber && !IsStopped (); i++)
{
  ArrayInitialize (F, 0.0);

for (int j = 0; j < particlesNumber && !IsStopped (); j++)
{
  if (i == j) continue;

  summ1 = 0.0;
  summ2 = 0.0;

  for (int k = 0; k < coordinatesNumber && !IsStopped (); k++)
  {
    t1 = p [i].c [k] - p [j].c [k];
    summ1 += t1 * t1;

    //t2 = t1 * 0.5 - cB [k];
    //summ2 += t2 * t2;
  }

  //r = sqrt (summ1) / (sqrt (summ2) + e);
  r = sqrt (summ1);
        
  if (r == 0.0) r = 0.01;

  if (r >= radius)
  {
    b1 = 0.0;
    b2 = 1.0;
  }
  else
  {
    b1 = 1.0;
    b2 = 0.0;
  }

  c = p [i].f < p [j].f ? -1.0 : 1.0;

  q = p [j].q;

  Q = ((q * r * b1 / (radius * radius * radius)) + (q * b2 / (r * r))) * c;

  for (int k = 0; k < coordinatesNumber && !IsStopped (); k++)
  {
    F [k] += /*p [i].q */ Q * (p [j].c [k] - p [i].c [k]);
  }
}

  for (int k = 0; k < coordinatesNumber && !IsStopped (); k++)
  {
    V = p [i].c [k] - p [i].cPrev [k];
    U = RNDfromCI (0.0, 1.0);

    X = p [i].c [k] + speedCo * U * V + accelCo * U * coordinatesNumber * (F [k] / p [i].q);
        
    p [i].cNew [k] = SeInDiSp (X, rangeMin [k], rangeMax [k], rangeStep [k]);
  }
}

for (int i = 0; i < particlesNumber && !IsStopped (); i++)
{
  for (int k = 0; k < coordinatesNumber && !IsStopped (); k++)
  {
    p [i].cPrev [k] = p [i].c [k];
    p [i].c [k] = p [i].cNew [k];
  }
}

Y, en último lugar, sigue el método Revision ().
Al principio del método, se asigna a la variable fW el valor máximo de tipo double (DBL_MAX), para poder determinar más tarde la peor partícula con el valor mínimo de la función de aptitud.
A continuación, se realiza un ciclo a través de todas las partículas del sistema. Para cada partícula, se ejecutan los siguientes pasos:
- Si el valor f de la partícula actual es mayor que el valor fB (la mejor función de adaptabilidad de todas las partículas), el valor fB se actualizará con el valor f de la partícula actual, mientras que al array cB (mejor posición) se copiará a partir de la posición de la partícula actual.
- Si el valor de f de la partícula actual es menor que el valor de fW (la función de aptitud más pequeña de todas las partículas), entonces el valor de fW se actualizará con el valor de f de la partícula actual.

Así, este código encuentra las funciones de mejor y peor ajuste entre todas las partículas y actualiza los valores correspondientes.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CSS::Revision ()
{
  fW  = DBL_MAX;

  for (int i = 0; i < particlesNumber; i++)
  {
    if (p [i].f > fB)
    {
      fB = p [i].f;
      ArrayCopy (cB, p [i].c, 0, 0, WHOLE_ARRAY);
    }

    if (p [i].f < fW)
    {
      fW = p [i].f;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Resultados de las pruebas

Impresión del funcionamiento del algoritmo de búsqueda por parte del sistema de cargas en el banco de pruebas:

C_AO_CSS:50;0.1;0.7;0.01
=============================
5 Rastrigin's; Func runs 10000 result: 70.43726076935499
Score: 0.87276
25 Rastrigin's; Func runs 10000 result: 68.88569793414477
Score: 0.85353
500 Rastrigin's; Func runs 10000 result: 66.01225385184436
Score: 0.81793
=============================
5 Forest's; Func runs 10000 result: 0.4891262437640296
Score: 0.27667
25 Forest's; Func runs 10000 result: 0.1494549763925046
Score: 0.08454
500 Forest's; Func runs 10000 result: 0.07829232143185726
Score: 0.04429
=============================
5 Megacity's; Func runs 10000 result: 2.04
Score: 0.17000
25 Megacity's; Func runs 10000 result: 0.744
Score: 0.06200
500 Megacity's; Func runs 10000 result: 0.26880000000000004
Score: 0.02240
=============================
All score: 3.20412

La impresión de los resultados del algoritmo muestra el bajo resultado global. Llama la atención el hecho de que en la función Rastrigin para 10, 50 y 1000 variables los resultados del valor de la función de aptitud no son muy diferentes. Veamos a continuación lo que esto significa.

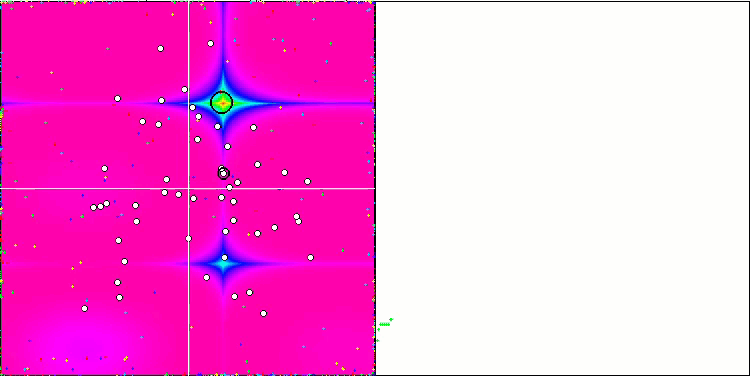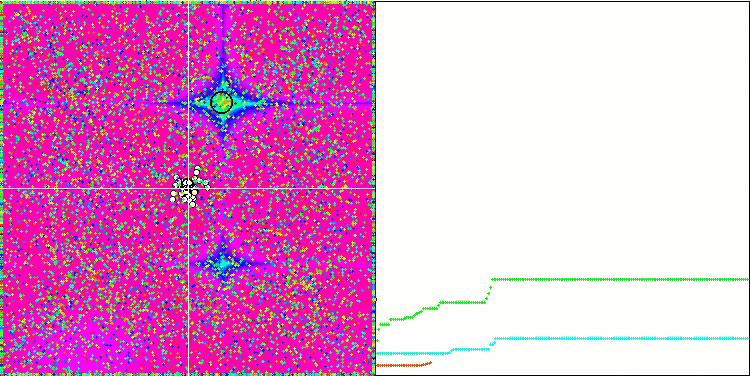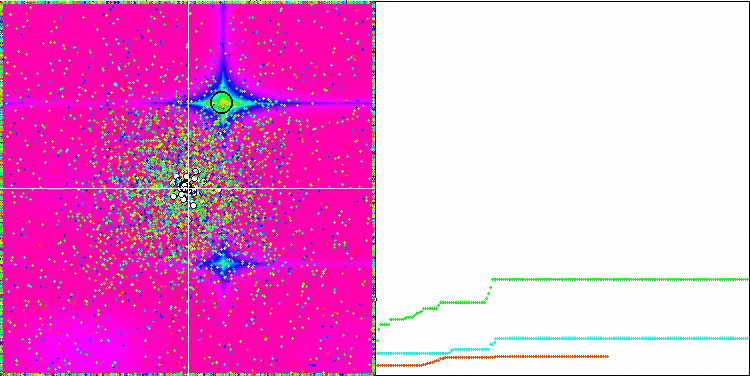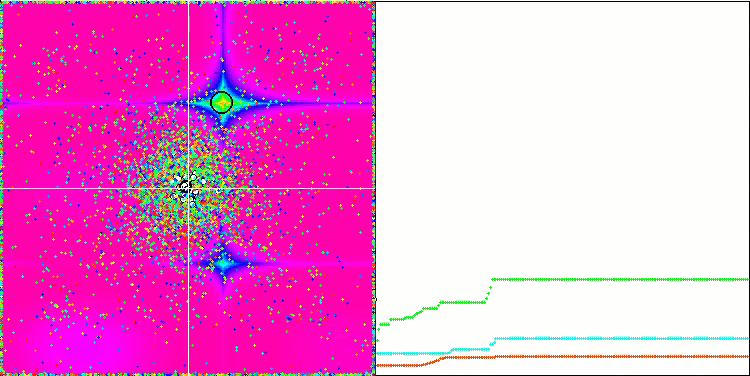
La visualización de la función de prueba Rastrigin muestra una separación claramente distinguible de la población de partículas por extremos locales significativos, lo cual significa que las regiones locales están bien definidas, pero este comportamiento no se observa en las funciones Forest y Megacity, en las que la población se comporta como una nube informe. Las largas partes horizontales del gráfico de convergencia indican la tendencia del algoritmo a atascarse en los extremos locales, aunque la excelente escalabilidad en la función Rastrigin suave compensa en cierto modo este enorme inconveniente del algoritmo.

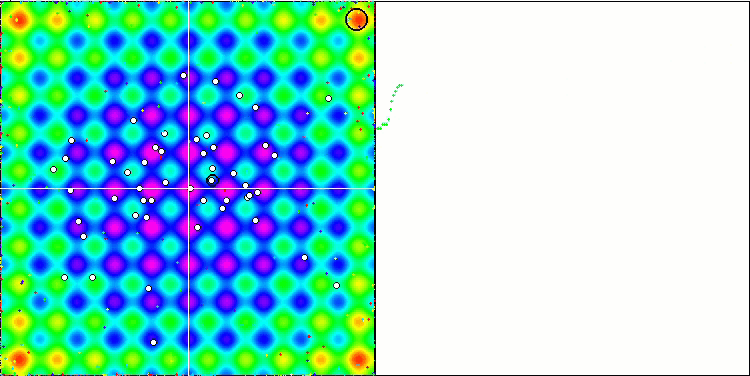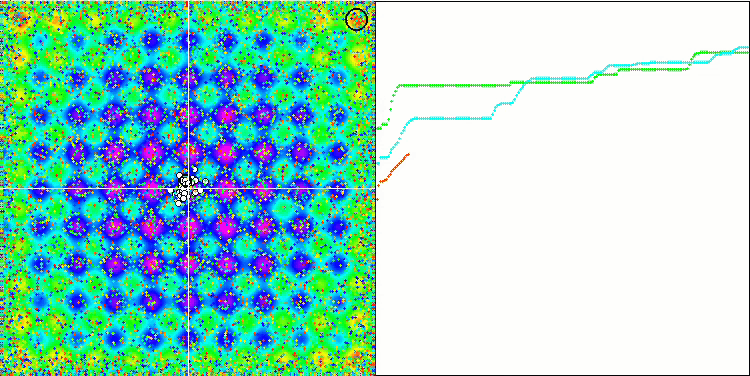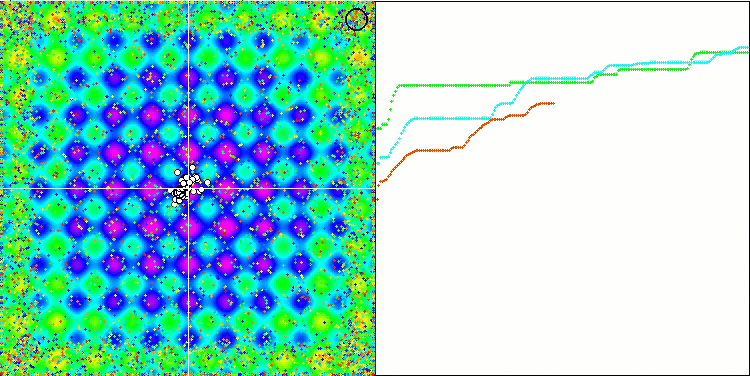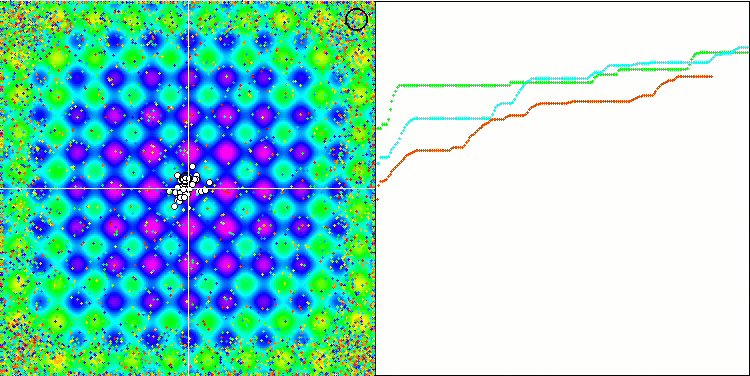
  CSS en la función de prueba Rastrigin.

  CSS en la función de prueba Forest.

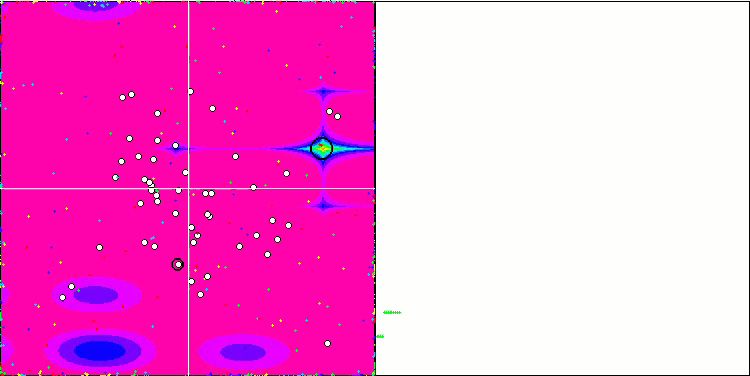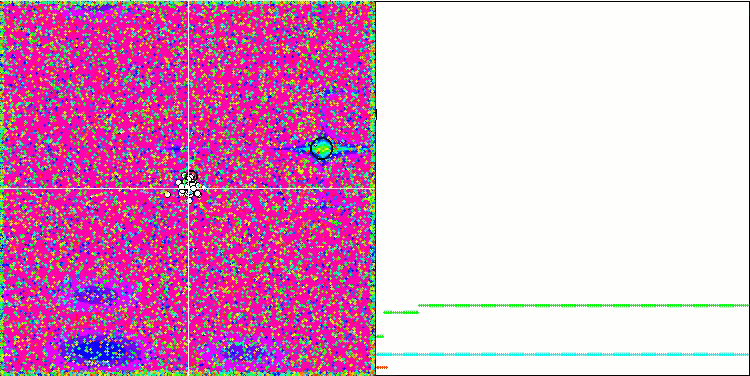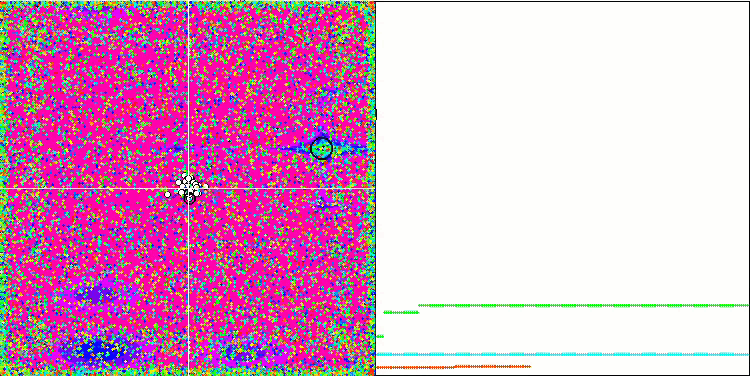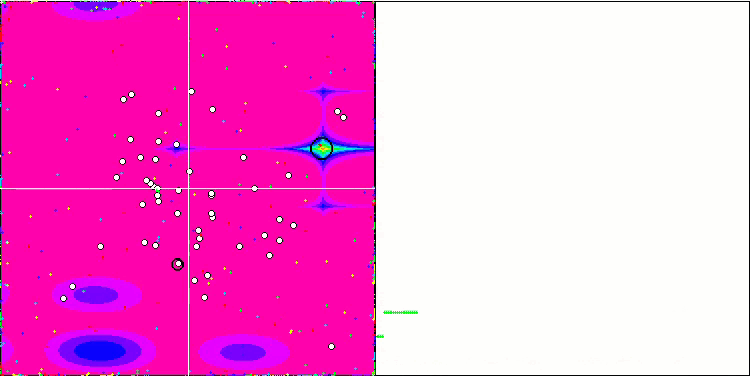
  CSS en la función de prueba Megacity.

Las pruebas del algoritmo CSS han identificado un nuevo líder en la optimización de funciones suaves, el anterior líder en la función Rastrigin era también un algoritmo inspirado en la naturaleza inanimada: la búsqueda electromagnética (EM), esta vez el nuevo récord supera al anterior en casi un 10%. Por desgracia, en la función Forest con un extremo global agudo y en la función discreta Megacity, el algoritmo muestra algunos de los peores resultados. Gracias al impresionante resultado en Rastrigin con 1000 variables, el algoritmo ha logrado situarse en el puesto 13 de 20 en cuanto a puntuación total. Para el número de 10000 ejecuciones asignadas por el reglamento de pruebas, el algoritmo CSS no ha podido acercarse al extremo global más del 90% (véanse las impresiones del funcionamiento en el banco de pruebas indicadas anteriormente).   

№	AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	SDS	stochastic Diffusion Search	0,99737	1,00000	0,58904	2,58641	0,96893	1,00000	0,95092	2,91985	1,00000	1,00000	0,72149	2,72149	100,000
2	SSG	saplings sowing and growing	1,00000	0,95313	0,51630	2,46944	0,72740	0,69680	1,00000	2,42421	0,69612	0,65918	1,00000	2,35531	87,506
3	HS	harmony search	0,99676	0,90817	0,44686	2,35179	1,00000	0,72930	0,44806	2,17736	0,91159	0,76578	0,41537	2,09274	79,501
4	ACOm	ant colony optimization M	0,34611	0,17142	0,15808	0,67562	0,86888	0,73719	0,77362	2,37968	0,91159	0,68163	0,05606	1,64929	55,026
5	IWO	invasive weed optimization	0,95828	0,63939	0,27647	1,87415	0,70773	0,34168	0,31773	1,36714	0,72927	0,32539	0,33289	1,38756	54,060
6	MEC	mind evolutionary computation	0,99270	0,48648	0,21148	1,69066	0,60762	0,29973	0,25459	1,16194	0,85083	0,31978	0,26170	1,43231	49,669
7	COAm	cuckoo optimization algorithm M	0,92400	0,44601	0,24120	1,61121	0,58378	0,25090	0,16526	0,99994	0,66298	0,25666	0,17083	1,09047	42,223
8	FAm	firefly algorithm M	0,59825	0,32387	0,15893	1,08106	0,51073	0,31182	0,49790	1,32045	0,31491	0,21880	0,35258	0,88629	36,941
9	ABC	artificial bee colony	0,78170	0,31182	0,19313	1,28664	0,53837	0,15816	0,13344	0,82998	0,51381	0,20758	0,13926	0,86064	32,977
10	BA	bat algorithm	0,40526	0,60773	0,78330	1,79629	0,20841	0,12884	0,25989	0,59714	0,27073	0,08135	0,17371	0,52579	32,236
11	GSA	gravitational search algorithm	0,70167	0,43098	0,00000	1,13265	0,31660	0,26845	0,33204	0,91710	0,54144	0,27208	0,00000	0,81352	31,522
12	BFO	bacterial foraging optimization	0,67203	0,29511	0,10957	1,07671	0,39702	0,19626	0,20652	0,79980	0,47514	0,25807	0,18932	0,92253	30,702
13	CSS	charged system search	0,56605	0,70573	1,00000	2,27178	0,14081	0,01980	0,16282	0,32343	0,09393	0,00000	0,03481	0,12874	29,743
14	EM	electroMagnetism-like algorithm	0,12235	0,44109	0,92752	1,49096	0,00000	0,02578	0,34880	0,37458	0,00000	0,00562	0,10924	0,11486	20,252
15	SFL	shuffled frog-leaping	0,40072	0,22627	0,24624	0,87323	0,20153	0,03057	0,02652	0,25862	0,24862	0,04769	0,06639	0,36270	14,050
16	MA	monkey algorithm	0,33192	0,31883	0,13582	0,78658	0,10012	0,05817	0,08932	0,24762	0,19889	0,03787	0,10720	0,34396	12,564
17	FSS	fish school search	0,46812	0,24149	0,10483	0,81445	0,12840	0,03696	0,06516	0,23052	0,15471	0,04208	0,08283	0,27961	11,880
18	PSO	particle swarm optimisation	0,20449	0,07816	0,06641	0,34906	0,18895	0,07730	0,21738	0,48363	0,21547	0,05049	0,01957	0,28553	9,246
19	RND	random	0,16826	0,09287	0,07438	0,33551	0,13496	0,03546	0,04715	0,21757	0,15471	0,03507	0,04922	0,23900	5,083
20	GWO	grey wolf optimizer	0,00000	0,00000	0,02093	0,02093	0,06570	0,00000	0,00000	0,06570	0,29834	0,06170	0,02557	0,38561	1,000

Conclusiones

Hemos tenido que hacer muchos experimentos y ediciones de código para que las partículas se movieran por el campo sin que se "pegaran" y "congelaran"; los autores del algoritmo no tuvieron en cuenta la influencia del número de parámetros optimizados en la calidad de la optimización (a medida que aumentaba la dimensionalidad del problema, la convergencia se deterioraba desproporcionadamente rápido), la adición del número de coordenadas a la fórmula ha permitido aumentar la influencia de la aceleración y mejorar las características del CSS (sin estos cambios el algoritmo mostraba muy malos resultados). Las leyes establecidas del movimiento de las partículas resultan demasiado caprichosas para cualquier cambio con fines investigativos y, por tanto, dificultan los intentos de mejorar el rendimiento de este interesante algoritmo de optimización.

El algoritmo de búsqueda de sistema cargado es un método eficaz para optimizar funciones suaves utilizando una nube de partículas cargadas mutuamente unidas por fuerzas de Coulomb. A la hora de usar este interesante algoritmo, debemos considerar su escasa idoneidad para problemas con un campo discreto del espacio de búsqueda, pero para funciones suaves con muchas variables es el mejor algoritmo de optimización de los considerados anteriormente. El CSS puede utilizarse en todas las áreas de optimización con un gran número de variables, no necesita ni información de gradiente ni continuidad del espacio de búsqueda.

Para visualizar mejor las ventajas e inconvenientes de cada algoritmo en comparación con los demás, la tabla anterior puede representarse utilizando la escala de colores de la figura 1. La clasificación por colores de la tabla ofrece una visión más clara de la posibilidad de aplicar cada algoritmo individual, según el problema de optimización específico. Así, podemos ver que por el momento no se ha encontrado ningún algoritmo absolutamente universal para la mejor solución de cualquier problema (quizá en futuros estudios seamos capaces de encontrar uno).

Por ejemplo, si consideramos el algoritmo de la primera línea de la clasificación SDS, no es el mejor en algunos problemas de prueba (las funciones suaves con muchas variables le vienen dadas por la media de la tabla). Si tomamos el algoritmo ACOm, sus resultados individuales están muy por debajo de la media de la tabla (resuelve sorprendentemente mal las funciones suaves), pero Forest y Megacity discreta se manejan muy bien (se diseñó originalmente para resolver problemas discretos, como el problema del viajante), aunque la escalabilidad deja mucho que desear.

El último algoritmo CSS presentado es un claro ejemplo de que vemos su lado más fuerte en la función Rastrigin con 1000 variables (quizás será una buena elección para entrenar redes neuronales con muchos parámetros), es decir, el mejor resultado entre todo el número de algoritmos de optimización analizados anteriormente, aunque en cuanto a los resultados totales no parece el mejor de la tabla, por lo que es muy importante elegir el algoritmo adecuado dependiendo de las especificidades del problema.

Las pruebas a gran escala de algoritmos de optimización con una amplia variedad de estrategias de búsqueda han revelado un hecho inesperado: la estrategia puede resultar incluso peor que si aplicamos una simple búsqueda aleatoria con selección del mejor resultado: RND ocupa el segundo lugar por la cola en lugar del último esperado, GWO ha sido peor que la búsqueda aleatoria con la excepción de Megacity discreta con 10 parámetros.

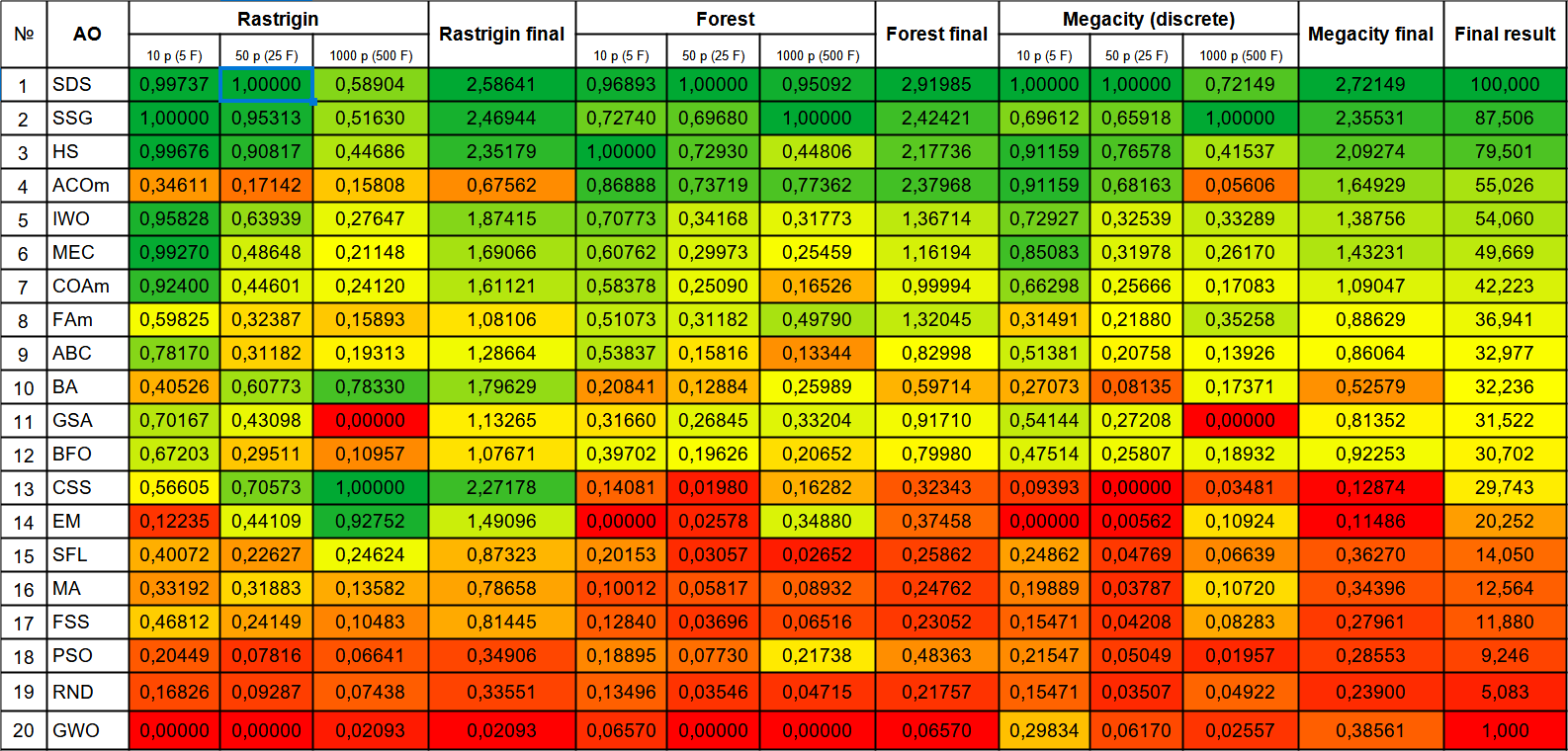
Figura 1. Gradación por colores de los algoritmos según sus respectivas pruebas.

Histograma de los resultados de los algoritmos de prueba en la figura 2 (en una escala de 0 a 100, cuanto más mejor, en el archivo hay un script para calcular la tabla de clasificación según la metodología de este artículo):

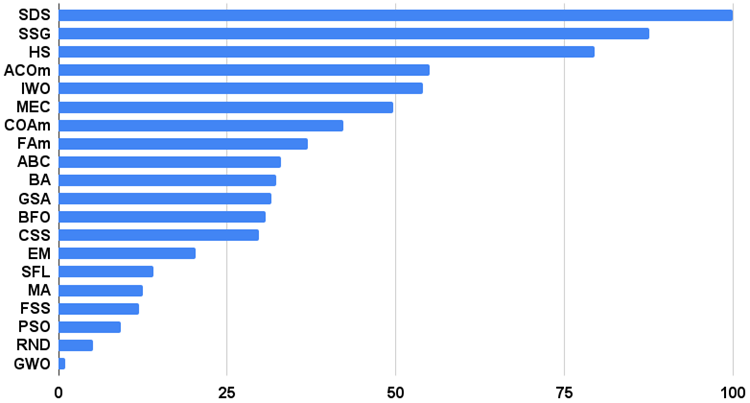
Figura 2. Histograma con los resultados finales de los algoritmos de prueba.

Ventajas e inconvenientes del algoritmo de búsqueda de sistema cargado (CSS):

Ventajas:
1. Alta escalabilidad en funciones suaves.
2. Posee un número reducido de parámetros externos.

Desventajas:
1. Muestra malos resultados en las funciones discretas.
2. Baja convergencia.
3. Tendencia a estancarse en los extremos locales.

Adjunto a cada artículo encontrará un archivo con versiones actualizadas de los códigos de los algoritmos descritos en artículos anteriores. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.