Algoritmos de optimización de la población: Algoritmo de salto de rana aleatorio (Shuffled Frog-Leaping, SFL)

MetaTrader 5 — Ejemplos | 22 febrero 2024, 07:58

318

Andrey Dik

Contenido:

1. Introducción
2. Descripción del algoritmo
3. Resultados de las pruebas

1. Introducción

El algoritmo de salto de rana aleatorio (SFL) fue propuesto por M. Eusuff y otros en 2003. Este algoritmo combina los principios del algoritmo memético y el algoritmo de enjambre de partículas, y su desarrollo se inspiró en el comportamiento de un grupo de ranas en busca de comida.

El algoritmo SFL se desarrolló originalmente como un método metaheurístico para resolver problemas de optimización combinatoria, y se basa en el uso de funciones matemáticas y en la búsqueda heurística informada.

El algoritmo SFL consta de varias poblaciones virtuales de ranas que interactúan entre sí: estas se denominan memeplexes. Las ranas virtuales desempeñan el papel de huéspedes o portadoras de memes, donde un meme representa una unidad de evolución cultural. Cada memeplex se busca localmente de forma independiente usando un método similar a la optimización por enjambre de partículas, pero haciendo hincapié en la búsqueda local.

Para permitir la investigación global, las ranas virtuales se barajan y reorganizan periódicamente en nuevos memeplexes usando un método similar al algoritmo de evolución compleja barajada. Además, se generarán ranas virtuales aleatorias y se sustituirán en la población para permitir la generación aleatoria de información mejorada.

El algoritmo SFL es un método eficaz para resolver problemas de optimización complejos y consigue soluciones óptimas en diversas aplicaciones. En este artículo repasaremos los principios básicos y la aplicación de este algoritmo, así como sus ventajas y desventajas.

2. Descripción del algoritmo

La memética es un enfoque de los modelos de transferencia de información evolutiva basado en el concepto de memes. Los memes, que son análogos de los genes, sirven como unidades de información cultural difundidas entre las personas a través de la imitación, el aprendizaje y otros medios. C.R. Dawkins introdujo el concepto de meme, así como los fundamentos de la memética, en 1976. Los memes pueden transmitirse verticalmente: partiendo de antecesores, padres, cuidadores, libros, artefactos culturales, etc. La transmisión horizontal de memes también es posible, y se realiza de persona a persona y de cultura a cultura. Aunque los memes representan información pura, su funcionamiento provoca cambios significativos en el comportamiento humano.

Los algoritmos meméticos (algoritmos M) se definen como algoritmos híbridos de optimización de búsqueda metaheurística basados en poblaciones y basados en el concepto de meme y el principio neodarwinista de evolución. En el contexto de los algoritmos M, un meme es una implementación de un algoritmo de optimización local que mejora las soluciones actuales en cada iteración o después de cierto número de iteraciones. Los algoritmos M pueden considerarse una hibridación de uno de los algoritmos de búsqueda global basados en poblaciones y uno o varios algoritmos de optimización local clásicos o basados en poblaciones. Los algoritmos M fueron originalmente propuestos como una opción para mejorar la eficacia de los algoritmos genéticos.

La eficacia de los algoritmos M depende en gran medida de los valores de sus parámetros libres: varios estudios han demostrado que la elección de los memes utilizados suponen una gran influencia en el rendimiento de estos algoritmos. Por ello, este problema ocupa uno de los lugares principales en los trabajos dedicados a los algoritmos M.

Los memes representan una de las ideas revolucionarias que conllevan la similitud entre la evolución de los genes y la evolución de la cultura humana. Dawkins denominó meme a una unidad de intercambio cultural, el análogo de un gen en la cultura. Un meme puede ser un gesto, una palabra o una idea: cualquier unidad de información cultural que pueda transmitirse de persona a persona mediante el aprendizaje por imitación supone un meme.

A diferencia de los algoritmos genéticos, los algoritmos meméticos imitan el proceso de evolución cultural. El enfoque desarrollado por Moscato usa una analogía con la evolución de los memes. El algoritmo memético consta de los siguientes pasos: búsqueda local, cooperación, competición y criterio de finalización de la búsqueda. La memética abarca una amplia clase de algoritmos unidos por una idea común: la inclusión del aprendizaje individual de los individuos en un algoritmo genético y el uso de información sobre la estructura del espacio de posibles soluciones. El problema del equilibrio entre la búsqueda poblacional y local puede considerarse un problema general sobre el equilibrio entre la exploración extensiva e intensiva del espacio de búsqueda.

En términos generales, un algoritmo memético incluye los siguientes componentes:

1. Búsqueda local. Para su aplicación, pueden utilizarse el algoritmo de recocido simulado y los algoritmos de elevación.
2. Cooperación. El intercambio de información entre individuos puede realizarse usando un procedimiento similar a la aplicación del operador de cruce de dos puntos en los algoritmos genéticos.
3. Competición. El procedimiento de selección resulta similar al de los algoritmos genéticos y suele consistir en seleccionar los individuos mejor adaptados de una población y eliminar los menos adaptados.
4. Criterios de finalización de la búsqueda. En los algoritmos meméticos, podemos incluir una estimación de la diversidad de los individuos, además de contar el número de iteraciones y estimar la mejora del resultado.

Los algoritmos meméticos suponen una amplia clase de algoritmos unidos por la idea común del entrenamiento individual por individuos y la explotación de la información sobre la estructura del espacio de posibles soluciones.

Los memes, como los genes, son replicadores, es decir, objetos capaces de autorreplicarse. Para los memes, la supervivencia y la reproducción dependen de la existencia de un medio que propague el meme. Los memes pueden modificarse para formar nuevos memes e iniciar una lucha por los recursos: las mentes de las personas.

Los memes suelen agruparse en complejos, o memeplexes, para reforzar su posición en la competencia por los portadores. Los memplexes son análogos a los conjuntos simbióticos de genes que componen los códigos genéticos de los organismos biológicos: un ejemplo de memeplex sería la religión. Los memplex ejercen un profundo impacto en la formación del comportamiento individual y social.

Vamos a pasar directamente al algoritmo SFL. La idea básica del algoritmo consiste en dividir toda la población de ranas con un líder global G en memes, es decir, grupos, cada uno de los cuales tiene un líder L (figura 1).

frogs1

Figura 1. Población de ranas con un líder global (G) dividida en memes con su líder local (L).

Dentro de cada meme, las ranas tenderán a acercarse al líder local. El liderazgo se actualizará si la posición de una de las ranas mejora. Los memes no se compartirán en el espacio de búsqueda y podrán tener solapamientos. Así, una rana en el territorio de un meme bien podría pertenecer a otro. Esto crea un entorno dinámico en el que las ranas podrán moverse espacialmente de un meme a otro, dependiendo de los cambios en sus posiciones en el espacio de búsqueda.

Analizaremos un problema de optimización condicional global en el que la función de aptitud estará sujeta a maximización. El algoritmo SFL incluirá los siguientes pasos básicos.

1.0 Inicialización del algoritmo
1.1 Creación de una población inicial de ranas con coordenadas aleatorias.
1.2 Determinación de la aptitud de cada rana.
1.3 Creación de memeplexes (subpoblaciones), distribución de las ranas en memeplexes.

2.0 Ciclo de búsqueda de la solución óptima
2.1 Para cada memeplex:
    2.1.1 Identificación de la mejor rana.
    2.1.2 Desplazamiento de las ranas restantes hacia la mejor rana del memeplex.
2.2 Si el traslado de la rana no ha mejorado su aptitud:
    2.2.1 Desplazamiento hacia la mejor rana a nivel global.
    2.2.2 Si esto tampoco ha mejorado la aptitud, desplazamiento de la rana a un lugar aleatorio del campo.

3.0 Medición de la adaptación de las ranas
3.1 Mide la aptitud de cada rana de la población.
3.2 Actualización de la información sobre la mejor rana en cada memeplex y en el conjunto de la población.

4.0 Determinación de la mejor rana global y la actualización de memeplexes
4.1 Determinamos la mejor rana global de la población.
4.2 Si se trata del último ciclo:
    4.2.1 Ponemos a cero del contador de ciclos de memplex.
    4.2.2 Generamos índices aleatorios para las ranas.
    4.2.3 Copiamos las ranas en memeplexes utilizando los nuevos índices.
    4.2.4 Identificamos la mejor rana de cada memeplex.
    4.2.5 Restablecemos la adaptación de la rana y el paso.
4.3 Si no es el último ciclo:
    4.3.1 Copiamos la aptitud y las coordenadas de las ranas de la población en las ranas de memeplex correspondientes.
    4.3.2 Identificamos la mejor rana de cada memeplex.
    4.3.3 Determinamos la dirección del siguiente salto de cada rana en función de su aptitud.

Así, la base del algoritmo SFL es una combinación de la búsqueda local dentro de cada memeplex y la búsqueda global mediante el intercambio de información sobre las posiciones de los mejores agentes de los memeplexes.
Este algoritmo supone una modificación del algoritmo SFL, en el que en la fase de búsqueda local el agente no se moverá exactamente en la dirección del mejor agente del memeplex correspondiente, sino en alguna dirección perturbada aleatoriamente. Se conocen hibridaciones tanto secuenciales como paralelas del algoritmo con muchos algoritmos poblacionales, como el algoritmo del sistema inmune artificial.

frog2

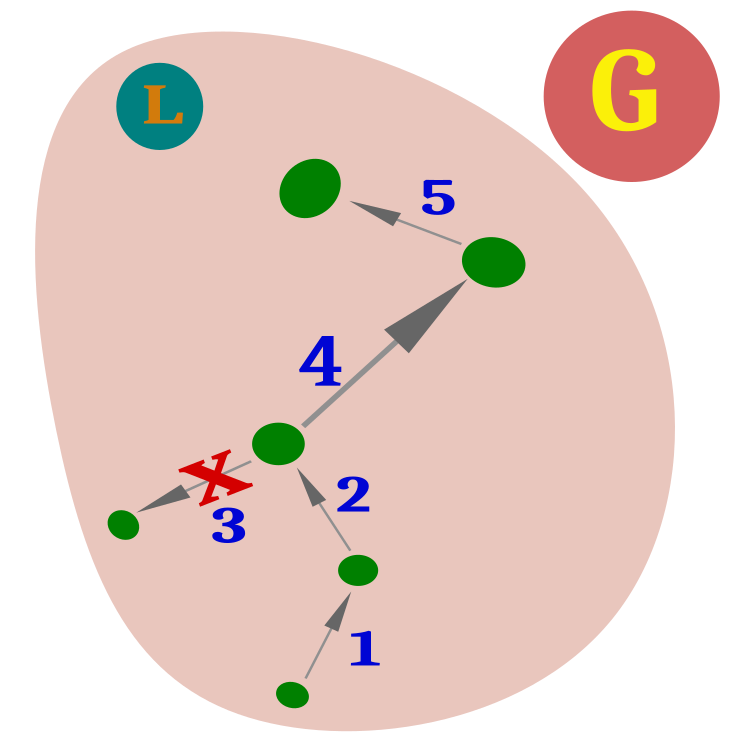
Figura 2. Salto de las ranas. Si el desplazamiento anterior no ha tenido éxito, el siguiente salto se realizará desde el mismo lugar.

La unidad lógica del algoritmo de optimización SFL es una rana que puede describirse mediante la estructura S_Frog, que representará un agente en el espacio de búsqueda.

La estructura S_Frog contendrá los siguientes campos:

c - array de coordenadas de la posición actual de la rana.
cPrev - array de coordenadas de la posición anterior de la rana.
f - valor de la función de aptitud para la posición actual de la rana.
fPrev - valor de la función de aptitud para la posición anterior de la rana.
frogStep - número del paso en el que se encuentra la rana.

//——————————————————————————————————————————————————————————————————————————————
struct S_Frog
{
  void Init (int coords)
  {
    ArrayResize (c,     coords);
    ArrayResize (cPrev, coords);
    f        = -DBL_MAX;
    fPrev    = -DBL_MAX;
    frogStep = 0;
  }
  double c     []; //coordinates
  double cPrev []; //previous coordinates
  double f;        //fitness
  double fPrev;    //previous fitness
  int    frogStep; //frog step
};
//——————————————————————————————————————————————————————————————————————————————

La estructura S_Memeplex describe el memeplex en el algoritmo. Contendrá los siguientes campos:

frogs - conjunto de ranas que componen el memplex.
fBest - mejor valor de la función de aptitud entre todas las ranas del memeplex.
cBest - array de coordenadas correspondientes al mejor valor de la función de aptitud en el memeplex.

//——————————————————————————————————————————————————————————————————————————————
struct S_Memeplex
{
  S_Frog frogs [];
  double fBest;     //best fitness
  double cBest [];  //best coordinates
};
//——————————————————————————————————————————————————————————————————————————————

La clase C_AO_SFL ofrece métodos para inicializar el algoritmo, desplazar las ranas y revisar la población. También contiene métodos auxiliares para convertir valores y generar números aleatorios.

Vamos a escribir una clase de algoritmo SFL que incluya los campos:

cB - array que almacena las mejores coordenadas (best coordinates);
fB - variable que almacena el valor de la función de aptitud para las mejores coordenadas;
frogs - array que almacena todas las ranas de la población;
mems - array que almacena los memeplexes (grupos de ranas);
rangeMax - array que almacena los valores máximos de cada coordenada de búsqueda;
rangeMin - array que almacena los valores mínimos de cada coordenada de búsqueda;
rangeStep - array que almacena los pasos de búsqueda para cada coordenada.

Métodos de clase abiertos:

Init - método de inicialización de los parámetros del algoritmo, admite los siguientes parámetros:
coordinatesNumberP - número de coordenadas de búsqueda;
populationSizeP - tamaño de la población (número de ranas);
numbMemsP - número de memeplexes (grupos de ranas);
numbCyclesP - número de ciclos en el memeplex;
frogStepsToLocalMaxP - número de pasos de la rana hasta el máximo local;
movConstantP - constante de movimiento (paso de búsqueda) de las ranas.

Moving - método que implementa el desplazamiento de las ranas en el espacio de búsqueda.
Revision - método que implementa la revisión de la población de ranas y actualiza las mejores coordenadas.
SeInDiSp - método auxiliar que implementa la conversión de un valor de un rango a otro con un paso especificado.
RNDfromCI - método auxiliar que genera un número aleatorio dentro de un intervalo dado.

Descripción de los campos privados de la clase:

coordinatesNumber - número de coordenadas de búsqueda;
frogsNumber- número de ranas en la población;
numbMems - número de memeplexes (grupos de ranas);
numbCycles - número de ciclos en el memeplex;
frogStepsToLocalMax - número de pasos de rana hasta el máximo local;
movConstant - constante de movimiento (paso de búsqueda) de las ranas;
memsFrogs - número de ranas en cada memeplex;
numbCyclesCNT - contador de ciclos;
vect - array que almacena un vector;
indexes - array que almacena los índices;
revision- bandera que indica la necesidad de revisar la población.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SFL
{
  //----------------------------------------------------------------------------
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates
  public: S_Frog frogs     []; //all frogs
  public: S_Memeplex mems  []; //memeplexes

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search


  public: void Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    numbMemsP,            //number of memeplexes
                     const int    numbCyclesP,          //number of cycles in the memeplex
                     const int    frogStepsToLocalMaxP, //frog steps to the local maximum
                     const double movConstantP);        //movement step (0.0 .. 1.0)

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber;   //coordinates number
  private: int    frogsNumber;         //frogs number
  private: int    numbMems;            //number of memeplexes
  private: int    numbCycles;          //number of cycles in the memeplex
  private: int    frogStepsToLocalMax; //frog steps to the local maximum
  private: double movConstant;         //movement step (0.0 .. 1.0)
  private: int    memsFrogs;           //number of frogs in the memplex
  private: int    numbCyclesCNT;       //cycle counter

  private: double vect    [];          //vector
  private: int    indexes [];          //indexes
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

Para inicializar el algoritmo, utilizaremos el método de inicialización Init, que tiene varios parámetros:

coordinatesNumberP - número de coordenadas
populationSizeP - tamaño de la población
numbMemsP - número de memeplexes
numbCyclesP - número de ciclos en el memeplex
frogStepsToLocalMaxP - número de pasos de la rana hasta el máximo local
movConstantP - paso de desplazamiento (de 0,0 a 1,0)

El método primero reiniciará el generador de números aleatorios y establecerá el valor inicial de la variable fB (-DBL_MAX) y revision (false).
A continuación, el método creará los arrays rangeMax, rangeMin, rangeStep, vect, indexes, cB, frogs y mems con los tamaños deseados.
El método inicializa cada rana en el array frogs y cada rana en cada memplex en el array mems utilizando el método Init, transmitiendo el número de coordenadas.
A continuación, el método establece el valor inicial de la variable fBest de cada memeplex en DBL_MAX y crea el array cBest para cada memeplex con el tamaño deseado.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SFL::Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    numbMemsP,            //number of memeplexes
                     const int    numbCyclesP,          //number of cycles in the memeplex
                     const int    frogStepsToLocalMaxP, //frog steps to the local maximum
                     const double movConstantP)         //movement step (0.0 .. 1.0)
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber   = coordinatesNumberP;
  frogsNumber         = populationSizeP;
  numbMems            = numbMemsP;
  numbCycles          = numbCyclesP;
  frogStepsToLocalMax = frogStepsToLocalMaxP;
  movConstant         = movConstantP;
  memsFrogs           = frogsNumber / numbMems;

  numbCyclesCNT       = 0;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);
  ArrayResize (vect,      coordinatesNumber);
  ArrayResize (indexes,   frogsNumber);

  ArrayResize (cB, coordinatesNumber);

  ArrayResize (frogs, frogsNumber);
  for (int i = 0; i < frogsNumber; i++)
  {
    frogs [i].Init (coordinatesNumber);
  }

  ArrayResize (mems, numbMems);
  for (int i = 0; i < numbMems; i++)
  {
    ArrayResize (mems [i].frogs, memsFrogs);
    for (int frgs = 0; frgs < memsFrogs; frgs++)
    {
      mems [i].frogs [frgs].Init (coordinatesNumber);
    }

    mems [i].fBest = -DBL_MAX;
    ArrayResize (mems [i].cBest, coordinatesNumber);
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método Moving está diseñado para desplazar las ranas por el espacio de búsqueda. El método es bastante amplio, así que lo dividiremos en partes.

Al principio del código, se comprobará el valor de la variable revision. Si es false, se ejecutará el siguiente bloque de código:

- Se fijará el valor inicial de la variable fB, que representa la mejor estimación de la función. En este caso se le asignará el valor -DBL_MAX (infinito negativo).
- Se iniciará un ciclo en el que se inicializará cada rana. Para cada rana:
- Se iniciará un ciclo en cada coordenada c.
- Se generará un valor aleatorio para la coordenada c utilizando la función RNDfromCI, que retornará un número aleatorio dentro del rango especificado.
- El valor de la coordenada c se llevará al intervalo mediante la función SeInDiSp, que permite desplazar el valor dentro del intervalo en un paso determinado.
- El valor de la función f para la rana se establecerá en -DBL_MAX.
- El valor de la función fPrev anterior para la rana se establecerá en -DBL_MAX.
- frogStep se fijará en 0.

- Se iniciará un ciclo en cada coordenada c.
- Se calculará el valor de vect[c], que es el producto de la diferencia entre los valores máximo y mínimo del rango por movConstante.
- La variable revision se establecerá en true para indicar que se ha realizado la inicialización.
- A la variable numbCyclesCNT se le asignará el valor 0.

Así, este código inicializará las ranas, establecerá los valores iniciales de la función y otros parámetros, y calculará el valor vect[c] para cada coordenada c.

if (!revision)
{
  fB = -DBL_MAX;

  for (int frgs = 0; frgs < frogsNumber; frgs++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      frogs [frgs].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      frogs [frgs].c [c] = SeInDiSp (frogs [frgs].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      frogs [frgs].f        = -DBL_MAX;
      frogs [frgs].fPrev    = -DBL_MAX;
      frogs [frgs].frogStep = 0;
    }
  }

  for (int c = 0; c < coordinatesNumber; c++)
  {
    vect [c] = (rangeMax [c] - rangeMin [c]) * movConstant;
  }

  revision      = true;
  numbCyclesCNT = 0;
}

Si el indicador revision es true, significará que el algoritmo ha entrado en la fase de desplazamiento de la rana. Ya hemos visto qué son las variables de método, así que no nos detendremos en ellas. Esta parte del código implementará el salto de rana según el paso individual para cada rana. En el primer paso la rana saltará hacia el líder local, el intento contará si la posición de la rana ha mejorado, de lo contrario la cuenta de pasos aumentará. Es decir, se asignará un número fijo de intentos para los saltos hacia el líder local en función de los parámetros externos del algoritmo.

La rana líder utilizará un principio de desplazamiento diferente al de todas las demás del memeplex. El líder simplemente saltará en una dirección aleatoria en una pequeña vecindad de su posición.

A diferencia del líder, todas las demás ranas saltarán hacia el líder según la siguiente fórmula:

coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c] * ((mems [m].cBest [c] - mems [m].frogs [frgs].cPrev [c]) / eDistance);

por la fórmula podemos ver que la nueva coordenada de la rana se obtendrá desplazándose hacia el líder en la distancia entre ambos, normalizada por la distancia euclídea para todas las coordenadas, con un componente aleatorio rnd introducido.

else
{
  int cnt = 0;
  double eDistance = 0.0; //euclidean distance
  double coordDiff = 0.0; //the difference in coordinates

  for  (int m = 0; m < numbMems; m++)
  {
    for (int frgs = 0; frgs < memsFrogs; frgs++)
    {
      //2.1 move the frogs towards the best one in the memeplex-----------------
      if (mems [m].frogs [frgs].frogStep < frogStepsToLocalMax)
      {
        if (mems [m].frogs [frgs].fPrev != -DBL_MAX && mems [m].fBest != -DBL_MAX)
        {
          if (mems [m].frogs [frgs].fPrev == mems [m].fBest)
          {
            for (int c = 0; c < coordinatesNumber; c++)
            {
              rnd = RNDfromCI (-1.0, 1.0);
              rnd = rnd < 0.0 ? -rnd * rnd : rnd * rnd;
              coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c] * 0.2;
              mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]);
            }
          }
          else
          {
            eDistance = 0.0;
            coordDiff = 0.0;

            //calculate Euclidean distance----------------------------------
            for (int c = 0; c < coordinatesNumber; c++)
            {
              coordDiff  = mems [m].cBest [c] - mems [m].frogs [frgs].cPrev [c];
              coordDiff *= coordDiff;
              eDistance += coordDiff;
            }

            eDistance = sqrt (eDistance);

            for (int c = 0; c < coordinatesNumber; c++)
            {
              rnd = RNDfromCI (-1.0, 1.0);
              coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c] * ((mems [m].cBest [c] - mems [m].frogs [frgs].cPrev [c]) / eDistance);
              mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]);
            }
          }
        }
        else
        {
          for (int c = 0; c < coordinatesNumber; c++)
          {
            rnd = RNDfromCI (-1.0, 1.0);
            rnd = rnd < 0.0 ? -rnd * rnd : rnd * rnd;
            coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c];
            mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]);
          }
        }
      }
      else
      {
        //2.2 move towards global if the move is worse than the previous one-----
        if (mems [m].frogs [frgs].frogStep /*==*/ >= frogStepsToLocalMax)
        {
          eDistance = 0.0;
          coordDiff = 0.0;

          //calculate Euclidean distance------------------------------------
          for (int c = 0; c < coordinatesNumber; c++)
          {
            coordDiff  = cB [c] - mems [m].frogs [frgs].cPrev [c];
            coordDiff *= coordDiff;
            eDistance += coordDiff;
          }

          eDistance = sqrt (eDistance);

          for (int c = 0; c < coordinatesNumber; c++)
          {
            rnd = RNDfromCI (-1.0, 1.0);
            coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c] * ((cB [c] - mems [m].frogs [frgs].cPrev [c]) / eDistance);
            mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]);
          }
        }
        //2.3 move randomly across the field --------------------------------
        else
        {
          for (int c = 0; c < coordinatesNumber; c++)
          {
            rnd = RNDfromCI (-1.0, 1.0);

            coord    = RNDfromCI (rangeMin [c], rangeMax [c]);
            mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]);
          }
        }
      }

      frogs [cnt] = mems [m].frogs [frgs];
      cnt++;
    }
  }


  //--------------------------------------------------------------------------
  numbCyclesCNT++;
}

El método Revision está diseñado para determinar el líder global en cada iteración del algoritmo y para determinar los líderes locales. Si se agota el número de ciclos asignados a los movimientos de las ranas dentro de cada memeplex, realizaremos un barajado: reasignaremos ranas a memeplexes aleatoriamente, intercambiando así información entre memeplexes. Este método también tendrá en cuenta los pasos de salto correspondientes: hacia dónde se desplazará la rana en la siguiente iteración (hacia el líder local o global o en una dirección aleatoria en el espacio de búsqueda).

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SFL::Revision ()
{
  //4.1 determine the globally best one by population-------------------------------
  for (int i = 0; i < frogsNumber; i++)
  {
    if (frogs [i].f > fB)
    {
      fB = frogs [i].f;
      ArrayCopy (cB, frogs [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  int cnt = 0;

  //if the last loop=========================================================
  if (numbCyclesCNT >= numbCycles)
  {
    //4.2.0 reset the memeplex cycle counter-----------------------------------
    numbCyclesCNT = 0;

    //4.2.1 generate random indices--------------------------------------
    for (int i = 0; i < frogsNumber; i++) indexes [i] = i;

    Shuffle (indexes, frogsNumber);

    //4.2.2 copy to memeplexes accidentally------------------------------------
    for  (int m = 0; m < numbMems; m++)
    {
      mems [m].fBest = -DBL_MAX;

      for (int frgs = 0; frgs < memsFrogs; frgs++)
      {
        mems [m].frogs [frgs] = frogs [indexes [cnt]];
        cnt++;

        //4.2.3 determine the best one in each memeplex---------------------------
        if (mems [m].frogs [frgs].f > mems [m].fBest)
        {
          mems [m].fBest = mems [m].frogs [frgs].f;
          ArrayCopy (mems [m].cBest, mems [m].frogs [frgs].c, 0, 0, WHOLE_ARRAY);
        }

        //4.2.4 reset frogs' fitness and step------------------------
        mems [m].frogs [frgs].f        = -DBL_MAX;
        mems [m].frogs [frgs].fPrev    = -DBL_MAX;
        mems [m].frogs [frgs].frogStep = 0;
      }
    }
  }
  //if NOT the last cycle======================================================
  else
  {
    for  (int m = 0; m < numbMems; m++)
    {
      for (int frgs = 0; frgs < memsFrogs; frgs++)
      {
        mems [m].frogs [frgs].frogStep++;

        //4.3.1 copy the fitness and coordinates of frogs from the population to the
        //corresponding frog memeplexes
        mems [m].frogs [frgs].f = frogs [cnt].f;
        ArrayCopy (mems [m].frogs [frgs].c, frogs [cnt].c, 0, 0, WHOLE_ARRAY);

        //4.3.2 determine the best one in each memeplex---------------------------
        if (frogs [cnt].f > mems [m].fBest)
        {
          mems [m].fBest = frogs [cnt].f;
          ArrayCopy (mems [m].cBest, frogs [cnt].c, 0, 0, WHOLE_ARRAY);
        }

        //4.3.3 determine the direction of the next jump------------------------
        if (mems [m].frogs [frgs].frogStep <= frogStepsToLocalMax)
        {
          if (mems [m].frogs [frgs].f > mems [m].frogs [frgs].fPrev)
          {
            mems [m].frogs [frgs].fPrev = mems [m].frogs [frgs].f;
            ArrayCopy (mems [m].frogs [frgs].cPrev, mems [m].frogs [frgs].c, 0, 0, WHOLE_ARRAY);
            mems [m].frogs [frgs].frogStep = 0;
          }
        }
        else
        {
          if (mems [m].frogs [frgs].frogStep >= frogStepsToLocalMax + 1)
          {
            if (mems [m].frogs [frgs].f > mems [m].frogs [frgs].fPrev)
            {
              mems [m].frogs [frgs].fPrev = mems [m].frogs [frgs].f;
              ArrayCopy (mems [m].frogs [frgs].cPrev, mems [m].frogs [frgs].c, 0, 0, WHOLE_ARRAY);
              mems [m].frogs [frgs].frogStep = 0;
            }
          }
          else
          {
            mems [m].frogs [frgs].f        = -DBL_MAX;
            mems [m].frogs [frgs].fPrev    = -DBL_MAX;
            mems [m].frogs [frgs].frogStep = 0;
          }
        }

        cnt++;
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

En el algoritmo de optimización de SFL, tendremos que barajar las ranas entre memeplexes aleatoriamente. El problema del barajado aleatorio resulta interesante porque su solución algorítmica no es trivial, pero gracias a Ronald Fisher y Frank Yates, el mundo cuenta con un algoritmo eficiente y rápido. En los artículos anteriores no usamos este concepto porque no era necesario. Se utiliza mucho en informática, sobre todo en algoritmos genéticos, criptografía y estadística.

Principales ventajas del algoritmo Fisher-Yates:
1. Simplicidad de aplicación: El algoritmo Fisher-Yates resulta fácil de aplicar en cualquier lenguaje de programación, y no requiere cálculos matemáticos complejos ni bibliotecas especiales.
2. Eficiencia: El algoritmo Fisher-Yates se ejecuta en tiempo lineal, lo cual significa que el tiempo de ejecución dependerá del número de elementos que haya que recolocar. Esto lo hace muy eficaz al trabajar con grandes conjuntos de datos.
3. Aleatoriedad: El algoritmo Fisher-Yates ofrece una alta aleatoriedad en las permutaciones. Esto resulta importante para muchas aplicaciones, como las pruebas aleatorias, el cifrado y las simulaciones.
4. Independencia de los datos de entrada: El algoritmo de Fisher-Yates puede aplicarse a cualquier conjunto de datos sin que haya necesidad de conocer su estructura o propiedades. Esto lo convierte en una herramienta versátil para muchas tareas.
5. Pseudoaleatoriedad: El algoritmo de Fisher-Yates genera permutaciones pseudoaleatorias que pueden usarse en muchas aplicaciones en las que se requiere aleatoriedad, pero no necesariamente verdadera aleatoriedad.

En general, el algoritmo Fisher-Yates es interesante por su simpleza, eficacia y versatilidad. Sin duda se trata de una herramienta útil para muchas tareas que implican aleatoriedad y permutaciones de datos.

//——————————————————————————————————————————————————————————————————————————————
void Shuffle (int & arr [], int size)
{
  int index, temp;
  for (int i = size - 1; i > 0; i--)
  {
    index = MathRand () % (i + 1);
    temp = arr [i];
    arr [i] = arr [index];
    arr [index] = temp;
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Resultados de las pruebas

Impresión del rendimiento del algoritmo SFL en el banco de pruebas:

C_AO_SFL:50;25;15;5;0.7
=============================
5 Rastrigin's; Func runs 10000 result: 66.52578871476199
Score: 0.82429
25 Rastrigin's; Func runs 10000 result: 52.38937199890908
Score: 0.64913
500 Rastrigin's; Func runs 10000 result: 44.5591163558836
Score: 0.55211
=============================
5 Forest's; Func runs 10000 result: 0.5762718670482314
Score: 0.32597
25 Forest's; Func runs 10000 result: 0.16329693292687839
Score: 0.09237
500 Forest's; Func runs 10000 result: 0.04968320483668511
Score: 0.02810
=============================
5 Megacity's; Func runs 10000 result: 3.1599999999999997
Score: 0.26333
25 Megacity's; Func runs 10000 result: 1.016
Score: 0.08467
500 Megacity's; Func runs 10000 result: 0.3004
Score: 0.02503
=============================
All score: 2.84501

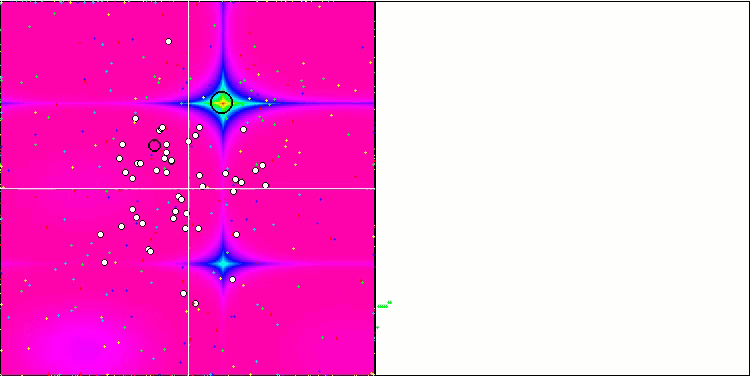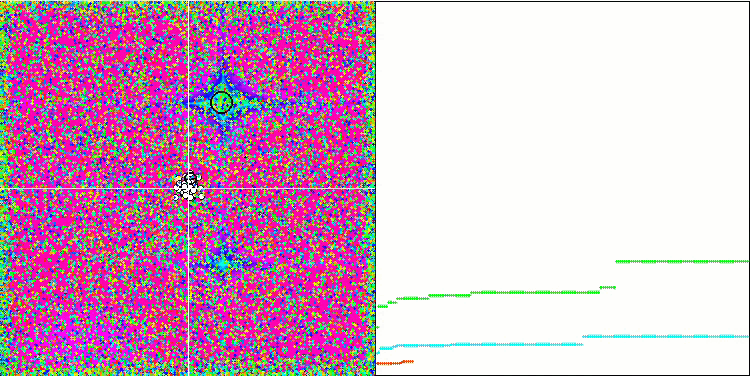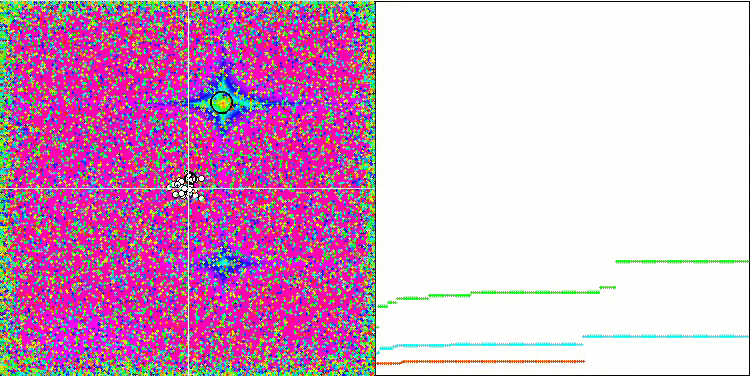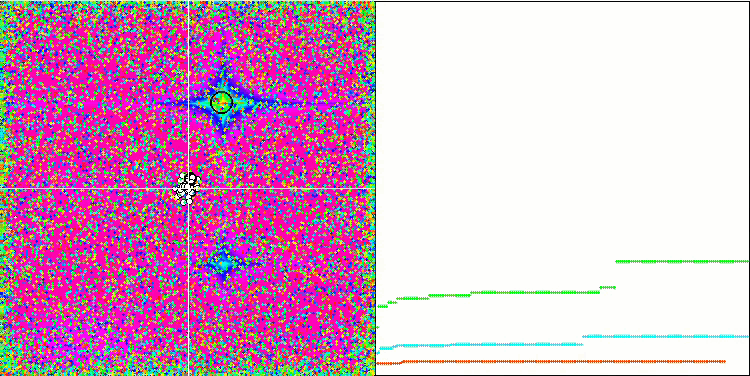
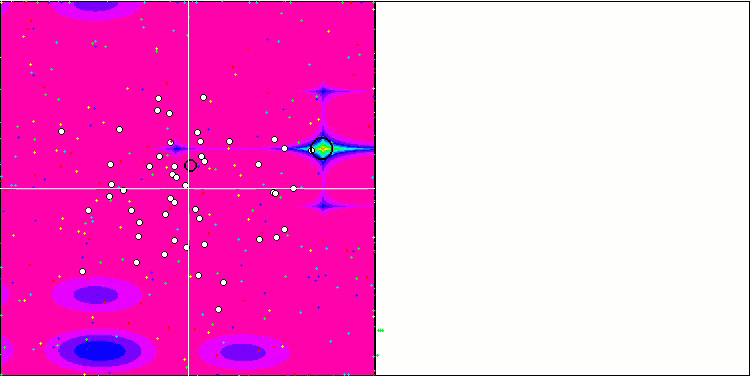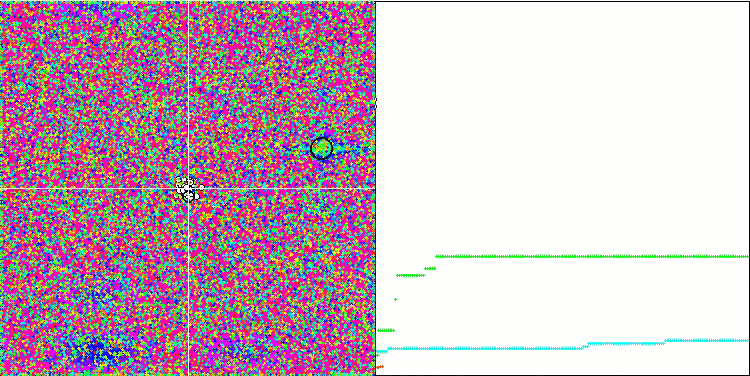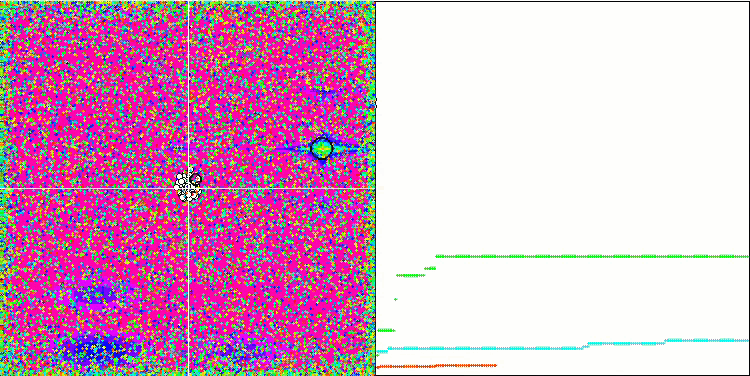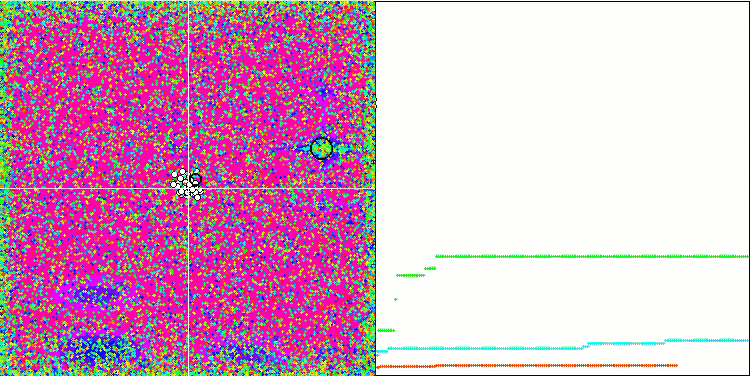
Al observar la animación del rendimiento del algoritmo SFL, no se detecta ninguna agrupación o clusterización en memes individuales, aunque se esperaba lo contrario. Los agentes (puntos) de optimización se distribuyen caóticamente en el campo y no existen regularidades en el movimiento de las partículas. Inmediatamente nos damos cuenta de la mala calidad de la convergencia del algoritmo, que, por desgracia, se manifiesta en el atrapamiento en los extremos locales, que se pueden identificar por las largas secciones suaves en el gráfico de convergencia. No obstante, a medida que aumenta el número de parámetros que hay que optimizar, disminuirá el "escalonamiento".

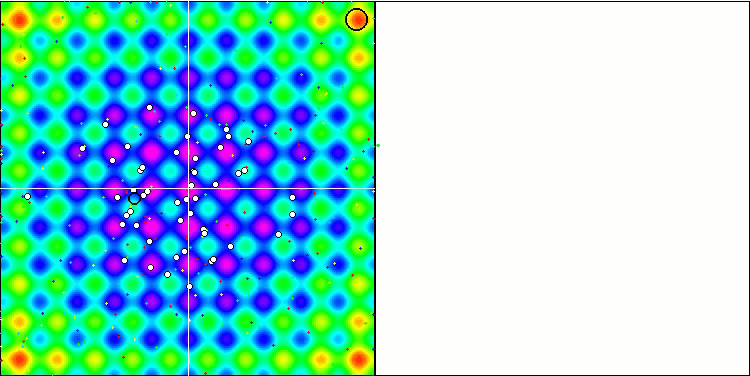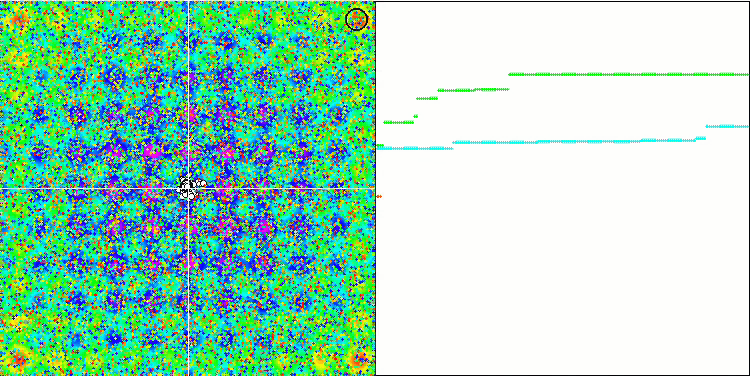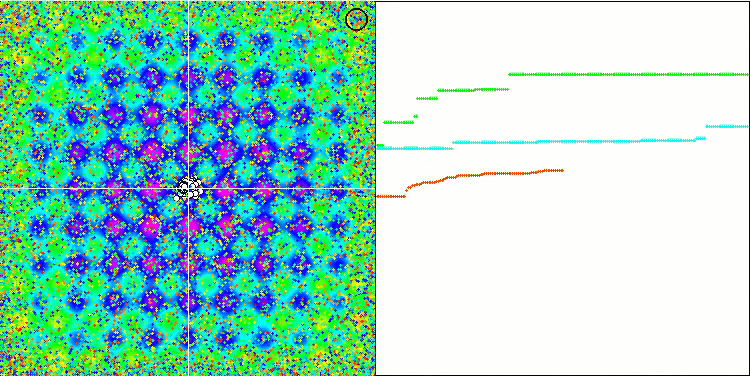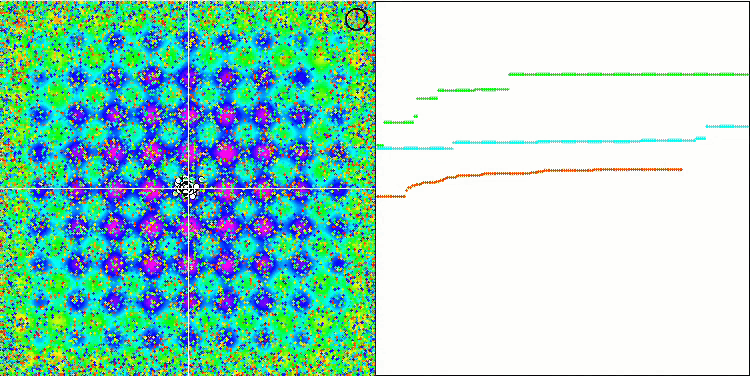
SFL en la función de prueba Rastrigin.

SFL en la función de prueba Forest.

SFL en la función de prueba Megacity.

Resumamos. Al analizar la tabla de resultados de las pruebas de algoritmos, podemos observar que el algoritmo SFL muestra resultados por debajo de la media como optimización. Aunque el SFL tiene alguna ventaja sobre la función Rastrigin suave, no resulta suficiente para recomendarlo como el algoritmo preferido para funciones suaves. En funciones con pliegues como Forest y Megacity, el algoritmo SFL obtiene peores resultados que las funciones suaves. Esto puede explicarse por el hecho de que en las partes suaves del rasgo optimizado, los saltos de rana no mejoran su posición, y regresan constantemente a su posición original sin poder "engancharse" al terreno.

AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
AO	Description	10 params (5 F)	50 params (25 F)	1000 params (500 F)	Rastrigin final	10 params (5 F)	50 params (25 F)	1000 params (500 F)	Forest final	10 params (5 F)	50 params (25 F)	1000 params (500 F)	Megacity final	Final result
SSG	plantones sembrando y creciendo	1.00000	1.00000	0.55665	2.55665	0.72740	0.94522	1.00000	2.67262	0.76364	0.85977	1.00000	2.62340	100.000
HS	harmony search	0.99676	0.95282	0.48178	2.43136	1.00000	0.98931	0.44806	2.43736	1.00000	1.00000	0.41537	2.41537	92.329
ACOm	ant colony optimization M	0.34611	0.17985	0.17044	0.69640	0.86888	1.00000	0.77362	2.64249	1.00000	0.88930	0.05606	1.94536	65.347
IWO	invasive weed optimization	0.95828	0.67083	0.29807	1.92719	0.70773	0.46349	0.31773	1.48896	0.80000	0.42067	0.33289	1.55356	61.104
COAm	cuckoo optimization algorithm M	0.92400	0.46794	0.26004	1.65199	0.58378	0.34034	0.16526	1.08939	0.72727	0.33025	0.17083	1.22835	47.612
FAm	firefly algorithm M	0.59825	0.33980	0.17135	1.10941	0.51073	0.42299	0.49790	1.43161	0.34545	0.28044	0.35258	0.97847	41.537
ABC	artificial bee colony	0.78170	0.32715	0.20822	1.31707	0.53837	0.21455	0.13344	0.88636	0.56364	0.26569	0.13926	0.96858	36.849
GSA	gravitational search algorithm	0.70167	0.45217	0.00000	1.15384	0.31660	0.36416	0.33204	1.01280	0.59395	0.35054	0.00000	0.94448	36.028
BA	bat algorithm	0.40526	0.63761	0.84451	1.88738	0.20841	0.17477	0.25989	0.64308	0.29698	0.09963	0.17371	0.57032	35.888
BFO	bacterial foraging optimization	0.67203	0.30963	0.11813	1.09979	0.39702	0.26623	0.20652	0.86976	0.52122	0.33211	0.18932	1.04264	34.693
EM	electroMagnetism-like algorithm	0.12235	0.46278	1.00000	1.58513	0.00000	0.03498	0.34880	0.38377	0.00000	0.00000	0.10924	0.10924	22.091
SFL	shuffled frog-leaping	0.40072	0.23739	0.26548	0.90360	0.20153	0.04147	0.02652	0.26952	0.27273	0.05535	0.06639	0.39446	15.203
MA	monkey algorithm	0.33192	0.33451	0.14644	0.81287	0.10012	0.07891	0.08932	0.26836	0.21818	0.04243	0.10720	0.36781	13.603
FSS	fish school search	0.46812	0.25337	0.11302	0.83451	0.12840	0.05013	0.06516	0.24369	0.16971	0.04796	0.08283	0.30050	12.655
PSO	particle swarm optimisation	0.20449	0.08200	0.07160	0.35809	0.18895	0.10486	0.21738	0.51119	0.23636	0.05903	0.01957	0.31496	10.031
RND	random	0.16826	0.09743	0.08019	0.34589	0.13496	0.04810	0.04715	0.23021	0.16971	0.03875	0.04922	0.25767	5.302
GWO	grey wolf optimizer	0.00000	0.00000	0.02256	0.02256	0.06570	0.00000	0.00000	0.06570	0.32727	0.07378	0.02557	0.42663	1.000

Conclusiones

El SFL es más bien un "complemento" para otros algoritmos de optimización que pueden utilizarse como lógica para desplazar agentes en memeplexes. El algoritmo SFL precisamente se inventó en sus inicios como una técnica para mejorar la calidad de la optimización de algoritmos ya existentes. Como algoritmo de optimización autónomo, el rendimiento del SFL se encuentra por debajo de la media de los algoritmos basados en poblaciones que hemos analizado anteriormente. El SFL tiene un gran margen para la experimentación con la combinación de pasos lógicos en el algoritmo que mejoran tanto la exploración como la explotación. El SFL es muy flexible y adaptable, lo cual lo hace adecuado para su uso especial en problemas de optimización específicos.

Histograma con los resultados de los algoritmos de prueba en la figura 3 (en una escala de 0 a 100, cuanto más mejor, en el archivo hay un script para calcular la tabla de clasificación según la metodología de este artículo).

chart

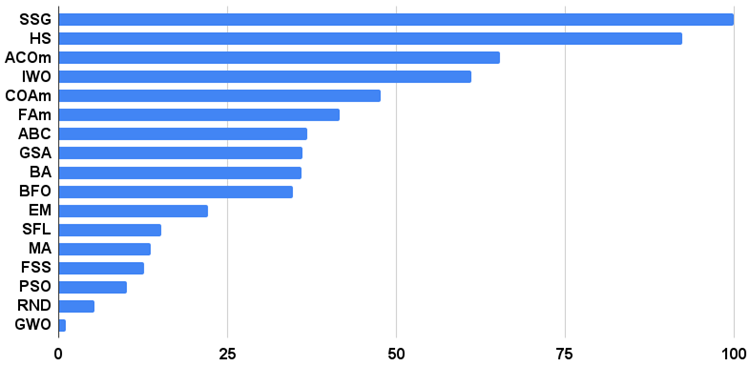
Figura 3. Histograma con los resultados finales de los algoritmos de prueba.

Ventajas e inconvenientes del algoritmo SFL:

Ventajas:
1. Posee un número reducido de parámetros externos.
2. Originalidad de la arquitectura del algoritmo, posibilidad de usar otros algoritmos de optimización en memes.

Desventajas:
1. Tiene una alta complejidad computacional.
2. Malos resultados con funciones suaves y discretas.
3. El algoritmo se atasca en funciones con "plataformas" horizontales planas.

En cada artículo adjuntamos un archivo que contiene versiones reales actualizadas de los códigos de los algoritmos descritos en los artículos anteriores. Los artículos se crean usando como base la experiencia acumulada del autor y su opinión personal, y tanto las conclusiones como los juicios se basan en los resultados de los experimentos.

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/13366

Archivos adjuntos |

Descargar ZIP

17_The_world_of_AO_SFL.zip (143.2 KB)

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Últimos comentarios | Pasar a la discusión en el foro de los operadores (11)

fxsaber | 20 sept. 2023 en 00:33

Stanislav Korotky #:

Sólo lo esbocé porque si voy a construir algún truco, debería ser sin problemas potenciales - me "enganchó" el uso de un bucle con búsqueda de cadenas (!) - puede ser super ineficiente en programas más grandes.

El ini-file no sólo contiene parámetros de cadena, sino también otros tipos de parámetros (aunque están representados por texto).

Un singleton en una fábrica está bien. Singleton en objeto función - en este caso sólo para la operatividad del ejemplo - se puede implementar la multiplicidad.

Yo uso la resolución de cadenas en la etapa de inicialización. Creo que se tarda menos de un milisegundo. Honestamente, no sentí ningún problema potencial.

Dmitry Fedoseev | 20 sept. 2023 en 06:16

fxsaber #:

¡Gracias al autor por hacer un gran trabajo y por la oportunidad gratuita de utilizarlo!

Estoy mirando un poco el código. Y reemplazado esta belleza con tal horror.

¿Cuál es la ganancia? Es realmente horrible. Lo siento, en todo caso)))

Dmitry Fedoseev | 20 sept. 2023 en 06:32

Stanislav Korotky #:

Por todos los medios, la creación de una función a petición debe estar en la propia clase (sin bailes de cadena y "atar" en fragmentos coincidentes de nombres de clase y elementos de enumeración). Hay una variante del autor allí. Aquí hay otro - algo como esto:

Functions.mqh archivo:

Usar en un script como este:

Lo siento, pero estoy equivocado, por supuesto, justo en esa línea de código:

static FunctionInstance *pointers[] = {C_Function::fabric<C_Skin>(), C_Function::fabric<C_Forest>(), C_Function::fabric<C_Megacity>(), C_Function::fabric<C_Rastrigin>(), C_Function::fabric<C_Universe>()};

no creará un objeto de cada tipo?

... Entonces, ¿cómo, sólo un tipo se utilizará durante todo el tiempo del programa.

fxsaber | 20 sept. 2023 en 07:25

Dmitry Fedoseev #:

¿Cuál es la ganancia? Quiero decir, es realmente horrible. Pido disculpas en todo caso)))

Es una pregunta difícil. No lo sé.

Stanislav Korotky | 20 sept. 2023 en 19:46

Dmitry Fedoseev #:

Lo siento, pero me equivoco por supuesto, justo en esa línea de código:

¿no se creará un objeto de cada tipo?

...entonces cómo, sólo se utilizará un tipo durante todo el tiempo del programa.

En esta línea se crean las fábricas. En efecto, están reservadas para todas las clases (en el momento de la puesta en marcha). Una fábrica crea un objeto de trabajo llamando explícitamente a create.

Teoría de categorías en MQL5 (Parte 21): Transformaciones naturales con ayuda de LDA

Este artículo, el número 21 de nuestra serie, continuaremos analizando las transformaciones naturales y cómo se pueden implementar mediante el análisis discriminante lineal. Como en el artículo anterior, la implementación se presentará en formato de clase de señal.

Teoría de categorías en MQL5 (Parte 20): Autoatención y transformador

Hoy nos apartaremos un poco de nuestros temas habituales y veremos parte del algoritmo de ChatGPT. ¿Tiene alguna similitud o concepto tomado de las transformaciones naturales? Intentaremos responder estas y otras preguntas usando nuestro código en formato de clase de señal.

Desarrollando un cliente MQTT para MetaTrader 5: metodología de TDD (Parte 3)

El presente artículo supone la tercera parte de la serie que describe las etapas de desarrollo de un cliente MQL5 nativo para el protocolo MQTT. En esta ocasión, hablaremos con detalle sobre la aplicación de un desarrollo basado en pruebas para implementar el intercambio de paquetes CONNECT/CONNACK. Al final de este paso, nuestro cliente DEBERÁ poder comportarse adecuadamente al lidiar con cualquier posible resultado del servidor al intentar conectarse.

Desarrollando un cliente MQTT para MetaTrader 5: metodología de TDD (Parte 2)

El artículo forma parte de una serie que describe las etapas de desarrollo de un cliente MQL5 nativo para el protocolo MQTT. En esta parte describiremos la organización de nuestro código, los primeros archivos de encabezado y las clases, así como la escritura de las pruebas. Este artículo también incluirá notas breves sobre un desarrollo basado en las pruebas y su aplicación a este proyecto.