Aplicación de la selección de características localizadas en Python y MQL5

Introducción

En el análisis del mercado financiero, los indicadores suelen mostrar una eficacia variable a medida que cambian las condiciones subyacentes. Por ejemplo, la volatilidad fluctuante puede hacer que indicadores que antes eran confiables se vuelvan ineficaces a medida que cambian los regímenes del mercado. Esta variabilidad explica la proliferación de indicadores utilizados por los traders, ya que ningún indicador por sí solo puede tener un buen desempeño consistente en todas las condiciones del mercado. Desde una perspectiva de aprendizaje automático, esto requiere una técnica de selección de características flexible que pueda adaptarse a ese comportamiento dinámico.

Muchos algoritmos de selección de características comunes priorizan las características que muestran poder predictivo en todo el espacio de características. Estas características suelen ser favorecidas incluso cuando sus relaciones con la variable objetivo no son lineales o están influenciadas por otras características. Sin embargo, este sesgo global puede ser problemático, ya que los modelos no lineales modernos pueden extraer información valiosa de características con fuertes capacidades predictivas locales o cuyas relaciones con la variable objetivo cambian dentro de regiones específicas del espacio de características.

En este artículo, exploramos un algoritmo de selección de características introducido en el artículo 'Local Feature Selection for Data Classification' de Narges Armanfard, James P. Reilly y Majid Komeili. Este método tiene como objetivo identificar características predictivas que a menudo se pasan por alto en las técnicas de selección tradicionales debido a su utilidad global limitada. Comenzaremos con una descripción general del algoritmo, seguido de su implementación en Python para crear modelos de clasificadores adecuados para exportar a MetaTrader 5.

Selección de funciones locales

El aprendizaje automático exitoso depende de la selección de características informativas que contribuyan a resolver el problema. En la clasificación supervisada, las características deben diferenciar eficazmente entre categorías de datos. Sin embargo, identificar estas características informativas puede ser un desafío, ya que las que no lo son pueden introducir ruido y degradar el rendimiento del modelo. Como resultado, la selección de características es a menudo un paso inicial fundamental en la construcción de modelos predictivos.

A diferencia de los métodos tradicionales que buscan un único subconjunto de características óptimas para todos los datos, la selección de características locales (Local Feature Selection, LFS) identifica subconjuntos óptimos para regiones locales específicas. Esta adaptabilidad podría ser particularmente útil para manejar datos no estacionarios. Además, LFS incorpora un clasificador que tiene en cuenta los distintos subconjuntos de características utilizados en diferentes muestras. Esto se logra mediante la agrupación por clases, seleccionando características que minimizan las distancias dentro de las clases y maximizan las distancias entre clases.

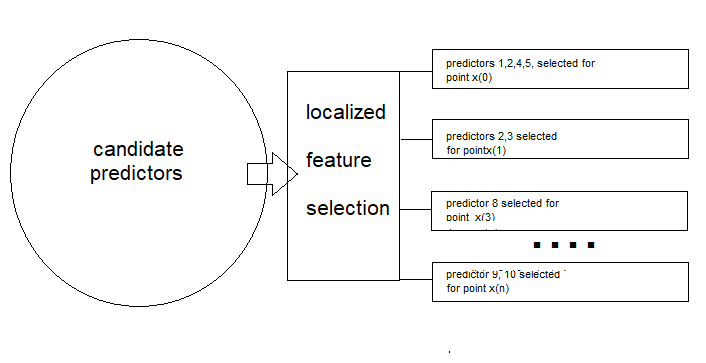
Este enfoque identifica un subespacio de características localmente óptimo en regiones superpuestas, lo que garantiza que cada muestra esté representada en múltiples espacios de características. Para entender mejor el concepto, consideremos un escenario en el que una empresa de telecomunicaciones busca predecir la pérdida de clientes, identificando a aquellos clientes que probablemente cierren sus cuentas. La empresa recopila diversas características de los clientes, entre ellas:

• Antigüedad del cliente: ¿Cuánto tiempo lleva el cliente en la empresa?
• Factura mensual: ¿Cuánto paga el cliente cada mes?
• Peso y altura del cliente.
• Número de llamadas realizadas al servicio de atención al cliente: Con qué frecuencia el cliente se pone en contacto con el soporte.

Imagínese seleccionar dos clientes leales que han estado con la empresa durante muchos años. Para cada una de las características descritas, probablemente habría diferencias mínimas entre estos clientes leales, ya que pertenecen a la misma clase. Ahora, compare esto con la diferencia entre un cliente de largo plazo y uno que canceló su suscripción poco después de registrarse. Si bien su peso y altura pueden no diferir mucho, otros predictores relevantes probablemente mostrarían una variación significativa.

El cliente leal obviamente tendrá una permanencia mucho más larga, podría estar más dispuesto a optar por un paquete de suscripción de mayor precio y es más probable que se comunique con el servicio de atención al cliente cuando surjan problemas en lugar de cancelar por frustración. Mientras tanto, métricas como el peso y la altura se mantendrían cerca del promedio de la población y no contribuirían significativamente a distinguir estos tipos de clientes.

El análisis de valores de características individuales en pares utilizando la distancia euclidiana revela que los predictores más relevantes tendrán la mayor distancia entre clases entre clientes, mientras que los predictores menos relevantes exhibirán la menor distancia entre clases. Esto hace que la selección de predictores efectivos sea clara: priorizamos pares con baja distancia intraclase y alta distancia interclase.

Si bien este enfoque parece eficaz, no logra tener en cuenta las variaciones locales dentro de los datos. Para abordar esto, debemos considerar cómo el poder predictivo puede diferir en varios dominios de características. Imagine un conjunto de datos con dos clases, donde una clase se divide en dos subconjuntos distintos. Un diagrama de dispersión de dos características de este conjunto de datos ilustra que el primer subconjunto puede estar bien separado de la Clase 1 usando la variable x1, pero no x2. Por el contrario, el segundo subconjunto puede estar bien separado utilizando x2, pero no x1.

Si solo consideramos la separación entre clases, el algoritmo podría seleccionar erróneamente x1 y x2, aunque solo uno sea verdaderamente efectivo en cada subconjunto. Esto sucede porque el algoritmo podría priorizar la gran distancia general entre los dos subconjuntos por sobre las distancias más pequeñas y más relevantes dentro de cada subconjunto. Para solucionar esto, los autores del artículo citado introdujeron un esquema de ponderación para las distancias. Al asignar pesos más altos a pares de casos que están más cerca entre sí y pesos más bajos a pares que están más lejos, el algoritmo puede reducir la influencia de valores atípicos dentro de una clase. Esto considera tanto las membresías de clases como la distribución global de distancias.

En resumen, el algoritmo LFS, como se describe en el artículo citado, consta de dos componentes principales. El primero es el proceso de selección de características, donde se selecciona un subconjunto de características para cada muestra. El segundo componente implica un mecanismo localizado que mide la similitud de una muestra de prueba con una clase específica, que se utiliza para fines de inferencia.

Selección de funciones

En esta sección, describiremos el procedimiento de aprendizaje empleado por el método LFS, paso a paso, con un poco de matemáticas. Comenzamos con la estructura esperada de los datos de entrenamiento. La implementación de la selección de características localizadas se realiza en un conjunto de datos con N muestras de entrenamiento, clasificadas en Z etiquetas de clase y acompañadas de M características o candidatos predictores.

Los datos de entrenamiento se pueden representar como una matriz X, donde las filas corresponden a las muestras y las columnas representan distintos candidatos predictores. Por tanto, la matriz X tiene N filas y M columnas. Cada muestra se denomina X(i), en referencia a la fila i-ésima de la matriz. Las etiquetas de clase se almacenan en un vector de columnas separado Y, con cada etiqueta asignada a una muestra correspondiente (fila) en la matriz.

El objetivo final de la aplicación del método LFS es determinar, para cada muestra de entrenamiento X(i), un vector binario F(i) de tamaño M que indique qué predictores candidatos son más relevantes para determinar la etiqueta de clase correspondiente. La matriz F tendrá las mismas dimensiones que X.

Utilizando la distancia euclidiana, el algoritmo apunta a minimizar la distancia promedio entre la muestra actual y otras muestras con la misma etiqueta de clase, mientras maximiza la distancia promedio entre la muestra actual y aquellas con diferentes etiquetas de clase. Además, las distancias deben ponderarse para favorecer las muestras en el mismo vecindario que la muestra actual, introduciendo el vector de columna de pesos W. Dado que los pesos (W) y el vector binario F(i) no están disponibles inicialmente, se utiliza un procedimiento iterativo para estimar los vectores W y F(i) óptimos.

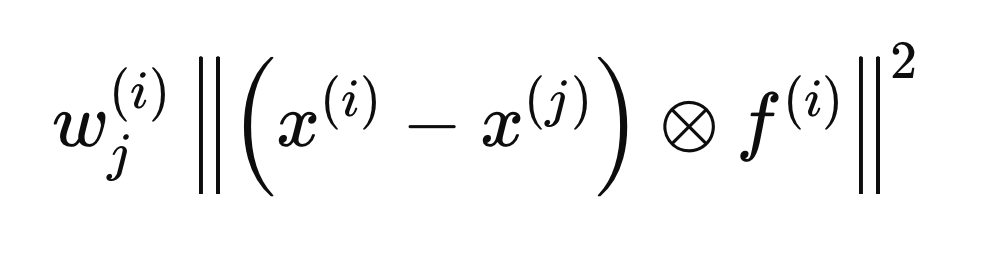
Cálculo de las distancias intraclase e interclase

Cada paso descrito en las siguientes secciones corresponde a cálculos realizados para una sola muestra, X(i), para determinar el vector F(i) óptimo. El proceso comienza inicializando todas las entradas de F a cero y estableciendo los pesos iniciales en 1. A continuación, calculamos las distancias intraclase e interclase con respecto a X(i). La inclusión del vector F(i) en los cálculos de distancia garantiza que sólo se consideren las variables consideradas relevantes (aquellas iguales a 1). Para mayor comodidad matemática, las distancias euclidianas se elevan al cuadrado, lo que da como resultado la siguiente ecuación de distancia.

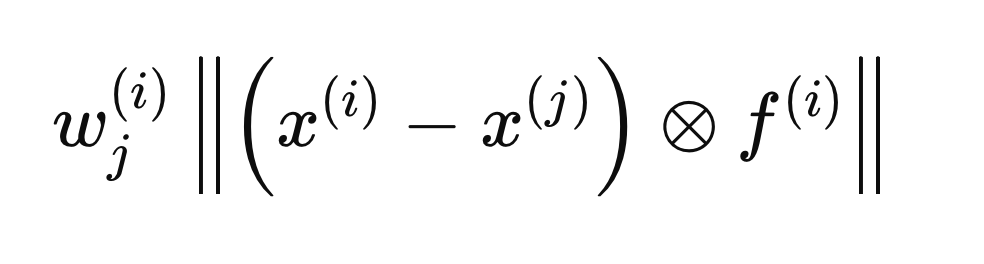
El círculo con una "x" encerrada denota un operador para la multiplicación elemento por elemento. Las distancias intraclase e interclase se calculan utilizando la fórmula anterior, pero con diferentes j elementos (filas) de X. La distancia intraclase se calcula utilizando los j elementos que comparten la misma etiqueta de clase que X(i),

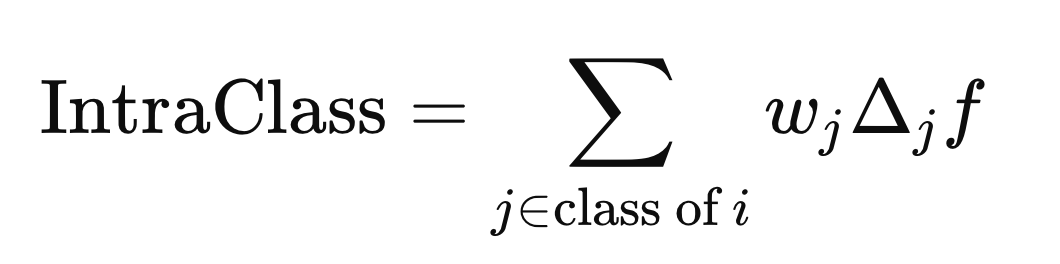
Mientras que la distancia entre clases se calcula utilizando los j elementos con cualquier etiqueta de clase diferente de Y(i).

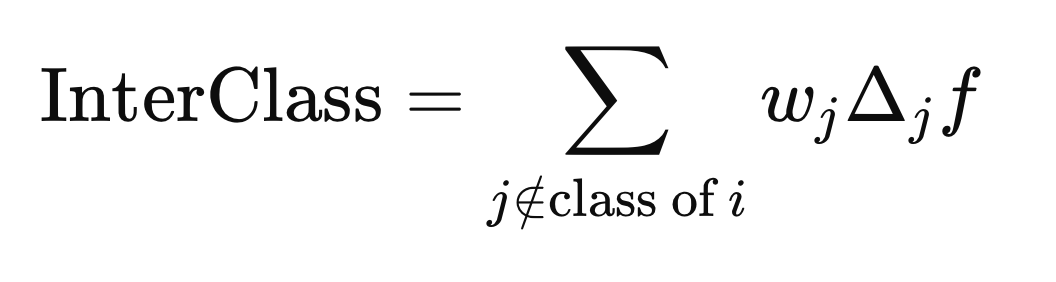
Calculando los pesos

Para la muestra X(i), calculamos un vector de pesos (W), que tiene una longitud N, tal que si X(j) está lejos de X(i), su peso debería ser pequeño y, a la inversa, si está cerca, el peso debería ser mayor. La ponderación no debe penalizar las muestras simplemente porque tienen una etiqueta de clase diferente. Como F(i) aún no es óptimo, las variables seleccionadas para definir la base de los vecindarios aún son desconocidas. El artículo citado aborda esta cuestión promediando los pesos calculados a partir de iteraciones anteriores de refinamiento de pesos.

Cuando se incluye un vector F en la definición de la distancia entre dos muestras, se considera dentro del espacio métrico definido por F(i). El cálculo de pesos óptimos se realiza definiendo distancias en términos de un espacio métrico diferente, al que nos referiremos como F(z), como se indica en la fórmula siguiente.

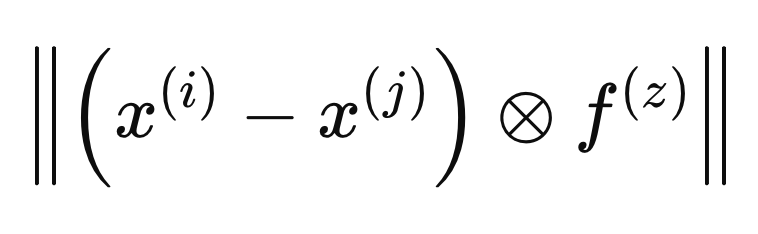
Para garantizar que los pesos no penalicen a las muestras simplemente por estar en una clase diferente, calculamos la distancia mínima entre X(i) y todas las demás muestras de la misma clase en el espacio métrico definido por F(z).

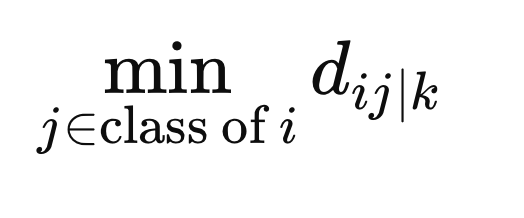
Además, calculamos la distancia mínima desde las muestras con una etiqueta de clase diferente a X(i).

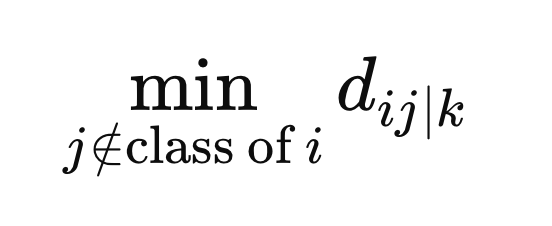
Éstos son los valores finales necesarios para definir los pesos. Los pesos se calculan como el promedio de todos los espacios métricos, dado por el exponencial negativo de la diferencia entre la distancia y la distancia mínima para un espacio métrico particular, z.

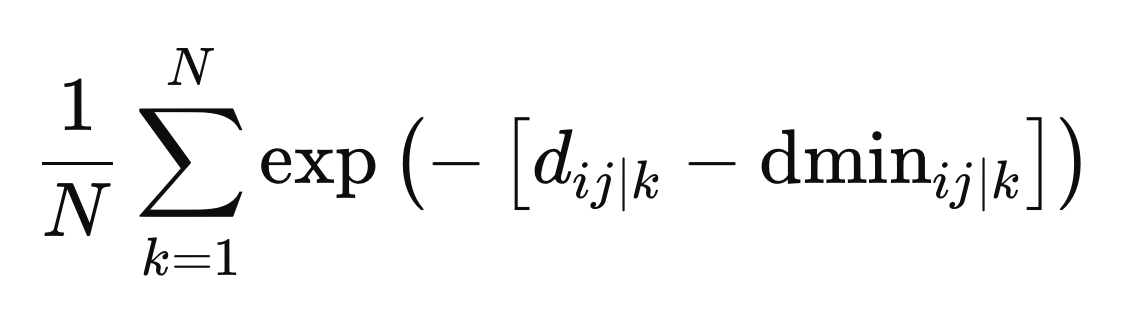
Objetivos en conflicto

En esta fase, hemos obtenido las ponderaciones óptimas, lo que nos permite abordar el reto de encontrar el equilibrio adecuado entre la separación interclases e intraclases. Se trata de conciliar dos objetivos contrapuestos: minimizar la separación intraclase (hacer que los puntos de datos de una misma clase sean lo más parecidos posible) y maximizar la separación interclase (hacer que las distintas clases sean lo más distintas posible). Lograr ambos objetivos a la perfección con el mismo conjunto de predictores suele ser inviable.

Un enfoque viable es el método de restricción Epsilon, que encuentra un compromiso entre estos objetivos en conflicto. Este método funciona resolviendo primero uno de los problemas de optimización (normalmente el problema de maximización) y luego abordando el problema de minimización con la restricción adicional de que la función maximizada permanezca por encima de un cierto umbral.

En primer lugar, maximizamos la separación entre clases y registramos el valor máximo de esta función, denotado como épsilon (ϵ), que representa la mayor separación posible entre clases. A continuación, minimizamos la separación intraclase para varios valores de un parámetro β (que va de 0 a 1), con la restricción de que la separación interclase para la solución minimizada debe permanecer mayor o igual a βϵ.

El parámetro β sirve como factor de compromiso, equilibrando la atención entre los dos objetivos: cuando β se fija en 1, la separación entre clases tiene prioridad absoluta, mientras que cuando β se fija en 0, la atención se desplaza por completo a minimizar la separación intraclase. Se imponen cuatro restricciones a ambas tareas de optimización:

• Todos los elementos de F deben estar comprendidos entre 0 y 1, ambos inclusive.
• La suma de los elementos de un vector F debe ser inferior o igual a un hiperparámetro especificado por el usuario, que rige el número máximo de predictores que pueden activarse.
• La suma de los elementos de un vector F debe ser mayor o igual que uno, lo que garantiza que se activa al menos un predictor para cada muestra.
  

Para la minimización intraclase, existe una restricción adicional heredada de la operación de maximización inicial: el valor de la maximización de la función debe ser al menos igual al producto de β y ϵ.

Las funciones y restricciones implicadas son lineales, lo que indica que las tareas de optimización son problemas de programación lineal. Los problemas de programación lineal estándar pretenden maximizar una función objetivo sujeta a restricciones que especifican umbrales que no deben superarse.

La programación lineal implica la optimización de una función objetivo lineal sujeta a restricciones lineales. La función objetivo, normalmente denominada "z", es una combinación lineal de variables de decisión. Las restricciones se expresan como desigualdades o igualdades lineales, limitando los valores de las variables de decisión. Más allá de las restricciones especificadas por el usuario, existen restricciones implícitas de no negatividad en las variables de decisión y restricciones de no negatividad en los lados derechos de las desigualdades.

Si bien la forma estándar supone variables de decisión no negativas y desigualdades "menores o iguales que", estas restricciones se pueden relajar mediante transformaciones. Al multiplicar ambos lados de una desigualdad por -1, podemos manejar desigualdades "mayores o iguales" y lados derechos negativos. Además, los coeficientes no positivos que involucran variables de decisión se pueden transformar en coeficientes positivos mediante la creación de nuevas variables.

El método del punto interior es un algoritmo eficiente para resolver problemas de programación lineal, especialmente cuando se trata de tareas de optimización a gran escala. Nuestra implementación en Python empleará este método para encontrar eficientemente una solución óptima. Una vez alcanzada la convergencia, obtendremos un vector F(i) óptimo. Sin embargo, es importante tener en cuenta que estos valores no están en el formato requerido (1 o 0). Esto se corrige en el paso final del método LFS.

Pruebas beta

El problema con el vector F(i) calculado es que consta de valores reales en lugar de valores binarios. El objetivo del procedimiento LFS es identificar las variables más relevantes para cada muestra, que se representa mediante una matriz F binaria donde los valores son 0 o 1. Un valor de 0 indica que la variable correspondiente se considera irrelevante o se omite.

Para convertir los valores reales del vector F(i) en valores binarios, utilizamos un método de Monte Carlo para encontrar el mejor equivalente binario. Esto implica repetir el proceso una cantidad de veces especificada por el usuario, lo cual es un hiperparámetro clave del método LFS. Para cada iteración, comenzamos con un vector binario donde cada candidato a predictor se establece inicialmente en 1, utilizando los valores continuos F(i) como probabilidades para cada predictor. Luego verificamos si el vector binario satisface las restricciones del procedimiento de minimización y calculamos el valor de su función objetivo. El vector binario con el valor mínimo de la función objetivo se elige como el vector final F(i).

Posprocesamiento para selección de características

LFS selecciona de forma independiente candidatos predictores óptimos para cada muestra, lo que hace que no sea práctico informar un único conjunto definitivo. Para abordar esto, contamos la frecuencia de inclusión de cada predictor en subconjuntos óptimos. Esto permite a los usuarios establecer un umbral e identificar los predictores que aparecen con mayor frecuencia como los más relevantes. Es importante destacar que la relevancia de un predictor dentro de este conjunto no implica su valor individual; su valor podría residir en su interacción con otros predictores.

Esta es una ventaja clave de LFS: su capacidad de identificar predictores que pueden ser individualmente insignificantes pero valiosos cuando se combinan con otros. Este paso de preprocesamiento es importante para los modelos de predicción modernos, que se destacan por discernir relaciones complejas entre variables. Al eliminar predictores irrelevantes, LFS agiliza el proceso de modelado y mejora el rendimiento del modelo.

Implementación en Python: LFSpy

En esta sección, exploramos la aplicación práctica del algoritmo LFS, centrándonos primero en su uso como técnica de selección de características y discutiendo brevemente sus capacidades de clasificación de datos. Todas las demostraciones se realizarán en Python utilizando el paquete LFSpy, que implementa los aspectos de selección de características y clasificación de datos del algoritmo LFS. El paquete está disponible en PyPI, donde se puede encontrar información detallada sobre él.

Primero, instale el paquete LFSpy.

pip install LFSpy

A continuación, importe la clase LocalFeatureSelection desde LFSpy.

desde LFSpy importar LocalFeatureSelection

Se puede crear una instancia de LocalFeatureSelection llamando al constructor paramétrico.

lfs = LocalFeatureSelection(alpha=8,tau=2,n_beta=20,nrrp=2000)

El constructor admite los siguientes parámetros opcionales:

Nombre del parámetro	Tipo de datos	Descripción
alpha	integer	El número máximo de predictores seleccionados de todos los candidatos a predictores. El valor predeterminado es 19.
gamma	double	Un nivel de tolerancia que rige la relación entre muestras con etiquetas de clase diferentes y aquellas con la misma etiqueta de clase dentro de una región local. El valor predeterminado es 0,2.
tau	integer	El número de iteraciones a través de todo el conjunto de datos (equivalente al número de épocas en el aprendizaje automático tradicional). El valor predeterminado es 2 y se recomienda establecer este valor en un número de un solo dígito, normalmente no más de 5.
sigma	double	Controla la ponderación de las observaciones en función de su distancia. Un valor mayor que 1 reduce la ponderación. El valor predeterminado es 1.
n_beta	integer	El número de valores beta probados al convertir los vectores F continuos a sus equivalentes binarios.
nrrp	integer	El número de iteraciones para pruebas beta. Este valor debe ser al menos 500 y aumentar con el tamaño del conjunto de datos de entrenamiento. El valor predeterminado es 2000.
knn	integer	Se aplica específicamente a tareas de clasificación. Especifica el número de vecinos más cercanos a comparar para la categorización. El valor predeterminado es 1.

Después de inicializar una instancia de la clase LFSpy, utilizamos el método fit() con al menos dos parámetros de entrada: una matriz bidimensional de muestras de entrenamiento, que consta de predictores candidatos, y una matriz unidimensional de etiquetas de clase correspondientes.

lfs.fit(xtrain,ytrain)

Una vez ajustado el modelo, llamar a fstar devuelve la matriz de inclusión F, que consta de unos y ceros para indicar las características seleccionadas. Tenga en cuenta que esta matriz está transpuesta con respecto a la orientación de las muestras de entrenamiento.

fstar = lfs.fstar

El método predict() se utiliza para clasificar muestras de prueba según el modelo aprendido y devuelve las etiquetas de clase correspondientes a los datos de prueba.

predicted_classes = lfs.predict(test_samples)

El método score() calcula la precisión del modelo comparando las etiquetas de clase previstas con las etiquetas conocidas. Devuelve la fracción de muestras de prueba que se clasificaron correctamente.

accuracy = lfs.score(test_data,test_labels)

Ejemplos de LFSpy

Para la primera demostración práctica, generamos varios miles de variables aleatorias distribuidas uniformemente dentro del intervalo [−1,1][−1,1]. Estas variables se organizan en una matriz con un número específico de columnas. Luego creamos un vector de etiquetas {0, 1} correspondientes a cada fila, dependiendo de si los valores en dos columnas arbitrarias son ambos negativos o ambos positivos. El objetivo de esta demostración es determinar si el método LFS puede identificar los predictores más relevantes en este conjunto de datos. Evaluamos los resultados sumando el número de veces que se selecciona cada predictor (indicado por un 1) en la matriz de inclusión binaria F. El código que implementa esta prueba se muestra a continuación.

import numpy as np
import pandas as pd
from LFSpy import LocalFeatureSelection
from timeit import default_timer as timer

#number of random numbers to generate
datalen = 500 

#number of features the dataset will have
datavars = 5

#set random number seed
rng_seed = 125
rng = np.random.default_rng(rng_seed)

#generate the numbers
data = rng.uniform(-1.0,1.0,size=datalen)

#shape our dataset
data = data.reshape([datalen//datavars,datavars])

#set up container for class labels
class_labels = np.zeros(shape=data.shape[0],dtype=np.uint8)

#set the class labels
for i in range(data.shape[0]):
    class_labels[i] = 1 if (data[i,1] > 0.0 and data[i,2] > 0.0) or (data[i,1] < 0.0 and data[i,2] < 0.0) else 0

#partition our training data
xtrain = data
ytrain = class_labels

#initialize the LFS object
lfs = LocalFeatureSelection(rr_seed=rng_seed,alpha=8,tau=2,n_beta=20,nrrp=2000)

#start timer
start = timer()

#train the model
lfs.fit(xtrain,ytrain)

#output training duration
print("Training done in ", timer()-start , " seconds. ")

#get the inclusion matrix
fstar = lfs.fstar

#add up all ones for each row of the inclusion matrix
ibins = fstar.sum(axis=1)

#calculate the percent of times a candidate was selected
original_crits = 100.0 * ibins.astype(np.float64)/np.float64(ytrain.shape[0])

#output the results
print("------------------------------> Percent of times selected <------------------------------" )
for i in range(original_crits.shape[0]):
   print( f" Variable at column {i}, selected {original_crits[i]} %")

La salida de ejecutar LFSdemo.py

Training done in  45.84896759999992  seconds. 
Python  ------------------------------> Percent of times selected <------------------------------
Python   Variable at column 0, selected 19.0 %
Python   Variable at column 1, selected 81.0 %
Python   Variable at column 2, selected 87.0 %
Python   Variable at column 3, selected 20.0 %
Python   Variable at column 4, selected 18.0 %

Es curioso que una de las variables relevantes fuera seleccionada con una frecuencia ligeramente mayor que la otra, a pesar de que desempeñan papeles idénticos en la predicción de la clase. Esto sugiere que matices sutiles dentro de los datos podrían estar influyendo en el proceso de selección. Lo que está claro es que ambas variables fueron elegidas consistentemente con mayor frecuencia que los predictores irrelevantes, lo que indica su importancia para determinar la clase. La ejecución relativamente lenta del algoritmo probablemente se deba a su naturaleza de un solo subproceso, lo que puede obstaculizar su rendimiento en conjuntos de datos más grandes.

LFS para clasificación de datos

Dada la naturaleza local de LFS, construir un clasificador a partir de él requiere más esfuerzo en comparación con los métodos tradicionales de selección de características con sesgo global. El artículo referenciado analiza una arquitectura de clasificador propuesta, en la que no profundizaremos aquí. Se recomienda a los lectores interesados consultar el artículo citado para obtener detalles completos. En esta sección nos centraremos en la implementación.

El método predict() de la clase LocalFeatureSelection evalúa la similitud de clases. Toma datos de prueba que coinciden con la estructura de los datos de entrenamiento y devuelve etiquetas de clase predichas en función de los patrones aprendidos por el modelo LFS entrenado. En la próxima demostración de código, ampliaremos el script anterior para crear un modelo de clasificador LFS, exportarlo en formato JSON, cargarlo usando un script MQL5 y clasificar un conjunto de datos fuera de la muestra. El código utilizado para exportar un modelo LFS está contenido en JsonModel.py. Este archivo define la función lfspy2json(), que serializa el estado y los parámetros de un modelo LocalFeatureSelection en un archivo JSON. Esto permite guardar el modelo en un formato que se puede leer y utilizar fácilmente en código MQL5, lo que facilita la integración con MetaTrader 5. El código completo se muestra a continuación.

# Copyright 2024, MetaQuotes Ltd.
# https://www.mql5.com

from LFSpy import LocalFeatureSelection
import json 

MQL5_FILES_FOLDER = "MQL5\\FILES"
MQL5_COMMON_FOLDER = "FILES"

def lfspy2json(lfs_model:LocalFeatureSelection, filename:str):
    """
    function export a LFSpy model to json format 
    readable from MQL5 code.
    
    param: lfs_model should be an instance of LocalFeatureSelection
    param: filename or path to file where lfs_model
    parameters will be written to
    
    """
    if not isinstance(lfs_model,LocalFeatureSelection):
        raise TypeError(f'invalid type supplied, "lfs_model" should be an instance of LocalFeatureSelection')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "alpha":lfs_model.alpha,
            "gamma":lfs_model.gamma,
            "tau":lfs_model.tau,
            "sigma":lfs_model.sigma, 
            "n_beta":lfs_model.n_beta,
            "nrrp":lfs_model.nrrp,
            "knn":lfs_model.knn,
            "rr_seed":lfs_model.rr_seed,
            "num_observations":lfs_model.training_data.shape[1],
            "num_features":lfs_model.training_data.shape[0],
            "training_data":lfs_model.training_data.tolist(),
            "training_labels":lfs_model.training_labels.tolist(),
            "fstar":lfs_model.fstar.tolist()
          }
          
    
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return 

La función toma un objeto LocalFeatureSelection y un nombre de archivo como entradas. Serializa los parámetros del modelo como un objeto JSON y los guarda bajo el nombre de archivo especificado. El módulo también define dos constantes, MQL5_FILES_FOLDER y MQL5_COMMON_FOLDER, que representan las rutas de directorio para las carpetas accesibles en una instalación estándar de MetaTrader 5. Esta es solo una parte de la solución para la integración con MetaTrader 5. La otra parte está implementada en código MQL5, que se presenta en lfspy.mqh. Este archivo incluido contiene la definición de la clase Clfspy, que facilita la carga de un modelo LFS guardado en formato JSON para fines de inferencia. El código completo se proporciona a continuación.

//+------------------------------------------------------------------+
//|                                                        lfspy.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<JAson.mqh>
#include<Files/FileTxt.mqh>
#include<np.mqh>
//+------------------------------------------------------------------+
//|structure of model parameters                                     |
//+------------------------------------------------------------------+
struct LFS_PARAMS
  {
   int               alpha;
   int               tau;
   int               n_beta;
   int               nrrp;
   int               knn;
   int               rr_seed;
   int               sigma;
   ulong             num_features;
   double            gamma;
  };
//+------------------------------------------------------------------+
//|  class encapsulates LFSpy model                                  |
//+------------------------------------------------------------------+
class Clfspy
  {
private:
   bool              loaded;
   LFS_PARAMS        model_params;
   matrix train_data,
          fstar;
   vector            train_labels;
   //+------------------------------------------------------------------+
   //|  helper function for parsing model from file                     |
   //+------------------------------------------------------------------+
   bool              fromJSON(CJAVal &jsonmodel)
     {

      model_params.alpha = (int)jsonmodel["alpha"].ToInt();
      model_params.tau = (int)jsonmodel["tau"].ToInt();
      model_params.sigma = (int)jsonmodel["sigma"].ToInt();
      model_params.n_beta = (int)jsonmodel["n_beta"].ToInt();
      model_params.nrrp = (int)jsonmodel["nrrp"].ToInt();
      model_params.knn = (int)jsonmodel["knn"].ToInt();
      model_params.rr_seed = (int)jsonmodel["rr_seed"].ToInt();
      model_params.gamma = jsonmodel["gamma"].ToDbl();

      ulong observations = (ulong)jsonmodel["num_observations"].ToInt();
      model_params.num_features = (ulong)jsonmodel["num_features"].ToInt();

      if(!train_data.Resize(model_params.num_features,observations) || !train_labels.Resize(observations) ||
         !fstar.Resize(model_params.num_features,observations))
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }


      for(int i=0; i<int(model_params.num_features); i++)
        {
         for(int j = 0; j<int(observations); j++)
           {
            if(i==0)
               train_labels[j] = jsonmodel["training_labels"][j].ToDbl();
            train_data[i][j] = jsonmodel["training_data"][i][j].ToDbl();
            fstar[i][j] = jsonmodel["fstar"][i][j].ToDbl();
           }
        }

      return true;
     }
   //+------------------------------------------------------------------+
   //| helper classification function                                   |
   //+------------------------------------------------------------------+
   matrix            classification(matrix &testing_data)
     {
      int N = int(train_labels.Size());
      int H = int(testing_data.Cols());

      matrix out(H,2);

      for(int i = 0; i<H; i++)
        {
         vector column = testing_data.Col(i);
         vector result = class_sim(column,train_data,train_labels,fstar,model_params.gamma,model_params.knn);
         if(!out.Row(result,i))
           {
            Print(__FUNCTION__, " row insertion failure ", GetLastError());
            return matrix::Zeros(1,1);
           }
        }

      return out;
     }
   //+------------------------------------------------------------------+
   //| internal feature classification function                         |
   //+------------------------------------------------------------------+
   vector            class_sim(vector &test,matrix &patterns,vector& targets, matrix &f_star, double gamma, int knn)
     {
      int N = int(targets.Size());
      int n_nt_cls_1 = (int)targets.Sum();
      int n_nt_cls_2 = N - n_nt_cls_1;
      int M = int(patterns.Rows());
      int NC1 = 0;
      int NC2 = 0;
      vector S = vector::Zeros(N);

      S.Fill(double("inf"));

      vector NoNNC1knn = vector::Zeros(N);
      vector NoNNC2knn = vector::Zeros(N);
      vector NoNNC1 = vector::Zeros(N);
      vector NoNNC2 = vector::Zeros(N);
      vector radious = vector::Zeros(N);
      double r = 0;
      int k = 0;
      for(int i = 0; i<N; i++)
        {
         vector fs = f_star.Col(i);
         matrix xpatterns = patterns * np::repeat_vector_as_rows_cols(fs,patterns.Cols(),false);
         vector testpr = test * fs;
         vector mtestpr = (-1.0 * testpr);
         matrix testprmat = np::repeat_vector_as_rows_cols(mtestpr,xpatterns.Cols(),false);
         vector dist = MathAbs(sqrt((pow(testprmat + xpatterns,2.0)).Sum(0)));
         vector min1 = dist;
         np::sort(min1);
         vector min_uniq = np::unique(min1);
         int m = -1;
         int no_nereser = 0;
         vector NN(dist.Size());
         while(no_nereser<int(knn))
           {
            m+=1;
            double a1  = min_uniq[m];
            for(ulong j = 0; j<dist.Size(); j++)
               NN[j]=(dist[j]<=a1)?1.0:0.0;
            no_nereser = (int)NN.Sum();
           }
         vector bitNN = np::bitwiseAnd(NN,targets);
         vector Not = np::bitwiseNot(targets);
         NoNNC1knn[i] = bitNN.Sum();
         bitNN = np::bitwiseAnd(NN,Not);
         NoNNC2knn[i] = bitNN.Sum();
         vector A(fs.Size());
         for(ulong v =0; v<A.Size(); v++)
            A[v] = (fs[v]==0.0)?1.0:0.0;
         vector f1(patterns.Cols());
         vector f2(patterns.Cols());
         if(A.Sum()<double(M))
           {
            for(ulong v =0; v<A.Size(); v++)
               A[v] = (A[v]==1.0)?0.0:1.0;
            matrix amask = matrix::Ones(patterns.Rows(), patterns.Cols());
            amask *= np::repeat_vector_as_rows_cols(A,patterns.Cols(),false);
            matrix patternsp = patterns*amask;
            vector testp = test*(amask.Col(0));
            vector testa = patternsp.Col(i) - testp;
            vector col = patternsp.Col(i);
            matrix colmat = np::repeat_vector_as_rows_cols(col,patternsp.Cols(),false);
            double Dist_test = MathAbs(sqrt((pow(col - testp,2.0)).Sum()));
            vector Dist_pat  = MathAbs(sqrt((pow(patternsp - colmat,2.0)).Sum(0)));
            vector eerep = Dist_pat;
            np::sort(eerep);
            int remove = 0;
            if(targets[i] == 1.0)
              {
               vector unq = np::unique(eerep);
               k = -1;
               NC1+=1;
               if(remove!=1)
                 {
                  int Next = 1;
                  while(Next == 1)
                    {
                     k+=1;
                     r = unq[k];
                     for(ulong j = 0; j<Dist_pat.Size(); j++)
                       {
                        if(Dist_pat[j] == r)
                           f1[j] = 1.0;
                        else
                           f1[j] = 0.0;
                        if(Dist_pat[j]<=r)
                           f2[j] = 1.0;
                        else
                           f2[j] = 0.0;
                       }
                     vector f2t = np::bitwiseAnd(f2,targets);
                     vector tn = np::bitwiseNot(targets);
                     vector f2tn = np::bitwiseAnd(f2,tn);
                     double nocls1clst = f2t.Sum() - 1.0;
                     double nocls2clst = f2tn.Sum();
                     if(gamma *(nocls1clst/double(n_nt_cls_1-1)) < (nocls2clst/(double(n_nt_cls_2))))
                       {
                        Next = 0 ;
                        if((k-1) == 0)
                           r = unq[k];
                        else
                           r = 0.5 * (unq[k-1] + unq[k]);
                        if(r==0.0)
                           r = pow(10.0,-6.0);
                        r = 1.0*r;
                        for(ulong j = 0; j<Dist_pat.Size(); j++)
                          {
                           if(Dist_pat[j]<=r)
                              f2[j] = 1.0;
                           else
                              f2[j] = 0.0;
                          }
                        f2t = np::bitwiseAnd(f2,targets);
                        f2tn = np::bitwiseAnd(f2,tn);
                        nocls1clst = f2t.Sum() - 1.0;
                        nocls2clst = f2tn.Sum();
                       }
                    }
                  if(Dist_test<r)
                    {
                     patternsp = patterns * np::repeat_vector_as_rows_cols(fs,patterns.Cols(),false);
                     testp = test * fs;
                     dist = MathAbs(sqrt((pow(patternsp - np::repeat_vector_as_rows_cols(testp,patternsp.Cols(),false),2.0)).Sum(0)));
                     min1 = dist;
                     np::sort(min1);
                     min_uniq = np::unique(min1);
                     m = -1;
                     no_nereser = 0;
                     while(no_nereser<int(knn))
                       {
                        m+=1;
                        double a1  = min_uniq[m];
                        for(ulong j = 0; j<dist.Size(); j++)
                           NN[j]=(dist[j]<a1)?1.0:0.0;
                        no_nereser = (int)NN.Sum();
                       }
                     bitNN = np::bitwiseAnd(NN,targets);
                     Not = np::bitwiseNot(targets);
                     NoNNC1[i] = bitNN.Sum();
                     bitNN = np::bitwiseAnd(NN,Not);
                     NoNNC2[i] = bitNN.Sum();
                     if(NoNNC1[i]>NoNNC2[i])
                        S[i] = 1.0;
                    }
                 }
              }
            if(targets[i] == 0.0)
              {
               vector unq = np::unique(eerep);
               k=-1;
               NC2+=1;
               int Next;
               if(remove!=1)
                 {
                  Next =1;
                  while(Next==1)
                    {
                     k+=1;
                     r = unq[k];
                     for(ulong j = 0; j<Dist_pat.Size(); j++)
                       {
                        if(Dist_pat[j] == r)
                           f1[j] = 1.0;
                        else
                           f1[j] = 0.0;
                        if(Dist_pat[j]<=r)
                           f2[j] = 1.0;
                        else
                           f2[j] = 0.0;
                       }
                     vector f2t = np::bitwiseAnd(f2,targets);
                     vector tn = np::bitwiseNot(targets);
                     vector f2tn = np::bitwiseAnd(f2,tn);
                     double nocls1clst = f2t.Sum() ;
                     double nocls2clst = f2tn.Sum() -1.0;
                     if(gamma *(nocls2clst/double(n_nt_cls_2-1)) < (nocls1clst/(double(n_nt_cls_1))))
                       {
                        Next = 0 ;
                        if((k-1) == 0)
                           r = unq[k];
                        else
                           r = 0.5 * (unq[k-1] + unq[k]);
                        if(r==0.0)
                           r = pow(10.0,-6.0);
                        r = 1.0*r;
                        for(ulong j = 0; j<Dist_pat.Size(); j++)
                          {
                           if(Dist_pat[j]<=r)
                              f2[j] = 1.0;
                           else
                              f2[j] = 0.0;
                          }
                        f2t = np::bitwiseAnd(f2,targets);
                        f2tn = np::bitwiseAnd(f2,tn);
                        nocls1clst = f2t.Sum();
                        nocls2clst = f2tn.Sum() -1.0;
                       }
                    }
                  if(Dist_test<r)
                    {
                     patternsp = patterns * np::repeat_vector_as_rows_cols(fs,patterns.Cols(),false);
                     testp = test * fs;
                     dist = MathAbs(sqrt((pow(patternsp - np::repeat_vector_as_rows_cols(testp,patternsp.Cols(),false),2.0)).Sum(0)));
                     min1 = dist;
                     np::sort(min1);
                     min_uniq = np::unique(min1);
                     m = -1;
                     no_nereser = 0;
                     while(no_nereser<int(knn))
                       {
                        m+=1;
                        double a1  = min_uniq[m];
                        for(ulong j = 0; j<dist.Size(); j++)
                           NN[j]=(dist[j]<a1)?1.0:0.0;
                        no_nereser = (int)NN.Sum();
                       }
                     bitNN = np::bitwiseAnd(NN,targets);
                     Not = np::bitwiseNot(targets);
                     NoNNC1[i] = bitNN.Sum();
                     bitNN = np::bitwiseAnd(NN,Not);
                     NoNNC2[i] = bitNN.Sum();
                     if(NoNNC2[i]>NoNNC1[i])
                        S[i] = 1.0;
                    }
                 }
              }
           }
         radious[i] = r;
        }
      vector q1 = vector::Zeros(N);
      vector q2 = vector::Zeros(N);
      for(int i = 0; i<N; i++)
        {
         if(NoNNC1[i] > NoNNC2knn[i])
            q1[i] = 1.0;
         if(NoNNC2[i] > NoNNC1knn[i])
            q2[i] = 1.0;
        }

      vector ntargs = np::bitwiseNot(targets);
      vector c1 = np::bitwiseAnd(q1,targets);
      vector c2 = np::bitwiseAnd(q2,ntargs);

      double sc1 = c1.Sum()/NC1;
      double sc2 = c2.Sum()/NC2;

      if(sc1==0.0 && sc2==0.0)
        {
         q1.Fill(0.0);
         q2.Fill(0.0);

         for(int i = 0; i<N; i++)
           {
            if(NoNNC1knn[i] > NoNNC2knn[i])
               q1[i] = 1.0;
            if(NoNNC2knn[i] > NoNNC1knn[i])
               q2[i] = 1.0;

            if(!targets[i])
               ntargs[i] = 1.0;
            else
               ntargs[i] = 0.0;
           }

         c1 = np::bitwiseAnd(q1,targets);
         c2 = np::bitwiseAnd(q2,ntargs);

         sc1 = c1.Sum()/NC1;
         sc2 = c2.Sum()/NC2;
        }

      vector out(2);

      out[0] = sc1;
      out[1] = sc2;

      return out;
     }
public:
   //+------------------------------------------------------------------+
   //|    constructor                                                   |
   //+------------------------------------------------------------------+
                     Clfspy(void)
     {
      loaded = false;
     }
   //+------------------------------------------------------------------+
   //|  destructor                                                      |
   //+------------------------------------------------------------------+
                    ~Clfspy(void)
     {
     }
   //+------------------------------------------------------------------+
   //|  load a LFSpy trained model from file                            |
   //+------------------------------------------------------------------+
   bool              load(const string file_name, bool FILE_IN_COMMON_DIRECTORY = false)
     {
      loaded = false;
      CFileTxt modelFile;
      CJAVal js;
      ResetLastError();
      if(modelFile.Open(file_name,FILE_IN_COMMON_DIRECTORY?FILE_READ|FILE_COMMON:FILE_READ,0)==INVALID_HANDLE)
        {
         Print(__FUNCTION__," failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         if(!js.Deserialize(modelFile.ReadString()))
           {
            Print("failed to read from ",file_name,".Error -",::GetLastError());
            return false;
           }
         loaded = fromJSON(js);
        }
      return loaded;
     }
   //+------------------------------------------------------------------+
   //|   make a prediction based specific inputs                        |
   //+------------------------------------------------------------------+
   vector            predict(matrix &inputs)
     {
      if(!loaded)
        {
         Print(__FUNCTION__, " No model available, Load a model first before calling this method ");
         return vector::Zeros(1);
        }

      if(inputs.Cols()!=train_data.Rows())
        {
         Print(__FUNCTION__, " input matrix does np::bitwiseNot match with shape of expected model inputs (columns)");
         return vector::Zeros(1);
        }

      matrix testdata = inputs.Transpose();

      matrix probs = classification(testdata);
      vector classes = vector::Zeros(probs.Rows());

      for(ulong i = 0; i<classes.Size(); i++)
         if(probs[i][0] > probs[i][1])
            classes[i] = 1.0;

      return classes;

     }
   //+------------------------------------------------------------------+
   //| get the parameters of the loaded model                           |
   //+------------------------------------------------------------------+
   LFS_PARAMS        getmodelparams(void)
     {
      return model_params;
     }


  };
//+------------------------------------------------------------------+

Hay dos métodos principales que los usuarios deben comprender en esta clase:

• El método load() toma un nombre de archivo como entrada, que debe apuntar al modelo LFS exportado.
• El método predict() toma una matriz con el número requerido de columnas y devuelve un vector de etiquetas de clase, correspondiente al número de filas en la matriz de entrada.
  

Veamos cómo funciona todo esto en la práctica. Comenzamos con el código Python. El archivo LFSmodelExportDemo.py prepara conjuntos de datos dentro y fuera de la muestra utilizando números generados aleatoriamente. Los datos fuera de la muestra se guardan como un archivo CSV. Se entrena un modelo LFS utilizando los datos de la muestra, luego se serializa y se guarda en formato JSON. Probamos el modelo con los datos fuera de la muestra y registramos los resultados para que luego podamos compararlos con la misma prueba realizada en MetaTrader 5. El código Python se muestra a continuación.

# Copyright 2024, MetaQuotes Ltd.
# https://www.mql5.com
# imports
import MetaTrader5 as mt5
import numpy as np
import pandas as pd
from JsonModel import lfspy2json, LocalFeatureSelection, MQL5_COMMON_FOLDER, MQL5_FILES_FOLDER
from os import path
from sklearn.metrics import accuracy_score, classification_report

#initialize MT5 terminal
if not mt5.initialize():
    print("MT5 initialization failed ")
    mt5.shutdown()
    exit() # stop the script if mt5 not initialized
  
#we want to get the path to the MT5 file sandbox
#initialize TerminalInfo instance    
terminal_info = mt5.terminal_info()

#model file name
filename = "lfsmodel.json"

#build the full path
modelfilepath = path.join(terminal_info.data_path,MQL5_FILES_FOLDER,filename)

#number of random numbers to generate
datalen = 1000

#number of features the dataset will have
datavars = 5

#set random number seed
rng_seed = 125
rng = np.random.default_rng(rng_seed)

#generate the numbers
data = rng.uniform(-1.0,1.0,size=datalen)

#shape our dataset
data = data.reshape([datalen//datavars,datavars])

#set up container for class labels
class_labels = np.zeros(shape=data.shape[0],dtype=np.uint8)

#set the class labels
for i in range(data.shape[0]):
    class_labels[i] = 1 if (data[i,1] > 0.0 and data[i,2] > 0.0) or (data[i,1] < 0.0 and data[i,2] < 0.0) else 0

#partition our data
train_size = 100
xtrain = data[:train_size,:]
ytrain = class_labels[:train_size]

#load testing data (out of sample)
test_data = data[train_size:,:]
test_labels = class_labels[train_size:]

#here we prepare the out of sample data for export using pandas
#the data will be exported in a single csv file
colnames = [ f"var_{str(col+1)}" for col in range(test_data.shape[1])]
testdata = pd.DataFrame(test_data,columns=colnames)

#the last column will be the target labels
testdata["c_labels"]=test_labels

#display first 5 samples
print("Out of sample dataframe head \n", testdata.head())
#display last 5 samples
print("Out of sample dataframe tail \n", testdata.tail())

#build the full path of the csv file
testdatafilepath=path.join(terminal_info.data_path,MQL5_FILES_FOLDER,"testdata.csv")

#try save the file
try:
    testdata.to_csv(testdatafilepath)
except Exception as e:
    print(" Error saving iris test data ")
    print(e) 
else:
    print(" test data successfully saved to csv file ")  

#initialize the LFS object
lfs = LocalFeatureSelection(rr_seed=rng_seed,alpha=8,tau=2,n_beta=20,nrrp=2000)

#train the model
lfs.fit(xtrain,ytrain)

#get the inclusion matrix
fstar = lfs.fstar

#add up all ones for each row of the inclusion matrix
bins = fstar.sum(axis=1)

#calculate the percent of times a candidate was selected
percents = 100.0 * bins.astype(np.float64)/np.float64(ytrain.shape[0])
index = np.argsort(percents)[::-1]

#output the results
print("------------------------------> Percent of times selected <------------------------------" )
for i in range(percents.shape[0]):
   print(f" Variable  {colnames[index[i]]}, selected {percents[index[i]]} %")


#conduct out of sample test of trained model
accuracy = lfs.score(test_data,test_labels)
print(f" Out of sample accuracy is {accuracy*100.0} %")


#export the model
try:
    lfspy2json(lfs,modelfilepath)
except Exception as e:
    print(" Error saving lfs model ")
    print(e)
else:
   print("lfs model saved to \n ", modelfilepath)

A continuación, nos centramos en un script de MetaTrader 5, LFSmodelImportDemo.mq5. Aquí, leemos los datos fuera de muestra producidos por el script de Python y cargamos el modelo entrenado. Luego se prueba el conjunto de datos fuera de la muestra y se comparan los resultados con los obtenidos de la prueba de Python. El código MQL5 se presenta a continuación.

//+------------------------------------------------------------------+
//|                                           LFSmodelImportDemo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<lfspy.mqh>
//script inputs
input string OutOfSampleDataFile = "testdata.csv";
input bool   OutOfSampleDataInCommonFolder = false;
input string LFSModelFileName = "lfsmodel.json";
input bool   LFSModelInCommonFolder = false;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   matrix testdata = np::readcsv(OutOfSampleDataFile,OutOfSampleDataInCommonFolder);
   
   if(testdata.Rows()<1)
    {
     Print(" failed to read csv file ");
     return;
    }
    
   
   vector testlabels = testdata.Col(testdata.Cols()-1);
   testdata = np::sliceMatrixCols(testdata,1,testdata.Cols()-1);
   
  
   Clfspy lfsmodel;
   
   if(!lfsmodel.load(LFSModelFileName,LFSModelInCommonFolder))
    {
     Print(" failed to load the iris lfs model ");
     return;
    }
    
   vector y_pred = lfsmodel.predict(testdata);
   
   vector check = MathAbs(testlabels-y_pred);
   
   Print("Accuracy is " , (1.0 - (check.Sum()/double(check.Size()))) * 100.0, " %");
  }
//+------------------------------------------------------------------+

La salida de la ejecución del script Python LFSmodelExportDemo.py.

Python  Out of sample dataframe head 
Python         var_1     var_2     var_3     var_4     var_5  c_labels
Python  0  0.337773 -0.210114 -0.706754  0.940513  0.434695         1
Python  1 -0.009701 -0.119561 -0.904122 -0.409922  0.619245         1
Python  2  0.442703  0.295811  0.692888  0.618308  0.682659         1
Python  3  0.694853  0.244405 -0.414633 -0.965176  0.929655         0
Python  4  0.120284  0.247607 -0.477527 -0.993267  0.317743         0
Python  Out of sample dataframe tail 
Python          var_1     var_2     var_3     var_4     var_5  c_labels
Python  95  0.988951  0.559262 -0.959583  0.353533 -0.570316         0
Python  96  0.088504  0.250962 -0.876172  0.309089 -0.158381         0
Python  97 -0.215093 -0.267556  0.634200  0.644492  0.938260         0
Python  98  0.639926  0.526517  0.561968  0.129514  0.089443         1
Python  99 -0.772519 -0.462499  0.085293  0.423162  0.391327         0
Python  test data successfully saved to csv file 

Python  ------------------------------> Percent of times selected <------------------------------
Python   Variable  var_3, selected 87.0 %
Python   Variable  var_2, selected 81.0 %
Python   Variable  var_4, selected 20.0 %
Python   Variable  var_1, selected 19.0 %
Python   Variable  var_5, selected 18.0 %
Python   Out of sample accuracy is 92.0 %
Python  lfs model saved to 
Python    C:\Users\Zwelithini\AppData\Roaming\MetaQuotes\Terminal\FB9A56D617EDDDFE29EE54EBEFFE96C1\MQL5\FILES\lfsmodel.json

Salida de la ejecución del script MQL5 LFSmodelImportDemo.mq5.

LFSmodelImportDemo (BTCUSD,D1)  Accuracy is 92.0 %

Comparando los resultados, podemos ver que la salida de ambos programas coincide, lo que indica que el método de exportación del modelo funciona como se esperaba.

Conclusión

La selección de características locales ofrece un enfoque innovador para la selección de características, especialmente adecuado para entornos dinámicos como los mercados financieros. Al identificar características localmente relevantes, LFS supera las limitaciones de los métodos tradicionales que se basan en un único conjunto de características globales. La adaptabilidad del algoritmo a patrones de datos variables, su capacidad para gestionar relaciones no lineales y su capacidad para equilibrar objetivos conflictivos lo convierten en una herramienta valiosa para construir modelos de aprendizaje automático. Si bien el paquete LFSpy proporciona una implementación práctica de LFS, existe potencial para optimizar aún más su eficiencia computacional, especialmente para conjuntos de datos de gran escala. En conclusión, LFS presenta un enfoque prometedor para las tareas de clasificación en dominios caracterizados por datos complejos y en evolución.

Nombre del archivo	Descripción
Mql5/include/np.mqh	Archivo Include que contiene definiciones genéricas para varias funciones de utilidad de matrices y vectores.
Mql5/include/lfspy.mqh	Archivo Include que contiene la definición de la clase Clfspy que proporciona la funcionalidad de inferencia del modelo LFS en los programas MetaTrader 5.
Mql5/scripts/JsonModel.py	Módulo local de Python que contiene la definición de la función que permite exportar el modelo LFS en formato JSON.
Mql5/scripts/LFSdemo.py	Un script de Python que demuestra cómo utilizar la clase LocalFeatureSelection para la selección de características utilizando variables aleatorias.
Mql5/scripts/LFSmodelExportDemo.py	Un script de Python que demuestra cómo exportar el modelo LFS para su uso en MetaTrader 5.
Mql5/scripts/LFSmodelImportDemo.mq5	Un script MQL5 que muestra cómo cargar y utilizar un modelo LFS exportado en un programa MetaTrader 5.