
Optimización del búfalo africano - African Buffalo Optimization (ABO)
Contenido
Introducción
El algoritmo de Optimización del Búfalo Africano (ABO) es un enfoque metaheurístico inspirado en el asombroso comportamiento de estos animales en libertad. Basado en la interacción social y las estrategias de supervivencia de los búfalos africanos, el algoritmo ABO fue desarrollado en 2015 por los científicos Julius Beneoluchi Odili y Mohd Nizam Kahar.
Los búfalos africanos son conocidos por su capacidad para defenderse colectivamente y coordinarse de forma coherente al buscar comida y agua. Estos animales viven en grandes manadas, lo cual les protege de los depredadores y favorece la formación de grupos densos donde los adultos cuidan de los jóvenes y débiles. Cuando son atacados por depredadores, los búfalos muestran una impresionante capacidad de coordinación: pueden formar un círculo alrededor de los miembros vulnerables de la manada o atacar al enemigo mediante un esfuerzo concertado.
Los principios básicos del algoritmo ABO reflejan aspectos clave del comportamiento del búfalo. En primer lugar, la comunicación: los búfalos usan señales sonoras para coordinar sus acciones, lo que en el algoritmo se corresponde con el intercambio de información entre agentes. En segundo lugar, el aprendizaje: los búfalos aprenden de su propia experiencia y de la experiencia de otros miembros de la manada, lo que en el algoritmo se realiza mediante la actualización de las posiciones de los agentes según la información recopilada.
El comportamiento único de los búfalos africanos los convierte en una interesante fuente de inspiración para crear algoritmos de optimización. Estos animales son capaces de adaptarse a los cambios de su entorno, iniciando migraciones estacionales en busca de comida y agua, y recorriendo largas distancias en busca de condiciones favorables. Durante las migraciones, los búfalos usan estrategias de búsqueda que les permiten encontrar recursos y evitar peligros con eficacia.
Así, el comportamiento altamente coordinado, colectivamente defensivo y adaptativo del búfalo africano proporciona un fuerte incentivo para el desarrollo de algoritmos de optimización como el ABO. Estos aspectos hacen del algoritmo una herramienta eficaz para resolver problemas complejos, inspirada en los mecanismos naturales que garantizan que estos asombrosos animales sobrevivan y prosperen en su entorno natural.
Implementación del algoritmo
El algoritmo de Optimización del Búfalo Africano (ABO) usa los instintos de comportamiento del búfalo africano, como la cooperación y la interacción social, para resolver problemas de optimización. Sus principios de funcionamiento son los siguientes:
1. El algoritmo comienza inicializando una población de búfalos, donde cada búfalo representa una solución potencial en el espacio de soluciones. Las posiciones de los búfalos se inicializan aleatoriamente en un espacio concreto.
2. Cada solución (posición del búfalo) se evalúa usando una función de aptitud. Si la aptitud actual del búfalo es mejor que su mejor aptitud anterior "bp_max", se mantendrá su posición. Del mismo modo, si la aptitud es mejor que la mejor aptitud de toda la manada "bg_max", también se conservará esta posición.
3. El algoritmo actualiza las posiciones de los búfalos basándose en dos señales principales: "maaa" (quedarse y explotar) y "waaa" (moverse y explorar). Estas señales ayudan a los búfalos a optimizar su búsqueda de fuentes de alimento.
4.W.k + 1 = W.k + lp * r1 * (bgmaxt.k - m.k) + lp * r2 * (bpmax.k - m.k): Esta ecuación actualiza el desplazamiento del búfalo. W.k representa el desplazamiento para la exploración, y m.k representa la posición actual de los búfalos para la explotación. lp1 y lp2 son los factores de aprendizaje, mientras que r1 y r2 son números aleatorios en el intervalo [0,1]. bgmax es la mejor posición en la manada, y bpmax es la mejor posición de un búfalo concreto.
En esta ecuación (bgmaxt.k - m.k) representa la señal "maaaa" y (bpmax.k - m.k) representa la señal "waaa".
5. A continuación, se actualiza la posición del búfalo k con respecto a su posición actual personal y al desplazamiento calculado en la fórmula anterior, usando la siguiente ecuación: m.k + 1 = λ * (W.k + m.k). Esta ecuación determina la nueva posición del búfalo, donde λ es el coeficiente de desplazamiento.
6. Si no se cumplen los criterios de parada, volveremos al paso 2 para actualizar de nuevo los valores de aptitud.
7. Cuando se alcanza el criterio de parada, el algoritmo termina y muestra un vector de posición que representa la mejor solución encontrada para el problema dado.
Vamos a describir ahora la estructura "S_Buffalo" y la clase "C_AO_ABO", que implementan la base del algoritmo.
- S_Buffalo es la estructura que representa un búfalo. Contiene un array "w" que describe el vector de desplazamiento del agente en el algoritmo.
- El constructor de la clase establece parámetros como el tamaño de la población "popSize", los factores de aprendizaje "lp1", "lp2" y el valor "lambda" que se usan en el algoritmo.
- El método "SetParams" permite establecer los parámetros del algoritmo usando como base los valores almacenados en el array "params".
- El método "Init" sirve para inicializar el algoritmo. Adopta límites de búsqueda mínimo y máximo, el paso de búsqueda y el número de épocas.
- Los métodos "Moving" y "Revision" aplican las principales etapas del algoritmo de optimización: el desplazamiento (búsqueda de una nueva solución) y la revisión (comprobación y actualización de las soluciones).
- Los campos de clase "lp1", "lp2" y "lambda" se usan para controlar el comportamiento del algoritmo.
- El array "b" de tipo "S_Buffalo" almacena las instancias de búfalo que participan en el proceso de optimización.
//—————————————————————————————————————————————————————————————————————————————— struct S_Buffalo { double w []; }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— class C_AO_ABO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ABO () { } C_AO_ABO () { ao_name = "ABO"; ao_desc = "African Buffalo Optimization"; ao_link = "https://www.mql5.com/es/articles/16024"; popSize = 50; // размер популяции lp1 = 0.7; // фактор обучения 1 lp2 = 0.5; // фактор обучения 2 lambda = 0.3; // лямбда для уравнения движения ArrayResize (params, 4); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "lp1"; params [1].val = lp1; params [2].name = "lp2"; params [2].val = lp2; params [3].name = "lambda"; params [3].val = lambda; } void SetParams () { popSize = (int)params [0].val; lp1 = params [1].val; lp2 = params [2].val; lambda = params [3].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double lp1; // фактор обучения 1 double lp2; // фактор обучения 2 double lambda; // лямбда для уравнения движения private: //------------------------------------------------------------------- S_Buffalo b []; }; //——————————————————————————————————————————————————————————————————————————————
El método "Init" de la clase "C_AO_ABO" se encarga de inicializar los parámetros del algoritmo. Parámetros del método:
- rangeMinP [] - array que indica los valores mínimos de los rangos de parámetros.
- rangeMaxP [] - array indica los valores máximos para los rangos de parámetros.
- rangeStepP [] - el array especifica los pasos para cambiar los valores de los parámetros.
- epochsP - número de épocas (iteraciones), por defecto es igual a 0. Este parámetro sirve para definir el número de iteraciones del proceso de optimización.
Lógica de funcionamiento del método:
1. Inicialización estándar: el método llama primero a "StandardInit" con los arrays transmitidos "rangeMinP", "rangeMaxP" y "rangeStepP". Si esta inicialización falla, se retornará "false".
2. Inicialización de la población:
- El método redimensiona el array "b" al valor "popSize", que se corresponde con el número de agentes de búsqueda en la población.
- Para cada agente de la población (en un ciclo de 0 a "popSize"): el tamaño del array "b[i].w" se cambia por el valor "coords", que se corresponde con el número de coordenadas (parámetros de tarea optimizados) de cada individuo.
- El array "b[i].w" se inicializa con ceros usando "ArrayInitialize".
3. Si todas las operaciones se realizan correctamente, el método retornará "true", lo cual indicá que la inicialización se ha realizado correctamente.
El método "Init" se encargará de preparar las estructuras de datos necesarias para el algoritmo, garantizando la correcta inicialización de los parámetros y la población. Se trata de un paso importante antes de ejecutar el algoritmo principal que usará estos datos para la optimización.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ABO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (b, popSize); for (int i = 0; i < popSize; i++) { ArrayResize(b [i].w, coords); ArrayInitialize (b [i].w, 0.0); } return true; } //——————————————————————————————————————————————————————————————————————————————
El método "Moving" de la clase "C_AO_ABO" se encargará de desplazar la población de búfalos por el espacio de búsqueda durante el proceso de optimización. A continuación veremos una descripción detallada de su funcionamiento:
1. El método comprueba primero si se ha realizado la revisión "if (!revision)", si aún no se ha realizado la revisión, inicializará la población con valores aleatorios:
- El ciclo exterior recorre todos los individuos de la población "popSize".
- El ciclo interior recorre todas las coordenadas "coords".
Para cada parámetro:
- En primer lugar, se genera un valor aleatorio entre "rangeMin [c]" y "rangeMax [c]" usando el método"u.RNDfromCI".
- A continuación, este valor se verifica y ajusta usando el método"u.SeInDiSp", que limita el valor dentro de un rango dado por el paso "rangeStep [c]".
- Una vez finalizada la inicialización, "revision" se establece en "true" y el método finaliza la ejecución.
2. Lógica principal de desplazamiento de los búfalos. Si la revisión ya se ha realizado, el método procederá a actualizar la posición del búfalo en el espacio:
- Las variables "w", "m", "r1", "r2", "bg" y "bp" se inicializan para los cálculos posteriores.
- El ciclo exterior recorre todos los individuos de la población "popSize".
- El ciclo interior recorre todas las coordenadas "coords":
- Luego se generan dos valores aleatorios "r1" y "r2" para actualizar la posición de los búfalos, introduciendo un elemento de aleatoriedad en su comportamiento.
- Después "bg" y "bp" obtienen los valores de sus respectivos arrays: "cB [c]" (mejores coordenadas globales de la manada) y "a [i].cB [c]" (mejores coordenadas individuales del búfalo).
- A continuación, "m" obtiene el valor del elemento del vector de posición actual "a [i].c [c]" y "w" obtiene el valor del elemento del vector de desplazamiento actual "b [i].w [c]" del búfalo en la coordenada correspondiente.
- El valor del vector de desplazamiento "b [i].w [c]" se actualiza mediante una fórmula que tiene en cuenta la mejor posición global y local del búfalo: b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m).
- A continuación, la posición en la coordenada "m" correspondiente se actualiza considerando el factor "lambda".
- Por último, se calcula el nuevo valor de la coordenada del agente de búsqueda "a[i].c[c]" y se corrige con ayuda de "u.SeInDiSp".
El método "Moving" se encarga de inicializar y actualizar la posición y desplaza a los miembros de la población durante la optimización. Usa valores aleatorios para inicializar y actualizar las posiciones de los búfalos de la misma manera, utilizando números aleatorios basados en las mejores posiciones globales y locales conocidas de los animales de la manada.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double w = 0.0; double m = 0.0; double r1 = 0.0; double r2 = 0.0; double bg = 0.0; double bp = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { r1 = u.RNDfromCI (0, lp1); r2 = u.RNDfromCI (0, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; w = b [i].w [c]; b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m); m = lambda * (m + b [i].w [c]); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
El método "Revision" de la clase "C_AO_ABO" se encarga de actualizar la mejor función y los valores de los parámetros en la población. Descripción del método:
1. La variable "ind" se inicializará con el valor "-1". Se usará para almacenar un índice de individuos con la mejor función.
2. Búsqueda del mejor individuo global:
- El ciclo "for" recorre todos los agentes de la población "popSize":
- Para cada agente, se comprueba si su valor de la función de aptitud "a[i].f" supera el mejor valor global "fB" actual.
- Si es así, "fB" se actualizará y el índice de este agente se almacenará en la variable "ind".
- Una vez finalizado el ciclo, si se ha encontrado un agente mejor (es decir, "ind" no es igual a "-1"), se llamará a la función "ArrayCopy", que copiará los parámetros "c" de este agente en el array global de mejores parámetros "cB".
3. Actualización de los mejores valores locales:
- El segundo ciclo "for" itera de nuevo todos los agentes de la población.
- Para cada agente, se comprueba si el valor de su función de aptitud "a[i].f" supera su mejor valor "a[i].fB" local.
- Si es así, se actualiza el mejor valor local "a[i].fB" y las coordenadas de este agente se copian a su mejor array de coordenadas local "cB".
El método revision realiza dos tareas principales:
- Busca y actualiza el valor de la función de mejor ajuste global y los parámetros relacionados.
- Luego actualiza los valores y parámetros de la función de mejor ajuste local para cada agente de la población.
Esta lógica es característica de aquellos algoritmos de optimización para los que resulta importante realizar un seguimiento tanto de los óptimos globales como de los locales para mejorar la búsqueda de soluciones.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
Bien, ya hemos desglosado la implementación completa del algoritmo, que es bastante simple, y ahora podemos pasar a la fase de pruebas.
Veamos cómo funciona la versión de los autores del algoritmo ABO:
=============================
5 Hilly's; Func runs: 10000; result: 0.8495807203797128
25 Hilly's; Func runs: 10000; result: 0.5186057937632769
500 Hilly's; Func runs: 10000; result: 0.2642792490546295
=============================
5 Forest's; Func runs: 10000; result: 0.6554510234450559
25 Forest's; Func runs: 10000; result: 0.41662244493546935
500 Forest's; Func runs: 10000; result: 0.21044033116304034
=============================
5 Megacity's; Func runs: 10000; result: 0.6015384615384616
25 Megacity's; Func runs: 10000; result: 0.26430769230769224
500 Megacity's; Func runs: 10000; result: 0.11120000000000112
=============================
All score: 3.89203 (43.24%)
Digamos que no es un mal resultado. Sin embargo, yo no sería yo si no intentara mejorar el algoritmo. En la versión del autor, la nueva posición del búfalo se calcula a partir de un cálculo previo del vector de desplazamiento (incremento hasta la posición actual) basado en la información sobre la mejor posición global en la manada, la mejor posición del búfalo en cuestión y su posición actual. Este vector de desplazamiento actúa como una especie de inercia en movimiento.
Se me ocurrió renunciar a la inercia y utilizar directamente la información sobre las mejores posiciones tanto mías como de la manada, aplicando el cálculo a la posición actual. Vamos a comentar el fragmento de código del autor y a escribir uno nuevo, más simple, deshaciéndonos de un parámetro externo: lambda. El nuevo código aparece resaltado en verde.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double w = 0.0; double m = 0.0; double r1 = 0.0; double r2 = 0.0; double bg = 0.0; double bp = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { /* r1 = u.RNDfromCI (0, lp1); r2 = u.RNDfromCI (0, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; w = b [i].w [c]; b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m); m = lambda * (m + b [i].w [c]); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); */ r1 = u.RNDfromCI (-lp1, lp1); r2 = u.RNDfromCI (-lp2, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; m = m + r1 * (bg - m) + r2 * (bp - m); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Estos son los resultados después de modificar la lógica de desplazamiento del búfalo:
=============================
5 Hilly's; Func runs: 10000; result: 0.833371781687727
25 Hilly's; Func runs: 10000; result: 0.6224659624836805
500 Hilly's; Func runs: 10000; result: 0.2996410968574058
=============================
5 Forest's; Func runs: 10000; result: 0.9217022975045926
25 Forest's; Func runs: 10000; result: 0.5861755787948962
500 Forest's; Func runs: 10000; result: 0.19722782275756043
=============================
5 Megacity's; Func runs: 10000; result: 0.6100000000000001
25 Megacity's; Func runs: 10000; result: 0.4315384615384614
500 Megacity's; Func runs: 10000; result: 0.13224615384615512
=============================
All score: 4.63437 (51.49%)
Los resultados han mejorado casi un 10%: Un 51,49% frente a un 43,24%. Las mejoras resultan especialmente notables en funciones con 50 y 1.000 parámetros, mientras que en funciones con 10 parámetros los cambios son casi inapreciables. Esto indica una mejora en la capacidad del algoritmo para escalar en problemas de alta dimensionalidad.
Ahora tenemos una idea más que probar: ¿y si no usamos la mejor posición de un búfalo en la fórmula, sino la mejor posición de uno seleccionado al azar de la manada, desplazando al mismo tiempo la probabilidad al principio de la lista de individuos de la población? Esto es fácil de comprobar y solo requerirá unos pocos cambios en el código. Desplazar la probabilidad al principio de la lista de población garantiza que el número aleatorio [0,0;1,0] se eleve a una potencia, descartando la parte fraccionaria del número resultante. En este caso, se usa la potencia "4".
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double w = 0.0; double m = 0.0; double r1 = 0.0; double r2 = 0.0; double bg = 0.0; double bp = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { /* r1 = u.RNDfromCI (0, lp1); r2 = u.RNDfromCI (0, lp2); bg = cB [c]; bp = a [i].cB [c]; m = a [i].c [c]; w = b [i].w [c]; b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m); m = lambda * (m + b [i].w [c]); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); */ r1 = u.RNDfromCI (-lp1, lp1); r2 = u.RNDfromCI (-lp2, lp2); bg = cB [c]; //bp = a [i].cB [c]; double r = u.RNDprobab (); int ind = (int)pow (r - 1, 4); bp = a [ind].cB [c]; m = a [i].c [c]; m = m + r1 * (bg - m) + r2 * (bp - m); a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Para aplicar la selección probabilística de individuos en una población con un desplazamiento hacia los mejores toros, necesitaremos realizar la clasificación según el nivel de aptitud de los individuos en el métodoRevision. Afortunadamente, el método "Sorting_fB" correspondiente ya ha sido añadido en un artículo anterior.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ABO::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting_fB (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Veamos los resultados de aplicar la selección probabilística de la mejor posición del búfalo en el rebaño para utilizarla en la fórmula de cálculo de la nueva posición en el algoritmo ABO:
ABO|African Buffalo Optimization|50.0|0.1|0.8|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.841272551476775
25 Hilly's; Func runs: 10000; result: 0.5701677694693293
500 Hilly's; Func runs: 10000; result: 0.28850644933225034
=============================
5 Forest's; Func runs: 10000; result: 0.9015705858486595
25 Forest's; Func runs: 10000; result: 0.49493378365495344
500 Forest's; Func runs: 10000; result: 0.1919604395333699
=============================
5 Megacity's; Func runs: 10000; result: 0.5692307692307692
25 Megacity's; Func runs: 10000; result: 0.35261538461538455
500 Megacity's; Func runs: 10000; result: 0.12010769230769343
=============================
All score: 4.33037 (48.12%)
El rendimiento global del algoritmo ha empeorado, pero sigue siendo superior al de la versión "pura" del autor. A este respecto, registraremos los resultados del primer experimento de la modificación del algoritmo y los introduciremos en la tabla de clasificación. Me gustaría señalar que para cada versión del algoritmo se han seleccionado parámetros externos con el fin de garantizar el máximo rendimiento en todas las pruebas, ya que modificar la lógica del algoritmo conlleva un cambio en su comportamiento en el espacio de búsqueda.
Resultados de las pruebas
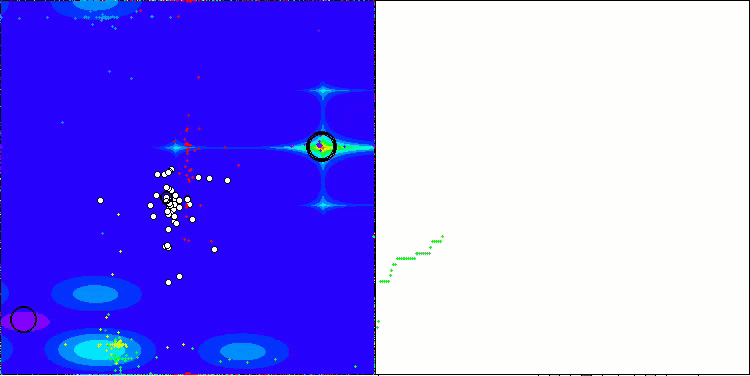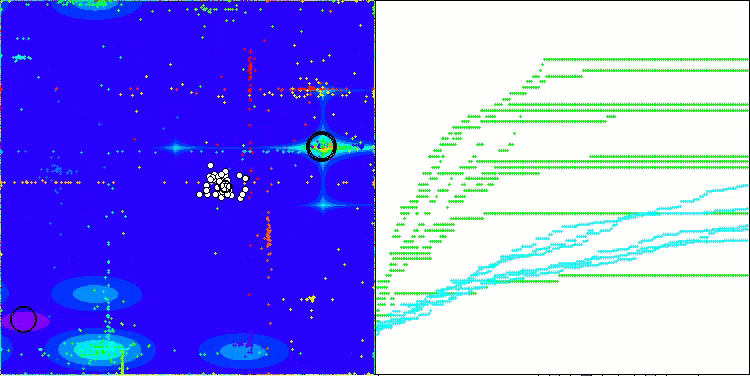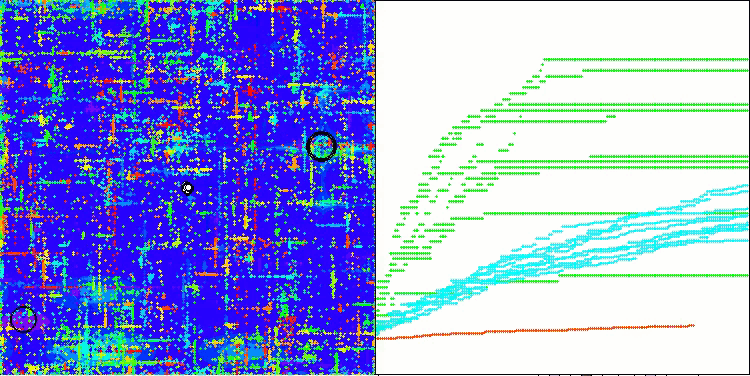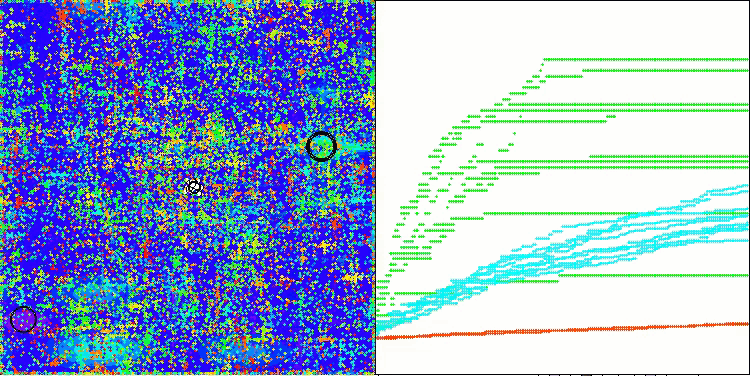
En la visualización del rendimiento del algoritmo ABO, podemos observar una elaboración bastante buena de partes significativas del hiperespacio, lo cual indica una gran capacidad para explorar la superficie de la función optimizada. Desgraciadamente, la pequeña modificación, aunque mejora la escalabilidad del algoritmo, aumenta la probabilidad de atascarse en problemas de pequeña dimensionalidad, lo que puede apreciarse en la dispersión de los resultados (líneas verdes del gráfico de convergencia en la visualización).
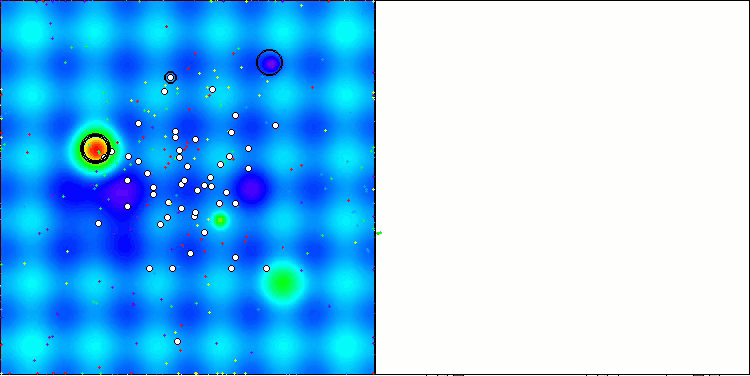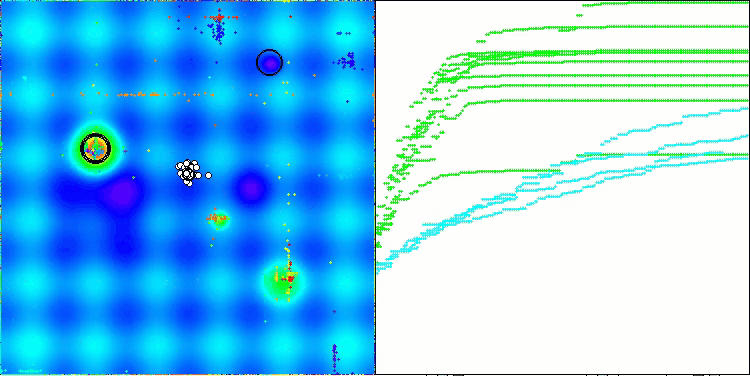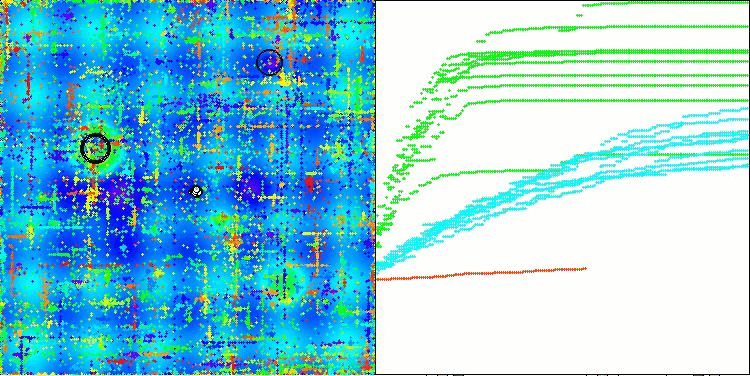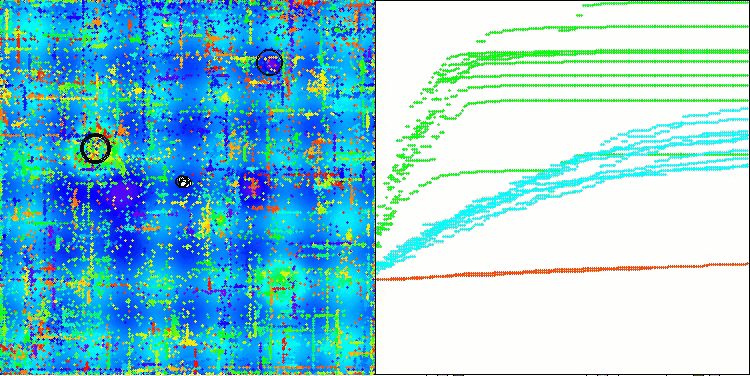
ABO en la función de prueba Hilly
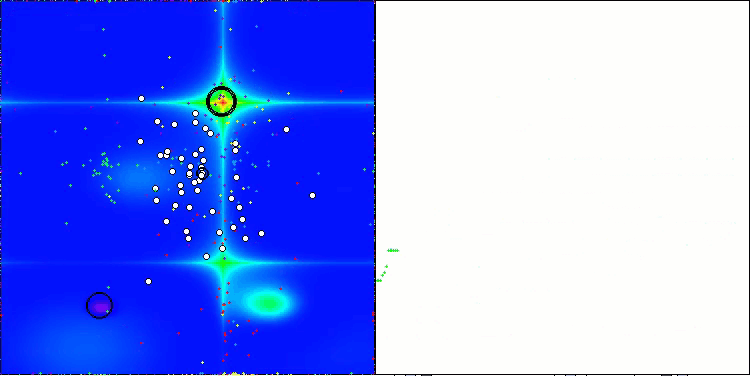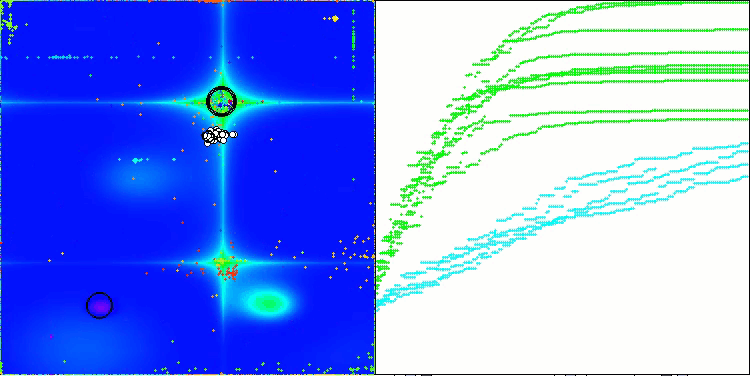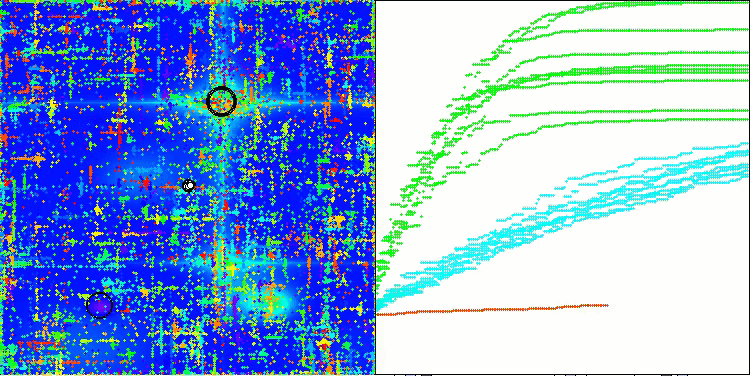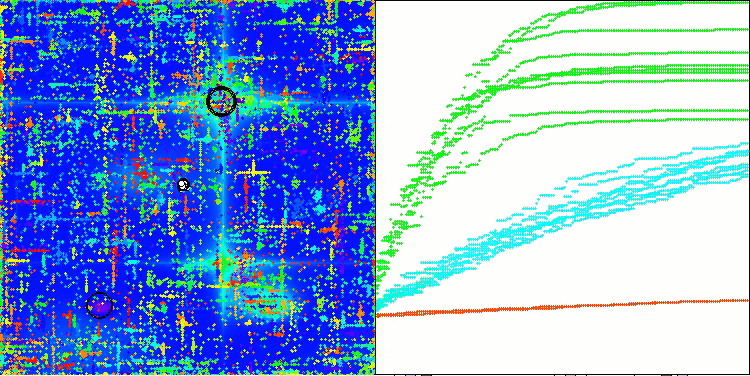
ABO en la función de prueba Forest
ABO en la función de prueba Megacity
Al final de las pruebas, el algoritmo ocupa un estable 19º puesto en la clasificación general de algoritmos de optimización.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration optimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 8 | ESG | evolution of social groups | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 9 | SIA | simulated isotropic annealing | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 10 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 11 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 12 | TSEA | turtle shell evolution algorithm | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 13 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 14 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 15 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 16 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 17 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 18 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 19 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 20 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 21 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 22 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 23 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 24 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 25 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 26 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 27 | ABH | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4.127 | 45,85 |
| 28 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 29 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 30 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3.657 | 40,63 |
| 31 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 32 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 33 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 34 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 35 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 36 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 37 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 38 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 39 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 40 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 41 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 42 | AAA | algae adaptive algorithm | 0,50007 | 0,32040 | 0,25525 | 1,07572 | 0,37021 | 0,22284 | 0,16785 | 0,76089 | 0,27846 | 0,14800 | 0,09755 | 0,52402 | 2,361 | 26,23 |
| 43 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
| 44 | IWDm | intelligent water drops M | 0,54501 | 0,37897 | 0,30124 | 1,22522 | 0,46104 | 0,14704 | 0,04369 | 0,65177 | 0,25833 | 0,09700 | 0,02308 | 0,37842 | 2,255 | 25,06 |
| 45 | PSO | particle swarm Optimization | 0,59726 | 0,36923 | 0,29928 | 1,26577 | 0,37237 | 0,16324 | 0,07010 | 0,60572 | 0,25667 | 0,08000 | 0,02157 | 0,35823 | 2,230 | 24,77 |
Conclusiones
Hoy hemos presentado al lector algunas versiones del algoritmo ABO, la original y otra con pequeñas modificaciones. Los cambios en la lógica del algoritmo han simplificado los cálculos en cada paso de la optimización y han reducido los parámetros externos de tres a dos (sin contar el parámetro responsable del tamaño de la población), lo que tuvo un efecto positivo en los resultados globales. El nuevo algoritmo también establece un equilibrio diferente entre la exploración de un nuevo espacio de soluciones y la explotación de las buenas soluciones ya encontradas.
A pesar de la tendencia del algoritmo a atascarse en problemas de baja dimensionalidad, muestra una gran eficacia en aplicaciones prácticas. La visualización del rendimiento del algoritmo ha demostrado su capacidad de explorar en profundidad zonas significativas del hiperespacio, lo que también indica su mayor capacidad de exploración. Como resultado, la nueva versión del algoritmo ha demostrado ser más potente y eficiente que la original, mostrando una buena escalabilidad en todos los tipos de funciones de prueba, incluidas las discretas.
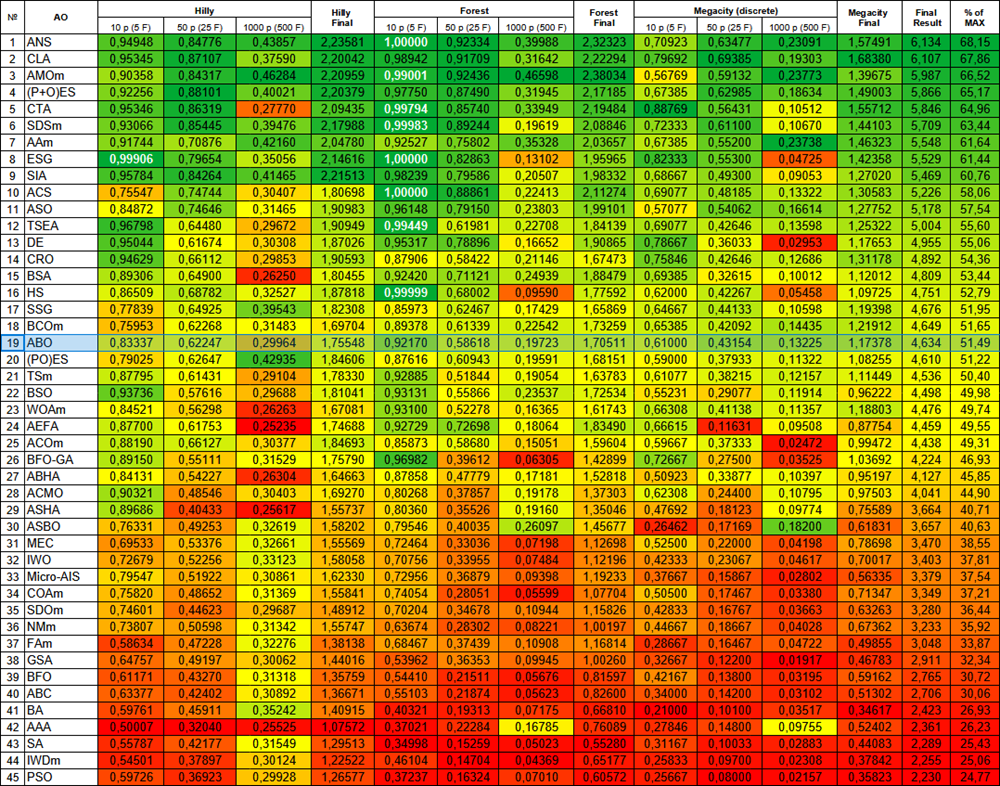
Figura 1. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados superiores o iguales a 0,99 aparecen resaltados en blanco.
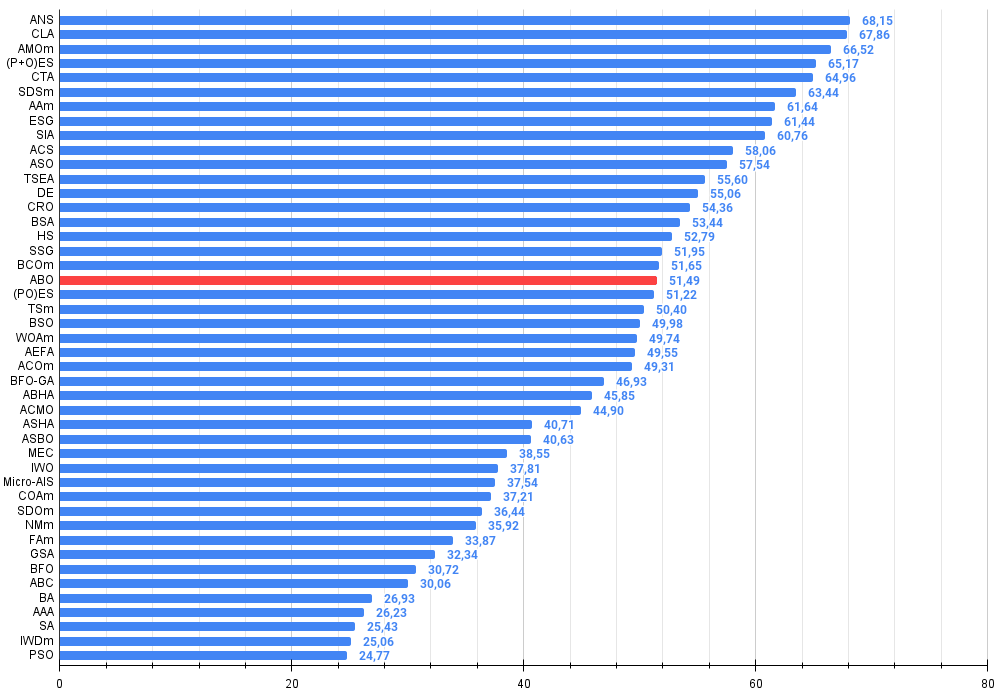
Figura 2. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor,
donde 100 es el máximo resultado teórico posible; el script para calcular la tabla de clasificación está en el archivo)
Ventajas e inconvenientes del algoritmo ABO:
Ventajas:
- Es rápido.
- Aplicación muy simple.
- Posee una buena escalabilidad.
- Pocos parámetros externos.
Desventajas:
- Gran dispersión de resultados en funciones de pequeña dimensionalidad.
- Falta de mecanismos de anti-interferencia.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16024
 Características del Wizard MQL5 que debe conocer (Parte 37): Regresión de procesos gaussianos con núcleos Matérn y lineales
Características del Wizard MQL5 que debe conocer (Parte 37): Regresión de procesos gaussianos con núcleos Matérn y lineales
 Introducción a MQL5 (Parte 9): Comprensión y uso de objetos en MQL5
Introducción a MQL5 (Parte 9): Comprensión y uso de objetos en MQL5
 Redes neuronales en el trading: Segmentación guiada
Redes neuronales en el trading: Segmentación guiada
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso