MetaTrader 5 / Ejemplos
English Русский 中文 Deutsch 日本語 Português
preview
Algoritmos de optimización de la población: Algoritmo de recocido simulado (Simulated Annealing, SA). Parte I

Algoritmos de optimización de la población: Algoritmo de recocido simulado (Simulated Annealing, SA). Parte I

MetaTrader 5 — Ejemplos | 5 junio 2024, 10:05
320 0
Andrey Dik
Andrey Dik

Contenido:

1. Introducción
2. Descripción del algoritmo
3. Resultados de las pruebas


1. Introducción

El algoritmo de optimización de recocido simulado (Simulated Annealing) fue desarrollado por Scott Kirkpatrick, George Gelatt y Mario Vecchi en 1983. En el estudio de las propiedades de líquidos y sólidos a alta temperatura, se comprueba que el metal pasa al estado líquido y las partículas se distribuyen aleatoriamente, mientras que el estado de mínima energía se alcanza bajo la condición de una temperatura inicial suficientemente alta y un tiempo de enfriamiento suficientemente largo. Si no se cumple, el material terminará en un estado metaestable con una energía no mínima, lo cual se denomina "recocido", que es el enfriamiento brusco del material. En este caso, la estructura de los átomos no tiene simetría (estado anisótropo, o de no uniformidad de las propiedades del material dentro de la red cristalina).

No obstante, durante el proceso de recocido lento, el material también pasa a un estado sólido, pero con átomos organizados y con simetría, por lo que se propuso utilizar este proceso para desarrollar un algoritmo de optimización que pudiera encontrar un óptimo global en problemas complejos. El algoritmo también se ha propuesto como método para resolver problemas de optimización combinatoria.

De esta manera, la idea básica del algoritmo se basa en un análogo matemático del proceso de recocido de metales. Durante el proceso de recocido, para distribuir uniformemente su energía interna, el metal se calienta a una temperatura elevada y luego se enfría lentamente, lo cual permite que las moléculas metálicas se muevan y se ordenen en estados más estables, al tiempo que se alivian las tensiones internas del metal y se eliminan los defectos intergranulares. El término "recocido" también está relacionado con la energía libre termodinámica, que es un atributo del material y depende de su estado.

El algoritmo de optimización de recocido simulado usa un proceso similar, y aplica operaciones similares al calentamiento y el enfriamiento de un material. El algoritmo comienza con una solución inicial, que puede ser aleatoria o derivada de iteraciones anteriores. Luego aplica operaciones de cambio de estado de la decisión, que pueden ser aleatorias o controladas, para obtener un nuevo estado, aunque sea peor que el actual. La probabilidad de tomar la peor decisión viene determinada por una función de "enfriamiento" que disminuye la probabilidad de tomar la peor decisión con el tiempo, lo cual permite al algoritmo "saltar" temporalmente de los óptimos locales y buscar mejores soluciones en otros lugares del espacio de búsqueda.

El algoritmo de recocido simulado se basa en tres conceptos esenciales:

  • La aplicación de la aleatoriedad: El algoritmo usa operaciones aleatorias para cambiar el estado de la solución y seleccionar el siguiente estado. Esto nos permite explorar distintas áreas del espacio de búsqueda y evitar quedarnos atascados en óptimos locales.
  • La toma de peores decisiones: El algoritmo SA es uno de los pocos algoritmos que favorece con cierta probabilidad las peores soluciones frente a las mejores.
  • La reducción gradual de la probabilidad de toma de peores decisiones: El algoritmo usa un proceso de "enfriamiento" que reduce la probabilidad de tomar decisiones peores con el tiempo. Esto nos permitirá explorar primero el espacio de búsqueda de forma más amplia y después centrarnos en mejorar la solución, equilibrando así la exploración y la explotación del espacio de búsqueda.

El algoritmo de optimización de recocido simulado es uno de los métodos usados en la metaheurística, que describe una clase de algoritmos para resolver problemas complejos de optimización. Estos se basan en métodos heurísticos que buscan soluciones aproximadas en el espacio de búsqueda sin requerir una iteración completa de todas las variantes posibles. La aleatoriedad es uno de los elementos clave de las metaheurísticas que permite descubrir regiones de soluciones nuevas y prometedoras. El presente algoritmo pertenece a un grupo de algoritmos denominados "métodos de optimización estocástica".

El algoritmo SA tiene desventajas que analizaremos a continuación. Se han desarrollado otros algoritmos basados en SA, como el "Adaptive Simulated Annealing, ASA", o el "Quantum Normalisation, QN" (también llamado "Quantum Annealing, QA").


2. Descripción del algoritmo

La versión básica del algoritmo de recocido simulado de los autores es extremadamente sencilla, pero no resulta fácil imaginar cómo funciona el algoritmo sin una representación visual de los gráficos del proceso de cambio de temperatura y del gráfico de probabilidad de toma de peores decisiones.

Vayamos poco a poco. El algoritmo parte de una temperatura inicial elevada (parámetro externo), que se corresponde con el calentamiento del material en metalurgia. Una temperatura elevada implica una energía elevada de las moléculas que pasan de un estado energético diferente a un estado energético inferior o superior. De manera similar a este proceso de movimiento de alta energía en el metal, el sistema puede tomar decisiones peores con cierta probabilidad.

Si imaginamos a un esquiador descendiendo desde la cima de una montaña, una vez se encuentre en alguna llanura localizada, el esquiador podría pensar que ha llegado al pie de la montaña. Y para estar seguro de lo acertado de la decisión, deberá empeorar ligeramente su posición y ascender hasta cierta altura, para descender aún más rápido precipitarse hacia abajo. De eso se trata, de tomar decisiones peores con cierta probabilidad. Para saltar fuera de la "trampa" local, se desarrolló un algoritmo de recocido cuántico que simulaba los efectos cuánticos de hallarse en dos lugares al mismo tiempo, en el que se supone que es posible saltar por encima de las "paredes" usando la tunelización; pero tratando de deshacerse de algunos inconvenientes, el recocido cuántico topó con otros, en particular con el problema de la selección de la fuerza de transición cuántica.

Para describir el proceso de recocido simulado, se usan varias fórmulas sencillas. Fórmula para calcular la energía:

E = f (x)

Es decir, E representa el valor de la función de aptitud para el estado actual del agente.

Fórmula para calcular el cambio de energía:

ΔE = E_nuevo - E_viejo

donde:

  • ΔE - cambio de energía en la transición del estado actual a un nuevo estado (diferencia de valores de la función de aptitud en dos iteraciones consecutivas).
  • E_new - valor energético del nuevo estado
  • E_old - valor energético del estado anterior

Fórmula para calcular la probabilidad de tomar la peor decisión:

P = exp (-ΔE / T)

donde:

  • P - probabilidad de tomar la peor decisión
  • T - temperatura actual

El gráfico siguiente, que muestra la dependencia de la probabilidad P, muestra que a mayor ΔE corresponde una menor probabilidad. Esto significa que, conforme disminuya la temperatura, la probabilidad de transiciones de alta energía hacia el lado peor disminuirá más rápidamente que las transiciones con diferencias de energía más pequeñas. Es decir, el algoritmo asumirá cada vez menos "riesgos" al intentar escapar de la "trampa", prefiriendo solo mejorar la solución. En la figura 1 se muestra un gráfico con la dependencia de las probabilidades, y se utiliza una disminución lineal de la temperatura para mayor claridad, aunque el algoritmo utiliza un cambio no lineal de la temperatura.

delta ch

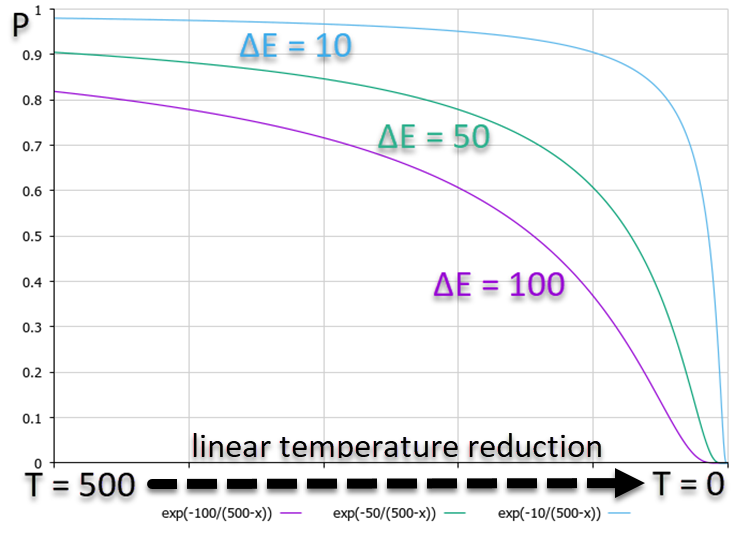
Figura 1. Gráfico de las probabilidades de decisión según el cambio de energía para el peor lado con una disminución lineal de la temperatura.

Fórmula para actualizar la temperatura:

Tnew = α * Tprev

donde:

  • α - coeficiente de enfriamiento, normalmente α se encuentra entre 0,8 y 0,99
  • Tnew - nueva temperatura
  • Tprev - temperatura anterior

La gráfica del cambio de temperatura en cada iteración con el coeficiente α = 0.99, 0.8, 0.5 y 0.1 a la temperatura inicial T = 500 se muestra en la figura 2. La temperatura disminuye gradualmente, lo cual se corresponde con el enfriamiento del material. La disminución de la temperatura en cada iteración provoca una disminución de la probabilidad de tomar peores decisiones, lo cual se corresponde con una disminución de la capacidad de las moléculas para cambiar su estado energético a medida que disminuye la temperatura.

Gráfico de temperatura

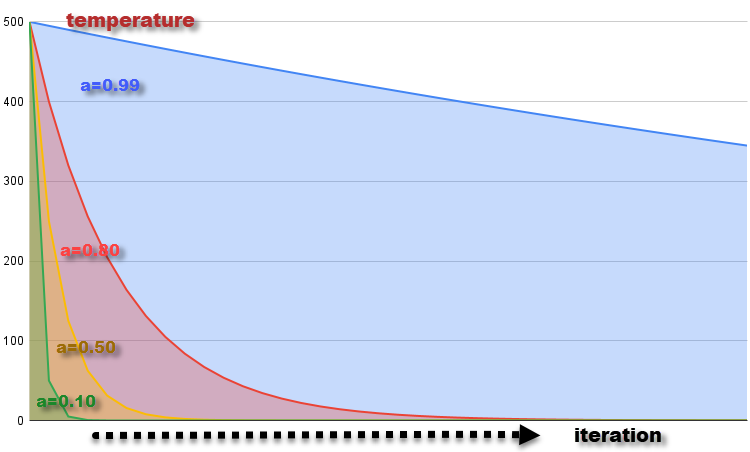
Figura 2. Gráfico de variación de la temperatura con coeficientes α = 0,99, 0,8, 0,5 y 0,1.

Fórmula para generar un nuevo estado del sistema:

x_new = GenerateNeighbor (x)

donde:

  • x_new - nuevo estado generado a partir del estado actual x
  • GenerateNeighbor (x) - función que genera un nuevo estado realizando cambios aleatorios con distribución uniforme en el estado actual.

Ahora, conociendo todos los fundamentos teóricos del algoritmo de recocido simulado, no deberíamos tener problemas para escribir el código de SA. Podemos representar el movimiento de las moléculas que cambian su estado energético y que son agentes como una estructura, S_Agent, que contiene información sobre el agente en el problema de optimización. Descripción de los campos y los métodos de la estructura:

  • Init (int coords): inicializa el agente y asigna memoria para los arrays "c" y "cPrev" de tamaño "coords". También establece los valores iniciales de "f" y "fPrev" en "-DBL_MAX" (infinito negativo)
  • c []: el array "c" representa las coordenadas del agente en el espacio de optimización
  • cPrev []: el array "cPrev" representa las coordenadas anteriores del agente
  • f: representa el valor de la función de aptitud para las coordenadas actuales del agente
  • fPrev: representa el valor anterior de la función de aptitud del agente
//————————————————————————————————————————
struct S_Agent
{
  void Init (int coords)
  {
    ArrayResize (c,     coords);
    ArrayResize (cPrev, coords);
    f     = -DBL_MAX;
    fPrev = -DBL_MAX;
  }

  double c     []; //coordinates
  double cPrev []; //previous coordinates
  double f;        //fitness
  double fPrev;    //previous fitness
};
//————————————————————————————————————————

Describiremos la clase de algoritmo SA y la llamaremos C_AO_SA. Resultará muy sencillo porque no contiene nada inusual que no hayamos usado antes, salvo variables y constantes térmicas específicas.

Campos y métodos de la clase:

  • cB []: array con las mejores coordenadas encontradas por el algoritmo de optimización en el momento de la iteración actual
  • fB: valor de la función de aptitud para las mejores coordenadas
  • a []: el array representa a los agentes, se utiliza para almacenar información sobre cada agente en el problema de optimización, cada elemento del array es un ejemplar de la estructura S_Agent
  • rangeMax []: array con los valores máximos del rango de búsqueda para cada coordenada; se utiliza para definir el límite superior de la búsqueda para cada coordenada del agente.
  • rangeMin []: array de los valores mínimos del rango de búsqueda para cada coordenada; se utiliza para definir el límite inferior de la búsqueda para cada coordenada del agente.
  • rangeStep []: array que representa los pasos de búsqueda para cada coordenada
  • Init (const int coordsP, const int popSizeP, const double tP, const double aP, const double dP): el método inicializa el algoritmo de optimización, acepta los parámetros: el número de coordenadas "coordsP", el tamaño de la población "popSizeP", la temperatura inicial "tP", el factor de reducción de la temperatura "aP" y el factor de difusión "dP", el método inicializa los campos de clase y agente
  • Moving (): método que desplaza los agentes durante el proceso de optimización y utiliza un algoritmo para determinar las nuevas coordenadas de los agentes.
  • Revision (): método que revisa y actualiza las mejores coordenadas y la función de aptitud basándose en los valores actuales de los agentes.
  • SeInDiSp (double In, double InMin, double InMax, double Step): método privado usado para normalizar el valor de "In" en el rango de "InMin" a "InMax" en pasos "Step".
  • RNDfromCI (double min, double max): método privado usado para generar un número aleatorio dentro de un rango dado de "min" a "max".

Cabe señalar que el coeficiente de difusión dP falta en la versión original SA. La cuestión es que la idea de los autores era generar un nuevo estado del sistema y, en consecuencia, una nueva coordenada de los agentes en el intervalo completo de "mín" a "máx" de cada coordenada, lo cual se correspondería con el movimiento caótico de las moléculas en todo el "volumen" del metal sometido al recocido. Mis experimentos han demostrado que los resultados mejoran si restringimos el intervalo de vibración de las moléculas a solo algún intervalo expresado en partes del intervalo total admisible. Este es el significado de este parámetro del coeficiente de difusión: limitar el área de posible mezcla de moléculas.

Para obtener resultados equivalentes a los del SA original, bastará con establecer este parámetro en 1 (por defecto, 0,2). 

//————————————————————————————————————————
class C_AO_SA
{
  //----------------------------------------------------------------------------
  public: double  cB [];  //best coordinates
  public: double  fB;     //FF of the best coordinates
  public: S_Agent a  [];  //agent

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,      //coordinates number
                     const int    popSizeP,     //population size
                     const double tP,           //temperature
                     const double aP,           //temperature reduction coefficient
                     const double dP);          //diffusion coefficient


  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;       //coordinates number
  private: int    popSize;      //population size

  private: double T;
  private: double α;
  private: double d;

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//————————————————————————————————————————

El método de inicialización es la función "Init", que inicializará todos los campos de la clase y asignará los tamaños de los arrays necesarios para el algoritmo de optimización. 

//————————————————————————————————————————
void C_AO_SA::Init (const int    coordsP,      //coordinates number
                    const int    popSizeP,     //population size
                    const double tP,           //temperature
                    const double aP,           //temperature reduction coefficient
                    const double dP)           //diffusion coefficient
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords     = coordsP;
  popSize    = popSizeP;
  T          = tP;
  α          = aP;
  d          = dP;

  ArrayResize (a, popSize);
  for (int i = 0; i < popSize; i++) a [i].Init (coords);

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//————————————————————————————————————————

Para desplazar agentes en el espacio de búsqueda, escribiremos el método "Moving". 
En la primera iteración, cuando se acaba de ejecutar el algoritmo, la variable - flag "revision" es igual a "false", deberemos inicializar los agentes de la población con los valores iniciales situados en el rango [min;max] de coordenadas con distribución uniforme. Los valores obtenidos de las coordenadas de los agentes se normalizan usando la función SeInDiS para cumplir el paso de movimiento requerido. A continuación, la bandera "revision" se establecerá en "true" para indicar que deberemos aplicar los operadores del algoritmo de recocido simulado en la siguiente iteración.

En la segunda iteración y siguientes, si se tratara del SA original, haríamos lo mismo que en la primera iteración, es decir, seguiríamos generando números aleatorios dentro de un rango dado con una distribución uniforme. En nuestra versión ligeramente modificada, haremos lo mismo, pero con un rango de valores ajustado, limitando así la región de interacción difusiva de las moléculas en el metal, mientras nos desplazaremos desde donde estaba la molécula en la iteración anterior. Los valores obtenidos de las coordenadas de los agentes se normalizan usando la función SeInDiS para cumplir el paso de movimiento requerido. 

//————————————————————————————————————————
void C_AO_SA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double rnd = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      rnd = RNDfromCI (-0.1, 0.1);
      a [i].c [c] = a [i].cPrev [c] + rnd * (rangeMax [c] - rangeMin [c]) * d;
      a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//————————————————————————————————————————
Si en el método "Moving" ejecutamos la generación de nuevos estados del sistema, es decir, movimos moléculas en el metal fundido, en el método "Revision" realizaremos el cálculo del "equilibrio térmico" y la probabilidad de transición de las moléculas a un nuevo estado.

Al principio del método comprobaremos los valores de todas las funciones de aptitud de los agentes, y si encontramos valores mejores que el global, entonces lo actualizaremos.

Luego, en un ciclo "for" realizamos las siguientes acciones para cada agente de la población:
  • el valor "ΔE" se calculará como el valor absoluto de la diferencia entre "a[i].f" y "a[i].fPrev", es decir, la diferencia entre los valores de la función de aptitud en la iteración actual y en la anterior.

Si el valor de "a[i].f" es mayor que el valor de "a[i].fPrev" (es decir, la adaptación actual es mejor que la anterior), se ejecutará el siguiente bloque de código:

  • el valor "a[i].fPrev" se sustituirá por el valor "a[i].f"
  • los valores del array "a[i].cPrev" se copiarán del array "a[i].c"

En caso contrario, se ejecutará el siguiente bloque de código (el valor actual de la función de aptitud es peor que el anterior):

  • el valor de probabilidad "P" se calculará como el exponente de la relación negativa entre "ΔE" y "T"
  • generaremos un número aleatorio del intervalo [0,0;1,0] para "rnd" que modele la probabilidad de transición a un nuevo estado que sea peor que el anterior.

Si el valor de "rnd" es inferior al valor "P" (es decir, se cumple la probabilidad), entonces:

  • el valor "a[i].fPrev" se sustituirá por el valor "a[i].f"
  • los valores del array "a[i].cPrev" se copiarán del array "a[i].c"

El valor de temperatura "T" se multiplicará por el coeficiente térmico "α", que posibilitará la disminución de la temperatura con cada nueva iteración. 

//————————————————————————————————————————
void C_AO_SA::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB) ind = i;
  }

  if (ind != -1)
  {
    fB = a [ind].f;
    ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
  }

  //----------------------------------------------------------------------------
  double rnd  = 0.0;
  double ΔE;
  double P;

  for (int i = 0; i < popSize; i++)
  {
    ΔE = fabs (a [i].f - a [i].fPrev);

    if (a [i].f > a [i].fPrev)
    {
      a [i].fPrev = a [i].f;
      ArrayCopy (a [i].cPrev, a [i].c, 0, 0, WHOLE_ARRAY);
    }
    else
    {
      P = exp (-ΔE / T);
      rnd = RNDfromCI (0, 1.0);

      if (rnd < P)
      {
        a [i].fPrev = a [i].f;
        ArrayCopy (a [i].cPrev, a [i].c, 0, 0, WHOLE_ARRAY);
      }

    }
  }

  T = α * T;
}
//————————————————————————————————————————


3. Resultados de las pruebas

Impresión del funcionamiento del algoritmo original en un banco de pruebas con generación de números aleatorios en todo el rango aceptable de valores:

C_AO_SA:50:1000.0:0.1:0.2
=============================
5 Rastrigin's; Func runs 10000 result: 61.3646399742684
Score: 0.76034
25 Rastrigin's; Func runs 10000 result: 47.454223750487884
Score: 0.58798
500 Rastrigin's; Func runs 10000 result: 39.06494648961887
Score: 0.48404
=============================
5 Forest's; Func runs 10000 result: 0.4708272303190655
Score: 0.26632
25 Forest's; Func runs 10000 result: 0.17553657864203864
Score: 0.09929
500 Forest's; Func runs 10000 result: 0.0538869772164491
Score: 0.03048
=============================
5 Megacity's; Func runs 10000 result: 2.6
Score: 0.21667
25 Megacity's; Func runs 10000 result: 1.0
Score: 0.08333
500 Megacity's; Func runs 10000 result: 0.3044
Score: 0.02537
=============================
All score: 2.55383

Y esta es una impresión del algoritmo ejecutándose en un banco de pruebas con el coeficiente de difusión añadido:

C_AO_SA:50:1000.0:0.1:0.2
=============================
5 Rastrigin's; Func runs 10000 result: 65.78409729002105
Score: 0.81510
25 Rastrigin's; Func runs 10000 result: 52.25447043222567
Score: 0.64746
500 Rastrigin's; Func runs 10000 result: 40.40159931988021
Score: 0.50060
=============================
5 Forest's; Func runs 10000 result: 0.5814827554067439
Score: 0.32892
25 Forest's; Func runs 10000 result: 0.23156336186841173
Score: 0.13098
500 Forest's; Func runs 10000 result: 0.06760002887601002
Score: 0.03824
=============================
5 Megacity's; Func runs 10000 result: 2.92
Score: 0.24333
25 Megacity's; Func runs 10000 result: 1.256
Score: 0.10467
500 Megacity's; Func runs 10000 result: 0.33840000000000003
Score: 0.02820
=============================
All score: 2.83750

De los resultados de estas dos pruebas se desprende que los resultados del algoritmo han mejorado notablemente con la aplicación del coeficiente de difusión. El algoritmo original ha necesitado mejoras para llegar a nuestra mesa. Resulta inesperado que un método de optimización tan conocido y popular obtenga resultados tan pobres, sobre todo porque sus aplicaciones son muy amplias, incluido su uso en el entrenamiento de redes neuronales.

La visualización del funcionamiento de SA no ha revelado ningún rasgo distintivo apreciable en el comportamiento de los agentes en el espacio de búsqueda, los puntos se han comportado caóticamente sin formar estructuras, de forma similar al movimiento browniano térmico. Además, podemos añadir que existe un atascamiento en los extremos locales y que la convergencia deja mucho que desear, aunque no existe falta de diversidad poblacional, es decir, la población no se agota al final de las iteraciones.

rastrigin

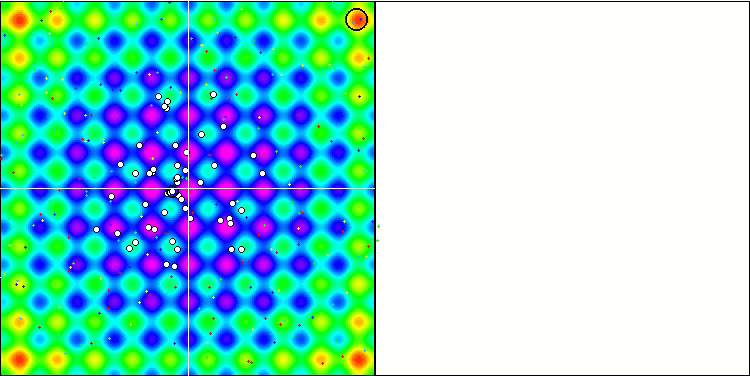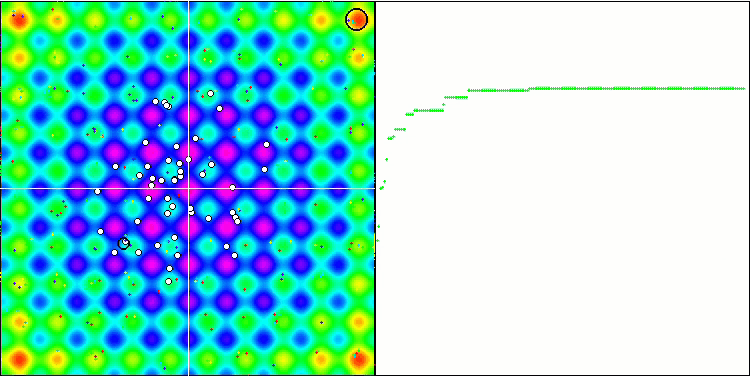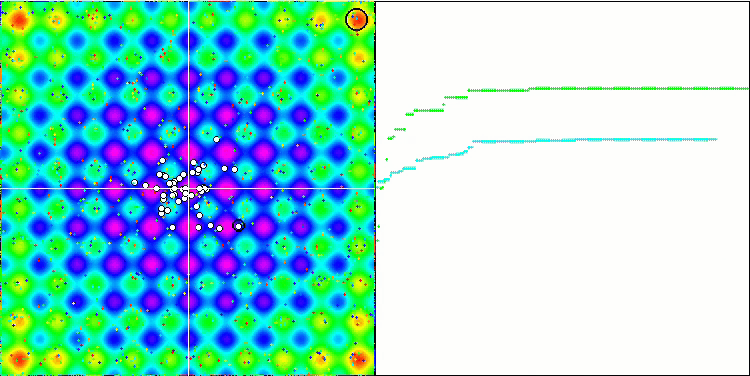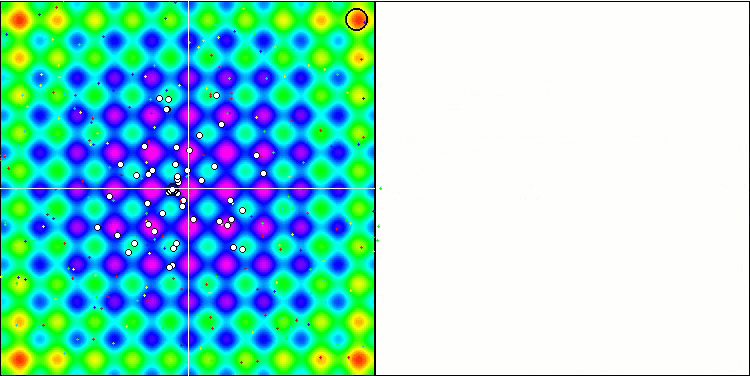
  SA en la función de prueba Rastrigin.

forest

  SA en la función de prueba Forest.

megacity

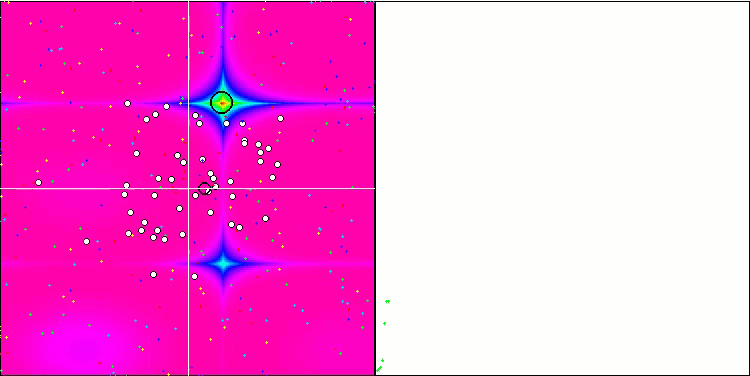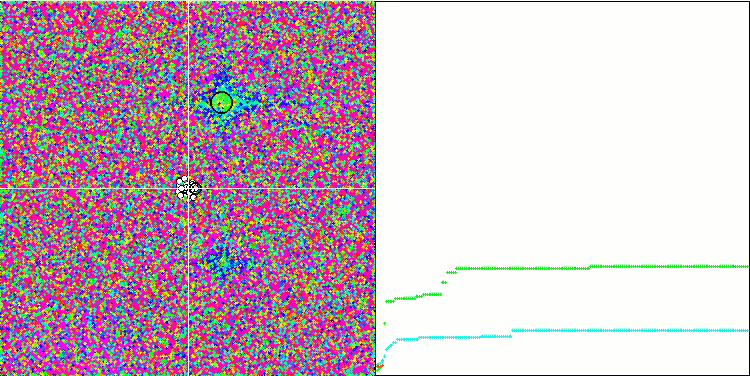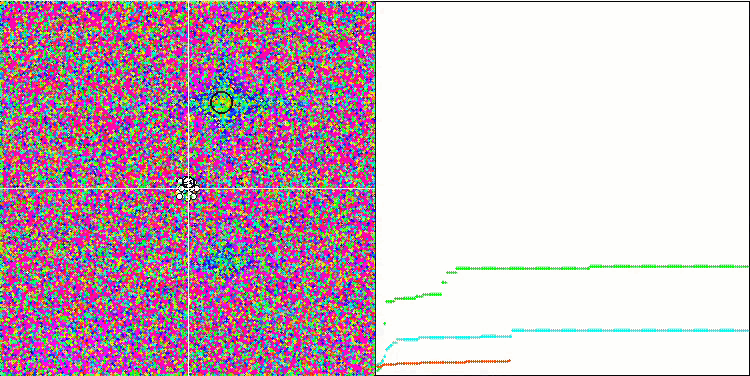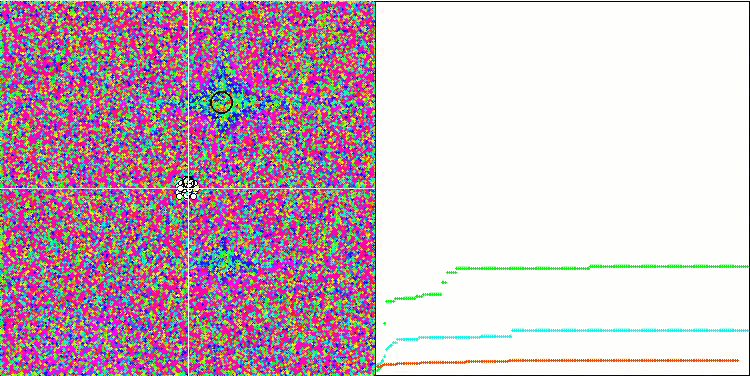
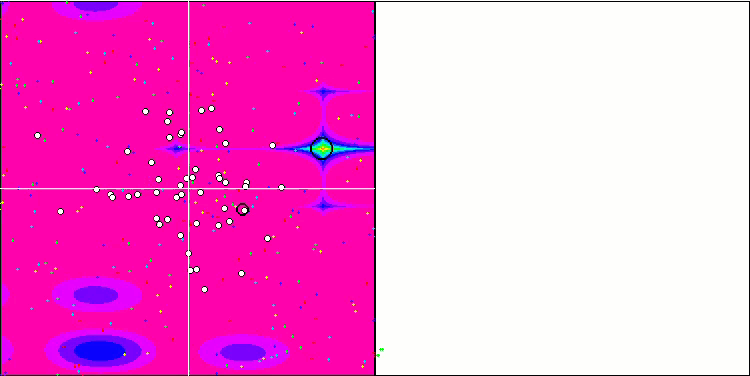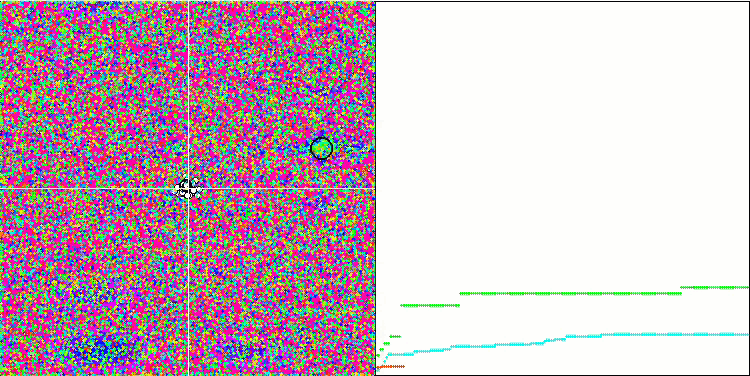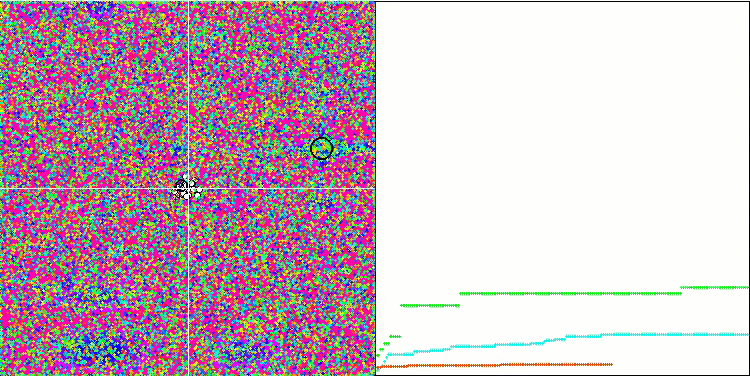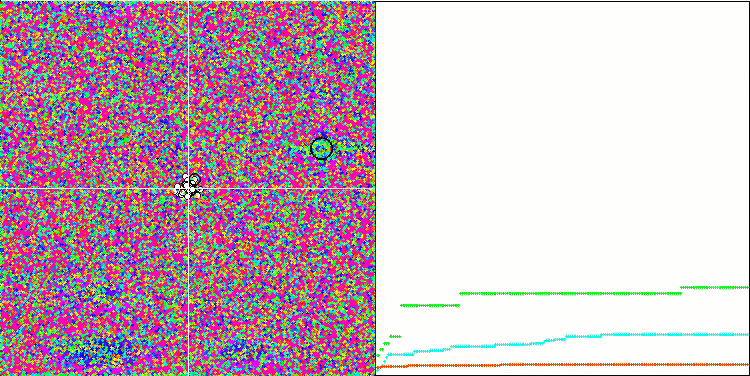
   SA en la función de prueba Megacity.


El algoritmo de recocido simulado ha ocupado el último lugar de la tabla. La tabla comparativa muestra que el algoritmo no presenta ninguna característica distintiva en las pruebas individuales: todos los resultados están por debajo de la media. Hay algoritmos como el CSS que muestran grandes resultados en pruebas individuales, aunque están en la parte inferior de la tabla; por desgracia, el algoritmo SA no es uno de ellos.

№

AO

Description

Rastrigin

Rastrigin final

Forest

Forest final

Megacity (discrete)

Megacity final

Final result

10 p (5 F)

50 p (25 F)

1000 p (500 F)

10 p (5 F)

50 p (25 F)

1000 p (500 F)

10 p (5 F)

50 p (25 F)

1000 p (500 F)

1

SDSm

stochastic diffusion search M

0,99809

1,00000

0,69149

2,68958

0,99265

1,00000

1,00000

2,99265

1,00000

1,00000

1,00000

3,00000

100,000

2

SSG

saplings sowing and growing

1,00000

0,92761

0,51630

2,44391

0,72120

0,65201

0,83760

2,21081

0,54782

0,61841

0,99522

2,16146

77,683

3

DE

differential evolution

0,98295

0,89236

0,51375

2,38906

1,00000

0,84602

0,65510

2,50112

0,90000

0,52237

0,12031

1,54268

73,099

4

HS

harmony search

0,99676

0,88385

0,44686

2,32747

0,99148

0,68242

0,37529

2,04919

0,71739

0,71842

0,41338

1,84919

70,623

5

IWO

invasive weed optimization

0,95828

0,62227

0,27647

1,85703

0,70170

0,31972

0,26613

1,28755

0,57391

0,30527

0,33130

1,21048

48,250

6

ACOm

ant colony optimization M

0,34611

0,16683

0,15808

0,67103

0,86147

0,68980

0,64798

2,19925

0,71739

0,63947

0,05579

1,41265

47,387

7

MEC

mind evolutionary computation

0,99270

0,47345

0,21148

1,67763

0,60244

0,28046

0,21324

1,09615

0,66957

0,30000

0,26045

1,23002

44,049

8

SDOm

spiral dynamics optimization M

0,69840

0,52988

0,33168

1,55996

0,59818

0,38766

0,37600

1,36183

0,35653

0,15262

0,25842

0,76758

40,289

9

NMm

Nelder-Mead method M

0,88433

0,48306

0,45945

1,82685

0,46155

0,24379

0,21903

0,92437

0,46088

0,25658

0,16810

0,88555

39,660

10

COAm

cuckoo optimization algorithm M

0,92400

0,43407

0,24120

1,59927

0,57881

0,23477

0,13842

0,95200

0,52174

0,24079

0,17001

0,93254

37,830

11

FAm

firefly algorithm M

0,59825

0,31520

0,15893

1,07239

0,50637

0,29178

0,41704

1,21519

0,24783

0,20526

0,35090

0,80398

33,139

12

ABC

artificial bee colony

0,78170

0,30347

0,19313

1,27829

0,53379

0,14799

0,11177

0,79355

0,40435

0,19474

0,13859

0,73768

29,766

13

BA

bat algorithm

0,40526

0,59145

0,78330

1,78002

0,20664

0,12056

0,21769

0,54488

0,21305

0,07632

0,17288

0,46225

29,499

14

CSS

charged system search

0,56605

0,68683

1,00000

2,25289

0,13961

0,01853

0,13638

0,29452

0,07392

0,00000

0,03465

0,10856

27,930

15

GSA

gravitational search algorithm

0,70167

0,41944

0,00000

1,12111

0,31390

0,25120

0,27812

0,84322

0,42609

0,25525

0,00000

0,68134

27,807

16

BFO

bacterial foraging optimization

0,67203

0,28721

0,10957

1,06881

0,39364

0,18364

0,17298

0,75026

0,37392

0,24211

0,18841

0,80444

27,542

17

EM

electroMagnetism-like algorithm

0,12235

0,42928

0,92752

1,47915

0,00000

0,02413

0,29215

0,31628

0,00000

0,00527

0,10872

0,11399

19,002

18

SFL

shuffled frog-leaping

0,40072

0,22021

0,24624

0,86717

0,19981

0,02861

0,02221

0,25063

0,19565

0,04474

0,06607

0,30646

13,200

19

SA

simulated annealing

0,36938

0,21640

0,10018

0,68595

0,20341

0,07832

0,09372

0,37545

0,16956

0,08422

0,10394

0,35772

13,138

20

MA

monkey algorithm

0,33192

0,31029

0,13582

0,77804

0,09927

0,05443

0,07482

0,22852

0,15652

0,03553

0,10669

0,29874

11,777

21

FSS

fish school search

0,46812

0,23502

0,10483

0,80798

0,12730

0,03458

0,05458

0,21647

0,12175

0,03947

0,08244

0,24366

11,332

22

IWDm

intelligent water drops M

0,26459

0,13013

0,07500

0,46972

0,28358

0,05445

0,05112

0,38916

0,22609

0,05659

0,05054

0,33322

10,423

23

PSO

particle swarm optimisation

0,20449

0,07607

0,06641

0,34696

0,18734

0,07233

0,18207

0,44175

0,16956

0,04737

0,01947

0,23641

8,426

24

RND

random

0,16826

0,09038

0,07438

0,33302

0,13381

0,03318

0,03949

0,20648

0,12175

0,03290

0,04898

0,20363

5,054

25

GWO

grey wolf optimizer

0,00000

0,00000

0,02093

0,02093

0,06514

0,00000

0,00000

0,06514

0,23478

0,05789

0,02545

0,31812

1,000


Conclusiones

El algoritmo de recocido simulado presenta varios puntos débiles que pueden limitar su eficacia en la resolución de algunos problemas de optimización. Algunos de estos puntos débiles serían:

  • Dependencia de la solución inicial: como muchos otros métodos de optimización, el algoritmo de recocido simulado puede depender de una solución inicial seleccionada al azar. Si la solución inicial es mala, el algoritmo podría quedarse atascado en un óptimo local y no encontrar un óptimo global.

    Es importante señalar que el algoritmo requiere el ajuste de parámetros como la "temperatura" inicial, el paso de cambio de la temperatura, que afectan a la probabilidad de tomar la peor decisión. Estos parámetros afectan al rendimiento y la calidad de las soluciones, por lo que la selección y el ajuste de los parámetros serán aspectos importantes a la hora de aplicar el algoritmo de recocido simulado a un problema de optimización concreto. La configuración de estos ajustes puede resultar complicada, y los ajustes incorrectos podrían dar lugar a malos resultados. Hemos elegido la configuración por defecto para obtener los mejores resultados en el conjunto de funciones de prueba.

  • Otro punto débil del algoritmo de recocido simulado es la posibilidad de quedarse atascado en los extremos locales. Esto ocurre cuando el algoritmo halla una solución óptima que es un extremo local pero no es un extremo global. En este caso, el algoritmo no podrá avanzar más y se detendrá en el óptimo local, cosa que se ve muy bien en la visualización de arriba.

  • Baja tasa de convergencia: El SA puede tardar en converger a la solución óptima, especialmente en problemas de optimización complejos. Esto se debe a que el algoritmo utiliza el azar y puede tomar peores decisiones, lo cual puede ralentizar el proceso de optimización.

  • Necesidad de un gran número de iteraciones: Para alcanzar una solución óptima, el algoritmo de recocido simulado puede necesitar un gran número de iteraciones. Esto podría ser un problema para las tareas en las que el tiempo de ejecución resulta un factor crítico.

  • Ineficacia en la resolución de problemas con un gran número de variables: El SA puede resultar ineficaz al resolver problemas con un gran número de variables, ya que el espacio de búsqueda puede ser demasiado grande. En este caso, otras técnicas de optimización, como los algoritmos genéticos o los métodos de optimización basados en el gradiente, podrían resultar más eficaces. El algoritmo procesa bien un número pequeño de variables (1-2), tan bien como cualquier algoritmo, incluso el RND aleatorio simple.

Hay varias mejoras que podemos aplicar al algoritmo de recocido simulado para mejorar su rendimiento y eficacia:

1. Modificación de la función de refrigeración: la función de refrigeración es un parámetro importante del algoritmo que controla la velocidad de refrigeración y la temperatura del sistema.

2. Uso de métodos más eficaces para elegir el siguiente estado: El SA utiliza la selección aleatoria del siguiente estado. No obstante, existen métodos más eficaces para seleccionar el siguiente estado, como los métodos de mutación y cruce.

3. Uso de parámetros adaptables: los parámetros del algoritmo, como la temperatura inicial y el coeficiente de refrigeración, pueden ajustarse de forma adaptable según las características del problema de optimización.

4. Uso de una combinación de algoritmos: El SA puede combinarse con otros algoritmos de optimización, como los algoritmos genéticos o los métodos de descenso de gradiente, para mejorar el rendimiento y la eficacia de la optimización.

La aplicación de distintas distribuciones de la variable aleatoria al generar un nuevo estado del sistema, en lugar de una uniforme, no ha ayudado a mejorar los resultados. Sin embargo, existe una forma de transformar drásticamente este algoritmo tan conocido y popular hasta el punto de que pueda competir con los líderes de la tabla por los primeros lugares. ¿Cómo es posible? - En la segunda parte del artículo, compartiremos este método y veremos todos los pasos de modificación realizados. Pero como sabemos, no existe una forma universal de mejorar ningún algoritmo de optimización: dependerá exclusivamente de la estrategia de búsqueda del propio algoritmo. Por ello, la mejora solo afectará al viejo (pero prácticamente inútil) algoritmo de recocido simulado.


rating table

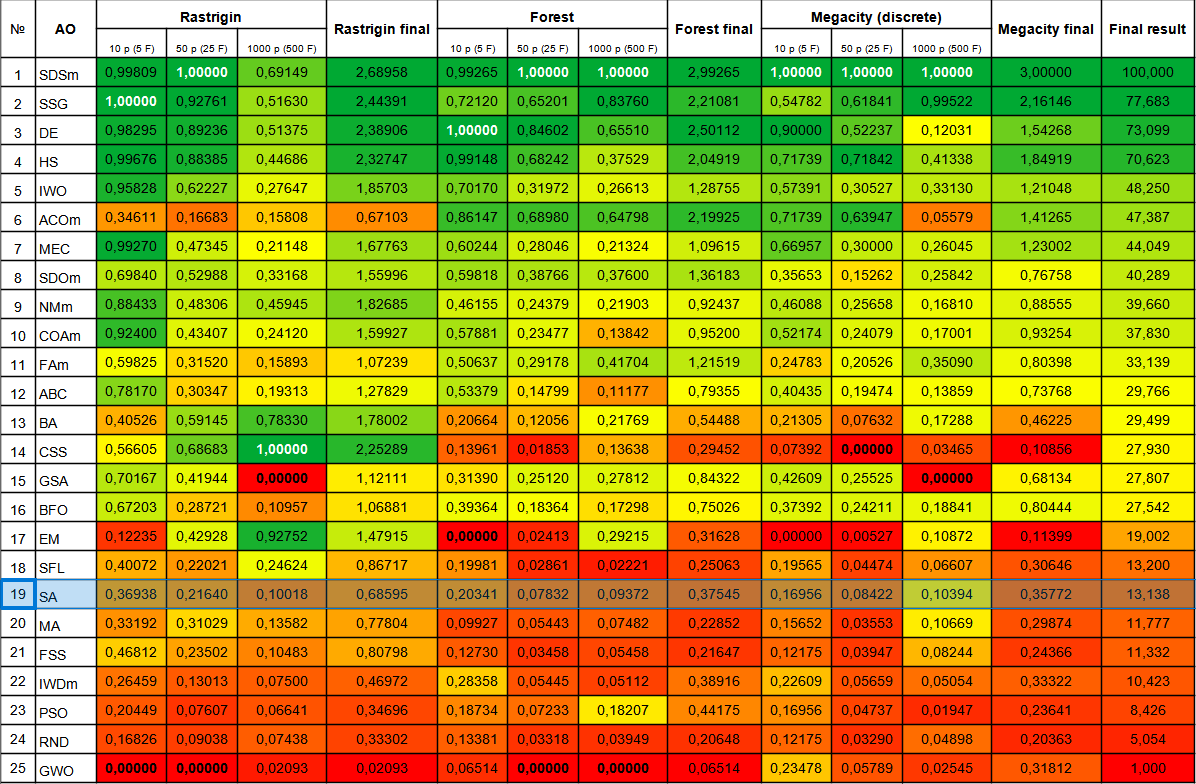
Figura 3. Gradación por colores de los algoritmos según sus respectivas pruebas.

chart

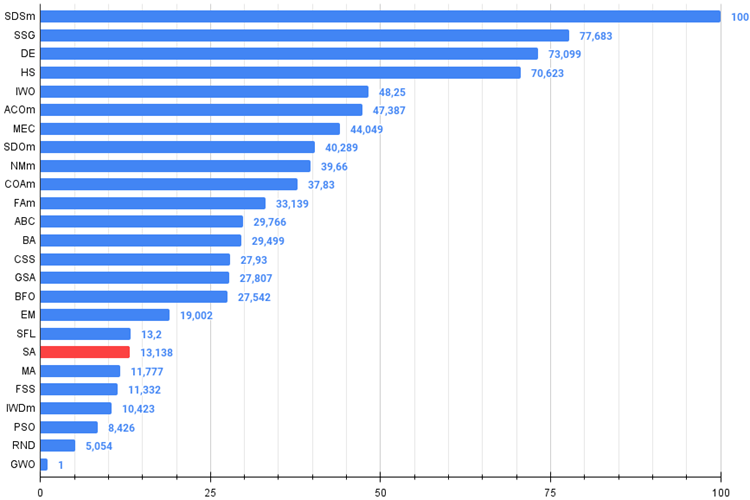
Figura 4. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor),

en el archivo hay un script para calcular la tabla de clasificación según la metodología de este artículo).

Ventajas e inconvenientes del algoritmo de recocido simulado (SA):

Ventajas:

  1. Tiene un número reducido de parámetros externos.
  2. Alta velocidad de funcionamiento.
  3. Aplicación muy simple.

Desventajas:

  1. Ajustes poco evidentes (no está claro cómo y a qué afecta la temperatura).
  2. Escalabilidad muy pobre.
  3. Gran variación de los resultados.
  4. Tendencia a estancarse en los extremos locales.
  5. Mala convergencia.

Adjuntamos al artículo un archivo con las versiones reales actualizadas de los códigos de los algoritmos descritos en los artículos anteriores. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/13851

Archivos adjuntos |
Descargar ZIP
25_The_world_of_AO_SA.zip (405.38 KB)
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores
Desarrollo de un sistema de repetición (Parte 39): Pavimentando el terreno (II) Desarrollo de un sistema de repetición (Parte 39): Pavimentando el terreno (II)
Antes de comenzar la segunda fase del desarrollo, es necesario reforzar algunas ideas. Entonces, ¿sabes cómo forzar al MQL5 a hacer lo que es necesario? ¿Has intentado ir más allá de lo que informa la documentación? Si no, prepárate. Porque empezaré a hacer cosas mucho más allá de lo que la mayoría hace normalmente.
Marcado de datos en el análisis de series temporales (Parte 4): Descomposición de la interpretabilidad usando el marcado de datos Marcado de datos en el análisis de series temporales (Parte 4): Descomposición de la interpretabilidad usando el marcado de datos
En esta serie de artículos, presentaremos varias técnicas de marcado de series temporales que pueden producir datos que se ajusten a la mayoría de los modelos de inteligencia artificial (IA). El marcado dirigido de datos puede hacer que un modelo de IA entrenado resulte más relevante para las metas y objetivos del usuario, mejorando la precisión del modelo y ayudando a este a dar un salto de calidad.
Redes neuronales: así de sencillo (Parte 67): Utilizamos la experiencia adquirida para afrontar nuevos retos Redes neuronales: así de sencillo (Parte 67): Utilizamos la experiencia adquirida para afrontar nuevos retos
En este artículo, seguiremos hablando de los métodos de recopilación de datos en una muestra de entrenamiento. Obviamente, en el proceso de entrenamiento será necesaria una interacción constante con el entorno, aunque con frecuencia se dan situaciones diferentes.
Patrones de diseño en MQL5 (Parte 3): Patrones conductuales 1 Patrones de diseño en MQL5 (Parte 3): Patrones conductuales 1
En el nuevo artículo de la serie sobre patrones de diseño, nos ocuparemos de los patrones conductuales para comprender cómo crear de forma eficaz métodos de interacción entre los objetos creados. Diseñando estos patrones conductuales, podremos entender cómo construir software reutilizable, extensible y comprobable.