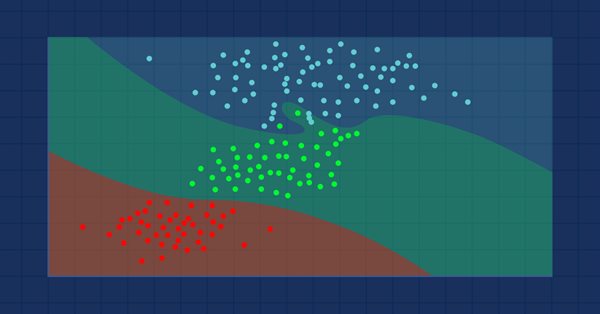
Aprendizaje automático y Data Science (Parte 9): Algoritmo de k vecinos más próximos (KNN)
Los pájaros del mismo plumaje se juntan (proverbio inglés): esta es la idea que subyace en el algoritmo KNN.
El algoritmo de k vecinos más próximos es un clasificador de aprendizaje no paramétrico supervisado que clasifica datos o predice su pertenencia a clases basándose en la proximidad. El algoritmo se usa principalmente para problemas de clasificación, pero también puede utilizarse para problemas de regresión. Con frecuencia se utiliza para realizar clasificaciones usando como base el supuesto de que varios puntos similares de un conjunto de datos pueden ser adyacentes. El método de k vecinos más próximos es uno de los algoritmos más sencillos del aprendizaje automático supervisado. En este artículo construiremos nuestro propio algoritmo de clasificación.
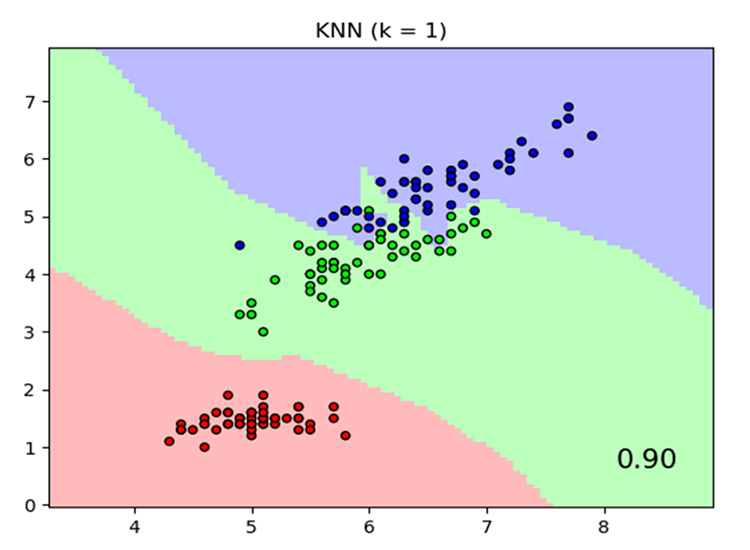
Fuente de la imagen: skicit-learn.org
Algunas observaciones:
- A menudo se usa como clasificador, pero también puede utilizarse para la regresión.
- El KNN es un algoritmo no paramétrico, lo cual significa que no hace suposiciones sobre los datos brutos.
- A menudo se denomina algoritmo de aprendizaje perezoso porque no aprende partiendo de una muestra de entrenamiento. El método almacena todos los datos y los usa posteriormente.
- El algoritmo KNN presupone la similitud entre los nuevos datos y el conjunto de datos disponible, y a partir de ahí, coloca los nuevos datos en una categoría con los datos más similares.
¿Cómo funciona el algoritmo KNN?
Antes de sumergirnos en la escritura del código, debemos comprender cómo funciona el algoritmo KNN:- Paso 1: seleccionamos del número de k vecinos
- Paso 2: hallamos la distancia euclidiana desde un punto hasta todos los miembros del conjunto de datos
- Paso 3: tomamos los k vecinos más próximos según la distancia euclidiana
- Paso 4: entre estos vecinos más próximos, contamos el número de puntos de datos en cada categoría
- Paso 5: asignamos los nuevos datos a la categoría cuyo número de vecinos sea máximo
Paso 1: seleccionamos el número de k vecinos
Este es un paso sencillo, solo tenemos que elegir el número k que usaremos en la clase CKNNnearestNearestbours. Ahora debemos plantearnos la cuestión de cómo factorizar k.
Factorización K
K es el número de vecinos más próximos que usaremos para votar a dónde asignar un valor/punto. Un valor pequeño de k provocará una gran cantidad de ruido en los datos clasificados, lo cual podría dar lugar a un mayor número de desviaciones, mientras que un valor muy grande de k hará que el algoritmo resulte mucho más lento. 
Esto ocurre con mayor frecuencia al usar 2 categorías para la clasificación. Más adelante, veremos qué se puede hacer en estas situaciones en las que hay muchas categorías para k vecinos.
Dentro de la biblioteca de clusterización, crearemos una función para recuperar las clases disponibles de la matriz del conjunto de datos y almacenarlas en el vector global de clases m_classesVector
vector CKNNNearestNeighbors::ClassVector() { vector t_vectors = Matrix.Col(m_cols-1); //target variables are found on the last column in the matrix vector temp_t = t_vectors, v = {t_vectors[0]}; for (ulong i=0, count =1; i<m_rows; i++) //counting the different neighbors { for (ulong j=0; j<m_rows; j++) { if (t_vectors[i] == temp_t[j] && temp_t[j] != -1000) { bool count_ready = false; for(ulong n=0;n<v.Size();n++) if (t_vectors[i] == v[n]) count_ready = true; if (!count_ready) { count++; v.Resize(count); v[count-1] = t_vectors[i]; temp_t[j] = -1000; //modify so that it can no more be counted } else break; //Print("t vectors vector ",t_vectors); } else continue; } } return(v); }
CKNNNearestNeighbors::CKNNNearestNeighbors(matrix<double> &Matrix_) { Matrix.Copy(Matrix_); k = (int)round(MathSqrt(Matrix.Rows())); k = k%2 ==0 ? k+1 : k; //make sure the value of k is an odd number m_rows = Matrix.Rows(); m_cols = Matrix.Cols(); m_classesVector = ClassVector(); Print("classes vector | Neighbors ",m_classesVector); }
Información mostrada:
2022.10.31 05:40:33.825 TestScript classes vector | Neighbors [1,0]
Si se ha fijado, existe una línea en el constructor que asegura que el valor de k será un número impar: se genera por defecto como la raíz cuadrada del número total de filas del conjunto de datos/número de puntos de datos. Este será el caso cuando no nos preocupemos por el valor K, es decir, no ajustemos el algoritmo. Existe otro constructor que permitirá establecer el valor de k, pero después seguirá comprobando si k es impar. El valor en este caso será 3, para 9 filas: √9 = 3 (número impar).
CKNNNearestNeighbors:: CKNNNearestNeighbors(matrix<double> &Matrix_, uint k_) { k = k_; if (k %2 ==0) printf("K %d is an even number, It will be added by One so it becomes an odd Number %d",k,k=k+1); Matrix.Copy(Matrix_); m_rows = Matrix.Rows(); m_cols = Matrix.Cols(); m_classesVector = ClassVector(); Print("classes vector | Neighbors ",m_classesVector); }
Para empezar, usaremos el siguiente conjunto de datos al crear la biblioteca. A continuación, veremos cómo podemos utilizar la información comercial y aplicar el algoritmo en MetaTrader 5.

Así se ven los datos en el MetaEditor:
matrix Matrix = {//weight(kg) | height(cm) | class {51, 167, 1}, //underweight {62, 182, 0}, //Normal {69, 176, 0}, //Normal {64, 173, 0}, //Normal {65, 172, 0}, //Normal {56, 174, 1}, //Underweight {58, 169, 0}, //Normal {57, 173, 0}, //Normal {55, 170, 0} //Normal };
Paso 2: hallamos la distancia euclidiana desde un punto hasta todos los miembros del conjunto de datos
Asumiendo que no sabemos calcular el IMC, necesitaremos saber si una persona que pesa 57 kg y mide 170 cm tiene un peso insuficiente o inferior al normal.
vector v = {57, 170}; nearest_neighbors = new CKNNNearestNeighbors(Matrix); //calling the constructor and passing it the matrix nearest_neighbors.KNNAlgorithm(v); //passing this new points to the algorithm
Lo primero que hará la función KNNAlgorithm será hallar la distancia euclidiana entre un punto dado y todos los puntos del conjunto de datos.
vector vector_2; vector euc_dist; euc_dist.Resize(m_rows); matrix temp_matrix = Matrix; temp_matrix.Resize(Matrix.Rows(),Matrix.Cols()-1); //remove the last column of independent variables for (ulong i=0; i<m_rows; i++) { vector_2 = temp_matrix.Row(i); euc_dist[i] = Euclidean_distance(vector_,vector_2); }
La propia función para calcular la distancia euclidiana tendrá el siguiente aspecto:
double CKNNNearestNeighbors:: Euclidean_distance(const vector &v1,const vector &v2) { double dist = 0; if (v1.Size() != v2.Size()) Print(__FUNCTION__," v1 and v2 not matching in size"); else { double c = 0; for (ulong i=0; i<v1.Size(); i++) c += MathPow(v1[i] - v2[i], 2); dist = MathSqrt(c); } return(dist); }
En esta biblioteca, hemos elegido la distancia euclidiana para medir la distancia entre dos puntos, pero no es la única forma. También podemos utilizar la distancia en línea recta y la distancia Manhattan; ya hablamos de algunas de ellas en un artículo anterior.
Print("Euclidean distance vector\n",euc_dist); Output -----------> CS 0 19:29:09.057 TestScript Euclidean distance vector CS 0 19:29:09.057 TestScript [6.7082,13,13.41641,7.61577,8.24621,4.12311,1.41421,3,2]
Ahora vamos a rellenar la última columna de la matriz usando la distancia euclidiana:
if (isdebug) { matrix dbgMatrix = Matrix; //temporary debug matrix dbgMatrix.Resize(dbgMatrix.Rows(),dbgMatrix.Cols()+1); dbgMatrix.Col(euc_dist,dbgMatrix.Cols()-1); Print("Matrix w Euclidean Distance\n",dbgMatrix); ZeroMemory(dbgMatrix); }
Información mostrada:
CS 0 19:33:48.862 TestScript Matrix w Euclidean Distance CS 0 19:33:48.862 TestScript [[51,167,1,6.7082] CS 0 19:33:48.862 TestScript [62,182,0,13] CS 0 19:33:48.862 TestScript [69,176,0,13.41641] CS 0 19:33:48.862 TestScript [64,173,0,7.61577] CS 0 19:33:48.862 TestScript [65,172,0,8.24621] CS 0 19:33:48.862 TestScript [56,174,1,4.12311] CS 0 19:33:48.862 TestScript [58,169,0,1.41421] CS 0 19:33:48.862 TestScript [57,173,0,3] CS 0 19:33:48.862 TestScript [55,170,0,2]]
Para explicarlo mejor, mostraremos estos datos en forma de imagen:
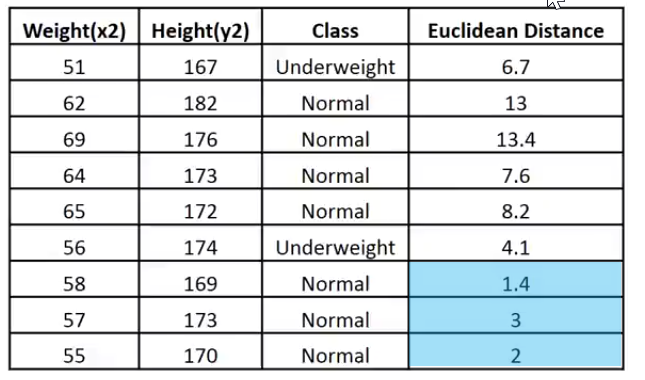
Como el valor de k es 3, los 3 vecinos más próximos pertenecerán a la clase Normal, por lo que visualmente entenderemos que este punto pertenece a la categoría Normal. Ahora vamos a escribir el código para esta toma de decisión.
Identificar y monitorear a los vecinos más próximos usando vectores resultará muy difícil. Los arrays serán la opción más flexible para dividir y modificar la forma. Utilizaremos arrays en nuestro proceso.
int size = (int)m_target.Size(); double tarArr[]; ArrayResize(tarArr, size); double eucArray[]; ArrayResize(eucArray, size); for(ulong i=0; i<m_target.Size(); i++) //convert the vectors to array { tarArr[i] = m_target[i]; eucArray[i] = euc_dist[i]; } double track[], NN[]; ArrayCopy(track, tarArr); int max; for(int i=0; i<(int)m_target.Size(); i++) { if(ArraySize(track) > (int)k) { max = ArrayMaximum(eucArray); ArrayRemove(eucArray, max, 1); ArrayRemove(track, max, 1); } } ArrayCopy(NN, eucArray); Print("NN "); ArrayPrint(NN); Print("Track "); ArrayPrint(track);
En el código anterior identificaremos a los vecinos más próximos y los almacenaremos en el array NN, también monitorearemos sus valores de clase o qué clase ocupan en el vector global de valores objetivo. Además, eliminaremos los valores máximos del array hasta que quede un array de valores más pequeños de tamaño k (vecinos más próximos).
Obtendremos el resultado siguiente:
CS 0 05:40:33.825 TestScript NN CS 0 05:40:33.825 TestScript 1.4 3.0 2.0 CS 0 05:40:33.825 TestScript Track CS 0 05:40:33.825 TestScript 0.0 0.0 0.0
El proceso de votación:
//--- Voting process vector votes(m_classesVector.Size()); for(ulong i=0; i<votes.Size(); i++) { int count = 0; for(ulong j=0; j<track.Size(); j++) { if(m_classesVector[i] == track[j]) count++; } votes[i] = (double)count; if(votes.Sum() == k) //all members have voted break; } Print("votes ", votes);
Información mostrada:
2022.10.31 05:40:33.825 TestScript votes [0,3]
¿Recuerda que un vector de votos ordena los votos en función del vector global de clases del conjunto de datos?
2022.10.31 06:43:30.095 TestScript classes vector | Neighbors [1,0]
Aquí, de los 3 vecinos seleccionados para votar, 3 han votado que los datos pertenecen a la clase de los ceros (0), y ningún miembro ha votado por la clase de los unos (1).
Veamos qué podría ocurrir si seleccionáramos 5 vecinos para votar, es decir, si el valor de K fuera 5.
CS 0 06:43:30.095 TestScript NN CS 0 06:43:30.095 TestScript 6.7 4.1 1.4 3.0 2.0 CS 0 06:43:30.095 TestScript Track CS 0 06:43:30.095 TestScript 1.0 1.0 0.0 0.0 0.0 CS 0 06:43:30.095 TestScript votes [2,3]
Ahora la decisión final será fácil: ganará la clase con más votos. En este caso, el peso se clasificará como normal, con un índice de 0.
if(isdebug) Print(vector_, " belongs to class ", (int)m_classesVector[votes.ArgMax()]);
Información mostrada:
2022.10.31 06:43:30.095 TestScript [57,170] belongs to class 0
Ahora todo funciona perfectamente. Vamos a cambiar el tipo de KNNAlgorithm de void a int para que la función retorne el valor de la clase a la que pertenece el valor. Esto podría resultar útil en el comercio real, pues suministraremos nuevos valores para los cuales esperamos una salida inmediata del algoritmo.
int KNNAlgorithm(vector &vector_);
Probando el modelo y determinando su precisión.
Nuestro modelo ya está listo. Ahora, como con cualquier otro método de aprendizaje automático supervisado, deberemos entrenarlo y probarlo con datos que resulten nuevos para él. Las pruebas nos ayudarán a comprender cómo funciona nuestro modelo con distintos conjuntos de datos.
float TrainTest(double train_size=0.7)
Por defecto, el 70% del conjunto de datos se usará para el entrenamiento y el 30% restante para las pruebas.
Vamos a escribir el código de la función para separar el conjunto de datos en una fase de entrenamiento y una fase de prueba:
//--- Split the matrix matrix default_Matrix = Matrix; int train = (int)MathCeil(m_rows*train_size), test = (int)MathFloor(m_rows*(1-train_size)); if (isdebug) printf("Train %d test %d",train,test); matrix TrainMatrix(train,m_cols), TestMatrix(test,m_cols); int train_index = 0, test_index =0; //--- for (ulong r=0; r<Matrix.Rows(); r++) { if ((int)r < train) { TrainMatrix.Row(Matrix.Row(r),train_index); train_index++; } else { TestMatrix.Row(Matrix.Row(r),test_index); test_index++; } } if (isdebug) Print("TrainMatrix\n",TrainMatrix,"\nTestMatrix\n",TestMatrix);
Información mostrada:
CS 0 09:51:45.136 TestScript TrainMatrix CS 0 09:51:45.136 TestScript [[51,167,1] CS 0 09:51:45.136 TestScript [62,182,0] CS 0 09:51:45.136 TestScript [69,176,0] CS 0 09:51:45.136 TestScript [64,173,0] CS 0 09:51:45.136 TestScript [65,172,0] CS 0 09:51:45.136 TestScript [56,174,1] CS 0 09:51:45.136 TestScript [58,169,0]] CS 0 09:51:45.136 TestScript TestMatrix CS 0 09:51:45.136 TestScript [[57,173,0] CS 0 09:51:45.136 TestScript [55,170,0]]
Así, el entrenamiento del algoritmo del vecino más próximo será muy sencillo. Podríamos pensar que no existe aprendizaje en absoluto porque, como se ha mencionado anteriormente, este algoritmo en sí no intenta comprender patrones en el conjunto de datos, a diferencia de métodos como la regresión logística o la SVM: simplemente almacenará los datos durante el entrenamiento, y estos datos se utilizarán posteriormente para las pruebas.
Entrenamiento:
Matrix.Copy(TrainMatrix); //That's it ??? Pruebas:
//--- Testing the Algorithm vector TestPred(TestMatrix.Rows()); vector v_in = {}; for (ulong i=0; i<TestMatrix.Rows(); i++) { v_in = TestMatrix.Row(i); v_in.Resize(v_in.Size()-1); //Remove independent variable TestPred[i] = KNNAlgorithm(v_in); Print("v_in ",v_in," out ",TestPred[i]); }
Información mostrada:
CS 0 09:51:45.136 TestScript v_in [57,173] out 0.0 CS 0 09:51:45.136 TestScript v_in [55,170] out 0.0
Todas las pruebas resultarían inútiles si no midiéramos la precisión de nuestro modelo con un conjunto de datos determinado.
Matriz de confusión
Ya hemos hablado de esto en el segundo artículo de esta serie.
matrix CKNNNearestNeighbors::ConfusionMatrix(vector &A,vector &P) { ulong size = m_classesVector.Size(); matrix mat_(size,size); if (A.Size() != P.Size()) Print("Cant create confusion matrix | A and P not having the same size "); else { int tn = 0,fn =0,fp =0, tp=0; for (ulong i = 0; i<A.Size(); i++) { if (A[i]== P[i] && P[i]==m_classesVector[0]) tp++; if (A[i]== P[i] && P[i]==m_classesVector[1]) tn++; if (P[i]==m_classesVector[0] && A[i]==m_classesVector[1]) fp++; if (P[i]==m_classesVector[1] && A[i]==m_classesVector[0]) fn++; } mat_[0][0] = tn; mat_[0][1] = fp; mat_[1][0] = fn; mat_[1][1] = tp; } return(mat_); }
Dentro de TrainTest(), hemos añadido el siguiente código al final de la función para finalizar la función y retornar la precisión:
matrix cf_m = ConfusionMatrix(TargetPred,TestPred); vector diag = cf_m.Diag(); float acc = (float)(diag.Sum()/cf_m.Sum())*100; Print("Confusion Matrix\n",cf_m,"\nAccuracy ------> ",acc,"%"); return(acc);
Información mostrada:
CS 0 10:34:26.681 TestScript Confusion Matrix CS 0 10:34:26.681 TestScript [[2,0] CS 0 10:34:26.681 TestScript [0,0]] CS 0 10:34:26.681 TestScript Accuracy ------> 100.0%
Obviamente, la precisión debería ser del cien por cien: el modelo solo ha ofrecido dos puntos de datos para comprobar, todos pertenecientes a la clase cero (clase normal), que es la correcta.
Actualmente disponemos de una biblioteca K-Nearest Neighbours totalmente funcional. Veamos cómo podemos usarla para predecir los precios de varios símbolos de divisas y acciones.
Preparando el conjunto de datos
Recuerde que estamos trabajando con un aprendizaje supervisado, es decir, deberá existir cierta intervención humana a la hora de crear los datos y asignarles etiquetas, para que los modelos sepan cuáles son sus objetivos y puedan comprender la relación entre las variables independientes y las variables objetivo.
Las variables independientes serán las lecturas del indicador y los indicadores de volumen. La variable objetivo será 1 si el mercado ha ascendido y 0 si ha descendido. Esto será una señal de compra y una señal de venta, respectivamente, al probar y utilizar el modelo para comerciar.
int OnInit() { //--- Preparing the dataset atr_handle = iATR(Symbol(),timeframe,period); volume_handle = iVolumes(Symbol(),timeframe,applied_vol); CopyBuffer(atr_handle,0,1,bars,atr_buffer); CopyBuffer(volume_handle,0,1,bars,volume_buffer); Matrix.Col(atr_buffer,0); //Independent var 1 Matrix.Col(volume_buffer,1); //Independent var 2 //--- Target variables vector Target_vector(bars); MqlRates rates[]; ArraySetAsSeries(rates,true); CopyRates(Symbol(),PERIOD_D1,1,bars,rates); for (ulong i=0; i<Target_vector.Size(); i++) //putting the labels { if (rates[i].close > rates[i].open) Target_vector[i] = 1; //bullish else Target_vector[i] = 0; } Matrix.Col(Target_vector,2); //---
La lógica para encontrar las variables independientes será la siguiente: si la vela se ha cerrado por encima del cierre, hablaremos de una vela alcista; la variable objetivo para las variables independientes será 1, en caso contrario, será 0.
Pero cuando estamos trabajando en una vela diaria, se pueden dar muchos movimientos de precio dentro de esas 24 horas de una sola vela. Esta lógica no resultaría adecuada para crear un scalper o un robot que comercie en periodos más cortos. Hay otro pequeño fallo en la lógica: si el precio de cierre es superior al precio de apertura, denotaremos la variable objetivo como 1, de lo contrario denotaremos 0, pero con frecuencia hay situaciones en las que el precio de apertura es igual al precio de cierre. Sin embargo, esta situación rara vez ocurre en los marcos temporales mayores, así que esta será nuestra forma de evitar errores.
La información no supone asesoramiento financiero o comercial alguno.
Vamos a mostrar los 10 últimos valores de las barras, 10 filas de nuestro array de conjunto de datos:
CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) ATR,Volumes,Class Matrix CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [[0.01139285714285716,12295,0] CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [0.01146428571428573,12055,0] CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [0.01122142857142859,10937,0] CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [0.01130000000000002,13136,0] CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [0.01130000000000002,15305,0] CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [0.01097857142857144,13762,1] CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [0.0109357142857143,12545,1] CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [0.01116428571428572,18806,1] CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [0.01188571428571429,19595,1] CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [0.01137142857142859,15128,1]]
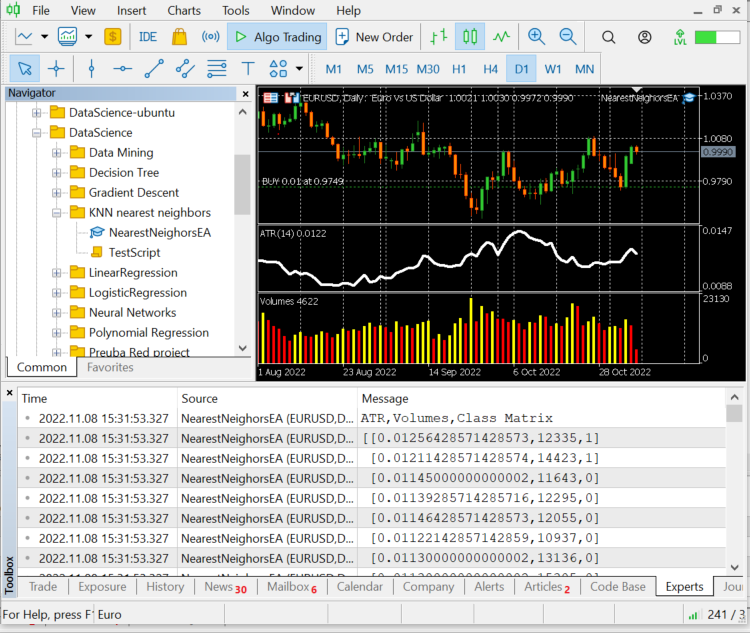
Los datos se han agrupado según las velas y los indicadores pertinentes, y ahora se transmiten al algoritmo.
nearest_neigbors = new CKNNNearestNeighbors(Matrix,k);
nearest_neigbors.TrainTest();
Información mostrada:
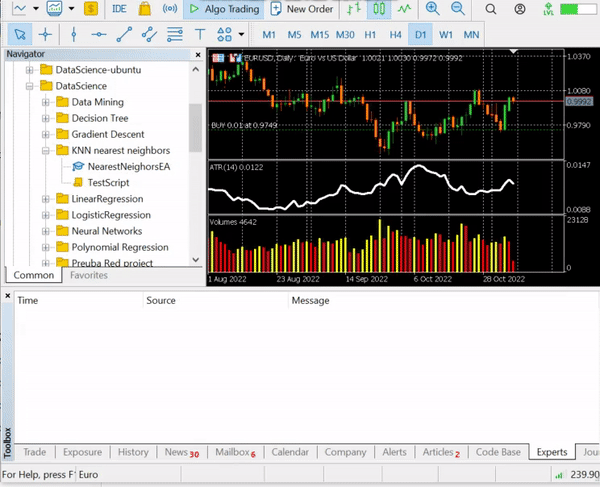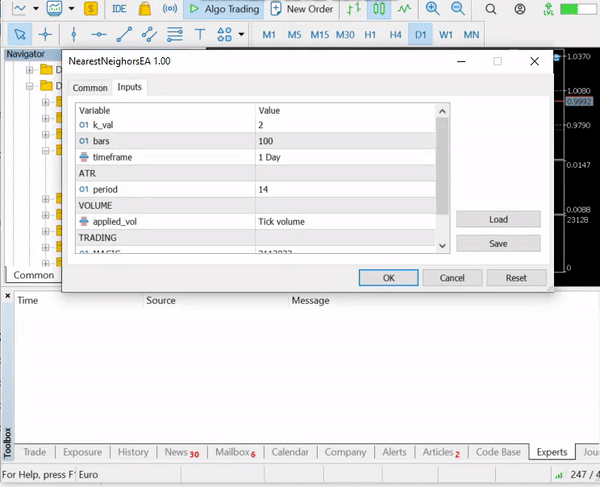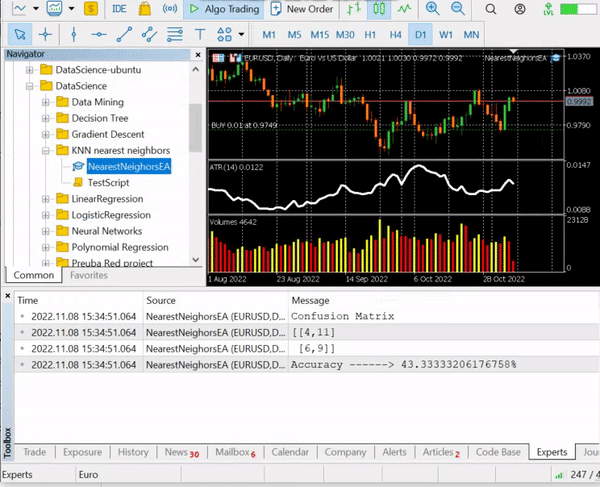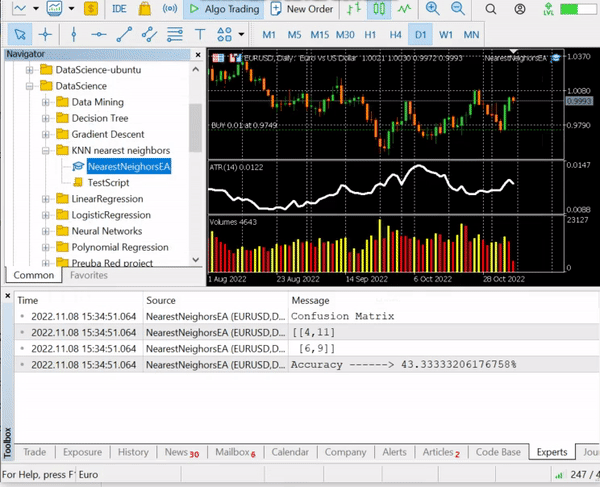
El resultado será una precisión de alrededor del 43,33%, lo cual no está mal teniendo en cuenta que no buscábamos el valor óptimo de k. A continuación, iteraremos por los distintos valores de k y elegiremos el que ofrezca la mayor precisión.
for(uint i=0; i<bars; i++) { printf("<<< k %d >>>",i); nearest_neigbors = new CKNNNearestNeighbors(Matrix,i); nearest_neigbors.TrainTest(); delete(nearest_neigbors); }
Información mostrada:
...... CS 0 16:22:28.013 NearestNeighorsEA (EURUSD,D1) <<< k 24 >>> CS 0 16:22:28.013 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 46.66666793823242% CS 0 16:22:28.014 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 46.66666793823242% CS 0 16:22:28.014 NearestNeighorsEA (EURUSD,D1) <<< k 26 >>> CS 0 16:22:28.014 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 40.0% CS 0 16:22:28.014 NearestNeighorsEA (EURUSD,D1) <<< k 27 >>> CS 0 16:22:28.015 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 40.0% CS 0 16:22:28.015 NearestNeighorsEA (EURUSD,D1) <<< k 28 >>> CS 0 16:22:28.015 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 56.66666793823242% CS 0 16:22:28.016 NearestNeighorsEA (EURUSD,D1) <<< k 29 >>> CS 0 16:22:28.016 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 56.66666793823242% CS 0 16:22:28.016 NearestNeighorsEA (EURUSD,D1) <<< k 30 >>> ..... ..... CS 0 16:22:28.017 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 60.000003814697266% CS 0 16:22:28.017 NearestNeighorsEA (EURUSD,D1) <<< k 31 >>> CS 0 16:22:28.017 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 60.000003814697266% CS 0 16:22:28.017 NearestNeighorsEA (EURUSD,D1) <<< k 32 >>> CS 0 16:22:28.018 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 56.66666793823242% CS 0 16:22:28.018 NearestNeighorsEA (EURUSD,D1) <<< k 33 >>> CS 0 16:22:28.018 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 56.66666793823242% CS 0 16:22:28.018 NearestNeighorsEA (EURUSD,D1) <<< k 34 >>> CS 0 16:22:28.019 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 50.0% CS 0 16:22:28.019 NearestNeighorsEA (EURUSD,D1) <<< k 35 >>> CS 0 16:22:28.019 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 50.0% CS 0 16:22:28.019 NearestNeighorsEA (EURUSD,D1) <<< k 36 >>> CS 0 16:22:28.020 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 53.333335876464844% CS 0 16:22:28.020 NearestNeighorsEA (EURUSD,D1) <<< k 37 >>> CS 0 16:22:28.020 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 53.333335876464844% CS 0 16:22:28.020 NearestNeighorsEA (EURUSD,D1) <<< k 38 >>> CS 0 16:22:28.021 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 56.66666793823242% CS 0 16:22:28.021 NearestNeighorsEA (EURUSD,D1) <<< k 39 >>> CS 0 16:22:28.021 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 56.66666793823242% CS 0 16:22:28.021 NearestNeighorsEA (EURUSD,D1) <<< k 40 >>> CS 0 16:22:28.022 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 56.66666793823242% CS 0 16:22:28.022 NearestNeighorsEA (EURUSD,D1) <<< k 41 >>> ..... .... CS 0 16:22:28.023 NearestNeighorsEA (EURUSD,D1) <<< k 42 >>> CS 0 16:22:28.023 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 63.33333206176758% CS 0 16:22:28.023 NearestNeighorsEA (EURUSD,D1) <<< k 43 >>> CS 0 16:22:28.024 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 63.33333206176758% CS 0 16:22:28.024 NearestNeighorsEA (EURUSD,D1) <<< k 44 >>> CS 0 16:22:28.024 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 66.66667175292969% CS 0 16:22:28.024 NearestNeighorsEA (EURUSD,D1) <<< k 45 >>> CS 0 16:22:28.025 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 66.66667175292969% CS 0 16:22:28.025 NearestNeighorsEA (EURUSD,D1) <<< k 46 >>> CS 0 16:22:28.025 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 56.66666793823242% CS 0 16:22:28.025 NearestNeighorsEA (EURUSD,D1) <<< k 47 >>> .... ....
Este no es el mejor método para determinar el valor de k. Para encontrar los valores óptimos podemos usar un método de comprobación cruzada. Bien, hemos obtenido un rendimiento máximo con el valor k en la región de cuarenta. Ahora vamos a probar este algoritmo en un entorno comercial.
void OnTick() { vector x_vars(2); //vector to store atr and volumes values double atr_val[], volume_val[]; CopyBuffer(atr_handle,0,0,1,atr_val); CopyBuffer(volume_handle,0,0,1,volume_val); x_vars[0] = atr_val[0]; x_vars[1] = volume_val[0]; //--- int signal = 0; double volume = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN); MqlTick ticks; SymbolInfoTick(Symbol(),ticks); double ask = ticks.ask, bid = ticks.bid; if (isNewBar() == true) //we are on the new candle { signal = nearest_neigbors.KNNAlgorithm(x_vars); //Calling the algorithm if (signal == 1) { if (!CheckPosionType(POSITION_TYPE_BUY)) { m_trade.Buy(volume,Symbol(),ask,0,0); if (ClosePosType(POSITION_TYPE_SELL)) printf("Failed to close %s Err = %d",EnumToString(POSITION_TYPE_SELL),GetLastError()); } } else { if (!CheckPosionType(POSITION_TYPE_SELL)) { m_trade.Sell(volume,Symbol(),bid,0,0); if (ClosePosType(POSITION_TYPE_BUY)) printf("Failed to close %s Err = %d",EnumToString(POSITION_TYPE_BUY),GetLastError()); } } } }
El asesor experto ha aprendido a abrir y cerrar operaciones, ahora lo probaremos en el simulador de estrategias, pero primero echaremos un vistazo a la llamada del algoritmo completo en el asesor:
#include "KNN_nearest_neighbors.mqh"; CKNNNearestNeighbors *nearest_neigbors; matrix Matrix; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { // gathering data to Matrix has been ignored nearest_neigbors = new CKNNNearestNeighbors(Matrix,_k); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- delete(nearest_neigbors); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { vector x_vars(2); //vector to store atr and volumes values //adding live indicator values from the market has been ignored //--- int signal = 0; if (isNewBar() == true) //we are on the new candle { signal = nearest_neigbors.KNNAlgorithm(x_vars); //trading actions } }
Prueba en el simulador de estrategias con EURUSD desde el 01.06.2022 hasta el 03.11.2022 (en el modo "Todos los ticks"):
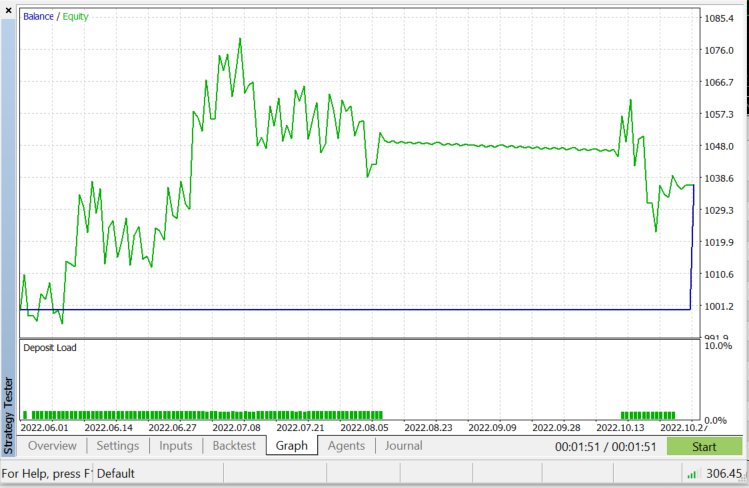
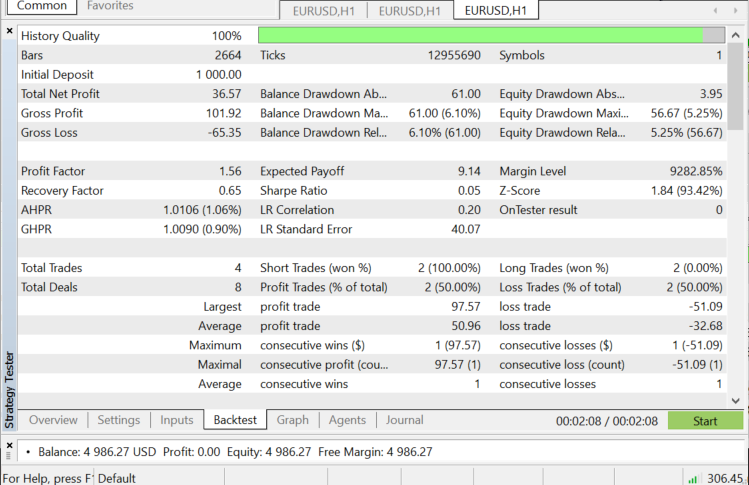
¿Cuándo podemos usar el algoritmo KNN?
Resulta importante saber dónde utilizar este algoritmo, porque no todos los problemas pueden resolverse con él, al igual que sucede con cualquier otra técnica de aprendizaje automático.
- Cuando el conjunto de datos está marcado
- Cuando no hay ruido en el conjunto de datos
- Cuando el conjunto de datos es pequeño (esto también es necesario para el rendimiento)
Ventajas:
- Es muy fácil de entender y aplicar
- Se basa en puntos de datos locales, lo cual resulta positivo para los conjuntos de datos que incluyen muchos grupos con clústeres locales.
Desventajas
Cada vez que utilicemos todos los datos de entrenamiento disponibles para la predicción, esto implicará que todos los datos deberán estar almacenados y listos para usarse cada vez que aparezca un nuevo punto para la clasificación.
Reflexiones finales
Como ya hemos dicho, este algoritmo es un buen clasificador, pero no para un conjunto de datos complejo, por lo que, con toda probabilidad, resultará mejor para predecir acciones e índices: dejamos su uso a la discreción del lector. Al probar el algoritmo en el asesor, han surgido problemas de rendimiento en el simulador de estrategias. Hemos seleccionado 50 barras y el asesor se ejecuta en una nueva barra. El simulador se queda atascado en cada vela durante unos 20-30 segundos, el tiempo necesario para que el algoritmo inicie todo el proceso. Este es un problema del simulador, pero en el comercio real todo sucede más rápido. Siempre existe margen para la mejora, especialmente en las siguientes líneas de código. No hemos podido obtener los valores de los indicadores en la función Init, así que hemos tenido que obtenerlos y utilizarlos para la previsión del mercado en un solo lugar.
if (isNewBar() == true) //new candlestick { if (MQLInfoInteger(MQL_TESTER) || MQLInfoInteger(MQL_OPTIMIZATION)) { gather_data(); nearest_neigbors = new CKNNNearestNeighbors(Matrix,_k); signal = nearest_neigbors.KNNAlgorithm(x_vars); delete(nearest_neigbors); }
¡Gracias por su atención!
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/11678
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso