MetaTrader 5 / Negociação
English Русский 中文 Español Deutsch 日本語
preview
Ciência de dados e Aprendizado de Máquina (parte 09): O algoritmo K-vizinhos mais próximos (KNN)

Ciência de dados e Aprendizado de Máquina (parte 09): O algoritmo K-vizinhos mais próximos (KNN)

MetaTrader 5 — Negociação | 7 fevereiro 2023, 09:23
447 1
Omega J Msigwa
Omega J Msigwa

Pássaros de mesma pena voam juntos -- Ideia por trás do Algoritmo KNN.

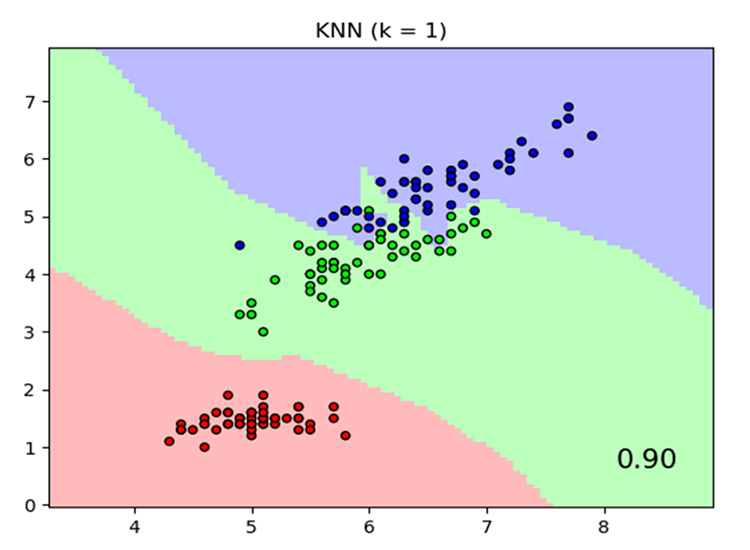
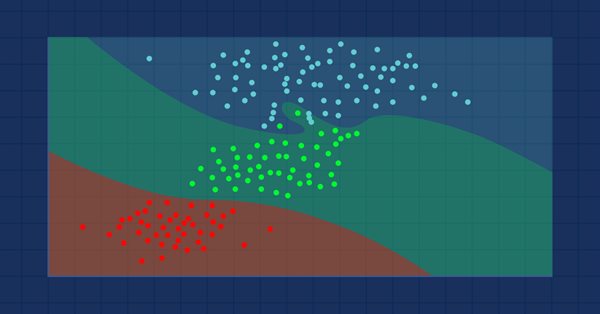
O algoritmo K-vizinhos mais próximos é um classificador de aprendizado supervisionado não paramétrico que usa a proximidade para fazer classificações ou previsões sobre o agrupamento de um ponto de dados individual. Embora esse algoritmo seja usado principalmente para problemas de classificação, ele também pode ser usado para resolver um problema de regressão. Ele é frequentemente usado como um algoritmo de classificação devido à suposição de que pontos semelhantes no conjunto de dados podem ser encontrados próximos uns dos outros; O algoritmo de k-vizinhos mais próximos é um dos algoritmos mais simples em aprendizado de máquina supervisionado. Construiremos nosso algoritmo neste artigo como um classificador.


algoritmo kNN

Fonte da imagem:skicit-learn.org

Algumas coisas a serem observadas:

  1.  Geralmente ele é usado como um classificador, mas ele também pode ser usado para regressão.
  2.  K-NN é um algoritmo não paramétrico, o que significa que ele não faz nenhuma suposição sobre os dados subjacentes.
  3.  Muitas vezes, ele é chamado de algoritmo de aprendizado preguiçoso porque ele não aprende com o conjunto de treinamento. Em vez disso, ele armazena os dados e os usa durante o tempo de ação.
  4.  O algoritmo KNN assume a semelhança entre os novos dados e o conjunto de dados disponível e coloca os novos dados na categoria mais semelhante às categorias disponíveis.

Como funciona o KNN?

Antes de mergulharmos na escrita do código, vamos entender como o algoritmo KNN funciona;
  • Passo 01: Selecionamos o número k dos vizinhos
  • Passo 02:Calculamos a distância euclidiana de um ponto para todos os membros do conjunto de dados
  • Passo 03:Pegamos os K vizinhos mais próximos de acordo com a distância euclidiana
  • Passo 04:Entre esses vizinhos mais próximos, contamos o número de pontos de dados em cada categoria
  • Passo 05:Atribuímos os novos pontos de dados àquela categoria para a qual o número de vizinhos é máximo

Passo 01: Selecionando o número k de vizinhos

Este é um passo simples, tudo o que precisamos fazer é selecionar o número de k que vamos usar em nossa classe CKNNnearestNeighbors, isso agora levanta uma questão de como fatoramos k.

Como Fatoramos K?

K é o número de vizinhos mais próximos a serem usados para votar sobre onde o valor/ponto fornecido deve pertencer. Escolher o menor número de k levará a muito ruído nos pontos de dados classificados, o que pode levar a um maior número de viés, enquanto o maior número de k torna o algoritmo significativamente mais lento. 
O valor k precisa ser um número ímpar para evitar ficar preso no processo de decisão, eis o que isso significa porque o processo de votação requer um número k de vizinhos. Se for definido como 4, então 2 membros votam que o ponto fornecido pertence à categoria A então os 2 votos restantes pertencem à categoria B?? Como você vai decidir qual lado ganhou a decisão?


Este caso ocorre mais quando há 2 categorias para classificar, veremos o que nós podemos fazer se situações como esta acontecerem mais tarde quando houver muitas categorias para os k vizinhos.

Dentro de nossa biblioteca Clustering, vamos criar a função para obter as classes disponíveis da matriz de conjuntos de dados e armazená-las em um vetor global de classes chamado m_classesVector

vector CKNNNearestNeighbors::ClassVector()
 {
   vector t_vectors = Matrix.Col(m_cols-1); //target variables are found on the last column in the matrix
   vector temp_t = t_vectors, v = {t_vectors[0]};
   
   for (ulong i=0, count =1; i<m_rows; i++) //counting the different neighbors
    {
      for (ulong j=0; j<m_rows; j++)
         {
            if (t_vectors[i] == temp_t[j] && temp_t[j] != -1000)
               {                   
                  bool count_ready = false;
                  
                  for(ulong n=0;n<v.Size();n++)
                      if (t_vectors[i] == v[n])
			 count_ready = true;
                    
                    if (!count_ready)
                      {
                        count++;
                        v.Resize(count);
                        
                        v[count-1] = t_vectors[i]; 
                        
                        temp_t[j] = -1000; //modify so that it can no more be counted
                      }
                    else 
			break;
                  //Print("t vectors vector ",t_vectors);
               }
             else
		 continue;
         }
    }
   
   return(v);
 } 

CKNNNearestNeighbors::CKNNNearestNeighbors(matrix<double> &Matrix_)
  {
    Matrix.Copy(Matrix_);

    k = (int)round(MathSqrt(Matrix.Rows())); 
    k = k%2 ==0 ? k+1 : k; //make sure the value of k ia an odd number    
    
    m_rows = Matrix.Rows();
    m_cols = Matrix.Cols();
    
   m_classesVector = ClassVector();
   Print("classes vector | Neighbors ",m_classesVector);
  }

Saída:

2022.10.31 05:40:33.825 TestScript      classes vector | Neighbors [1,0]

Se você prestou atenção ao construtor, há uma linha que garante que o valor de k seja um número ímpar depois que ele foi gerado por padrão como a raiz quadrada do número total de linhas no conjunto de dados/número de pontos de dados, caso em que alguém decida não se preocupar com o valor de K, ou seja, decidiu não ajustar o algoritmo; Existe o outro construtor que permite ajustar o valor de k, mas o valor é verificado para garantir que seja um número ímpar; O valor de K neste caso é 3, dado 9 linhas então √9 = 3 (número ímpar)

CKNNNearestNeighbors:: CKNNNearestNeighbors(matrix<double> &Matrix_, uint k_)
 {
   k = k_;
   
   if (k %2 ==0)
      printf("K %d is an even number, It will be added by One so it becomes an odd Number %d",k,k=k+1);
      
   Matrix.Copy(Matrix_);
   
   m_rows = Matrix.Rows();
   m_cols = Matrix.Cols();
   
   m_classesVector = ClassVector();
   Print("classes vector | Neighbors ",m_classesVector);
 }

Para construir a biblioteca, vamos usar o conjunto de dados abaixo, depois veremos como nós podemos usar as informações de negociação para fazer algo com isso na MetaTrader.

Aqui está como esses dados se parecem no MetaEditor;

    matrix Matrix = 
      {//weight(kg) | height(cm) | class
         {51, 167,   1}, //underweight
         {62, 182,   0}, //Normal
         {69, 176,   0}, //Normal
         {64, 173,   0}, //Normal
         {65, 172,   0}, //Normal
         {56, 174,   1}, //Underweight
         {58, 169,   0}, //Normal
         {57, 173,   0}, //Normal
         {55, 170,   0}  //Normal
      };    

Passo 02: Calcular a distância euclidiana de um ponto a todos os membros do conjunto de dados

Supondo que não saibamos calcular o índice de massa corporal, queremos saber se a pessoa com o peso de 57kg e altura de 170cm pertence entre a categoria abaixo do peso e a categoria Normal.

    vector v = {57, 170};
    
    nearest_neighbors = new CKNNNearestNeighbors(Matrix); //calling the constructor and passing it the matrix
    nearest_neighbors.KNNAlgorithm(v);  //passing this new points to the algorithm

A primeira coisa que a função KNNAlgorithm faz é encontrar a Distância Euclidiana entre o ponto dado e todos os pontos no conjunto de dados.

   vector vector_2;
   vector euc_dist;
   euc_dist.Resize(m_rows);
   
   matrix temp_matrix = Matrix;
   temp_matrix.Resize(Matrix.Rows(),Matrix.Cols()-1); //remove the last column of independent variables
   
   for (ulong i=0; i<m_rows; i++)
      {
         vector_2 = temp_matrix.Row(i);
         euc_dist[i] = Euclidean_distance(vector_,vector_2);
      }      

Dentro da função Distância Euclidiana;

double CKNNNearestNeighbors:: Euclidean_distance(const vector &v1,const vector &v2)
 {
   double dist = 0;
   
   if (v1.Size() != v2.Size()) 
	Print(__FUNCTION__," v1 and v2 not matching in size");
   else
    {
       double c = 0;
         for (ulong i=0; i<v1.Size(); i++)
               c += MathPow(v1[i] - v2[i], 2); 

        dist = MathSqrt(c);
    } 
    
    return(dist);
 }

Eu escolhi a distância Euclidiana como um método para medir a distância entre os dois pontos nesta biblioteca, mas esta não é a única maneira, você pode usar vários métodos como a Distância Retilínea e a distância de Manhattan, alguns foram discutidos no artigo anterior.

Print("Euclidean distance vector\n",euc_dist);

Output  -----------> 

CS      0       19:29:09.057    TestScript   Euclidean distance vector
CS      0       19:29:09.057    TestScript   [6.7082,13,13.41641,7.61577,8.24621,4.12311,1.41421,3,2]

Agora, vamos incorporar a distância euclidiana à última coluna da matriz;

   if (isdebug)
      {  
         matrix dbgMatrix = Matrix; //temporary debug matrix
         dbgMatrix.Resize(dbgMatrix.Rows(),dbgMatrix.Cols()+1);
         dbgMatrix.Col(euc_dist,dbgMatrix.Cols()-1);
         
         Print("Matrix w Euclidean Distance\n",dbgMatrix);
         
         ZeroMemory(dbgMatrix);
      }

Saída:

CS      0       19:33:48.862    TestScript   Matrix w Euclidean Distance
CS      0       19:33:48.862    TestScript   [[51,167,1,6.7082]
CS      0       19:33:48.862    TestScript    [62,182,0,13]
CS      0       19:33:48.862    TestScript    [69,176,0,13.41641]
CS      0       19:33:48.862    TestScript    [64,173,0,7.61577]
CS      0       19:33:48.862    TestScript    [65,172,0,8.24621]
CS      0       19:33:48.862    TestScript    [56,174,1,4.12311]
CS      0       19:33:48.862    TestScript    [58,169,0,1.41421]
CS      0       19:33:48.862    TestScript    [57,173,0,3]
CS      0       19:33:48.862    TestScript    [55,170,0,2]]

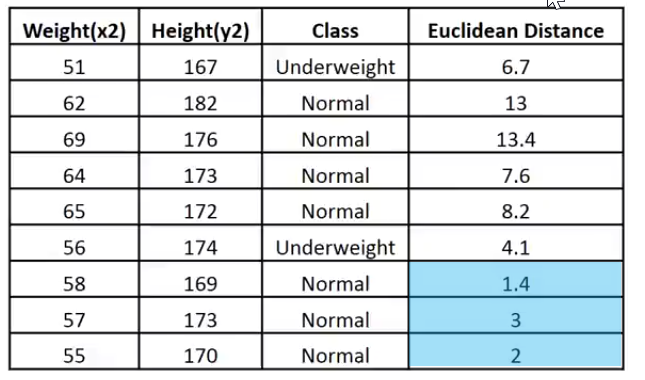
Deixe-me colocar esses dados em uma imagem para facilitar a interpretação:

Dado que o valor de k é 3, os 3 vizinhos mais próximos pertencem à classe Normal, portanto, sabemos manualmente que o ponto fornecido se enquadra na categoria Normal. Agora, vamos programar para a tomada dessa decisão. 

Para poder determinar os vizinhos mais próximos e rastreá-los será muito difícil fazer com vetores, arrays são flexíveis para fatiar e remodelar, vamos encerrar este processo usando-os

   int size = (int)m_target.Size();

   double tarArr[];
   ArrayResize(tarArr, size);
   double eucArray[];
   ArrayResize(eucArray, size);

   for(ulong i=0; i<m_target.Size(); i++)  //convert the vectors to array
     {
      tarArr[i] = m_target[i];
      eucArray[i] = euc_dist[i];
     }

   double track[], NN[];
   ArrayCopy(track, tarArr);


   int max; 
   for(int i=0; i<(int)m_target.Size(); i++)
     {
      if(ArraySize(track) > (int)k)
        {
         max = ArrayMaximum(eucArray);
         ArrayRemove(eucArray, max, 1);
         ArrayRemove(track, max, 1);
        }
     }
   ArrayCopy(NN, eucArray);

   Print("NN ");
   ArrayPrint(NN);
   Print("Track ");
   ArrayPrint(track);

No bloco de código acima, determinamos os vizinhos mais próximos e os armazenamos em um array NN, também monitoramos seus valores de classe/qual classe eles estão no vetor global de valores de destino. Além disso, removemos os valores máximos da matriz até ficarmos com a matriz de tamanho k de valores menores (vizinhos mais próximos).

Abaixo está a Saída:

CS      0       05:40:33.825    TestScript    NN 
CS      0       05:40:33.825    TestScript    1.4 3.0 2.0
CS      0       05:40:33.825    TestScript    Track 
CS      0       05:40:33.825    TestScript    0.0 0.0 0.0

Processo de votação:

//--- Voting process

   vector votes(m_classesVector.Size());

   for(ulong i=0; i<votes.Size(); i++)
     {
      int count = 0;
      for(ulong j=0; j<track.Size(); j++)
        {
         if(m_classesVector[i] == track[j])
            count++;
        }

      votes[i] = (double)count;

      if(votes.Sum() == k)  //all members have voted
         break;
     }
   Print("votes ", votes);

Saída:

2022.10.31 05:40:33.825 TestScript   votes [0,3]

O vetor de votos organiza os votos com base no vetor global de classes disponíveis no conjunto de dados, lembra?

2022.10.31 06:43:30.095 TestScript   classes vector | Neighbors [1,0]

Isso agora nos diz que dos 3 vizinhos que foram selecionados para votar, 3 deles votaram que os dados fornecidos pertencem à classe de zeros(0) e nenhum membro votou na classe de Ones(1).

Vamos ver o que poderia ter acontecido se 5 vizinhos fossem escolhidos para votar, ou seja, o valor de K era 5.

CS      0       06:43:30.095    TestScript   NN 
CS      0       06:43:30.095    TestScript   6.7 4.1 1.4 3.0 2.0
CS      0       06:43:30.095    TestScript   Track 
CS      0       06:43:30.095    TestScript   1.0 1.0 0.0 0.0 0.0
CS      0       06:43:30.095    TestScript   votes [2,3]

Agora, a decisão final é fácil de fazer, a classe com o maior número de votos venceu a decisão. Nesse caso, o peso fornecido pertence à classe normal codificada como 0.

   if(isdebug)
      Print(vector_, " belongs to class ", (int)m_classesVector[votes.ArgMax()]);

Saída:

2022.10.31 06:43:30.095 TestScript      [57,170] belongs to class 0

Ótimo, agora tudo funciona bem, vamos mudar o tipo do KNNAlgorithm de void para int, para fazê-lo retornar o valor da classe à qual o valor fornecido pertence, isso pode ser útil na negociação ao vivo, pois estaremos conectando os novos valores que esperamos uma saída imediata do algoritmo.

   int               KNNAlgorithm(vector &vector_);

Testando o modelo e encontrando a sua precisão.

Agora que nós temos o modelo, assim como qualquer outra técnica de aprendizado de máquina supervisionado, precisamos treiná-lo e testá-lo nos dados que ele não viu antes. O processo de teste nos ajudará a entender como o nosso modelo pode funcionar em diferentes conjuntos de dados.

float TrainTest(double train_size=0.7)

Por padrão, 70% do conjunto de dados será usado para treinamento, enquanto os 30% restantes serão usados para teste.

Precisamos codificar a função para dividir o conjunto de dados para a fase de treinamento e a fase de teste:

^//--- Split the matrix
   
   matrix default_Matrix = Matrix; 
   
   int train = (int)MathCeil(m_rows*train_size),
       test  = (int)MathFloor(m_rows*(1-train_size));
   
   if (isdebug) printf("Train %d test %d",train,test);

   matrix TrainMatrix(train,m_cols), TestMatrix(test,m_cols);
   int train_index = 0, test_index =0;

//---
   
   for (ulong r=0; r<Matrix.Rows(); r++)
      {
         if ((int)r < train)
           {
             TrainMatrix.Row(Matrix.Row(r),train_index);
             train_index++;
           }
         else
           {
             TestMatrix.Row(Matrix.Row(r),test_index);
             test_index++;
           }     
      }

   if (isdebug) Print("TrainMatrix\n",TrainMatrix,"\nTestMatrix\n",TestMatrix);
  

Saída:

CS      0       09:51:45.136    TestScript   TrainMatrix
CS      0       09:51:45.136    TestScript   [[51,167,1]
CS      0       09:51:45.136    TestScript    [62,182,0]
CS      0       09:51:45.136    TestScript    [69,176,0]
CS      0       09:51:45.136    TestScript    [64,173,0]
CS      0       09:51:45.136    TestScript    [65,172,0]
CS      0       09:51:45.136    TestScript    [56,174,1]
CS      0       09:51:45.136    TestScript    [58,169,0]]
CS      0       09:51:45.136    TestScript   TestMatrix
CS      0       09:51:45.136    TestScript   [[57,173,0]
CS      0       09:51:45.136    TestScript    [55,170,0]]

Portanto, o treinamento do algoritmo do vizinho mais próximo é muito simples, você pode considerar que não há treinamento porque, como dito anteriormente, esse algoritmo em si não tenta entender os padrões no conjunto de dados, ao contrário dos métodos como regressão logística ou SVM, ele apenas armazena os dados durante o treinamento, esses dados serão usados para fins de teste.

Treinamento:

   Matrix.Copy(TrainMatrix); //That's it ???

Testando:

//--- Testing the Algorithm
   
   vector TestPred(TestMatrix.Rows());
   vector v_in = {};
   
   for (ulong i=0; i<TestMatrix.Rows(); i++)
     {
        v_in = TestMatrix.Row(i);
        v_in.Resize(v_in.Size()-1); //Remove independent variable
        
        TestPred[i] = KNNAlgorithm(v_in);
        
        Print("v_in ",v_in," out ",TestPred[i]);
     }  

Saída:

CS      0       09:51:45.136    TestScript   v_in [57,173] out 0.0
CS      0       09:51:45.136    TestScript   v_in [55,170] out 0.0

Todos os testes seriam inúteis se não medíssemos a precisão do nosso modelo no conjunto de dados fornecido.

Matriz de Confusão.

Explicado anteriormente no segundo artigo desta série.

matrix CKNNNearestNeighbors::ConfusionMatrix(vector &A,vector &P)
 {
   ulong size = m_classesVector.Size();
   matrix mat_(size,size);
   
   if (A.Size() != P.Size()) 
      Print("Cant create confusion matrix | A and P not having the same size ");
   else
     {
      
         int tn = 0,fn =0,fp =0, tp=0;
         for (ulong i = 0; i<A.Size(); i++)
            {              
               if (A[i]== P[i] && P[i]==m_classesVector[0])
                  tp++; 
               if (A[i]== P[i] && P[i]==m_classesVector[1])
                  tn++;
               if (P[i]==m_classesVector[0] && A[i]==m_classesVector[1])
                  fp++;
               if (P[i]==m_classesVector[1] && A[i]==m_classesVector[0])
                  fn++;
            }
            
       mat_[0][0] = tn; mat_[0][1] = fp;
       mat_[1][0] = fn; mat_[1][1] = tp;

    }
     
   return(mat_);    
 }

Dentro da TrainTest() ao final da função, eu adicionei o seguinte código para finalizar a função e retornar a sua Precisão;

   matrix cf_m = ConfusionMatrix(TargetPred,TestPred);
   vector diag = cf_m.Diag();
   float acc = (float)(diag.Sum()/cf_m.Sum())*100;
   
   Print("Confusion Matrix\n",cf_m,"\nAccuracy ------> ",acc,"%");
   
   return(acc);      

Saída:

CS      0       10:34:26.681    TestScript   Confusion Matrix
CS      0       10:34:26.681    TestScript   [[2,0]
CS      0       10:34:26.681    TestScript    [0,0]]
CS      0       10:34:26.681    TestScript   Accuracy ------> 100.0%

Claro, a precisão tinha que ser cem por cento, o modelo recebeu apenas dois pontos de dados para teste em que todos eles pertenciam à classe zero (A classe normal), o que é verdade.

Até este ponto, nós temos uma biblioteca K-vizinhos mais próximos totalmente funcional. Vamos ver como podemos usá-la para prever o preço de diferentes instrumentos forex e ações.

Preparando o conjunto de dados.

Lembre-se de que este é um aprendizado supervisionado, o que significa que deve haver interferência humana para criar os dados e rotulá-los, para que os modelos saibam quais são seus objetivos, para que possam entender a relação entre as variáveis independentes e de destino.

As variáveis independentes de escolha são as leituras do ATRe o indicador de volumes, enquanto a variável de destino será definida como 1 se o mercado subir e 0 se o mercado cair, isso se tornará o sinal de compra e o sinal de venda, respectivamente, ao testar e usar o modelo para negociar.

int OnInit()
  {
//--- Preparing the dataset 

    atr_handle = iATR(Symbol(),timeframe,period);
    volume_handle = iVolumes(Symbol(),timeframe,applied_vol);
    
    CopyBuffer(atr_handle,0,1,bars,atr_buffer);
    CopyBuffer(volume_handle,0,1,bars,volume_buffer); 
    
    Matrix.Col(atr_buffer,0); //Independent var 1
    Matrix.Col(volume_buffer,1); //Independent var 2
    
//--- Target variables

    vector Target_vector(bars);
    
    MqlRates rates[];
    ArraySetAsSeries(rates,true);
    CopyRates(Symbol(),PERIOD_D1,1,bars,rates);
    
    for (ulong i=0; i<Target_vector.Size(); i++) //putting the labels
     {
       if (rates[i].close > rates[i].open)
          Target_vector[i] = 1; //bullish
       else
          Target_vector[i] = 0;
     }

   Matrix.Col(Target_vector,2);
        
//---

A lógica de encontrar as variáveis independentes é que se o fechamento de uma vela foi acima de sua abertura, em outras palavras, a vela de alta, a variável de destino para as variáveis independentes é 1, caso contrário, 0.

Agora, lembre-se de que estamos na vela diária, uma única vela tem muitos movimentos de preço nessas 24 horas, essa lógica pode não ser boa ao tentar fazer um scalper ou algo que negocie em períodos menores, também há uma pequena falha na lógica, porque se o preço de fechamento for maior que o preço de abertura, significa que a variável-alvo é como 1, caso contrário, significa 0, mas geralmente é onde o preço de abertura é igual ao preço de fechamento, certo? Eu entendo, mas esta situação raramente acontece em tempos gráficos maiores, então esta é minha maneira de dar espaço ao modelo para erros. 

A propósito, isso não é um conselho financeiro ou de negociação.

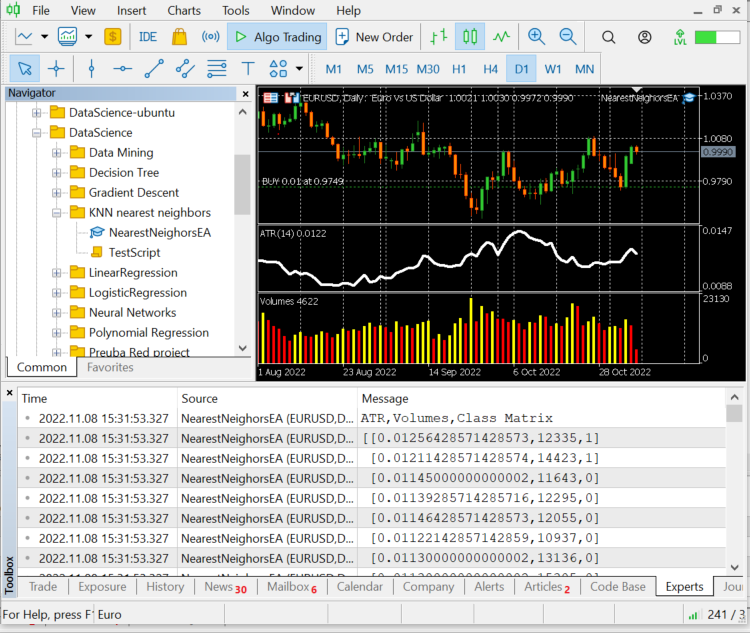
então vamos imprimir os valores das últimas 10 barras, 10 linhas de nossa matriz de conjunto de dados;

CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)   ATR,Volumes,Class Matrix
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)   [[0.01139285714285716,12295,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01146428571428573,12055,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01122142857142859,10937,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01130000000000002,13136,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01130000000000002,15305,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01097857142857144,13762,1]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.0109357142857143,12545,1]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01116428571428572,18806,1]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01188571428571429,19595,1]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01137142857142859,15128,1]]


Os dados foram bem classificados de suas respectivas velas e indicadores, agora vamos passar para o algoritmo.

    nearest_neigbors = new CKNNNearestNeighbors(Matrix,k); 
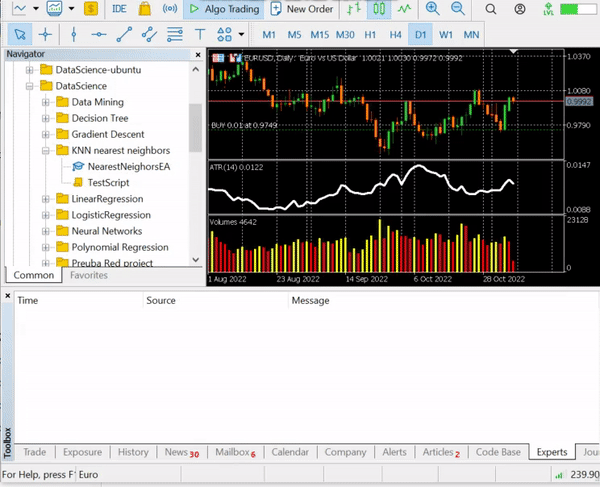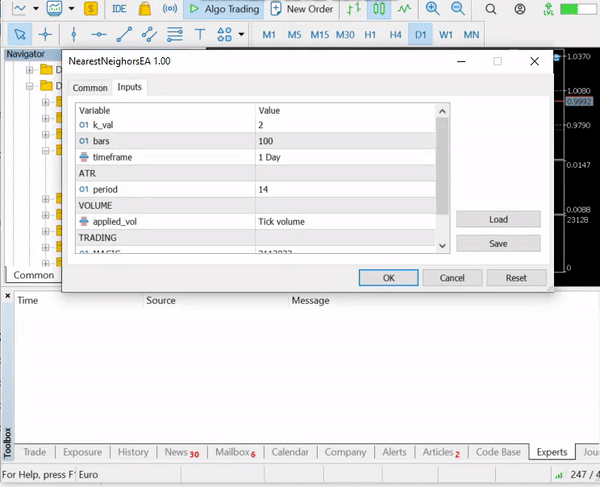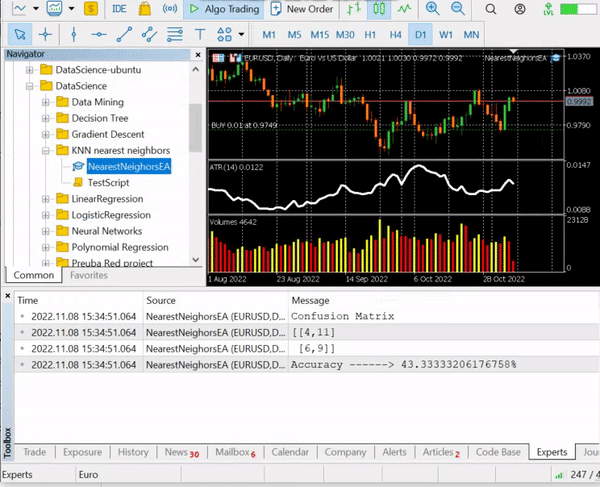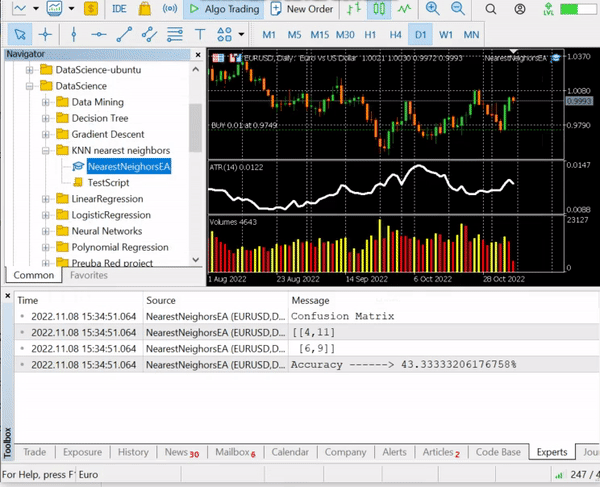
    nearest_neigbors.TrainTest();

Saída:


Temos uma precisão de cerca de 43,33%, nada mal considerando que não nos preocupamos em encontrar o valor ideal de k. vamos repetir diferentes valores de k e escolher aquele que oferecem uma melhor precisão.

    for(uint i=0; i<bars; i++)
      {
        printf("<<< k %d >>>",i);
        nearest_neigbors = new CKNNNearestNeighbors(Matrix,i); 
        nearest_neigbors.TrainTest(); 
        
        delete(nearest_neigbors);
      }

Saída:

......
CS      0       16:22:28.013    NearestNeighorsEA (EURUSD,D1)   <<< k 24 >>>
CS      0       16:22:28.013    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 46.66666793823242%
CS      0       16:22:28.014    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 46.66666793823242%
CS      0       16:22:28.014    NearestNeighorsEA (EURUSD,D1)   <<< k 26 >>>
CS      0       16:22:28.014    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 40.0%
CS      0       16:22:28.014    NearestNeighorsEA (EURUSD,D1)   <<< k 27 >>>
CS      0       16:22:28.015    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 40.0%
CS      0       16:22:28.015    NearestNeighorsEA (EURUSD,D1)   <<< k 28 >>>
CS      0       16:22:28.015    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.016    NearestNeighorsEA (EURUSD,D1)   <<< k 29 >>>
CS      0       16:22:28.016    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.016    NearestNeighorsEA (EURUSD,D1)   <<< k 30 >>>
.....
.....
CS      0       16:22:28.017    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 60.000003814697266%
CS      0       16:22:28.017    NearestNeighorsEA (EURUSD,D1)   <<< k 31 >>> 
CS      0       16:22:28.017    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 60.000003814697266%
CS      0       16:22:28.017    NearestNeighorsEA (EURUSD,D1)   <<< k 32 >>> 
CS      0       16:22:28.018    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.018    NearestNeighorsEA (EURUSD,D1)   <<< k 33 >>> 
CS      0       16:22:28.018    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.018    NearestNeighorsEA (EURUSD,D1)   <<< k 34 >>> 
CS      0       16:22:28.019    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 50.0%
CS      0       16:22:28.019    NearestNeighorsEA (EURUSD,D1)   <<< k 35 >>> 
CS      0       16:22:28.019    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 50.0%
CS      0       16:22:28.019    NearestNeighorsEA (EURUSD,D1)   <<< k 36 >>> 
CS      0       16:22:28.020    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 53.333335876464844%
CS      0       16:22:28.020    NearestNeighorsEA (EURUSD,D1)   <<< k 37 >>> 
CS      0       16:22:28.020    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 53.333335876464844%
CS      0       16:22:28.020    NearestNeighorsEA (EURUSD,D1)   <<< k 38 >>> 
CS      0       16:22:28.021    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.021    NearestNeighorsEA (EURUSD,D1)   <<< k 39 >>> 
CS      0       16:22:28.021    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.021    NearestNeighorsEA (EURUSD,D1)   <<< k 40 >>> 
CS      0       16:22:28.022    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.022    NearestNeighorsEA (EURUSD,D1)   <<< k 41 >>>
.....
....
CS      0       16:22:28.023    NearestNeighorsEA (EURUSD,D1)   <<< k 42 >>>
CS      0       16:22:28.023    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 63.33333206176758%
CS      0       16:22:28.023    NearestNeighorsEA (EURUSD,D1)   <<< k 43 >>>
CS      0       16:22:28.024    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 63.33333206176758%
CS      0       16:22:28.024    NearestNeighorsEA (EURUSD,D1)   <<< k 44 >>>
CS      0       16:22:28.024    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 66.66667175292969%
CS      0       16:22:28.024    NearestNeighorsEA (EURUSD,D1)   <<< k 45 >>>
CS      0       16:22:28.025    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 66.66667175292969%
CS      0       16:22:28.025    NearestNeighorsEA (EURUSD,D1)   <<< k 46 >>>
CS      0       16:22:28.025    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.025    NearestNeighorsEA (EURUSD,D1)   <<< k 47 >>>
....
....

Mesmo que este método para determinar o valor de k não seja a melhor maneira, pode-se usar o método de validação cruzada Loose One para encontrar os valores ideais de k. Parece que o desempenho máximo foi quando o valor de k estava na casa dos quarenta. Agora é a vez de usarmos o Algoritmo no ambiente de negociação.

void OnTick()
  {
  
    vector x_vars(2); //vector to store atr and volumes values
    double atr_val[], volume_val[];
    
    CopyBuffer(atr_handle,0,0,1,atr_val);
    CopyBuffer(volume_handle,0,0,1,volume_val);
    
    x_vars[0] = atr_val[0]; 
    x_vars[1] = volume_val[0];
    
//---
    int signal = 0;
    
    double volume = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN);
    
    MqlTick ticks;
    SymbolInfoTick(Symbol(),ticks);
    
    double ask = ticks.ask, bid = ticks.bid;
    
    
      if (isNewBar() == true) //we are on the new candle
         {
            signal = nearest_neigbors.KNNAlgorithm(x_vars); //Calling the algorithm
            
            if (signal == 1)
              {
                 if (!CheckPosionType(POSITION_TYPE_BUY))
                  {
                    m_trade.Buy(volume,Symbol(),ask,0,0);
                    if (ClosePosType(POSITION_TYPE_SELL))
                      printf("Failed to close %s Err = %d",EnumToString(POSITION_TYPE_SELL),GetLastError());
                  }
              }
            else 
              {
                if (!CheckPosionType(POSITION_TYPE_SELL))
                  {
                    m_trade.Sell(volume,Symbol(),bid,0,0);
                    if (ClosePosType(POSITION_TYPE_BUY))
                      printf("Failed to close %s Err = %d",EnumToString(POSITION_TYPE_BUY),GetLastError());
                  }
              }
         }
     
  }
  

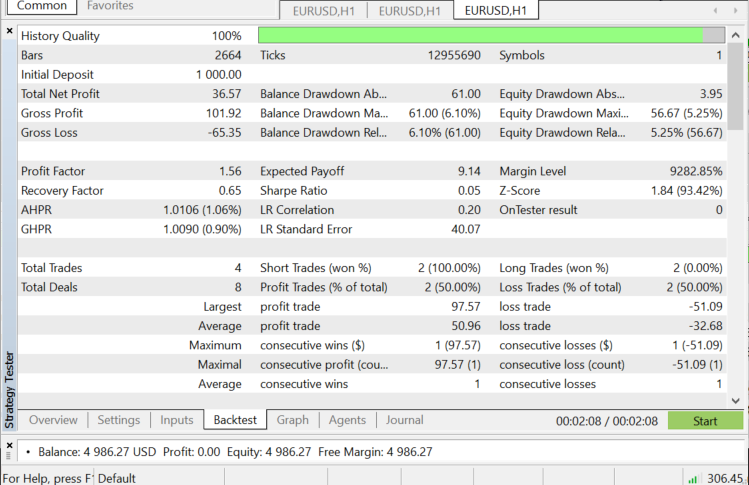
Agora que nosso EA é capaz de abrir negociações e fechá-las, deixe-me experimentá-lo no testador de estratégia, mas antes disso, esta é uma visão geral sobre como chamar o algoritmo em todo o Expert Advisor;

#include "KNN_nearest_neighbors.mqh";
CKNNNearestNeighbors *nearest_neigbors;

matrix Matrix;
//+------------------------------------------------------------------+
//| Expert initialization function                                     |
//+------------------------------------------------------------------+
int OnInit()
  { 
// gathering data to Matrix has been ignored
    
     nearest_neigbors = new CKNNNearestNeighbors(Matrix,_k); 
 
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- 

    delete(nearest_neigbors);
  }

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+

void OnTick()
  {
  
    vector x_vars(2); //vector to store atr and volumes values

//adding live indicator values from the market has been ignored 

//---
    int signal = 0;

      if (isNewBar() == true) //we are on the new candle
         {
            signal = nearest_neigbors.KNNAlgorithm(x_vars);
            //trading actions
         }
}

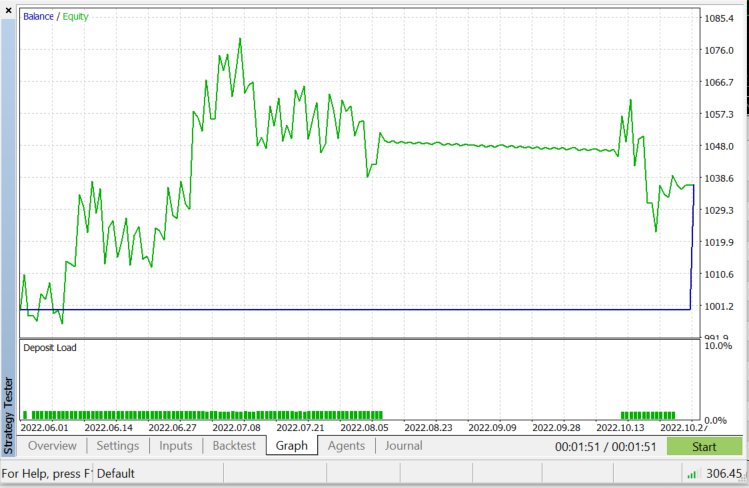
Testador de estratégia em EURUSD: de 01.06.2022 até 03.11.2022 (cada tick):



Quando usar o KNN?

É muito importante saber onde usar esse algoritmo, porque nem todos os problemas podem ser resolvidos por ele, assim como todas as técnicas de aprendizado de máquina.

  • Quando o conjunto de dados é rotulado
  • Quando o conjunto de dados é livre de ruído
  • Quando o conjunto de dados é pequeno (isso também é útil por motivos de desempenho)

Vantagens:

  • Ele é muito fácil de entender e implementar 
  • Ele é baseado em pontos de dados locais que podem ser benéficos para os conjuntos de dados envolvendo muitos grupos com clusters locais

Desvantagens:

Todos os dados de treinamento são usados toda vez que precisamos prever algo, isso significa que todos os dados devem estar armazenados e prontos para serem usados toda vez que houver um novo ponto a classificar.

Pensamentos finais:

como dito anteriormente, este algoritmo é um bom classificador, mas não em um conjunto de dados complexo, então acho que faria melhores preditores em ações e índices, deixo isso para você explorar, uma coisa que você verá ao testar este algoritmo em um EA é que ele causa problemas de desempenho no testador de estratégia, embora eu tenha escolhido 50 barras e feito o robô entrar em ação em uma nova barra, o testador ficaria preso em cada vela por cerca de 20 a 30 segundos apenas para permitir que o algoritmo fosse executado todo o processo, embora o processo seja mais rápido na negociação ao vivo, é exatamente o oposto no testador. Sempre há espaço para melhorias, especialmente nas seguintes linhas de código, porque eu não consegui extrair as leituras do indicador na função Init, então tive que extraí-los para treinar e usá-los para prever o mercado, tudo em um só lugar.

        if (isNewBar() == true) //we are on the new candle
         { 
           if (MQLInfoInteger(MQL_TESTER) || MQLInfoInteger(MQL_OPTIMIZATION)) 
             {
               gather_data();      
               nearest_neigbors = new CKNNNearestNeighbors(Matrix,_k); 
               signal = nearest_neigbors.KNNAlgorithm(x_vars);
               
               delete(nearest_neigbors);
             }      

Obrigado por ler.

Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/11678

Arquivos anexados |
Baixar como ZIP
KNN_nearest_neighbors.zip (67.49 KB)
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.

Outros artigos do autor

Últimos Comentários | Ir para discussão (1)
Antonio valeriano costa
Antonio valeriano costa | 21 fev 2023 em 01:47
Congratulations for the article! I'm looking back on updates.
Aprendendo a construindo um Expert Advisor que opera de forma automática (Parte 14): Automação (VI) Aprendendo a construindo um Expert Advisor que opera de forma automática (Parte 14): Automação (VI)
Aqui vamos realmente colocar todo o conhecimento desta sequencia em prática. Vamos finalmente construir um sistema 100% automático e funcional. Mas para fazer isto, você terá que aprender uma última coisa.
Ciência de Dados e Aprendizado de Máquina (Parte 08): Agrupamento K-Means em MQL5 Ciência de Dados e Aprendizado de Máquina (Parte 08): Agrupamento K-Means em MQL5
A mineração de dados é crucial para um cientista de dados e um trader porque, muitas vezes, os dados não são tão diretos quanto pensamos, o olho humano não consegue entender o padrão subjacente menor e as relações no conjunto de dados, talvez o algoritmo K-means pode nos ajudar com isso. Vamos descobrir...
DoEasy. Controles (Parte 25): Objeto WinForms Tooltip DoEasy. Controles (Parte 25): Objeto WinForms Tooltip
Neste artigo, começaremos a desenvolver o controle Tooltip (dica de ferramenta) e começaremos a criar novas primitivas gráficas para a biblioteca. Naturalmente, nem todo elemento tem uma dica de ferramenta, mas todo objeto gráfico pode ter uma.
Como desenvolver um sistema de negociação baseado no indicador Fractais Como desenvolver um sistema de negociação baseado no indicador Fractais
Aqui está um novo artigo da nossa série sobre como projetar um sistema de negociação com base nos indicadores técnicos mais populares. Nós aprenderemos um novo indicador que é o indicador Fractais e aprenderemos como desenvolver um sistema de negociação baseado nele para ser executado na plataforma MetaTrader 5.