Ejemplo de optimización estocástica y control óptimo

Introducción a la optimización estocástica y al control óptimo

La modelización estocástica y la optimización del control son métodos matemáticos que ayudan a resolver problemas bajo incertidumbre. Se utilizan en finanzas, ingeniería, inteligencia artificial y muchas otras áreas.

La modelización estocástica se utiliza para describir sistemas con elementos aleatorios, como los movimientos de los precios bursátiles o la cola de un restaurante. Se basa en variables aleatorias, distribuciones de probabilidad y procesos estocásticos. Métodos como Montecarlo y las cadenas de Markov pueden modelar estos procesos y predecir su comportamiento.

La optimización del control le ayuda a encontrar mejores soluciones para controlar los sistemas. Se utiliza para automatizar y mejorar el funcionamiento de diversos procesos, desde la conducción de automóviles hasta la operación de plantas químicas. Los métodos básicos incluyen el controlador cuadrático lineal, el control predictivo de modelos y el aprendizaje de refuerzo. La optimización del control estocástico combina ambos enfoques y se aplica a problemas en los que deben tomarse decisiones en ausencia de información completa sobre el futuro, por ejemplo, en inversiones o en la gestión de la cadena de suministro.

Estos métodos nos permiten modelar sistemas inciertos y tomar decisiones informadas en entornos complejos, lo que los convierte en herramientas importantes en el mundo moderno.

Asesor Experto (Expert Advisor, EA)

El asesor SMOC (Smart Money Optimal Control) utiliza una combinación de indicadores técnicos, modelos matemáticos y métodos de gestión del riesgo para tomar decisiones de negociación en el mercado de divisas, como ejemplo sencillo que demuestra sus capacidades.

Características principales:

1. Modelo de gestión predictiva: el EA utiliza un algoritmo de gestión óptimo para predecir futuros movimientos de precios y tomar decisiones comerciales.
2. Parámetros adaptativos: el sistema ajusta el horizonte de pronóstico y el tamaño del lote dependiendo de la volatilidad del mercado y la reducción de la cuenta.
3. Múltiples indicadores técnicos: Incluye medias móviles simples (SMA), SAR Parabólico, índice de fuerza relativa (RSI) y rango medio verdadero (ATR) para el análisis de tendencias y volatilidad.
4. Stop Loss y Take Profit dinámicos: El EA calcula y actualiza los niveles de SL y TP en función de la volatilidad del mercado.
5. Gestión del riesgo: Incluye funciones para ajustar el tamaño de la posición en función del saldo de la cuenta y la reducción.

Posibles áreas de aplicación:

• Estrategias comerciales a medio y largo plazo.
• Mercados con tendencias pronunciadas.
• Carteras que requieren una gestión de riesgos compleja.

Ventajas:

1. Enfoque adaptativo: el sistema se adapta a las condiciones cambiantes del mercado, aumentando potencialmente su resiliencia.
2. Análisis complejo: mediante la combinación de múltiples indicadores y modelos matemáticos, pretende reflejar diversos aspectos del comportamiento del mercado.
3. Contabilidad de riesgos: el asesor incluye protección contra caídas y determinación dinámica del tamaño de la posición.
4. Registro detallado: se mantiene un archivo de registro para el análisis del rendimiento y la depuración.

Contras:

1. Complejidad: Los algoritmos complejos pueden hacer que el sistema sea difícil de entender y optimizar.
2. Computacionalmente intensivo: los cálculos de control óptimo pueden ser computacionalmente intensivos, lo que potencialmente limita su uso en sistemas menos potentes.
3. Posible sobreajuste: con una gran cantidad de parámetros e indicadores, existe el riesgo de sobreajuste a los datos históricos.
4. Supuesto del mercado: La eficacia de la estrategia se basa en el supuesto de que el comportamiento de los precios pasados puede predecir movimientos futuros, lo que no siempre es cierto en los mercados financieros.

Características principales del asesor SMOC

Control predictivo de modelos (Model Predictive Control, MPC): el EA utiliza un algoritmo de control óptimo para predecir futuros movimientos de precios y tomar decisiones comerciales. Esto se implementa en la función OptimalControl().

//+------------------------------------------------------------------+
//| Function for optimal control using Model Predictive Control      |
//+------------------------------------------------------------------+
int OptimalControl( double currentPrice)
  {
   int predictionHorizon = CalculateAdaptiveHorizon();
   double mu = EstimateDrift();
   double sigma = EstimateVolatility();
   double baseThreshold = 0.001 ;
   double decisionThreshold = baseThreshold * ( 1 + ( 1 - successRate));
   double dt = 1.0 / 1440.0 ;

   double bestExpectedReturn = - DBL_MAX ;
   int bestDecision = 0 ;
   double bestU1 = 0 , bestU2 = 0 ;

// Optimize the search space
   double u1Start = 0.01 , u1End = 0.99 , u1Step = 0.01 ;
   double u2Start = 0.01 , u2End = 0.99 , u2Step = 0.01 ;

// Calculate historical average price
   int lookbackPeriod = 20 ; // You can adjust this
   double historicalPrices[];
   ArraySetAsSeries (historicalPrices, true );
   CopyClose ( Symbol (), PERIOD_CURRENT , 0 , lookbackPeriod, historicalPrices);
   double avgHistoricalPrice = ArraySum(historicalPrices) / lookbackPeriod;

   for ( double u1 = u1Start; u1 <= u1End; u1 += u1Step)
     {
       for ( double u2 = u2Start; u2 <= u2End; u2 += u2Step)
        {
         double expectedReturn = CalculateExpectedReturn(currentPrice, mu, sigma, dt, predictionHorizon, u1, u2);

         // Compare with historical average
         if (currentPrice > avgHistoricalPrice)
           {
            expectedReturn *= - 1 ; // Invert expected return to favor selling when price is high
           }

         if (expectedReturn > bestExpectedReturn)
           {
            bestExpectedReturn = expectedReturn;
            bestU1 = u1;
            bestU2 = u2;
           }
        }
     }

   LogMessage( StringFormat ( "OptimalControl - Best u1: %f, Best u2: %f, Best Expected Return: %f, Decision Threshold %f" ,
                           bestU1, bestU2, bestExpectedReturn, decisionThreshold));

   if (bestExpectedReturn > decisionThreshold)
       return 1 ; // Buy
   if (bestExpectedReturn < decisionThreshold)
       return - 1 ; // Sell
   return 0 ; // Hold
  }

Esto utiliza el control predictivo de modelos (MPC) para tomar decisiones comerciales óptimas. La función OptimalControl es el núcleo de este algoritmo, diseñado para determinar si comprar, vender o mantener en función de las condiciones y pronósticos actuales del mercado.

La función OptimalControl toma el precio actual como entrada y devuelve un entero que representa la decisión comercial:

• 1 para compras.
• -1 para ventas.
• 0 para mantener.

Componentes clave

1. Horizonte de pronóstico adaptativo: la función calcula un horizonte de pronóstico adaptativo, lo que permite al algoritmo ajustar el rango de pronóstico en función de las condiciones del mercado.
2. Evaluación de los parámetros del mercado: Evalúa los parámetros clave del mercado:
   • Deriva (μ): Rendimiento esperado de un activo.
   • Volatilidad (σ): Tasa de variación del precio de un activo.
3. Umbral de decisión: El umbral dinámico se calcula en función del umbral base y de la tasa de éxito del algoritmo. Esto adapta la sensibilidad del algoritmo a los cambios del mercado.
4. Proceso de optimización: La función utiliza la búsqueda en cuadrícula para optimizar dos parámetros de control (u1 y u2) en un espacio de búsqueda definido.
5. Comparación de precios históricos: El precio actual se compara con la media histórica para ajustar la estrategia en función de si el precio actual es relativamente alto o bajo.
6. Cálculo de la rentabilidad esperada: Para cada combinación de parámetros de control, se calcula la rentabilidad esperada mediante una función independiente (no mostrada en este fragmento de código).
7. Toma de decisiones: En función de la mejor rentabilidad esperada y del umbral de decisión, se decide si comprar, vender o mantener el activo.

Revisión detallada

1. La función comienza inicializando las variables y calculando los parámetros necesarios.
2. A continuación, entra en un bucle anidado para encontrar los parámetros de control óptimos (u1 y u2).
3. Para cada combinación de u1 y u2, se calcula la rentabilidad esperada.
4. Si el precio actual está por encima de la media histórica, invierte la rentabilidad esperada. Esto crea una tendencia a vender cuando los precios son altos y a comprar cuando son bajos.
5. Sigue la mejor rentabilidad esperada y los índices de referencia correspondientes.
6. Tras la optimización, se registran los mejores parámetros y la rentabilidad esperada.
7. Por último, compara la mejor rentabilidad esperada con el valor umbral para tomar una decisión comercial.

Ideas clave

• El algoritmo se adapta a las condiciones del mercado utilizando un horizonte adaptativo y un umbral dinámico.
• Implica tanto la optimización a corto plazo (utilizando el enfoque MPC) como la comprensión a largo plazo de las tendencias (utilizando comparaciones históricas de precios).
• El uso de la búsqueda en cuadrícula para la optimización permite explorar a fondo el espacio de parámetros, lo que puede conducir a decisiones más sólidas.

Posibles mejoras

1. La búsqueda en cuadrícula se puede reemplazar con un algoritmo de optimización más eficiente para mejorar el rendimiento.
2. La comparación de precios históricos puede hacerse más compleja, tal vez incluyendo múltiples períodos de tiempo.
3. Pueden añadirse funciones de gestión del riesgo para equilibrar la optimización de la rentabilidad con la minimización del riesgo.

 /+------------------------------------------------------------------+
//| Calculate expected return for given parameters                   |
//+------------------------------------------------------------------+
double CalculateExpectedReturn( double currentPrice, double mu, double sigma, double dt, int horizon, double u1, double u2)
  {
   double tempPrice = currentPrice;
   double totalReturn = 0 ;

   for ( int i = 0 ; i < horizon; i++)
     {
       double Z = MathSqrt (- 2.0 * MathLog (u1)) * MathCos ( 2.0 * M_PI * u2);
       double nextPrice = tempPrice * MathExp ((mu - 0.5 * sigma * sigma) * dt + sigma * MathSqrt (dt) * Z);
      totalReturn += nextPrice - tempPrice;
      tempPrice = nextPrice;
     }

   return totalReturn / horizon;
  }

Es un componente esencial de los modelos financieros y los sistemas de negociación algorítmica. Esta función estima la rentabilidad esperada de un activo en un horizonte temporal determinado utilizando un proceso estocástico conocido como Movimiento Browniano Geométrico (Geometric Brownian Motion, GBM).

 double CalculateExpectedReturn( double currentPrice, double mu, double sigma, double dt, int horizon, double u1, double u2)

Parámetros

1. currentPrice : Precio actual del activo.
2. mu : Parámetro de deriva (rendimiento esperado).
3. sigma: Parámetro de volatilidad.
4. dt: Paso temporal (normalmente 1/número de pasos por año).
5. Horizon: El número de pasos temporales a simular.
6. u1, u2: Números aleatorios utilizados para generar variables aleatorias con distribución normal.

Descripción general de las funciones

Esta función modela la trayectoria del precio de un activo utilizando el modelo geométrico de movimiento browniano, muy utilizado en matemáticas financieras para modelizar los precios de las acciones. A continuación, calcula la rentabilidad media a lo largo de la trayectoria modelizada.

Explicación detallada

1. Inicialización:
   • tempPrice se inicializa con el precio actual.
   • totalReturn se pone a 0 para acumular devoluciones.
2. Bucle de simulación: La función entra en un bucle que recorre el horizonte veces. En cada iteración: Generar una variable aleatoria normal :

 double Z = MathSqrt (- 2.0 * MathLog (u1)) * MathCos ( 2.0 * M_PI * u2);

Esta línea implementa la transformada Box-Muller para generar una variable aleatoria normal estándar. Este es un componente clave en la modelización de un paseo aleatorio en los precios de los activos.

Calcular el siguiente precio:

 double nextPrice = tempPrice * MathExp ((mu - 0.5 * sigma * sigma) * dt + sigma * MathSqrt (dt) * Z);

Esta línea implementa la fórmula del movimiento browniano geométrico:

• (mu - 0.5 * sigma * sigma) * dt es el componente de deriva
• sigma * MathSqrt(dt) * Z es el componente aleatorio de choque

Rentabilidad acumulada:

totalReturn += nextPrice - tempPrice;

La función calcula y acumula el rendimiento de cada paso.

Actualización de precios:

tempPrice = nextPrice;

El precio actual se actualiza para la siguiente iteración.

Calcular el rendimiento medio:

 return totalReturn / horizon;

La función devuelve la rentabilidad media a lo largo del horizonte simulado.

Importancia en la modelización financiera

1. Evaluación de riesgos: Mediante la simulación de múltiples trayectorias de precios, esta función ayuda a evaluar los riesgos potenciales asociados a un activo.
2. Preciación de opciones: Este tipo de modelización es fundamental en los modelos de valoración de opciones, especialmente los métodos Montecarlo.
3. Optimización de carteras: Los rendimientos esperados son datos clave en los algoritmos de optimización de carteras.
4. Estrategias de negociación: Las estrategias de negociación algorítmicas suelen utilizar los rendimientos esperados para tomar decisiones de compra/venta.

Limitaciones y consideraciones

1. Supuestos del modelo: El modelo GBM asume que los rendimientos se distribuyen normalmente y son independientes, lo que puede no ser siempre cierto en los mercados reales.
2. Estimación de parámetros: La precisión de la función depende en gran medida de la correcta estimación de 'mu' y 'sigma'.
3. Simulación única: Esta función realiza una simulación única. En la práctica, suelen realizarse varias simulaciones para obtener una estimación más fiable.
4. Horizonte temporal: La elección del horizonte y del 'dt' puede afectar significativamente a los resultados y debe elegirse cuidadosamente en función del caso de uso específico.

Esta función es un elemento fundamental en las finanzas cuantitativas y proporciona una manera de estimar rendimientos futuros basados en parámetros actuales del mercado. Su implementación en algoritmos comerciales permite la toma de decisiones basada en datos en entornos financieros complejos.

Parámetros adaptativos: el sistema ajusta su horizonte de pronóstico y el tamaño del lote en función de la volatilidad del mercado y la reducción de la cuenta. Esto se logra utilizando funciones como CalculateAdaptiveHorizon() y AdjustLotSizeForDrawdown().

//+------------------------------------------------------------------+
//| Calculate adaptive horizon                                       |
//+------------------------------------------------------------------+
int CalculateAdaptiveHorizon()
  {
   double currentVolatility = EstimateVolatility();
   int baseHorizon = 5 ;
   return MathMax (baseHorizon, MathMin ( 20 , ( int )(baseHorizon * ( 1 + currentVolatility))));
  }

 // Función para ajustar el tamaño del lote basado en drawdown
double AdjustLotSizeForDrawdown()
  {
   static int consecutiveLosses = 0 ;
   static double maxBalance = 0 ;

   double currentBalance = AccountInfoDouble ( ACCOUNT_BALANCE );
   double currentEquity = AccountInfoDouble ( ACCOUNT_EQUITY );

   if (currentBalance > maxBalance)
      maxBalance = currentBalance;

   double drawdown = (maxBalance - currentEquity) / maxBalance;

   double baseLotSize = CalculateDynamicLotSize();

   if (drawdown > 0.1 ) // 10% drawdown
     {
       return baseLotSize * 0.5 ; // Reducir el tamaño del lote a la mitad
     }
   else
       if (consecutiveLosses > 3 )
        {
         return baseLotSize * 0.75 ; // Reducir el tamaño del lote en un 25%
        }

   return baseLotSize;
  }

Este es un componente importante de la gestión del riesgo comercial. Esta función ajusta el tamaño del lote comercial en función de la reducción de la cuenta actual y la cantidad de pérdidas consecutivas.

Descripción general de las funciones

La función AdjustLotSizeForDrawdown está diseñada para ajustar dinámicamente el tamaño del lote de negociación con el fin de gestionar los riesgos en condiciones de mercado volátiles. Tiene en cuenta dos factores principales:

1. Disminución actual de la cuenta de negociación.
2. Número de derrotas consecutivas.

Componentes clave

1. Variables estáticas:
   • consecutiveLosses: Controla el número de operaciones perdedoras consecutivas.
   • maxBalance: Mantiene el saldo máximo alcanzado en la cuenta.
2. Información de la cuenta:
   • currentBalance: Saldo actual de la cuenta comercial.
   • currentEquity: Patrimonio actual de la cuenta de operaciones
3. Cálculo de la reducción : La reducción se calcula como una disminución porcentual desde el saldo máximo hasta el capital actual.
4. Tamaño de lote base: La función llama a CalculateDynamicLotSize() (no se muestra en este fragmento) para determinar el tamaño de lote base.
5. Ajuste del tamaño del lote: La función ajusta el tamaño del lote basándose en dos condiciones:
• Si la reducción supera el 10%.
• Si hubo más de 3 pérdidas consecutivas.

Explicación detallada

Actualización del saldo máximo:

 if (currentBalance > maxBalance)
   maxBalance = currentBalance;

Esto le permite hacer un seguimiento del saldo máximo alcanzado, lo que es crucial para calcular la reducción.

Cálculo de la reducción:

 double drawdown = (maxBalance - currentEquity) / maxBalance;

Calcula la reducción actual como porcentaje del saldo máximo.

Obtención del tamaño del lote base:

 double baseLotSize = CalculateDynamicLotSize();

Esto llama a una función separada para calcular el tamaño inicial del lote.

Ajuste por reducción elevada:

 if (drawdown > 0.1 ) // 10% drawdown
  {
   return baseLotSize * 0.5 ; // Reduce lot size by half
  }

Si la reducción supera el 10%, la función reduce el tamaño del lote a la mitad para reducir el riesgo.

Ajuste de pérdidas consecutivas:

 else if (consecutiveLosses > 3 )
  {
   return baseLotSize * 0.75 ; // Reduce lot size by 25%
  }

Si se producen más de 3 pérdidas consecutivas, la función reduce el tamaño del lote en un 25%.

Devolver valor predeterminado: Si no se cumple ninguna de las condiciones, la función devuelve el tamaño del lote base sin ajuste.

Importancia en la gestión de riesgos:

1. Protección contra reducciones: Al reducir el tamaño de los lotes en caso de reducciones significativas, esta función ayuda a proteger la cuenta frente a pérdidas adicionales en condiciones de mercado adversas.
2. Gestión de las rachas perdedoras: Ajustar las pérdidas consecutivas ayuda a mitigar los efectos de las rachas perdedoras, que pueden ser devastadoras psicológica y financieramente.
3. Ajuste dinámico del riesgo: Esta función le permite gestionar dinámicamente sus riesgos ajustándose a las condiciones actuales del mercado y a los resultados de las operaciones.

Consideraciones y posibles mejoras

1. Ajuste gradual: La función puede modificarse para implementar un ajuste más gradual de los tamaños de lote basado en diferentes niveles de reducción.
2. Mecanismo de recuperación: Se puede añadir un mecanismo adicional para aumentar gradualmente el tamaño de los lotes a medida que la cuenta se recupera de una reducción.
3. Tamaño máximo de lote: La introducción de un límite máximo de tamaño de lote puede proporcionar una capa adicional de gestión del riesgo.
4. Seguimiento de ganancias: La función puede ampliarse para realizar un seguimiento de las ganancias consecutivas y aumentar potencialmente el tamaño de los lotes durante los periodos favorables.

Esta característica es un aspecto vital de la gestión de riesgos en los sistemas comerciales, ya que ayuda a preservar el capital en condiciones de mercado difíciles y a mitigar los efectos de las rachas perdedoras.

Varios indicadores técnicos: El asesor incluye varios indicadores técnicos para el análisis:

• Medias móviles simples (Simple Moving Average, SMA)
• SAR Parabólico (Stop and Reverse, SAR)
• Índice de fuerza relativa (Relative Strength Index, RSI)
• Rango medio verdadero (Average True Range, ATR)

 // Initialize indicator handles
   smaHandle = iMA ( Symbol (), PERIOD_CURRENT , 50 , 0 , MODE_SMA , PRICE_CLOSE );
   psarHandle = iSAR ( Symbol (), PERIOD_CURRENT , 0.02 , 0.2 );
   rsiHandle = iRSI ( Symbol (), PERIOD_CURRENT , 14 , PRICE_CLOSE );
   atrHandle = iATR ( Symbol (), PERIOD_CURRENT , 14 );

Stop Loss y Take Profit dinámicos: El EA calcula y actualiza los niveles SL y TP en función de la volatilidad del mercado mediante las funciones CalculateDynamicSL() y CalculateDynamicTP().

 double CalculateDynamicSL( double price, int decision)
  {
   double atrValue[];
   if ( CopyBuffer (atrHandle, 0 , 0 , 1 , atrValue) <= 0 )
     {
      LogMessage( StringFormat ( "Error getting ATR values: %d" , GetLastError ()));
       return 0.0 ;
     }
   double volatility = atrValue[ 0 ];
   double dynamicSL = (decision == 1 ) ? price - (volatility * multi * 1.2 ) : price + (volatility * multi * 0.8 );

   return NormalizeDouble (dynamicSL, _Digits );
  }


double CalculateDynamicTP( double price, int decision)
  {
   double atrValue[];
   if ( CopyBuffer (atrHandle, 0 , 0 , 1 , atrValue) <= 0 )
     {
      LogMessage( StringFormat ( "Error getting ATR values: %d" , GetLastError ()));
       return 0.0 ;
     }
   double volatility = atrValue[ 0 ];
   double dynamicTP = (decision == 1 ) ? price + (volatility * multi * 1.8 ) : price - (volatility * multi * 2.2 );

   return NormalizeDouble (dynamicTP, _Digits );
  }

Esta función calcula niveles dinámicos de stop loss (SL) y take profit (TP) en función de la volatilidad actual del mercado, lo que mejora la gestión del riesgo y, potencialmente, los resultados de las operaciones.

Reseñas de funciones

Ambas funciones utilizan el indicador Average True Range (ATR) para medir la volatilidad del mercado y ajustar los niveles de SL y TP en consecuencia. Tienen en cuenta si la operación es una decisión de compra (1) o de venta (-1).

 double CalculateDynamicSL( double price, int decision)

Esta función calcula un nivel de Stop Loss dinámico basado en el precio actual, la dirección de la operación y la volatilidad del mercado.

 double CalculateDynamicTP( double price, int decision)

Esta función calcula un nivel dinámico de toma de beneficios basado en el precio actual, la dirección de la operación y la volatilidad del mercado.

Componentes clave

1. Indicador ATR: Ambas funciones utilizan el indicador ATR para medir la volatilidad del mercado.
2. Price: El precio de mercado actual del activo.
3. Decision: Un número entero (1 para comprar, presumiblemente -1 para vender) que indica la dirección de la operación.
4. Multiplicador: La variable global 'multi' se utiliza para ajustar el impacto de la volatilidad.

Explicación detallada

Función CalculateDynamicSL

Obtener valor ATR :

 double atrValue[];
if ( CopyBuffer (atrHandle, 0 , 0 , 1 , atrValue) <= 0 )
{
   LogMessage( StringFormat ( "Error getting ATR values: %d" , GetLastError ()));
   return 0.0 ;
}
double volatility = atrValue[ 0 ];

Este código recupera el último valor ATR, que refleja la volatilidad del mercado.

Calcular SL dinámico :

 double dynamicSL = (decision == 1 ) ? price - (volatility * multi * 1.2 ) : price + (volatility * multi * 0.8 );

Para una operación de compra (decision == 1) fija el SL por debajo del precio actual.

Para una operación de venta, el SL se fija por encima del precio actual.

La distancia se calcula como un múltiplo del ATR, ajustado mediante la variable multi y un factor (1.2 para las compras, 0.8 para las ventas, lo hice para mostrar la diferencia en el artículo).

Normalizar y volver:

 return NormalizeDouble (dynamicSL, _Digits );

El valor del SL se normaliza con el número apropiado de decimales para el instrumento negociado.

Función CalculateDynamicTP

Obtener el valor ATR: Esta parte es idéntica a la función SL.

Calcular el TP dinámico:

 double dynamicTP = (decision == 1 ) ? price + (volatility * multi * 1.8 ) : price - (volatility * multi * 2.2 );

Para una operación de compra, el TP se fija por encima del precio actual.

Para una operación de venta, el TP se fija por debajo del precio actual.

La distancia se calcula como un múltiplo del ATR ajustado por la variable multi y un factor (1.8 para compras, 2.2 para ventas, lo hice para mostrar la diferencia, puedes usar lo que necesites).

Normalizar y devolver: similar a la función SL.

Importancia en el comercio

1. Gestión del riesgo basada en la volatilidad : Utilizando el ATR, estas funciones adaptan los niveles de SL y TP a las condiciones actuales del mercado, proporcionando una gestión del riesgo más adecuada.
2. Relación riesgo/recompensa asimétrica : Los niveles TP se fijan más lejos del precio de entrada que los niveles SL, creando potencialmente una relación riesgo/recompensa favorable.
3. Ajuste dinámico : A medida que cambia la volatilidad del mercado, estas funciones ajustan automáticamente los niveles de SL y TP para las nuevas operaciones.

Consideraciones y posibles mejoras

1. Manejo de errores: Ambas funciones tienen un manejo básico de errores para recuperar ATR, pero esto puede ser extendido.
2. Configuración: Los multiplicadores (1.2, 0.8, 1.8, 2.2) pueden convertirse en parámetros para facilitar la configuración.
3. Distancia mínima: Implementar una distancia mínima para SL y TP puede evitar problemas en condiciones de volatilidad extremadamente baja.
4. Distancia máxima: Del mismo modo, se puede introducir una distancia máxima para limitar el riesgo en condiciones muy inestables.

Estas características representan un enfoque para fijar los niveles de SL y TP que se adapta a las condiciones del mercado para mejorar potencialmente los resultados de las operaciones y, al mismo tiempo, gestionar eficazmente el riesgo.

Gestión de riesgos: Incluye funciones para ajustar el tamaño de la posición en función del saldo de la cuenta y la reducción, implementadas en AdjustLotSizeForDrawdown() y CalculateDynamicLotSize().

 // Function to adjust the lot size based on drawdown
double AdjustLotSizeForDrawdown()
{
   // Static variables to keep track of consecutive losses and maximum balance
   static int consecutiveLosses = 0 ;
   static double maxBalance = 0 ;

   // Get current account balance and equity
   double currentBalance = AccountInfoDouble ( ACCOUNT_BALANCE );
   double currentEquity = AccountInfoDouble ( ACCOUNT_EQUITY );

   // Update the maximum balance if current balance is higher
   if (currentBalance > maxBalance)
      maxBalance = currentBalance;

   // Calculate the current drawdown as a percentage
   double drawdown = (maxBalance - currentEquity) / maxBalance;

   // Calculate the base lot size using a separate function
   double baseLotSize = CalculateDynamicLotSize();

   // If drawdown is greater than 10%, reduce lot size by half
   if (drawdown > 0.1 ) // 10% drawdown
   {
       return baseLotSize * 0.5 ; // Reduce lot size by half
   }
   else if (consecutiveLosses > 3 )
   {
       return baseLotSize * 0.75 ; // Reduce lot size by 25% after 3 consecutive losses
   }

   // Return the base lot size if no adjustments are needed
   return baseLotSize;
}

Esta función AdjustLotSizeForDrawdown() está diseñada para ajustar dinámicamente el tamaño del lote de negociación en función de la reducción de la cuenta y del rendimiento reciente. He aquí un desglose de sus principales funciones:

1. Utiliza variables estáticas para seguir las pérdidas consecutivas y el saldo máximo alcanzado.
2. Calcula la reducción actual comparando el saldo máximo con el capital actual.
3. La función aplica dos estrategias de gestión de riesgos:
   • Si la reducción supera el 10%, el tamaño del lote se reduce a la mitad.
   • Si se producen más de 3 pérdidas consecutivas, el tamaño del lote se reduce en un 25%.
4. El tamaño del lote base se calcula utilizando otra función llamada CalculateDynamicLotSize(), que no se muestra en este fragmento.
5. Si no se cumple ninguna de las condiciones de riesgo, la función devuelve el tamaño de lote base sin ajustar.

Este enfoque ayuda a proteger su cuenta de negociación durante los periodos de malos resultados o alta volatilidad, reduciendo el impacto. Es una forma sencilla pero eficaz de aplicar el dimensionamiento adaptativo de posiciones en la negociación algorítmica.

 // Function to dynamically calculate the lot size
double CalculateDynamicLotSize()
{
   // Get current account balance and equity
   double accountBalance = AccountInfoDouble ( ACCOUNT_BALANCE );
   double equity = AccountInfoDouble ( ACCOUNT_EQUITY );
   double riskPercentage = 0.01 ; // 1% risk per trade

   // Use the lower value between balance and equity to be conservative
   double baseAmount = MathMin (accountBalance, equity);

   // Calculate the value of a pip for the current symbol
   double tickSize = SymbolInfoDouble ( _Symbol , SYMBOL_TRADE_TICK_SIZE );
   double tickValue = SymbolInfoDouble ( _Symbol , SYMBOL_TRADE_TICK_VALUE );
   double pipValue = (tickValue / tickSize) * 10 ; // Assuming a pip is 10 ticks

   // Calculate lot size based on desired risk
   double riskAmount = baseAmount * riskPercentage;
   double stopLossPips = 50 ; // Adjust according to your strategy

   double lotSize1 = NormalizeDouble (riskAmount / (stopLossPips * pipValue), 2 );

   // Ensure the lotSize is within the allowed limits
   double minLot = SymbolInfoDouble ( _Symbol , SYMBOL_VOLUME_MIN );
   double maxLot = SymbolInfoDouble ( _Symbol , SYMBOL_VOLUME_MAX );
   double lotSize2 = MathMax (minLot, MathMin (maxLot, lotSize1));

   return lotSize2;
}

Esta función CalculateDynamicLotSize() está diseñada para calcular el tamaño de lote adecuado para operar en función del saldo de su cuenta, su tolerancia al riesgo y las condiciones actuales del mercado. He aquí un desglose de sus principales funciones:

1. Extrae la balanza por cuenta corriente y los fondos propios utilizando el menor de los dos valores para un enfoque más conservador.
2. La función utiliza un porcentaje fijo de riesgo por operación, en este caso fijado en el 1%.
3. Calcula el valor del pip para el símbolo de negociación actual, suponiendo que un pip equivale a 10 ticks.
4. A continuación, se calcula el tamaño del lote en función de:
   • Monto de riesgo (1% del monto base)
   • Stop loss predefinido en pips (en este ejemplo se establece en 50 pips)
   • Valor calculado del punto
5. La función garantiza que el tamaño de lote calculado esté dentro del tamaño de lote mínimo y máximo permitido para el símbolo de negociación.
6. Se devuelve el tamaño del lote final, normalizado a dos decimales.

Este enfoque dinámico del tamaño del lote ayuda a mantener un nivel de riesgo constante en las operaciones, independientemente del tamaño de la cuenta o las condiciones del mercado. Es un componente importante de una estrategia de gestión de riesgos y funciona en conjunto con la función AdjustLotSizeForDrawdown() que analizamos anteriormente.

La combinación de estas dos funciones proporciona un sistema sólido de gestión de riesgos que:

1. Ajusta el tamaño de las posiciones en función del rendimiento y la reducción de la cuenta.
2. Mantiene un porcentaje constante de riesgo por operación.
3. Se adapta a los cambios en los saldos de las cuentas y las condiciones del mercado.

Este enfoque puede ayudar a los operadores a mantener la disciplina y proteger su capital tanto en condiciones de mercado favorables como desafiantes.

Características importantes:

1. OptimalControl(double currentPrice): Esta es la función decisoria central del EA. Utiliza el Control Predictivo por Modelos para determinar si comprar, vender o mantener. Calcula el rendimiento esperado durante el horizonte de pronóstico y lo compara con el umbral de decisión.
2. CalculateExpectedReturn(...): Esta función calcula la rentabilidad esperada para un determinado conjunto de parámetros utilizados en la función OptimalControl.
3. ManageOpenOrder(int decision): Gestiona las órdenes abiertas existentes, decidiendo si cerrarlas en función del número de barras abiertas o si la decisión actual entra en conflicto con una posición abierta.
4. ExecuteTrade(int decision): Ejecuta una nueva operación basándose en la decisión de OptimalControl, estableciendo los niveles adecuados de Stop Loss y Take Profit.
5. UpdateSLTP(ulong ticket, int decision): Actualiza los niveles de Stop Loss y Take Profit de una posición existente en función de las condiciones actuales del mercado.
6. EstimateDrift() y EstimateVolatility(): Estas funciones estiman la deriva y la volatilidad de los precios que se utilizan en los cálculos de control óptimo.
7. IsTrendFavorable(int decision) y IsLongTermTrendFavorable(int decision): Estas funciones comprueban si la tendencia actual del mercado está en línea con la decisión de negociación utilizando medias móviles y RSI.
8. AdjustLotSizeForDrawdown() y CalculateDynamicLotSize(): Estas funciones ajustan el volumen de negociación en función de la reducción actual y del saldo de la cuenta, aplicando una gestión dinámica del riesgo.
9. LogMessage(string message): Registra eventos y decisiones importantes en un archivo para su posterior análisis y depuración.

Resultados

Marco temporal de 1 día.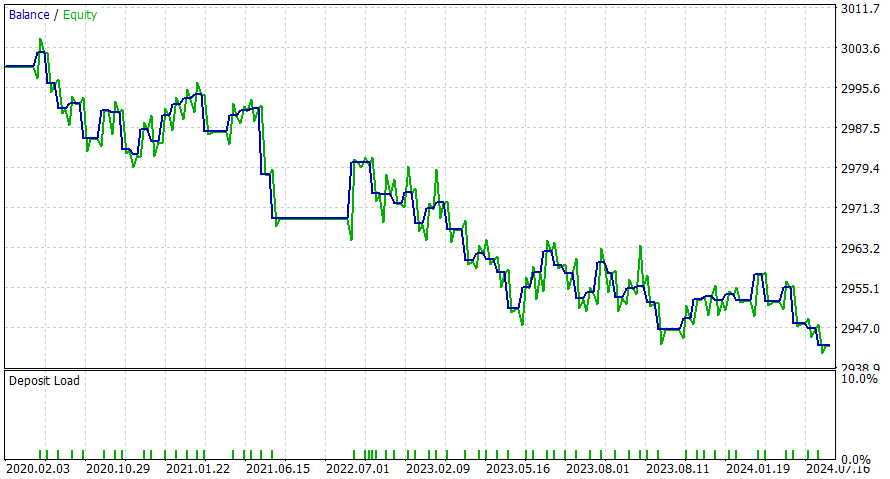

Marco temporal de 1 hora.

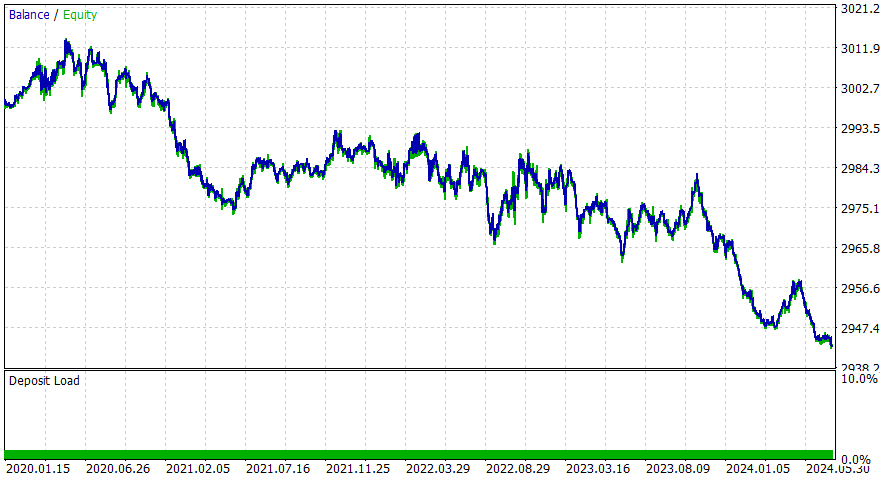
Marco temporal de 4 horas.

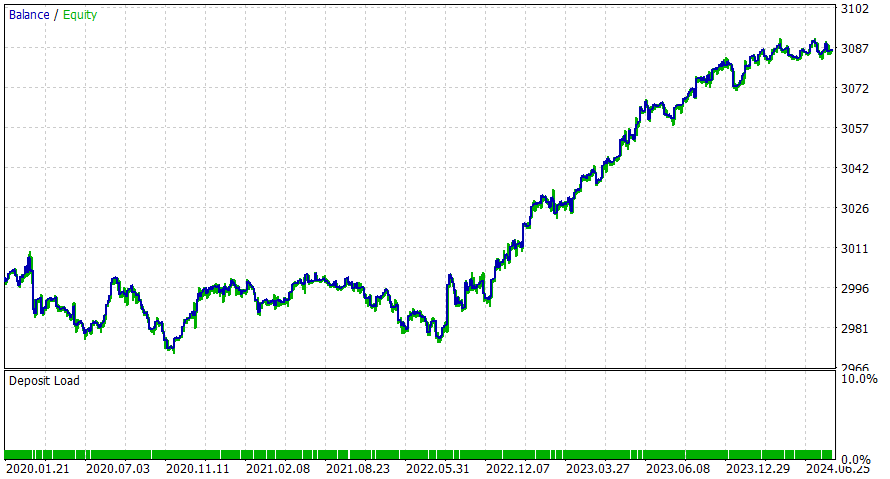
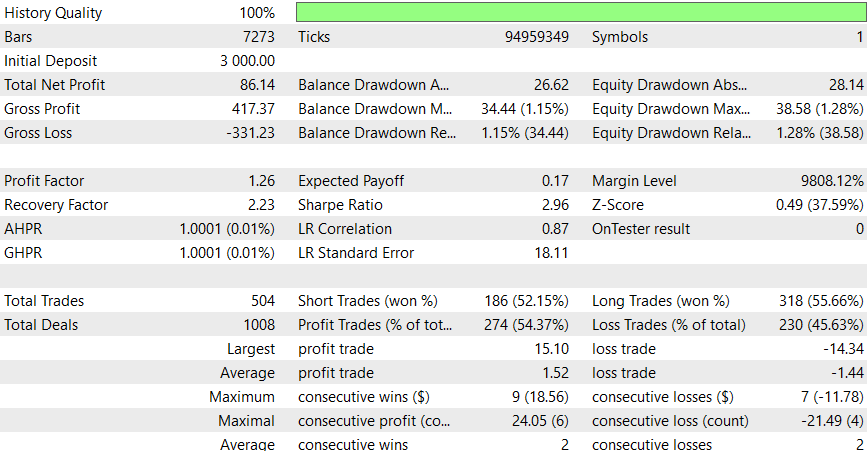
Marco temporal de 6 horas.

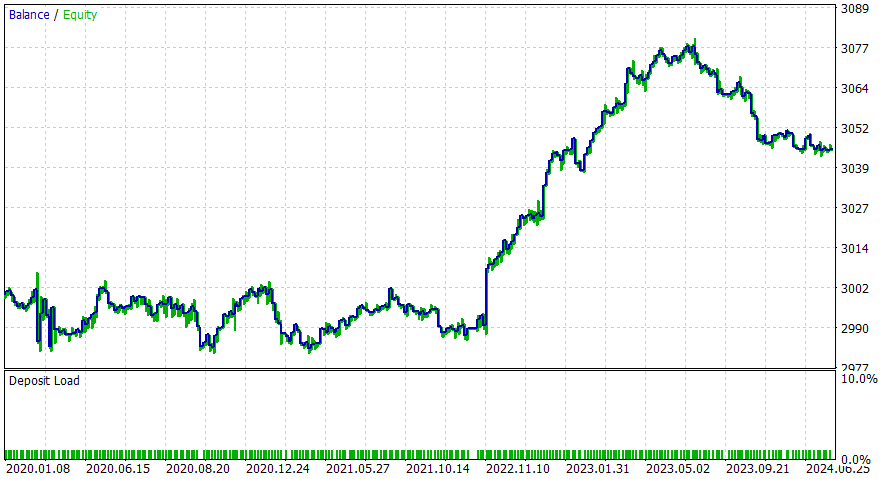
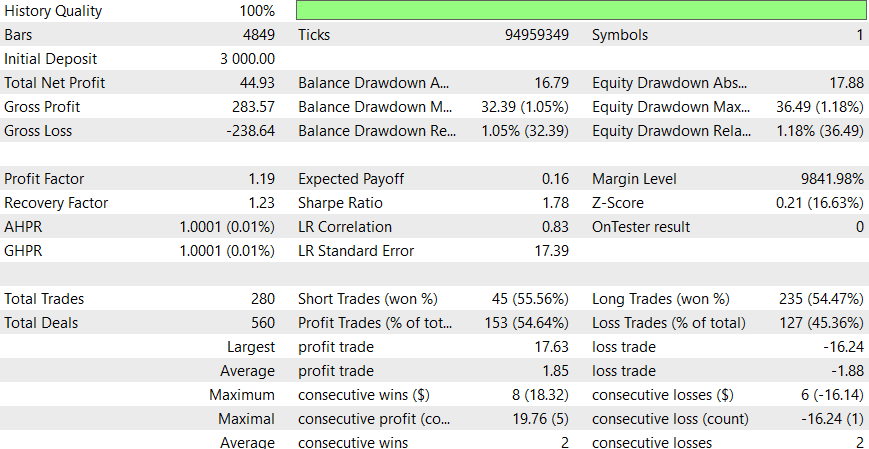
Este EA parece funcionar mejor durante el período intradiario, pero estoy seguro de que puede lograr mejores resultados agregando SL o aplicando la consideración de mejoras potenciales.

Conclusión

El Asesor Experto SMOC es una versión simplificada de un enfoque sofisticado para el trading automatizado con modelado estocástico y optimización del control. Combinando varios métodos de análisis, incluidos promedios móviles, RSI, ATR y algoritmos de control óptimo personalizados, tiene como objetivo tomar decisiones comerciales informadas. La naturaleza adaptativa del sistema, con características como el tamaño dinámico de los lotes y el ajuste del riesgo en función de las reducciones, muestra un enfoque en la sostenibilidad a largo plazo. Sin embargo, como ocurre con cualquier sistema comercial, será fundamental realizar pruebas retrospectivas y futuras exhaustivas para evaluar su rendimiento y confiabilidad en el mundo real.

Despedida: Este es sólo un ejemplo simple de un asesor avanzado.