Aprendizaje automático y Data Science (Parte 24): Predicción de series temporales de divisas mediante modelos de IA convencionales

Contenido

• ¿Qué es la predicción de series temporales?
• ¿Por qué y dónde se utilizan las predicciones de series temporales?
• Comparación entre modelos ML clásicos y modernos basados en series temporales
• Ingeniería de características para la predicción de series temporales
• Entrenamiento del modelo regresor LightGBM
• Prueba de Dickey-Fuller aumentada
• ¿Por qué importa la estacionalidad?
• Predicción de una variable estacionaria
• Creación del modelo de clasificación LightGBM
• Guardar el modelo clasificador LightGBM en ONNX
• Envolverlo todo en un robot de negociación
• Probar el modelo en el probador de estrategias
• Ventajas del uso de modelos ML clásicos y modernos para la predicción de series temporales
• Conclusión

¿Qué es la predicción de series temporales?

La predicción de series temporales es el proceso de utilizar datos pasados para predecir valores futuros en una secuencia de puntos de datos. Esta secuencia suele estar ordenada por tiempo, de ahí el nombre de serie temporal.

Variables principales en datos de series temporales 

Aunque podemos tener tantas variables de características como queramos en nuestros datos, cualquier dato para análisis de series temporales o predicción debe tener estas dos variables.

1. Time (Tiempo)
   
   Se trata de una variable independiente, que representa los puntos específicos en el tiempo en los que se observaron los puntos de datos.
   
   
2. Variable objetivo
   
   Es el valor que intentas predecir basándote en observaciones anteriores y, potencialmente, en otros factores. (por ejemplo, cotización de cierre diaria, temperatura horaria, tráfico de sitios web por minuto).

El objetivo de la predicción de series temporales es aprovechar los patrones y tendencias históricos de los datos para realizar predicciones informadas sobre valores futuros.

Este artículo asume que usted tiene un conocimiento básico de ONNX, la predicción de series temporales, y LightGBM (Light Gradient Boosting Machine). Por favor, lee estos artículos si no lo has hecho para mayor comprensión. 

¿Por qué y dónde se utiliza la predicción de series temporales?

El análisis de series temporales y la predicción pueden utilizarse en los siguientes escenarios:

• Predicción de valores futuros 
• Comprensión de los comportamientos anteriores
• Planificar el futuro, que podría depender del pasado
• Evaluar los logros actuales

Modelos de aprendizaje automático clásicos y modernos frente a los basados en series temporales

A diferencia de los modelos clásicos de aprendizaje automático, como la regresión lineal, la máquina de vectores de soporte (SVM, Support Vector Machine), las redes neuronales (NN, Neural Networks) y otros, de los que hemos hablado en artículos anteriores, cuyo objetivo es determinar relaciones entre variables características y realizar predicciones futuras basadas en estas relaciones aprendidas, los modelos de series temporales predicen valores futuros basándose en valores observados previamente.

Esta diferencia de enfoque significa que los modelos de series temporales están diseñados específicamente para tratar las dependencias temporales y los patrones inherentes a los datos secuenciales. Los modelos de predicción de series temporales, como ARIMA, SARIMA, Exponential Smoothing, RNN, LSTM y GRU, aprovechan los datos históricos para predecir puntos futuros de la serie, capturando tendencias, estacionalidad y otras estructuras temporales.

El siguiente diagrama de flujo ilustra varios modelos de aprendizaje automático utilizados para la predicción de series temporales. 

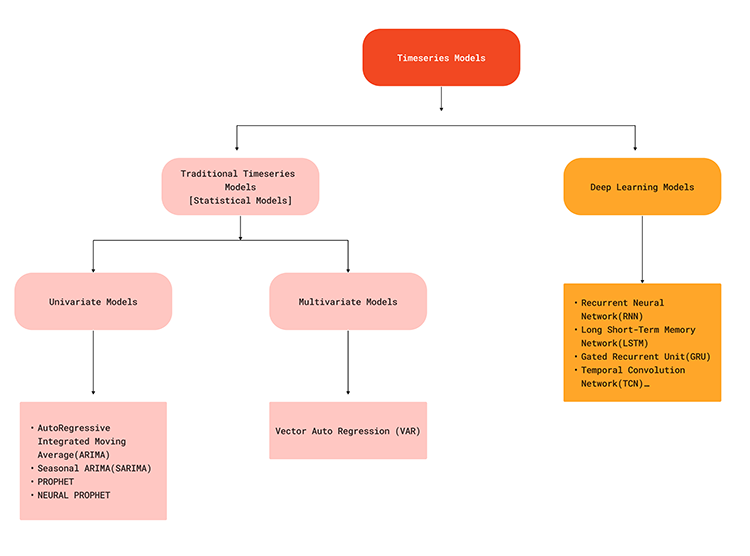
Dado que los modelos de series temporales son capaces de captar las dependencias temporales de los datos, pueden ofrecer una solución realista cuando se trata de hacer predicciones sobre el mercado de divisas, ya que todos sabemos que lo que ocurre actualmente en el mercado puede deberse a algunos factores que acaban de suceder en breve o en algún momento del pasado. Por ejemplo, las noticias publicadas sobre el EURUSD hace 5 minutos podrían ser uno de los factores de un cambio brusco del precio en el momento actual. Para entenderlo mejor, veamos las ventajas de la predicción de series temporales frente a la predicción tradicional con modelos de aprendizaje automático.

Aspecto	Predicción de series temporales	Predicción tradicional y moderna mediante ML
Dependencias temporales	Son capaces de captar patrones temporales, ya que tienen en cuenta el orden de los puntos de datos y las dependencias a lo largo del tiempo.	Los modelos tradicionales de ML tratan los puntos de datos como independientes, ignorando las dependencias temporales de los datos.
Tratamiento de tendencias y estacionalidad	Los modelos de series temporales, como ARIMA y algunos otros, incorporan componentes para tratar las tendencias y la estacionalidad.	Requiere extracción manual e ingeniería de características para captar tendencias y estacionalidad.
Autocorrelación	Modelos como ARIMA y LSTM pueden tener en cuenta la autocorrelación de los datos.	Suponen que cada característica es independiente, por lo que es posible que no tengan en cuenta la autocorrelación a menos que se modele explícitamente en las características.
Complejidad del modelo	Los modelos de series temporales están diseñados para datos secuenciales, por lo que se adaptan mejor a este tipo de tareas.	Los modelos tradicionales pueden requerir ingeniería de características para manejar adecuadamente los datos secuenciales. Esto añade complejidad al proceso
Jerarquías temporales	Puede ampliarse de forma natural a la predicción jerárquica de series temporales (por ejemplo, mensual, semanal).	Los modelos tradicionales pueden tener dificultades para realizar predicciones a múltiples escalas temporales sin ingeniería adicional.
Rendimiento predictivo	A menudo ofrece un mejor rendimiento predictivo en tareas dependientes del tiempo debido a la consideración del orden.	Puede rendir menos en tareas que dependen del tiempo.
Eficiencia computacional	Los modelos de series temporales pueden actualizarse incrementalmente con nuevos datos de forma eficiente.	Los modelos tradicionales pueden necesitar un reentrenamiento completo, que es más intensivo desde el punto de vista informático con nuevos datos.
Tendencias y estacionalidad interpretables	Los modelos como ARIMA proporcionan componentes interpretables para la tendencia y la estacionalidad.	Requiere pasos adicionales para interpretar las tendencias y la estacionalidad de las características de ingeniería.

A pesar de no ser buenos para la predicción de series temporales por defecto, los modelos de aprendizaje automático clásicos y modernos como LightGBM, XGBoost, CatBoost, etc. Puede seguir utilizándose para predecir series temporales si se le proporciona la información adecuada. La clave para lograrlo reside en la ingeniería de funciones.

Ingeniería de características para predicción de series temporales

En la predicción de series temporales, el objetivo es construir nuevas características y preparar las existentes de forma que acaben aportando información/componentes importantes para las series temporales, como: Tendencia, estacionalidad, patrones cíclicos, estacionariedad, autocorrelación y autocorrelación parcial, etc.

Hay muchos aspectos que se pueden tener en cuenta a la hora de crear nuevas características para un problema de series temporales, a continuación se indican algunos de ellos:

01: Funciones retrasadas

En los datos para el aprendizaje automático clásico, a menudo recopilamos datos como OPEN, HIGH, LOW, CLOSE, y algunos otros datos en la barra actual. Contiene la información actual en cada barra concreta y no ofrece información sobre lo que ocurrió antes de esa barra específica.

Al introducir características retardadas en nuestros datos, nos aseguramos de capturar las dependencias temporales de barras anteriores que, sin duda, tienen algo que ver con el precio de la barra actual.

MQL5

//--- getting Open, high, low and close prices
   
   ohlc_struct OHLC;
   
   OHLC.AddCopyRates(Symbol(), timeframe, start_bar, bars);
   time_vector.CopyRates(Symbol(), timeframe, COPY_RATES_TIME, start_bar, bars);
   
//--- Getting the lagged values of Open, High, low and close prices

   ohlc_struct  lag_1;
   lag_1.AddCopyRates(Symbol(), timeframe, start_bar+1, bars);
   
   ohlc_struct  lag_2;
   lag_2.AddCopyRates(Symbol(), timeframe, start_bar+2, bars);
   
   ohlc_struct  lag_3;
   lag_3.AddCopyRates(Symbol(), timeframe, start_bar+3, bars);

En el ejemplo anterior solo obtenemos tres retrasos. Dado que recopilamos estos datos diariamente, obtenemos la información de los tres días anteriores para 1000 barras.

Copiando MqlRates en vectores comenzando en start_bar+1 estamos obteniendo una barra anterior a la copia de tarifas comenzando en start_bar. Esto puede ser confuso a veces, por favor, consulte https://www.mql5.com/es/docs/series.

MQL5

input int bars = 1000;
input ENUM_TIMEFRAMES timeframe = PERIOD_D1;
input uint start_bar = 2; //StartBar|Must be >= 1

struct ohlc_struct 
{
   vector open;
   vector high;
   vector low;
   vector close;
   
   matrix MATRIX; //this stores all the vectors all-together
   
   void AddCopyRates(string symbol, ENUM_TIMEFRAMES tf, ulong start, ulong size)
    {
      open.CopyRates(symbol, tf, COPY_RATES_OPEN, start, size); 
      high.CopyRates(symbol, tf, COPY_RATES_HIGH, start, size); 
      low.CopyRates(symbol, tf, COPY_RATES_LOW, start, size); 
      close.CopyRates(symbol, tf, COPY_RATES_CLOSE, start, size); 
      
      this.MATRIX.Resize(open.Size(), 4); //we resize it to match one of the vector since all vectors are of the same size
      
      this.MATRIX.Col(open, 0);
      this.MATRIX.Col(high, 1);
      this.MATRIX.Col(low, 2);
      this.MATRIX.Col(close, 3);
    }
};

02: Estadísticas de balanceo

Las estadísticas móviles como la media, las desviaciones estándar y otras estadísticas de este tipo ayudan a resumir las tendencias recientes y la volatilidad dentro de una ventana. Aquí es donde entran en juego algunos indicadores como la media móvil para un periodo determinado, la desviación típica para un tiempo dado, etc.

int ma_handle = iMA(Symbol(),timeframe,30,0,MODE_SMA,PRICE_WEIGHTED); //The Moving averaege for 30 days
int stddev = iStdDev(Symbol(), timeframe, 7,0,MODE_SMA,PRICE_WEIGHTED); //The standard deviation for 7 days
   
vector SMA_BUFF, STDDEV_BUFF;
SMA_BUFF.CopyIndicatorBuffer(ma_handle,0,start_bar, bars);
STDDEV_BUFF.CopyIndicatorBuffer(stddev, 0, start_bar, bars);

Estas estadísticas continuas ofrecen una visión más amplia de la evolución del mercado y pueden captar fluctuaciones a largo plazo que no son evidentes en los datos retrospectivos.

03: Funciones de fecha-hora

Como se dijo anteriormente los datos de series temporales tienen la variable tiempo sin embargo, tener una variable Fecha-hora (Datetime) solamente no va a ayudar mucho, necesitamos extraer sus características.

Como sabemos, el mercado de divisas exhibe algunos patrones o se comporta de cierta manera durante momentos específicos. Por ejemplo: los viernes no suele haber mucha actividad de negociación y el mercado es volátil cuando hay un acontecimiento noticioso ese día concreto. También en algunos meses las actividades comerciales pueden cambiar para bien o para mal, lo mismo ocurre con algunos años. Por ejemplo: durante los años electorales de algunos países, como las elecciones estadounidenses.

Al introducir las características Fecha-Hora (Datetime), captamos explícitamente los patrones estacionales, lo que permitiría a nuestro modelo ajustar las predicciones en función de la época del año, un día o un mes concretos, etc.

Recopilemos las funciones Fecha-Hora en MQL5:

vector time_vector; //we want to add time vector 
time_vector.CopyRates(Symbol(), timeframe, COPY_RATES_TIME, start_bar, bars); //copy the time in seconds


ulong size = time_vector.Size(); 
vector DAY(size), DAYOFWEEK(size), DAYOFYEAR(size), MONTH(size);

MqlDateTime time_struct;
string time = "";
for (ulong i=0; i<size; i++)
  {
    time = (string)datetime(time_vector[i]); //converting the data from seconds to date then to string
    TimeToStruct((datetime)StringToTime(time), time_struct); //convering the string time to date then assigning them to a structure
    
    DAY[i] = time_struct.day;
    DAYOFWEEK[i] = time_struct.day_of_week;
    DAYOFYEAR[i] = time_struct.day_of_year;
    MONTH[i] = time_struct.mon;
  }

04: Diferenciación

La diferenciación de las series en los desfases estacionales elimina los patrones estacionales de los datos para lograr la estacionariedad, que suele ser un requisito para algunos modelos.

Intentemos diferenciar en lag1 los precios actuales.

MQL5

vector diff_lag_1_open = OHLC.open - lag_1.open;
vector diff_lag_1_high = OHLC.high - lag_1.high;
vector diff_lag_1_low = OHLC.low - lag_1.low;
vector diff_lag_1_close = OHLC.close - lag_1.close;

Puede diferenciar tantos retardos como desee, no está limitado únicamente al retardo 1.

Hasta este punto tenemos 26 variables independientes/características que es suficiente para nuestras variables independientes. Dado que estamos tratando de resolver un problema de regresión, recopilemos los precios de cierre como nuestro precio final variable objetivo.

vector TARGET_CLOSE;
TARGET_CLOSE.CopyRates(Symbol(), timeframe, COPY_RATES_CLOSE, start_bar-1, bars); //one bar forward

Siéntase libre de crear más características para su problema teniendo en cuenta otros aspectos que no hemos considerado a continuación.

05: Variables externas (características exógenas)

• Datos meteorológicos: Prueba a ver si te ayudan.
• Indicadores económicos: Incluidos el PIB, las tasas de desempleo, etc., para la predicción financiera.

06: Transformadas Fourier y Wavelet

Utilización de transformadas de Fourier u Wavelet para extraer patrones cíclicos y tendencias en el dominio de la frecuencia.

07: Codificación de destino

Puede crear características basadas en estadísticas agregadas (media, mediana) de la variable objetivo en diferentes periodos de tiempo.

El conjunto de datos final tiene 27 columnas:

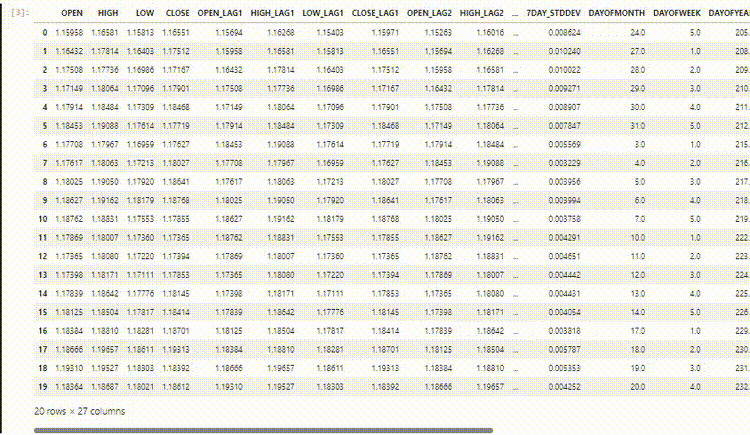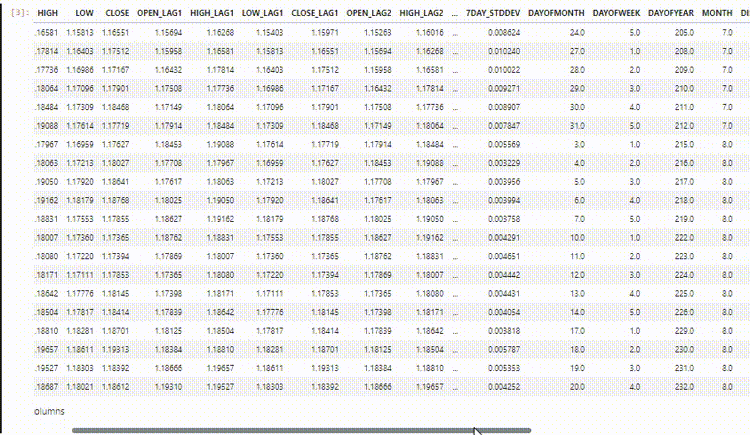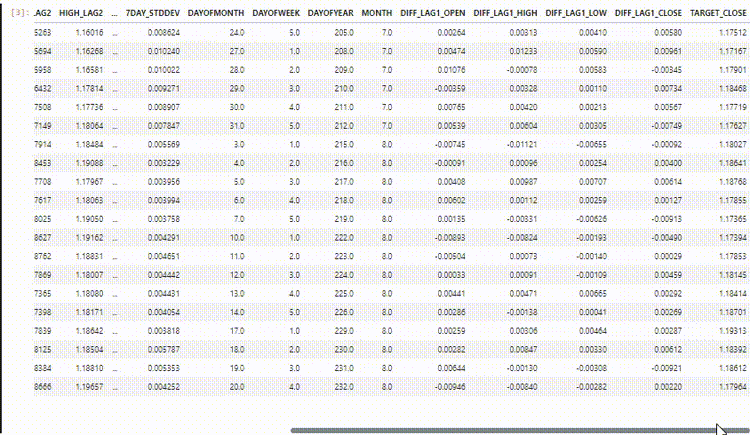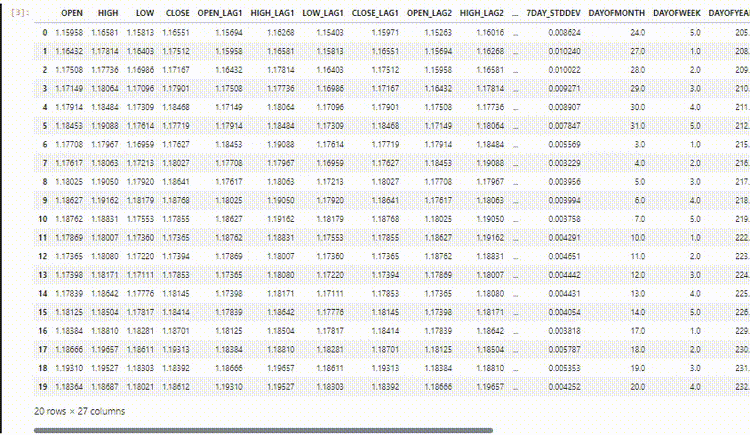
Entrenamiento del modelo regresor LightGBM

Ahora que tenemos todos los datos que necesitamos, pasemos a la parte de Python.

Podemos empezar dividiendo los datos en muestras de entrenamiento y de prueba.

Python

X = df.drop(columns=["TARGET_CLOSE"])
Y = df["TARGET_CLOSE"]

train_size = 0.7 #configure train size

train_size = round(train_size*df.shape[0])

x_train = X.iloc[:train_size,:]
x_test = X.iloc[train_size:, :]

y_train = Y.iloc[:train_size]
y_test = Y.iloc[train_size:]

print(f"x_train_size{x_train.shape}\nx_test_size{x_test.shape}\n\ny_train{y_train.shape}\ny_test{y_test.shape}")

Resultados:

x_train_size(700, 26)
x_test_size(300, 26)

y_train(700,)
y_test(300,)

Ajustemos el modelo a los datos de entrenamiento.

model = lgb.LGBMRegressor(**params)
model.fit(x_train, y_train)

Vamos a probar el modelo entrenado y, a continuación, trazar las predicciones y el r2_score.

Python

from sklearn.metrics import r2_score

test_pred = model.predict(x_test)

accuracy = r2_score(y_test, test_pred)

#showing actual test values and predictions

plt.figure(figsize=(8, 6))  
plt.plot(y_test, label='Actual Values')
plt.plot(test_pred, label='Predicted Values')
plt.xlabel('Index')
plt.ylabel('Values')
plt.title('Actual vs. Predicted Values')
plt.legend(loc="lower center")

# Add R-squared (accuracy) score in a corner
plt.text(0.05, 0.95, f"LightGBM (Accuracy): {accuracy:.4f}", ha='left', va='top', transform=plt.gca().transAxes, fontsize=10, bbox=dict(boxstyle='round', facecolor='white', alpha=0.7))

plt.grid(True)

plt.savefig("LighGBM Test plot")
plt.show()

Resultado:

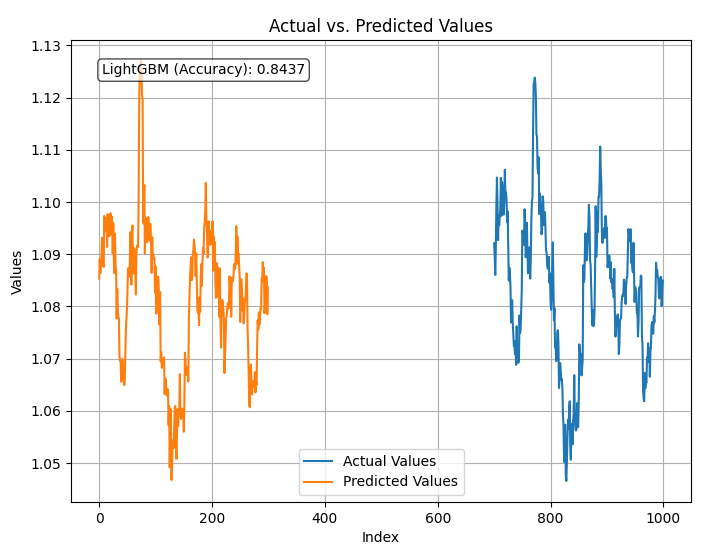
El modelo tiene una precisión del 84% en la predicción de los precios de cierre utilizando todos los datos que se le proporcionaron. Aunque parece una buena precisión, debemos examinar nuestras variables para seguir analizando y mejorando el modelo.

Utilizando la técnica de trazado incorporada de LightGBM (plot_importance), a continuación se muestra el trazado de la importancia de las características.

Python

# Plot feature importance using Gain
lgb.plot_importance(model, importance_type="gain", figsize=(8,6), title="LightGBM Feature Importance (Gain)")

plt.tight_layout()

plt.savefig("LighGBM feature importance(Gain)")
plt.show()

Resultado:

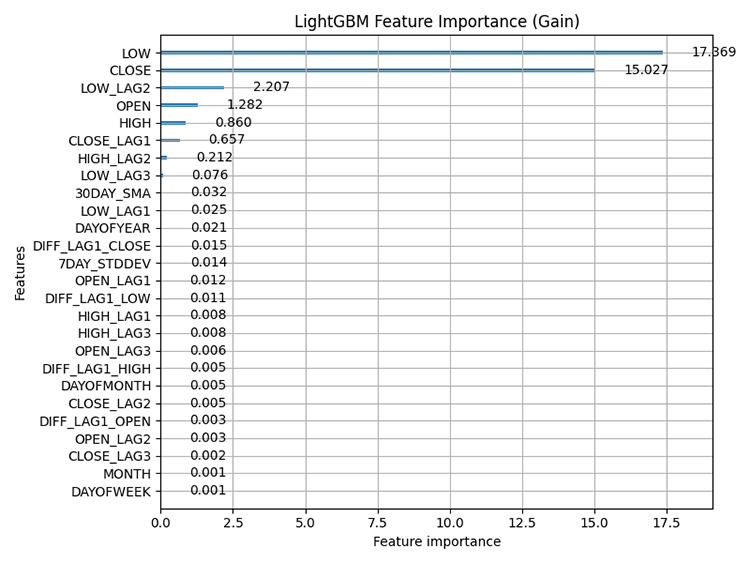
plot_importance: Hace referencia a las técnicas que evalúan la contribución relativa de cada característica (variable) de un conjunto de datos a las predicciones realizadas por el modelo. Nos ayuda a comprender qué características influyen más en las predicciones del modelo.

Es importante saber que los métodos basados en árboles, como LightGBM y XGBoost, calculan la importancia de las características de forma diferente a los modelos no basados en árboles, ya que tienen en cuenta la frecuencia con la que se utiliza una característica para tomar decisiones de división en los árboles y el impacto de esas divisiones en la predicción final.

También puede utilizar SHAP para comprobar la importancia de las características.

Python:

explainer = shap.TreeExplainer(model)
shap_values = explainer(x_train)  

shap.summary_plot(shap_values, x_train, max_display=len(x_train.columns), show=False)  # Show all features

# Adjust layout and set figure size
plt.subplots_adjust(left=0.12, bottom=0.1, right=0.9, top=0.9)  
plt.gcf().set_size_inches(6, 8) 
plt.tight_layout()

plt.savefig("SHAP_Feature_Importance_Summary_Plot.png")
plt.show()

Resultado:

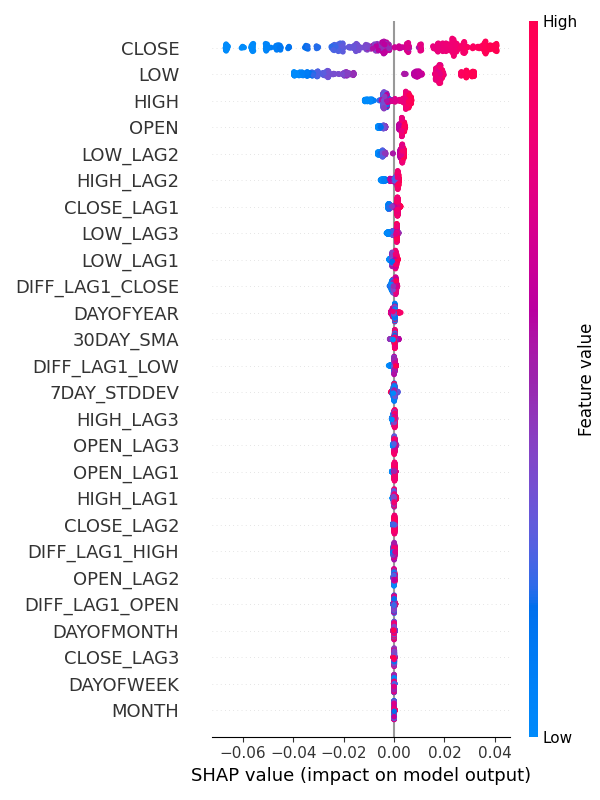
De los gráficos de importancia de las características se desprende claramente que las variables para captar los patrones estacionales como DAYOFWEEK, MONTH, DAYOFMONTH y DAYOFYEAR son algunas de las variables con menor contribución a las predicciones del modelo.

Curiosamente, todos ellos son estacionarios según la prueba Dickey-Fuller aumentada.

  

Prueba Dickey-Fuller aumentada (ADF, Augmented Dickey-Fuller)

Se trata de una prueba estadística utilizada para determinar si un conjunto de datos de series temporales es estacionario o no. La estacionariedad es una propiedad crucial para muchos métodos de predicción y análisis de series temporales.

Una variable estacionaria o un conjunto de datos estacionarios, se refiere a una serie cuyas propiedades estadísticas (media, varianza, autocorrelación) permanecen constantes a lo largo del tiempo. Por ejemplo, en el mercado de valores. La media de los valores OHLC puede aumentar o disminuir drásticamente a lo largo del tiempo, lo que hace que estos valores no sean estacionarios en su mayor parte, mientras que sus rendimientos, como la media o la varianza de la diferencia entre el máximo y el mínimo son estacionarios a lo largo del tiempo.

He realizado esta prueba con todo el conjunto de datos que tenemos.

from statsmodels.tsa.stattools import adfuller

def adf_test(series, signif=0.05):
  """
  Performs the ADF test on a pandas Series and interprets the results.

  Args:
      series: The pandas Series containing the time series data.
      signif: Significance level for the test (default: 0.05).

  Returns:
      A dictionary containing the test statistic, p-value, used lags,
      critical values, and interpretation of stationarity.
  """
  dftest = adfuller(series, autolag='AIC')
  adf_stat = dftest[0]  # Access test statistic
  pvalue = dftest[1]  # Access p-value
  usedlag = dftest[2]  # Access used lags
  critical_values = dftest[4]  # Access critical values

  interpretation = 'Stationary' if pvalue < signif else 'Non-Stationary'
  result = {'Statistic': adf_stat, 'p-value': pvalue, 'Used Lags': usedlag,
            'Critical Values': critical_values, 'Interpretation': interpretation}
  return result

for col in df.columns:
  adf_results = adf_test(df[col], signif=0.05)
  print(f"ADF Results for column {col}:\n {adf_results}")

De 27 variables, sólo 9 se detectaron estacionarias. Estas variables son: 

1. 7DAY_STDDEV
2. DAYOFMONTH
3. DAYOFWEEK
4. DAYOFYEAR
5. MONTH
6. DIFF_LAG1_OPEN
7. DIFF_LAG1_HIGH
8. DIFF_LAG1_LOW
9. DIFF_LAG1_CLOSE

Para averiguar fácilmente si las variables son estacionarias o no, basta con mirar el gráfico de distribución. Un dato bien distribuido en torno a la media es muy probablemente un dato estacionario.

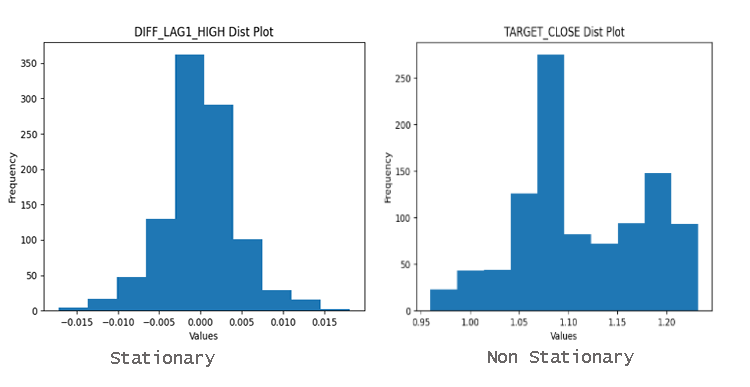
¿Por qué es importante la estacionalidad?

Muchos métodos estadísticos utilizados en el análisis y la predicción de series temporales presuponen la estacionalidad. Si una serie temporal no es estacionaria, estos métodos pueden producir resultados engañosos o inexactos. 

Imagínese intentar predecir el precio futuro de las acciones si las cotizaciones tienden constantemente al alza. El modelo de series temporales no sería capaz de captar la tendencia subyacente.

Los modelos de aprendizaje automático clásicos o incluso los denominados modernos, como el LightGBM que hemos utilizado, tienen la capacidad de manejar relaciones no lineales entre las características, lo que hace que se vean menos afectados por la estacionalidad presente en los datos. La importancia de las características para este modelo ha demostrado claramente que las características más importantes para nuestro modelo son las variables OHLC no estacionarias.

Sin embargo, esto no significa que variables como el día de la semana no influyan en el modelo. La importancia de las características es sólo una parte de la gran historia; en mi opinión, sigue siendo necesario el conocimiento del dominio.

No hay necesidad de eliminar esta variable porque está clasificada más abajo, ya que estoy seguro de que afecta al EURUSD. 

Predicción de una variable objetivo estacionaria

Disponer de una variable objetivo estacionaria mejora el rendimiento de muchos modelos de aprendizaje automático cuando se trata de predicción de series temporales, ya que los datos estacionarios tienen una constante (media, varianza, autocorrelación) a lo largo del tiempo. Como usted sabe predecir donde el mercado se moverá en la próxima vela es difícil, pero predecir la cantidad de pips o puntos para el próximo movimiento no es muy difícil.

Si podemos predecir la cantidad de puntos que generará la siguiente barra, podemos utilizarla para establecer objetivos de negociación (Stop Loss y Take Profit).

Para ello, tenemos que encontrar la diferencia de primer orden, restando el precio de cierre anterior del precio de cierre siguiente.

Python

Y = df["TARGET_CLOSE"] - df["CLOSE"] #first order differencing 

Al diferenciar los siguientes precios cercanos de los anteriores, obtenemos una variable estacionaria.

adf_results = adf_test(Y,signif=0.05)

print(f"ADF Results:\n {adf_results}")

Resultados:

ADF Results: {'Statistic': -23.37891429248752, 'p-value': 0.0, 'Used Lags': 1, 'Critical Values': {'1%': -3.4369193380671, '5%': -2.864440383452517, '10%': -2.56831430323573}, 'Interpretation': 'Stationary'}

Tras ajustar el modelo regresor a la nueva variable objetivo estacionaria y evaluar su rendimiento en el conjunto de datos de prueba, el resultado fue el siguiente.

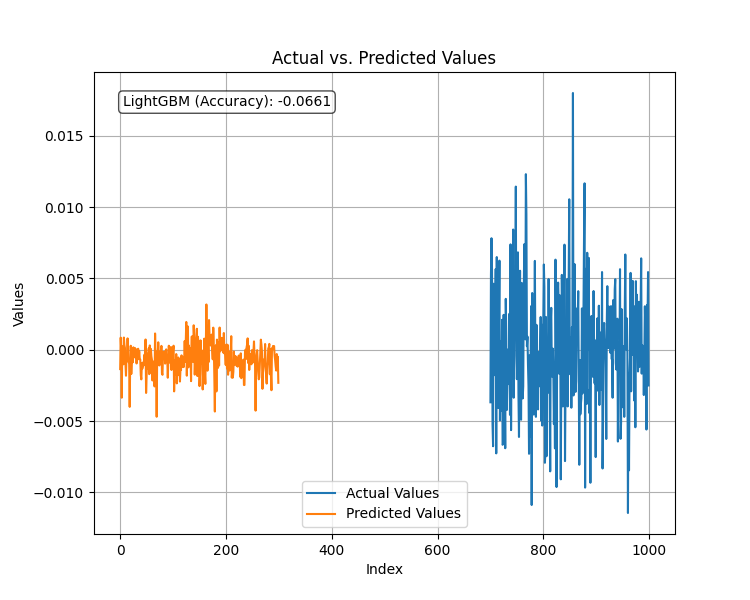
El modelo tuvo un rendimiento pésimo cuando la variable objetivo era estacionaria. Como siempre en el aprendizaje automático, puede haber muchos factores que lleven a esto, pero por ahora vamos a concluir que LightGBM no funciona bien para variables objetivo estacionarias. Vamos a ceñirnos al modelo de regresión elaborado para predecir los valores de cierre del objetivo.

Tener este modelo de regresión que predice los valores continuos del precio de cierre no es tan útil como tener un modelo que prediga las señales de trading como comprar o vender, para lograr esto necesitamos hacer otro modelo para predecir las señales de trading.

Construcción del modelo clasificador LightGBM

Para hacer un modelo clasificador, necesitamos preparar la variable objetivo como una variable objetivo binaria donde 1 representa una señal de compra mientras que 0 representa una señal de venta.

Python

Y = []
target_open = df["TARGET_OPEN"]
target_close = df["TARGET_CLOSE"]

for i in range(len(target_open)):
    if target_close[i] > target_open[i]: # if the candle closed above where it opened thats a buy signal
        Y.append(1)
    else: #otherwise it is a sell signal
        Y.append(0)

# split Y into irrespective training and testing samples 

y_train = Y[:train_size]
y_test = Y[train_size:]

I trained the LightGBM model inside a Pipeline with the StandardScaler technique.

Python

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

params = {
    'boosting_type': 'gbdt',  # Gradient Boosting Decision Tree
    'objective': 'binary',  # For binary classification (use 'regression' for regression tasks)
    'metric': ['auc','binary_logloss'],  # Evaluation metric
    'num_leaves': 25,  # Number of leaves in one tree
    'n_estimators' : 100, # number of trees
    'max_depth': 5,
    'learning_rate': 0.05,  # Learning rate
    'feature_fraction': 0.9  # Fraction of features to be used for each boosting round
}

pipe = Pipeline([
    ("scaler", StandardScaler()),
    ("lgbm", lgb.LGBMClassifier(**params))
])

# Fit the pipeline to the training data
pipe.fit(x_train, y_train)

Los resultados de las pruebas no fueron tan sorprendentes: Un 53% de precisión global.

Informe de clasificación:

Classification Report
               precision    recall  f1-score   support

           0       0.49      0.79      0.61       139
           1       0.62      0.30      0.40       161

    accuracy                           0.53       300
   macro avg       0.56      0.54      0.51       300
weighted avg       0.56      0.53      0.50       300

Matriz de confusión:

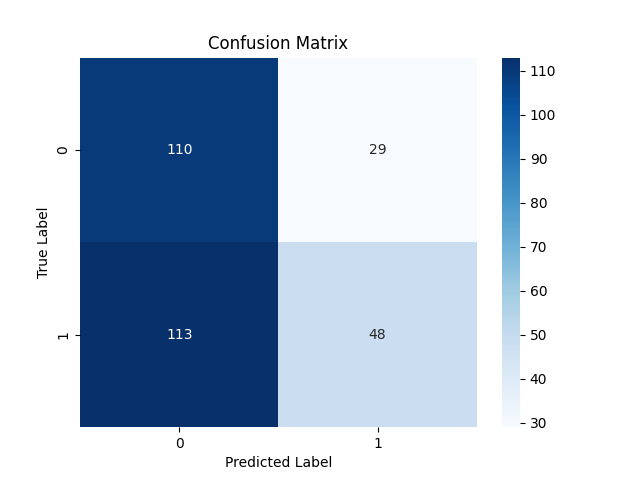
Guardar el modelo clasificador LightGBM en ONNX

Como hicimos anteriormente, guardar el modelo LightGBM en formato ONNX es sencillo y sólo requiere unas pocas líneas de código.

import onnxmltools
from onnxmltools.convert import convert_lightgbm
import onnxmltools.convert.common.data_types
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx import convert_sklearn, update_registered_converter

from skl2onnx.common.shape_calculator import (
    calculate_linear_classifier_output_shapes,
)  # noqa

from onnxmltools.convert.lightgbm.operator_converters.LightGbm import (
    convert_lightgbm,
)  # noqa

# registering onnx converter

update_registered_converter(
    lgb.LGBMClassifier,
    "GBMClassifier",
    calculate_linear_classifier_output_shapes,
    convert_lightgbm,
    options={"nocl": [False], "zipmap": [True, False, "columns"]},
)

# Final LightGBM conversion to ONNX

model_onnx = convert_sklearn(
    pipe,
    "pipeline_lightgbm",
    [("input", FloatTensorType([None, x_train.shape[1]]))],
    target_opset={"": 12, "ai.onnx.ml": 2},
)

# And save.
with open("lightgbm.Timeseries Forecasting.D1.onnx", "wb") as f:
    f.write(model_onnx.SerializeToString())

Envolverlo todo en un robot de negociación

Ahora que tenemos un modelo de aprendizaje automático guardado en ONNX podemos adjuntarlo directamente dentro de un Asesor Experto y utilizar el clasificador LightGBM para predicciones de series temporales en MetaTrader 5.

MQL5

#resource "\\Files\\lightgbm.Timeseries Forecasting.D1.onnx" as uchar lightgbm_onnx[] //load the saved onnx file 
#include <MALE5\LightGBM\LightGBM.mqh>
CLightGBM lgb;

Usando la clase LightGBM construida en el artículo anterior, pude inicializar el modelo y usarlo para hacer predicciones.

int OnInit()
  {
//---
   
   if (!lgb.Init(lightgbm_onnx)) //Initialize the LightGBM model
     return INIT_FAILED;
   
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---
    
   if (NewBar()) //Trade at the opening of a new candle
    {
     vector input_vector = input_data(); 
     long signal = lgb.predict_bin(input_vector);
     
   //---
     
      MqlTick ticks;
      SymbolInfoTick(Symbol(), ticks);
      
      if (signal==1) //if the signal is bullish
       {
          if (!PosExists(POSITION_TYPE_BUY)) //There are no buy positions
           {
             if (!m_trade.Buy(lotsize, Symbol(), ticks.ask, ticks.bid-stoploss*Point(), ticks.ask+takeprofit*Point())) //Open a buy trade
               printf("Failed to open a buy position err=%d",GetLastError());
           }
       }
      else if (signal==0) //Bearish signal
        {
          if (!PosExists(POSITION_TYPE_SELL)) //There are no Sell positions
            if (!m_trade.Sell(lotsize, Symbol(), ticks.bid, ticks.ask+stoploss*Point(), ticks.bid-takeprofit*Point())) //open a sell trade
               printf("Failed to open a sell position err=%d",GetLastError());
        }
      else //There was an error
        return;
    }
  }

La función input_data() se encarga de coleccionar los datos de forma similar a como se recogieron y almacenaron los datos en un archivo CSV en el script Feature engineering Timeseries predicción.mq5.

Prueba del modelo en el probador de estrategias

Por último, podemos probar el modelo en el entorno comercial. Dado que los datos se recogieron en un marco de tiempo diario podría ser una buena idea probarlo en un marco de tiempo inferior para evitar errores cuando «el mercado está cerrado», ya que estamos buscando señal de trading en la apertura de una nueva barra. También podemos establecer el tipo de modelización en precios abiertos para realizar pruebas más rápidas.

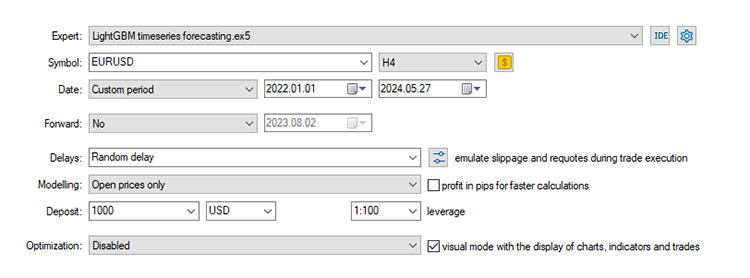
El EA realizó predicciones correctas aproximadamente el 5 % de las veces, dado que el Stop Loss y el Take Profit eran de 500 y 700 puntos respectivamente.

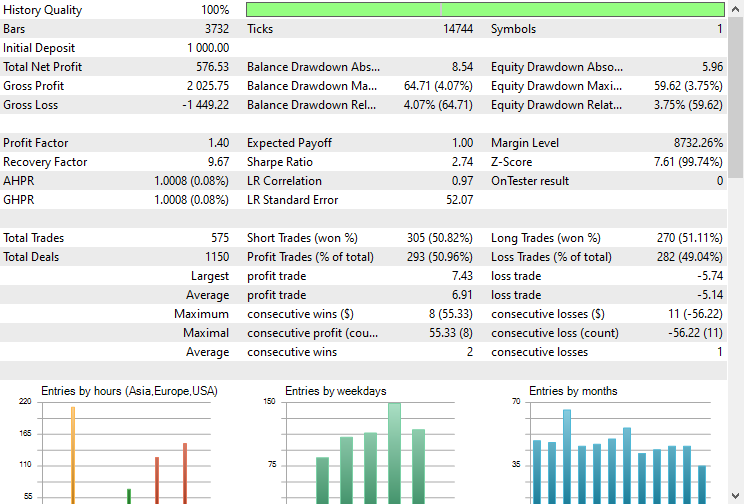
La curva de balance/equidad también era impresionante.

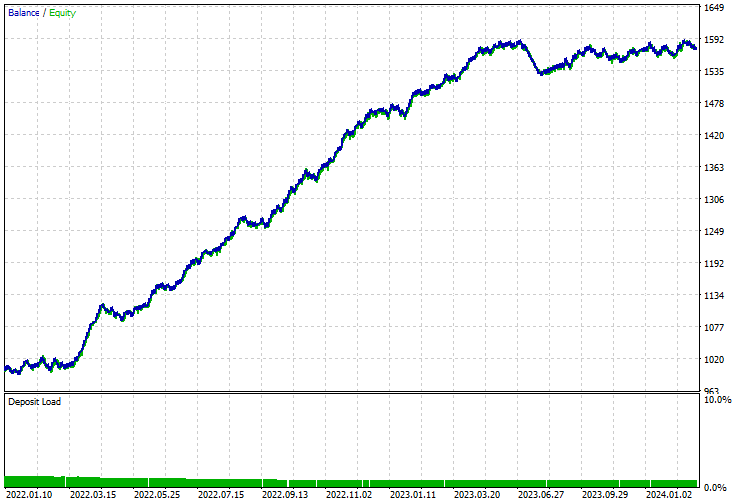
Ventajas del uso de modelos ML clásicos y modernos para la predicción de series temporales

El uso de modelos de aprendizaje automático de series no temporales para la predicción de series temporales presenta varias ventajas. A continuación se enumeran algunas de las principales ventajas:

1. Flexibilidad en la ingeniería de funciones

Los modelos clásicos de aprendizaje automático permiten una amplia ingeniería de características, que puede aprovecharse para incluir diversas variables externas y características derivadas. Puede utilizar su intelecto humano para analizar manualmente e incorporar todos los datos que considere útiles, incluidas características complejas como los desfases y las estadísticas móviles, como hicimos en este artículo.

2. Manejo de la no estacionalidad

En lugar de hacer estacionarias las series mediante diferenciación, puede incluir la tendencia y la estacionalidad directamente como características y el modelo aprenderá los patrones sin problemas.

3. Sin suposiciones sobre la distribución de datos

Muchos modelos clásicos de series temporales (como ARIMA) suponen que los datos siguen una distribución estadística específica. En cambio, los modelos clásicos y modernos de ML son más flexibles en cuanto a la distribución de los datos.

Los modelos como los árboles de decisión, los bosques aleatorios y el gradient boosting (incluido LightGBM) no asumen ninguna distribución específica de los datos.

4. Escalabilidad

Los modelos clásicos de ML pueden manejar grandes conjuntos de datos de forma más eficiente y suelen ser más fáciles de escalar.

5. Interacciones complejas

Los modelos clásicos de ML pueden captar relaciones complejas y no lineales entre las características y la variable objetivo.

6. Robustez frente a la falta de datos

Los modelos de aprendizaje automático suelen tener mejores mecanismos para tratar los datos que faltan que los modelos tradicionales de series temporales.

7. Métodos de conjunto

Puede utilizar fácilmente métodos de conjunto como bagging, boosting y stacking para mejorar el rendimiento del modelo combinando múltiples modelos para mejorar el rendimiento predictivo y la solidez.

8. Facilidad de uso e integración

Los modelos ML clásicos suelen ser más fáciles de usar y vienen con amplias bibliotecas y herramientas para implementación, visualización y evaluación.

Bibliotecas como Scikit-learn, LightGBM y XGBoost proporcionan herramientas integrales para crear, ajustar y evaluar estos modelos.

El resultado final

Tanto los modelos de aprendizaje automático clásicos como los modernos se pueden utilizar para el análisis y el pronóstico de series de tiempo sin problemas y pueden superar a los modelos de series de tiempo con la información, el ajuste y los procesos adecuados, como se analiza en este artículo. He decidido utilizar LightGBM como ejemplo, sin embargo, se puede aplicar cualquier modelo de aprendizaje automático clásico o moderno como SVM, Regresión lineal, Naïve Bayes, XGBoost, etc.

Paz.

Siga el desarrollo de modelos de aprendizaje automático y mucho más discutido en esta serie de artículos en este repositorio de GitHub.

Tabla de anexos

Nombre del archivo	Tipo de archivo	Descripción y uso
LightGBM timeseries forecasting.mq5	Asesor experto	Robot comercial para cargar el modelo ONNX y probar la estrategia comercial final en MetaTrader 5.
lightgbm.Timeseries Forecasting.D1.onnx	ONNX	Modelo LightGBM en formato ONNX.
LightGBM.mqh	Un "Include" (biblioteca).	Consiste en el código para cargar el formato del modelo ONNX y desplegarlo en lenguaje nativo MQL5.
Feature engineering Timeseries forecasting.mq5	Un script.	Se trata de un script en el que se recopilan todos los datos y se diseñan para el análisis de series temporales y la predicción.
forex-timeseries-forecasting-lightgbm.ipynb	Script Python (Jupyter Notebook)	Todo el código Python discutido en este artículo se puede encontrar dentro de este Jupyter Notebook.

Fuentes y referencias:

• Charla sobre series temporales: Estacionalidad (https://youtu.be/oY-j2Wof51c)
• Kishan Manani - Ingeniería de características para la predicción de series temporales | PyData Londres 2022 (https://www.youtube.com/watch?v=9QtL7m3YS9I)
• Predicción bursátil mediante técnicas de aprendizaje profundo: Un repaso (https://arxiv.org/abs/2212.12717)
• Retos de la predicción de series temporales (https://www.youtube.com/watch?v=rcdDl8qf0ZA)
• Estacionalidad y diferenciación (https://otexts.com/fpp2/stationarity.html)
• Cómo codificar atributos categóricos en Python (https://www.youtube.com/watch?v=nd7vc4MZQz4)