Aprendizaje automático y Data Science (Parte 8): Clusterización con el método de k-medias en MQL5
Los datos son como la basura: debemos comprender qué hacer con ellos antes de comenzar a recopilarlos.
Aprendizaje no supervisado
Este es un paradigma de aprendizaje automático para problemas que tienen datos de entrada sin procesar. A diferencia de los métodos de aprendizaje supervisado, como los métodos de regresión, las SVM, los árboles de decisión, las redes neuronales y muchos otros analizados en esta serie de artículos, donde siempre tenemos conjuntos de datos etiquetados con los que se entrenan nuestros modelos, en el aprendizaje no supervisado, los datos no se etiquetan de ninguna forma y el propio algoritmo debe encontrar las relaciones, patrones y dependencias existentes entre los ellos.
Algunos ejemplos de problemas de aprendizaje no supervisado son la clusterización, la reducción de la dimensionalidad y la estimación de la densidad.
Análisis de clústeres
El análisis de clústeres consiste en la ordenación de un conjunto de objetos en grupos de tal forma que los objetos con los mismos atributos se coloquen en los mismos grupos (clústeres).
Por ejemplo, en las tiendas, los productos semejantes se encuentran juntos porque alguien los ha clasificado en grupos. Cuando los datos del conjunto no se clasifican en grupos, el análisis de clústeres hará lo mismo: recopilará los valores de datos más similares en grupos (clústeres), destacando los datos del conjunto común.
El análisis de clústeres en sí mismo no es un algoritmo. Para resolver el problema principal, podemos usar varios algoritmos que se distinguen sustancialmente en su comprensión de lo que es un clúster.
Fuente de la imagen: Wikipedia
Los tres tipos de clusterización más conocidos son:- Exclusiva
- Superpuesta
- Jerárquica
Clusterización exclusiva
Esta es una clusterización dura en la que los puntos/elementos de los datos solo se pueden asignar a un clúster, como la clusterización de k-medias.
Agrupación superpuesta
Este es un tipo de clusterización suave, en la que los puntos/elementos de los datos pueden asignarse a varios clústeres a la vez. Por ejemplo, la clusterización difusa o método de c-medias.
Clusterización jerárquica
Este tipo de clusterización busca construir una jerarquía de clústeres.
¿Dónde se utilizan los algoritmos de clusterización?
Por ejemplo, Amazon y otros minoristas en línea utilizan técnicas de clusterización para recomendar productos similares en función de los clústeres creados previamente. Netflix hace lo mismo al recomendar películas al espectador.
En esencia, estos algoritmos se usan para identificar grupos de entidades o intereses similares en un conjunto de datos multidimensionales en diferentes campos, como el marketing, la biomedicina y las actividades geoespaciales.
Clusterización con el método de k-medias
No debe confundir este algoritmo con el método de k-vecinos más próximos, del que hablaremos en el próximo artículo.
El algoritmo de k-medias es una técnica de cuantificación vectorial que tiene como objetivo dividir n observaciones en k clústeres, donde cada observación pertenece al clúster con la media más cercana/el centroide más cercano, y además k < n. Se trata del algoritmo de clusterización más conocido y utilizado, y se basa en matemáticas bastante sencillas. Los procesos involucrados en el algoritmo se muestran a continuación. 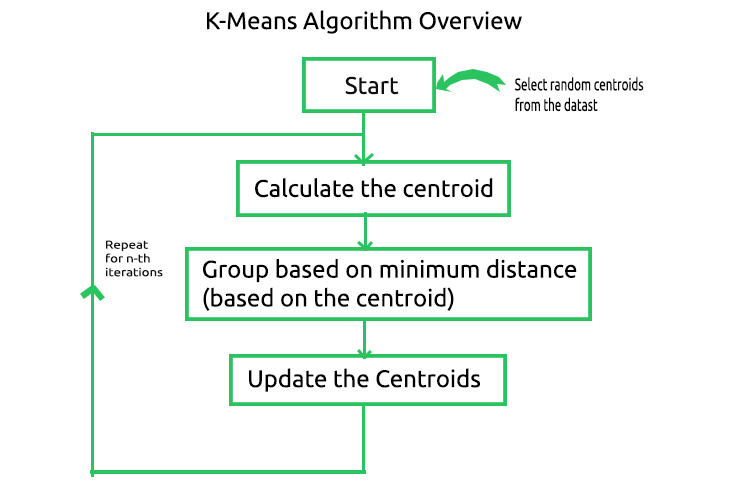
Para comprender cómo funciona este algoritmo, repasaremos todas las operaciones manualmente y automatizaremos el proceso escribiendo el código en el MetaEditor. Primero, crearemos una matriz para almacenar los centroides de nuestro conjunto de datos en una sección privada de la biblioteca CKMeans.
class CKMeans { private: ulong n; uint m_clusters; ulong m_cols; matrix InitialCentroids; //Intitial Centroids matrix vector cluster_assign; }
Como siempre, utilizaremos un conjunto de datos simple para crear la biblioteca y luego veremos cómo usar el algoritmo en una situación real con un conjunto de datos real.
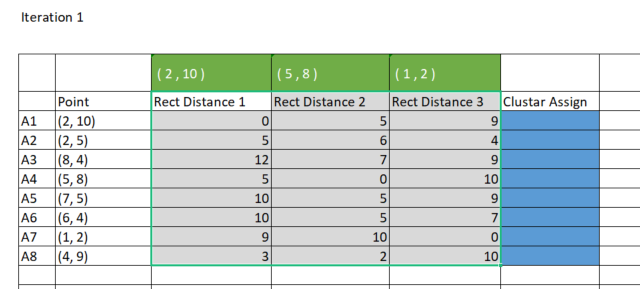
matrix DMatrix = { {2,10}, {2,5}, {8,4}, {5,8}, {7,5}, {6,4}, {1,2}, {4,9} };
1. Ejecutamos el algoritmo y 2. Cálculo de centroides
Para ejecutar el algoritmo, necesitaremos centros iniciales para cada uno de los clústeres que buscaremos. Por consiguiente, elegiremos centroides aleatorios y los almacenaremos en la matriz InitialCentroid.
m_cols = Matrix.Cols(); n = Matrix.Rows(); //number of elements | Matrix Rows InitialCentroids.Resize(m_clusters,m_cols); vector cluster_comb_v = {}; matrix cluster_comb_m = {}; vector rand_v = {}; for (ulong i=0; i<m_clusters; i++) { rand_v = Matrix.Row(i * m_clusters); InitialCentroids.Row(rand_v,i); } Print("Initial Centroids matrix\n",InitialCentroids);
Obtendremos los siguientes centroides iniciales:
CS 0 06:44:02.152 K-means test (EURUSD,M1) Initial Centroids matrix CS 0 06:44:02.152 K-means test (EURUSD,M1) [[2,10] CS 0 06:44:02.152 K-means test (EURUSD,M1) [5,8] CS 0 06:44:02.152 K-means test (EURUSD,M1) [1,2]]
Ya hemos terminado con la etapa inicial, que es muy importante. Según la imagen, el siguiente paso será calcular los centroides. ¿Pero no acabamos de encontrar los centroides? Sí, al principio no necesitaremos calcular los centroides, ya que disponemos de valores iniciales. Estos centroides se actualizarán más tarde.
3. Clusterización por distancia mínima
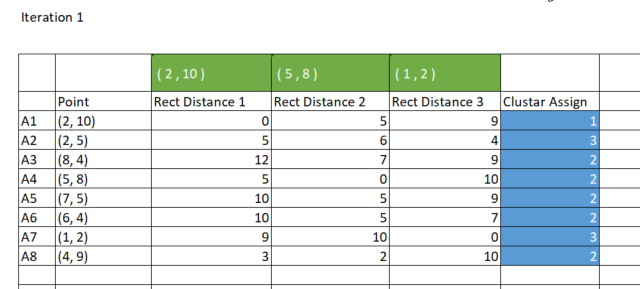
Ahora determinaremos la distancia entre cada punto en el conjunto de datos de los centroides obtenidos. Para ello, asignaremos un punto de datos al clúster cuyo centroide esté más cerca que otros centroides.
Para encontrar la distancia, podemos usar dos fórmulas matemáticas: la distancia euclidiana o la distancia en línea recta.
Distancia euclidiana
Este es un método para medir la distancia entre dos puntos usando el Teoremas de Pitágoras. La fórmula del cálculo se muestra a continuación:
Distancia en línea recta
La distancia en línea recta supone simplemente la suma de la diferencia en las coordenadas x e y entre dos puntos. La fórmula del cálculo se muestra a continuación:
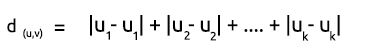
Para mayor simplicidad, es preferible usar el método de la línea recta a la hora de encontrar la distancia entre los centroides y los puntos. Vamos a construir una matriz en Excel.
Para hacer esto en MQL5, crearemos una matriz de 8 filas de 3 clústeres para almacenar las distancias en línea recta con las que distribuiremos los datos entre los clústeres. ¿Por qué precisamente tres grupos? Hemos elegido tres clústeres al inicializar la biblioteca, pero podemos tener cualquier número de clústeres según nuestros objetivos. Echaremos un vistazo más de cerca a este punto un poco más tarde. El constructor de la biblioteca se muestra a continuación.
CKMeans::CKMeans(int clusters=3) { m_clusters = clusters; }Después veremos cómo crear una matriz para almacenar las distancias en línea recta:
matrix rect_distance = {}; //matrix to store rectilinear distances rect_distance.Reshape(n,m_clusters);
Ahora calcularemos las distancias en línea recta y almacenaremos los resultados en la matriz rect_distance que acabamos de crear:
vector v_matrix = {}, v_centroid = {}; double output = 0; for (ulong i=0; i<rect_distance.Rows(); i++) for (ulong j=0; j<rect_distance.Cols(); j++) { v_matrix = Matrix.Row(i); v_centroid = InitialCentroids.Row(j); ZeroMemory(output); for (ulong k=0; k<v_matrix.Size(); k++) output += MathAbs(v_matrix[k] - v_centroid[k]); //Rectilinear distance rect_distance[i][j] = output; } Print("Rectilinear distance matrix\n",rect_distance);
Información mostrada:
CS 0 15:17:52.136 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 15:17:52.136 K-means test (EURUSD,M1) [[0,5,9] CS 0 15:17:52.136 K-means test (EURUSD,M1) [5,6,4] CS 0 15:17:52.136 K-means test (EURUSD,M1) [12,7,9] CS 0 15:17:52.136 K-means test (EURUSD,M1) [5,0,10] CS 0 15:17:52.136 K-means test (EURUSD,M1) [10,5,9] CS 0 15:17:52.136 K-means test (EURUSD,M1) [10,5,7] CS 0 15:17:52.136 K-means test (EURUSD,M1) [9,10,0] CS 0 15:17:52.136 K-means test (EURUSD,M1) [3,2,10]]
Como hemos dicho anteriormente, el método de clusterización de k-medias agrupa puntos de datos de forma que el punto con la distancia más pequeña respecto a un clúster en particular pertenezca a ese clúster. Cada columna en la matriz rect_distance representa un clúster, por lo que deberemos encontrar el valor mínimo en una fila: la columna con el valor mínimo se asignará a ese clúster. Mire la imagen de abajo.
Código en el que se determina el clúster necesario:
//--- Assigning the Clusters matrix cluster_cent = {}; //cluster centroids ulong cluster = 0; for (ulong i=0; i<rect_distance.Rows(); i++) { v_row = rect_distance.Row(i); cluster = v_row.ArgMin(); cluster_assign[i] = (uint)cluster; } Print("Assigned clusters\n",cluster_assign);
Información mostrada:
CS 0 15:17:52.136 K-means test (EURUSD,M1) Assigned clusters CS 0 15:17:52.136 K-means test (EURUSD,M1) [0,2,1,1,1,1,2,1]
Una vez que hayamos asignado los puntos a los clústeres correspondientes, agruparemos estos puntos en función de los clústeres recién encontrados. Si realizamos este proceso en Excel, obtendremos clústeres como este:
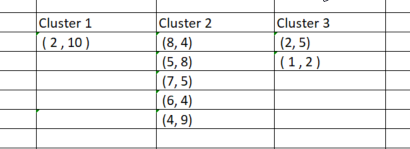
Agrupar manualmente los datos en clústeres resulta bastante sencillo, sin embargo, al intentar programar, las cosas son un poco más complicadas porque los clústeres siempre tendrán diferentes tamaños. Por consiguiente, si usamos una matriz para almacenar clústeres, las columnas tendrán un número de filas distinto. Usar el método de arrays resulta algo incómodo y también difícil de leer. Los archivos CSV resultan incómodos a la hora de almacenar valores, ya que necesitamos escribir dinámicamente columnas para cada uno de los grupos.
Nos surgió la idea de usar matrices de clúster 3 xn para almacenar los clústeres. Hablamos de una matriz de ceros inicialmente dimensionada para que el número de filas sea igual al número de clústeres y el número de columnas sea igual al número máximo que puede haber en un clúster.
Como resultado, cada clúster se almacena horizontalmente en la fila de la matriz.
Tendremos el resultado el siguiente:
CS 0 15:17:52.136 K-means test (EURUSD,M1) clustered Matrix CS 0 15:17:52.136 K-means test (EURUSD,M1) [[2,10,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0] CS 0 15:17:52.136 K-means test (EURUSD,M1) [2,5,1,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0] CS 0 15:17:52.136 K-means test (EURUSD,M1) [8,4,5,8,7,5,6,4,4,9,0,0,0,0,0,0,0,0,0,0,0,0,0,0]]Dado que esta matriz se transmite como referencia a la función KMeansClustering donde se realizan todas las operaciones, se podrá recuperar y los valores se podrán filtrar para eliminar los valores nulos después del último valor nulo no negativo.
void CKMeans::KMeansClustering(const matrix &Matrix, matrix &clustered_matrix)
4. Actualización del centroide
Para determinar los nuevos centroides de cada clúster, deberemos encontrar el promedio de todos los elementos individuales en el clúster. A continuación mostramos el código donde se realiza esto:
vector x_y_z = {0,0}; ZeroMemory(rand_v); for (ulong k=0; k<cluster_cent.Cols(); k++) { x_y_z.Resize(cluster_cent.Cols()); rand_v = cluster_cent.Col(k); x_y_z[k] = rand_v.Mean(); } InitialCentroids.Row(x_y_z, i); if (index >= n_each_cluster.Size()) break; } Print("New Centroids\n",InitialCentroids,"\nclustered Matrix\n",clustered_matrix);
Tendremos el resultado el siguiente:
CS 0 15:17:52.136 K-means test (EURUSD,M1) New Centroids CS 0 15:17:52.136 K-means test (EURUSD,M1) [[2,10] CS 0 15:17:52.136 K-means test (EURUSD,M1) [1.5,3.5] CS 0 15:17:52.136 K-means test (EURUSD,M1) [6,6]]
Hemos analizado el proceso de una iteración. Ahora resulta tedioso iterar desde el segundo paso hasta el último hasta que los datos se agrupen en los clústeres correspondientes. Esto se puede lograr de dos maneras: o bien se construye la lógica para que el proceso se detenga cuando los nuevos centroides para los clústeres dejen de cambiar y se encuentren los valores óptimos para todos los clústeres, o bien simplemente se establece un número limitado de iteraciones en el algoritmo. A nuestro juicio, el problema de la primera forma reside en la necesidad de un ciclo infinito para controlar la instrucción if, por eso mismo, necesitaremos un descanso. Parece tener más sentido limitar el algoritmo en cuanto al número de iteraciones.
Más abajo, mostramos al lector la función completa del algoritmo de clusterización de k-medias con la adición de iteraciones:
void CKMeans::KMeansClustering(const matrix &Matrix, matrix &clustered_matrix,int iterations = 10) { m_cols = Matrix.Cols(); n = Matrix.Rows(); //number of elements | Matrix Rows InitialCentroids.Resize(m_clusters,m_cols); cluster_assign.Resize(n); clustered_matrix.Resize(m_clusters, m_clusters*n); clustered_matrix.Fill(NULL); vector cluster_comb_v = {}; matrix cluster_comb_m = {}; vector rand_v = {}; for (ulong i=0; i<m_clusters; i++) { rand_v = Matrix.Row(i * m_clusters); InitialCentroids.Row(rand_v,i); } Print("Initial Centroids matrix\n",InitialCentroids); //--- vector v_row; vector n_each_cluster; //Each cluster content matrix rect_distance = {}; //matrix to store rectilinear distances rect_distance.Reshape(n,m_clusters); vector v_matrix = {}, v_centroid = {}; double output = 0; //--- for (int iter=0; iter<iterations; iter++) { printf("\n<<<<< %d >>>>>\n",iter ); for (ulong i=0; i<rect_distance.Rows(); i++) for (ulong j=0; j<rect_distance.Cols(); j++) { v_matrix = Matrix.Row(i); v_centroid = InitialCentroids.Row(j); ZeroMemory(output); for (ulong k=0; k<v_matrix.Size(); k++) output += MathAbs(v_matrix[k] - v_centroid[k]); //Rectilinear distance rect_distance[i][j] = output; } Print("Rectilinear distance matrix\n",rect_distance); //--- Assigning the Clusters matrix cluster_cent = {}; //cluster centroids ulong cluster = 0; for (ulong i=0; i<rect_distance.Rows(); i++) { v_row = rect_distance.Row(i); cluster = v_row.ArgMin(); cluster_assign[i] = (uint)cluster; } Print("Assigned clusters\n",cluster_assign); //--- Combining the clusters n_each_cluster.Resize(m_clusters); for (ulong i=0, index =0, sum_count = 0; i<cluster_assign.Size(); i++) { for (ulong j=0, count = 0; j<cluster_assign.Size(); j++) { //printf("cluster_assign[%d] cluster_assign[%d]",i,j); if (cluster_assign[i] == cluster_assign[j]) { count++; n_each_cluster[index] = (uint)count; cluster_comb_m.Resize(count, m_cols); cluster_comb_m.Row(Matrix.Row(j) , count-1); cluster_cent.Resize(count, m_cols); // New centroids cluster_cent.Row(Matrix.Row(j),count-1); sum_count++; } else continue; } //--- MatrixToVector(cluster_comb_m, cluster_comb_v); // solving for new cluster and updating the old ones if (iter == iterations-1) clustered_matrix.Row(cluster_comb_v, index); //--- index++; //--- vector x_y_z = {0,0}; ZeroMemory(rand_v); for (ulong k=0; k<cluster_cent.Cols(); k++) { x_y_z.Resize(cluster_cent.Cols()); rand_v = cluster_cent.Col(k); x_y_z[k] = rand_v.Mean(); } InitialCentroids.Row(x_y_z, i); if (index >= n_each_cluster.Size()) break; } Print("New Centroids\n",InitialCentroids);//,"\nclustered Matrix\n",clustered_matrix); } //end of iterations } //+------------------------------------------------------------------+
Así se verá el diario de registro del algoritmo tras 10 iteraciones:
CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 0 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[0,5,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5,6,4] CS 0 20:40:05.438 K-means test (EURUSD,M1) [12,7,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5,0,10] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10,5,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10,5,7] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9,10,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) [3,2,10]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,2,1,1,1,1,2,1] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[2,10] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [6,6]] CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 1 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[0,7,8] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5,2,5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [12,7,4] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5,8,3] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10,7,2] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10,5,2] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9,2,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [3,8,5]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,1,2,2,2,2,1,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[3,9.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [6.5,5.25]] CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 2 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[1.5,7,9.25] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5.5,2,4.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [10.5,7,2.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [3.5,8,4.25] CS 0 20:40:05.438 K-means test (EURUSD,M1) [8.5,7,0.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [8.5,5,1.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.5,2,8.75] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,8,6.25]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,1,2,0,2,2,1,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[3.666666666666667,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7,4.333333333333333]] CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 3 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[2.666666666666667,7,10.66666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5.666666666666666,2,5.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.333333333333334,7,1.333333333333333] CS 0 20:40:05.438 K-means test (EURUSD,M1) [2.333333333333333,8,5.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7.333333333333334,7,0.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7.333333333333334,5,1.333333333333333] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.666666666666666,2,8.333333333333332] CS 0 20:40:05.438 K-means test (EURUSD,M1) [0.3333333333333335,8,7.666666666666667]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,1,2,0,2,2,1,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[3.666666666666667,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7,4.333333333333333]] CS 0 20:40:05.438 K-means test (EURUSD,M1) ..... ..... ..... ..... CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) <<<<< 9 >>>>> CS 0 20:40:05.438 K-means test (EURUSD,M1) CS 0 20:40:05.438 K-means test (EURUSD,M1) Rectilinear distance matrix CS 0 20:40:05.438 K-means test (EURUSD,M1) [[2.666666666666667,7,10.66666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [5.666666666666666,2,5.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.333333333333334,7,1.333333333333333] CS 0 20:40:05.438 K-means test (EURUSD,M1) [2.333333333333333,8,5.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7.333333333333334,7,0.666666666666667] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7.333333333333334,5,1.333333333333333] CS 0 20:40:05.438 K-means test (EURUSD,M1) [9.666666666666666,2,8.333333333333332] CS 0 20:40:05.438 K-means test (EURUSD,M1) [0.3333333333333335,8,7.666666666666667]] CS 0 20:40:05.438 K-means test (EURUSD,M1) Assigned clusters CS 0 20:40:05.438 K-means test (EURUSD,M1) [0,1,2,0,2,2,1,0] CS 0 20:40:05.438 K-means test (EURUSD,M1) New Centroids CS 0 20:40:05.438 K-means test (EURUSD,M1) [[3.666666666666667,9] CS 0 20:40:05.438 K-means test (EURUSD,M1) [1.5,3.5] CS 0 20:40:05.438 K-means test (EURUSD,M1) [7,4.333333333333333]]
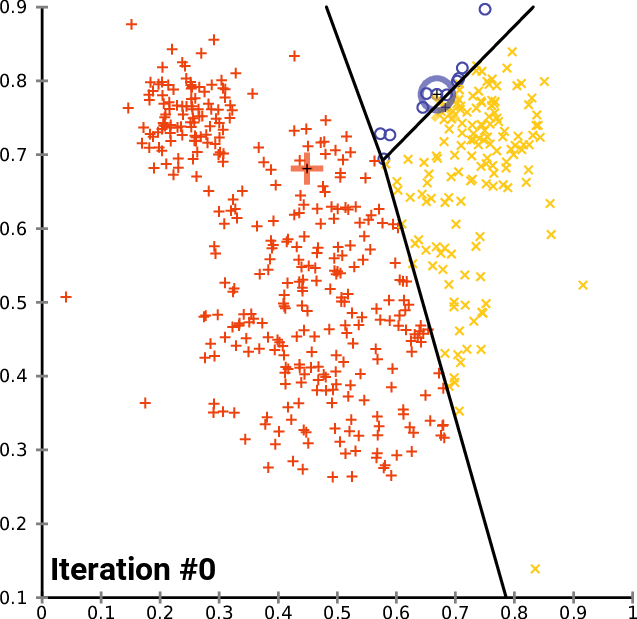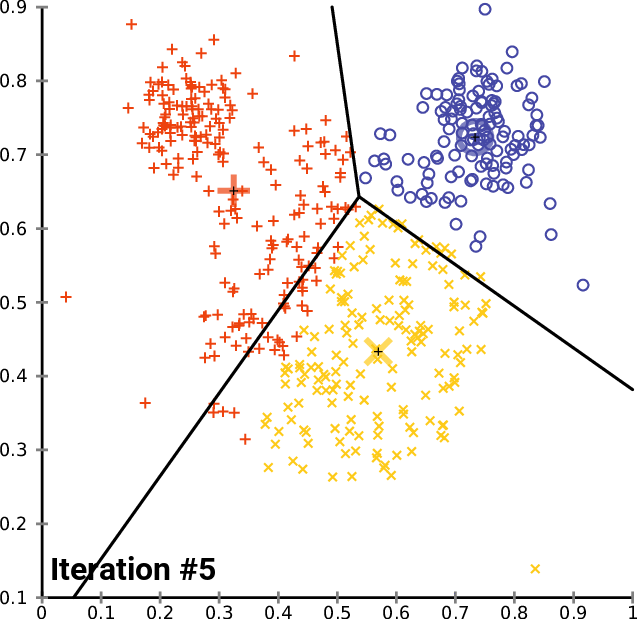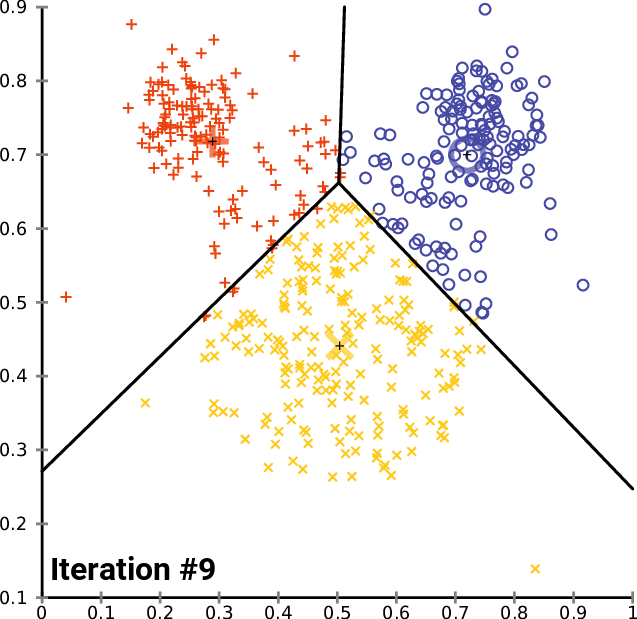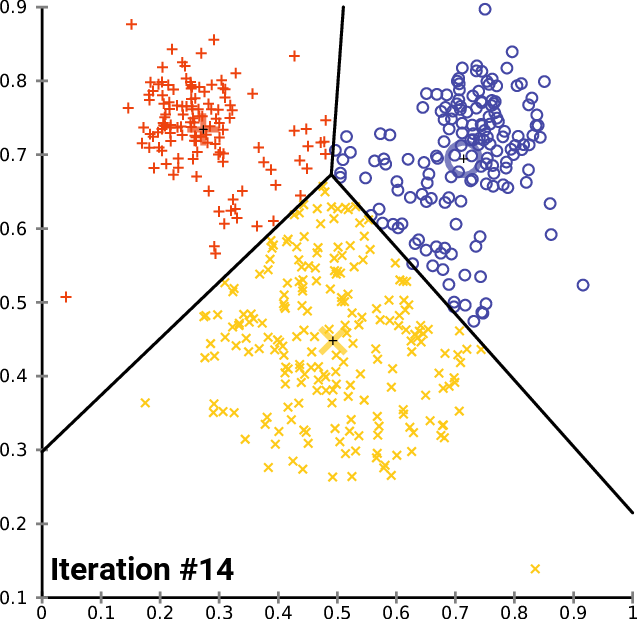
Ya después de dos iteraciones, el algoritmo ha convergido y determinado los valores óptimos para los centroides. Esto nos lleva a preguntarnos cuál será el número óptimo de iteraciones para este tipo de algoritmo. A diferencia del descenso de gradiente y otros algoritmos, la clusterización de k-medias no requiere una gran cantidad de iteraciones para alcanzar valores óptimos; a menudo, de 5 a 10 iteraciones bastan para clusterizar por completo un conjunto de datos simple.
Dentro del script K-Means Test
En la función principal del script de prueba, inicializaremos la biblioteca, llamaremos a la función k-MeansClustering, aplicaremos los clústeres a un eje y finalmente eliminaremos el objeto de la biblioteca. void OnStart() { //--- matrix DMatrix = { {2,10}, {2,5}, {8,4}, {5,8}, {7,5}, {6,4}, {1,2}, {4,9} }; int clusters =3; matrix clusterd_mat; clustering = new CKMeans(clusters); clustering.KMeansClustering(DMatrix,clusterd_mat); ObjectsDeleteAll(0,0); ScatterPlotsMatrix("graph",clusterd_mat,"cluster 1"); delete(clustering); }
A continuación, mostramos el diagrama de clústeres:
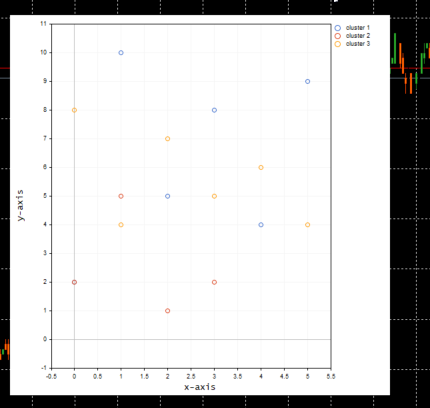
Antes de trazar los valores en el gráfico, llamaremos a una función dentro de la función ScatterPlotsMatrix() para filtrar los valores cero. Todos los valores que se encuentren exactamente en la línea del eje x o y en el gráfico deberán ignorarse.
vectortoArray(x,x_arr); FilterZeros(x_arr); graph.CurveAdd(x_arr,CURVE_POINTS," cluster "+string(i+1));
¿Cuál es el número correcto de clústeres k?
Ya hemos hablado sobre cómo funciona el algoritmo, pero no podemos simplemente llamar a la función principal de clusterización de k-medias y especificar el número de clústeres. ¿Cómo podemos saber que el número seleccionado de clústeres resulta óptimo?, no olvidemos que la inicialización afecta a todo el algoritmo. Para entender esto, veremos un método llamado el «método del codo» o «elbow method».
El método del codo
El método del codo se usa para encontrar el número óptimo de clústeres al realizar la clusterización con el método de k-medias, y traza la función de costes obtenida usando diferentes valores de clústeres (k).
A medida que aumente el número k, la función de costes disminuirá, esto se puede definir como sobreajuste.
Si observamos el gráfico del método del codo, podremos ver el punto en el que la dirección del gráfico cambia rápidamente, después de lo cual el gráfico comenzará a moverse en paralelo al eje x.
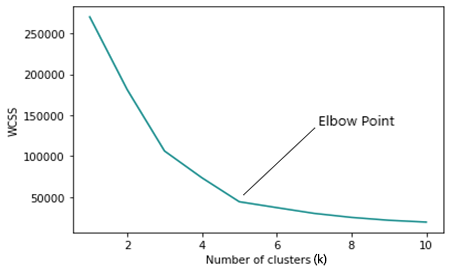
WCSS
La suma residual de cuadrados intracluster (WCSS) es la suma de las distancias al cuadrado entre cada punto y el centroide en el clúster.
Fórmula de cálculo:
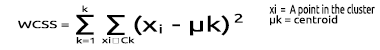
Como el método del codo es un método de optimización para la clusterización de k-medias, cada iteración del mismo requerirá una llamada a la función de clusterización de k-medias.
Por lo tanto, para ejecutar el método del codo y obtener resultados, deberemos cambiar algo en la función principal para la clusterización con el método de k-medias. Lo primero que deberemos cambiar es la obtención de centroides, porque cuando los clústeres seleccionados se vuelven iguales o cercanos al número de filas en la matriz, el método de selección aleatoria del centroide inicial deja de funcionar.
for (ulong i=0; i<m_clusters; i++) { rand_v = Matrix.Row(i); InitialCentroids.Row(rand_v,i); }
También deberemos modificar la lógica para que la cantidad máxima de clústeres iniciales no supere el número de muestras n que hay en el conjunto de datos. Como sabemos por la definición de la clusterización de k-medias, k < n.
void CKMeans::ElbowMethod(const int initial_k=1, int total_k=10, bool showPlot = true) { matrix clustered_mat, _centroids = {}; if (total_k > (int)n) total_k = (int)n; //>>k should always be less than n
El código para el método del codo se muestra completo a continuación;
void CKMeans::ElbowMethod(const int initial_k=1, int total_k=10, bool showPlot = true) { matrix clustered_mat, _centroids = {}; if (total_k > (int)n) total_k = (int)n; //k should always be less than n vector centroid_v={}, x_y_z={}; vector short_v = {}; //vector for each point vector minus_v = {}; //vector to store the minus operation output double wcss = 0; double WCSS[]; ArrayResize(WCSS,total_k); double kArray[]; ArrayResize(kArray,total_k); for (int k=initial_k, count_k=0; k<ArraySize(WCSS)+initial_k; k++, count_k++) { wcss = 0; m_clusters = k; KMeansClustering(clustered_mat,_centroids,1); for (ulong i=0; i<_centroids.Rows(); i++) { centroid_v = _centroids.Row(i); x_y_z = clustered_mat.Row(i); FilterZero(x_y_z); for (ulong j=0; j<x_y_z.Size()/m_cols; j++) { VectorCopy(x_y_z,short_v,uint(j*m_cols),(uint)m_cols); //--- WCSS (within cluster sum of squared residuals) minus_v = (short_v - centroid_v); minus_v = MathPow(minus_v,2); wcss += minus_v.Sum(); } } WCSS[count_k] = wcss; kArray[count_k] = k; } Print("WCSS"); ArrayPrint(WCSS); Print("kArray"); ArrayPrint(kArray); //--- Plotting the Elbow on the graph if (showPlot) { ObjectDelete(0,"elbow"); ScatterCurvePlots("elbow",kArray,WCSS,WCSS,"Elbow line","k","WCSS"); } }
Aquí tenemos lo que genera este bloque de código:
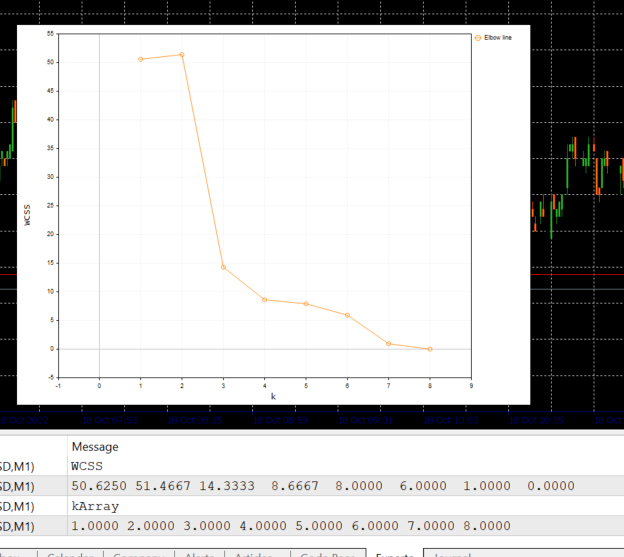
Mirando el gráfico de Elbow, nos queda claro que el número óptimo de clústeres es 3. Los valores de WCSS se han desplomado en este punto, de 51,4667 a 14,333.
Ya tenemos todo lo necesario para implementar el algoritmo de clusterización de k-medias en MQL5, así que vamos a ver cómo podemos implementar este algoritmo en el campo del trading.
Veamos cómo podemos agrupar los mismos datos de precio de mercado en varios clústeres:
matrix DMatrix = {}; DMatrix.Resize(bars, 1); //columns determines the dimension of the dataset 1D won't be visualized properly vector column_v = {}; column_v.CopyRates(symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,1,bars); DMatrix.Col(column_v,0);
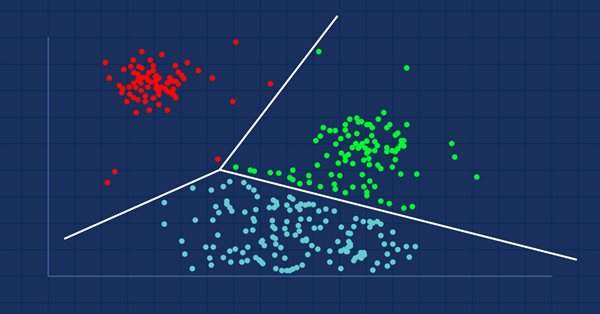
Acabamos de reemplazar la matriz con una matriz nx1 para los valores de precio de mercado. Esta vez usaremos una matriz unidimensional. Dado el código del algoritmo, no obtendremos una buena visualización y clusterización de matrices unidimensionales; por ejemplo, mire el resultado de la operación de clusterización completa para el símbolo NASDAQ en 20 barras en los gráficos a continuación.
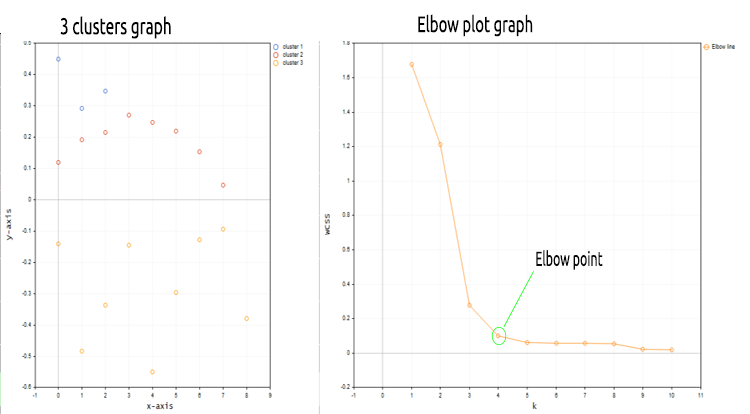
De acuerdo con el método del codo en el gráfico anterior, una cantidad de clústeres igual a cuatro resulta adecuada aquí. Los clústeres se ven mucho mejor cuando están dibujados en el gráfico.
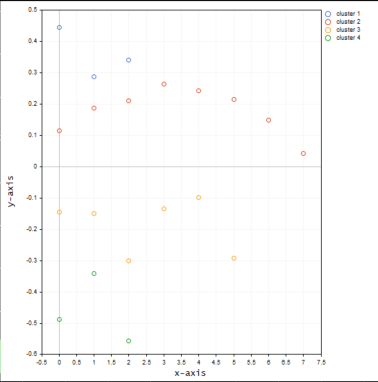
Ahora pondremos los valores del mismo símbolo en una matriz 3D y veremos qué sucede con los clústeres.
matrix DMatrix = {}; DMatrix.Resize(bars, 3); //columns determines the dimension of the dataset 1D won't be visualized properly vector column_v = {}; ulong start = 0; for (ulong i=0; i<2; i++) { column_v.CopyRates(symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,start,bars); DMatrix.Col(column_v,i); start += bars; }
A continuación, mostramos cómo se verán los clústeres en el gráfico:
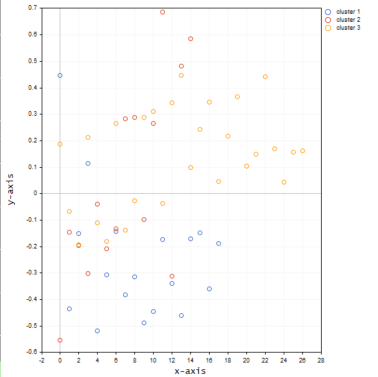
Por lo visto las matrices 3D al realizar la clusterización en un eje ofrecen muchos valores atípicos en los clústeres.
Podríamos considerar el uso de una matriz superior a una unidimensional para agrupar diferentes muestras cuyos valores se encuentren, por ejemplo, en diferentes niveles/escalas. Puede probar con los valores del indicador RSI o la media móvil, pero la opción ideal sería incluir siempre estos valores en una matriz unidimensional, es decir, en una sola columna de la matriz. Puede experimentar y compartir los resultados en el apartado de discusión.
Antes de mostrar los gráficos, hemos olvidado mencionar que hemos normalizado los valores de los precios de NASDAQ usando la técnica Mean-Normalization.
MeanNormalization(DMatrix);
Entonces los datos estarán bien distribuidos en el gráfico. Código completo:
void MeanNormalization(matrix &mat) { vector v = {}; for (ulong i=0; i<mat.Cols(); i++) { v = mat.Col(i); MeanNormalization(v); mat.Col(v,i); } } //+------------------------------------------------------------------+ void MeanNormalization(vector &v) { double mean = v.Mean(), max = v.Max(), min = v.Min(); for (ulong i=0; i<v.Size(); i++) v[i] = (v[i] - mean) / (max - min); }
Reflexiones finales
La clusterización con K-medias es un algoritmo muy útil que debería encontrarse en la caja de herramientas de cada tráder y de cualquiera que trabaje con datos. Una cosa importante a recordar es que el algoritmo está fuertemente influenciado por los inicializadores. Si buscamos el algoritmo óptimo usando el método del codo, comenzando con 2 clústeres, podremos obtener un número óptimo de clústeres distinto al número 4 elegido inicialmente. Además, los centroides iniciales resultan muy importantes, por lo que hemos tenido que añadir datos de entrada a la función principal de clusterización. Esto nos permite comprender si necesitamos elegir los centroides iniciales al azar o si tenemos que elegir las tres primeras filas de la matriz.void CKMeans::KMeansClustering(matrix &clustered_matrix,matrix ¢roids,int iterations = 1,bool rand_cluster =false)
El argumento de la función rand_cluster para elegir aleatoriamente un centroide se establece en false por defecto en caso de llamar a la función de clusterización en la función del método elbow. Esto se debe a que la opción de elegir centroides aleatorios al buscar clústeres óptimos no funciona. Funciona cuando conocemos el número de clústeres.
Reciba mis mejores deseos.
Los archivos de código MQL5 del artículo se adjuntan más abajo. En los archivos zip, el código se ha modificado ligeramente: hemos eliminado algunas líneas para mejorar el rendimiento, mientras que hemos añadido otras simplemente para facilitar la comprensión de lo que sucede dentro del proceso.
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/11615
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Aprendiendo a diseñar un sistema de trading con Fractals
Aprendiendo a diseñar un sistema de trading con Fractals
 Redes neuronales: así de sencillo (Parte 31): Algoritmos evolutivos
Redes neuronales: así de sencillo (Parte 31): Algoritmos evolutivos
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
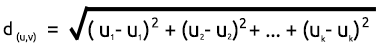
En primer lugar, me gustaría dar las gracias al autor por compartir este artículo. Espero que el autor, además de explicar estas teorías, puede dar ejemplos de cómo K-mean clustering se utiliza en el comercio real, si no hay un ejemplo correspondiente, este u otros artículos del autor son prácticamente indistinguibles de los libros de texto. El aprendizaje automático se utiliza en muchos campos.
Estaría bien que el autor ilustrara mejor estas teorías de aprendizaje automático con ejemplos de mecanismos de trading de MT5. Gracias de nuevo por compartir.
Nuevo artículo Data Science and Machine Learning (Part 08): K-Means Clustering in plain MQL5 ha sido publicado:
Autor: Omega J Msigwa
hola Omega J Msigwa, gracias por tu articulo tan util.
¿me estoy perdiendo algo o en el código anterior te refieres a DMatrix?
Hola Omega J Msigwa, gracias por su artículo tan útil.
¿me estoy perdiendo algo o en el código anterior te refieres a DMatrix?
Me refiero a Matrix como se explica en el artículo, ya que este código se encuentra bajo la función