Redes neuronales: así de sencillo (Parte 32): Aprendizaje Q distribuido

MetaTrader 5 — Sistemas comerciales | 23 febrero 2023, 16:37

656

Dmitriy Gizlyk

Introducción

En el artículo "Redes neuronales: así de sencillo (Parte 27): Aprendizaje Q profundo (DQN)" ya vimos el método de aprendizaje Q. Recordamos al lector que entonces aproximamos la función Q, que supone una función de dependencia de la recompensa del estado del sistema y de la acción realizada, pero el problema es que el mundo real es polifacético. Al evaluar la situación actual, no siempre podemos considerar todos los factores que influyen, y, en consecuencia, no existirá una relación directa entre los parámetros evaluados del estado del sistema, la acción emprendida y la recompensa obtenida. Al aproximar la función Q solo obtendremos una media del valor más probable de la recompensa esperada. Al mismo tiempo, no veremos toda la distribución de recompensas obtenidas durante el entrenamiento del modelo. Al mismo tiempo, el valor medio estará sujeto a distorsiones como consecuencia de caídas bruscas significativas. En 2017, se presentaron 2 artículos en los que los autores proponían algoritmos para estudiar la distribución de los valores de recompensa. En ambos artículos, los autores lograron mejorar significativamente los resultados del aprendizaje Q clásico en juegos de ordenador Atari.

1. Características del aprendizaje Q distribuido

El aprendizaje Q distribuido, al igual que el aprendizaje Q original, lleva a cabo una aproximación de la función de utilidad de la acción. Así que, como antes, aproximaremos la función Q para predecir la recompensa esperada. La principal diferencia será que no aproximaremos un valor de recompensa individual por una acción realizada en un estado concreto, sino toda la distribución de probabilidad de la recompensa esperada. Hay que decir que, debido a la limitación de recursos, obviamente, no podremos estimar la probabilidad de que aparezca cada valor de recompensa individual, pero podemos dividir todo el rango posible de valores de recompensa en varios rangos distintos: los cuantiles.

Para determinar los cuantiles, se introducen hiperparámetros adicionales: el valor mínimo (Vmin), el valor máximo (Vmax) del rango de recompensas esperadas y el número de cuantiles (N). A continuación, calcularemos el intervalo de valores de un cuantil usando la fórmula:

A diferencia del método de aprendizaje Q original, que se aproximaba al valor natural de la recompensa, el algoritmo de aprendizaje Q distribuido se aproxima a la distribución de probabilidad de obtener una recompensa dentro de un cuantil al realizar una acción concreta en una condición determinada. Es precisamente el traslado del problema al plano de la distribución de probabilidad lo que permite reclasificar el problema de aproximación de la función Q como un problema de clasificación estándar, y de ahí se deriva un cambio en la función de pérdida. Si el aprendizaje Q original utiliza la desviación estándar como función de pérdida, en el método de aprendizaje Q distribuido, en cambio, utilizaremos LogLoss. Ya nos familiarizamos con esta característica al estudiar el Policy Gradient.

LogLoss

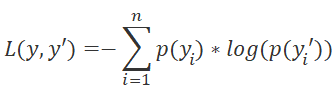
En general, esto nos permitirá aproximar la distribución de probabilidad de la recompensa para cada par estado-acción. Y esto significará que, a la hora de elegir una acción, podremos determinar con mayor precisión el nivel de recompensa esperado y la probabilidad de obtenerla. Resulta especialmente valioso el hecho de que podamos estimar las probabilidades de un determinado nivel de recompensa en lugar de su valor promedio. Esto nos permitirá utilizar un enfoque basado en el riesgo para evaluar la probabilidad de recompensas positivas y negativas al tomar medidas partiendo del estado actual del sistema.

Dicho factor tiene mayor efecto cuando el entorno retorna recompensas tanto positivas como negativas como resultado de realizar las mismas acciones a partir de situaciones similares. Si usamos el aprendizaje Q original y promediamos la recompensa esperada en estas situaciones, lo más probable será que obtengamos un valor cercano a "0", y la acción será omitida. En el caso del aprendizaje Q distribuido, en cambio, tendremos la oportunidad de estimar la probabilidad de recompensas reales, por lo que utilizar un enfoque basado en el riesgo nos permitirá tomar la decisión correcta.

Aquí debemos señalar que cuando un agente realiza cualquiera de las acciones posibles, el entorno estará obligado a darnos una recompensa. En consecuencia, para cualquier acción del agente partiendo del estado actual del entorno esperaríamos obtener una recompensa con una probabilidad del 100%, y la suma de las probabilidades de la acción de cada agente debería dar "1". Este resultado se puede lograr utilizando la función SoftMax en términos de acciones posibles.

Obviamente, seguiremos utilizando todas las herramientas del algoritmo de aprendizaje Q original. Estos incluyen el búfer de reproducción de experiencia y el modelo Target Net para predecir futuras recompensas. Y, naturalmente, utilizaremos un factor de descuento para futuras recompensas.

El entrenamiento del modelo se basará en los principios del aprendizaje Q original, y el proceso tomará como base la conocida ecuación de Bellman.

Ecuación de Bellman

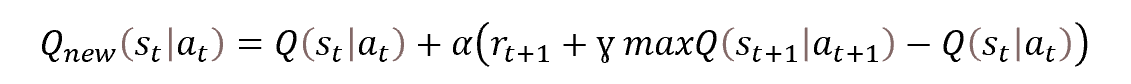
Como ya hemos mencionado, usaremos Target Net para estimar los valores previstos de las recompensas futuras. Como ya sabrá, se trata de una copia «congelada» del modelo de entrenamiento. Aquí me gustaría decir unas palabras sobre sus enfoques de uso.

Una de las características del aprendizaje por refuerzo, y del aprendizaje Q en particular, es la capacidad de construir estrategias de acción para conseguir el mejor resultado posible. Para permitir la construcción de una estrategia, la ecuación de Bellman incluye un valor del estado futuro. De hecho, la evaluación del estado futuro del entorno debería incluir la máxima recompensa posible desde el estado hasta el final de la sesión. Sin este indicador, el modelo solo aprendería a predecir la recompensa esperada para la transición del estado actual a uno nuevo.

Pero veamos el proceso desde otro ángulo. No tendremos una recompensa completa real hasta el final de la sesión, así que utilizaremos una segunda red neuronal para predecir los datos que faltan. Para evitar entrenar 2 modelos en paralelo, utilizaremos una copia del modelo entrenado con pesos congelados para predecir las recompensas de un estado futuro. Pero, ¿cómo de precisas serán las predicciones de un modelo no entrenado? Es probable que resulten completamente aleatorias, y al fijar valores aleatorios a los objetivos del modelo de entrenamiento, solo distorsionaremos la percepción del entorno y dirigiremos el entrenamiento del modelo en una dirección falsa.

Al mismo tiempo, renunciando al uso de Target Net desde el inicio, podremos entrenar el modelo para predecir la recompensa de la transición actual con cierta precisión. Sí, en ese caso el modelo no podrá construir una estrategia, pero esta será solo la primera etapa del entrenamiento. Si disponemos de un modelo capaz de realizar predicciones sensatas con un paso de antelación, podremos utilizarlo como Target Net, y entonces podremos perfeccionar nuestro modelo para construir una estrategia dos pasos por delante.

Este será exactamente el planteamiento, con la actualización por etapas de Target Net, y el uso de proyecciones razonables de los valores del estado futuro permitirá al modelo construir la estrategia adecuada. Solo así podremos obtener los resultados deseados.

Ahora, diremos unas palabras sobre el factor de descuento del valor de las recompensas futuras. Esta es nuestra herramienta para gestionar la previsión del modelo al construir la estrategia. Dicho hiperparámetro determina en gran medida el tipo de estrategia construida. El uso de un coeficiente próximo a "1" indicará al modelo que construya una estrategia larga. Acto seguido, el modelo elaborará estrategias de inversión a largo plazo.

Por el contrario, aproximando este parámetro a "0", haremos que el modelo se olvide de las recompensas futuras y se centre más en los beneficios a corto plazo. Construiremos una estrategia de scalping, por así decirlo. Obviamente, el marco temporal usado también influirá en el mantenimiento de la posición.

Resumiendo lo anterior:

El método de aprendizaje Q distribuido se basa en el aprendizaje Q clásico y lo complementa.
Como modelo se utilizará una red neuronal.
Al entrenar el modelo, aproximaremos la distribución de la probabilidad de la recompensa esperada por pasar a un nuevo estado según el par estado-acción.
La distribución se representará usando un conjunto de cuantiles de un rango de recompensa fijo.
El número de cuantiles y el rango de valores posibles vendrán determinados por los hiperparámetros.
La distribución para cada acción posible estará representada por el mismo vector de probabilidad.
Para normalizar la distribución de probabilidad, utilizaremos la función SoftMax en el contexto de cada acción individual.
El entrenamiento del modelo se basará en la ecuación de Bellman.
El enfoque probabilístico del problema requerirá el uso de LogLoss como función de pérdida.
Para estabilizar el proceso de aprendizaje, se usará la heurística del algoritmo de aprendizaje Q original (Target Net, búfer de reproducción de la experiencia).

Y como siempre, a la parte teórica le seguirá la aplicación práctica del enfoque usando MQL5.

2. Implementación usando MQL5

Al comenzar a aplicar el método de aprendizaje Q distribuido usando MQL5, deberemos realizar un plan de trabajo. Como hemos mencionado en la parte teórica del artículo, el método se basará en el algoritmo de aprendizaje Q original. Ya hemos aplicado este algoritmo anteriormente, por lo que resultará lógico crear un nuevo asesor basado en el asesor previamente implementado.

El uso del enfoque probabilístico requerirá cambios en el bloque de transmisión de valores objetivo del modelo.

A la salida del modelo, tendremos que normalizar los datos usando la función SoftMax. Esta función ya se introdujo y aplicó en el artículo de Policy Gradient. En el artículo mencionado, también normalizamos las probabilidades. En aquel momento, hablábamos de probabilidades de elección de acciones, así que normalizamos los datos en toda la capa neuronal. Ahora tendremos que normalizar las probabilidades de distribución de cada acción por separado. Esto implicará que no podremos utilizar la clase CNeuronSoftMaxOCL creada anteriormente en su forma pura.

En este caso, tendremos dos opciones: podemos crear una nueva clase o actualizar una ya existente. Nos decantamos por la segunda opción. Recuerde la estructura de la clase creada anteriormente.

class CNeuronSoftMaxOCL    :  public CNeuronBaseOCL
  {
protected:
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return true; }

public:
                     CNeuronSoftMaxOCL(void) {};
                    ~CNeuronSoftMaxOCL(void) {};
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);   
   virtual bool      calcOutputGradients(CArrayFloat *Target, float& error) override;
   //---
   virtual int       Type(void) override  const   {  return defNeuronSoftMaxOCL; }
  };

Lo primero que haremos será añadir la variable para almacenar el número de vectores normalizados, iHeads, así como el método para especificar este parámetro, SetHeads. Por defecto, se indicará 1 vector, que se corresponderá con la normalización de los datos dentro de toda la capa.

class CNeuronSoftMaxOCL    :  public CNeuronBaseOCL
  {
protected:
   uint              iHeads;
.........
.........
public:
                     CNeuronSoftMaxOCL(void) : iHeads(1) {};
                    ~CNeuronSoftMaxOCL(void) {};
.........
.........
   virtual void      SetHeads(int heads)  { iHeads = heads; }
.........
.........
  };

Como ya sabemos, añadir una nueva variable no cambiará por sí mismo la lógica de los métodos de la clase: luego deberemos introducir cambios en el algoritmo de los métodos. En primer lugar, nos interesarán los métodos de pasada directa e inversa. El método feedForward se encargará de la pasada directa. Permítanme recordarles que el método anterior solo organizará el algoritmo auxiliar para llamar al núcleo del programa OpenCL correspondiente: todos los cálculos se efectuarán en modo multihilo en el lado OpenCL del contexto. Por lo tanto, antes de realizar cambios en las operaciones de cola del kernel, primero deberemos realizar cambios en el lado OpenCL del programa.

Reflexionemos un poco. Una característica especial de la función SoftMax es la normalización de los datos de manera que la suma del vector completo de resultados sea igual a "1". Permítame recordarle la fórmula matemática de la función.

SoftMax

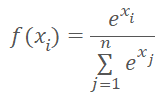
Como podrá ver, para normalizar los datos se usa la suma de los valores exponenciales del vector completo de datos sin procesar. Utilizando un array de datos local, hemos organizado la transmisión de datos entre los hilos individuales de un único kernel, lo cual nos ha permitido crear una implementación multihilo de esta función en el lado OpenCL del contexto. El algoritmo que hemos creado se ejecutará en un espacio de tareas unidimensional y normalizará los valores dentro de un único vector. Para resolver los problemas del nuevo algoritmo, tendremos que dividir el volumen total de datos sin procesar en varias partes iguales, y luego normalizar cada parte por separado. El número actual de estas piezas, desconocido, podría suponer una cierta complicación,

pero también hay una "cara positiva de la moneda": la normalización de cada unidad individual podrá realizarse independientemente de las demás, y encajará perfectamente con nuestro concepto de computación multihilo. Y esto significará que podremos ejecutar ejemplares adicionales de un kernel creado previamente para normalizar datos distribuidos.

Solo nos quedará asignar el volumen total de datos sin procesar y los búferes de resultados a los bloques correspondientes. Como ya hemos mencionado, antes ejecutábamos el kernel en un espacio de tareas unidimensional. La tecnología OpenCL nos permite usar un espacio de tareas tridimensional. En este caso, la tercera dimensión sería innecesaria. La segunda dimensión, en cambio, podremos utilizarla para identificar la unidad de normalización.

Así, al añadir otra dimensión del espacio de tareas, implementaremos la posibilidad de realizar la normalización distribuida en la clase SoftMax_FeedForward creada anteriormente, eso sí, seguirá habiendo cambios en el código del kernel, aunque serán poco significativos. Al fin y al cabo, tendremos que añadir el procesamiento del espacio de tareas de la segunda dimensión al algoritmo del kernel.

Los parámetros del kernel permanecen inalterados. En ellas transmitiremos los punteros a los búferes de datos, así como el tamaño del vector de normalización de datos.

__kernel void SoftMax_FeedForward(__global float *inputs,
                                  __global float *outputs,
                                  const uint total)
  {
   uint i = (uint)get_global_id(0);
   uint l = (uint)get_local_id(0);
   uint h = (uint)get_global_id(1);
   uint ls = min((uint)get_local_size(0), (uint)256);
   uint shift_head = h * total;

En el cuerpo del kernel, solicitaremos inmediatamente los identificadores de los hilos en ambas dimensiones del espacio de tareas. Estos definirán el volumen de trabajo realizado por el hilo actual y los desplazamientos en los búferes de datos de los elementos que se van a procesar. La primera dimensión nos indicará el lugar que ocupa el hilo en el algoritmo de normalización de datos, mientras que a partir de la segunda dimensión, determinaremos el desplazamiento en los búferes de datos. Hemos resaltado las líneas añadidas en el código anterior.

A continuación, en nuestro algoritmo de kernel se realizará un ciclo por la primera etapa de la suma de los valores exponenciales de los datos sin procesar. Aquí realizaremos una corrección del desplazamiento hasta el primer elemento del bloque de datos de origen normalizado (resaltado en el código).

Tenga en cuenta que solo utilizaremos el desplazamiento para el búfer de datos de origen global, sin tener en cuenta el conjunto de datos locales. La cuestión es que cada grupo de trabajo trabajará de forma aislada y utilizará su propio conjunto de datos locales.

   __local float temp[256];
   uint count = 0;
   if(l < 256)
      do
        {
         uint shift = shift_head + count * ls + l;
         temp[l] = (count > 0 ? temp[l] : 0) + (shift < ((h + 1) * total) ? exp(inputs[shift]) : 0);
         count++;
        }
      while((count * ls + l) < total);
   barrier(CLK_LOCAL_MEM_FENCE);

En el bloque anterior recogimos partes de la suma total en los elementos del array local. A continuación, se realizará un ciclo de consolidación de la suma total de los valores del array local. Aquí solo trabajaremos con un array local. Este proceso resultará completamente independiente de la segunda dimensión de nuestro espacio de tareas y permanecerá inalterado.

   count = ls;
   do
     {
      count = (count + 1) / 2;
      if(l < 256)
         temp[l] += (l < count && (l + count) < total ? temp[l + count] : 0);
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);
//---
   float sum = temp[0];

Al final del kernel, normalizaremos los datos sin procesar y almacenaremos el valor resultante en el búfer de resultados. Aquí, como en el primer bucle, utilizaremos el desplazamiento en los búferes de datos globales calculado anteriormente.

   if(sum != 0)
     {
      count = 0;
      while((count * ls + l) < total)
        {
         uint shift = shift_head + count * ls + l;
         if(shift < ((h + 1) * total))
            outputs[shift] = exp(inputs[shift] / 10) / (sum + 1e-37f);
         count++;
        }
     }
  }

Luego utilizaremos un enfoque similar al realizar cambios en el kernel de distribución de gradiente a la capa SoftMax_HiddenGradient anterior. Solo añadiremos el desplazamiento en los búferes de datos globales sin cambiar el algoritmo general del kernel.

__kernel void SoftMax_HiddenGradient(__global float* outputs,
                                     __global float* output_gr,
                                     __global float* input_gr)
  {
   size_t i = get_global_id(0);
   size_t outputs_total = get_global_size(0);
   size_t h = get_global_id(1);
   uint shift = h * outputs_total;
   float output = outputs[shift + i];
   float result = 0;
   for(int j = 0; j < outputs_total ; j++)
      result += outputs[shift + j] * output_gr[shift + j] * ((float)(i == j) - output);
   input_gr[shift + i] = result;
  }

No realizaremos ningún cambio en el kernel para determinar la desviación respecto a la distribución de referencia SoftMax_OutputGradient. Como este kernel determinará la desviación en un elemento de secuencia concreto, y dará absolutamente igual de qué unidad forme parte el elemento individual.

__kernel void SoftMax_OutputGradient(__global float* outputs,
                                     __global float* targets,
                                     __global float* output_gr)
  {
   size_t i = get_global_id(0);
   output_gr[i] = targets[i] / (outputs[i] + 1e-37f);
  }

Con esto daremos por concluido nuestro trabajo en el lado OpenCL del programa, así que podemos volver al código de nuestra clase CNeuronSoftMaxOCL. En primer lugar, hemos introducido cambios en el kernel de pasada directa. De forma similar, introduciremos cambios en los métodos de nuestra clase.

No añadiremos ni cambiaremos parámetros en los kernels. Como consecuencia, el algoritmo de preparación de datos y la llamada al kernel permanecerán inalterados. Los únicos cambios afectarán a la especificación del espacio de tareas.

Primero definiremos la dimensionalidad del vector de normalización de datos. Se podrá determinar fácilmente dividiendo el tamaño del búfer de resultados por el número de vectores a normalizar. Después almacenaremos el valor resultante en la variable local tamaño, y rellenaremos inmediatamente el array del espacio de tareas global_work_size. En la primera dimensión, especificaremos el tamaño del vector de normalización calculado anteriormente, mientras que en la segunda dimensión, especificaremos el número de estos vectores.

Para poder sincronizar los hilos e intercambiar datos entre ellos, crearemos previamente un grupo de trabajo igual al espacio de tareas global. Al fin y al cabo, hemos normalizado los datos dentro del búfer de datos al completo. Ahora la situación resulta un poco distinta, y tenemos varios bloques individuales en el búfer de datos para normalizar. Al construir el kernel de pasada directa, hemos observado que el trabajo con el array de datos local no cambia. Esto es posible gracias a que hemos planeado asignar la normalización de cada vector a un grupo de trabajo independiente. Por consiguiente, en este caso, necesitaremos crear un array del espacio de tareas local_work_size aparte del grupo local.

Las dimensiones del espacio de tareas global y local deberán ser las mismas. En consecuencia, necesitaremos definir un espacio de tareas local bidimensional. Además, el número de hilos globales deberá ser múltiplo del número de hilos locales en cada dimensión individual del espacio de tareas.

Antes, especificábamos el espacio tareas global en el tamaño de un vector normalizable en la primera dimensión y el número de estos vectores en la segunda dimensión. En cada grupo de trabajo, tenemos previsto normalizar solo un vector. Entonces lo lógico sería especificar también el tamaño de un vector normalizado en la primera dimensión del espacio de tareas local, mientras que en la segunda dimensión indicaremos "1", que se corresponde con el vector.

A continuación, le mostraremos el código modificado para el método feedForward. Todos los cambios han sido resaltados a color. Como podrá ver, no son muchos, pero resulta vital tener en cuenta todos los puntos clave.

bool CNeuronSoftMaxOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!OpenCL || !NeuronOCL)
      return false;
   uint global_work_offset[2] = {0, 0};
   uint size = Output.Total() / iHeads;
   uint global_work_size[2] = { size, iHeads };
   uint local_work_size[2] = { size, 1 };
   OpenCL.SetArgumentBuffer(def_k_SoftMax_FeedForward, def_k_softmaxff_inputs, NeuronOCL.getOutputIndex());
   OpenCL.SetArgumentBuffer(def_k_SoftMax_FeedForward, def_k_softmaxff_outputs, getOutputIndex());
   OpenCL.SetArgument(def_k_SoftMax_FeedForward, def_k_softmaxff_total, size);
   if(!OpenCL.Execute(def_k_SoftMax_FeedForward, 2, global_work_offset, global_work_size, local_work_size))
     {
      printf("Error of execution kernel SoftMax FeedForward: %d", GetLastError());
      return false;
     }
//---
   return true;
  }

Hemos realizado cambios similares en el método de distribución del gradiente de error a la capa anterior calcInputGradients. Solo con este método hemos evitado crear grupos de trabajo.

bool CNeuronSoftMaxOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(NeuronOCL) == POINTER_INVALID)
      return false;
   uint global_work_offset[2] = {0, 0};
   uint size = Output.Total() / iHeads;
   uint global_work_size[2] = {size, iHeads};
   OpenCL.SetArgumentBuffer(def_k_SoftMax_HiddenGradient, def_k_softmaxhg_input_gr, NeuronOCL.getGradientIndex());
   OpenCL.SetArgumentBuffer(def_k_SoftMax_HiddenGradient, def_k_softmaxhg_output_gr, getGradientIndex());
   OpenCL.SetArgumentBuffer(def_k_SoftMax_HiddenGradient, def_k_softmaxhg_outputs, getOutputIndex());
   if(!OpenCL.Execute(def_k_SoftMax_HiddenGradient, 2, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel SoftMax InputGradients: %d", GetLastError());
      return false;
     }
//---
   return true;
  }

La adición de la normalización distribuida será una característica de diseño y deberá reflejarse en los métodos de archivo del robot. Vamos a continuar con la clase CNeuronSoftMaxOCL. Debemos decir que no hemos creado previamente los métodos de trabajo con archivos para esta clase. La funcionalidad de los métodos similares de la clase padre era suficiente para nosotros, pero añadir una nueva variable cuyo valor necesitamos almacenar para restablecer correctamente el funcionamiento del objeto requiere que redefinamos dichos métodos.

Como siempre, empezaremos con el método de almacenamiento de datos Save. Su algoritmo es bastante simple. En los parámetros, el método obtendrá el manejador del archivo para escribir los datos. Normalmente, estos métodos empiezan comprobando que el manejador obtenido sea correcto. No es que vayamos a crear un bloque de controles: en su lugar, llamaremos al mismo método de la clase padre y le transmitiremos el manejador resultante. Este enfoque nos permitirá resolver dos tareas con una sola línea de código. Todos los controles necesarios ya estarán implementados en el método de la clase padre, lo cual significa que tendrán una función de control. Asimismo, implementaremos el almacenamiento de todos los objetos y variables heredados. Como consecuencia, también se cumplirá la función de almacenamiento de datos. Solo tendremos que comprobar el resultado del método de la clase padre para hacernos una idea del estado de la funcionalidad especificada.

Una vez que el método de la clase padre se haya ejecutado con éxito, todo lo que deberemos hacer es guardar el valor de la nueva variable y finalizar el método.

bool CNeuronSoftMaxOCL::Save(const int file_handle)
  {
   if(!CNeuronBaseOCL::Save(file_handle))
      return false;
   if(FileWriteInteger(file_handle, iHeads) <= 0)
      return false;
//---
   return true;
  }

El método de carga de datos CNeuronSoftMaxOCL está construido de forma casi idéntica. En él, solo hemos añadido un control para el número mínimo de vectores normalizables.

bool CNeuronSoftMaxOCL::Load(const int file_handle)
  {
   if(!CNeuronBaseOCL::Load(file_handle))
      return false;
   iHeads = (uint)FileReadInteger(file_handle);
   if(iHeads <= 0)
      iHeads = 1;
//---
   return true;
  }

Con esto damos por finalizado nuestro trabajo con la clase CNeuronSoftMaxOCL. Solo tendremos que añadir la posibilidad de especificación del número de vectores normalizados por parte del usuario. No realizaremos ningún cambio en el objeto de la descripción de la capa neuronal. Para especificar el número de vectores normalizados, por otra parte, utilizaremos el parámetro step. En el método de inicialización de la red neuronal CNet::Create, al crear la capa SoftMax, añadiremos la transmisión del parámetro especificado al ejemplar creado de la clase CNeuronSoftMaxOCL. Los cambios se destacarán en el código siguiente.

void CNet::Create(CArrayObj *Description)
  {
.........
.........
//---
   for(int i = 0; i < total; i++)
     {
.........
.........
      if(!!opencl)
        {
.........
.........
         CNeuronSoftMaxOCL *softmax = NULL;
         switch(desc.type)
           {
.........
.........
            case defNeuronSoftMaxOCL:
               softmax = new CNeuronSoftMaxOCL();
               if(!softmax)
                 {
                  delete temp;
                  return;
                 }
               if(!softmax.Init(outputs, 0, opencl, desc.count, desc.optimization, desc.batch))
                 {
                  delete softmax;
                  delete temp;
                  return;
                 }
               softmax.SetHeads(desc.step);
               if(!temp.Add(softmax))
                 {
                  delete softmax;
                  delete temp;
                  return;
                 }
               softmax = NULL;
               break;
.........
.........
           }
        }
.........
.........
//---
   return;
  }

Para aplicar este método no será necesario modificar la arquitectura de la red neuronal.

El proceso de aprendizaje del modelo se implementará en el asesor experto "DistQ-learning.mq5". Este asesor se creó a partir del asesor "Q-learning.mq5", utilizado para entrenar el modelo con el método de aprendizaje Q original.

El algoritmo de aprendizaje Q distribuido implicará la introducción de hiperparámetros adicionales que definirán el rango de recompensas esperadas y el número de cuantiles de la distribución de probabilidad.

En la implementación propuesta, hemos abordado la cuestión desde un ángulo diferente. Al igual que en las pruebas anteriores, crearemos el modelo usando la herramienta NetCreator . Luego determinaremos el número de cuantiles según el tamaño de la capa de resultados del modelo. Obviamente, teniendo en cuenta el número de acciones posibles. Este se especifica usando el parámetro Action del asesor.

int                  Actions     =  3;

En el proceso de aprendizaje, necesitaremos hacer coincidir un valor de recompensa específico del entorno con un cuantil concreto. Para ello, partiremos de los supuestos que enumeraremos a continuación. La política de recompensas previamente desarrollada preverá recompensas tanto positivas como negativas. Recompensas y multas, por así decirlo. Vamos a suponer que la mediana del vector se corresponderá con una recompensa nula. Para estimar el tamaño del cuantil en la dimensión natural de la recompensa, introduciremos el parámetro externo Step.

input double               Step = 5e-4;

Los demás parámetros externos del asesor permanecerán inalterados.

En la función de inicialización OnInit del asesor, cuando el modelo se haya cargado correctamente, definiremos el número de cuantiles según el tamaño de la capa neuronal de la salida del modelo y el número del cuantil mediano.

int OnInit()
  {
.........
.........
//---
   float temp1, temp2;
   if(!StudyNet.Load(FileName + ".nnw", dError, temp1, temp2, dtStudied, false) ||
      !TargetNet.Load(FileName + ".nnw", dError, temp1, temp2, dtStudied, false))
      return INIT_FAILED;
   if(!StudyNet.TrainMode(true))
      return INIT_FAILED;
//---
   if(!StudyNet.GetLayerOutput(0, TempData))
      return INIT_FAILED;
   HistoryBars = TempData.Total() / 12;
   StudyNet.getResults(TempData);
   action_dist = TempData.Total() / Actions;
   if(action_dist <= 0)
      return INIT_PARAMETERS_INCORRECT;
   action_midle = (action_dist + 1) / 2;
//---
.........
.........
//---
   return(INIT_SUCCEEDED);
  }

Después pasaremos a la función de aprendizaje del modelo. El bloque de preparación de datos no se modificará en este caso. Al fin y al cabo, no vamos a cambiar en absoluto los datos de la muestra de entrenamiento. Los cambios solo afectarán al bloque de resultados objetivo para predecir la recompensa prevista.

En primer lugar, prepararemos un vector para el valor proyectado del estado futuro. Este vector contendrá 3 elementos: un valor para cada acción. Para calcular los valores vectoriales, utilizaremos operaciones vectoriales. Primero transferiremos el búfer de resultados de Target Net a la matriz de filas. A continuación, reformatearemos la matriz en una matriz tabular de 3 filas: una fila por cada acción. En cada fila, encontraremos el elemento con mayor probabilidad, convirtiendo a continuación los cuantiles de los elementos máximos en la expresión natural de la recompensa.

void Train(void)
  {
//---
.........
.........
//---
   for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++)
     {
.........
.........
      for(int batch = 0; batch < (Batch * UpdateTarget); batch++)
        {
.........
.........
//---
         vectorf add = vectorf::Zeros(Actions); 
         if(use_target)
           {
            if(!TargetNet.feedForward(GetPointer(State2), 12, true))
               return;
            TargetNet.getResults(TempData);
            vectorf temp;
            TempData.GetData(temp);
            matrixf target = matrixf::Zeros(1, temp.Size());
            if(!target.Row(temp, 0) || !target.Reshape(Actions, action_dist))
               return;
            add = DiscountFactor * (target.ArgMax(1) - action_midle) * Step;
           }

Una vez determinado el valor previsto del estado futuro, podremos preparar un búfer de valores objetivo para nuestro modelo. Primero, realizaremos un pequeño trabajo preparatorio. Para ello, rellenaremos el búfer de recompensa con valores cero y determinaremos el beneficio potencial del estado actual del sistema a 1 vela hacia adelante.

         Rewards.BufferInit(Actions * action_dist, 0);
         double reward = Rates[i].close - Rates[i].open;

Los siguientes pasos dependerán de la dirección de la vela. Si la vela es alcista, daremos una recompensa positiva a la acción de compra y una recompensa negativa aumentada a la acción de venta. Además, daremos una recompensa negativa por "estar fuera del mercado" como penalización por el beneficio no realizado. Asimismo, añadiremos a la recompensa obtenida el valor del coste del estado futuro calculado anteriormente. Pero si antes al construir el algoritmo original de aprendizaje Q, en el búfer de variables objetivo especificábamos las recompensas como expresión natural, ahora definiremos el cuantil de la recompensa de cada acción, anotando la probabilidad "1" del suceso correspondiente. Las probabilidades nulas permanecerán en los elementos restantes de la memoria intermedia.

         if(reward >= 0)
           {
            int rew = (int)fmax(fmin((2 * reward + add[0]) / Step + action_midle, action_dist - 1), 0);
            if(!Rewards.Update(rew, 1))
               return;
            rew = (int)fmax(fmin((-5 * reward + add[1]) / Step + action_midle, action_dist - 1), 0) + action_dist;
            if(!Rewards.Update(rew, 1))
               return;
            rew = (int)fmax(fmin((-reward + add.Max()) / Step + action_midle, action_dist - 1), 0) + 2 * action_dist;
            if(!Rewards.Update(rew, 1))
               return;
           }

Para la vela bajista, el algoritmo será similar. La única diferencia será la recompensa y la penalización por las acciones de compra y venta.

         else
           {
            int rew = (int)fmax(fmin((5 * reward + add[0]) / Step + action_midle, action_dist - 1), 0);
            if(!Rewards.Update(rew, 1))
               return;
            rew = (int)fmax(fmin((-2 * reward + add[1]) / Step + action_midle, action_dist - 1), 0) + action_dist;
            if(!Rewards.Update(rew, 1))
               return;
            rew = (int)fmax(fmin((reward + add.Max()) / Step + action_midle, action_dist - 1), 0) + 2 * action_dist;
            if(!Rewards.Update(rew, 1))
               return;
           }

El resto del código de la función permanecerá inalterado, al igual que todo el código asesor no descrito aquí. Podrá encontrar el código completo del asesor en el archivo adjunto.

3. Simulación

Utilizando el asesor creado anteriormente, entrenaremos un modelo compuesto por:

3 capas convolucionales de preprocesamiento,
3 capas ocultas totalmente conectadas de 1000 neuronas cada una,
1 capa de toma de decisiones totalmente conectada de 45 neuronas (15 neuronas por 3 distribuciones de probabilidad de las acciones),
1 capa SoftMax para normalizar las distribuciones de probabilidad.

El entrenamiento se basará en los datos históricos de los últimos 2 años del instrumento EURUSD. Los datos procederán del marco temporal H1. La lista de indicadores utilizados y sus parámetros permanecerán invariables a lo largo de toda la serie.

El modelo entrenado se probará en el simulador de estrategias con los datos históricos de las 2 últimas semanas no incluidas en la muestra de entrenamiento. De este modo, preservaremos la pureza del experimento, y el modelo se probará con nuevos datos.

Para probar el modelo en el simulador de estrategias, crearemos el asesor experto "DistQ-learning-test.mq5". Este asesor será casi una copia completa de EA "Q-learning-test.mq5", con el que probamos el modelo entrenado por el método de aprendizaje Q original. El único cambio en el código de asesor será la adición de la función de selección de acciones GetAction.

En los parámetros, la función obtendrá el puntero al búfer de la distribución de probabilidad resultante de la evaluación de la situación actual por parte del modelo. No olvidemos que este búfer contiene las distribuciones de probabilidad para todas las acciones posibles. Para facilitar el tratamiento de los datos, transferiremos los valores del búfer a una matriz, y cambiaremos el formato de la matriz al formato tabular con un número de filas igual al número de acciones posibles del agente.

A continuación, determinaremos los cuantiles con la recompensa más probable para cada acción individual,

int GetAction(CBufferFloat* probability)
  {
   vectorf prob;
   if(!probability.GetData(prob))
      return -1;
   matrixf dist = matrixf::Zeros(1, prob.Size());
   if(!dist.Row(prob, 0))
      return -1;
   if(!dist.Reshape(Actions, prob.Size() / Actions))
      return -1;
   prob = dist.ArgMax(1);

comparando después los rendimientos esperados de compra y venta en el estado actual. Si el rendimiento esperado es igual, elegiremos la acción con mayor probabilidad de obtener una recompensa.

   if(prob[0] == prob[1])
     {
      if(prob[2] > prob[0])
         return 2;
      if(dist[0, (int)prob[0]] >= dist[1, (int)prob[1]])
         return 0;
      else
         return 1;
     }

En caso contrario, seleccionaremos la acción con la máxima recompensa esperada.

//---
   return (int)prob.ArgMax();
  }

Como podemos ver, en este caso estaremos utilizando una estrategia codiciosa de selección de acciones con rendimientos máximos.

Podrá encontrar el código completo del asesor en el archivo adjunto.

Según los resultados del funcionamiento del asesor de prueba en el simulador de estrategias de MetaTrader 5 durante las 2 semanas analizadas con respecto a las señales del modelo, hemos obtenido un beneficio de alrededor de 20 dólares. Recordemos que todas las operaciones se han realizado con un lote mínimo fijo. En el siguiente gráfico podemos apreciar fácilmente una clara tendencia al alza del balance.

Prueba del modelo en el simulador de estrategias

Prueba del modelo de aprendizaje Q distribuido

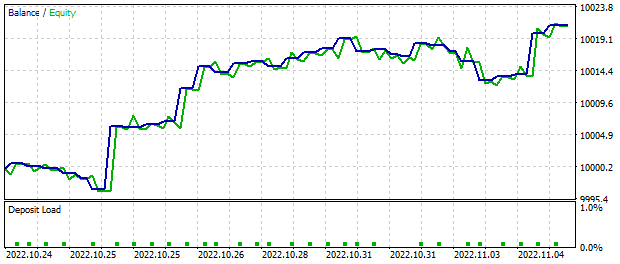
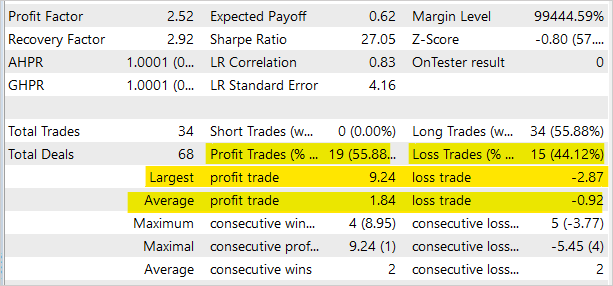
Las estadísticas comerciales muestran casi un 56% de transacciones rentables. Sin embargo, tenga en cuenta que el asesor experto ha sido creado exclusivamente para probar el modelo en el simulador de estrategias y no resulta adecuado para el comercio real en los mercados financieros.

En el archivo adjunto, encontrará el código completo de todos los programas usados en el artículo.

Conclusión

En este artículo, nos hemos familiarizado con otro algoritmo para el aprendizaje de modelos con refuerzo: el aprendizaje Q distribuido. Como resultado de la utilización de este algoritmo, el modelo analiza la distribución de probabilidad de las recompensas al realizar una acción determinada en un estado concreto del entorno. Estudiar la distribución de probabilidades en lugar de predecir la recompensa media ofrece más información sobre la naturaleza de la recompensa y mejora la estabilidad del aprendizaje del modelo. Además, conocer la distribución de probabilidad de los rendimientos esperados nos permite evaluar mejor sus riesgos al comerciar.

La prueba del modelo entrenado en el simulador de estrategias de MetaTrader 5 ha demostrado la potencial rentabilidad del enfoque. El algoritmo merece una mayor elaboración posterior, y ha justificado su uso a la hora de construir soluciones comerciales.

En el archivo adjunto, podrá encontrar el código completo de todos los programas y bibliotecas usados.

Enlaces

Programas usados en el artículo.

#	Nombre	Tipo	Descripción
1	DistQ-learning.mq5	Asesor	Asesor para la optimización de modelos
2	DistQ-learning-test.mq5	Asesor	Asesor Experto para probar modelos en el Simulador de Estrategias
3	NeuroNet.mqh	Biblioteca de clases	Biblioteca para organizar modelos de redes neuronales
4	NeuroNet.cl	Biblioteca	Biblioteca de código OpenCL para organizar modelos de redes neuronales
5	NetCreator.mq5	Asesor	Herramienta de construcción de modelos
6	NetCreatotPanel.mqh	Biblioteca de clases	Biblioteca de clases para crear una herramienta

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/11716

Archivos adjuntos |

Descargar ZIP

MQL5.zip (82.71 KB)

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores

Cómo trabajar con líneas usando MQL5

En este artículo, hablaremos sobre cómo trabajar con las líneas más importantes, como las líneas de tendencia, apoyo y resistencia, usando las herramientas de MQL5.

Características del Wizard MQL5 que debe conocer (Parte 04): Análisis Discriminante Lineal

El tráder moderno está casi siempre a la búsqueda de nuevas ideas, probando constantemente nuevas estrategias, modificándolas y descartando las que han fracasado. En esta serie de artículos, trataremos de demostrar que el Wizard MQL5 es la verdadera columna vertebral para un tráder en su búsqueda.

DoEasy. Elementos de control (Parte 26): Mejoramos el objeto WinForms "ToolTip" y comenzamos a desarrollar "ProgressBar"

En este artículo, completaremos el desarrollo del control ToolTip y comenzaremos a desarrollar el objeto WinForms ProgressBar. A medida que trabajemos en los objetos, desarrollaremos una funcionalidad universal para animar los controles y sus componentes.

Aprendizaje automático y Data Science (Parte 9): Algoritmo de k vecinos más próximos (KNN)

Se trata de un algoritmo perezoso que no aprende a partir de una muestra de entrenamiento, sino que almacena todas las observaciones disponibles y clasifica los datos en cuanto recibe una nueva muestra. A pesar de su sencillez, este método se usa en muchas aplicaciones del mundo real.