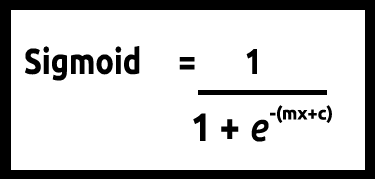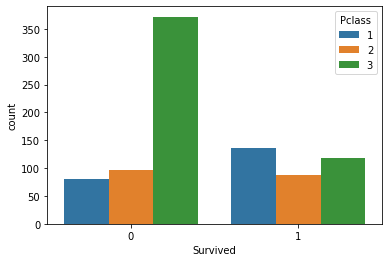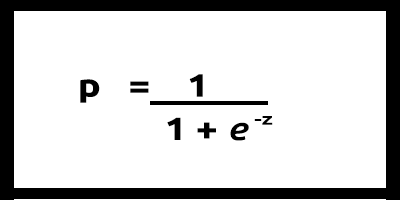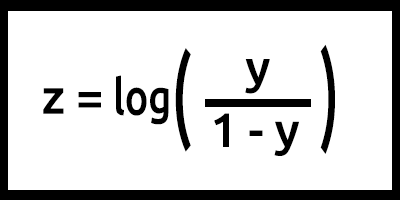
Aprendizaje automático y Data Science (Parte 02): Regresión logística
A diferencia de la regresión lineal de la que hablamos en la parte 01, la regresión logística es un método de clasificación basado en la regresión lineal.
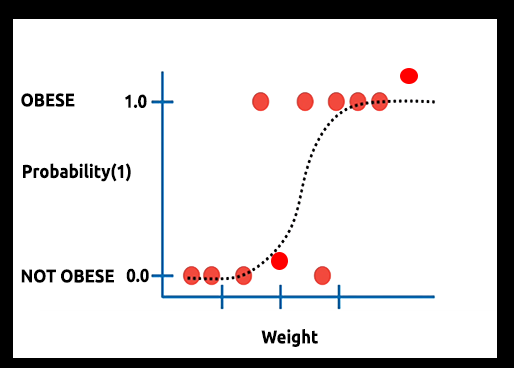
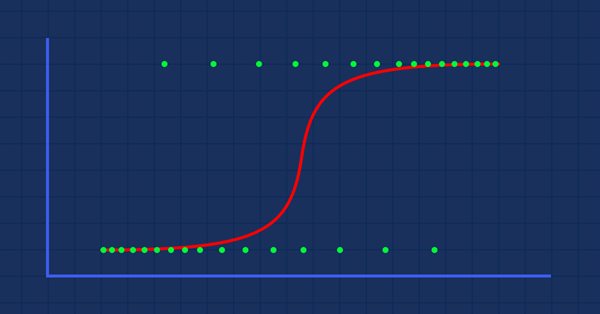
Teoría: Supongamos que dibujamos un gráfico que muestra la probabilidad de que alguien sea obeso frente a su peso.
En este caso, no podremos utilizar un modelo lineal, usaremos otra técnica para transformar esta línea en una curva S conocida como Sigmoide.
Como la Regresión Logística produce resultados en un formato binario que se usa para predecir el resultado de la variable dependiente categórica, el resultado deberá ser discreto/categórico como:
- 0 o 1
- Sí o No
- Verdadero o falso
- Alto o Bajo
- Comprar o vender
En la biblioteca que vamos a crear, ignoraremos otros valores discretos. Nos centraremos en el binario (0,1).
Como nuestros valores de y deben estar entre 0 y 1, nuestra línea deberá recortarse en 0 y 1. Esto puede lograrse usando la fórmula
Lo cual nos dará este gráfico
El modelo lineal se transmite a una función logística (sigmoide/p) =1/1+e^t donde t es el modelo lineal cuyo resultado son valores entre 0 y 1. Esto representa la probabilidad de que un punto de datos pertenezca a una clase.
En lugar de utilizar y de un modelo lineal como dependiente, su función se mostrará como " p" se utiliza como dependiente
p = 1/1+e^-(c+m1x1+m2x2+....+mnxn), caso de valores múltiples
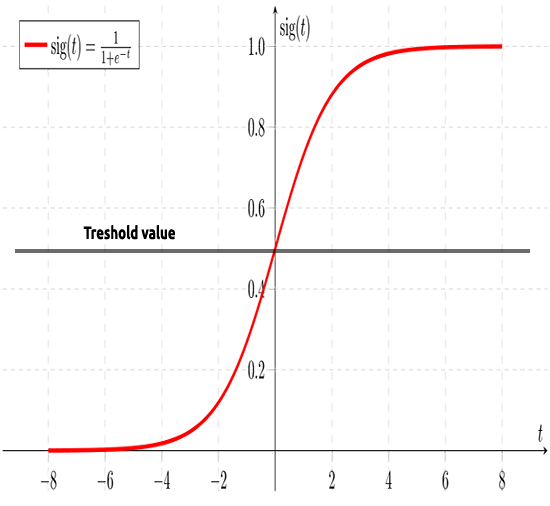
Como hemos dicho anteriormente, la curva sigmoidea tiene como objetivo convertir los valores infinitos en una salida en formato binario (0 o 1). Pero si tenemos un punto de datos situado en 0,8, ¿cómo podremos decidir si el valor es cero o uno? Aquí es donde entran en acción los valores umbral.
El umbral indica la probabilidad de ganar o perder, y está situado en 0,5 (el centro de 0 y 1).
Cualquier valor superior o igual a 0,5 se redondeará a uno, por lo que se considerará ganador, mientras que cualquier valor inferior a 0,5 se redondeará a 0, considerándose por consiguiente perdedor. En este punto, es el momento de ver la diferencia entre las regresiones lineal y logística.
La regresión lineal frente a la regresión logística
| Lineal | Regresión logística |
|---|---|
| Variable continua | Variable categórica |
| Resuelve los problemas de regresión | Resuelve los problemas de clasificación |
| El modelo tiene una ecuación recta | El modelo tiene una ecuación logística |
Antes de sumergirnos en lo referente a la codificación y los algoritmos de clasificación de datos, hay varios pasos que podrían ayudarnos a entender los datos y facilitarnos la construcción de nuestro modelo:
- Recogida y análisis de datos
- Limpieza de datos
- Comprobación de la exactitud
01: Recogida y análisis de datos
En esta sección, escribiremos un montón de código python para visualizar nuestros datos. Empezaremos importando las bibliotecas que vamos a utilizar para extraer y visualizar los datos en el cuaderno Jupyter.
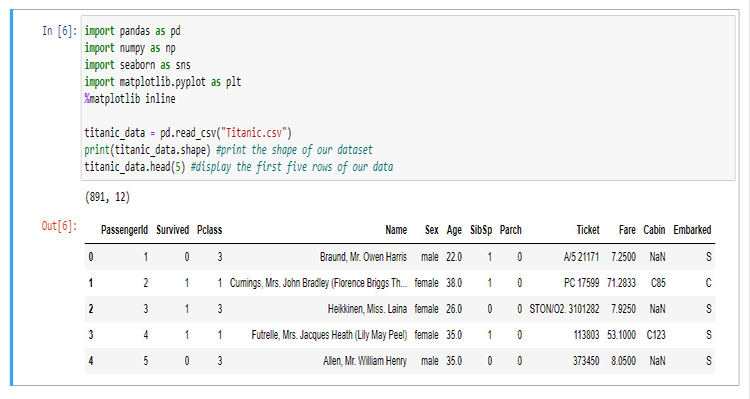
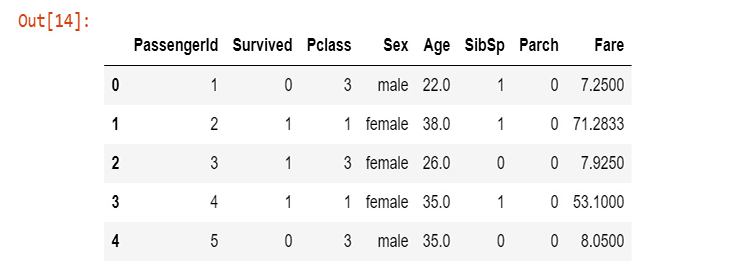
Para la construcción de nuestra biblioteca, utilizaremos los datos del Titanic: para los que no estén al tanto, nos referimos a los datos del accidente del barco que se hundió en el Atlántico Norte el 15 de abril de 1912 tras chocar con un iceberg, Wikipedia. Todos los códigos de Python y el conjunto de datos se pueden encontrar en mi GitHub, cuyo enlace se encuentra al final del artículo.
Las columnas significan
survival - Supervivencia (0 = No; 1 = Sí)
class - Clase del pasajero (1 = 1º; 2 = 2º; 3 = 3º)
name - Nombre
sex - Sexo
age - Edad
sibsp - Número de hermanos/cónyuges a bordo
parch - Número de padres/hijos a bordo
ticket - Número de billete
fare - Tarifa de pasajero
cabin - Cabina
embarked - Puerto de embarque (C = Cherburgo; Q = Queenstown; S = Southampton)
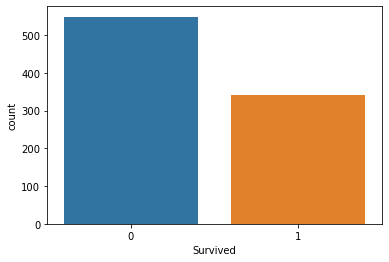
Ahora que tenemos nuestros datos recogidos y almacenados en la variable titanic_data, vamos a visualizar los datos en columnas, empezando por la columna de supervivencia.
sns.countplot(x="Survived", data = titanic_data)
salida
Esto nos dice que solo una minoría de los pasajeros sobrevivió al accidente, aproximadamente la mitad de los pasajeros que iban en el barco sobrevivieron.
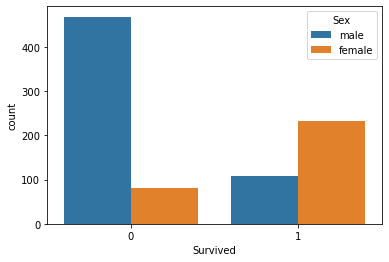
Vamos a visualizar el número de la supervivencia según el sexo
sns.countplot(x='Survived', hue='Sex', data=titanic_data)
Desconocemos qué sucedió con los hombres ese día, pero las mujeres sobrevivieron más del doble que ellos
Vamos a visualizar el número de la supervivencia según los grupos de clase
sns.countplot(x='Sobrevivido', hue='Pclass', data=titanic_data)
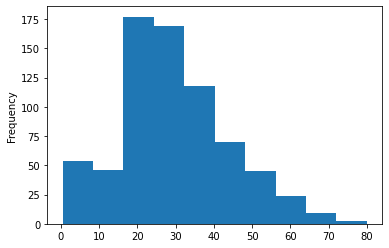
Vamos a dibujar el histograma de los grupos de edad de los pasajeros que estaban en el barco, aquí no podemos usar los gráficos de conteo para visualizar nuestros datos, ya que hay muchos valores de edad distintos en nuestro conjunto de datos que no están organizados.
titanic_data['Age'].plot.hist()Salida:
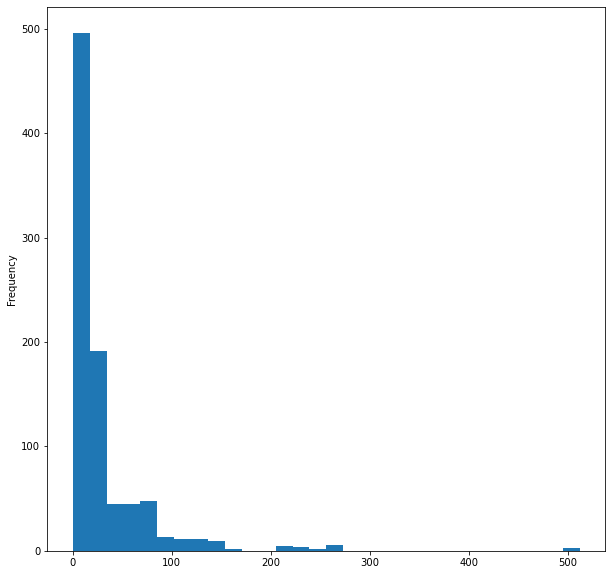
Por último, visualizaremos el histograma de la tarifa en el barco
titanic_data['Fare'].plot.hist(bins=30, figsize=(10,10))
Eso es todo en cuanto a la visualización de los datos, aunque hemos visualizado solo 5 columnas de 12 porque son columnas importantes, ahora vamos a limpiar nuestros datos.
02: Limpiando nuestros datos
Aquí, limpiaremos nuestros datos eliminando los valores NaN (perdidos) y evitando/eliminando las columnas innecesarias en el conjunto de datos.
Al usar la regresión logística es necesario tener valores dobles y enteros por lo que tendremos que evitar los valores string no significativos; en este caso, ignoraremos las siguientes columnas:
- La columna del nombre (no tiene ninguna información significativa)
- La columna de entradas (no tiene ningún sentido para la supervivencia del accidente)
- La columna de la cabina (tiene demasiados valores perdidos, incluso las primeras 5 filas lo demuestran)
- Los embarcados (nos parece irrelevante)
Para ello, abriremos el archivo CSV en WPS office y eliminaremos manualmente las columnas; podemos usar cualquier programa de hoja de cálculo de nuestra elección.
Después de eliminar las columnas usando una hoja de cálculo, visualizaremos los nuevos datos.
new_data = pd.read_csv(r'C:\Users\Omega Joctan\AppData\Roaming\MetaQuotes\Terminal\892B47EBC091D6EF95E3961284A76097\MQL5\Files\titanic.csv') new_data.head(5)
Salida:
Ahora tenemos los datos depurados, aunque todavía nos faltan los valores en la columna de la edad, por no mencionar que tenemos valores string en la columna del sexo. Vamos a arreglar el problema con un poco de código. Crearemos un codificador de etiquetas para convertir la línea con los hombres y las mujeres en 0 y 1 respectivamente.
void CLogisticRegression::LabelEncoder(string &src[],int &EncodeTo[],string members="male,female") { string MembersArray[]; ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(members,separator,MembersArray); //convert members list to an array ArrayResize(EncodeTo,ArraySize(src)); //make the EncodeTo array same size as the source array int binary=0; for(int i=0;i<ArraySize(MembersArray);i++) // loop the members array { string val = MembersArray[i]; binary = i; //binary to assign to a member int label_counter = 0; for (int j=0; j<ArraySize(src); j++) { string source_val = src[j]; if (val == source_val) { EncodeTo[j] = binary; label_counter++; } } Print(MembersArray[binary]," total =",label_counter," Encoded To = ",binary); } }
Para obtener la matriz fuente llamada src[] también hemos programado una función que permite obtener los datos de una columna específica en un archivo CSV y luego ponerlos en una matriz de valores string MembersArray[], vamos a comprobarlo:
void CLogisticRegression::GetDatatoArray(int from_column_number, string &toArr[]) { int handle = FileOpen(m_filename,FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI,m_delimiter); int counter=0; if (handle == INVALID_HANDLE) Print(__FUNCTION__," Invalid csv handle err=",GetLastError()); else { int column = 0, rows=0; while (!FileIsEnding(handle)) { string data = FileReadString(handle); column++; //--- if (column==from_column_number) //if column in the loop is the same as the desired column { if (rows>=1) //Avoid the first column which contains the column's header { counter++; ArrayResize(toArr,counter); toArr[counter-1]=data; } } //--- if (FileIsLineEnding(handle)) { rows++; column=0; } } } FileClose(handle); }
Dentro de nuestro testscript.mq5, así es como se llaman correctamente las funciones y se inicializa la biblioteca:
#include "LogisticRegressionLib.mqh"; CLogisticRegression Logreg; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- Logreg.Init("titanic.csv",","); string Sex[]; int SexEncoded[]; Logreg.GetDatatoArray(4,Sex); Logreg.LabelEncoder(Sex,SexEncoded,"male,female"); ArrayPrint(SexEncoded); }
Impresión de la salida, después de ejecutar con éxito el script,
total de hombres =577 Codificado a = 0
total de mujeres =314 Codificado a = 1
[ 0] 0 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 0 1 0 1 1 0 0 1 0 0 1 1 0 0 0 0 0 1 1 1 1 0 1 1 0 0 1 0 1 0 0 1 1 0 0 1 0 1 0 0 1 0 0 0 0 1 0 1 0 0 1 0 0 0
[ 75] 0 0 0 0 1 0 0 1 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 0 1 0 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 1 1 0 0 1 0 0 0 1 1 1 0 0 0 0 1 0 0
... ... ... ...
... ... ... ...
[750] 1 0 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 0 0 0 0 1 0 1 0 0 1 0 1 1 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 1 0 1 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0
[825] 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 0 0 0 1 1 0 1 1 0 0 0 0 1 0 0 1 1 0 0 0 1 1 0 1 0 0 1 0 1 1 0 0
Antes de codificar sus valores, tenemos que prestar atención a los miembros="hombre,mujer" en su argumento de función, el primer valor que aparezca en su línea será codificado como 0; como podemos ver, en la columna de los hombres aparece primero, por lo que todos los hombres serán codificados a 0 , y las mujeres serán codificadas a 1. Sin embargo, esta función no estará restringida a dos valores, podemos codificar todo lo que queramos, siempre que la línea tenga algún sentido para nuestros datos.
Valores perdidos
Si prestamos atención a la columna de la edad, veremos que hay valores que faltan. Los valores ausentes pueden deberse principalmente a una razón... la muerte. En nuestro conjunto de datos, esto hace imposible identificar la edad de un individuo; podemos identificar esas lagunas mirando el conjunto de datos, aunque eso podría llevarnos mucho tiempo, especialmente en conjuntos de datos grandes, ya que también estamos usando pandas para visualizar nuestros datos. Vamos a encontrar las filas que faltan en todas las columnas
titanic_data.isnull().sum()
La salida será:
PassengerId 0
Survived 0
Pclass 0
Sex 0
Age 177
SibSp 0
Parch 0
Fare 0
dtype: int64
De 891, 177 filas de nuestra columna de edad tienen valores perdidos (NAN).
Ahora, vamos a reemplazar los valores que faltan en nuestra columna, sustituyendo para ello los valores por la media de todos los valores.
void CLogisticRegression::FixMissingValues(double &Arr[]) { int counter=0; double mean=0, total=0; for (int i=0; i<ArraySize(Arr); i++) //first step is to find the mean of the non zero values { if (Arr[i]!=0) { counter++; total += Arr[i]; } } mean = total/counter; //all the values divided by their total number Print("mean ",MathRound(mean)," before Arr"); ArrayPrint(Arr); for (int i=0; i<ArraySize(Arr); i++) { if (Arr[i]==0) { Arr[i] = MathRound(mean); //replace zero values in array } } Print("After Arr"); ArrayPrint(Arr); }
Esta función encuentra la media de todos los valores no nulos y luego sustituye todos los valores nulos de la matriz por el valor medio.
La salida se da después de ejecutar con éxito la función. Como podemos ver, todos los valores cero han sido reemplazados con 30,0, que era la edad media de los pasajeros en el Titanic.
media de 30,0 antes de Arr
[ 0] 22.0 38.0 26.0 35.0 35.0 0.0 54.0 2.0 27.0 14.0 4.0 58.0 20.0 39.0 14.0 55.0 2.0 0.0 31.0 0.0 35.0 34.0 15.0 28.0 8.0 38.0 0.0 19.0 0.0 0.0
... ... ... ... ... ... ... ... ...
[840] 20.0 16.0 30.0 34.5 17.0 42.0 0 .0 35.0 28.0 0 .0 4.0 74.0 9.0 16.0 44.0 18.0 45.0 51.0 24.0 0 .0 41.0 21.0 48.0 0.0 24.0 42.0 27.0 31.0 0 .0 4.0
[870] 26.0 47.0 33.0 47.0 28.0 15.0 20.0 19.0 0 .0 56.0 25.0 33.0 22.0 28.0 25.0 39.0 27.0 19.0 0 .0 26.0 32.0
Después de Arr
[ 0] 22.0 38.0 26.0 35.0 35.0 30.0 54.0 2.0 27.0 14.0 4.0 58.0 20.0 39.0 14.0 55.0 2.0 30.0 31.0 30.0 35.0 34.0 15.0 28.0 8.0 38.0 30.0 19.0 30. 0 30.0
... ... ... ... ... ... ... ... ...
[840] 20.0 16.0 30.0 34.5 17.0 42.0 30.0 35.0 28.0 30.0 4.0 74.0 9.0 16.0 44.0 18.0 45.0 51.0 24.0 30.0 41.0 21.0 48.0 30.0 24.0 42.0 27.0 31.0 30.0 4.0
[870] 26.0 47.0 33.0 47.0 28.0 15.0 20.0 19.0 30.0 56.0 25.0 33.0 22.0 28.0 25.0 39.0 27.0 19.0 30.0 26.0 32.0
Construyendo del modelo de regresión logística
En primer lugar, vamos a construir nuestra regresión logística, donde tendremos una variable independiente y una variable dependiente. Más adelante, ampliaremos el modelo para la solución completa de nuestro problema.
Construiremos el modelo sobre dos variables Supervivencia frente a Edad, y averiguaremos cuáles son las posibilidades de que una persona sobreviva en función de su Edad.
Hasta ahora, sabemos que en el fondo del modelo logístico hay un modelo lineal. Empezaremos codificando las funciones que hacen posible el modelo lineal.
Coefficient_of_X() e y_intercept() estas funciones no son nuevas, las construimos en el primer artículo de esta serie; recomendamos su lectura para obtener más información sobre estas funciones y la regresión lineal en general.
double CLogisticRegression::y_intercept() { // c = y - mx return (y_mean-coefficient_of_X()*x_mean); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CLogisticRegression::coefficient_of_X() { double m=0; //--- { double x__x=0, y__y=0; double numerator=0, denominator=0; for (int i=0; i<ArraySize(m_xvalues); i++) { x__x = m_xvalues[i] - x_mean; //right side of the numerator (x-side) y__y = m_yvalues[i] - y_mean; //left side of the numerator (y-side) numerator += x__x * y__y; //summation of the product two sides of the numerator denominator += MathPow(x__x,2); } m = numerator/denominator; } return (m); }
Ahora, programaremos el modelo logístico a partir de la fórmula.
Tenga en cuenta que z también se denomina log-odds porque la inversa de la sigmoidea establece que z puede definirse como el logaritmo de la probabilidad de la etiqueta 1 (por ejemplo, "survived") dividido por la probabilidad de la etiqueta 0 (por ejemplo, "not survived"):
En este caso, y = mx+c (recuerda del modelo lineal).
Convirtiendo esto en código el resultado será,
double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1);
Preste atención a lo que hemos hecho aquí: en el valor de z, la fórmula es log(y/1-y), pero el código se escribe como log(y_)-log(1-y_); ¡Recuerde de las Leyes de los logaritmos en matemáticas! La división de logaritmos con la misma base da lugar a la resta de los exponentes, Leer.
Este es básicamente nuestro modelo cuando la fórmula está programada, pero hay muchas cosas que suceden dentro de nuestra función LogisticRegression() , aquí tenemos todo lo que hay dentro de la función:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7) { int arrsize = ArraySize(x); //the input array size double p_hat =0; //store the probability //--- int train_size = (int)MathCeil(arrsize*train_size_split); int test_size = (int)MathFloor(arrsize*(1-train_size_split)); ArrayCopy(m_xvalues,x,0,0,train_size); ArrayCopy(m_yvalues,y,0,0,train_size); //--- y_mean = mean(m_yvalues); x_mean = mean(m_xvalues); // Training our model in the background double c = y_intercept(), m = coefficient_of_X(); //--- Here comes the logistic regression model int TrainPredicted[]; double sigmoid = 0; ArrayResize(TrainPredicted,train_size); //resize the array to match the train size Print("Training starting..., train size=",train_size); for (int i=0; i<train_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); double odds_ratio = p_hat/(1-p_hat); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d ",i,m_xvalues[i],TrainPredicted[i]); } //--- Testing our model if (train_size_split<1.0) //if there is room for testing { ArrayRemove(m_xvalues,0,train_size); //clear our array ArrayRemove(m_yvalues,0,train_size); //clear our array from train data ArrayCopy(m_xvalues,x,0,train_size,test_size); //new values of x, starts from where the training ended ArrayCopy(m_yvalues,y,0,train_size,test_size); //new values of y, starts from where the testing ended Print("start testing...., test size=",test_size); ArrayResize(Predicted,test_size); //resize the array to match the test size for (int i=0; i<test_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); double odds_ratio = p_hat/(1-p_hat); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d , Original survival=%.1f ",i,m_xvalues[i],Predicted[i],m_yvalues[i]); } }
Ahora, vamos a entrenar y probar nuestro modelo en nuestro TestScript.mq5
double Age[]; Logreg.GetDatatoArray(5,Age); Logreg.FixMissingValues(Age); double y_survival[]; int Predicted[]; Logreg.GetDatatoArray(2,y_survival); Logreg.LogisticRegression(Age,y_survival,Predicted);
La salida de un script ejecutado con éxito será:
Training starting..., train size=624
0 Age =22.00 survival_Predicted =0
1 Age =38.00 survival_Predicted =0
... .... ....
622 Age =20.00 survival_Predicted =0
623 Age =21.00 survival_Predicted =0
start testing...., test size=267
0 Age =21.00 survival_Predicted =0
1 Age =61.00 survival_Predicted =1
.... .... ....
265 Age =26.00 survival_Predicted =0
266 Age =32.00 survival_Predicted =0
Genial. Nuestro modelo ya funciona y al menos podemos obtener los resultados de él, pero ¿hace el modelo buenas predicciones?
Tenemos que verificar su exactitud.
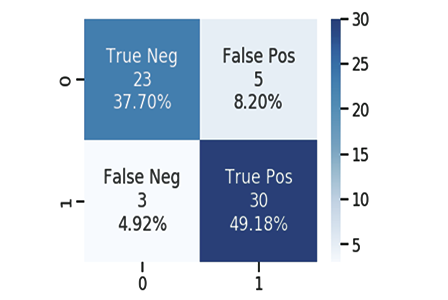
La matriz de confusión
Como todos sabemos, todo modelo bueno o malo puede hacer predicciones. Hemos creado un archivo CSV para las predicciones que nuestro modelo ha hecho junto con los valores originales de los datos de prueba sobre la supervivencia de los pasajeros: una vez más, 1 indica sobrevivió, 0 indica no sobrevivió.
Aquí vemos unas 10 columnas:
| Original | Predicción | |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 2 | 0 | 1 |
| 3 | 1 | 0 |
| 4 | 0 | 0 |
| 5 | 0 | 0 |
| 6 | 1 | 1 |
| 7 | 0 | 1 |
| 8 | 1 | 0 |
| 9 | 0 | 0 |
Calculamos la matriz de confusión usando:
- TP - Verdadero Positivo
- TN - Verdadero Negativo
- FP - Falso Positivo
- FN - Falso Negativo
Ahora bien, qué son estos valores?
TP (Verdadero Positivo)
Es cuando el valor original es positivo (1), y su modelo también predice positivo (1)
TN (Verdadero Negativo)
Es cuando el valor original es negativo (0), y su modelo también predice negativo (0)
FP (Falso Positivo)
Es cuando el valor original es negativo (0), pero su modelo predice un positivo (1)
FN (Falso Negativo)
Es cuando el valor original es positivo (1), pero su modelo predice un negativo (0)
Ahora que conocemos los valores, vamos a calcular la matriz de confusión para la muestra anterior como ejemplo
| Original | Predicción | TP/TN/FP/FN | |
|---|---|---|---|
| 0 | 0 | 0 | TN |
| 1 | 0 | 1 | FP |
| 2 | 0 | 1 | FP |
| 3 | 1 | 0 | FN |
| 4 | 0 | 0 | TN |
| 5 | 0 | 0 | TN |
| 6 | 1 | 1 | TP |
| 7 | 0 | 1 | FP |
| 8 | 1 | 0 | FN |
| 9 | 0 | 0 | TN |
La matriz de confusión se puede usar para calcular la precisión de nuestro modelo utilizando esta fórmula.
De nuestra tabla:
- TN = 4
- TP = 1
- FN = 2
- FP = 3
Precisión = 1 + 5 / 4 + 1 + 2 + 3
Precisión = 0,5
En este caso, nuestra precisión será del 50% (0,5*100% convirtiéndolo en porcentaje)
Ahora, ya entendemos cómo funciona la matriz de confusión 1X1. Es momento de convertirla en código y analizar la precisión de nuestro modelo en todo el conjunto de datos.
void CLogisticRegression::ConfusionMatrix(double &y[], int &Predicted_y[], double& accuracy) { int TP=0, TN=0, FP=0, FN=0; for (int i=0; i<ArraySize(y); i++) { if ((int)y[i]==Predicted_y[i] && Predicted_y[i]==1) TP++; if ((int)y[i]==Predicted_y[i] && Predicted_y[i]==0) TN++; if (Predicted_y[i]==1 && (int)y[i]==0) FP++; if (Predicted_y[i]==0 && (int)y[i]==1) FN++; } Print("Confusion Matrix \n ","[ ",TN," ",FP," ]","\n"," [ ",FN," ",TP," ] "); accuracy = (double)(TN+TP) / (double)(TP+TN+FP+FN); }
Regresemos ahora a nuestra función principal en la clase conocida como LogisticRegression(). Esta vez la convertiremos en una función doble que retornará la precisión del modelo; también vamos a reducir el número de métodos Print() pero añadiéndolos a una sentencia if, ya que no queremos imprimir los valores cada vez, a menos que deseemos depurar nuestra clase. Todos los cambios se resaltan en azul:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7) { double accuracy =0; //Accuracy of our Train/Testmodel int arrsize = ArraySize(x); //the input array size double p_hat =0; //store the probability //--- int train_size = (int)MathCeil(arrsize*train_size_split); int test_size = (int)MathFloor(arrsize*(1-train_size_split)); ArrayCopy(m_xvalues,x,0,0,train_size); ArrayCopy(m_yvalues,y,0,0,train_size); //--- y_mean = mean(m_yvalues); x_mean = mean(m_xvalues); // Training our model in the background double c = y_intercept(), m = coefficient_of_X(); //--- Here comes the logistic regression model int TrainPredicted[]; double sigmoid = 0; ArrayResize(TrainPredicted,train_size); //resize the array to match the train size Print("Training starting..., train size=",train_size); for (int i=0; i<train_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d ",i,m_xvalues[i],TrainPredicted[i]); } ConfusionMatrix(m_yvalues,TrainPredicted,accuracy); //be careful not to confuse the train predict values arrays printf("Train Model Accuracy =%.5f",accuracy); //--- Testing our model if (train_size_split<1.0) //if there is room for testing { ArrayRemove(m_xvalues,0,train_size); //clear our array ArrayRemove(m_yvalues,0,train_size); //clear our array from train data ArrayCopy(m_xvalues,x,0,train_size,test_size); //new values of x, starts from where the training ended ArrayCopy(m_yvalues,y,0,train_size,test_size); //new values of y, starts from where the testing ended Print("start testing...., test size=",test_size); ArrayResize(Predicted,test_size); //resize the array to match the test size for (int i=0; i<test_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d , Original survival=%.1f ",i,m_xvalues[i],Predicted[i],m_yvalues[i]); } ConfusionMatrix(m_yvalues,Predicted,accuracy); printf("Testing Model Accuracy =%.5f",accuracy); } return (accuracy); //Lastly, the testing Accuracy will be returned }
Si el script se ejecuta con éxito, veremos lo siguiente:
Training starting..., train size=624
Confusion matrix
[ 378 0 ]
[ 246 0 ]
Train Model Accuracy =0.60577
start testing...., test size=267
Confusion matrix
[ 171 0 ]
[ 96 0 ]
Testing Model Accuracy =0.64045
¡Hurra! Ahora podemos corroborar lo bueno que es nuestro modelo a través de los números, aunque la precisión del 64,045% en los datos de prueba no sea lo suficientemente buena como para utilizar el modelo en la realización de predicciones (en nuestra opinión), al menos por ahora, tenemos una biblioteca que podría ayudarnos a clasificar los datos utilizando la regresión logística.
Seguimos con algunas explicaciones sobre la función principal:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7)
La entrada train_size_split sirve para dividir los datos en entrenamiento y de prueba. Por defecto, la división es de 0,7, lo cual significa que el 70% de los datos se usarán para el entrenamiento y el 30% restante para la prueba .
Entropía cruzada binaria, también conocida como función de pérdida
Al igual que el error cuadrático medio es la función de error para la regresión lineal, la entropía cruzada binaria será la función de coste para la regresión logística.
Teoría:
Veamos cómo funciona en dos casos de uso de la regresión logística, es decir, cuando la salida real es 0 y 1
01: Cuando el valor de salida real sea 1
Consideremos el modelo para dos muestras de entrada p1 = 0,4 y p2 = 0,6. Se espera que p1 sea penalizado más que p2 porque se encuentra muy lejos de 1 en comparación con p1.
Desde un punto de vista matemático, el logaritmo negativo de un número pequeño es un número grande, y viceversa.
Para penalizar las entradas usaremos la fórmula
penalización = -log(p)
En estos dos casos
- Penalización = -log(0,4)=0,4 es decir, la penalización sobre p1 es de 0,4
- Penalización = -log(0,6)=0,2 es decir, la penalización sobre p2 es de 0,2
02: Cuando el valor de salida real sea 0
Consideremos la salida del modelo para dos muestras de entrada, p1 = 0,4 y p2= 0,6 (igual que en el caso anterior). Es de esperar que p2 se penalice más que p1 porque se encuentra lejos de 0, pero tenga en cuenta que la salida del modelo logístico es la probabilidad de que una muestra sea positiva. Para penalizar las probabilidades de entrada necesitamos encontrar la probabilidad de que una muestra sea negativa, y eso es fácil, aquí está la fórmula
Probabilidad de que la muestra sea negativa = 1-probabilidad de que la muestra sea positiva
Por lo tanto, para hallar la sanción en este caso, la fórmula de la sanción será
penalización = -log(1-p)
En estos dos casos
- penalización = -log(1-p) = -log(1-0,4) =0,2, es decir, la penalización es de 0,2
- penalización = -log(1-p) = -log(1-0,6) =0,4, es decir, la penalización es de 0,4
La penalización en p2 es mayor que en p1 (funciona como se esperaba), ¡genial!
Ahora, la penalización para una sola muestra de entrada cuya salida del modelo es p y el valor de salida verdadero es y puede calcularse como sigue:
si la muestra de entrada es positiva y=1:
penalización = -log(p)
Si no:
penalización = -log(1-p)
Una ecuación de una sola línea equivalente a la declaración del bloque if-else anterior puede escribirse como
penalización = -( y*log(p) + (1-y)*log(1-p) )
donde
y = valores reales en nuestro conjunto de datos
p = probabilidad predicha bruta del modelo (antes del redondeo)
Vamos a demostrar que esta ecuación es equivalente a la declaración if-else anterior
01: cuando los valores de salida y = 1
penalización = -( 1*log(p) + (1-1)*log(1-p) ) = -log(p) por lo tanto probado
02: cuando el valor de salida y = 0
penalización = -( 0*log(p) + (1-0)* log(1-p) ) = log(1-p) por lo tanto probado
Finalmente, la función de pérdida logarítmica para N muestras de entrada tiene el aspecto siguiente
La pérdida logarítmica indica lo cerca que está la probabilidad de predicción del valor real/verdadero correspondiente (0 o 1, en el caso de la clasificación binaria). Cuanto más se aleje la probabilidad prevista del valor real, mayor será el valor de la pérdida logarítmica.
Las funciones de coste, como la pérdida logarítmica y muchas otras, pueden usarse como métrica de lo bueno que es el modelo, pero el mayor uso se da al optimizar el modelo para los mejores parámetros usando el descenso de gradiente u otros algoritmos de optimización(lo discutiremos en series posteriores, permanezca atento).
Si se puede medir, se puede mejorar. Ese es el objetivo principal de las funciones de coste.
De nuestro conjunto de datos de prueba y de entrenamiento se desprende que nuestra pérdida logarítmica se sitúa entre 0,64 y 0,68, lo cual no resulta ideal (a grandes rasgos).
conjunto de datos de entrenamiento
Logloss =0,6858006105398738
conjunto de datos de prueba
Logloss =0,6599503403665642
Así es como podemos convertir nuestra función de pérdida logarítmica en código
double CLogisticRegression::LogLoss(double &rawpredicted[]) { double log_loss =0; double penalty=0; for (int i=0; i<ArraySize(rawpredicted); i++ ) { penalty += -((m_yvalues[i]*log(rawpredicted[i])) + (1-m_yvalues[i]) * log(1-rawpredicted[i])); //sum all the penalties if (m_debug) printf("penalty =%.5f",penalty); } log_loss = penalty/ArraySize(rawpredicted); //all the penalties divided by their total number Print("Logloss =",log_loss); return(log_loss); }
Para obtener el resultado de la predicción en bruto, tenemos que volver a los bucles for principales de prueba y entrenamiento y almacenar los datos en la matriz de predicción en bruto justo antes del proceso de redondeo de las probabilidades.
El reto de regresión logística dinámica múltiple
El mayor reto al que nos hemos enfrentado al construir las bibliotecas de regresión lineal y logística, tanto en este artículo como en el anterior, es el de las funciones de regresión dinámica múltiple en las que podamos utilizar estas para múltiples columnas de datos sin tener que codificar las cosas rigurosamente para cada dato añadido a nuestro modelo. En el artículo anterior, codificamos dos funciones con el mismo nombre, la única diferencia entre ellas era el número de datos con los que podía trabajar cada modelo: una era capaz de trabajar con dos variables independientes y la otra con cuatro, respectivamente:
void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[],double& C[],double& D[]);
Sin embargo, este método resulta inconveniente: se siente como una forma prematura de codificación de las cosas y viola las reglas del código limpio y DRY (no repitas principios que la POO está tratando de ayudarte a lograr).
A diferencia de python, con funciones flexibles que podrían tomar un gran número de argumentos funcionales con la ayuda de *args y **kwargs, en MQL5 esto podría lograrse usando solo líneas, por lo que podemos deducir. Este sería un buen punto de partida.
void CMultipleLogisticRegression::MLRInit(string x_columns="3,4,5,6,7,8")
La entrada x_columns representa todas las columnas de las variables independientes que usaremos en nuestra biblioteca; estas columnas requerirán que tengamos múltiples arrays independientes para cada una de las columnas pero no hay manera de que podamos crear arrays dinámicamente, por lo que el uso de arrays se puede descartar aquí.
Podemos crear múltiples archivos CSV de forma dinámica y utilizarlos como arrays, seguro, pero esto hará que nuestros programas consuman más recursos informáticos en comparación con el uso de arrays, sobre todo al tratar con datos múltiples, eso por no hablar de que los bucles while que usaremos frecuentemente para abrir los archivos ralentizarán todo el proceso; no estoy 100% seguro, así que corregidme si me equivoco.
Eso sí, todavía podemos ceñirnos a la forma mencionada.
Hemos descubierto el camino a seguir para usar matrices: vamos a almacenar todos los datos de todas las columnas en una matriz, y luego usaremos los datos por separado de esa única matriz.
int start = 0; if (m_debug) //if we are on debug mode print Each Array vs its row for (int i=0; i<x_columns_total; i++) { ArrayCopy(EachXDataArray,m_AllDataArray,0,start,rows_total); start += rows_total; Print("Array Number =",i," From column number ",m_XColsArray[i]); ArrayPrint(EachXDataArray); }
Dentro del bucle for, podemos manipular los datos en los arrays y realizar todos los cálculos para el modelo para todas las columnas de la forma que deseemos. Hemos probado este método, pero aún no hemos llevado el intento a buen puerto. La razón por la que hemos expuesto esta hipótesis es simple: para que todos los que lean este artículo entiendan dicho desafío. En la sección de comentarios, recibiremos con mucho gusto cualquier idea sobre cómo codificar esta función de regresión logística dinámica múltiple; el intento completo del autor se encuentra en este enlace https://www.mql5.com/en/code/38894.
Este intento no ha tenido éxito, pero creemos que vale la pena compartirlo.
Ventajas de la regresión logística
- No asume con respecto a la distribución de clases en el espacio de características.
- Fácilmente ampliable a múltiples clases (regresión multinomial)
- Visión probabilística natural de las predicciones de clase
- Rápido de entrenar
- Muy rápido en la clasificación de registros desconocidos
- Buena precisión para muchos conjuntos de datos sencillos
- Resistente al sobreajuste
- Puede interpretar los coeficientes del modelo como un indicador de la importancia de las características
Desventajas
- Construye límites lineales
Reflexiones finales
Eso es todo por este artículo. La regresión logística se usa en múltiples campos de la vida real, por ejemplo, en la clasificación de correos electrónicos como spam y no spam, la detección de la escritura manual, y muchas otras cosas interesantes.
Está claro que no vamos a utilizar los algoritmos de regresión logística para clasificar los datos del Titanic, o en cualquiera de los campos mencionados, sin embargo, especialmente en la plataforma MetaTrader 5, como hemos mencionado antes, el conjunto de datos se ha usado solo por el bien de la construcción de la biblioteca en comparación con la salida lograda en python, que tenemos el enlace > https://github.com/MegaJoctan/LogisticRegression-MQL5-and-python En el siguiente artículo, veremos cómo podemos usar los modelos logísticos para predecir las caídas de la bolsa.
Como este artículo se ha hecho demasiado largo, dejaremos que el lector se dedique por su cuenta a la tarea de la regresión múltiple.
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/10626
 Cómo avanzar en el aprendizaje automático
Cómo avanzar en el aprendizaje automático
 Aprendiendo a diseñar un sistema comercial basado en CCI
Aprendiendo a diseñar un sistema comercial basado en CCI
 Aprendiendo a diseñar un sistema comercial basado en MACD
Aprendiendo a diseñar un sistema comercial basado en MACD
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso