Características del Wizard MQL5 que debe conocer (Parte 04): Análisis Discriminante Lineal
483
0
El análisis discriminante lineal (LDA) es una técnica de reducción de la dimensionalidad muy común para problemas de clasificación. Al igual que sucede con los mapas de Kohonen descritos en el artículo anterior, si vamos a utilizar datos multidimensionales (con muchos atributos o variables) para clasificar las observaciones, el LDA nos ayudará a transformar los datos para que las clases resulten lo más distintas posibles. Siendo más rigurosos, el LDA encuentra una proyección lineal de los datos en un subespacio dimensional más bajo que optimiza alguna medida de separación de clases. La dimensionalidad de este subespacio nunca superará el número de clases. En este artículo, veremos cómo podemos usar el LDA como una señal, un indicador de trailing y una herramienta de administración de capital. En primer lugar, analizaremos la teoría y luego pasaremos a la aplicación práctica del LDA.
El LDA es muy similar a los métodos PCA, QDA y ANOVA. Todas estas abreviaturas se descifrarán en breve. En este artículo, no profundizaremos en todos estos métodos, solo resaltaremos sus diferencias.
1) Análisis de componentes principales (principal components analysis, PCA):
El LDA es muy similar al PCA. A veces incluso surge la pregunta de si tiene sentido realizar el PCA seguido de la regularización del LDA (para evitar el ajuste de curvas). Este es un tema amplio que podemos tratar en otro artículo.
La diferencia crucial entre los métodos de reducción 2D es que el PCA intenta encontrar ejes con varianza máxima para todo el conjunto de datos, con la suposición de que cuanto más dispersos estén los datos, más separables serán, mientras que el LDA intenta encontrar los ejes que realmente separan los datos en función de la clasificación.
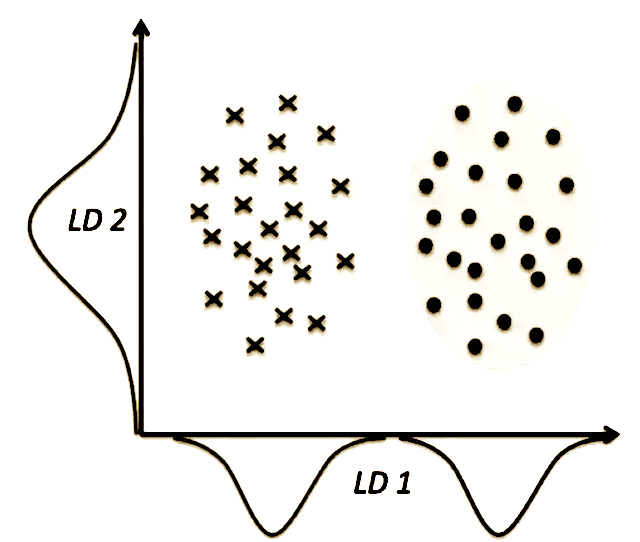
La figura anterior muestra claramente que el PCA nos dará LD2, mientras que el LDA nos dará LD1. Esto hará que la diferencia principal (y por lo tanto la ventaja del LDA) entre el PCA y el LDA resulte absolutamente obvia: el hecho de que una función tenga una varianza alta no significa que resulte útil para la predicción de clases.
2) Análisis cuadrático discriminante (quadratic discriminant analysis, QDA):
El QDA es una generalización del LDA como clasificador. El LDA asume que las distribuciones condicionales de una clase son gaussianas con la misma matriz de covarianza si queremos que realice alguna clasificación.
El QDA no hace suposiciones sobre homocedasticidad y trata de evaluar la covarianza de todas las clases. Si bien dicho algoritmo puede parecer más sólido (con menos suposiciones), también implica que será necesario valorar muchos más parámetros. Es bien sabido que el número de parámetros crece de forma cuadrática con el número de clases. Por lo tanto, si no podemos garantizar que nuestras estimaciones de covarianza sean fiables, resultará poco deseable utilizar QDA.
Después de todo esto, podría darse cierta confusión sobre la relación entre el LDA y el QDA, por ejemplo, a la hora de juzgar cuál es mejor para la reducción de dimensionalidad y cuál es mejor para la clasificación, etc. En dicho caso, el post CrossValidated (en inglés) y todos los enlaces proporcionados en él podrían servirle de ayuda.
3) Análisis de varianza (analysis of variance, ANOVA):
A primera vista, el LDA y ANOVA intentan dividir la variable observada en múltiples variables independientes/dependientes. Sin embargo, la herramienta utilizada por ANOVA, según la Wikipedia, es una versión espejo de la que utiliza el LDA:
"El LDA está estrechamente relacionado con el análisis de varianza (ANOVA) y el análisis de regresión, que también tratan de expresar una variable dependiente como una combinación lineal de otras características o dimensiones. Sin embargo, ANOVA utiliza variables categóricas independientes y una variable discriminante independiente, mientras que el análisis discriminante utiliza variables continuas independientes y una variable categórica independiente (es decir, una marca de clase)".
El LDA generalmente se define de la siguiente manera.
Asumimos que:
- n es el número de clases
- μ es la media de todas las observaciones
- N i es el número de observaciones en la clase i
- μ i es el valor medio i de la clase
- Σi es la matriz de dispersión de la clase i
SW es la matriz de dispersión intraclase, obtenida como
SW = ∑ i = 1 n Σ i
SB es la matriz de dispersión entre clases, obtenida como
SB = ∑ i = 1 n N i ( μ i − μ ) ( μ i − μ ) T
Diagonalizamos SW − 1 SB para obtener sus valores propios y sus vectores propios.
Seleccionamos los valores k propios más grandes y sus vectores propios vinculados. Luego proyectamos nuestras observaciones sobre el subespacio formado por estos vectores.
Esto significará que formaremos una matriz A, cuyas columnas supondrán vectores propios k ,seleccionados anteriormente. La clase CLDA en la biblioteca ALGLIB hace exactamente eso mismo y clasifica los vectores según sus valores propios en orden descendente, lo cual significa que solo necesitaremos seleccionar el mejor vector predictor para hacer una predicción.
Como en artículos anteriores, usaremos la biblioteca de código MQL al implementar el LDA para nuestro asesor experto. Concretamente, confiaremos en la clase CLDA en el archivo dataanalysis.mqh.
Analizaremos el LDA para la pareja de divisas USDJPY en 2022 en el marco temporal diario. La selección de los datos de entrada para el asesor experto dependerá en gran medida del usuario. En nuestro caso para este LDA, la entrada tendrá una variable y un componente de clase. Necesitaremos preparar estos datos antes de ejecutar las pruebas. Como no vamos a ocuparnos de los precios de cierre, por defecto el LDA "se mantendrá" (en su estado original). Después aplicaremos la normalización y la discretización a las variables y componentes de clase de nuestros datos. La normalización implicará que todos los datos estén entre el mínimo y el máximo especificados, mientras que la discretización implicará que los datos se conviertan a un valor booleano (verdadero o falso). A continuación, le mostraremos los preparativos para los cinco conjuntos de datos de nuestra señal:
- El seguimiento de los datos de las variables discretas del cambio en el precio de cierre para que coincidan con las categorías de clase.
- Los datos de las variables normalizadas de los cambios sin procesar en los precios de cierre que van desde -1.0 a +1.0.
- Los datos de variable continuos en los cambios sin procesar en el precio de cierre.
- Los precios de cierre sin procesar.
La normalización mostrará el cambio del precio de cierre como una proporción del rango de las últimas 2 barras en términos decimales (de -1.0 a +1.0), mientras que la discretización mostrará si el precio ha subido (índice 2), permaneciendo en un rango neutral (índice 1), o disminuido (lo que implica un índice 0). Vamos a poner a prueba todos los tipos de datos para comprobar el rendimiento. Esta preparación se realizará usando el método de datos mostrado a continuación. Los cuatro tipos de datos se ajustan usando el parámetro de entrada m_signal_regulizer para definir una zona neutral para nuestros datos y así reducir el ruido blanco.
//+------------------------------------------------------------------+ //| Data Set method | //| INPUT PARAMETERS | //| Index - int, read index within price buffer. | //| | //| Variables | //| - whether data component is variables or . | //| classifier. | //| OUTPUT | //| double - Data depending on data set type | //| | //| DATA SET TYPES | //| 1. Discretized variables. - 0 | //| | //| 2. Normalized variables. - 1 | //| | //| 3. Continuized variables. - 2 | //| | //| 4. Raw data variables. - 3 | //| | //+------------------------------------------------------------------+ double CSignalDA::Data(int Index,bool Variables=true) { m_close.Refresh(-1); m_low.Refresh(-1); m_high.Refresh(-1); if(Variables) { if(m_signal_type==0) { return(fabs(Close(StartIndex()+Index)-Close(StartIndex()+Index+1))<m_signal_regulizer*Range(Index)?1.0:((Close(StartIndex()+Index)>Close(StartIndex()+Index+1))?2.0:0.0)); } else if(m_signal_type==1) { if(fabs(Close(StartIndex()+Index)-Close(StartIndex()+Index+1))<m_signal_regulizer*Range(Index)) { return(0.0); } return((Close(StartIndex()+Index)-Close(StartIndex()+Index+1))/fmax(m_symbol.Point(),fmax(High(StartIndex()+Index),High(StartIndex()+Index+1))-fmin(Low(StartIndex()+Index),Low(StartIndex()+Index+1)))); } else if(m_signal_type==2) { if(fabs(Close(StartIndex()+Index)-Close(StartIndex()+Index+1))<m_signal_regulizer*Range(Index)) { return(0.0); } return(Close(StartIndex()+Index)-Close(StartIndex()+Index+1)); } else if(m_signal_type==3) { if(fabs(Close(StartIndex()+Index)-Close(StartIndex()+Index+1))<m_signal_regulizer*Range(Index)) { return(Close(StartIndex()+Index+1)); } return(Close(StartIndex()+Index)); } } return(fabs(Close(StartIndex()+Index)-Close(StartIndex()+Index+1))<m_signal_regulizer*Range(Index)?1.0:((Close(StartIndex()+Index)>Close(StartIndex()+Index+1))?2.0:0.0)); }
Usaremos una dimensionalidad de cuatro, lo que significa que cada valor del indicador ofrecerá cuatro variables. Entonces, para mayor brevedad, en nuestro caso, veremos los últimos cuatro valores del indicador para cada conjunto de datos de entrenamiento. Nuestra clasificación también resultará básica. Solo analizaremos dos clases (mínimo) en el componente de clase de cada conjunto de datos. Asimismo, necesitaremos establecer el número de puntos de datos en nuestro conjunto de entrenamiento. Este valor se almacenará en el parámetro de entrada m_signal_points.
La salida del LDA suele ser una matriz de coeficientes. Estos coeficientes se clasificarán en vectores, y el producto de punto de cualquiera de estos vectores y el punto de datos actual del indicador deberá producir un valor que luego se comparará con valores similares producidos por el producto del conjunto de datos de entrenamiento para clasificar estas unidades de datos nuevas/actuales. Por ello, si nuestro conjunto de entrenamiento tuviera solo dos puntos de datos con proyecciones LDA de 0 y 1, y nuestro nuevo valor arrojara un producto escalar de 0.9, concluiríamos que se encuentra en la misma categoría que el punto de datos, cuya proyección LDA es de 1, dado que está más cerca de uno. Por otro lado, si el producto diera un valor de 0.1, consideraríamos que este nuevo dato debería pertenecer a la misma categoría que el dato cuya proyección LDA ha sido de 0.
Los conjuntos de datos de entrenamiento rara vez constan de solo dos puntos de datos, por lo que, en la práctica, tomaremos el "centroide" de cada clase como comparación para derivar el producto escalar del nuevo punto de datos y el vector LDA de salida. Este "centroide" constituirá el promedio de la proyección LDA para cada clase.
Para clasificar cada punto de datos como alcista o bajista, simplemente observaremos el cambio en el precio de cierre después del valor del indicador. Si es positivo, entonces el punto de datos será alcista; si es negativo, entonces el punto de datos será bajista. Además, podría darse un movimiento lateral. Para simplificar, equipararemos el movimiento lateral con un signo alcista.
La clase ExpertSignal generalmente usa valores enteros normalizados (0-100) para ponderar las decisiones largas y cortas. Como las proyecciones LDA serán necesariamente del tipo double, las normalizaremos como mostramos a continuación para que entren en el rango de -1.0 a +1.0 (negativo para las bajistas y positivo para las alcistas).
// best eigen vector is the first for(int v=0;v<__S_VARS;v++){ _unknown_centroid+= (_w[0][v]*_z[0][v]); } // if(fabs(_centroids[__S_BULLISH]-_unknown_centroid)<fabs(_centroids[__S_BEARISH]-_unknown_centroid) && fabs(_centroids[__S_BULLISH]-_unknown_centroid)<fabs(_centroids[__S_WHIPSAW]-_unknown_centroid)) { _da=(1.0-(fabs(_centroids[__S_BULLISH]-_unknown_centroid)/(fabs(_centroids[__S_BULLISH]-_unknown_centroid)+fabs(_centroids[__S_WHIPSAW]-_unknown_centroid)+fabs(_centroids[__S_BEARISH]-_unknown_centroid)))); } else if(fabs(_centroids[__S_BEARISH]-_unknown_centroid)<fabs(_centroids[__S_BULLISH]-_unknown_centroid) && fabs(_centroids[__S_BEARISH]-_unknown_centroid)<fabs(_centroids[__S_WHIPSAW]-_unknown_centroid)) { _da=-1.0*(1.0-(fabs(_centroids[__S_BEARISH]-_unknown_centroid)/(fabs(_centroids[__S_BULLISH]-_unknown_centroid)+fabs(_centroids[__S_WHIPSAW]-_unknown_centroid)+fabs(_centroids[__S_BEARISH]-_unknown_centroid)))); }
Luego, este valor se normalizará fácilmente al número entero típico (0-100) esperado por la clase de señal.
if(_da>0.0) { result=int(round(100.0*_da)); }
para la función long Check y,
if(_da<0.0) { result=int(round(-100.0*_da)); }
para la función short Check.
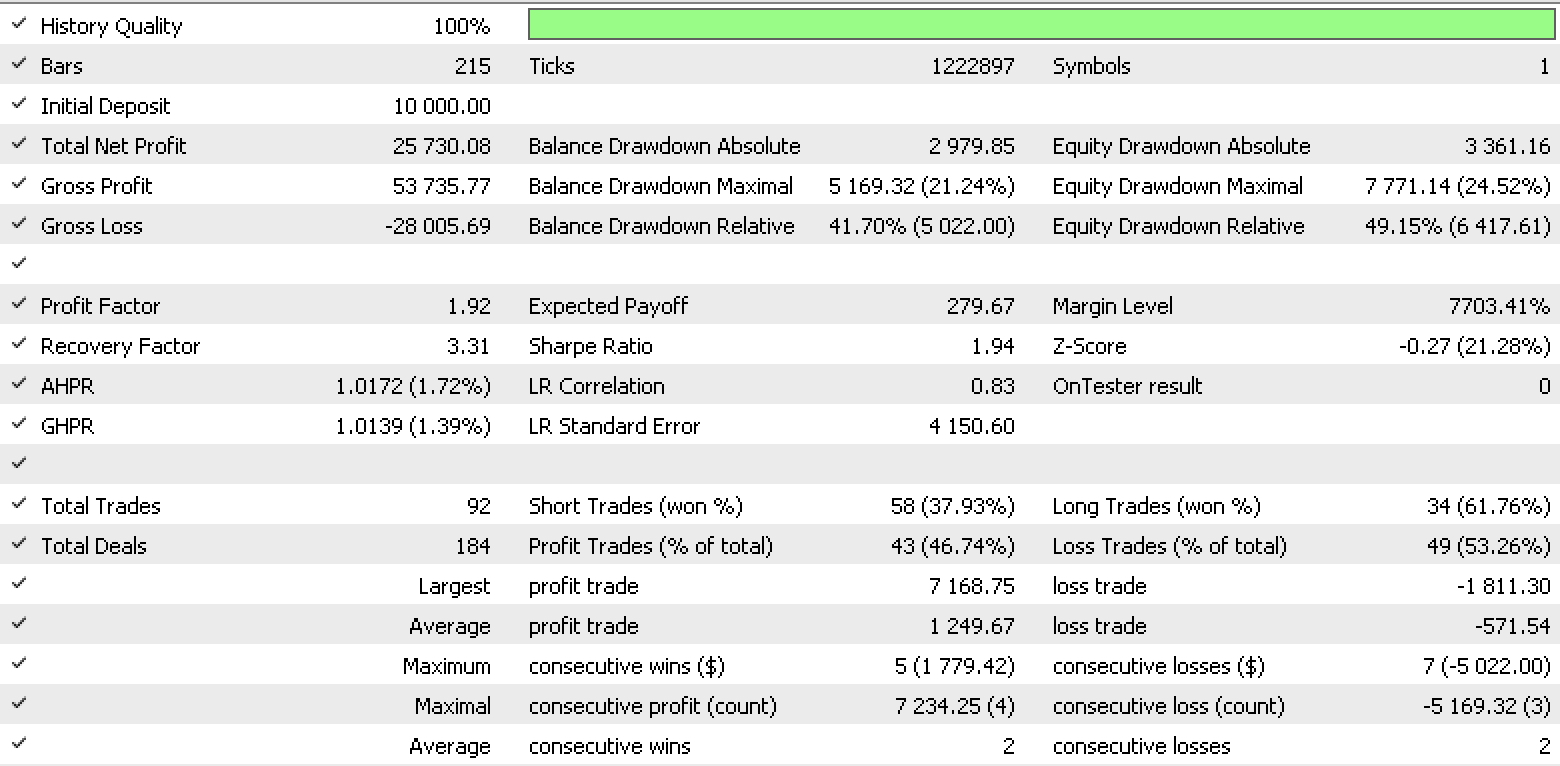
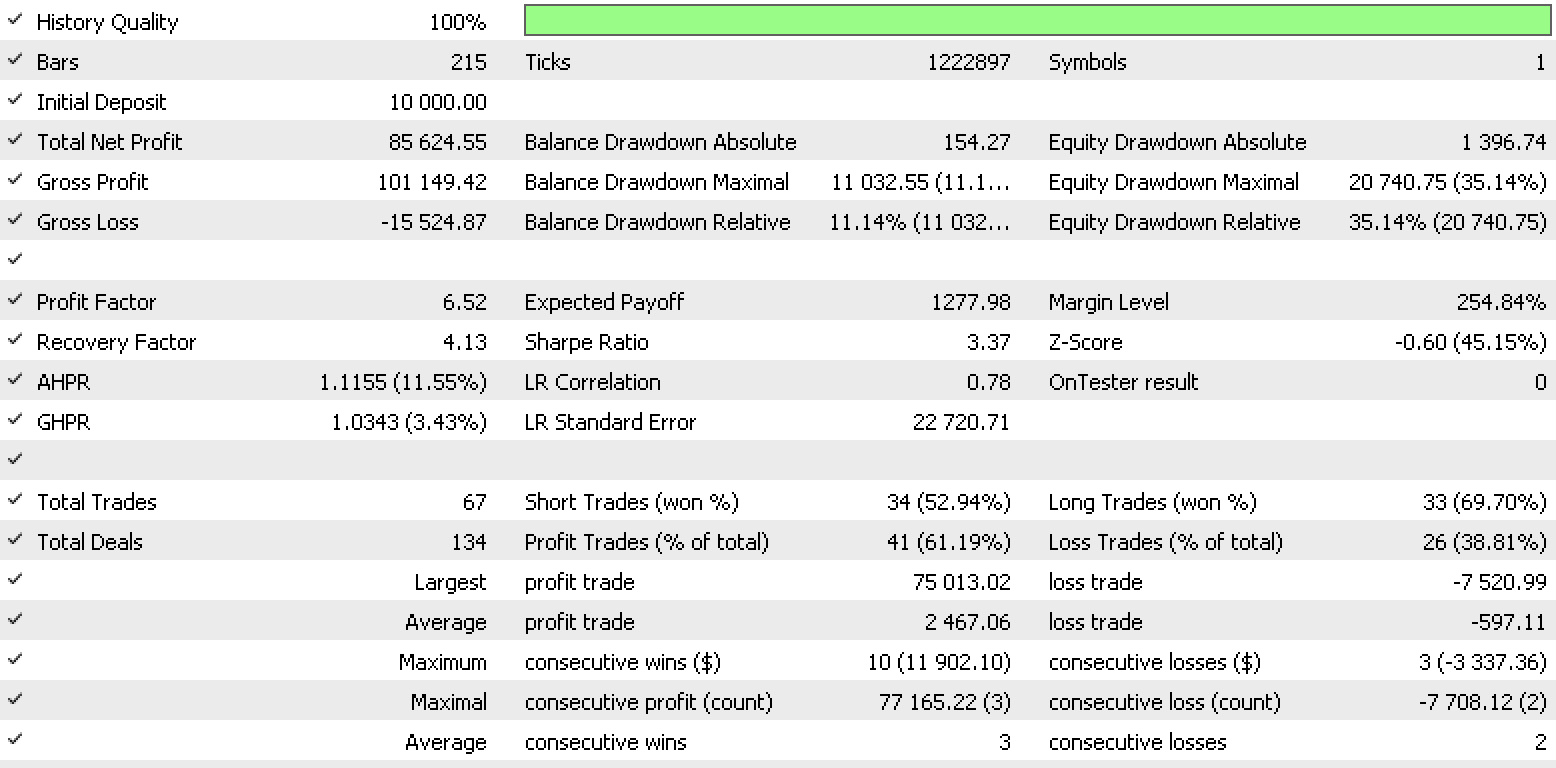
Por consiguiente, la pasada de prueba para cada uno de los tipos de datos de entrada ofrecerá los siguientes informes del simulador de estrategias.
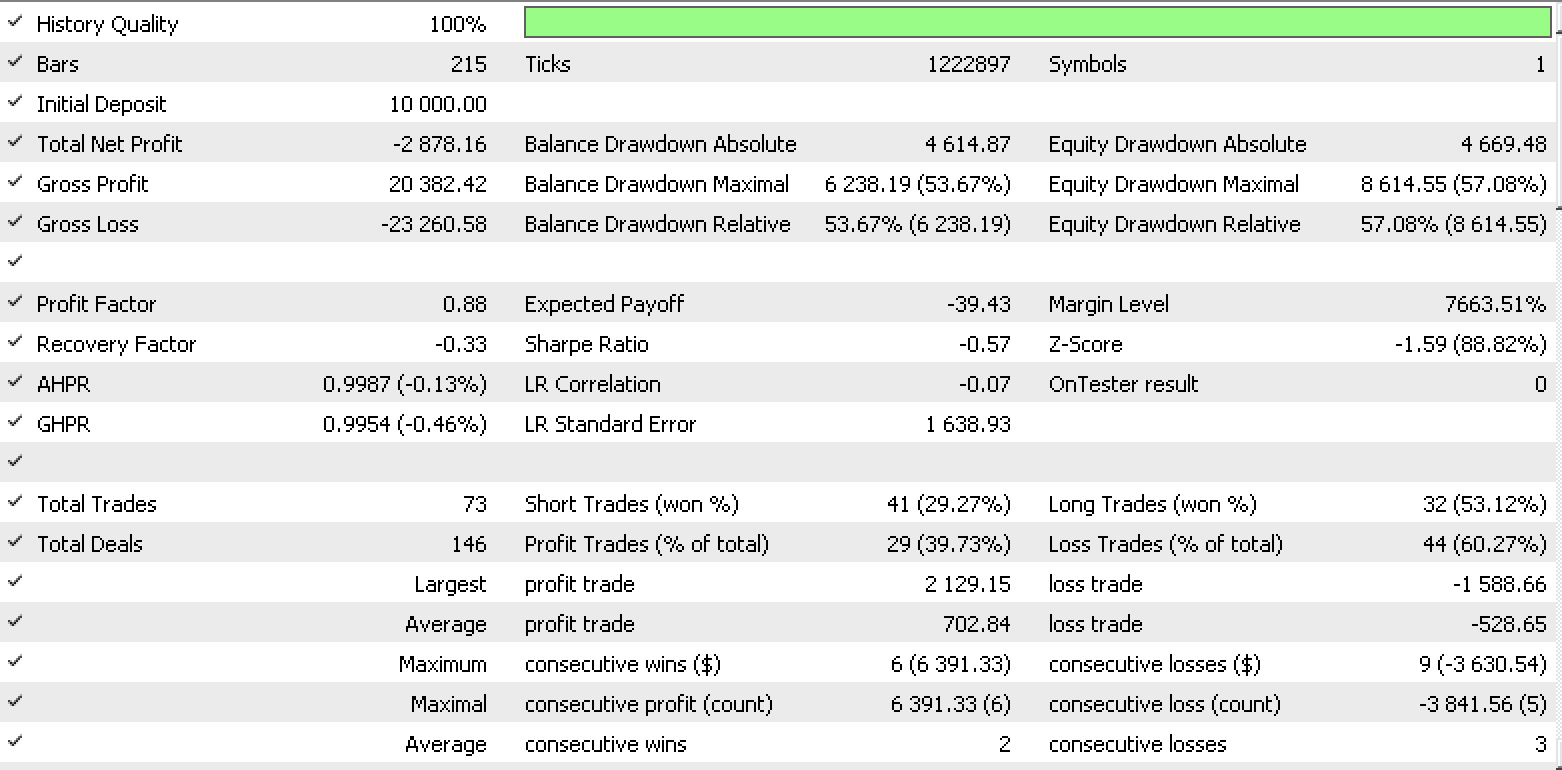
Informe de conjunto de datos 1
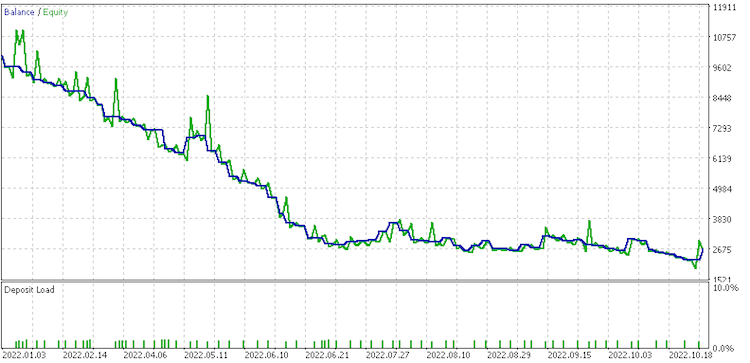
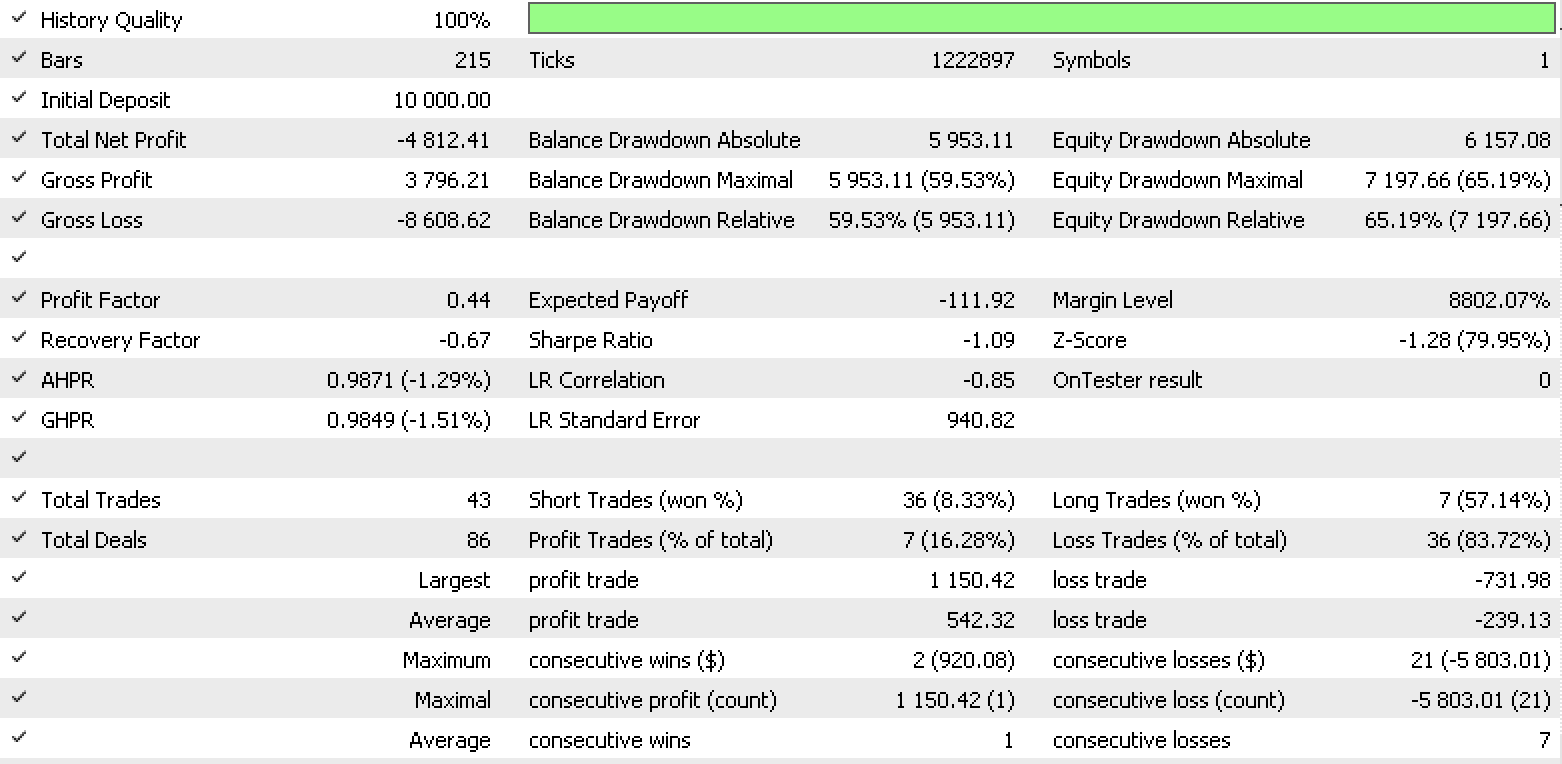
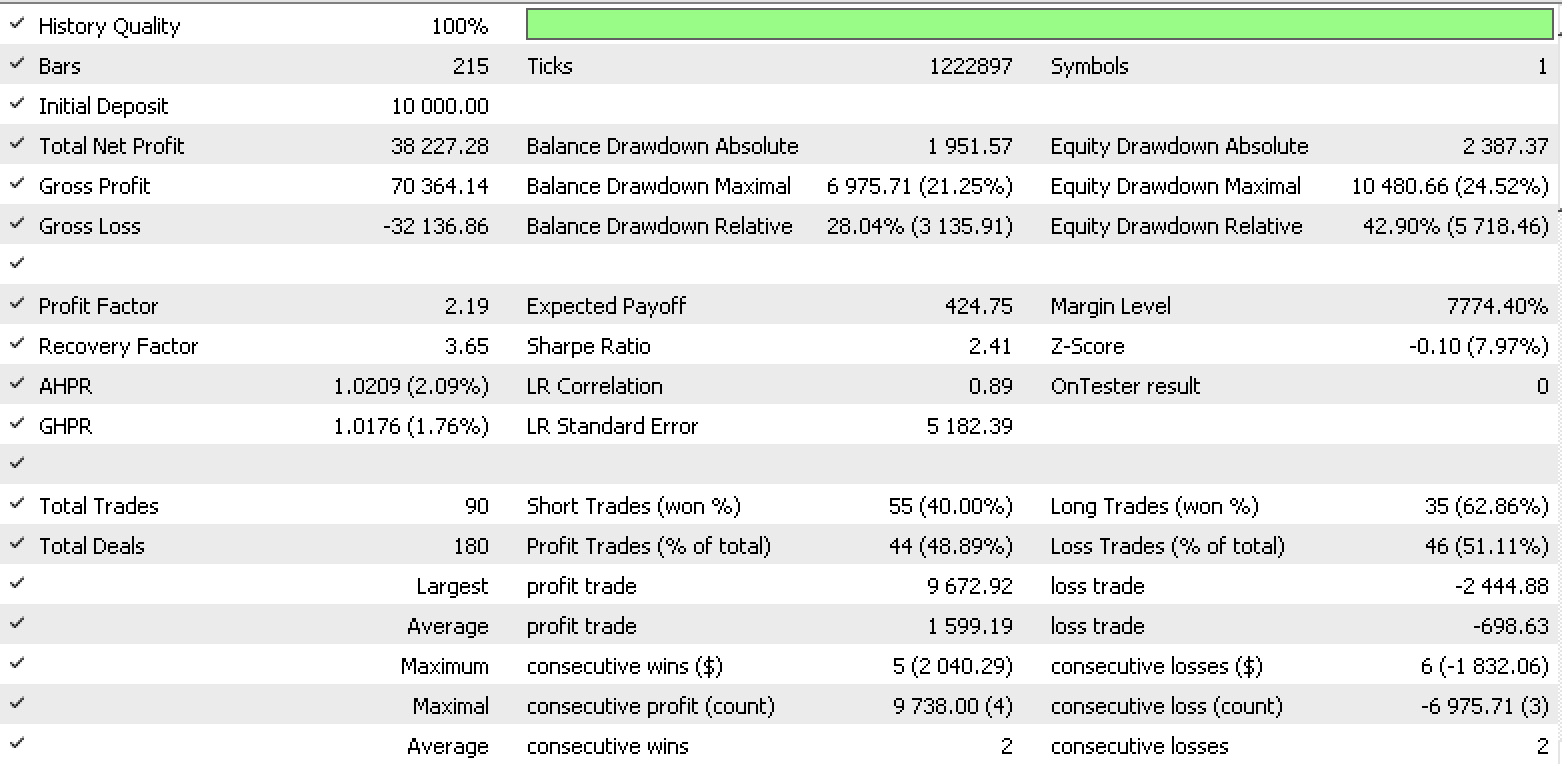
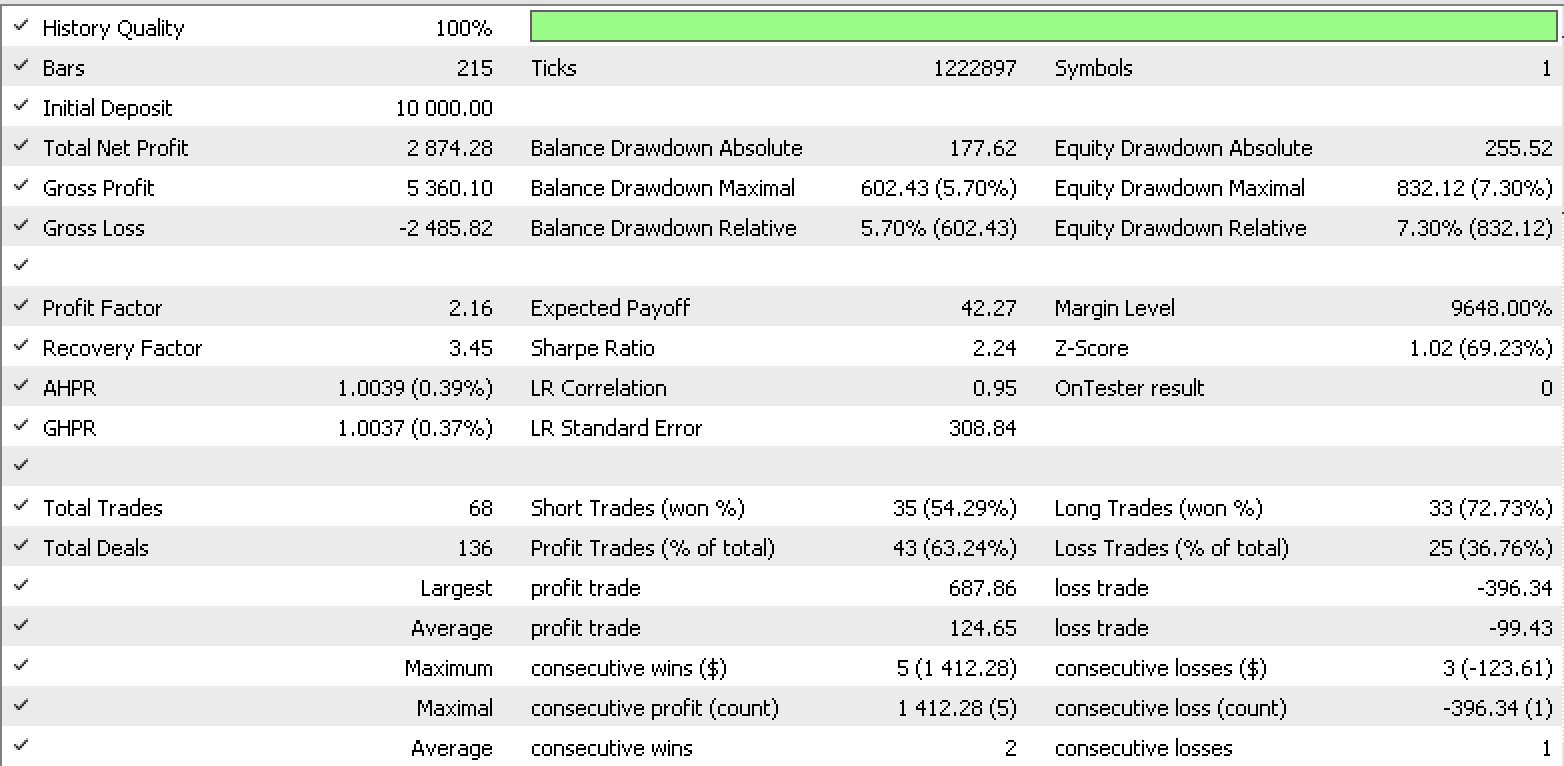
Informe de conjunto de datos 2
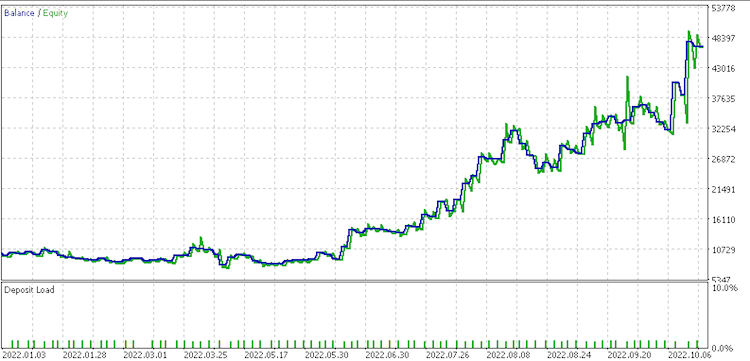
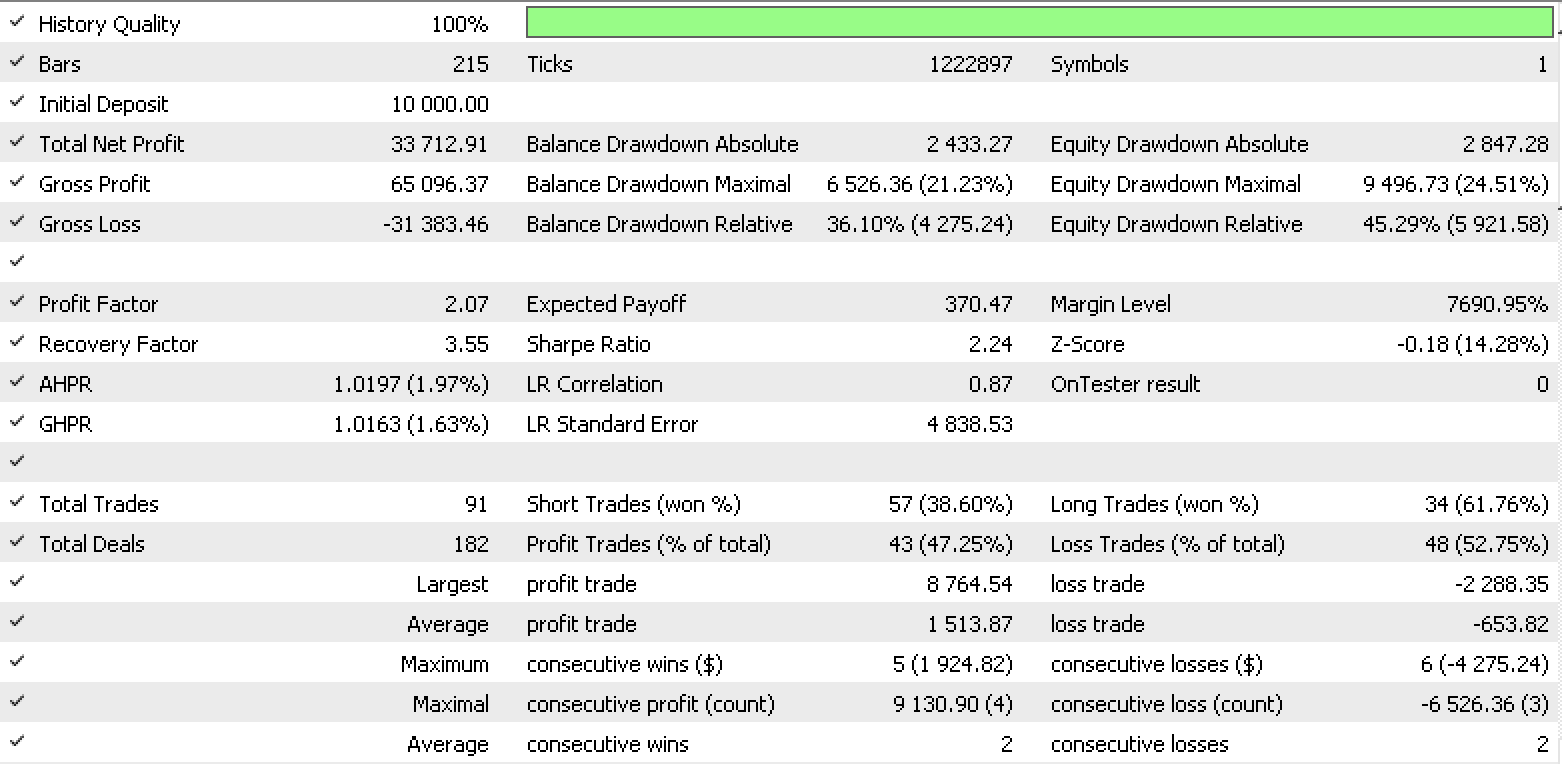
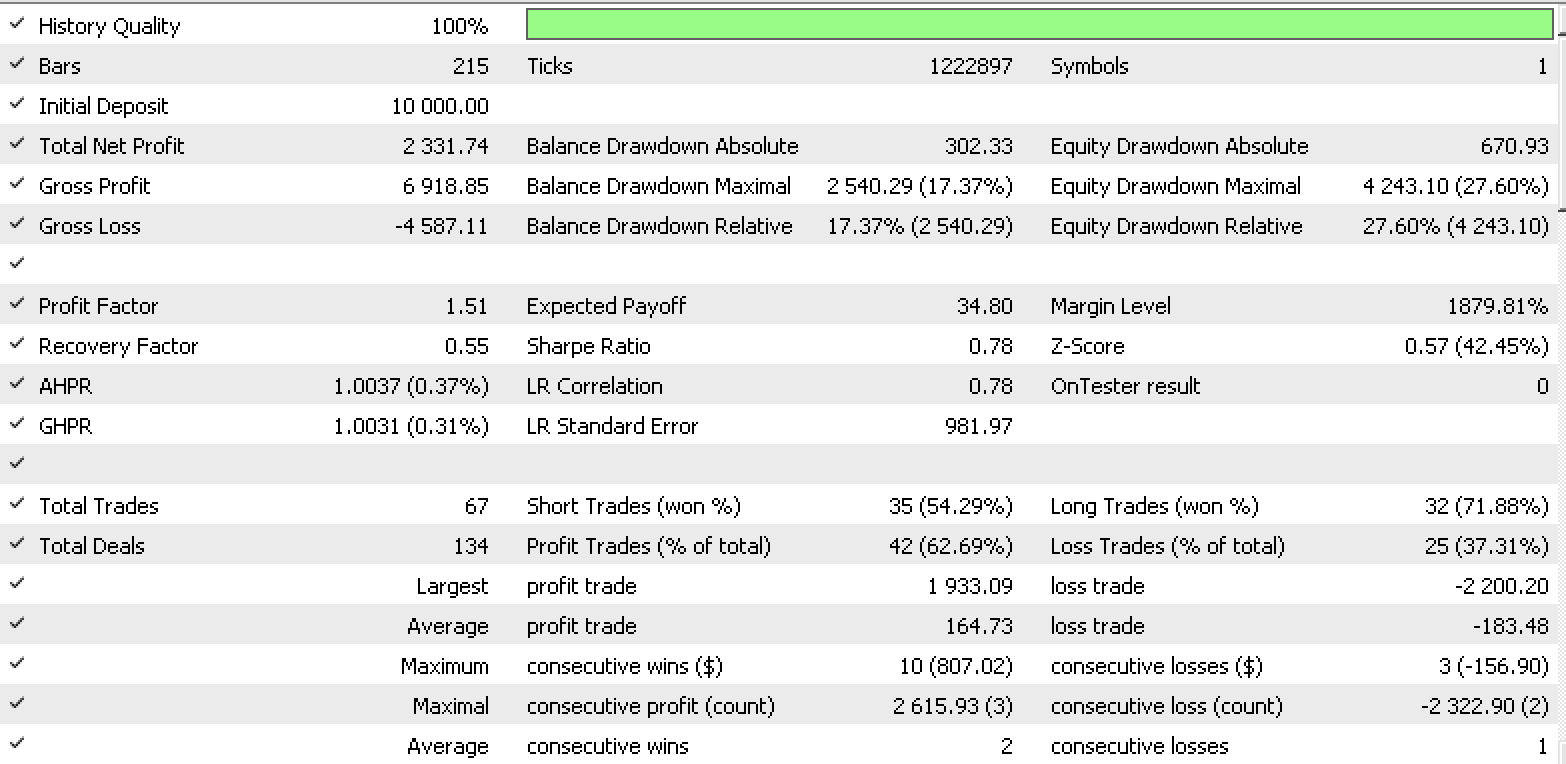
Informe de conjunto de datos 3
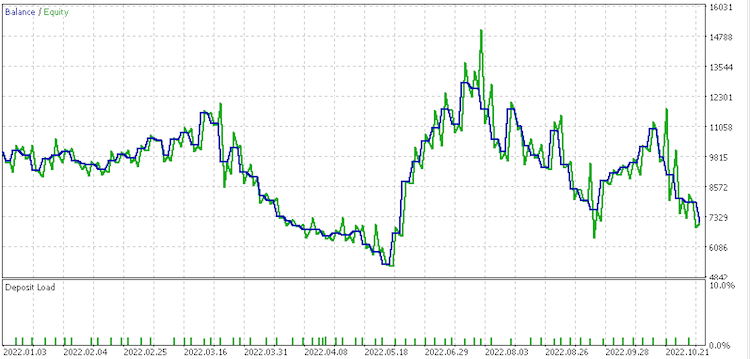
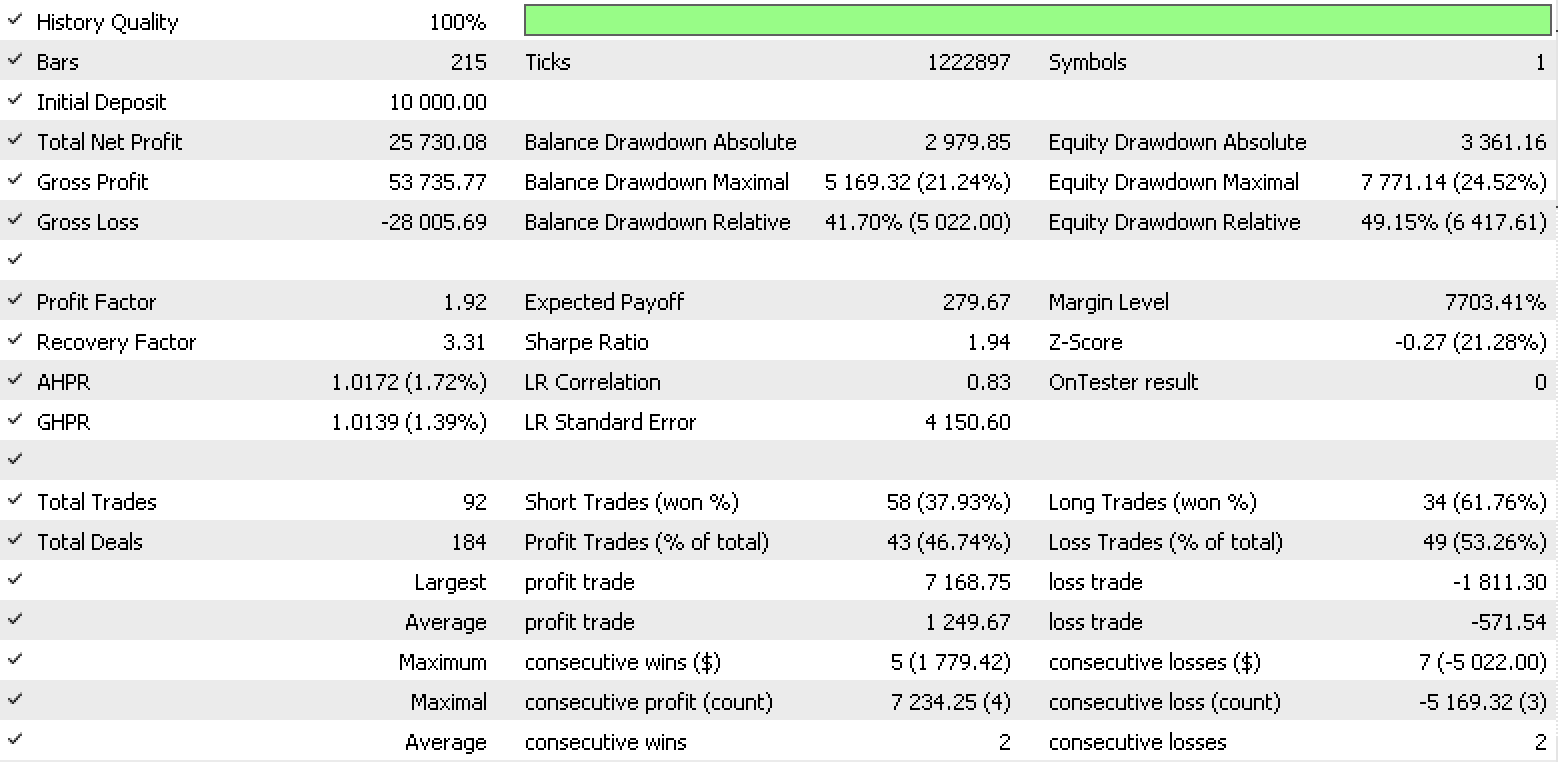
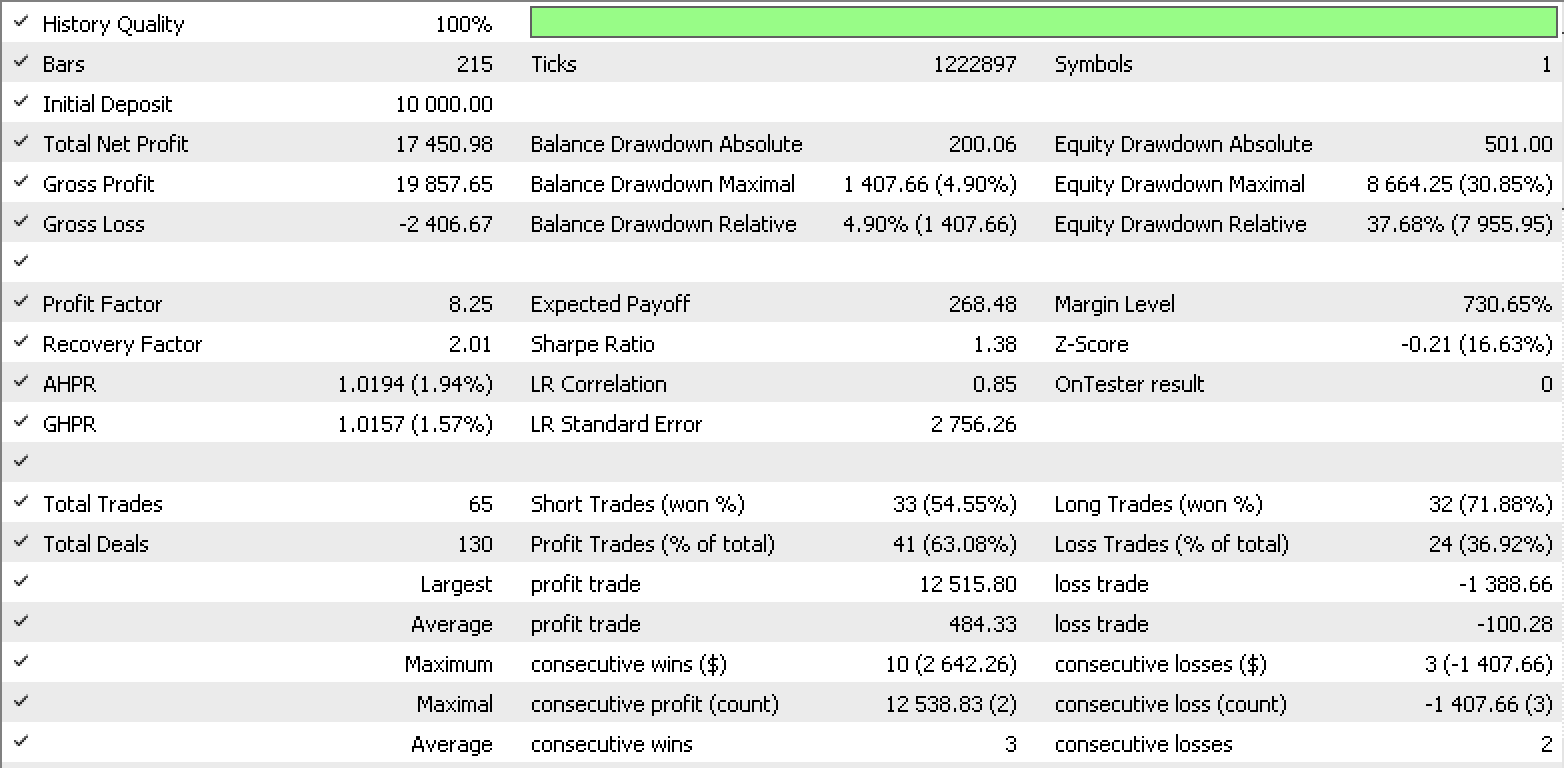
Informe de conjunto de datos 4
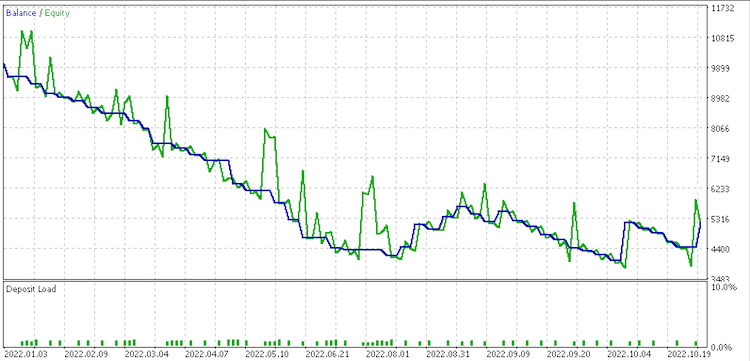
Estos informes demuestran el potencial del LDA como herramienta para tráders.
La clase ExpertTrailing ajustará o establecerá un stop loss para una posición abierta. El resultado clave mostrado aquí es el valor doble del nuevo stop loss. Por ello, dependiendo de la posición abierta, analizaremos los precios High y Low como nuestros conjuntos de datos primarios. Estos se prepararán de la siguiente manera para los precios High y Low con la selección según el tipo de posición abierta: -
- El seguimiento de los datos de las variables discretas de cambio de precio (High o Low) para que coincidan con las categorías de la clase.
- Los datos de las variables normalizadas de los cambios sin procesar (high or low) del precio (High o Low) en el rango de -1.0 a +1.0.
- Los datos de las variables continuas de los cambios de precio sin procesar (High o Low).
- Los precios sin procesar (High o Low).
Al igual que sucede con la clase de señal, el LDA se emitirá como un valor double normalizado. Como dicho valor resultará inútil para determinar el stop loss, lo ajustaremos como mostramos a continuación, según el tipo de posición abierta, para determinar el precio del stop loss.
int _index =StartIndex(); double _min_l=Low(_index),_max_l=Low(_index),_min_h=High(_index),_max_h=High(_index); for(int d=_index;d<m_trailing_points+_index;d++) { _min_l=fmin(_min_l,Low(d)); _max_l=fmax(_max_l,Low(d)); _min_h=fmin(_min_h,High(d)); _max_h=fmax(_max_h,High(d)); } if(Type==POSITION_TYPE_BUY) { _da*=(_max_l-_min_l); _da+=_min_l; } else if(Type==POSITION_TYPE_SELL) { _da*=(_max_h-_min_h); _da+=_max_h; }
Aquí también mostraremos cómo ajustar y establecer nuestros nuevos niveles de stop loss. Para las posiciones largas:
m_long_sl=ProcessDA(StartIndex(),POSITION_TYPE_BUY); double level =NormalizeDouble(m_symbol.Bid()-m_symbol.StopsLevel()*m_symbol.Point(),m_symbol.Digits()); double new_sl=NormalizeDouble(m_long_sl,m_symbol.Digits()); double pos_sl=position.StopLoss(); double base =(pos_sl==0.0) ? position.PriceOpen() : pos_sl; //--- sl=EMPTY_VALUE; tp=EMPTY_VALUE; if(new_sl>base && new_sl<level) sl=new_sl;
Aquí determinaremos el punto de precio bajo probable para la siguiente barra para una posición larga abierta ('m_long_sl') y luego lo estableceremos como nuestro nuevo stop loss si resulta mayor que el precio de apertura de la posición o si su stop loss actual se encuentra por debajo de Bid menos el stop loss. Los precios Low serán el tipo de datos usado en el cálculo.
El stop loss para las posiciones cortas se establecerá de forma inversa.
Entonces, una ejecución de prueba para cada uno de los tipos de datos de entrada, usando el tipo de datos ... para la señal, arrojará los siguientes resultados.
Informe de conjunto de datos 1
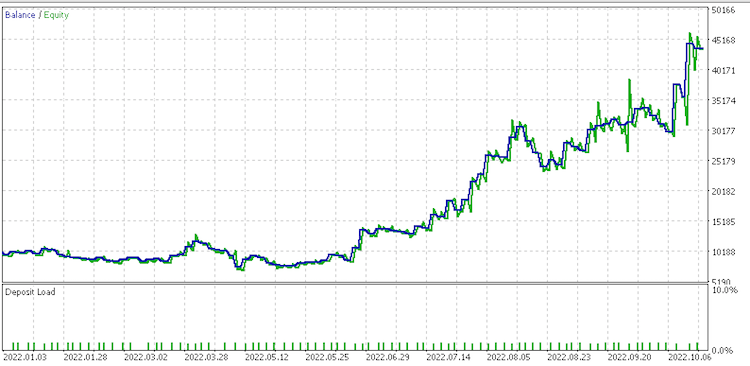
Informe de conjunto de datos 2
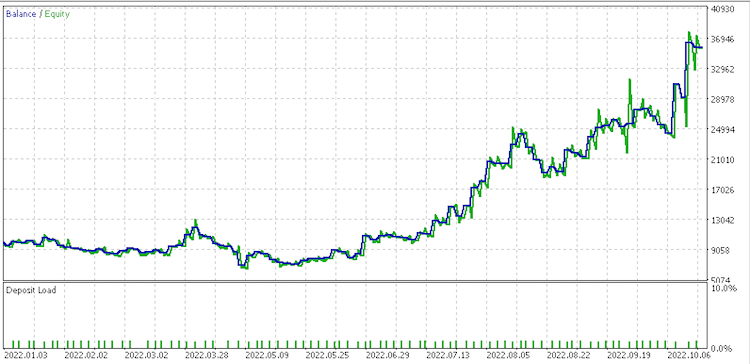
Informe de conjunto de datos 3
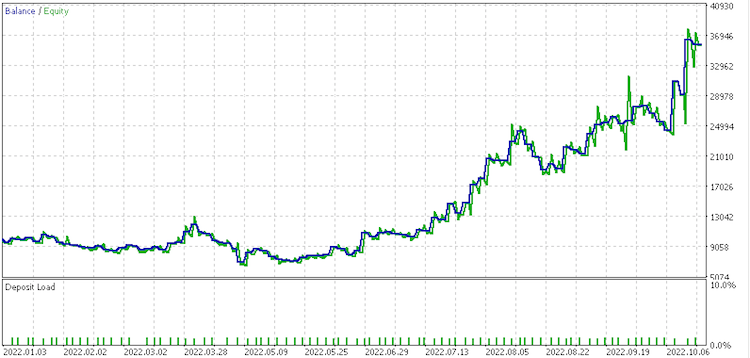
Informe de conjunto de datos 4
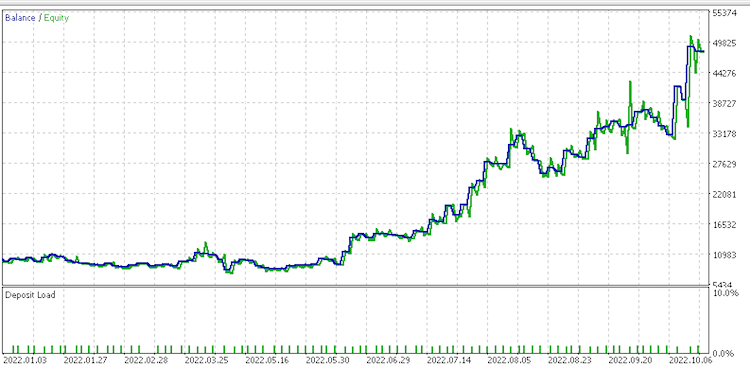
Estos informes posiblemente indiquen que el conjunto de cambios continuos sin procesar .data sea el que mejor se ajusta, dado su factor de recuperación de 6,82.
La clase ExpertMoney establecerá el tamaño del lote de nuestra posición. Esto podría deberse al rendimiento anterior, por lo que crearemos la clase OptimizedVolume. No obstante, el LDA puede ayudar con el tamaño inicial si estamos considerando la volatilidad o un rango entre precios altos y bajos. De esta forma, nuestro conjunto de datos principal será el rango de la barra de precios. Vamos a comprobar si el rango de la barra de precios está aumentando o disminuyendo. Prepararemos los siguientes datos:-
- El seguimiento de los datos de las variables discretasde cambio del valor del rango para coincidir con las categorías de clase.
- Los datos de las variables normalizadas de los cambios sin procesar del valor del intervalo de -1.0 a +1.0.
- Los datos de variable continuos en cambios sin procesar del rango de valores.
- Los valores de rango sin procesar.
Al igual que sucede con las clases de señal y seguimiento, el LDA se generará como un valor double normalizado. Como en el caso anterior, no nos aportará nada, por lo que haremos los ajustes que se muestran a continuación para proyectar mejor el nuevo intervalo de barras.
int _index =StartIndex(); double _min_l=Low(_index),_max_h=High(_index); for(int d=_index;d<m_money_points+_index;d++) { _min_l=fmin(_min_l,Low(d)); _max_h=fmax(_max_h,High(d)); } _da*=(_max_h-_min_l); _da+=(_max_h-_min_l);
Las dos funciones de espejo serán responsables de establecer el volumen abierto, dependiendo de si el asesor abre una posición larga o corta. A continuación, le mostraremos los aspectos más destacados de una posición larga.
double _da=ProcessDA(StartIndex()); if(m_symbol==NULL) return(0.0); sl=m_symbol.Bid()-_da; //--- select lot size double _da_1_lot_loss=(_da/m_symbol.TickSize())*m_symbol.TickValue(); double lot=((m_percent/100.0)*m_account.FreeMargin())/_da_1_lot_loss; //--- calculate margin requirements for 1 lot if(m_account.FreeMarginCheck(m_symbol.Name(),ORDER_TYPE_BUY,lot,m_symbol.Ask())<0.0) { printf(__FUNCSIG__" insufficient margin for sl lot! "); lot=m_account.MaxLotCheck(m_symbol.Name(),ORDER_TYPE_BUY,m_symbol.Ask(),m_percent); } //--- return trading volume return(Optimize(lot));
Lo notable aquí es que determinaremos el cambio pronosticado de precio del rango y restaremos esa predicción a nuestro precio Bid (también deberíamos haber restado el nivel de stop): esto nos dará un stop loss ajustado al riesgo. Y si usamos el parámetro de entrada Percent como parámetro de riesgo máximo de pérdida, podremos calcular un tamaño de lote que limite nuestro porcentaje de reducción al valor Percent si encontramos una reducción por debajo del precio Bid previsto.
Por lo tanto, una ejecución de prueba para cada uno de los tipos de datos de entrada, utilizando el tipo de datos de cierre sin procesar para la señal y... el trailing arrojará los siguientes resultados.
Informe de conjunto de datos 1
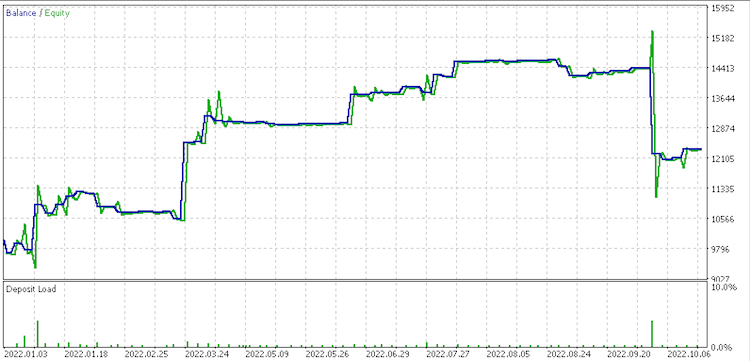
Informe de conjunto de datos 2
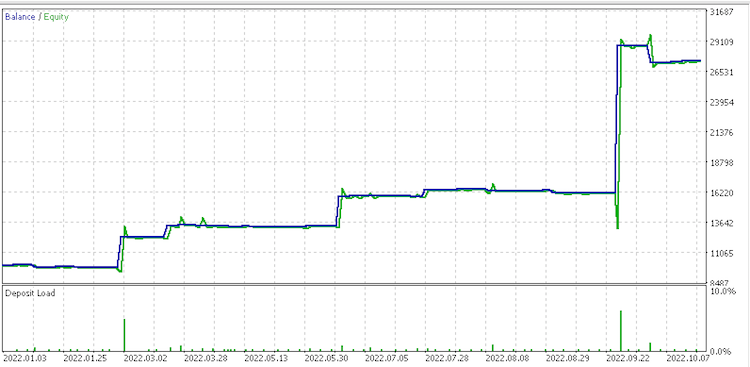
Informe de conjunto de datos 3
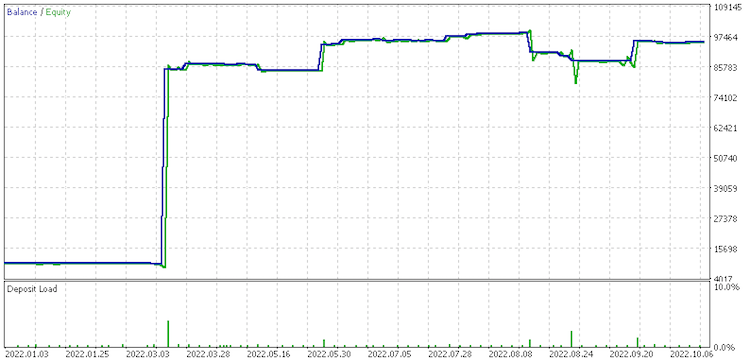
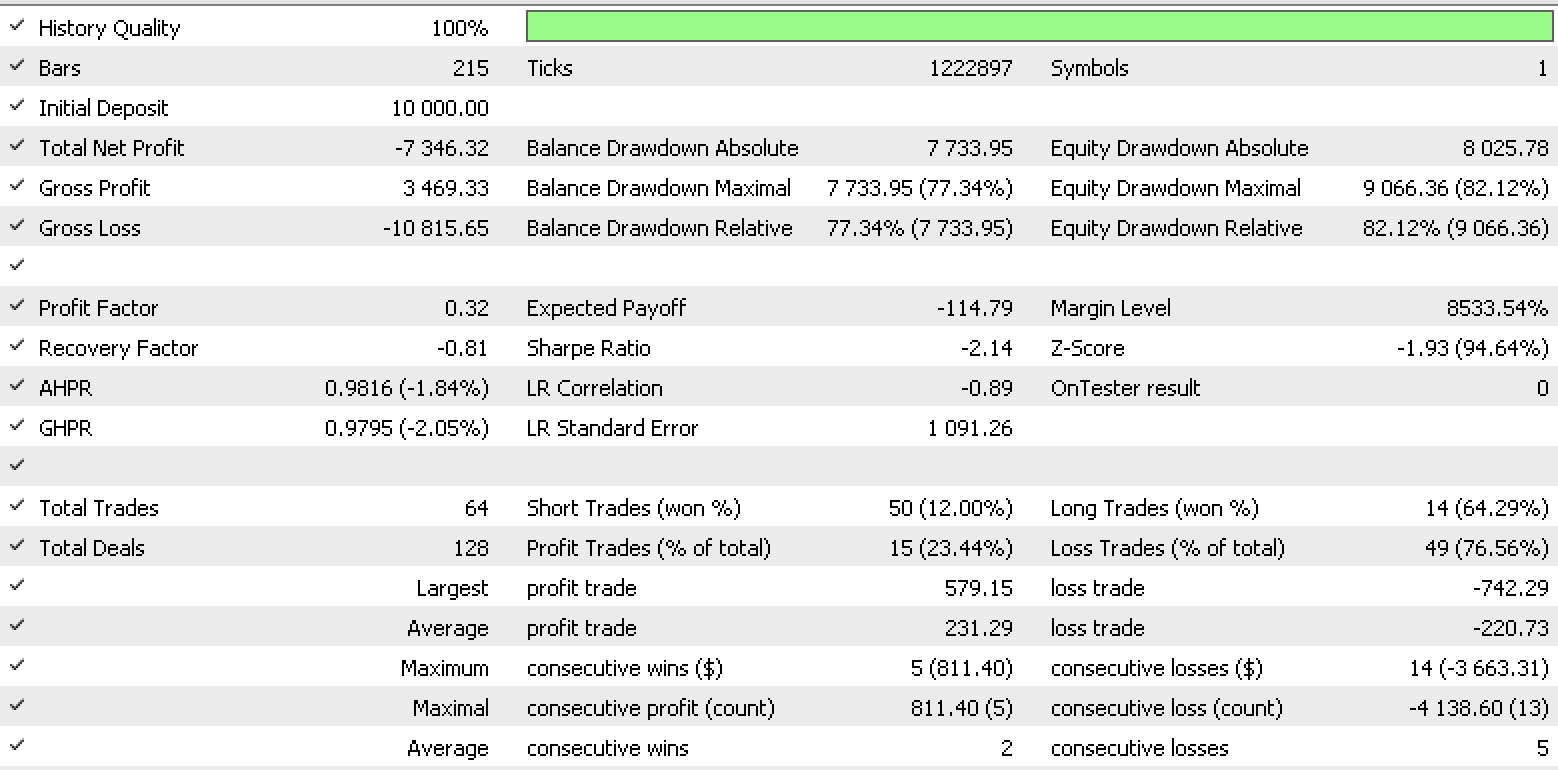
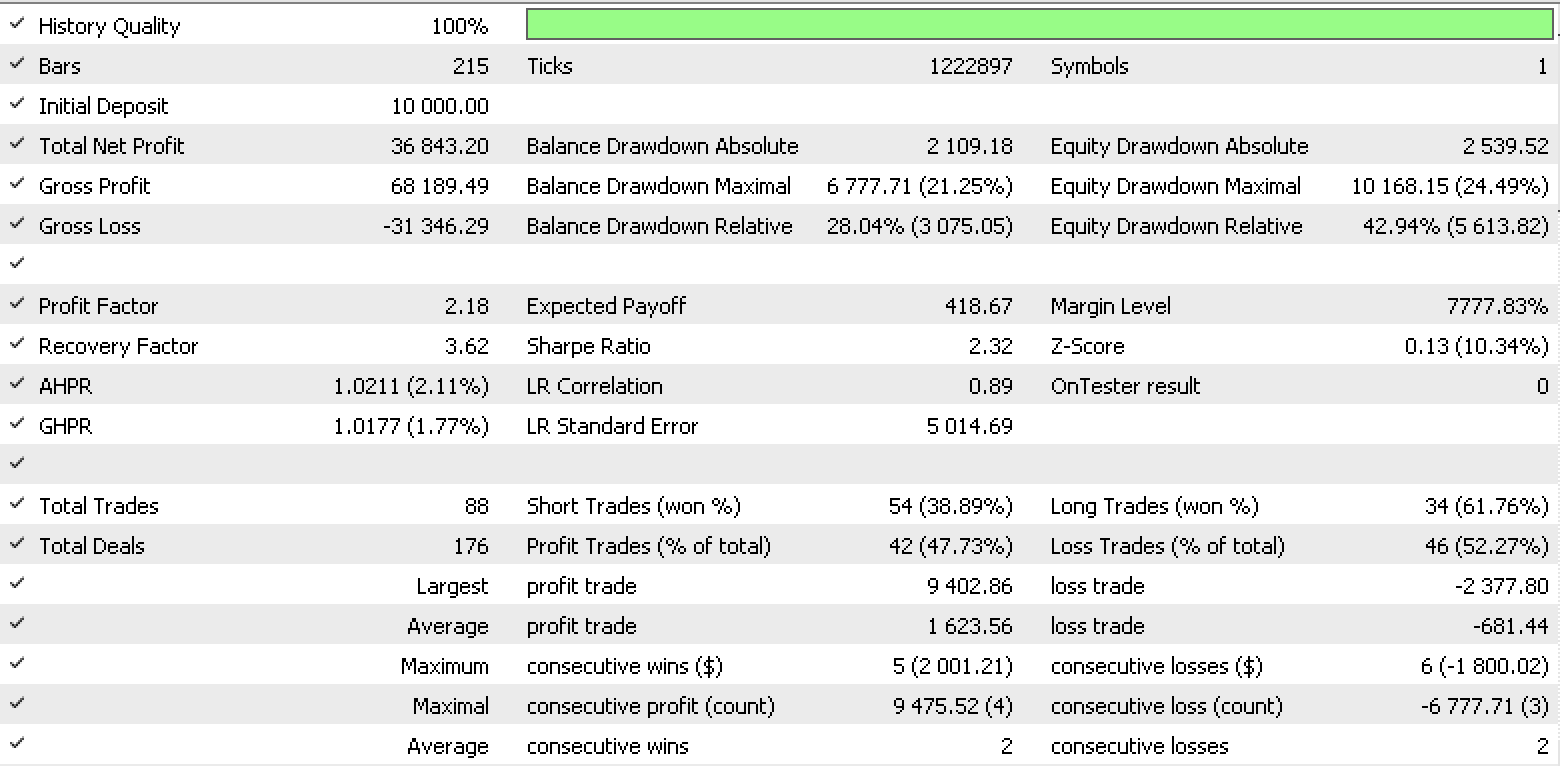
Informe de conjunto de datos 4
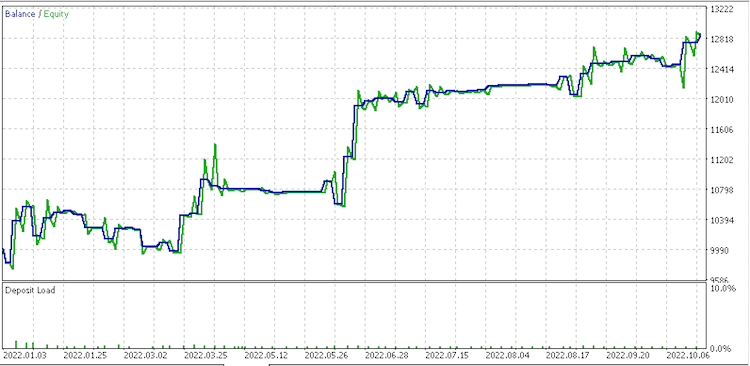
Por lo visto, el conjunto de datos de cambios discretos en los valores de rango es el más prometedor para la gestión del dinero. También deberemos tener en cuenta que existe una gran diferencia en los resultados de los conjuntos de datos al gestionar el capital dado que todos usan la misma señal y la misma configuración de trailing.
En el artículo hemos destacado las posibilidades del uso del análisis discriminante como herramienta comercial en un asesor experto. Obviamente, un solo artículo no puede abarcar este tema al completo. Podríamos realizar un análisis más detallado utilizando conjuntos de datos más diversos que cubran periodos más largos.
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/11687
Redes neuronales: así de sencillo (Parte 32): Aprendizaje Q distribuido
Aprendizaje automático y Data Science (Parte 9): Algoritmo de k vecinos más próximos (KNN)
Cómo trabajar con líneas usando MQL5
DoEasy. Elementos de control (Parte 25): El objeto WinForms «Tooltip»
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso