データサイエンスと機械学習（第09回）:K近傍法(KNN)

MetaTrader 5 — トレーディング | 16 1月 2023, 13:05

397

Omega J Msigwa

羽の鳥が群がる - KNNアルゴリズムの背後にあるアイデア

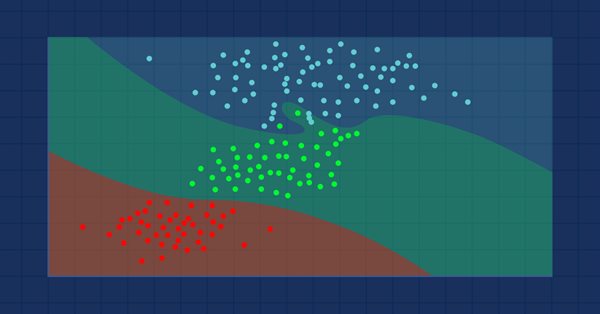
K近傍法は、近接性を使用して個々のデータポイントのグループ化に関する分類または予測をおこなうノンパラメトリック教師あり学習分類器です。このアルゴリズムは主に分類問題に使用されますが、回帰問題の解決にも使用できます。データセット内の類似したポイントは互いに近くにあるという仮定により、分類アルゴリズムとしてよく使用されます。近傍法は、教師あり機械学習における最もシンプルなアルゴリズムの1つです。この記事では、アルゴリズムを分類器として構築します。

kNNアルゴリズム

画像ソース：skicit-learn.org

注意事項：

分類器としてよく使用されますが、回帰にも使用できます。
K-NNはノンパラメトリックアルゴリズムです。つまり、基礎となるデータについて何の仮定も立てません。
訓練セットから学習しないため、遅延学習アルゴリズムと呼ばれることがよくあります。代わりに、データを保存し、行動時に使用します。
KNNアルゴリズムは、新しいデータと利用可能なデータセットの間の類似性を想定し、利用可能なカテゴリに最も類似しているカテゴリに新しいデータを配置します。

KNNの仕組み

コードの記述に入る前に、KNNアルゴリズムがどのように機能するかを理解しましょう。

手順01：近傍数kを選択する
手順02：ポイントからデータセットのすべてのメンバーまでのユークリッド距離を計算する
手順03：ユークリッド距離に従ってK個の最近傍を取得する
手順04：これらの最近傍の中で、各カテゴリのデータポイントの数を数える
手順05：隣接数が最大であるカテゴリに新しいデータポイントを割り当てる

手順01：近傍数kを選択する

これは簡単なステップです。必要なのは、CKNNnearestNeighborsクラスで使用するkの数を選択することだけです。ここで、kをどのように因数分解するかという問題が生じます。

Kを因数分解する方法

Kは、指定された値/ポイントがどこに属するべきかについて投票するために使用する最近傍の数です。小さい数のkを選択すると、分類されたデータポイントに多くのノイズが発生し、バイアスの数が大きくなる可能性があります。一方、kの数が大きいと、アルゴリズムが大幅に遅くなります。

決定プロセスで行き詰まらないように、kの値は奇数である必要があります。これが意味するのは、投票プロセスではk個の隣人が必要であります。4のように設定されていて、2個のメンバーが特定のポイントがカテゴリAに属すと投票して残りの2票がカテゴリBに属すと投票した場合、どちら側が決定に勝ったかをどのように決定できるでしょうか。

このケースは、分類するカテゴリが2つある場合に最も多く発生します。このような状況が後でk個の隣接カテゴリに多数のカテゴリがあるときに発生した場合に何ができるかを見ていきます。

クラスタリングライブラリ内で、データセットの行列から利用可能なクラスを取得し、それらをm_classesVectorという名前のクラスのグローバルベクトルに格納する関数を作成しましょう。

vector CKNNNearestNeighbors::ClassVector()
 {
   vector t_vectors = Matrix.Col(m_cols-1); //target variables are found on the last column in the matrix
   vector temp_t = t_vectors, v = {t_vectors[0]};
   
   for (ulong i=0, count =1; i<m_rows; i++) //counting the different neighbors
    {
      for (ulong j=0; j<m_rows; j++)
         {
            if (t_vectors[i] == temp_t[j] && temp_t[j] != -1000)
               {                   
                  bool count_ready = false;
                  
                  for(ulong n=0;n<v.Size();n++)
                      if (t_vectors[i] == v[n])
			 count_ready = true;
                    
                    if (!count_ready)
                      {
                        count++;
                        v.Resize(count);
                        
                        v[count-1] = t_vectors[i]; 
                        
                        temp_t[j] = -1000; //modify so that it can no more be counted
                      }
                    else 
			break;
                  //Print("t vectors vector ",t_vectors);
               }
             else
		 continue;
         }
    }
   
   return(v);
 }

CKNNNearestNeighbors::CKNNNearestNeighbors(matrix<double> &Matrix_)
  {
    Matrix.Copy(Matrix_);

    k = (int)round(MathSqrt(Matrix.Rows())); 
    k = k%2 ==0 ? k+1 : k; //make sure the value of k ia an odd number    
    
    m_rows = Matrix.Rows();
    m_cols = Matrix.Cols();
    
   m_classesVector = ClassVector();
   Print("classes vector | Neighbors ",m_classesVector);
  }

出力

2022.10.31 05:40:33.825 TestScript      classes vector | Neighbors [1,0]

コンストラクタに注意を払うと、データセット内の行の総数/データポイント数の平方根としてデフォルトで生成された後、kの値が奇数であることを保証する行があります。これは、Kの値を気にしないことにした場合、つまり、アルゴリズムを調整しないことにした場合です。kの値を調整できる別のコンストラクタがありますが、その値が奇数であることが確認されます。この場合のKの値は3で、行数が9であるため、√9=3（奇数）です。

CKNNNearestNeighbors:: CKNNNearestNeighbors(matrix<double> &Matrix_, uint k_)
 {
   k = k_;
   
   if (k %2 ==0)
      printf("K %d is an even number, It will be added by One so it becomes an odd Number %d",k,k=k+1);
      
   Matrix.Copy(Matrix_);
   
   m_rows = Matrix.Rows();
   m_cols = Matrix.Cols();
   
   m_classesVector = ClassVector();
   Print("classes vector | Neighbors ",m_classesVector);
 }

ライブラリを構築するために、以下のデータセットを使用します。その後、MetaTraderで取引情報を使用して何かを作成する方法を確認します。

このデータがMetaEditorでどのように表示されるかを次に示します。

    matrix Matrix = 
      {//weight(kg) | height(cm) | class
         {51, 167,   1}, //underweight
         {62, 182,   0}, //Normal
         {69, 176,   0}, //Normal
         {64, 173,   0}, //Normal
         {65, 172,   0}, //Normal
         {56, 174,   1}, //Underweight
         {58, 169,   0}, //Normal
         {57, 173,   0}, //Normal
         {55, 170,   0}  //Normal
      };

手順02：ポイントからデータセットのすべてのメンバーまでのユークリッド距離を計算する

体格指数の計算方法がわからないとして、体重57kg、身長170cmの人がやせ型と普通型のどちらに属するかを知りたいとします。

    vector v = {57, 170};
    
    nearest_neighbors = new CKNNNearestNeighbors(Matrix); //calling the constructor and passing it the matrix
    nearest_neighbors.KNNAlgorithm(v);  //passing this new points to the algorithm

KNNAlgorithm関数が最初におこなうことは、指定されたポイントとデータセット内のすべてのポイントの間のユークリッド距離を見つけることです。

   vector vector_2;
   vector euc_dist;
   euc_dist.Resize(m_rows);
   
   matrix temp_matrix = Matrix;
   temp_matrix.Resize(Matrix.Rows(),Matrix.Cols()-1); //remove the last column of independent variables
   
   for (ulong i=0; i<m_rows; i++)
      {
         vector_2 = temp_matrix.Row(i);
         euc_dist[i] = Euclidean_distance(vector_,vector_2);
      }

ユークリッド距離関数の内部：

double CKNNNearestNeighbors:: Euclidean_distance(const vector &v1,const vector &v2)
 {
   double dist = 0;
   
   if (v1.Size() != v2.Size()) 
	Print(__FUNCTION__," v1 and v2 not matching in size");
   else
    {
       double c = 0;
         for (ulong i=0; i<v1.Size(); i++)
               c += MathPow(v1[i] - v2[i], 2); 

        dist = MathSqrt(c);
    } 
    
    return(dist);
 }

このライブラリで2点間の距離を測定する方法としてユークリッド距離を選択しましたが、これが唯一の方法ではなく、L₁-距離やマンハッタン距離、などのいくつかの方法を使用できます。いくつかは、以前の記事で議論されました。

Print("Euclidean distance vector\n",euc_dist);

Output  -----------> 

CS      0       19:29:09.057    TestScript   Euclidean distance vector
CS      0       19:29:09.057    TestScript   [6.7082,13,13.41641,7.61577,8.24621,4.12311,1.41421,3,2]

それでは、ユークリッド距離を行列の最後の列に埋め込みましょう。

   if (isdebug)
      {  
         matrix dbgMatrix = Matrix; //temporary debug matrix
         dbgMatrix.Resize(dbgMatrix.Rows(),dbgMatrix.Cols()+1);
         dbgMatrix.Col(euc_dist,dbgMatrix.Cols()-1);
         
         Print("Matrix w Euclidean Distance\n",dbgMatrix);
         
         ZeroMemory(dbgMatrix);
      }

出力

CS      0       19:33:48.862    TestScript   Matrix w Euclidean Distance
CS      0       19:33:48.862    TestScript   [[51,167,1,6.7082]
CS      0       19:33:48.862    TestScript    [62,182,0,13]
CS      0       19:33:48.862    TestScript    [69,176,0,13.41641]
CS      0       19:33:48.862    TestScript    [64,173,0,7.61577]
CS      0       19:33:48.862    TestScript    [65,172,0,8.24621]
CS      0       19:33:48.862    TestScript    [56,174,1,4.12311]
CS      0       19:33:48.862    TestScript    [58,169,0,1.41421]
CS      0       19:33:48.862    TestScript    [57,173,0,3]
CS      0       19:33:48.862    TestScript    [55,170,0,2]]

このデータを簡単に解釈できるようにイメージしてみましょう。

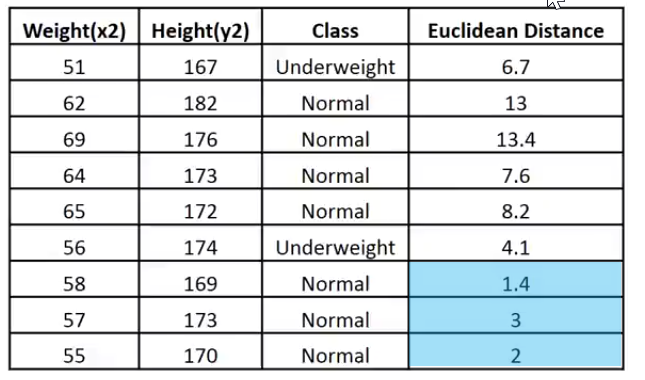
kの値が3の場合、3個の最近傍はすべてNormalクラスに分類されるため、指定されたポイントがNormalカテゴリに分類されることが手動でわかります。この決定をおこなうためのコードを作成しましょう。

最近傍を決定してそれらを追跡できるようにするために、ベクトルを使用するのは非常に困難です。配列は、スライスと再形成に対して柔軟です。それらを使用して、このプロセスをまとめましょう。

   int size = (int)m_target.Size();

   double tarArr[];
   ArrayResize(tarArr, size);
   double eucArray[];
   ArrayResize(eucArray, size);

   for(ulong i=0; i<m_target.Size(); i++)  //convert the vectors to array
     {
      tarArr[i] = m_target[i];
      eucArray[i] = euc_dist[i];
     }

   double track[], NN[];
   ArrayCopy(track, tarArr);


   int max; 
   for(int i=0; i<(int)m_target.Size(); i++)
     {
      if(ArraySize(track) > (int)k)
        {
         max = ArrayMaximum(eucArray);
         ArrayRemove(eucArray, max, 1);
         ArrayRemove(track, max, 1);
        }
     }
   ArrayCopy(NN, eucArray);

   Print("NN ");
   ArrayPrint(NN);
   Print("Track ");
   ArrayPrint(track);

上記のコードブロックでは、最近傍を決定し、それらをNN配列に格納します。また、それらのクラス値/ターゲット値のグローバルベクトルにあるクラスも追跡します。その上で、配列内の最大値を削除して、小さい値のkサイズの配列（最近隣）を残すまで削除します。

以下は出力です。

CS      0       05:40:33.825    TestScript    NN 
CS      0       05:40:33.825    TestScript    1.4 3.0 2.0
CS      0       05:40:33.825    TestScript    Track 
CS      0       05:40:33.825    TestScript    0.0 0.0 0.0

投票プロセス：

//--- Voting process

   vector votes(m_classesVector.Size());

   for(ulong i=0; i<votes.Size(); i++)
     {
      int count = 0;
      for(ulong j=0; j<track.Size(); j++)
        {
         if(m_classesVector[i] == track[j])
            count++;
        }

      votes[i] = (double)count;

      if(votes.Sum() == k)  //all members have voted
         break;
     }
   Print("votes ", votes);

出力

2022.10.31 05:40:33.825 TestScript   votes [0,3]

投票ベクトルは、データセットで使用可能なクラスのグローバルベクトルに基づいて投票を配置することを覚えていらっしゃるでしょうか。

2022.10.31 06:43:30.095 TestScript   classes vector | Neighbors [1,0]

これは、投票をおこなうために選択された3つの隣人のうち3人が、指定されたデータが0のクラスに属することに投票し、1のクラスに投票したメンバーはいないことを示しています。

5個の隣人が投票するように選ばれた場合、つまりKの値が5だった場合に何が起こるか見てみましょう。

CS      0       06:43:30.095    TestScript   NN 
CS      0       06:43:30.095    TestScript   6.7 4.1 1.4 3.0 2.0
CS      0       06:43:30.095    TestScript   Track 
CS      0       06:43:30.095    TestScript   1.0 1.0 0.0 0.0 0.0
CS      0       06:43:30.095    TestScript   votes [2,3]

これで、最終的な決定は、投票数が最も多いクラスが決定を勝ち取った簡単なものになります。この場合、指定された重みは、0としてエンコードされた通常のクラスに属します。

   if(isdebug)
      Print(vector_, " belongs to class ", (int)m_classesVector[votes.ArgMax()]);

出力

2022.10.31 06:43:30.095 TestScript      [57,170] belongs to class 0

これで、すべて正常に動作します。KNNAlgorithmのタイプをvoidからintに変更して、指定された値が属するクラスの値を返すようにしましょう。これはライブ取引で役立つ可能性があります。アルゴリズムからの即時の出力が期待されます。

   int               KNNAlgorithm(vector &vector_);

モデルをテストし、その精度を確認します。

モデルができたので、他の教師あり機械学習手法と同様に、モデルを訓練して、まだ見ていないデータでテストする必要があります。テストプロセスは、モデルがさまざまなデータセットでどのように機能するかを理解するのに役立ちます。

float TrainTest(double train_size=0.7)

デフォルトでは、データセットの70%が訓練に使用され、残りの30%がテストに使用されます。

訓練フェーズとテストフェーズのデータセットを分割する関数をコーディングする必要があります。

^//--- Split the matrix
   
   matrix default_Matrix = Matrix; 
   
   int train = (int)MathCeil(m_rows*train_size),
       test  = (int)MathFloor(m_rows*(1-train_size));
   
   if (isdebug) printf("Train %d test %d",train,test);

   matrix TrainMatrix(train,m_cols), TestMatrix(test,m_cols);
   int train_index = 0, test_index =0;

//---
   
   for (ulong r=0; r<Matrix.Rows(); r++)
      {
         if ((int)r < train)
           {
             TrainMatrix.Row(Matrix.Row(r),train_index);
             train_index++;
           }
         else
           {
             TestMatrix.Row(Matrix.Row(r),test_index);
             test_index++;
           }     
      }

   if (isdebug) Print("TrainMatrix\n",TrainMatrix,"\nTestMatrix\n",TestMatrix);

出力

CS      0       09:51:45.136    TestScript   TrainMatrix
CS      0       09:51:45.136    TestScript   [[51,167,1]
CS      0       09:51:45.136    TestScript    [62,182,0]
CS      0       09:51:45.136    TestScript    [69,176,0]
CS      0       09:51:45.136    TestScript    [64,173,0]
CS      0       09:51:45.136    TestScript    [65,172,0]
CS      0       09:51:45.136    TestScript    [56,174,1]
CS      0       09:51:45.136    TestScript    [58,169,0]]
CS      0       09:51:45.136    TestScript   TestMatrix
CS      0       09:51:45.136    TestScript   [[57,173,0]
CS      0       09:51:45.136    TestScript    [55,170,0]]

したがって、最近傍アルゴリズムの訓練は非常に単純です。訓練がまったくないと考えるかもしれません。前に述べたように、このアルゴリズム自体は、ロジスティック回帰や SVM などの方法とは異なり、データセット内のパターンを理解しようとはしません。トレーニング中にデータを保存するだけで、このデータはテスト目的で使用されます。

訓練

   Matrix.Copy(TrainMatrix); //That's it ???

テスト

//--- Testing the Algorithm
   
   vector TestPred(TestMatrix.Rows());
   vector v_in = {};
   
   for (ulong i=0; i<TestMatrix.Rows(); i++)
     {
        v_in = TestMatrix.Row(i);
        v_in.Resize(v_in.Size()-1); //Remove independent variable
        
        TestPred[i] = KNNAlgorithm(v_in);
        
        Print("v_in ",v_in," out ",TestPred[i]);
     }

出力

CS      0       09:51:45.136    TestScript   v_in [57,173] out 0.0
CS      0       09:51:45.136    TestScript   v_in [55,170] out 0.0

与えられたデータセットでモデルがどれだけ正確かを測定しなければ、すべてのテストは無駄になります。

混同行列

この連載の第2稿で説明しました。

matrix CKNNNearestNeighbors::ConfusionMatrix(vector &A,vector &P)
 {
   ulong size = m_classesVector.Size();
   matrix mat_(size,size);
   
   if (A.Size() != P.Size()) 
      Print("Cant create confusion matrix | A and P not having the same size ");
   else
     {
      
         int tn = 0,fn =0,fp =0, tp=0;
         for (ulong i = 0; i<A.Size(); i++)
            {              
               if (A[i]== P[i] && P[i]==m_classesVector[0])
                  tp++; 
               if (A[i]== P[i] && P[i]==m_classesVector[1])
                  tn++;
               if (P[i]==m_classesVector[0] && A[i]==m_classesVector[1])
                  fp++;
               if (P[i]==m_classesVector[1] && A[i]==m_classesVector[0])
                  fn++;
            }
            
       mat_[0][0] = tn; mat_[0][1] = fp;
       mat_[1][0] = fn; mat_[1][1] = tp;

    }
     
   return(mat_);    
 }

関数の最後にあるTrainTest（）内に、次のコードを追加して関数を終了し、精度を返します。

   matrix cf_m = ConfusionMatrix(TargetPred,TestPred);
   vector diag = cf_m.Diag();
   float acc = (float)(diag.Sum()/cf_m.Sum())*100;
   
   Print("Confusion Matrix\n",cf_m,"\nAccuracy ------> ",acc,"%");
   
   return(acc);

出力

CS      0       10:34:26.681    TestScript   Confusion Matrix
CS      0       10:34:26.681    TestScript   [[2,0]
CS      0       10:34:26.681    TestScript    [0,0]]
CS      0       10:34:26.681    TestScript   Accuracy ------> 100.0%

もちろん、精度は100%である必要がありました。モデルには、テスト用に2つのデータポイントのみが与えられました。これらのデータポイントはすべて、ゼロのクラス（通常のクラス）に属していました。これは真実です。

ここまでで、完全に機能するk近傍法ライブラリが完成しました。それを使用して、さまざまな外国為替商品と株式の価格を予測する方法を見てみましょう。

データセットの準備

これは教師あり学習であり、データを作成してラベルを付けるために人間の介入が必要であることを忘れないでください。これにより、モデルは目標が何であるかを認識し、独立変数とターゲット変数の間の関係を理解できるようになります。

選択する独立変数は、ATRとボリューム指標からの読み取り値です。ターゲット変数は、市場が上昇した場合は1に設定され、市場が下落した場合は0に設定されます。これは、モデルをテストおよび使用して取引するときに、それぞれ買いシグナルと売りシグナルになります。

int OnInit()
  {
//--- Preparing the dataset 

    atr_handle = iATR(Symbol(),timeframe,period);
    volume_handle = iVolumes(Symbol(),timeframe,applied_vol);
    
    CopyBuffer(atr_handle,0,1,bars,atr_buffer);
    CopyBuffer(volume_handle,0,1,bars,volume_buffer); 
    
    Matrix.Col(atr_buffer,0); //Independent var 1
    Matrix.Col(volume_buffer,1); //Independent var 2
    
//--- Target variables

    vector Target_vector(bars);
    
    MqlRates rates[];
    ArraySetAsSeries(rates,true);
    CopyRates(Symbol(),PERIOD_D1,1,bars,rates);
    
    for (ulong i=0; i<Target_vector.Size(); i++) //putting the labels
     {
       if (rates[i].close > rates[i].open)
          Target_vector[i] = 1; //bullish
       else
          Target_vector[i] = 0;
     }

   Matrix.Col(Target_vector,2);
        
//---

独立変数を見つけるロジックは、ローソク足の終値が強気のローソク足の始値を上回っていた場合です。独立変数のターゲット変数は1で、それ以外の場合は0です。

ここで、日足を使用していることを思い出してください。1本のローソク足には24時間で多くの価格変動があります。このロジックは、スキャルパーまたはより短い期間で取引されるものを作成しようとする場合には適切ではない可能性があります。小さな欠陥もあります。ロジックでは、終値が始値よりも大きい場合、ターゲット変数を1として示します。それ以外の場合は0を示しますが、始値が終値と等しい場合がよくあります。理解はしていますが、この状況がより長い時間枠で発生することはめったにないため、これは私がモデルにエラーの余地を与える方法です。

ちなみに、これは金融や取引のアドバイスではありません。

最後の10本のバーの値、データセット行列の10行を出力してみましょう。

CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)   ATR,Volumes,Class Matrix
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)   [[0.01139285714285716,12295,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01146428571428573,12055,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01122142857142859,10937,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01130000000000002,13136,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01130000000000002,15305,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01097857142857144,13762,1]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.0109357142857143,12545,1]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01116428571428572,18806,1]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01188571428571429,19595,1]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01137142857142859,15128,1]]

データはそれぞれのローソク足と指標から適切に分類されています。それをアルゴリズムに渡しましょう。

    nearest_neigbors = new CKNNNearestNeighbors(Matrix,k); 
    nearest_neigbors.TrainTest();

出力

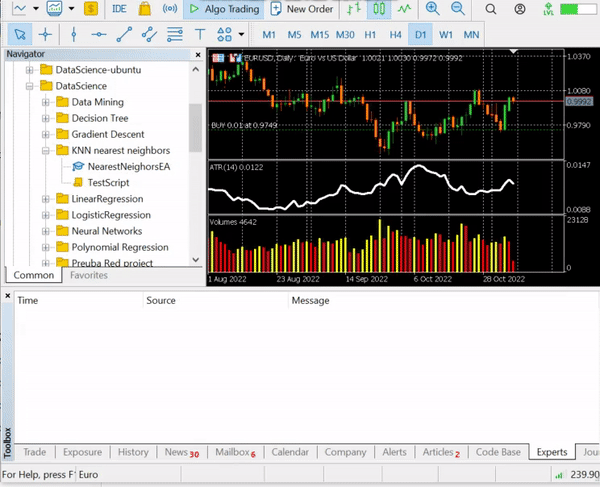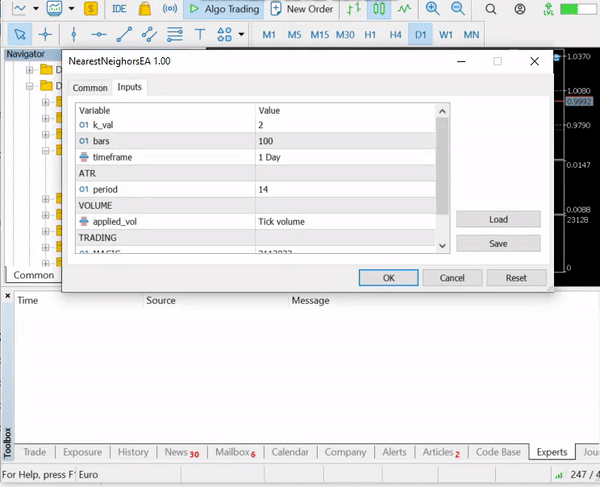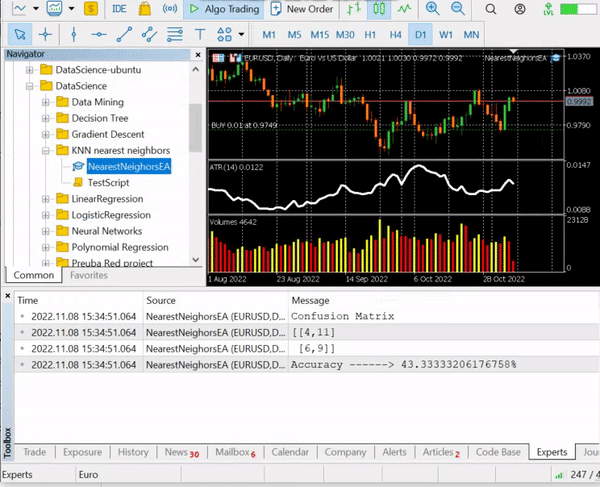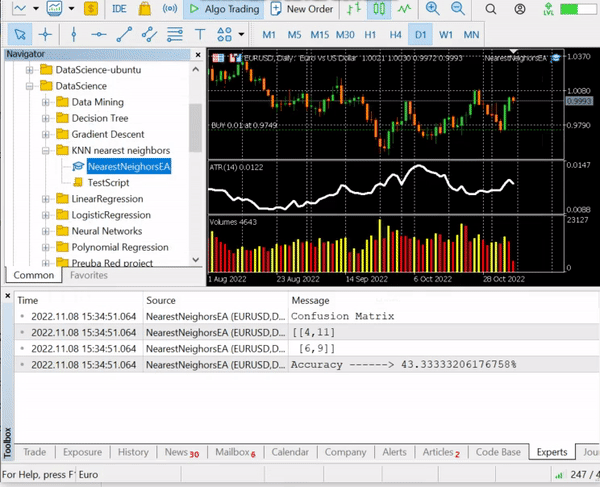
約43.33%の精度があり、kの最適値をわざわざ見つけなかったことを考えると悪くありません。さまざまなkの値をループして、より精度の高い値を選択してみましょう。

    for(uint i=0; i<bars; i++)
      {
        printf("<<< k %d >>>",i);
        nearest_neigbors = new CKNNNearestNeighbors(Matrix,i); 
        nearest_neigbors.TrainTest(); 
        
        delete(nearest_neigbors);
      }

出力

......
CS      0       16:22:28.013    NearestNeighorsEA (EURUSD,D1)   <<< k 24 >>>
CS      0       16:22:28.013    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 46.66666793823242%
CS      0       16:22:28.014    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 46.66666793823242%
CS      0       16:22:28.014    NearestNeighorsEA (EURUSD,D1)   <<< k 26 >>>
CS      0       16:22:28.014    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 40.0%
CS      0       16:22:28.014    NearestNeighorsEA (EURUSD,D1)   <<< k 27 >>>
CS      0       16:22:28.015    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 40.0%
CS      0       16:22:28.015    NearestNeighorsEA (EURUSD,D1)   <<< k 28 >>>
CS      0       16:22:28.015    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.016    NearestNeighorsEA (EURUSD,D1)   <<< k 29 >>>
CS      0       16:22:28.016    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.016    NearestNeighorsEA (EURUSD,D1)   <<< k 30 >>>
.....
.....
CS      0       16:22:28.017    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 60.000003814697266%
CS      0       16:22:28.017    NearestNeighorsEA (EURUSD,D1)   <<< k 31 >>> 
CS      0       16:22:28.017    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 60.000003814697266%
CS      0       16:22:28.017    NearestNeighorsEA (EURUSD,D1)   <<< k 32 >>> 
CS      0       16:22:28.018    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.018    NearestNeighorsEA (EURUSD,D1)   <<< k 33 >>> 
CS      0       16:22:28.018    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.018    NearestNeighorsEA (EURUSD,D1)   <<< k 34 >>> 
CS      0       16:22:28.019    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 50.0%
CS      0       16:22:28.019    NearestNeighorsEA (EURUSD,D1)   <<< k 35 >>> 
CS      0       16:22:28.019    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 50.0%
CS      0       16:22:28.019    NearestNeighorsEA (EURUSD,D1)   <<< k 36 >>> 
CS      0       16:22:28.020    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 53.333335876464844%
CS      0       16:22:28.020    NearestNeighorsEA (EURUSD,D1)   <<< k 37 >>> 
CS      0       16:22:28.020    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 53.333335876464844%
CS      0       16:22:28.020    NearestNeighorsEA (EURUSD,D1)   <<< k 38 >>> 
CS      0       16:22:28.021    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.021    NearestNeighorsEA (EURUSD,D1)   <<< k 39 >>> 
CS      0       16:22:28.021    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.021    NearestNeighorsEA (EURUSD,D1)   <<< k 40 >>> 
CS      0       16:22:28.022    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.022    NearestNeighorsEA (EURUSD,D1)   <<< k 41 >>>
.....
....
CS      0       16:22:28.023    NearestNeighorsEA (EURUSD,D1)   <<< k 42 >>>
CS      0       16:22:28.023    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 63.33333206176758%
CS      0       16:22:28.023    NearestNeighorsEA (EURUSD,D1)   <<< k 43 >>>
CS      0       16:22:28.024    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 63.33333206176758%
CS      0       16:22:28.024    NearestNeighorsEA (EURUSD,D1)   <<< k 44 >>>
CS      0       16:22:28.024    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 66.66667175292969%
CS      0       16:22:28.024    NearestNeighorsEA (EURUSD,D1)   <<< k 45 >>>
CS      0       16:22:28.025    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 66.66667175292969%
CS      0       16:22:28.025    NearestNeighorsEA (EURUSD,D1)   <<< k 46 >>>
CS      0       16:22:28.025    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.025    NearestNeighorsEA (EURUSD,D1)   <<< k 47 >>>
....
....

kの値を決定するこの方法は最善の方法ではありませんが、一つ抜き交差検証法を使用してkの最適値を見つけることができます。どうやら、パフォーマンスのピークはkの値が40代のときだったようです。取引環境でアルゴリズムを使用する時が来ました。

void OnTick()
  {
  
    vector x_vars(2); //vector to store atr and volumes values
    double atr_val[], volume_val[];
    
    CopyBuffer(atr_handle,0,0,1,atr_val);
    CopyBuffer(volume_handle,0,0,1,volume_val);
    
    x_vars[0] = atr_val[0]; 
    x_vars[1] = volume_val[0];
    
//---
    int signal = 0;
    
    double volume = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN);
    
    MqlTick ticks;
    SymbolInfoTick(Symbol(),ticks);
    
    double ask = ticks.ask, bid = ticks.bid;
    
    
      if (isNewBar() == true) //we are on the new candle
         {
            signal = nearest_neigbors.KNNAlgorithm(x_vars); //Calling the algorithm
            
            if (signal == 1)
              {
                 if (!CheckPosionType(POSITION_TYPE_BUY))
                  {
                    m_trade.Buy(volume,Symbol(),ask,0,0);
                    if (ClosePosType(POSITION_TYPE_SELL))
                      printf("Failed to close %s Err = %d",EnumToString(POSITION_TYPE_SELL),GetLastError());
                  }
              }
            else 
              {
                if (!CheckPosionType(POSITION_TYPE_SELL))
                  {
                    m_trade.Sell(volume,Symbol(),bid,0,0);
                    if (ClosePosType(POSITION_TYPE_BUY))
                      printf("Failed to close %s Err = %d",EnumToString(POSITION_TYPE_BUY),GetLastError());
                  }
              }
         }
     
  }

EAが取引を開始して終了できるようになったので、ストラテジーテスターで試してみましょう。その前に、エキスパートアドバイザー(EA)全体でのアルゴリズム呼び出しの概要を以下に示します。

#include "KNN_nearest_neighbors.mqh";
CKNNNearestNeighbors *nearest_neigbors;

matrix Matrix;
//+------------------------------------------------------------------+
//| Expert initialization function                                     |
//+------------------------------------------------------------------+
int OnInit()
  { 
// gathering data to Matrix has been ignored
    
     nearest_neigbors = new CKNNNearestNeighbors(Matrix,_k); 
 
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- 

    delete(nearest_neigbors);
  }

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+

void OnTick()
  {
  
    vector x_vars(2); //vector to store atr and volumes values

//adding live indicator values from the market has been ignored 

//---
    int signal = 0;

      if (isNewBar() == true) //we are on the new candle
         {
            signal = nearest_neigbors.KNNAlgorithm(x_vars);
            //trading actions
         }
}

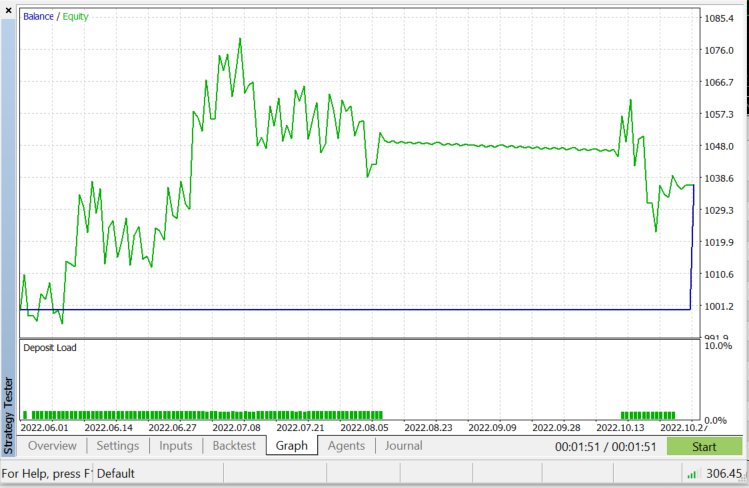
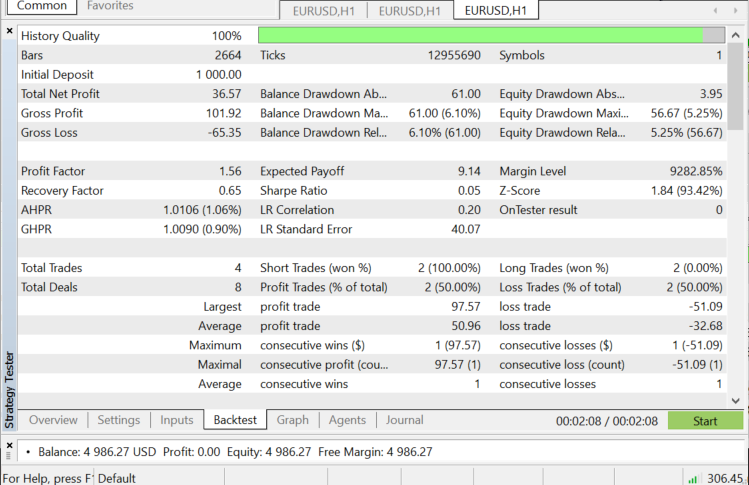
EURUSDのストラテジーテスター：2022.06.01から2022.11.03まで（すべてのティック）：

KNNをいつ使用するか

このアルゴリズムをどこで使用するかを知ることは非常に重要です。なぜなら、すべての問題がすべての機械学習技術のように解決できるわけではないからです。

データセットがラベル付けされている場合
データセットにノイズがない場合
データセットが小さい場合（これはパフォーマンス上の理由からも役立ちます）

メリット

理解して実装するのは非常に簡単です。
これはローカルデータポイントに基づいており、ローカルクラスターを持つ多くのグループを含むデータセットに役立つ可能性があります。

欠点

すべての訓練データは、何かを予測する必要があるたびに使用されます。つまり、すべてのデータを保存し、分類する新しいポイントが発生するたびに使用できるようにしておく必要があります。

最後に

前に述べたように、このアルゴリズムは優れた分類器ですが、複雑なデータセットではそうではありません。そのため、株式や指数のより良い予測子になると思います。ご自分でお試しください。EAでこのアルゴリズムをテストすると、ストラテジーテスターでパフォーマンスの問題が発生することがわかります。これは、50本のバーを選択し、新しいバーでロボットにアクションをとらせたにもかかわらずです。テスターは、アルゴリズムがプロセス全体を実行できるようにするために、すべてのローソク足で20秒から30秒ほど立ち往生しますが、ライブ取引ではプロセスが高速になります。テスターでは正反対です。Init関数で指標の読み取り値を抽出できなかったため、特に次のコード行の下では、改善の余地が常にあります。そのため、それらを抽出して訓練し、市場を予測するためにすべて1か所で使用する必要がありました。

        if (isNewBar() == true) //we are on the new candle
         { 
           if (MQLInfoInteger(MQL_TESTER) || MQLInfoInteger(MQL_OPTIMIZATION)) 
             {
               gather_data();      
               nearest_neigbors = new CKNNNearestNeighbors(Matrix,_k); 
               signal = nearest_neigbors.KNNAlgorithm(x_vars);
               
               delete(nearest_neigbors);
             }

ご精読ありがとうございました。

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/11678

添付されたファイル |

ZIPをダウンロード

KNN_nearest_neighbors.zip (67.49 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。