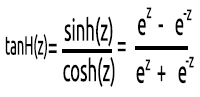
Aprendizaje automático y Data Science - Redes neuronales (Parte 01): Análisis de redes neuronales con conexión directa
"...cansado de saber demasiado y entender muy poco".
- Jan Karon, «La Casa de Holly Springs»
Introducción
Las redes neuronales parecen una nueva moda que ofrece una forma de acercarse al Santo Grial del trading. Los programas basados en redes neuronales impresionan porque parecen buenos a la hora de predecir los movimientos del mercado, y son generalmente buenos en cualquier tarea. Yo también creo que tienen un gran potencial a la hora de predecir o clasificar partiendo de nuevos datos no preparados.
Pero, por muy buenas que sean, las redes son creadas y optimizadas por personas que entiendan lo que están haciendo. Debemos entender que no solo el perceptrón multicapa debe tener la arquitectura adecuada, sino que el propio tipo de problema a resolver deberá involucrar a las redes neuronales, no solo a los modelos de regresión lineal o logística o cualquier otro método de aprendizaje automático.
Visto que las redes neuronales son un tema muy amplio, al igual que el aprendizaje automático en general, he decidido iniciar una subserie aparte. Así que continuaremos analizando otros aspectos del aprendizaje automático en otra rama de esta serie.
En este artículo, veremos los fundamentos de las redes neuronales y desglosaremos algunas de las cuestiones básicas que creo importantes para que los entusiastas del aprendizaje automático puedan dominar el campo.
¿Qué es una red neuronal artificial?
Las redes neuronales artificiales (RNA, redes neuronales) son sistemas informáticos inspirados en las redes neuronales biológicas de un cerebro vivo.
Perceptrón multicapa y red neuronal profunda
En las discusiones sobre redes neuronales, es frecuente encontrar el término Perceptrón Multicapa (MLP). Se trata del tipo de red neuronal más común. Un perceptrón multicapa constituye una red formada por una capa de entrada, una capa oculta y una capa de salida. A causa de su simplicidad, requieren una corta curva de aprendizaje para aprender la representación de los datos y producir resultados.
Esferas de aplicación:
El perceptrón multicapa suele usarse para datos que no son linealmente separables, como el análisis de regresión. Debido a su simplicidad, resultan los más adecuados para tareas complejas de clasificación y modelización predictiva. Se utilizan para la traducción automática, la previsión meteorológica, la detección de fraudes, las previsiones en el mercado de valores, las predicciones de calificación crediticia y muchos otros aspectos.
Las redes neuronales profundas, en cambio, comparten una estructura común pero contienen demasiadas capas ocultas. Si su red contiene más de tres (3) capas ocultas, podrá considerarla una red neuronal profunda. Debido a su naturaleza compleja, dichas redes requieren largos periodos de entrenamiento para la red con los datos de entrada, y también necesitan potentes computadoras con unidades de procesamiento especializadas, como las unidades de procesamiento tensorial (TPU) y los procesadores de aprendizaje profundo.
Esferas de aplicación:
Debido a la profundidad de sus capas, las redes neuronales profundas son algoritmos potentes, por lo que suelen usarse para tareas de cálculo complejas. Uno de estos retos es la visión por computadora.
Tabla de diferencias:
| Perceptrón multicapa | Red neuronal profunda |
|---|---|
| El número de capas ocultas es pequeño | El número de capas ocultas es grande |
| Aprendizaje rápido | Largos periodos de entrenamiento |
| Bastará con un hardware con GPU | Requiere un equipo con TPU |
Echemos un vistazo ahora a los tipos de redes neuronales.
Existen muchos tipos de redes neuronales y se dividen en tres clases principales:
- Redes neuronales con conexión directa
- Redes neuronales convolucionales
- Redes neuronales recurrentes
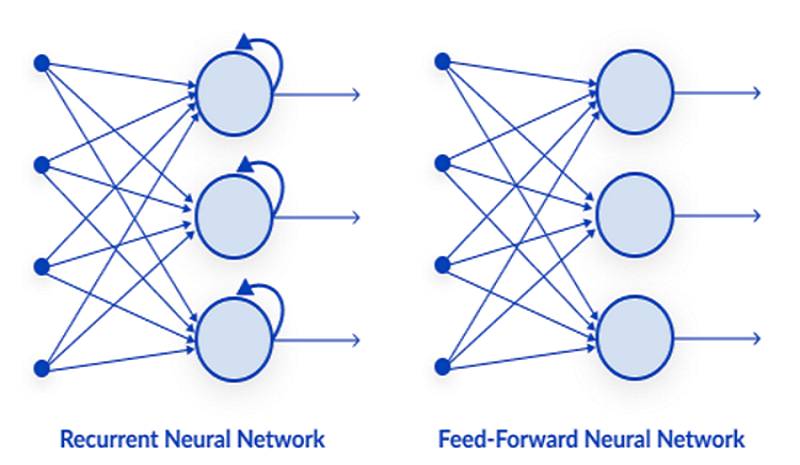
01: Red neuronal con conexión directa
Es uno de los tipos más simples de red neuronal. Aquí los datos pasan por los distintos nodos de entrada hasta alcanzar el nodo de salida. A diferencia del método de propagación inversa, aquí los datos se transmiten en una sola dirección.
En pocas palabras, la propagación inversa realiza los mismos procesos en una red neuronal que la propagación directa, en la que los datos se transfieren de la capa de entrada a la de salida, salvo que en la propagación inversa, una vez que la salida de la red llega a la capa de salida, recibe el valor real de la clase. Comparándolo con el valor pronosticado, el modelo verifica si sus predicciones han sido erróneas o correctas. Si la predicción es incorrecta, los datos se devolverán a la red y los parámetros se actualizarán para corregir la predicción. Esto sería un algoritmo de autoaprendizaje.
02: Red neuronal recurrente
Una red neuronal recurrente es un tipo de red neuronal artificial en la que la salida de una capa concreta se guarda y vuelve a la capa de entrada. Esto ayuda a predecir el resultado de la capa.
Las redes neuronales recurrentes se usan para resolver problemas relacionados con:
- Datos de series temporales
- Datos de texto
- Datos de audio
El uso más común en los datos de texto es la recomendación de las siguientes palabras para la IA, por ejemplo Cómo + se + siente + ...
03: Red neuronal convolucional
Las redes neuronales convolucionales se utilizan con mucha frecuencia. Por ejemplo, en proyectos de procesamiento de imágenes y vídeos.
Así, la inteligencia artificial (IA) para la detección y clasificación de imágenes consta en redes neuronales convolucionales.
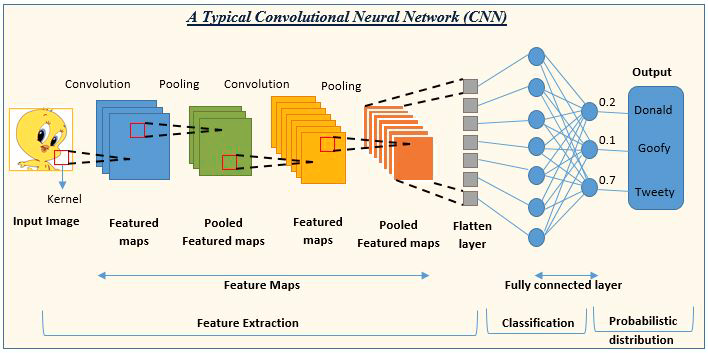
Fuente de la imagen: analyticsvidhya.com
Ya hemos visto los tipos de redes neuronales, ahora nos centraremos en el tema principal de este artículo las redes neuronales con conexión directa.
Redes neuronales con conexión directa
A diferencia de otros tipos de redes neuronales más complejas, en este tipo de red neuronal no hay propagación inversa, es decir, los datos solo se transmiten en una dirección. Una red neuronal con conexión directa puede tener una o más capas ocultas.
El siguiente esquema muestra cómo funciona esta red neuronal.
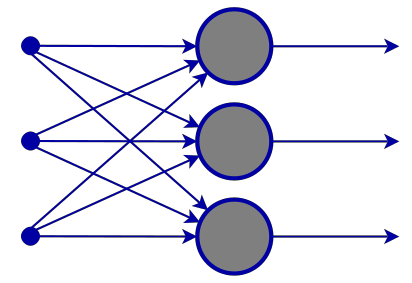
Capa de entrada
El esquema de la red neuronal muestra que hay una capa de entrada. En el fondo, una capa de entrada es simplemente una representación de los datos. En la capa de entrada no se realizan cálculos.
Capa oculta
La capa oculta es donde se realiza la mayor parte del trabajo de la red neuronal.
Para entender mejor cómo funciona, analizaremos un nodo de la segunda capa oculta.
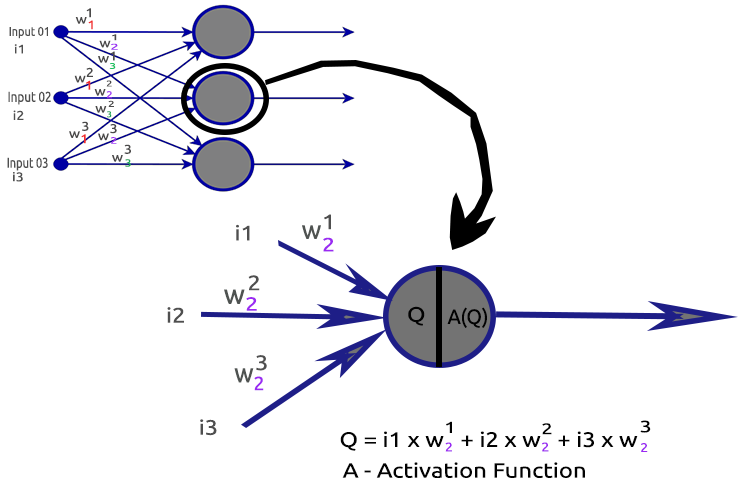
Procesos implicados:
- Hallazgo del producto escalar de los datos de entrada y sus respectivas pesos
- Adición del producto escalar resultante al desplazamiento
- Transmisión del resultado de la segunda acción a la función de activación
¿Qué es el desplazamiento?
El desplazamiento permite mover a la regresión lineal se hacia arriba y hacia abajo para ajustar mejor la línea de predicción a los datos. Es lo mismo que Intercept en la regresión lineal.
Este parámetro se explicará mejor en la sección Perceptrón multicapa con un solo nodo en la capa oculta.
La importancia del desplazamiento también está bien explicada en este hilo.
¿Qué son los coeficientes de peso?
Los pesos reflejan la importancia de las entradas, y actúan como coeficientes de la ecuación que se intenta resolver. Los pesos negativos reducen el valor de la salida, y viceversa. Cuando una red neuronal se entrena con un conjunto de datos, se inicializa con un conjunto de pesos. Dichos pesos se optimizan durante el periodo de entrenamiento y se obtiene el valor óptimo de los pesos.
¿Qué es la función de activación?
La función de activación no es más que una función matemática que toma los datos de entrada y produce una señal de salida.
Tipos de funciones de activación
Hay muchas funciones de activación con sus variantes, pero aquí están las más usadas:
- Relu
- Sigmoide
- TanH
- Softmax
Es muy importante saber qué función de activación usar y dónde hacerlo. Dicho esto, cuántas veces me he encontrado con artículos en internet que sugieren que la función de activación debe usarse donde no corresponde. Veamos los tipos con más detalle.
01: RELU
RELU significa «unidad lineal rectificada».
Es la función de activación más usada en las redes neuronales. Resulta más simple que otras, es fácil de escribir como código y su resultado es fácil de interpretar, por eso es tan popular. Esta función emite los datos directamente si la capa de entrada es un número positivo; en caso contrario, emite cero.
La lógica es la siguiente
if x < 0 : return 0
else return x
Esta función se usa mejor al resolver problemas de regresión.
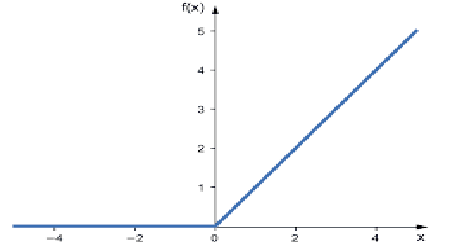
Los valores de salida van de cero a infinito positivo.
En MQL5, el código de la función será el siguiente:
double CNeuralNets::Relu(double z) { if (z < 0) return(0); else return(z); }
La RELU resuelve el problema del gradiente de fuga que sufren las funciones sigmoideas y TanH (para más detalles, podrá leer el artículo sobre la propagación inversa).
02: Sigmoide
¿Le resulta familiar? ¿Recuerda el artículo sobre la regresión logística?
La fórmula sigmoidea es la siguiente:
![]()
El uso de esta función resulta más adecuado en tareas de clasificación, especialmente al clasificar solo una o dos clases.
Los valores de salida van de cero a uno (probabilidad).
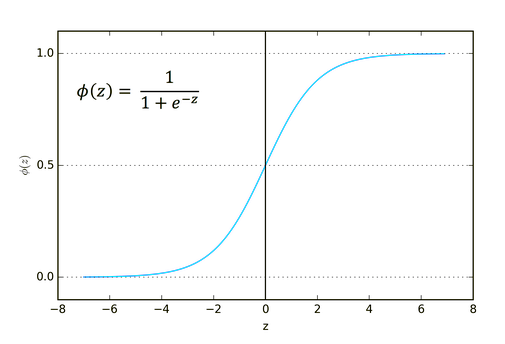
Por ejemplo, su red tiene dos nodos en la salida. El primer nodo es para el gato y el segundo para el perro. Si la salida del primer nodo es mayor que 0,5, esto indicará un gato, y al contrario para el perro.
En MQL5, el código de la función será el siguiente:
double CNeuralNets::Sigmoid(double z) { return(1.0/(1.0+MathPow(e,-z))); }
03: TanH
La función de tangente hiperbólica.
Esta función viene dada por la fórmula
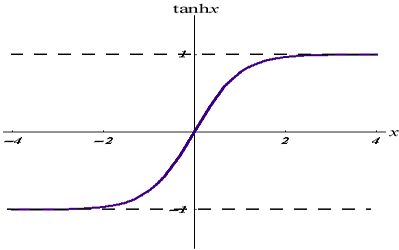
Su horario es el siguiente:
Esta función de activación es similar a la sigmoidea, pero mejor.
Sus valores de salida van de -1 a 1.
El uso de esta función resulta adecuado para redes neuronales de clasificación multiclase.
Su código MQL5 se muestra a continuación:
double CNeuralNets::tanh(double z) { return((MathPow(e,z) - MathPow(e,-z))/(MathPow(e,z) + MathPow(e,-z))); }
04: SoftMax
Alguien preguntó una vez por qué no existía un gráfico de la función SoftMax. A diferencia de las otras funciones de activación, SoftMax no se usa en las capas ocultas, sino solo en la capa de salida, y solo debe utilizarse cuando queremos convertir la salida de una red neuronal multiclase en términos de probabilidad.
La función SoftMax predice una distribución de probabilidad polinómica.
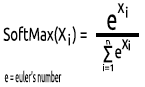
Por ejemplo, tenemos las salidas de una red neuronal de regresión: [1,3,2]. Si aplicamos la función SoftMax a este valor de salida, la salida pasará a ser [0,09003, 0,665240, 0,244728].
Los valores de salida de esta función van de 0 hasta 1.
En MQL5, el código de la función será el siguiente:
void CNeuralNets::SoftMax(double &Nodes[]) { double TempArr[]; ArrayCopy(TempArr,Nodes); ArrayFree(Nodes); double proba = 0, sum=0; for (int j=0; j<ArraySize(TempArr); j++) sum += MathPow(e,TempArr[j]); for (int i=0; i<ArraySize(TempArr); i++) { proba = MathPow(e,TempArr[i])/sum; Nodes[i] = proba; } ArrayFree(TempArr); }
Ahora que entendemos en qué consiste una neurona de la capa oculta, procederemos a escribir su código.
void CNeuralNets::Neuron(int HLnodes, double bias, double &Weights[], double &Inputs[], double &Outputs[] ) { ArrayResize(Outputs,HLnodes); for (int i=0, w=0; i<HLnodes; i++) { double dot_prod = 0; for(int j=0; j<ArraySize(Inputs); j++, w++) { if (m_debug) printf("i %d w %d = input %.2f x weight %.2f",i,w,Inputs[j],Weights[w]); dot_prod += Inputs[j]*Weights[w]; } Outputs[i] = ActivationFx(dot_prod+bias); } }
Dentro de ActivationFx(), podemos seleccionar qué función de activación se ha seleccionado al llamar al constructor NeuralNets.
double CNeuralNets::ActivationFx(double Q) { switch(A_fx) { case SIGMOID: return(Sigmoid(Q)); break; case TANH: return(tanh(Q)); break; case RELU: return(Relu(Q)); break; default: Print("Unknown Activation Function"); break; } return(0); }
Explicaciones adicionales sobre el código:
La función Neuron() no es solo un nodo dentro de una capa oculta, todas las operaciones de la capa oculta se realizan dentro de esta función. Los nodos de todas las capas ocultas tendrán el mismo tamaño que el nodo de entrada, hasta el nodo de salida final. He seleccionado esta estructura porque voy a realizar una clasificación usando esta red neuronal en un conjunto de datos generados aleatoriamente.
La siguiente, función a continuación, FeedForwardMLP(), es una estructura NxN, es decir, si tenemos tres nodos de entrada y seleccionamos tres capas ocultas, cada capa oculta tendrá tres nodos ocultos. Echemos un vistazo a la figura:
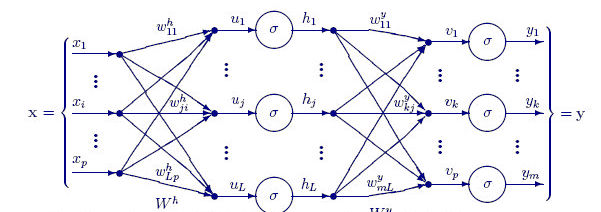
A continuación, mostramos la función FeedForwardMLP():
void CNeuralNets::FeedForwardMLP(int HiddenLayers, double &MLPInputs[], double &MLPWeights[], double &bias[], double &MLPOutput[]) { double L_weights[], L_inputs[], L_Out[]; ArrayCopy(L_inputs,MLPInputs); int HLnodes = ArraySize(MLPInputs); int no_weights = HLnodes*ArraySize(L_inputs); int weight_start = 0; for (int i=0; i<HiddenLayers; i++) { if (m_debug) printf("<< Hidden Layer %d >>",i+1); ArrayCopy(L_weights,MLPWeights,0,weight_start,no_weights); Neuron(HLnodes,bias[i],L_weights,L_inputs,L_Out); ArrayCopy(L_inputs,L_Out); ArrayFree(L_Out); ArrayFree(L_weights); weight_start += no_weights; } if (use_softmax) SoftMax(L_inputs); ArrayCopy(MLPOutput,L_inputs); if (m_debug) { Print("\nFinal MLP output(s)"); ArrayPrint(MLPOutput,5); } }
Las operaciones de búsqueda de productos escalares en una red neuronal podrían realizarse usando operaciones matriciales. No obstante, para dejar las cosas claras a todo el mundo en este primer artículo, he elegido el método del ciclo. La próxima vez usaremos la multiplicación de matrices.
Ya nos hemos familiarizado con la arquitectura seleccionada por defecto para construir nuestra biblioteca. Ahora surge la cuestión de la(s) arquitectura(s) de las redes neuronales.
Si abrimos Google y buscamos imágenes de redes neuronales, veremos miles, si no decenas de miles de imágenes con diferentes estructuras de redes neuronales, por ejemplo, como estas:
Ahora, la pregunta del millón: ¿qué arquitectura de red neuronal es la mejor?
«Nadie está tan lejos de la verdad como quien conoce las respuestas a todas las preguntas».
Vamos a profundizar en el tema y entenderemos qué es necesario y qué no.
Capa de entradaEl número de entradas que componen esta capa debe ser igual al número de características (columnas del conjunto de datos).
Capa de salida
La definición del tamaño (número de neuronas) viene definida por las clases del conjunto de datos para la red neuronal de clasificación. Para las tareas de tipo regresivo, el número de neuronas vendrá determinado por la configuración del modelo elegido. Para un regresor, una capa de salida suele ser más que suficiente.
Capas ocultas
Si la tarea no es muy complicada, una o dos capas ocultas bastarán. De hecho, dos capas ocultas serán suficientes para la gran mayoría de los problemas. Pero, ¿cuántos nodos debe haber en cada capa oculta? No estoy seguro de esto, pero creo que dependerá del rendimiento. Es decir, será precisamente el desarrollador quien deberá explorar y probar diferentes nodos para ver qué es lo que mejor funciona para un determinado tipo de tarea. Antes de jugar con los nodos, deberemos ocuparnos de los otros tipos de redes neuronales de los que hemos hablado antes.
Hay un hilo estupendo sobre este tema en stats.stackexchange.com (adjunto aquí el enlace.
Creo que el mismo número de nodos que la capa de entrada para todas las capas ocultas sería ideal para una red neuronal con conexión directa. Estos son los ajustes con los que trabajo la mayor parte del tiempo.
Perceptrón multicapa con un nodo y una capa oculta - modelo lineal
Si prestamos atención a las operaciones realizadas dentro de un solo nodo de la capa oculta de la red neuronal, veremos lo siguiente:
Q = wi * Ii + b
Y aquí tenemos la ecuación de regresión lineal:
Y = mi * xi + c
¿Nota el parecido? Teóricamente es lo mismo: esta operación es una regresión lineal, lo cual nos lleva de nuevo a la importancia del desplazamiento de la capa oculta. El desplazamiento es una constante para un modelo lineal, lo cual añade flexibilidad a nuestro modelo para ajustarse a un conjunto de datos determinado. Sin él, todos los modelos pasarán entre los ejes x e y en el punto cero (0).
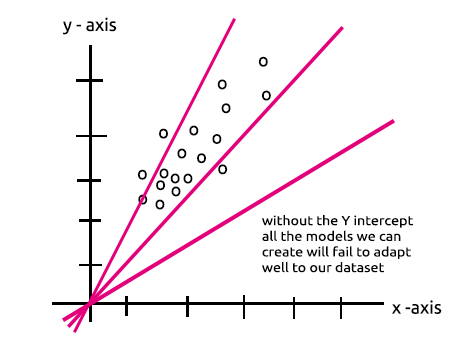
Los pesos y los desplazamientos se actualizarán a medida que se entrene la red neuronal. Los parámetros que produzcan menos errores para nuestro modelo serán guardados y recordados en el conjunto de datos para las pruebas.
Ahora construiremos un modelo de perceptrón multicapa para clasificar las dos clases. Esto nos ayudará a comprender mejor el uso. Pero antes de hacerlo, generaremos el conjunto de datos aleatorio con datos marcados con los que trabajará nuestra red neuronal. La función mostrada a continuación crea un conjunto aleatorio de datos: el segundo conjunto se multiplicará por 5 y el primer conjunto se multiplicará por 2 solo para obtener datos a diferentes escalas.
void MakeBlobs(int size=10) { ArrayResize(data_blobs,size); for (int i=0; i<size; i++) { data_blobs[i].sample_1 = (i+1)*(2); data_blobs[i].sample_2 = (i+1)*(5); data_blobs[i].class_ = (int)round(nn.MathRandom(0,1)); } }
El resultado será un conjunto de datos como éste:
QK 0 18:27:57.298 TestScript (EURUSD,M1) CNeural Nets Initialized activation = SIGMOID UseSoftMax = No IR 0 18:27:57.298 TestScript (EURUSD,M1) [sample_1] [sample_2] [class_] LH 0 18:27:57.298 TestScript (EURUSD,M1) [0] 2.0000 5.0000 0 GG 0 18:27:57.298 TestScript (EURUSD,M1) [1] 4.0000 10.0000 0 NL 0 18:27:57.298 TestScript (EURUSD,M1) [2] 6.0000 15.0000 1 HJ 0 18:27:57.298 TestScript (EURUSD,M1) [3] 8.0000 20.0000 0 HQ 0 18:27:57.298 TestScript (EURUSD,M1) [4] 10.0000 25.0000 1 OH 0 18:27:57.298 TestScript (EURUSD,M1) [5] 12.0000 30.0000 1 JF 0 18:27:57.298 TestScript (EURUSD,M1) [6] 14.0000 35.0000 0 DL 0 18:27:57.298 TestScript (EURUSD,M1) [7] 16.0000 40.0000 1 QK 0 18:27:57.298 TestScript (EURUSD,M1) [8] 18.0000 45.0000 0 QQ 0 18:27:57.298 TestScript (EURUSD,M1) [9] 20.0000 50.0000 0
La siguiente parte consistirá en generar valores aleatorios para los pesos y los desplazamientos.
generate_weights(weights,ArraySize(Inputs));
generate_bias(biases);
Este será el resultado:
RG 0 18:27:57.298 TestScript (EURUSD,M1) weights QS 0 18:27:57.298 TestScript (EURUSD,M1) 0.7084 -0.3984 0.6182 0.6655 -0.3276 0.8846 0.5137 0.9371 NL 0 18:27:57.298 TestScript (EURUSD,M1) biases DD 0 18:27:57.298 TestScript (EURUSD,M1) -0.5902 0.7384
Veamos ahora todas las operaciones de la función principal de nuestro script:
#include "NeuralNets.mqh"; CNeuralNets *nn; input int batch_size =10; input int hidden_layers =2; data data_blobs[]; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- nn = new CNeuralNets(SIGMOID); MakeBlobs(batch_size); ArrayPrint(data_blobs); double Inputs[],OutPuts[]; ArrayResize(Inputs,2); ArrayResize(OutPuts,2); double weights[], biases[]; generate_weights(weights,ArraySize(Inputs)); generate_bias(biases); Print("weights"); ArrayPrint(weights); Print("biases"); ArrayPrint(biases); for (int i=0; i<batch_size; i++) { Print("Dataset Iteration ",i); Inputs[0] = data_blobs[i].sample_1; Inputs[1]= data_blobs[i].sample_2; nn.FeedForwardMLP(hidden_layers,Inputs,weights,biases,OutPuts); } delete(nn); }
Qué debemos tener en cuenta:
- El número de desplazamientos coincide con el número de capas ocultas.
- Número total de pesos = cuadrado del número de entradas multiplicado por el número de capas ocultas. Esto es ahora posible porque nuestra red tiene el mismo número de nodos que la capa de entrada/salida de la red (todas las capas tienen el mismo número de nodos desde la entrada hasta la salida).
- Siguiendo el mismo principio, digamos que si tenemos 3 nodos de entrada, todas las capas ocultas tendrán 3 nodos excepto la última capa. Veamos qué sucede con esta capa.
Si se observamos un conjunto de datos generado aleatoriamente, podremos ver dos objetos/columnas de entrada en el conjunto de datos. Así que he decidido añadir dos capas ocultas. Aquí hay un resumen de los logs sobre la forma en que nuestro modelo realizará los cálculos (para evitar obtener estos logs, ponga el modo de depuración debug mode en el valor false)..
NL 0 18:27:57.298 TestScript (EURUSD,M1) Dataset Iteration 0 EJ 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 1 >> GO 0 18:27:57.298 TestScript (EURUSD,M1) NS 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 EI 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 2.00000 x weight 0.70837 FQ 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 5.00000 x weight -0.39838 QP 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product -0.57513 + bias -0.590 = -1.16534 RH 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.23770 CQ 0 18:27:57.298 TestScript (EURUSD,M1) OE 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 CO 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 2.00000 x weight 0.61823 FI 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 5.00000 x weight 0.66553 PN 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 4.56409 + bias -0.590 = 3.97388 GM 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.98155 DI 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 2 >> GL 0 18:27:57.298 TestScript (EURUSD,M1) NF 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 FH 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 0.23770 x weight -0.32764 ID 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 0.98155 x weight 0.88464 QO 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 0.79044 + bias 0.738 = 1.52884 RK 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.82184 QG 0 18:27:57.298 TestScript (EURUSD,M1) IH 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 DQ 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 0.23770 x weight 0.51367 CJ 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 0.98155 x weight 0.93713 QJ 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 1.04194 + bias 0.738 = 1.78034 JP 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.85574 EI 0 18:27:57.298 TestScript (EURUSD,M1) GS 0 18:27:57.298 TestScript (EURUSD,M1) Final MLP output(s) OF 0 18:27:57.298 TestScript (EURUSD,M1) 0.82184 0.85574 CN 0 18:27:57.298 TestScript (EURUSD,M1) Dataset Iteration 1 KH 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 1 >> EM 0 18:27:57.298 TestScript (EURUSD,M1) DQ 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 QH 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 4.00000 x weight 0.70837 PD 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 10.00000 x weight -0.39838 HR 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product -1.15027 + bias -0.590 = -1.74048 DJ 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.14925 OP 0 18:27:57.298 TestScript (EURUSD,M1) CK 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 MN 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 4.00000 x weight 0.61823 NH 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 10.00000 x weight 0.66553 HI 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 9.12817 + bias -0.590 = 8.53796 FO 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.99980 RG 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 2 >> IR 0 18:27:57.298 TestScript (EURUSD,M1) PD 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 RN 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 0.14925 x weight -0.32764 HF 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 0.99980 x weight 0.88464 EM 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 0.83557 + bias 0.738 = 1.57397 EL 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.82835 KE 0 18:27:57.298 TestScript (EURUSD,M1) GN 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 LS 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 0.14925 x weight 0.51367 FL 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 0.99980 x weight 0.93713 KH 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 1.01362 + bias 0.738 = 1.75202 IR 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.85221 OH 0 18:27:57.298 TestScript (EURUSD,M1) IM 0 18:27:57.298 TestScript (EURUSD,M1) Final MLP output(s) MH 0 18:27:57.298 TestScript (EURUSD,M1) 0.82835 0.85221
Ahora fíjese en los resultados finales del perceptrón multicapa en todas las iteraciones. Notará un comportamiento extraño cuando las salidas tienen los mismos valores: hay varias razones para este problema. A juzgar por esta discusión, uno de dichas razones sería el uso de una función de activación incorrecta en la capa de salida. Aquí es donde la función de activación SoftMax nos resulta útil.
Entiendo que la función sigmoidea solo retorna probabilidades cuando en la capa de salida hay un nodo que tiene que clasificar una clase. En este caso, necesitaremos la salida de una función sigmoidal que nos dirá si algo pertenece a una determinada clase o no, pero esta es otra historia. Si sumamos las salidas de los nodos finales, obtendremos uno (1) en la mayoría de los casos. Es decir, está claro que no son probabilidades, porque la probabilidad no puede superar el valor 1.
Si aplicamos SoftMax a la última capa, los resultados serán los siguientes:
First Iteration outputs [0.4915 0.5085] , Second Iteration Outputs [0.4940 0.5060]
El resultado puede interpretarse como [probabilidad de pertenencia a la clase 0 probabilidad de pertenencia a la clase 1] en este caso.
Al menos, ahora tendremos probabilidades en las que basarnos para interpretar algo significativo de nuestra red.
Reflexiones finales
Todavía no hemos terminado de trabajar con la red neuronal con conexión directa, pero al menos por ahora tenemos cierta comprensión de la teoría y las cosas más importantes que nos ayudarán a dominar las redes neuronales en MQL5. La red neuronal de conexión directa que se ha diseñado está pensada con fines clasificatorios, por lo que las funciones de activación correspondientes serán la sigmoidal y la función de TanH, según el conjunto de datos y las clases a seleccionar en ese conjunto de datos. No podemos cambiar la capa de salida en ella para que devuelva algo con lo que podamos jugar, como en el nodo de capas ocultas. La introducción de matrices nos ayudará a dinamizar todas estas operaciones de modo que podamos construir una red neuronal estándar para cualquier tarea. Ese será el objetivo de esta serie de artículos, así que permanezca atento.
También es importante saber cuándo podemos utilizar una red neuronal, ya que no todas las tareas deben ser resueltas por redes neuronales. Si podemos resolver el problema con una regresión lineal, un modelo lineal podrá ofrecer incluso mejores resultados. Esta es una de las cosas que deberemos tener en cuenta.
Repositorio de GitHub: https://github.com/MegaJoctan/NeuralNetworks-MQL5
Bibliografía adicional
-
Neural Networks for Pattern Recognition (Advanced Texts in Econometrics)
-
Neural Networks: Tricks of the Trade (Lecture Notes in Computer Science, 7700)
-
Deep Learning (Adaptive Computation and Machine Learning series)
Artículos:
-
Aprendizaje automático y data science (Parte 01): Regresión lineal
-
Aprendizaje automático y data science (Parte 02): Regresión logística
-
Aprendizaje automático y data science (Parte 03): Regresión matricial
-
Aprendizaje automático y data science (Parte 06): Descenso de gradiente
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/11275
 Redes neuronales: así de sencillo (Parte 23): Creamos una herramienta para el Transfer Learning
Redes neuronales: así de sencillo (Parte 23): Creamos una herramienta para el Transfer Learning
 Aprendiendo a diseñar un sistema de trading con Bears Power Index
Aprendiendo a diseñar un sistema de trading con Bears Power Index
 Creación simple de indicadores complejos usando objetos
Creación simple de indicadores complejos usando objetos
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso