Redes neuronales en el trading: Aprendizaje jerárquico de características en nubes de puntos

Introducción

Los conjuntos de puntos geométricos son conjuntos de puntos en el espacio euclidiano. Como conjunto, estos datos tienen que ser invariables a las permutaciones de sus miembros. Además, la métrica de distancia define vecindades locales que pueden presentar diversas propiedades. Por ejemplo, la densidad y otros atributos de los puntos pueden no resultar uniformes en distintas zonas.

En el artículo anterior nos familiarizamos con el método PointNet, cuya idea principal consiste en aprender la codificación espacial de cada punto y luego agregar todos los objetos individuales en una firma global de nube de puntos. PointNet no fija una estructura local. Sin embargo, el uso de una estructura local ha demostrado ser importante para el éxito de las arquitecturas convolucionales. Los modelos convergentes toman los datos de origen definidos en redes convencionales y son capaces de capturar progresivamente objetos a escalas cada vez mayores a lo largo de una jerarquía con resolución múltiple. En los niveles inferiores, las neuronas poseen campos receptivos más pequeños, mientras que en los niveles superiores tienen campos receptivos más grandes. La capacidad de abstraer patrones locales a lo largo de la jerarquía ofrece una mayor generalizabilidad.

Un enfoque similar se aplicó en el modelo PointNet++, presentado en el artículo "PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space". La idea general de PointNet++ consiste en dividir un conjunto de puntos en regiones locales superpuestas según una métrica de distancia en el espacio subyacente. Al igual que las redes convolucionales, PointNet++ extrae características locales captando pequeñas estructuras geométricas de vecindades reducidas. A continuación, estos objetos locales se agrupan en elementos más grandes y se procesan para producir objetos de nivel superior. Dicho proceso se repite hasta obtener las características de todo el conjunto de puntos.

Al proyectar PointNet++, los autores del método abordan dos problemas: la partición del conjunto de puntos y la abstracción de conjuntos de puntos o características locales mediante el entrenamiento de características locales. Estos dos problemas están relacionados porque al particionar un conjunto de puntos, resulta necesario crear estructuras comunes entre particiones para compartir los pesos de las características locales entrenadas de forma similar a los modelos convolucionales. Los autores del método eligen PointNet como dispositivo de entrenamiento local, que supone una arquitectura eficiente para procesar un conjunto desordenado de puntos y extraer características semánticas. Además, esta arquitectura resulta resistente a la corrupción de los datos de origen. Como elemento básico, PointNet abstrae conjuntos de puntos u objetos locales en representaciones de nivel superior. Desde este punto de vista, PointNet++ aplica PointNet de forma recursiva a la seccionalización anidada de los datos de origen.

Un problema que aún persiste es el método de creación de particiones de nubes de puntos superpuestas: cada región se define como una esfera de vecindad en el espacio euclidiano, cuyos parámetros incluyen la ubicación del centroide y la escala. Para abarcar uniformemente todo el conjunto, se seleccionan los centroides entre los puntos de origen dados por el algoritmo de muestreo más alejado del futuro. En comparación con los modelos convolucionales volumétricos que exploran el espacio en pasos fijos, los campos receptivos locales de PointNet++ dependen tanto de los datos de entrada como de las métricas, lo cual aumenta su eficacia.

1. El algoritmo PointNet

La arquitectura PointNet usa una sola operación MaxPooling para agregar todo el conjunto de puntos. Los autores de PointNet++ construyen una arquitectura jerárquica de agrupación de puntos con una abstracción gradual de las áreas locales a lo largo de la jerarquía.

La estructura jerárquica propuesta consta de una serie de niveles de abstracción establecidos. En cada nivel, la nube de puntos se procesa y abstrae para crear un nuevo conjunto de datos con un menor número de elementos. La capa de abstracción especificada consta de tres capas clave: la capa de Muestreo, la capa de Agrupación y la capa PointNet. La capa de muestreo selecciona un conjunto de puntos de la nube de puntos original que determina los centroides de las áreas locales. A continuación, la capa de agrupación crea conjuntos de puntos locales buscando objetos "vecinos" alrededor de dichos centroides. La capa PointNet usa mini-PointNet para codificar patrones de regiones locales en vectores de características.

El nivel de abstracción toma una matriz N×(d+C) como datos de entrada, que contiene N puntos con una dimensionalidad d de coordenadas y una dimensionalidad C de características. Y retorna una matriz N′×(d+C′), donde N′ representa puntos submuestreados con la dimensionalidad C′ del nuevo vector de características que resume el contexto local.

Los autores de PointNet++ proponen usar un muestreo iterativo de los puntos más alejados para seleccionar un subconjunto de puntos centroides. En comparación con el muestreo aleatorio, este enfoque abarca mejor un conjunto completo de puntos con el mismo número de centroides. A diferencia de las redes convolucionales, que exploran un espacio vectorial independiente de la distribución de los datos, la estrategia de muestreo propuesta genera campos receptivos según los datos origen.

Los datos de entrada para la capa de agrupamiento suponen una nube de puntos de tamaño N×(d+C) y las coordenadas de un conjunto de centroides de tamaño N′×d. El resultado son grupos de conjuntos de puntos de tamaño N′×K×(d+C), donde cada grupo corresponde a una región local y K es el número de puntos en la vecindad del centroide.

Obsérvese que K varía de un grupo a otro, pero la capa PointNet posterior es capaz de convertir un número flexible de puntos en un vector de longitud fija de objetos de la región local.

En las redes neuronales convolucionales, la región local de un píxel consta de píxeles con índices de matriz dentro de una cierta distancia Manhattan (tamaño del núcleo) del píxel. En una nube de puntos seleccionada de un espacio métrico, la vecindad de un punto se define por la distancia métrica.

Durante el proceso de agrupación, el modelo encuentra todos los puntos que se hallan dentro de un radio del punto solicitado (el límite superior K se establece en los hiperparámetros).

En la capa PointNet, los datos de entrada suponen N′ regiones de puntos locales con un tamaño de datos N′×K×(d+C). Cada región local de la salida se abstrae mediante su centroide y un objeto local que codifica la vecindad del mismo. El tamaño del tensor resultante es N′×(d+C).

Las coordenadas de los puntos del área local se traducen primero a un sistema de coordenadas local relativo al punto centroide:

para i = 1, 2,…, K y j = 1, 2,…, d, donde es la coordenada del centroide.

Los autores del método usan PointNet como elemento básico para el aprendizaje de patrones locales. El uso de coordenadas relativas junto con objetos puntuales permite captar las relaciones entre puntos de una región local.

Con frecuencia ocurre que un conjunto de puntos tiene una densidad desigual en distintas zonas. Esta heterogeneidad plantea un reto importante para el estudio de las características de los conjuntos de puntos. Las características aprendidas en datos densos pueden no aplicarse a regiones con muestreo disperso. Por ello, los modelos entrenados para una nube de puntos dispersa podrían no reconocer las estructuras locales finas.

Lo ideal consiste en explorar la nube de puntos con la mayor precisión posible para captar los detalles más pequeños en las zonas densamente muestreadas. Sin embargo, este escrutinio no resulta eficaz en zonas de baja densidad de puntos, ya que los patrones localizados pueden verse distorsionados por la falta de valores. En este caso, debemos buscar modelos a mayor escala en una vecindad mayor. Para lograr este objetivo, los autores de PointNet++ proponen capas PointNet adaptables a la densidad que se entrenan para combinar objetos de regiones de diferentes escalas cuando cambia la densidad de la muestra original.

En PointNet++, cada capa de abstracción extrae múltiples escalas de patrones locales y los combina de forma inteligente según la densidad de puntos locales. El artículo del autor nos presenta dos tipos de capas adaptables a la densidad.

Una forma sencilla pero eficaz de capturar patrones multiescala consiste en aplicar capas de agrupación con distintas escalas y, a continuación, asignar los PointNets adecuados para extraer las características de cada escala. Los objetos a diferentes escalas se combinan para formar un objeto multiescala.

De esta forma, entrenaremos a la red para que aprenda una estrategia optimizada de combinación de funciones multiescala. Esto se logra descartando aleatoriamente los puntos de partida con probabilidad aleatoria para cada instancia.

El enfoque descrito anteriormente requiere grandes recursos computacionales porque ejecuta una PointNet local en vecindades a gran escala para cada punto centroide. Un enfoque alternativo, que evita estos costosos cálculos conservando la capacidad de agregar información de forma adaptativa según las propiedades distributivas de los puntos, es la concatenación de los dos vectores. Un vector se obtiene sumando los objetos de cada subárea del nivel Li-1 inferior utilizando un nivel de abstracción determinado. El otro vector será una característica que se obtiene procesando directamente todos los puntos de origen de la región local utilizando un único PointNet.

Cuando la densidad del área local es baja, el primer vector puede resultar menos fiable que el segundo, ya que la subárea del cálculo del primer vector contiene aún más puntos dispersos y sufre más la falta de muestreo. En tal caso, el segundo vector debería tener más peso. Por otra parte, cuando la densidad de área local es alta, el primer vector ofrece información con detalles más finos porque tiene la capacidad de comprobar de forma recursiva con mayor resolución en niveles inferiores.

Este método es más eficiente desde el punto de vista computacional, ya que evita la extracción de características en vecindades a gran escala en los niveles más bajos.

En la capa de abstracción, el conjunto original de puntos se submuestrea, sin embargo, en una tarea de segmentación como el etiquetado semántico de puntos, resulta deseable obtener características puntuales para todos los puntos de origen. Una solución sería muestrear continuamente todos los puntos como centroides en todos los niveles de abstracción dados, lo cual, sin embargo, conllevará un elevado coste computacional. Otro método consiste en propagar los objetos de los puntos submuestreados a los puntos originales.

A continuación le presentamos la visualización del método PointNet++ realizada por el autor.

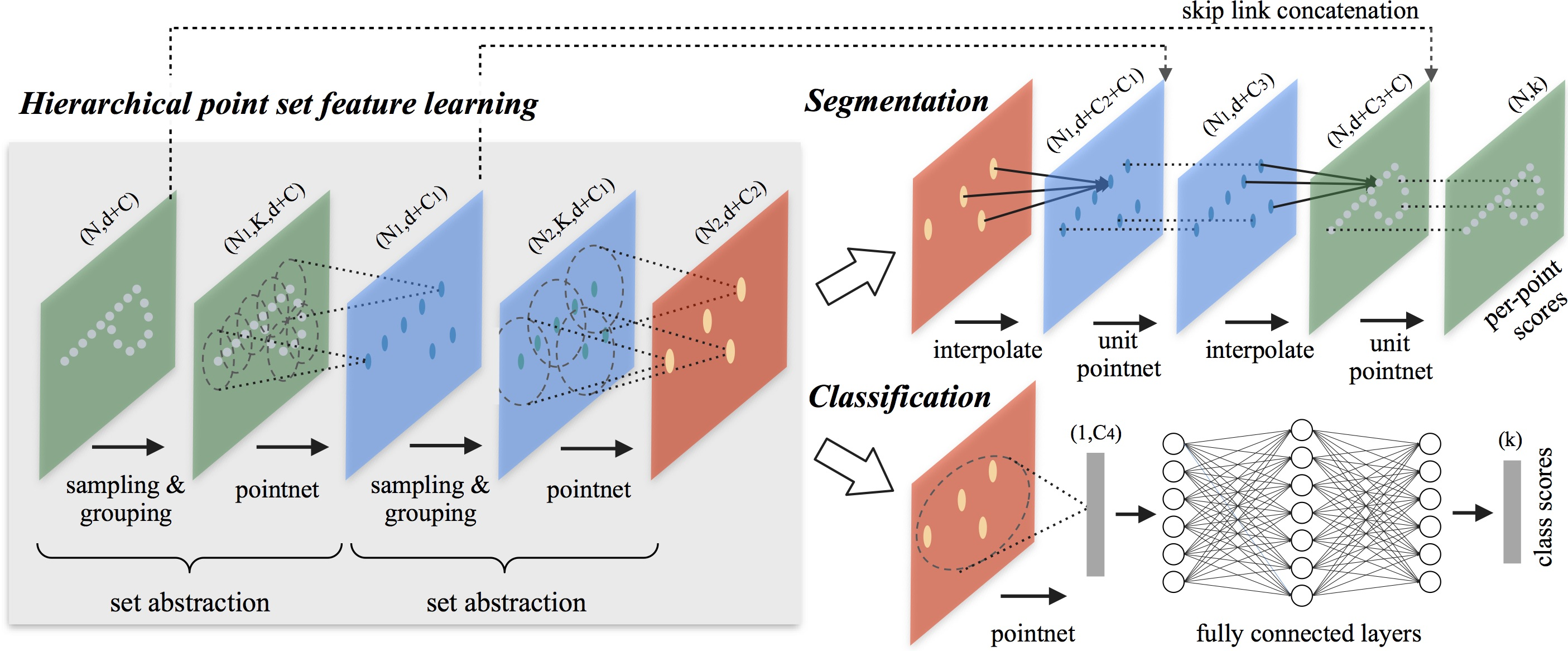
2. Implementación con MQL5

Tras analizar los aspectos teóricos del método PointNet++, pasaremos a la parte práctica de nuestro artículo, donde implementaremos nuestra visión de los enfoques propuestos usando MQL5. Y debemos decir que nuestra aplicación presenta algunas diferencias con respecto a la versión del autor descrita anteriormente. Pero vayamos por orden.

Dividiremos nuestro trabajo en 2 bloques. En primer lugar, crearemos una capa de submuestreo de datos locales que combinará las capas de Muestreo y Agrupación descritas anteriormente. Y luego construiremos una clase de nivel superior que ensamblará los bloques individuales en un único algoritmo PointNet++.

2.1 Incorporación de un programa OpenCL

Implementaremos el algoritmo de submuestreo local en la clase CNeuronPointNet2Local. Pero antes de empezar a trabajar en él, aún deberemos completar la funcionalidad de nuestro programa OpenCL.

En primer lugar, crearemos el kernel CalcDistance en el que definiremos la distancia entre los puntos de la nube analizada.

Aquí cabe señalar que definiremos la distancia en el espacio multidimensional de características de la descripción de puntos. Y el resultado del kernel será una matriz N×N con valores cero en la diagonal.

En los parámetros del kernel, obtendremos los punteros a los dos búferes de datos (los datos de origen y los datos para escribir los resultados) y una constante que especificará la dimensionalidad del vector de características de puntos.

__kernel void CalcDistance(__global const float *data,
                           __global float *distance,
                           const int dimension
                          )
  {
   const size_t main = get_global_id(0);
   const size_t slave = get_local_id(1);
   const int total = (int)get_local_size(1);

Y en el cuerpo del kernel, identificaremos el flujo en el espacio de tareas.

En la salida, esperamos obtener una matriz cuadrada. Por consiguiente, crearemos un espacio de tareas bidimensional del tamaño correspondiente. Así, en cada flujo individual, calcularemos el valor de un elemento de la matriz de resultados.

Debemos decir que aquí se producirá la primera desviación respecto al algoritmo del autor, pues no determinaremos iterativamente los centroides de las regiones locales. En nuestra aplicación, cada punto de la nube actuará como centroide del área local. Y para hacer realidad la adaptabilidad de los tamaños de las regiones, normalizaremos las distancias a cada punto de la nube. Para posibilitar la normalización de la distancia, necesitaremos intercambiar datos entre flujos separados. Y para ello, crearemos grupos de trabajo locales según las filas de la matriz de resultados del kernel.

Para intercambiar los datos dentro de un grupo de trabajo, crearemos un array local.

   __local float Temp[LOCAL_ARRAY_SIZE];
   int ls = min((int)total, (int)LOCAL_ARRAY_SIZE);

Y definiremos las constantes de desplazamiento hasta los elementos requeridos en los búferes de datos.

   const int shift_main = main * dimension;
   const int shift_slave = slave * dimension;
   const int shift_dist = main * total + slave;

A continuación, crearemos un ciclo para calcular la distancia entre dos objetos en un espacio multidimensional.

//--- calc distance
   float dist = 0;
   if(main != slave)
     {
      for(int d = 0; d < dimension; d++)
         dist += pow(data[shift_main + d] - data[shift_slave + d], 2.0f);
     }

Tenga en cuenta que los cálculos solo se realizarán para elementos no diagonales. Al fin y al cabo, la distancia desde un punto hasta sí mismo será "0". Y no malgastaremos recursos en cálculos innecesarios.

El siguiente paso consistirá en determinar la distancia máxima dentro del grupo de trabajo. En primer lugar, recopilaremos los valores máximos de los bloques individuales en un array local.

//--- Look Max
   for(int i = 0; i < total; i += ls)
     {
      if(!isinf(dist) && !isnan(dist))
        {
         if(i <= slave && (i + ls) > slave)
            Temp[slave - i] = max((i == 0 ? 0 : Temp[slave - i]), dist);
        }
      else
         if(i == 0)
            Temp[slave] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }

Y luego encontraremos el valor máximo en el array.

   int count = ls;
   do
     {
      count = (count + 1) / 2;
      if(slave < count && (slave + count) < ls)
        {
         if(Temp[slave] < Temp[slave + count])
            Temp[slave] = Temp[slave + count];
         Temp[slave + count] = 0;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Una vez hallado el valor máximo hasta el punto analizado, dividiremos por él las distancias calculadas anteriormente. Como resultado, todas las distancias entre puntos se normalizarán en el intervalo [0, 1].

//--- Normalize
   if(Temp[0] > 0)
      dist /= Temp[0];
   if(isinf(dist) || isnan(dist))
      dist = 1;
//--- result
   distance[shift_dist] = dist;
  }

Y guardaremos el valor obtenido en el elemento correspondiente del búfer global de resultados.

Obviamente, somos conscientes de que es probable que la distancia máxima dentro de un análisis de 2 puntos separados sea diferente. Y al normalizar los valores dentro de las escalas individuales perdamos esta diferencia. Pero ahí radica el elemento de adaptación de los campos receptivos.

Si el punto analizado se encuentra dentro de la nube de valores, resulta bastante obvio que el punto que esté a la máxima distancia de él se hallará en uno de los bordes de la nube. Por otra parte, si el punto que hay que analizar está en el borde de la nube, entonces el punto más alejado de él se encontrará en el borde opuesto de la nube. Y en el segundo caso, la distancia entre los puntos será mayor. Como consecuencia, el campo receptivo también será mayor en el segundo caso.

Pero también esperamos que la densidad de puntos sea mayor dentro de la nube que en los bordes. Y en este caso estará bastante justificado aumentar los campos receptivos en los márgenes de la nube de puntos analizada.

Además, los autores del método PointNet++ proponen calcular los desplazamientos locales de los puntos desde el centroide correspondiente y, a continuación, aplicar mini-PointNet a esas submuestras locales de datos. Pero tras la aparente sencillez de las acciones se oculta un problema de aplicación bastante serio.

Como ya hemos señalado, el número de elementos de cada área local es diferente y no se conoce de antemano. Aquí existe un problema con el tamaño de los búferes de datos asignados. Obviamente, podemos limitar el número máximo de puntos en el campo receptivo y declarar el tamaño del búfer "con margen", pero esto conllevará un aumento del consumo de memoria y de la complejidad computacional de todo el modelo, y como consecuencia, veremos cómo la complejidad del entrenamiento aumenta y el rendimiento del modelo disminuye.

En su lugar, adoptaremos un enfoque más sencillo y universal. Así, hemos abandonado el cálculo de las compensaciones locales, y para el entrenamiento de características puntuales, utilizaremos una matriz de parámetros de pesos para todas las características, de forma similar a PointNet vainilla, solo que realizaremos la operación MaxPooling dentro de los campos receptivos. Para ello creamos un nuevo kernel FeedForwardLocalMax, en cuyos parámetros transmitiremos los punteros a 3 búferes de datos: las características de puntos, la distancia normalizada entre puntos y el búfer de resultados. También añadiremos una constante para el radio del campo receptivo.

__kernel void FeedForwardLocalMax(__global const float *matrix_i,
                                  __global const float *distance,
                                  __global float *matrix_o,
                                  const float radius
                                 )
  {
   const size_t i = get_global_id(0);
   const size_t total = get_global_size(0);
   const size_t d = get_global_id(1);
   const size_t dimension = get_global_size(1);

Planeamos ejecutar este kernel en un espacio de tareas bidimensional. En la primera dimensión, indicaremos el número de características de la nube de puntos, y en la segunda, la dimensionalidad de características de un elemento. En el cuerpo del kernel, identificaremos directamente el flujo actual en ambas dimensiones del espacio de tareas. En este caso, cada flujo funcionará independientemente de los demás y no necesitaremos crear grupos de trabajo ni intercambiar datos entre flujos.

A continuación, definiremos las constantes de desplazamiento en los búferes de datos.

   const int shift_dist = i * total;
   const int shift_out = i * dimension + d;

Y luego organizaremos un ciclo para determinar el valor máximo.

   float result = -3.402823466e+38;
   for(int k = 0; k < total; k++)
     {
      if(distance[shift_dist + k] > radius)
         continue;
      int shift = k * dimension + d;
      result = max(result, matrix_i[shift]);
     }
   matrix_o[shift_out] = result;
  }

Obsérvese que antes de comprobar el valor del elemento siguiente, se comprobará necesariamente que se encuentre dentro del campo receptivo del elemento correspondiente de la nube de puntos.

Una vez completadas las iteraciones del ciclo, almacenaremos el valor resultante en el búfer de resultados.

Del mismo modo, creamos un kernel de pasada inversa CalcInputGradientLocalMax para distribuir el gradiente de error a los elementos correspondientes. Los algoritmos de kernel de pasada directa e inversa tienen muchas similitudes, y le sugiero que se familiarice con él. Encontrará el código completo de todos los kernels en el archivo adjunto. Ahora comenzaremos a trabajar en el programa principal.

2.2 Clase de submuestreo local

Ya hemos realizado el trabajo preparatorio en la parte del programa OpenCL y ahora pasaremos a trabajar en la clase de submuestreo local. Durante la implementación de los kernels de los programas OpenCL, ya hemos empezado a discutir parcialmente los principios de la construcción de los algoritmos. Y durante la implementación de los métodos de la clase CNeuronPointNet2Local, llegaremos a conocerlos con más detalle y veremos su implementación en el código. Le mostramos la estructura de la nueva clase a continuación:

class CNeuronPointNet2Local   :  public CNeuronConvOCL
  {
protected:
   float                fRadius;
   uint                 iUnits;
   //---
   CBufferFloat         cDistance;
   CNeuronConvOCL       cFeatureNet[3];
   CNeuronBatchNormOCL  cFeatureNetNorm[3];
   CNeuronBaseOCL       cLocalMaxPool;
   CNeuronConvOCL       cFinalMLP;
   //---
   virtual bool         CalcDistance(CNeuronBaseOCL *NeuronOCL);
   virtual bool         LocalMaxPool(void);
   virtual bool         LocalMaxPoolGrad(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override ;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronPointNet2Local(void) {};
                    ~CNeuronPointNet2Local(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint window_out, float radius,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronPointNet2LocalOCL; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

En la estructura presentada arriba podemos percibir varios objetos de capas neuronales internas y 2 variables cuyo propósito conoceremos durante la implementación de los métodos de la clase.

Aquí también vemos el ya familiar conjunto de métodos redefinidos. Además existen 3 métodos en consonancia con los kernels creados anteriormente:

• CalcDistance(CNeuronBaseOCL *NeuronOCL);
• LocalMaxPool(void);
• LocalMaxPoolGrad(void).

Como ya habrá adivinado, se trata de métodos para poner los kernels en la cola de ejecución. Ya hemos estudiado el algoritmo, así que no nos detendremos más en él dentro de este artículo.

También querría señalar que heredaremos de la clase de capa de convolución CNeuronConvOCL. Esta situación no es frecuente en nuestra práctica y se relaciona con el procesamiento independiente de las características locales del grupo.

Todos los objetos internos de la clase se declaran estáticamente, lo cual nos permitirá dejar el constructor y el destructor de la clase vacíos, La inicialización de una nueva instancia de objeto se realizará en el método Init.

bool CNeuronPointNet2Local::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                 uint window, uint units_count, uint window_out, float radius, 
                                 ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronConvOCL::Init(numOutputs, myIndex, open_cl, 128, 128, window_out, 
                                        units_count, 1, optimization_type, batch))
      return false;

En los parámetros del método, obtendremos las constantes básicas que definirán la arquitectura del objeto. Todas ellas están en consonancia con parámetros similares de la capa de convolución. Solo se añadirá un parámetro, radius, que definirá el radio de la ventana receptiva del elemento.

En el cuerpo del método llamaremos inmediatamente al método homónimo de la clase padre, en el que ya está implementado el control necesario de los datos recibidos y la inicialización de los objetos heredados. Y aquí vale la pena señalar que los valores transmitidos al método de la clase padre son un poco diferentes de los valores que obtenemos del programa externo. Esto se debe a las peculiaridades de uso de los objetos de la clase padre, de las que hablaremos más adelante en el proceso de implementación del método feedForward.

Tras ejecutar con éxito las operaciones del método de la clase padre, guardaremos algunas de las constantes resultantes, otras han sido almacenadas como parte de las operaciones de la clase padre.

   fRadius = MathMax(0.1f, radius);
   iUnits = units_count;

A continuación, inicializaremos los objetos internos. En primer lugar, crearemos un búfer para registrar las distancias entre los objetos de la nube de puntos analizada. Como ya hemos dicho, se tratará de una matriz cuadrada.

   cDistance.BufferFree();
   if(!cDistance.BufferInit(iUnits * iUnits, 0) ||
      !cDistance.BufferCreate(OpenCL))
      return false;

Para la extracción de características puntuales, crearemos un bloque de 3 capas convolucionales y 3 capas de normalización de lotes similar al bloque de extracción de características del algoritmo PointNet. No crearemos un bloque de proyección de datos de origen porque suponemos que existe en la clase de nivel superior.

   if(!cFeatureNet[0].Init(0, 0, OpenCL, window, window, 64, iUnits, 1, optimization, iBatch))
      return false;
   if(!cFeatureNetNorm[0].Init(0, 1, OpenCL, 64 * iUnits, iBatch, optimization))
      return false;
   cFeatureNetNorm[0].SetActivationFunction(LReLU);
   if(!cFeatureNet[1].Init(0, 2, OpenCL, 64, 64, 128, iUnits, 1, optimization, iBatch))
      return false;
   if(!cFeatureNetNorm[1].Init(0, 3, OpenCL, 128 * iUnits, iBatch, optimization))
      return false;
   cFeatureNetNorm[1].SetActivationFunction(LReLU);
   if(!cFeatureNet[2].Init(0, 4, OpenCL, 128, 128, 256, iUnits, 1, optimization, iBatch))
      return false;
   if(!cFeatureNetNorm[2].Init(0, 5, OpenCL, 256 * iUnits, iBatch, optimization))
      cFeatureNetNorm[2].SetActivationFunction(None);

Aquí también crearemos una capa para registrar los resultados de MaxPooling local.

   if(!cLocalMaxPool.Init(0, 6, OpenCL, cFeatureNetNorm[2].Neurons(), optimization, iBatch))
      return false;

Y añadiremos una capa del MLP resultante.

   if(!cFinalMLP.Init(0, 7, OpenCL, 256, 256, 128, iUnits, 1, optimization, iBatch))
      return false;
   cFinalMLP.SetActivationFunction(LReLU);

Planeamos usar la funcionalidad heredada como segunda capa.

Tenga en cuenta que, a diferencia del PointNet vainilla, también utilizaremos capas convolucionales en la salida. Esto se debe al procesamiento independiente de los descriptores de área local.

Al completar las operaciones del método de inicialización, indicaremos explícitamente la ausencia de la función de activación de nuestra clase y retornaremos el resultado lógico de las operaciones al programa que realiza la llamada.

   SetActivationFunction(None);
   return true;
  }

Una vez inicializado el nuevo objeto, pasaremos a construir los algoritmos de pasada directa en el método feedForward. En los parámetros de este método, obtendremos el puntero al objeto de datos de origen.

bool CNeuronPointNet2Local::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!CalcDistance(NeuronOCL))
      return false;

Como hemos mencionado antes, no tenemos previsto realizar la proyección de datos en el espacio canónico como parte de esta clase. Tenemos previsto que esta operación se realice en el nivel superior si es necesario. Por ello, realizaremos inmediatamente cálculos de distancia entre los elementos de los datos de origen.

A continuación, organizaremos un ciclo para calcular las características de los elementos analizados.

   CNeuronBaseOCL *temp = NeuronOCL;
   uint total = cFeatureNet.Size();
   for(uint i = 0; i < total; i++)
     {
      if(!cFeatureNet[i].FeedForward(temp))
         return false;
      if(!cFeatureNetNorm[i].FeedForward(cFeatureNet[i].AsObject()))
         return false;
      temp = cFeatureNetNorm[i].AsObject();
     }

Y realizaremos las operaciones MaxPooling para las regiones locales de puntos.

   if(!LocalMaxPool())
      return false;

Al final de las operaciones del método, aplicaremos un MLP independiente de dos capas a los descriptores de todas las regiones locales.

   if(!cFinalMLP.FeedForward(cLocalMaxPool.AsObject()))
      return false;
   if(!CNeuronConvOCL::feedForward(cFinalMLP.AsObject()))
      return false;
//---
   return true;
  }

Luego usaremos la capa interna cFinalMLP como primera capa MLP. Y las operaciones de la segunda capa se realizarán gracias a la funcionalidad heredada de la clase padre.

No se olvide de supervisar las operaciones en cada fase. Y tras completar con éxito todas las operaciones, retornaremos el resultado lógico de su ejecución al programa que realiza la llamada.

Los algoritmos de pasada inversa se implementarán en los métodos calcInputGradients y updateInputWeights. El primer método distribuirá el gradiente de error entre todos los elementos en función de su influencia en el resultado final. Su algoritmo está construido en plena concordancia con el método de pasada directa considerado, pero el flujo de operaciones se realiza en orden inverso. En el segundo método, se actualizarán los parámetros del modelo entrenado. Aquí solo llamaremos al método homónimo de los objetos internos que contienen los parámetros a entrenar. Los algoritmos de ambos métodos son fáciles de entender, por lo que le recomiendo que los estudie por su cuenta. Permítame recordarle que el código completo de esta clase y todos sus métodos se pueden encontrar en el archivo adjunto.

2.3 Construcción del algoritmo PointNet

Ya hemos realizado un trabajo considerable. Y ahora llegamos a la "línea de meta" de nuestra realización. En esta fase, ensamblaremos los distintos "ladrillos" en un único algoritmo PointNet++. Y realizaremos este trabajo dentro de la clase CNeuronPointNet2OCL, cuya estructura se presenta a continuación.

class CNeuronPointNet2OCL   :  public CNeuronPointNetOCL
  {
protected:
   CNeuronPointNetOCL   *cTNetG;
   CNeuronBaseOCL       *cTurnedG;
   //---
   CNeuronPointNet2Local caLocalPointNet[2];
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override ;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
public:
                     CNeuronPointNet2OCL(void) {};
                    ~CNeuronPointNet2OCL(void) ;
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint output, bool use_tnets,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronPointNet2OCL; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Por extraño que parezca, en esta clase declararemos solo 2 objetos estáticos de muestreo local de los datos y 2 objetos dinámicos que se inicializarán en caso de que necesitemos proyectar los datos al espacio canónico. Esta simplicidad externa se logra heredando de la clase PointNet vainilla, dentro de la cual ya está implementada la mayor parte de la funcionalidad.

Como ya hemos dicho, los objetos dinámicos solo se inicializarán cuando sea necesario. Por consiguiente, dejaremos el constructor de la clase vacío, pero en el destructor comprobaremos la presencia de punteros reales a objetos dinámicos y los borraremos si es necesario.

CNeuronPointNet2OCL::~CNeuronPointNet2OCL(void)
  {
   if(!!cTNetG)
      delete cTNetG;
   if(!!cTurnedG)
      delete cTurnedG;
  }

La inicialización del objeto de clase se realizará como de costumbre en el método Init. En los parámetros de los métodos, obtendremos las constantes básicas que definen las arquitecturas de las clases. Y aquí las hemos preservado completamente de la clase padre.

bool CNeuronPointNet2OCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,

                               uint window, uint units_count, uint output, bool use_tnets, 
                               ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronPointNetOCL::Init(numOutputs, myIndex, open_cl, 64, units_count, 
                                output, use_tnets, optimization_type, batch))
      return false;

En el cuerpo del método, llamaremos directamente al método análogo de la clase padre. Después comprobaremos si es necesario crear objetos de proyección de los datos iniciales en el espacio canónico.

//--- Init T-Nets
   if(use_tnets)
     {
      if(!cTNetG)
        {
         cTNetG = new CNeuronPointNetOCL();
         if(!cTNetG)
            return false;
        }
      if(!cTNetG.Init(0, 0, OpenCL, window, units_count, window * window, false, optimization, iBatch))
         return false;

Aquí, de ser necesario, primero crearemos los objetos requeridos y luego los inicializaremos.

      if(!cTurnedG)
        {
         cTurnedG = new CNeuronBaseOCL();
         if(!cTurned1)
            return false;
        }
      if(!cTurnedG.Init(0, 1, OpenCL, window * units_count, optimization, iBatch))
         return false;
     }

Si el usuario no ha especificado la necesidad de crear objetos de proyección, comprobaremos si existen punteros reales a los objetos. Y si los hay, eliminaremos los objetos innecesarios.

   else
     {
      if(!!cTNetG)
         delete cTNetG;
      if(!!cTurnedG)
         delete cTurnedG;
     }

A continuación, inicializaremos dos objetos de muestreo de datos locales con diferentes radios de ventana receptiva. Luego finalizaremos el método.

   if(!caLocalPointNet[0].Init(0, 0, OpenCL, window, units_count, 64, 0.2f, optimization, iBatch))
      return false;
   if(!caLocalPointNet[1].Init(0, 0, OpenCL, 64, units_count, 64, 0.4f, optimization, iBatch))
      return false;
//---
   return true;
  }

Obsérvese que comenzamos con una ventana receptiva pequeña seguida de una ampliación. Al hacerlo, no ampliaremos la ventana receptiva hasta alcanzar una cobertura total, ya que esto lo realizará la funcionalidad heredada de la clase PointNet vainilla.

Una vez hayamos terminado con el método de inicialización de la clase de objeto, construiremos el algoritmo de pasada directa en el método feedForward.

bool CNeuronPointNet2OCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- LocalNet
   if(!cTNetG)
     {
      if(!caLocalPointNet[0].FeedForward(NeuronOCL))
         return false;
     }

En los parámetros del método, obtendremos el puntero al objeto de datos de origen. Y en el cuerpo del método, primero comprobaremos si es necesario proyectar los datos de origen en el espacio canónico. El algoritmo de acciones aquí será similar al que construimos al implementar el método de la clase PointNet vainilla. Si no se requiere proyección de datos, pasaremos inmediatamente el puntero resultante al método de pasada directa de la primera capa de muestreo local de datos.

En caso contrario, generaremos primero la matriz de proyección de datos.

   else
     {
      if(!cTurnedG)
         return false;
      if(!cTNetG.FeedForward(NeuronOCL))
         return false;

A continuación, se realizará la proyección de los datos de origen multiplicándolos por la matriz de proyección.

      int window = (int)MathSqrt(cTNetG.Neurons());
      if(IsStopped() ||
         !MatMul(NeuronOCL.getOutput(), cTNetG.getOutput(), cTurnedG.getOutput(), 
                                    NeuronOCL.Neurons() / window, window, window))
         return false;

Y solo entonces transmitiremos los valores obtenidos al método de pasada directa de la capa de muestreo de datos.

      if(!caLocalPointNet[0].FeedForward(cTurnedG.AsObject()))
         return false;
     }

A continuación, realizaremos el muestreo con un tamaño de ventana receptiva mayor.

   if(!caLocalPointNet[1].FeedForward(caLocalPointNet[0].AsObject()))
      return false;

Y en el último pasada transmitiremos los datos enriquecidos al método de pasada directa de la clase padre, donde se determina el descriptor de la nube de puntos analizada en su conjunto.

   if(!CNeuronPointNetOCL::feedForward(caLocalPointNet[1].AsObject()))
      return false;
//---
   return true;
  }

Como puede ver, gracias a una estructura de herencia bastante compleja, hemos podido construir un método de pasada directa conciso para nuestra nueva clase. Los mismos algoritmos cortos se utilizarán también para los métodos de pasada inversa, que le sugiero que lea por su cuenta en el archivo adjunto. Permítame recordarle que el código completo de todas las clases y sus módulos utilizados en la preparación de este artículo se puede encontrar en el archivo adjunto. Ahí también se facilita el código completo de los programas modelo de entrenamiento e interacción con el entorno. Aquí vale la pena decir que este último se ha transferido íntegramente del artículo anterior sin ningún ajuste. Además, hemos conservado prácticamente la arquitectura de los modelos. De hecho, en la arquitectura del codificador de estado del entorno, solo hemos modificado el tipo de una capa, manteniendo los demás parámetros totalmente intactos.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronPointNet2OCL;
   descr.window = BarDescr;                        // Variables
   descr.count = HistoryBars;                      // Units
   descr.window_out = LatentCount;                 // Output Dimension
   descr.step = int(true);                         // Use input and feature transformation
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Y resulta aún más interesante ver los resultados de entrenamiento de la nueva política del Actor.

3. Simulación

Aquí hemos terminado de hacer realidad nuestra visión de los enfoques propuestos por los autores del método PointNet++. Y ahora es el momento de evaluar la eficacia de nuestra aplicación con datos históricos reales. Como ya hemos hecho antes, entrenaremos los modelos con los datos históricos del instrumento EURUSD para todo el año 2023, el marco temporal H1 y los parámetros de todos los indicadores por defecto. La prueba del modelo entrenado se realizará en el simulador de estrategias de MetaTrader 5.

Como ya hemos dicho, nuestro nuevo modelo se distinguirá del anterior en que solo tiene una capa. Además, nuestra nueva capa no será más que una versión mejorada del trabajo anterior. Y resulta aún más interesante comparar los resultados de los dos modelos. Y para que la comparación resulte lo más justa posible, entrenaremos los modelos con una muestra de entrenamiento totalmente conservada de trabajos anteriores.

Sí, siempre digo que para obtener mejores resultados en el entrenamiento del modelo, es necesario actualizar periódicamente la muestra de entrenamiento. Solo entonces esta coincidirá con la política real del Actor, lo cual permitirá una evaluación más precisa de sus acciones y ajustes políticos. Pero en este caso, no puedo rechazar la tentación de comparar dos métodos similares y evaluar la eficacia del enfoque jerárquico. En el último artículo, pudimos entrenar una política de Actor capaz de generar beneficios en esta muestra de entrenamiento, y esperamos no obtener peores resultados con el nuevo modelo.

Como resultado del entrenamiento, el nuevo modelo ha sido capaz de aprender una política capaz de generar beneficios tanto en las muestras de entrenamiento como en las de prueba. A continuación le mostramos los resultados de las pruebas del nuevo modelo.

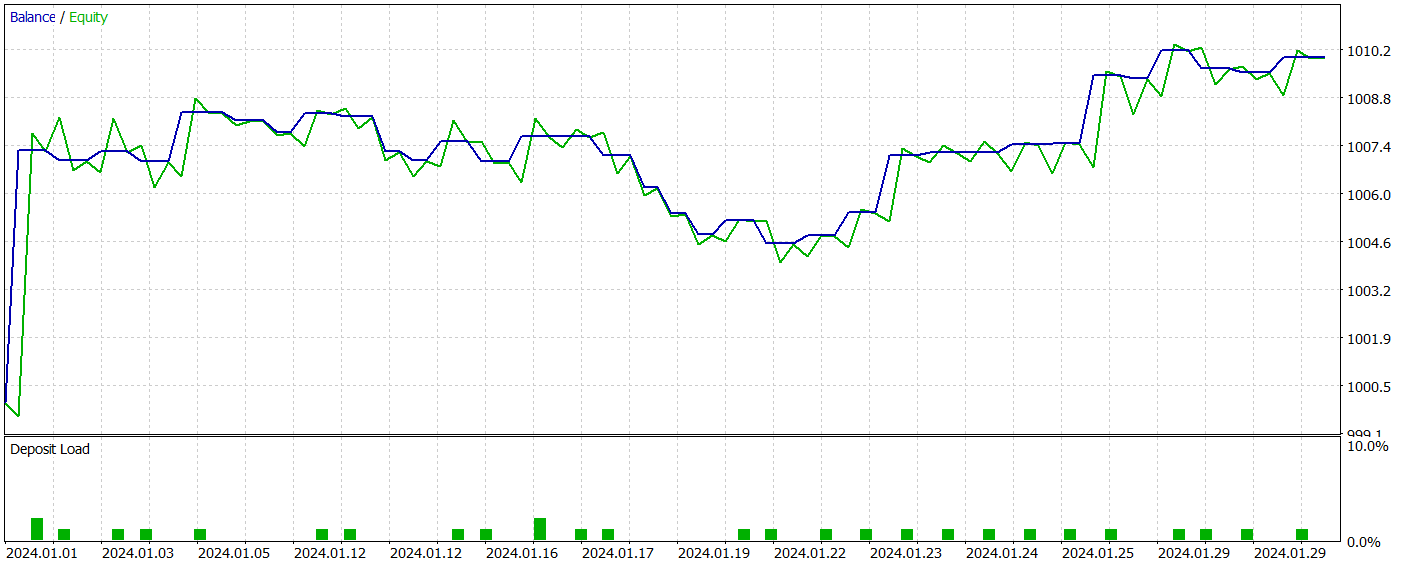
Tengo que decir que resulta bastante difícil comparar el rendimiento de los dos modelos. Durante el periodo de prueba, ambos modelos han generado aproximadamente los mismos beneficios. Las desviaciones en la reducción tanto del saldo como de la equidad se sitúan en el nivel de error. Sin embargo, el nuevo modelo ha hecho menos transacciones y el valor del factor de beneficio ha aumentado.

Sin embargo, el reducido número de transacciones realizadas por ambos modelos no nos permite extraer conclusiones sobre su eficacia a más largo plazo.

Conclusión

El uso del método PointNet++ permite analizar eficazmente patrones locales y globales en datos financieros complejos considerando su estructura multidimensional. Un enfoque perfeccionado del procesamiento de datos puntuales mejora la precisión de las previsiones y la estabilidad de las estrategias comerciales, lo que puede provocar decisiones más informadas y acertadas en mercados dinámicos.

En la parte práctica del artículo hemos hecho realidad nuestra visión de los enfoques propuestos por los autores del método PointNet++. Y debemos decir que durante las pruebas el modelo ha sido capaz de generar beneficios en la muestra de prueba. No obstante, los programas presentados son de demostración y solo pretenden ilustrar el funcionamiento del método.

Enlaces

• PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL