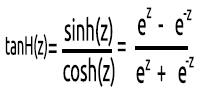
データサイエンスと機械学習—ニューラルネットワーク（第01回）：フィードフォワードニューラルネットワークの解明

MetaTrader 5 — トレーディングシステム | 15 11月 2022, 13:37

671

Omega J Msigwa

「…知りすぎて理解が少なすぎることにうんざりしている。」

― Jan Karon、Home to Holly Springs

はじめに

ニューラルネットワークは、聖杯の取引システムを構築するための、素晴らしく新しい方法のように思われます。多くのトレーダーは、ニューラルネットワークで作成されたプログラムに驚かされます。それらは、基本的に市場の動きを予測するのが得意であるが、目の前のあらゆるタスクに長けているようだからです。私も、訓練されていない/見たことのないデータに基づいて予測または分類することに関して、それらが大きな可能性を秘めていると信じています.

どんなに優れたものであっても、知識のある人が構築する必要があり、時には最適化が必要です。多層パーセプトロンが正しいアーキテクチャにあるということだけでなく、問題のタイプが、単なる線形回帰モデルやロジスティック回帰モデル、またはその他の機械学習手法ではなく、ニューラルネットワークを必要とするものだということを保証するためにです。

ニューラルネットワークはより広いテーマであり、一般的に機械学習もそうです。そのため、ニューラルネットワークのサブヘッダーを追加することにしました。機械学習の他の側面については、連載の他のサブヘッダーで進めます。

この記事では、ニューラルネットワークの基本を確認し、機械学習愛好家がこの主題を習得するために理解することが重要であると私が考える基本的な質問のいくつかに答えます。

人工ニューラルネットワークとは

通常ニューラルネットワークと呼ばれる人工ニューラルネットワーク(ANN)は、動物の脳を構成する生物学的ニューラルネットワークに着想を得たコンピューティングシステムです。

多層パーセプトロンとディープニューラルネットワークの比較

ニューラルネットワークについて議論する際に、多層パーセプトロン(MLP)という用語をよく耳にします。これは、最も一般的なタイプのニューラルネットワークに他なりません。MLPは、入力層、隠れ層、および出力層で構成されるネットワークです。シンプルであるため、データ内の表現を学習して出力を生成するために必要な訓練時間は短くなります。

適用

MLPは通常、回帰分析など、線形に分離できないデータに使用されます。シンプルであるため、複雑な分類タスクや予測モデリングに最適です。それらは、機械翻訳、天気予報、不正行為の検出、株式市場の予測、信用格付けの予測、および考えられる他の多くの側面に使用されています.

一方、ディープニューラルネットワークは共通の構造を持っており、唯一の違いは、隠れ層が多すぎることです。ネットワークに3つ以上の隠れ層がある場合、それはディープニューラルネットワークであると考えてください。複雑な性質のため、入力データでネットワークをさらに訓練するには長い期間が必要であり、テンソルプロセッシングユニット(TPU)とニューラルプロセッシングユニット(NPU)などの特殊な処理ユニットを備えた強力なコンピュータが必要です。

適用

DNNは層の深さによる強力なアルゴリズムであるため、通常は複雑な計算タスクを処理するために使用されます。コンピュータビジョンはそのようなタスクの1つです。

相違点の表

MLP	DNN
少数の隠れ層	多数の隠れ層
短い訓練期間	より長い訓練時間
GPU対応デバイスで十分	TPU対応デバイスで十分

次に、ニューラルネットワークの種類を見てみましょう。

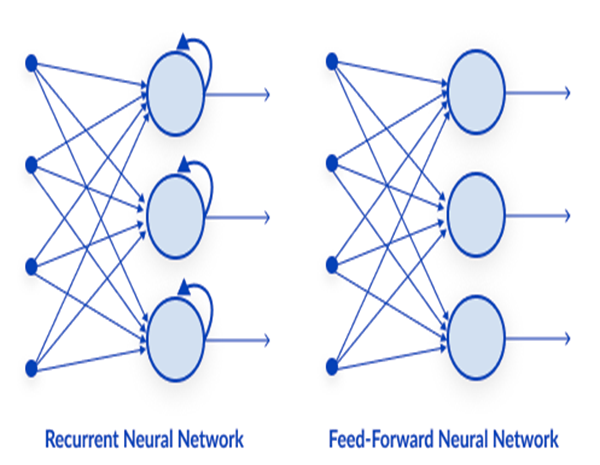
ニューラルネットワークには多くの種類がありますが、大まかに3つの主要なクラスに分類されます。

フィードフォワードニューラルネットワーク
畳み込みニューラルネットワーク
再帰型ニューラルネットワーク

01：フィードフォワードニューラルネットワーク

これは、最も単純なタイプのニューラルネットワークの1つです。フィードフォワードニューラルネットワークでは、データは出力ノードに到達するまで、さまざまな入力ノードを通過します。バックプロパゲーションとは対照的に、ここではデータは一方向にのみ移動します。

簡単に言えば、バックプロパゲーションは、データが入力層から出力層に渡されるフィードフォワードと同じプロセスをニューラルネットワークで実行します。ただし、バックプロパゲーションでは、ネットワークの出力が出力層に到達した後、クラスの実際の値を確認し、それを予測した値と比較して、モデルがおこなった予想がどの程度間違っているか正しいかを確認します。間違った予測をおこなった場合は、データをネットワークに逆方向に渡し、そのパラメータを更新して、次回の予測が正しくなるようにします。これは自己学習型のアルゴリズムです。

02：再帰型ニューラルネットワーク

再帰型ニューラルネットワークは、特定の層の出力が保存され、入力層にフィードバックされる人工ニューラルネットワークの一種です。これは、層の結果を予測するのに役立ちます。

再帰型ニューラルネットワークは、以下に関連する問題を解決するために使用されます。

時系列データ
テキストデータ
音声データ

テキストデータの最も一般的な用途は、たとえばAIが話す次の単語を推奨することです。例：How + are + you +?

03：畳み込みニューラルネットワーク(CNN)

CNNはディープラーニングコミュニティで猛威を振るっています。それらは、画像およびビデオ処理プロジェクトで優勢です。

たとえば、画像の検出と分類のAIは、畳み込みニューラルネットワークで構成されています。

畳み込みニューラルネットワークの画像

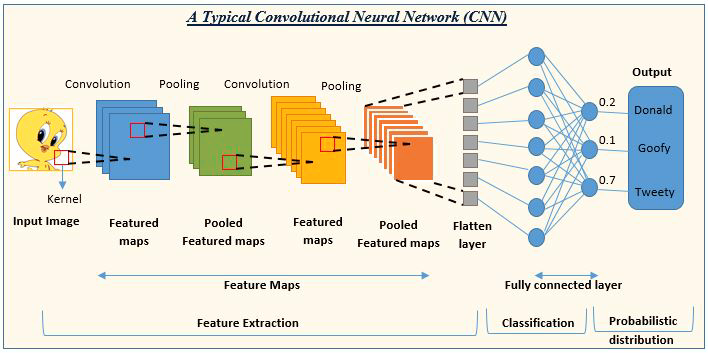
画像ソース：analyticsvidhya.com

ニューラルネットワークの種類を確認したので、この記事のメイントピックであるフィードフォワードニューラルネットワークに焦点を移しましょう。

フィードフォワードニューラルネットワーク

他のより複雑なタイプのニューラルネットワークとは異なり、バックプロパゲーションはありません。つまり、このタイプのニューラルネットワークではデータが一方向にのみ流れます。フィードフォワードニューラルネットワークには、1つの隠れ層または複数の隠れ層があります。

このネットワークが作動する理由を見てみましょう。

フィードフォワードニューラルネット

入力層

ニューラルネットワークの画像から、入力層があるように見えますが、奥深くでは、入力層は単なるプレゼンテーションです。入力層では計算は実行されません。

隠れ層

隠れ層は、ネットワーク内の作業の大部分がおこなわれる場所です。

明確にするために、2番目の隠れ層ノードを分析してみましょう。

2番目のノードの分析

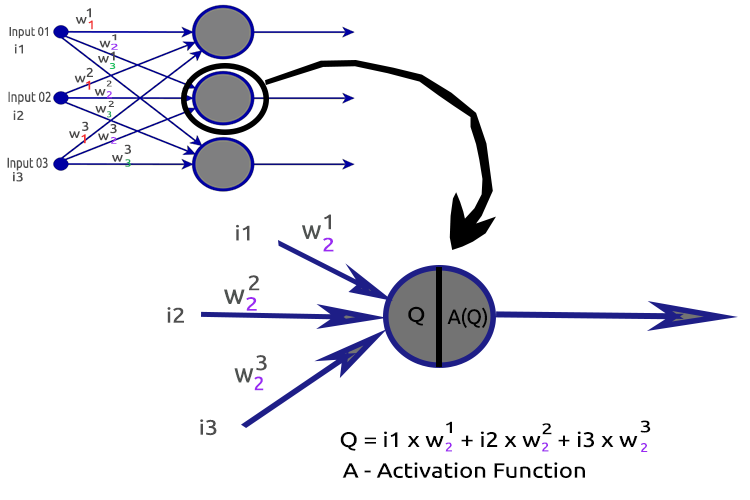
関連するプロセス

入力とそれぞれの重みの内積を求める
得られた内積をバイアスに加算する
2の結果を活性化関数に渡す

バイアスについて

バイアスを使用すると、線形回帰を上下にシフトして、予測線をデータによりよく適合させることができます。これは、線形回帰直線の切片と同じです。

このパラメータは、「ノードが1つ、隠れ層が1つのMLPは線形モデル」セクションでよく理解できます。

バイアスの重要性は、このStackでよく説明されています。

重みについて

重みは、解決しようとしている方程式の係数である入力の重要性を反映しています。負の重みは出力の値を減らし、その逆も同様です。ニューラルネットワークは、訓練データセットで訓練されると、一連の重みで初期化されます。これらの重みは訓練期間中に最適化され、重みの最適値が生成されます。

活性化関数について

活性化関数は、入力を受け取って出力を生成する数学関数に他なりません。

活性化関数の種類

活性化関数には多くの変型がありますが、最も一般的に使用されるものを次に示します。

ReLU
シグモイド
tanH
ソフトマックス

どの活性化関数をどこで使用するかは非常に重要です。活性化関数を無関係な場所で使用することを提案しているオンラインの記事を何度見たことかわかりません。これを詳しく見てみましょう。

01：ReLU

ReLUはRectified Linear Activation Functionの略です。

これは、ニューラルネットワークで最も使用される活性化関数です。最も単純で、コーディングも簡単で、出力の解釈も容易であるため、人気があります。この関数は、入力が正の数の場合は入力を直接出力し、それ以外の場合はゼロを出力します。

次がロジックです。

if x < 0 : return 0

else return x

この関数は、回帰問題の解決に使用することをお勧めします。

ReLU画像グラフ

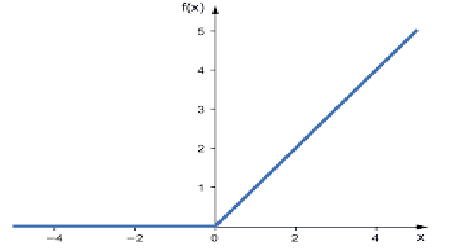
その出力範囲はゼロから正の無限大です。

そのMQL5コードは次のとおりです。

double CNeuralNets::Relu(double z)
 {
   if (z < 0) return(0);
   else return(z);
 }

ReLUは、シグモイドとTanHが被る勾配消失問題を解決します（これについては、バックプロパゲーションに関する記事で説明します）。

02：シグモイド

おなじみでしょうか。ロジスティック回帰を思い出してください。

式は次のとおりです。

この関数は、分類問題、特に1つまたは2つのクラスのみを分類する場合に使用することをお勧めします。

その出力範囲は0から1（確率項）までです。

シグモイドグラフ

たとえば、ネットワークの出力に2つのノードがあるとします。最初のノードは猫用で、もう1つは犬用です。最初のノードの出力が0.5より大きい場合は出力を選択して、それが猫であることを示し、犬の場合は同じですが逆であることを示します。

そのMQL5コードは次のとおりです。

double CNeuralNets::Sigmoid(double z)
 { 
   return(1.0/(1.0+MathPow(e,-z)));
 }

03：tanH

双曲正接関数です。

次の式で与えられます。

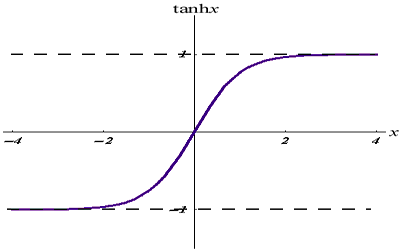
そのグラフは次のようになります。

この活性化関数はシグモイドに似ていますが、より優れています。

その出力範囲は-1から1です。

この関数は、多クラス分類ニューラルネットワークで使用することをお勧めします。

そのMQL5コードを以下に示します。

double CNeuralNets::tanh(double z)
 {
   return((MathPow(e,z) - MathPow(e,-z))/(MathPow(e,z) + MathPow(e,-z)));
 }

04：ソフトマックス

なぜソフトマックス関数のグラフがないのか、誰かが尋ねたことがあります。他の活性化関数とは異なり、ソフトマックスは隠れ層では使用されずに出力層でのみ使用され、マルチクラスニューラルネットワークの出力を確率項に変換する場合にのみ使用する必要があります。

ソフトマックスは、多項確率分布を予測します。

ソフトマックス活性化関数式

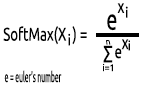
たとえば、回帰ニューラルネットの出力が[1,3,2]で、この出力にソフトマックス関数を適用すると、出力は[0.09003,0.665240,0.244728]になります。

この関数の出力範囲は0から1です。

そのMQL5コードは次のようになります。

void CNeuralNets::SoftMax(double &Nodes[])
 {
   double TempArr[];
   ArrayCopy(TempArr,Nodes);  ArrayFree(Nodes);
   
   double proba = 0, sum=0;
    
   for (int j=0; j<ArraySize(TempArr); j++)    sum += MathPow(e,TempArr[j]);
    
    for (int i=0; i<ArraySize(TempArr); i++)
      {
         proba = MathPow(e,TempArr[i])/sum;
         Nodes[i] = proba;
     } 
     
    ArrayFree(TempArr);
 }

隠れ層の単一のニューロンが何で構成されているかを理解したので、それをコーディングしましょう。

void CNeuralNets::Neuron(int HLnodes,
                        double bias,
                        double &Weights[],
                        double &Inputs[],
                        double &Outputs[]
                       )
 {
   ArrayResize(Outputs,HLnodes);
   
   for (int i=0, w=0; i<HLnodes; i++)
    {
      double dot_prod = 0;
      for(int j=0; j<ArraySize(Inputs); j++, w++)
        {
            if (m_debug) printf("i %d  w %d = input %.2f x weight %.2f",i,w,Inputs[j],Weights[w]);
            dot_prod += Inputs[j]*Weights[w];
        }
        
      Outputs[i] = ActivationFx(dot_prod+bias);
    }     
 }

ActivationFx()内では、NeuralNetsコンストラクタを呼び出すときに活性化関数を選択できます。

double CNeuralNets::ActivationFx(double Q)
 {
   switch(A_fx)
     {
      case  SIGMOID:
        return(Sigmoid(Q));
        break;
      case TANH:
         return(tanh(Q));
         break;
      case RELU:
         return(Relu(Q));
         break;
      default:
         Print("Unknown Activation Function");
        break;
     }
   return(0);
 }

コードに関する詳細な説明

Neuron()関数では、隠れ層内の単一のノードではなく、隠れ層のすべての操作がその1つの関数内で実行されます。すべての隠れ層のノードは、最終的な出力ノードまで、入力ノードと同じサイズになります。この構造を選択したのは、ランダムに生成されたデータセットでこのニューラルネットワークを使用して分類をおこなうためです。

以下のFeedForwardMLP()関数はNxN構造です。つまり、3つの入力ノードがあり、3つの隠れ層を選択した場合、各隠れ層に3つの隠れノードがあることになります。画像をご覧ください。

nxnニューラルネットワーク

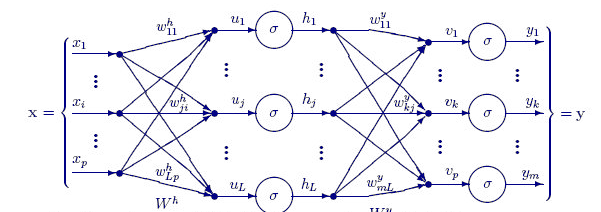
FeedForwardMLP()関数は次のとおりです。

void   CNeuralNets::FeedForwardMLP(int HiddenLayers,
           double &MLPInputs[],
           double &MLPWeights[],
           double &bias[],
           double &MLPOutput[])
 {
    
    double L_weights[], L_inputs[], L_Out[];
    
    ArrayCopy(L_inputs,MLPInputs);
    
    int HLnodes = ArraySize(MLPInputs);
    int no_weights = HLnodes*ArraySize(L_inputs);
    int weight_start = 0;
    
    for (int i=0; i<HiddenLayers; i++)
      {
        
        if (m_debug) printf("<< Hidden Layer %d >>",i+1);
        ArrayCopy(L_weights,MLPWeights,0,weight_start,no_weights);

        Neuron(HLnodes,bias[i],L_weights,L_inputs,L_Out);
        
        ArrayCopy(L_inputs,L_Out);
        ArrayFree(L_Out);
        
        ArrayFree(L_weights);
        
        weight_start += no_weights;
      }
     
    if (use_softmax)  SoftMax(L_inputs);
    ArrayCopy(MLPOutput,L_inputs);
    if (m_debug)
      {
       Print("\nFinal MLP output(s)");
       ArrayPrint(MLPOutput,5);
      }
 }

ニューラルネットワークで内積を求める操作は、行列演算で処理できますが、この最初の記事では、すべての読者に理解しやすいようにループメソッドを選択しました。次回は行列乗算を使用します。

ライブラリを構築するためにデフォルトで選択したアーキテクチャを見てきました。これにより、ニューラルネットワークアーキテクチャに関する疑問が生じます。

Googleでニューラルネットワークの画像を検索すると、何万とは言わずとも何千ものさまざまなニューラルネットワーク構造を持つ画像がヒットします。たとえば、次のような画像があります。

ニューラルネットワークアーキテクチャ

100万ドルの価値がある問題は、最適なニューラルネットワークアーキテクチャは何かということです。

「すべての答えを知っている人ほど間違っている人はいない」- トマス・マートン.

物事を分解して、何が必要で何が必要でないかを理解しましょう。

入力層

この層を構成する入力の数は、特徴（データセット内の列）の数と同じにする必要があります。

出力層

サイズ（ニューロンの数）は、分類ニューラルネットワークのデータセット内のクラスによって決定されます。回帰タイプの問題の場合、ニューロンの数は、選択したモデル構成によって決定されます。多くの場合、リグレッサーに対して1つの出力層で十分です。

隠れ層

問題が十分に複雑でない場合は、1つまたは2つの隠れ層で十分です。実際、問題の大部分には2つの隠れ層で十分です。ただし、各隠れ層にはいくつのノードが必要でしょうか。これについてはよくわかりませんが、パフォーマンスに依存すると思います。開発者が、さまざまなノードを調べて試して、特定の種類の問題に最適なものを確認するべきだと思います。また、これで実験してみる前に、前に説明した他のタイプのニューラルネットワークを認識してください。

このテーマについて、stats.stackexchange.comに素晴らしいトピックがあります。こちらです。

すべての隠れ層で入力層と同じ数のノードを持つことは、フィードフォワードニューラルネットワークにとって理想的だと思います。これは、私がほとんどの場合使用する構成です。

ノードが1つ、隠れ層が1つのMLPは線形モデルです。

ニューラルネットワークの隠れ層の1つのノード内でおこなわれる操作に注意を払うと、次のことがわかります。

Q = wi * Ii + b

一方、線形回帰方程式は次のとおりです。

Y = mi * xi + c

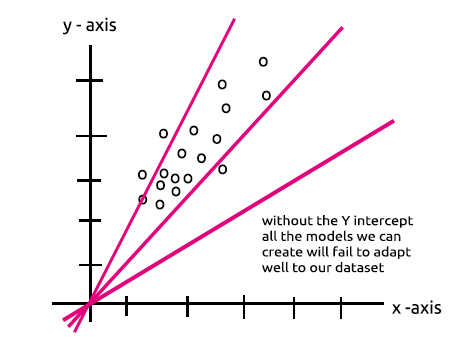
類似点にお気づきでしょうか。それらは理論的には同じものです。この操作は線形回帰であり、隠れ層のバイアスの重要性を思い起こさせます。バイアスは、指定されたデータセットに適合するようにモデルの柔軟性を追加する役割を持つ線形モデルの定数です。それがなければ、すべてのモデルがx軸とy軸の間をゼロで通過します。

切片なしの線形回帰

ニューラルネットワークを訓練すると、重みとバイアスが更新されます。モデルのエラーが少ないパラメータは、テストデータセットに保持され、記憶されます。

ポイントを明確にするために、2クラス分類のMLPを作成します。その前に、ラベル付けされたサンプルを使用してランダムデータセットを生成し、ニューラルネットワークで確認します。以下の関数はランダムなデータセットを作成し、2番目のサンプルに5を掛け、最初のサンプルに2を掛けて異なるスケールのデータを取得します。

void MakeBlobs(int size=10) 
 { 
     ArrayResize(data_blobs,size);
     for (int i=0; i<size; i++) 
       {   
         data_blobs[i].sample_1 = (i+1)*(2); 
         
         data_blobs[i].sample_2 = (i+1)*(5); 
         
         data_blobs[i].class_ = (int)round(nn.MathRandom(0,1));
       }  
 }

ここでデータセットを出力すると、次のようになります。

QK      0       18:27:57.298    TestScript (EURUSD,M1)  CNeural Nets Initialized activation = SIGMOID UseSoftMax = No
IR      0       18:27:57.298    TestScript (EURUSD,M1)      [sample_1] [sample_2] [class_]
LH      0       18:27:57.298    TestScript (EURUSD,M1)  [0]     2.0000     5.0000        0
GG      0       18:27:57.298    TestScript (EURUSD,M1)  [1]     4.0000    10.0000        0
NL      0       18:27:57.298    TestScript (EURUSD,M1)  [2]     6.0000    15.0000        1
HJ      0       18:27:57.298    TestScript (EURUSD,M1)  [3]     8.0000    20.0000        0
HQ      0       18:27:57.298    TestScript (EURUSD,M1)  [4]    10.0000    25.0000        1
OH      0       18:27:57.298    TestScript (EURUSD,M1)  [5]    12.0000    30.0000        1
JF      0       18:27:57.298    TestScript (EURUSD,M1)  [6]    14.0000    35.0000        0
DL      0       18:27:57.298    TestScript (EURUSD,M1)  [7]    16.0000    40.0000        1
QK      0       18:27:57.298    TestScript (EURUSD,M1)  [8]    18.0000    45.0000        0
QQ      0       18:27:57.298    TestScript (EURUSD,M1)  [9]    20.0000    50.0000        0

次の部分は、ランダムな重み値とバイアスを生成することです。

     generate_weights(weights,ArraySize(Inputs));
     generate_bias(biases);

出力は次のとおりです。

RG      0       18:27:57.298    TestScript (EURUSD,M1)  weights
QS      0       18:27:57.298    TestScript (EURUSD,M1)   0.7084 -0.3984  0.6182  0.6655 -0.3276  0.8846  0.5137  0.9371
NL      0       18:27:57.298    TestScript (EURUSD,M1)  biases
DD      0       18:27:57.298    TestScript (EURUSD,M1)  -0.5902  0.7384

それでは、スクリプトのメイン関数の操作全体を見てみましょう。

#include "NeuralNets.mqh";
CNeuralNets *nn;

input int batch_size =10;
input int hidden_layers =2;

data data_blobs[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---     
     nn = new CNeuralNets(SIGMOID);
           
     MakeBlobs(batch_size);
     
     ArrayPrint(data_blobs);
       
     double Inputs[],OutPuts[];
     
     ArrayResize(Inputs,2);     ArrayResize(OutPuts,2);
     
     double weights[], biases[];
     generate_weights(weights,ArraySize(Inputs));
     generate_bias(biases);
     
     Print("weights"); ArrayPrint(weights);
     Print("biases"); ArrayPrint(biases);
     
     for (int i=0; i<batch_size; i++)
       {
         Print("Dataset Iteration ",i);
         Inputs[0] = data_blobs[i].sample_1; Inputs[1]= data_blobs[i].sample_2;    
         nn.FeedForwardMLP(hidden_layers,Inputs,weights,biases,OutPuts);
       }
       
     delete(nn);    
  }

注意事項：

バイアスの数は、隠れ層の数と同じです。
重みの総数 = 入力の二乗数に隠れ層の数を掛けたもの。これは、私たちのネットワークが入力層/ネットワークの前の層と同じ数のノードを持っているという事実によって可能になりました（すべての層は入力から出力まで同じ数のノードを持っています）。
同じ原則に従います。たとえば、3つの入力ノードがある場合、すべての隠れ層に3つのノードがありますが、処理方法を確認しようとしている最後の層を除きます。

ランダムに生成されたデータセットを見ると、データセット内に2つの入力特徴/列があることがわかります。ここでは2つの隠れ層を選択しました。モデルがどのように計算を実行するかについてのログの簡単な概要を以下に示します（コードでdebugをfalseに設定するとこれらのログは出力されなくなります）。

NL      0       18:27:57.298    TestScript (EURUSD,M1)  Dataset Iteration 0
EJ      0       18:27:57.298    TestScript (EURUSD,M1)  << Hidden Layer 1 >>
GO      0       18:27:57.298    TestScript (EURUSD,M1)  
NS      0       18:27:57.298    TestScript (EURUSD,M1)   HLNode 1
EI      0       18:27:57.298    TestScript (EURUSD,M1)  i 0  w 0 = input 2.00000 x weight 0.70837
FQ      0       18:27:57.298    TestScript (EURUSD,M1)  i 0  w 1 = input 5.00000 x weight -0.39838
QP      0       18:27:57.298    TestScript (EURUSD,M1)  dot_Product -0.57513 + bias -0.590 = -1.16534
RH      0       18:27:57.298    TestScript (EURUSD,M1)  Activation function Output =0.23770
CQ      0       18:27:57.298    TestScript (EURUSD,M1)  
OE      0       18:27:57.298    TestScript (EURUSD,M1)   HLNode 2
CO      0       18:27:57.298    TestScript (EURUSD,M1)  i 1  w 2 = input 2.00000 x weight 0.61823
FI      0       18:27:57.298    TestScript (EURUSD,M1)  i 1  w 3 = input 5.00000 x weight 0.66553
PN      0       18:27:57.298    TestScript (EURUSD,M1)  dot_Product 4.56409 + bias -0.590 = 3.97388
GM      0       18:27:57.298    TestScript (EURUSD,M1)  Activation function Output =0.98155
DI      0       18:27:57.298    TestScript (EURUSD,M1)  << Hidden Layer 2 >>
GL      0       18:27:57.298    TestScript (EURUSD,M1)  
NF      0       18:27:57.298    TestScript (EURUSD,M1)   HLNode 1
FH      0       18:27:57.298    TestScript (EURUSD,M1)  i 0  w 0 = input 0.23770 x weight -0.32764
ID      0       18:27:57.298    TestScript (EURUSD,M1)  i 0  w 1 = input 0.98155 x weight 0.88464
QO      0       18:27:57.298    TestScript (EURUSD,M1)  dot_Product 0.79044 + bias 0.738 = 1.52884
RK      0       18:27:57.298    TestScript (EURUSD,M1)  Activation function Output =0.82184
QG      0       18:27:57.298    TestScript (EURUSD,M1)  
IH      0       18:27:57.298    TestScript (EURUSD,M1)   HLNode 2
DQ      0       18:27:57.298    TestScript (EURUSD,M1)  i 1  w 2 = input 0.23770 x weight 0.51367
CJ      0       18:27:57.298    TestScript (EURUSD,M1)  i 1  w 3 = input 0.98155 x weight 0.93713
QJ      0       18:27:57.298    TestScript (EURUSD,M1)  dot_Product 1.04194 + bias 0.738 = 1.78034
JP      0       18:27:57.298    TestScript (EURUSD,M1)  Activation function Output =0.85574
EI      0       18:27:57.298    TestScript (EURUSD,M1)  
GS      0       18:27:57.298    TestScript (EURUSD,M1)  Final MLP output(s)
OF      0       18:27:57.298    TestScript (EURUSD,M1)  0.82184 0.85574
CN      0       18:27:57.298    TestScript (EURUSD,M1)  Dataset Iteration 1
KH      0       18:27:57.298    TestScript (EURUSD,M1)  << Hidden Layer 1 >>
EM      0       18:27:57.298    TestScript (EURUSD,M1)  
DQ      0       18:27:57.298    TestScript (EURUSD,M1)   HLNode 1
QH      0       18:27:57.298    TestScript (EURUSD,M1)  i 0  w 0 = input 4.00000 x weight 0.70837
PD      0       18:27:57.298    TestScript (EURUSD,M1)  i 0  w 1 = input 10.00000 x weight -0.39838
HR      0       18:27:57.298    TestScript (EURUSD,M1)  dot_Product -1.15027 + bias -0.590 = -1.74048
DJ      0       18:27:57.298    TestScript (EURUSD,M1)  Activation function Output =0.14925
OP      0       18:27:57.298    TestScript (EURUSD,M1)  
CK      0       18:27:57.298    TestScript (EURUSD,M1)   HLNode 2
MN      0       18:27:57.298    TestScript (EURUSD,M1)  i 1  w 2 = input 4.00000 x weight 0.61823
NH      0       18:27:57.298    TestScript (EURUSD,M1)  i 1  w 3 = input 10.00000 x weight 0.66553
HI      0       18:27:57.298    TestScript (EURUSD,M1)  dot_Product 9.12817 + bias -0.590 = 8.53796
FO      0       18:27:57.298    TestScript (EURUSD,M1)  Activation function Output =0.99980
RG      0       18:27:57.298    TestScript (EURUSD,M1)  << Hidden Layer 2 >>
IR      0       18:27:57.298    TestScript (EURUSD,M1)  
PD      0       18:27:57.298    TestScript (EURUSD,M1)   HLNode 1
RN      0       18:27:57.298    TestScript (EURUSD,M1)  i 0  w 0 = input 0.14925 x weight -0.32764
HF      0       18:27:57.298    TestScript (EURUSD,M1)  i 0  w 1 = input 0.99980 x weight 0.88464
EM      0       18:27:57.298    TestScript (EURUSD,M1)  dot_Product 0.83557 + bias 0.738 = 1.57397
EL      0       18:27:57.298    TestScript (EURUSD,M1)  Activation function Output =0.82835
KE      0       18:27:57.298    TestScript (EURUSD,M1)  
GN      0       18:27:57.298    TestScript (EURUSD,M1)   HLNode 2
LS      0       18:27:57.298    TestScript (EURUSD,M1)  i 1  w 2 = input 0.14925 x weight 0.51367
FL      0       18:27:57.298    TestScript (EURUSD,M1)  i 1  w 3 = input 0.99980 x weight 0.93713
KH      0       18:27:57.298    TestScript (EURUSD,M1)  dot_Product 1.01362 + bias 0.738 = 1.75202
IR      0       18:27:57.298    TestScript (EURUSD,M1)  Activation function Output =0.85221
OH      0       18:27:57.298    TestScript (EURUSD,M1)  
IM      0       18:27:57.298    TestScript (EURUSD,M1)  Final MLP output(s)
MH      0       18:27:57.298    TestScript (EURUSD,M1)  0.82835 0.85221

ここで、すべての反復の最終的なMLP出力に注意してください。出力が同じ値を持つ傾向があるという奇妙な動作に気付くでしょう。この問題には、このStackで説明されているように、いくつかの原因があり、そのうちの1つは出力層で間違った活性化関数を使用していることです。ここで、ソフトマックス活性化関数の出番です。

私の理解では、シグモイド関数は、出力層に単一のノードがあり、1つのクラスを分類する必要がある場合にのみ確率を返します。この場合、何かが特定のクラスに属しているかどうかを示すために、シグモイドの出力が必要になります。、しかし、マルチクラスでは別の話です。最終ノードの出力を合計すると、ほとんどの場合、値が1を超えます。確率は1の値を超えることはできないため、これは確率ではないことがわかります。

ソフトマックスを最後の層に適用すると、出力は次のようになります。

最初の反復出力[0.49150.5085]、2番目の反復出力[0.49400.5060]

この場合、出力を[クラス0に属する確率　クラス1に属する確率]として解釈できます。

少なくとも今は、ネットワークから意味のあるものを解釈するために信頼できる可能性があります。

最後に

フィードフォワードニューラルネットワークはまだ終わっていませんが、少なくとも今のところ、MQL5でニューラルネットワークを習得するのに役立つ理論と最も重要なことは理解できました。設計されたフィードフォワードニューラルネットワークは分類目的のものであるため、データセットで分類するサンプルとクラスに応じて、適切な活性化関数はシグモイドとtanhになります。出力層を変更して、操作したいものを返すことはできませんでした。また、隠れ層のノードも変更できませんでした。行列の導入により、このすべての操作が動的になり、あらゆるタスクに対して非常に標準的なニューラルネットワークを構築できるようになります。これがこの連載の目標です。引き続きご注目ください。

すべてのタスクをニューラルネットワークで解決する必要があるわけではないため、ニューラルネットワークをいつ使用するかを知ることも重要です。タスクを線形回帰で解決できる場合、線形モデルはニューラルネットワークよりも優れていることがあります。これは、心に留めておくべきことの1つです。

GitHubリポジトリ:https://github.com/MegaJoctan/NeuralNetworks-MQL5

参考文献|書籍

記事の参照