Redes neuronales en el trading: Transformer para nubes de puntos (Pointformer)
Introducción
La detección de objetos en nubes de puntos es bastante importante para muchas aplicaciones del mundo real. En comparación con las imágenes, las nubes de puntos pueden ofrecer una geometría detallada y captar la estructura de un escenario. Por otra parte, las nubes de puntos son irregulares, lo cual plantea un gran reto para el aprendizaje eficiente de las características.
Los modelos basados en la arquitectura del Transformer han logrado grandes avances en el ámbito del procesamiento del lenguaje natural. Resultan muy eficaces en el aprendizaje de representaciones dependientes del contexto y en la captura de dependencias de largo alcance en la secuencia original. El Transformer y su mecanismo asociado de Self-Attention no solo cumplen el requisito de invarianza de la permutación, sino que también han demostrado ser altamente expresivos. Sin embargo, la aplicación directa del Transformer a las nubes de puntos resulta desorbitadamente cara, ya que el coste del cálculo crece de forma cuadrática con el tamaño de los datos de origen.
Los autores del método Pointformer intentan resolver este problema en el artículo "3D Object Detection with Pointformer". Este método permite un aprendizaje eficaz de las características aprovechando la superioridad de los modelos del Transformer en datos estructurados en conjuntos. El Pointformer es una estructura U-Net con bloques de Pointformer multiescala. El bloque Pointformer se compone de módulos basados en el Transformer que son a la vez expresivos y amigables con la tarea de detección de objetos.
Los autores del método utilizan 3 módulos del Transfotmer en su solución arquitectónica:
- El Trasformador Local (LT) se utiliza para modelar interacciones punto a punto en una región local. Este analiza las características dependientes del contexto de una región a nivel del objeto.
- El Local-Global Transformer (LGT) permite integrar funciones locales y globales con mayor resolución.
- El Global Transformer(GT) está diseñado para explorar representaciones conscientes del contexto a nivel de escenario.
Como resultado, Pointformer puede captar tanto las dependencias locales como las globales, mejorando así el rendimiento del aprendizaje de características para escenarios con múltiples objetos desordenados.
1. El algoritmo de Pointformer
Al estudiar las nubes de puntos, debemos considerar su naturaleza irregular y desordenada, así como su tamaño cambiante. Los autores del método Pointformer han desarrollado módulos basados en el Transformer para las operaciones con conjuntos de puntos. Los módulos propuestos no solo aumentan la expresividad de la extracción de características locales, sino que también incorporan información global a las representaciones de puntos.
La unidad Pointformer consta de tres módulos: El Local Transformer (LT), el Local-Global Transformer (LGT) y el Global Transformer (GT). Para cada bloque, LT obtiene primero los datos de origen del bloque anterior (alta resolución) y extrae características para un nuevo conjunto con menos elementos (baja resolución). A continuación, el LGT utiliza un mecanismo de atención cruzada multinivel para integrar las características de ambas resoluciones. Por último, el GT se utiliza para capturar vistas sensibles al contexto. En cuanto al bloque de aumento del muestro, los autores del método utilizan el módulo de propagación de funciones PointNet++.
Para construir una representación jerárquica de un escenario de nube de puntos, los autores de Pointformer utilizan una metodología de alto nivel para construir bloques de aprendizaje de características con diferentes resoluciones. En primer lugar, se usa una muestra de los puntos más alejados (FPS) como conjunto de centroides para seleccionar un subconjunto de puntos. Para cada centroide, se seleccionan los puntos de la región local dentro de un radio concreto. A continuación, estos objetos se agrupan en torno a los centroides y se transmiten como una secuencia de puntos a la capa del Transformer. Se aplica un bloque del Transformer común a todas las zonas locales. Y a medida que se aplican más capas del Transformer al bloque Pointformer, la expresividad del módulo aumenta y permite extraer mejores representaciones.
Además, se consideran las correlaciones de características entre puntos vecinos. En algunas circunstancias, los puntos vecinos pueden resultar incluso más informativos que el punto del centroide. Así, al usar la transferencia de información entre todos los puntos, los objetos de la región local se consideran por igual, lo que hace más eficaz el módulo de extracción de características locales.
El muestreo de puntos más lejanos (FPS) se utiliza ampliamente en muchos sistemas de nubes de puntos porque puede generar puntos de muestreo casi homogéneos conservando la forma original. Esto garantiza que la mayoría de los puntos puedan ser abarcados por un número limitado de centroides. Sin embargo, existen dos grandes problemas con el FPS:
- Es sensible a los valores atípicos, lo cual provoca una gran inestabilidad, especialmente cuando se trata de nubes de puntos reales.
- Los puntos de muestra FPS son un subconjunto de la nube de puntos original, lo cual dificulta la inferencia de la información geométrica original en los casos en que los objetos están parcialmente superpuestos o no se capturan suficientes puntos de objeto.
Como la mayoría de los puntos están fijados en la superficie de los objetos, la segunda cuestión puede cobrar mayor importancia, ya que las sugerencias se generan a partir de una muestra de puntos, lo que provoca una desconexión natural entre sugerencia y validez.
Para superar estos inconvenientes, los autores del método Pointformer proponen un módulo de refinamiento de coordenadas de puntos mediante mapas de Self-Attention. En primer lugar, se retiran los mapas de Self-Attention de la última capa del bloque del Transformer para cada cabeza de atención. Y luego se calcula la media de los mapas de atención. A continuación, se calculan las coordenadas refinadas del centroide ponderando los valores de todos los puntos de la región local por los coeficientes medios correspondientes de los mapas de Self-Attention. Con el módulo de refinamiento propuesto, las coordenadas del centroide se desplazan de forma adaptativa para aproximarse a los centros de los objetos.
La información global que representa los contextos de la escenario y las correlaciones de límites entre distintos objetos resulta igual de valiosa para las tareas de detección. Pointformer usa las capacidades de los módulos del Transformer para modelar relaciones no locales. En concreto, el módulo Global Transformer está diseñado para transferir información a través de toda la nube de puntos. Todos los puntos se recogen en un grupo y sirven como datos de entrada para el módulo GT.
El uso del Transformer a nivel de escenario, captura representaciones sensibles al contexto y facilita la transferencia de información entre diferentes objetos. Además, las representaciones globales pueden resultar especialmente útiles para detectar objetos con muy pocos puntos.
El Local-Global Transformer también es un módulo clave para combinar las funciones locales y globales extraídas por los módulos LT y GT. El LGT utiliza un módulo de atención cruzada multiescala y genera relaciones entre centroides de baja resolución y puntos de alta resolución. Formalmente, aquí se usa el mecanismo de atención cruzada del Transformer. Los resultados del LT sirven como Query, mientras que los datos del GT de mayor resolución (nivel anterior) se utilizan para Key y Value.
La codificación de la posición forma parte integrante de los modelos del Transformer. Es el único mecanismo que codifica información sobre la posición de cada token en la secuencia original. Al adaptar los Transformers a los datos de nubes de puntos, la codificación posicional desempeña un papel más importante, ya que las coordenadas de las nubes de puntos suponen características valiosas que indican estructuras locales.
A continuación le presentamos la visualización del autor del método Pointformer.

2. Implementación con MQL5
Tras repasar los aspectos teóricos del método Pointformer, pasaremos a la parte práctica de este artículo, donde implementaremos nuestra visión de los enfoques propuestos utilizando herramientas MQL5.
Al examinar en detalle los enfoques propuestos, observamos algunas similitudes con el método PointNet++ Ambos algoritmos usan el muestreo de los puntos más alejados para formar centroides. Y las operaciones básicas de ambos métodos se basan en la agrupación de puntos en torno a centroides. Por eso hemos decidido utilizar el objeto CNeuronPointNet2OCL como objeto padre para construir una nueva clase CNeuronPointFormer, cuya estructura se presenta a continuación.
class CNeuronPointFormer : public CNeuronPointNet2OCL { protected: CNeuronMLMHSparseAttention caLocalAttention[2]; CNeuronMLCrossAttentionMLKV caLocalGlobalAttention[2]; CNeuronMLMHAttentionMLKV caGlobalAttention[2]; CNeuronLearnabledPE caLocalPE[2]; CNeuronLearnabledPE caGlobalPE[2]; CNeuronBaseOCL cConcatenate; CNeuronConvOCL cScale; //--- CBufferFloat *cbTemp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override ; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronPointFormer(void) {}; ~CNeuronPointFormer(void) { delete cbTemp; } //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, uint output, bool use_tnets, ENUM_OPTIMIZATION optimization_type, uint batch) override; //--- virtual int Type(void) override const { return defNeuronPointFormer; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
En CNeuronPointNet2OCL, utilizaremos 2 niveles de escalas para extraer características locales. Y en la nueva clase, mantendremos un nivel de escalado similar, pero llevaremos la calidad de la extracción de características a un nuevo nivel, gracias a los módulos de atención propuestos. Esto se evidencia en las matrices de las capas neuronales internas, con cuyo propósito nos familiarizaremos a medida que implementemos los métodos de nuestra nueva clase CNeuronPointFormer.
Entre los objetos internos, solo hay un búfer declarado dinámicamente, que borraremos en el destructor de la clase. En este caso, dejaremos el constructor de la clase vacío, mientras que la inicialización de todos los objetos internos se realiza en el método Init, cuyos parámetros se transfieren sin cambios desde la clase padre.
bool CNeuronPointFormer::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, uint output, bool use_tnets, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronPointNet2OCL::Init(numOutputs, myIndex, open_cl, window, units_count, output, use_tnets, optimization_type, batch)) return false;
En el cuerpo del método, como es habitual, llamaremos primero al método homónimo de la clase padre, que controla los parámetros recibidos e inicializa los objetos heredados.
Aquí conviene recordar que creamos 2 capas internas de submuestreo local en la clase padre, a cuya salida obtendremos un vector de 64 elementos para cada punto de la nube analizada.
Después de cada capa de discretización local, añadiremos los módulos de atención propuestos por los autores del método Pointformer. La arquitectura modular de las dos capas será idéntica. Por ello, organizamos la inicialización de los objetos en un ciclo.
for(int i = 0; i < 2; i++) { if(!caLocalAttention[i].Init(0, i*5, OpenCL, 64, 16, 4, units_count, 2, optimization, iBatch)) return false;
En primer lugar, inicializaremos el módulo de atención local, cuya función será desempeñada por el bloque de atención dispersa CNeuronMLMHSparseAttention.
Aquí debemos decir que nos hemos apartado ligeramente del algoritmo propuesto por los autores del método Pointformer, pero manteniendo, a mi juicio, la lógica de la acción. En el módulo de atención local, los autores del método han enriquecido los puntos del área local con características comunes, lo que permite centrar la atención en el objeto de generalización. Obviamente, los puntos que pertenezcan al mismo objeto tendrán más dependencias. El uso de un bloque de atención dispersa permite ir más allá de una única área local y destacar elementos con una fuerte dependencia. Esto puede compararse con la definición de los niveles de apoyo y resistencia que el precio ha tocado varias veces en diferentes partes del intervalo histórico analizado.
A continuación, inicializaremos el bloque de atención local-global, donde aumentaremos la información local del objeto con semitonos de los datos de origen.
if(!caLocalGlobalAttention[i].Init(0, i*5+1, OpenCL, 64, 16, 4, 64, 2, units_count, units_count, 2, 2, optimization, iBatch)) return false;
Mientras que la unidad de atención global está diseñada para identificar representaciones dependientes del contexto a nivel de escenario.
if(!caGlobalAttention[i].Init(0, i*5+2, OpenCL, 64, 16, 4, 2, units_count, 2, 2, optimization, iBatch)) return false;
Y, por supuesto, añadiremos capas internas de codificación posicional entrenable. Aquí utilizaremos codificaciones posicionales separadas para la representación local y global.
if(!caLocalPE[i].Init(0, i*5+3, OpenCL, 64*units_count, optimization, iBatch)) return false; if(!caGlobalPE[i].Init(0, i*5+4, OpenCL, 64*units_count, optimization, iBatch)) return false; }
Cabe mencionar que no utilizaremos el bloque de refinamiento de coordenadas del centroide propuesto por los autores del método Pointformer. En primer lugar, al aplicar el algoritmo PointNet++, definiremos cada punto de la nube como el centroide del área local. En consecuencia, modificar las coordenadas de los puntos puede distorsionar el conjunto de la escenario. Por otro lado, la función de refinamiento de la posición del centroide se realiza parcialmente usando capas de codificación de posición entrenadas.
Ahora diremos unas palabras sobre el escalado de la extracción de características. Los objetos anteriormente inicializados no indican en modo alguno una diferencia en el ámbito de la extracción de características. Pero hay dos puntos a considerar. En la clase padre, utilizaremos diferentes radios de discretización local. Y aquí añadiremos diferentes niveles de atención localizada dispersa.
caLocalAttention[0].Sparse(0.1f); caLocalAttention[1].Sparse(0.3f);
Luego concatenaremos los resultados de los dos niveles de atención global en un único tensor.
if(!cConcatenate.Init(0, 10, OpenCL, 128 * units_count, optimization, iBatch)) return false;
Y haremos descender su dimensionalidad a los datos de origen del bloque de extracción del descriptor global de la nube de puntos que se inicializó en el método de la clase padre.
if(!cScale.Init(0, 11, OpenCL, 128, 128, 64, units_count, 1, optimization, iBatch)) return false;
Al final del método de inicialización, añadiremos la creación de un búfer intermedio de almacenamiento de datos.
if(!!cbTemp) delete cbTemp; cbTemp = new CBufferFloat(); if(!cbTemp || !cbTemp.BufferInit(caGlobalAttention[0].Neurons(), 0) || !cbTemp.BufferCreate(OpenCL)) return false; //--- return true; }
Después retornaremos el resultado lógico de las operaciones al programa que realiza la llamada y finalizaremos el método.
La siguiente etapa de nuestro trabajo consistirá en construir un algoritmo de pasada directa en el método feedForward. Y aquí, a diferencia del método de inicialización, no podremos utilizar completamente el método análogo de la clase padre. En el nuevo método, tendremos que combinar operaciones sobre objetos heredados y añadidos.
En los parámetros del método de pasada directa obtendremos un puntero al objeto de datos de origen, como antes. Y en el cuerpo del método guardaremos inmediatamente el puntero recibido en una variable local.
bool CNeuronPointFormer::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- LocalNet CNeuronBaseOCL *inputs = NeuronOCL;
En la mayoría de los casos, no almacenaremos el puntero resultante en una variable local porque no tiene sentido. Pero en este método, tendremos que implementar el algoritmo de operación secuencial de 2 bloques anidados de extracción de características de diferente escala. Y en el cuerpo del ciclo, resulta más cómodo trabajar con una variable local a la que podemos asignar punteros a varios objetos.
E inmediatamente después crearemos el ciclo anterior.
for(int i = 0; i < 2; i++) { if(!cTNetG || i > 0) { if(!caLocalPointNet[i].FeedForward(inputs)) return false; }
En el cuerpo del ciclo, primero realizaremos operaciones de discretización local cuyos objetos hayan sido declarados e inicializados en la clase padre.
Recordemos que el algoritmo de la clase padre permite proyectar los datos de origen en el espacio canónico. Y esta operación se realizará solo antes de la primera capa de muestreo local. Por lo tanto, primero comprobaremos si es necesario proyectar los datos de origen y, si no lo es, realizaremos inmediatamente la operación de discretización local.
En caso contrario, generaremos primero la matriz de proyección.
else { if(!cTurnedG) return false; if(!cTNetG.FeedForward(inputs)) return false;
Luego realizaremos la operación de proyección de los datos iniciales.
int window = (int)MathSqrt(cTNetG.Neurons()); if(IsStopped() || !MatMul(NeuronOCL.getOutput(), cTNetG.getOutput(), cTurnedG.getOutput(), NeuronOCL.Neurons() / window, window, window)) return false;
Y solo después discretizaremos los datos locales.
if(!caLocalPointNet[i].FeedForward(cTurnedG.AsObject())) return false; }
Desde la capa local de muestreo de datos, la información se transferirá al módulo local de atención.
//--- Local Attention if(!caLocalAttention[i].FeedForward(caLocalPointNet[i].AsObject())) return false;
Obsérvese que transmitiremos los datos al módulo de atención local sin codificación de posición. Al mismo tiempo, querría recordarle que el algoritmo Self-Attention resulta invariable con respecto a la secuencia de los objetos analizados. Así, en el bloque de atención local, identificaremos objetos con un alto grado de influencia mutua independientemente de sus coordenadas.
Suena un poco ilógico decir "análisis en el bloque de atención local sin referencia a las coordenadas". Parece que la atención local implica una cierta limitación de las coordenadas analizadas, pero le animo a verlo de otra manera. Tenemos un gráfico de precios. Podemos dividir la información sobre los precios en 2 categorías: coordenadas y características. La coordenada será el tiempo, mientras que el nivel de precios será una característica. Si eliminamos las coordenadas (datos temporales), obtendremos una especie de nube de puntos en el espacio de características. Y en el nivel en el que el valor del instrumento era más frecuente, el número de puntos será mayor. Al mismo tiempo, estos puntos pueden estar muy separados en el tiempo, pero estas son las zonas que más a menudo actúan como niveles de apoyo y resistencia. Por ello, nuestro módulo de atención local trabajará en un espacio de características locales.
Pero a continuación, añadiremos la codificación de posición tanto al resultado del módulo de atención local como al resultado de la capa de muestreo de datos locales.
//--- Position Encoder if(!caLocalPE[i].FeedForward(caLocalAttention[i].AsObject())) return false; if(!caGlobalPE[i].FeedForward(caLocalPointNet[i].AsObject())) return false;
Y en el siguiente paso del módulo de atención local-global, enriqueceremos los datos de atención local con información del contexto global, considerando las coordenadas de los objetos.
//--- Local to Global Attention if(!caLocalGlobalAttention[i].FeedForward(caLocalPE[i].AsObject(), caGlobalPE[i].getOutput())) return false;
Y las operaciones de nuestro ciclo se completarán con el módulo de atención global, que enriquecerá la información de los objetos con el contexto general de la escenario.
//--- Global Attention if(!caGlobalAttention[i].FeedForward(caLocalGlobalAttention[i].AsObject())) return false; inputs = caGlobalAttention[i].AsObject(); }
Y antes de pasar a la siguiente iteración del ciclo, no nos olvidaremos de cambiar el puntero al objeto de datos de origen en la variable local.
Tras completar con éxito todas las iteraciones de nuestro ciclo secuencial de enumeración de capas internas, concatenaremos los resultados de todos los módulos de atención global en un único tensor, lo que nos permitirá seguir considerando las características de los objetos a diferentes escalas.
if(!Concat(caGlobalAttention[0].getOutput(), caGlobalAttention[1].getOutput(), cConcatenate.getOutput(), 64, 64, cConcatenate.Neurons() / 128)) return false;
Luego reduciremos ligeramente el tamaño del tensor concatenado utilizando la capa de escalado.
if(!cScale.FeedForward(cConcatenate.AsObject())) return false;
Y pasaremos los datos recibidos al método de pasada directa de la clase CNeuronPointNetOCL que es el ancestro de nuestra clase padre. Implementa un mecanismo para generará un descriptor global de la nube de puntos.
if(!CNeuronPointNetOCL::feedForward(cScale.AsObject())) return false; //--- return true; }
No olvide controlar el proceso de ejecución de las operaciones en cada paso. Y después de la ejecución exitosa de todas las operaciones del método, devolveremos su resultado lógico al programa que realiza la llamada.
A continuación, pasaremos a la construcción de algoritmos de pasada inversa. Y aquí, como usted sabrá, tenemos 2 métodos para implementar:
- calcInputGradients - distribución del gradiente de error a todos los objetos según su influencia en el resultado global;
- updateInputWeights - actualiza los parámetros entrenados del modelo.
Para construir el algoritmo del segundo método, podemos tomar simplemente el método de pasada directa presentado anteriormente, dejando solo la jerarquía de llamada a los métodos de objetos con los parámetros entrenables en ella. Y luego reemplazar la llamada al método de pasada directa por el método de actualización de parámetros. Podrá ver el resultado en el archivo adjunto.
En cambio, con el algoritmo del método de distribución de gradientes de error calcInputGradients deberemos trabajar un poco. Como antes, el algoritmo del método seguirá el flujo de operaciones de pasada directa exactamente igual que antes, pero en orden inverso. Sin embargo, existen matices a considerar relacionados con el paralelismo de los flujos de información.
En los parámetros del método obtendremos el puntero al objeto de la capa anterior, al que tendremos que pasar el gradiente de error según la influencia de los datos iniciales en el resultado del modelo.
bool CNeuronPointFormer::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
En el cuerpo del método comprobaremos directamente la relevancia del puntero obtenido. Y es que, si no resulta válido, realizar otras operaciones perderá todo su sentido.
Debemos decir que el gradiente de error en el nivel de resultado de nuestra capa ya está contenido en el búfer de datos correspondiente en el momento de llamar a este método. Así que lo haremos descender a la capa interna de escalado llamando al método correspondiente de la clase antecesora.
if(!CNeuronPointNetOCL::calcInputGradients(cScale.AsObject())) return false;
A continuación, ejecutaremos el gradiente de error hasta la capa de datos concatenados.
if(!cConcatenate.calcHiddenGradients(cScale.AsObject())) return false;
Y lo distribuiremos a los módulos correspondientes de atención global.
if(!DeConcat(caGlobalAttention[0].getGradient(), caGlobalAttention[1].getGradient(), cConcatenate.getGradient(), 64, 64, cConcatenate.Neurons() / 128)) return false;
Y aquí deberemos pasar sistemáticamente el gradiente de error por los módulos de todas las capas internas. Para ello, organizaremos un ciclo de iteración inversa.
CNeuronBaseOCL *inputs = caGlobalAttention[0].AsObject(); for(int i = 1; i >= 0; i--) { //--- Global Attention if(!caLocalGlobalAttention[i].calcHiddenGradients(caGlobalAttention[i].AsObject())) return false;
En él, definiremos en primer lugar el gradiente de error a nivel del módulo de atención local-global. Y luego lo distribuiremos a las capas de la codificación posicional entrenada.
if(!caLocalPE[i].calcHiddenGradients(caLocalGlobalAttention[i].AsObject(), caGlobalPE[i].getOutput(), caGlobalPE[i].getGradient(), (ENUM_ACTIVATION)caGlobalPE[i].Activation())) return false;
A continuación, desde las capas de codificación posicional correspondientes, transferiremos el gradiente de error hasta el módulo de atención local y la capa de muestreo local.
if(!caLocalAttention[i].calcHiddenGradients(caLocalPE[i].AsObject())) return false; if(!caLocalPointNet[i].calcHiddenGradients(caGlobalPE[i].AsObject())) return false;
Ahora observe que el módulo de atención local también utiliza los resultados de la capa de muestreo local como entrada. Por ello, deberá transmitir su parte del gradiente de error a este objeto. Sin embargo, el búfer de datos correspondiente ya contiene el gradiente de error de la capa de codificación posicional que no querríamos perder. Por consiguiente, antes de transmitir el gradiente de error desde el módulo de atención local, necesitaremos almacenar la información existente en un búfer de almacenamiento temporal de datos.
Y aquí deberemos considerar que hemos creado deliberadamente un puntero dinámico al objeto búfer de almacenamiento. Además, haremos que su tamaño sea igual al búfer de gradientes de error de la capa de muestreo local. Y esto nos permitirá realizar un simple intercambio de punteros a objetos en lugar de copiar datos.
CBufferFloat *temp = caLocalPointNet[i].getGradient();
caLocalPointNet[i].SetGradient(cbTemp, false);
cbTemp = temp;
Y ahora podremos realizar con seguridad la transferencia del gradiente de error desde el módulo de atención local sin temor a perder los datos guardados anteriormente.
if(!caLocalPointNet[i].calcHiddenGradients(caLocalAttention[i].AsObject())) return false; if(!SumAndNormilize(caLocalPointNet[i].getGradient(), cbTemp, caLocalPointNet[i].getGradient(), 64, false, 0, 0, 0, 1)) return false;
Y luego sumaremos el gradiente de error a partir de los dos flujos de información.
Nuestro siguiente paso consistirá en pasar el gradiente de error a la capa de datos de origen. Pero aquí también hay un matiz a considerar. Dependiendo de la iteración del ciclo, pasaremos el gradiente de error a la capa del módulo de atención global de la capa interna anterior, o al objeto de datos de origen obtenido en los parámetros del método. En este último caso, el algoritmo será similar al método de la clase padre. Pero en el primero, deberemos recordar que arriba ya hemos guardado el gradiente de error por deconcatenación de datos del módulo de generación del descriptor global de la nube de datos analizada. En este caso también intercambiaremos los punteros a los búferes de datos. Al fin y al cabo, por algo se han creado del mismo tamaño.
if(i > 0) { temp = inputs.getGradient(); inputs.SetGradient(cbTemp, false); cbTemp = temp; }
A continuación comprobaremos si es necesario corregir el gradiente de error para la proyección del espacio canónico. Si no es necesario, pasaremos el gradiente al objeto correspondiente inmediatamente.
if(!cTNetG || i > 0) { if(!inputs.calcHiddenGradients(caLocalPointNet[i].AsObject())) return false; }
Si, por el contrario, la pasada directa se proyectaba en el espacio canónico, pasaremos primero el gradiente de error hasta el nivel del módulo de la capa de proyección.
else { if(!cTurnedG) return false; if(!cTurnedG.calcHiddenGradients(caLocalPointNet[i].AsObject())) return false;
Luego distribuiremos el gradiente de error entre los datos de origen y la matriz de proyección.
int window = (int)MathSqrt(cTNetG.Neurons()); if(IsStopped() || !MatMulGrad(inputs.getOutput(), inputs.getGradient(), cTNetG.getOutput(), cTNetG.getGradient(), cTurnedG.getGradient(), inputs.Neurons() / window, window, window)) return false;
Y corregiremos el gradiente de la matriz de proyección según el error de desviación de la matriz ortogonal.
if(!OrthoganalLoss(cTNetG, true)) return false;
Aquí también organizaremos las operaciones de intercambio de búferes de datos para preservar los gradientes de error de los dos flujos de información.
CBufferFloat *temp = inputs.getGradient(); inputs.SetGradient(cTurnedG.getGradient(), false); cTurnedG.SetGradient(temp, false);
Después transferiremos el gradiente de error del módulo de generación de la matriz de proyección en el espacio canónico al nivel de los datos de origen.
if(!inputs.calcHiddenGradients(cTNetG.AsObject())) return false;
Y sumaremos el gradiente de error a nivel de datos de origen a partir de los dos flujos de información.
if(!SumAndNormilize(inputs.getGradient(), cTurnedG.getGradient(), inputs.getGradient(), 1, false, 0, 0, 0, 1)) return false; }
A continuación, volveremos a determinar si es necesario sumar el gradiente de error de otros flujos de información y cambiaremos el puntero en la variable local al objeto de datos de origen. Y entonces pasaremos a la siguiente iteración del ciclo.
if(i > 0) { if(!SumAndNormilize(inputs.getGradient(), cbTemp, inputs.getGradient(), 64, false, 0, 0, 0, 1)) return false; inputs = caGlobalAttention[i - 1].AsObject(); } else inputs = NeuronOCL; } //--- return true; }
Cuando todas las iteraciones de nuestro ciclo de retroceso de la capa interna se hayan completado, devolveremos al programa que realiza la llamada el valor lógico del resultado de las operaciones de nuestro método de distribución del gradiente de error y lo finalizaremos.
Con esto concluye nuestra revisión de los algoritmos de construcción de los métodos para nuestra nueva clase de implementación de los enfoques propuestos por los autores del método Pointformer y CNeuronPointFormer. Podrá ver el código completo de esta clase y todos sus métodos en el archivo adjunto.
Y después solemos describir la arquitectura del modelo en el que estamos introduciendo la nueva clase. Esta vez será bastante sencillo. Como siempre, introduciremos la nueva clase en el modelo de Codificador del entorno. Utilizaremos el modelo del artículo anterior como arquitectura básica. Al mismo tiempo, la arquitectura del modelo permanecerá prácticamente inalterada. Simplemente sustituiremos en ella el tipo de capa de la clase padre por uno nuevo con todos los demás parámetros intactos. Estos ajustes no requerirán cambios en la arquitectura de los modelos del Actor y el Crítico, ni tampoco en los algoritmos de los programas de entrenamiento de modelos e interacción con el entorno, que también se transferirán sin cambios. Por lo tanto, no nos detendremos en estos puntos en el presente artículo. Podrá ver la arquitectura completa de todos los modelos en el archivo adjunto. También le presentamos allí el código completo de todos los programas utilizados en la elaboración del artículo.
3. Simulación
Hemos trabajado mucho para implementar nuestra visión de los enfoques propuestos por los autores del método Pointformer usando MQL5.
Hago hincapié en que la aplicación presentada en el artículo muestra algunas diferencias con el algoritmo presentado en el artículo del autor. Por consiguiente, los resultados obtenidos pueden ser en cierta medida distintos al rendimiento del algoritmo del autor.
Y ahora es el momento de ver los resultados de nuestro trabajo. Como antes, para entrenar los modelos usaremos los datos históricos reales para 2023 del instrumento financiero EURUSD y el marco temporal H1. Los parámetros de todos los indicadores analizados se han usado por defecto.
En primer lugar, realizaremos un entrenamiento iterativo offline del modelo ejecutando el asesor experto "...\PointFormer\Study.mq5" en tiempo real. Este asesor experto no realiza transacciones comerciales. Su algoritmo solo incluye el entrenamiento del modelo.
Las primeras iteraciones del entrenamiento se realizarán sobre los datos de las pasadas recogidas al entrenar los modelos a partir de trabajos anteriores. La estructura y los parámetros de los datos analizados no han cambiado.
A continuación, actualizaremos los datos de la muestra de entrenamiento para que sean lo más parecidos posible a la política de acción actual del Actor. Esto permitirá evaluar mejor sus acciones en el proceso de entrenamiento y ajustar correctamente la dirección de la optimización de la política. Para ello, ejecutaremos el modo de optimización lenta para el asesor de interacción con el entorno "...\PointFormer\Research.mq5" en el simulador de estrategias.
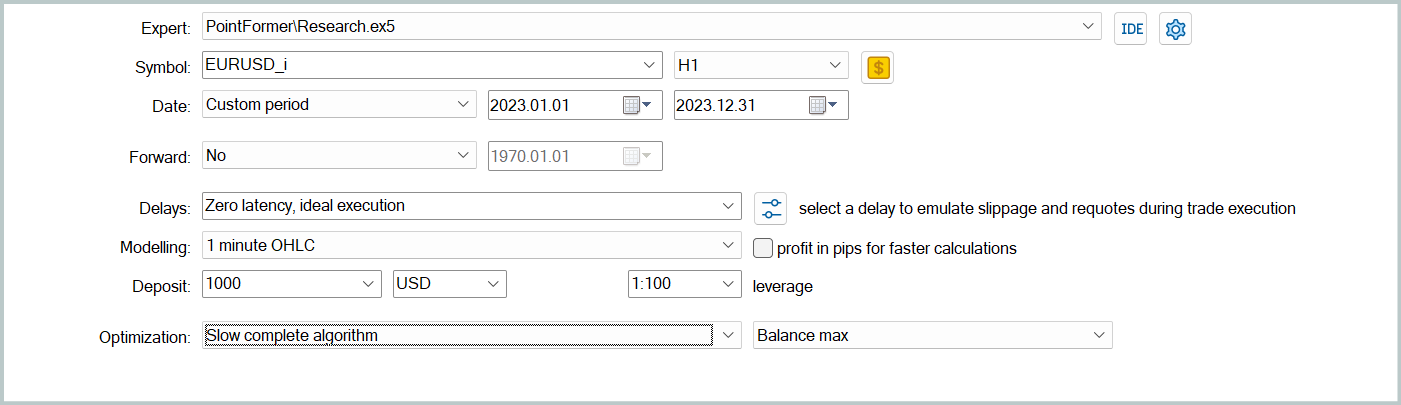
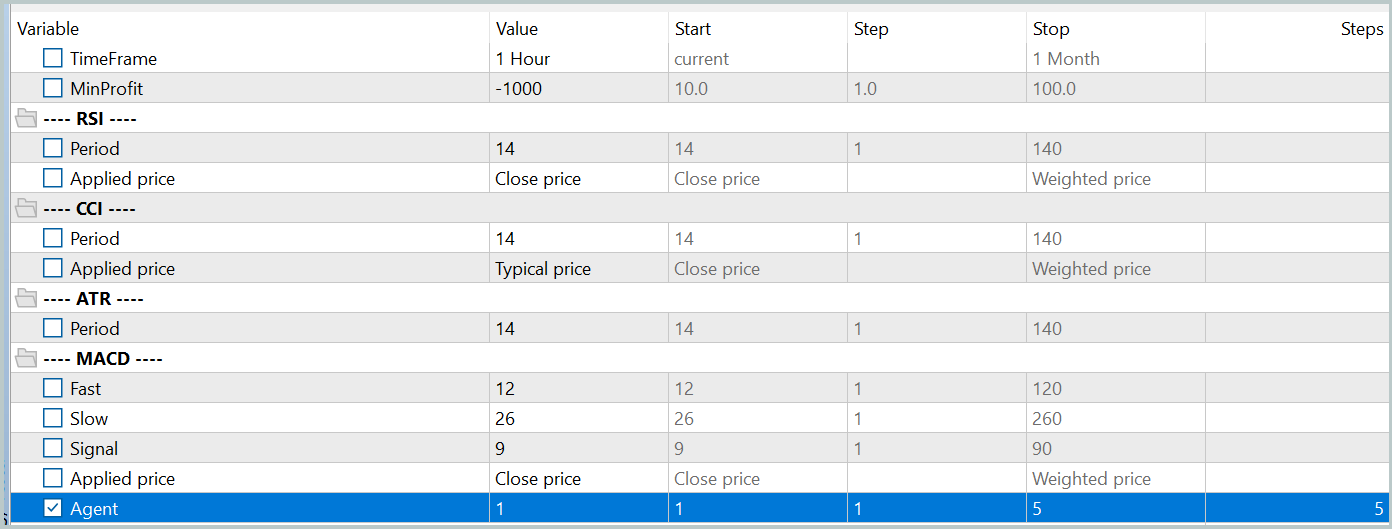
A continuación, repetiremos el proceso de entrenamiento de los modelos.
El entrenamiento del modelo y la actualización de la muestra de entrenamiento se realizarán iterativamente varias veces. Una buena señal del final del proceso de entrenamiento podría ser la obtención de resultados aceptables en todas las pasadas de la última iteración de actualización de la muestra de entrenamiento.
No obstante, deberá tenerse en cuenta que son aceptables ligeras diferencias en los resultados de las pasadas individuales. Esto se debe al uso de la política estocástica del Actor, que implica cierta estocasticidad de las acciones dentro del rango entrenado. A medida que se entrenen los modelos, disminuirá la estocasticidad de las acciones. Sin embargo, resultará aceptable alguna variación, por supuesto, si no cambia fundamentalmente la rentabilidad de la política.
Tras realizar varias iteraciones de entrenamiento de los modelos y actualizar la muestra de entrenamiento, hemos conseguido obtener una política capaz de generar beneficios tanto en la muestra de entrenamiento como en la de prueba.
Probaremos el modelo entrenado en el simulador de estrategias de MetaTrader 5 con los datos históricos de enero de 2024, manteniendo todos los demás parámetros intactos. Ahora le presentamos los resultados de las pruebas.
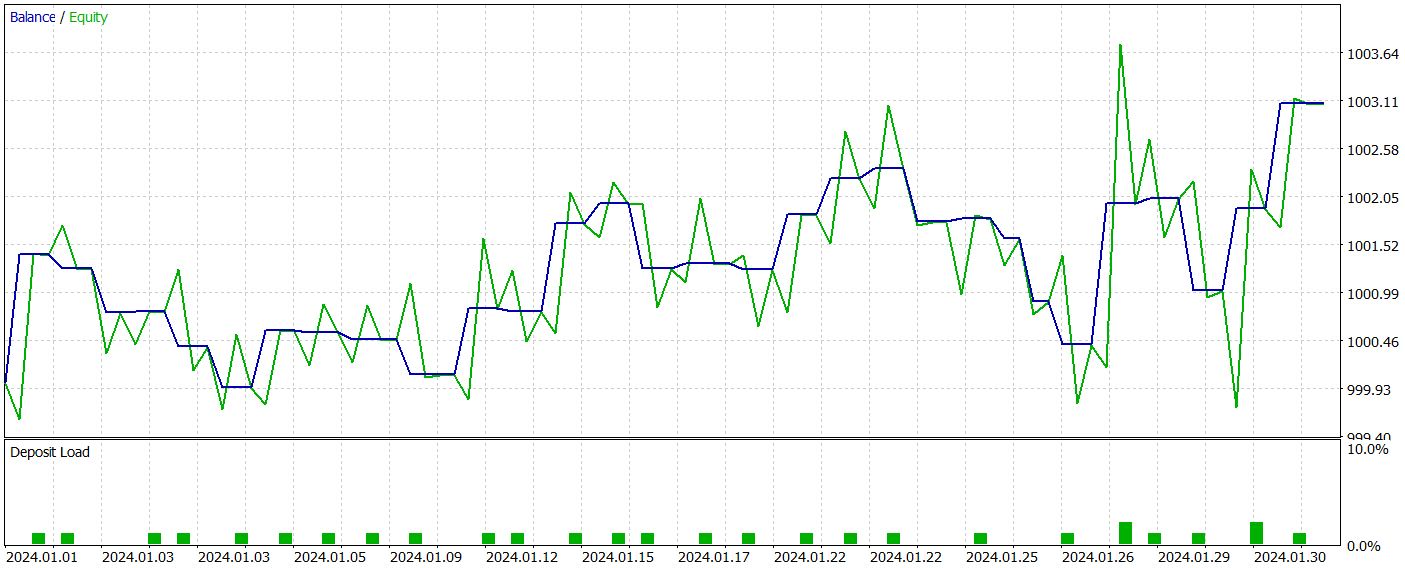
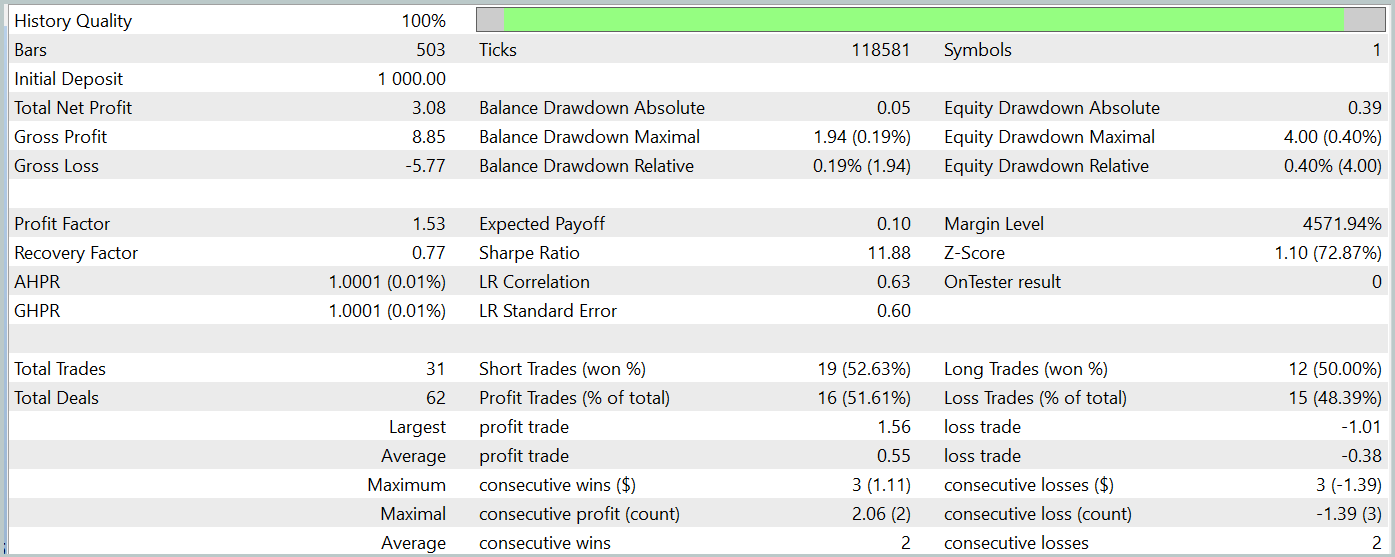
Durante el periodo de pruebas, el modelo entrenado solo ha realizado 31 transacciones comerciales, la mitad de las cuales se han cerrado con beneficio. Al mismo tiempo, las operaciones rentables máximas y medias han superado prácticamente en un 50% los indicadores similares de las transacciones no rentables, permitiendo fijar el valor del índice del factor de beneficio a un nivel de 1,53. Pero a pesar de que el gráfico de balance tiende a crecer, el bajo número de transacciones comerciales realizadas no nos permite sacar una conclusión sobre la eficacia del funcionamiento del modelo en un intervalo de tiempo largo.
Conclusión
En este artículo, hemos introducido el método Pointformer, que ofrece una nueva arquitectura para trabajar con nubes de puntos. El algoritmo propuesto combina Transformers locales y globales para extraer eficazmente patrones espaciales tanto locales como globales de los datos multidimensionales. El Pointformer utiliza mecanismos de atención para procesar la información considerando el contexto espacial, y favorece el aprendizaje según la importancia de cada punto.
En la parte práctica del artículo, hemos implementado nuestra visión de los enfoques propuestos usando MQL5. Asimismo, hemos entrenado y probado el modelo utilizando los algoritmos propuestos. Y los resultados demuestran el potencial del método a la hora de analizar estructuras de datos complejas.
No obstante, cabe señalar que debemos seguir investigando y optimizando para comprender mejor las capacidades de Pointformer en el contexto de los datos financieros.
Enlaces
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de Modelos |
| 4 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 5 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 6 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15820
 Introducción a Connexus (Parte 1): ¿Cómo utilizar la función WebRequest?
Introducción a Connexus (Parte 1): ¿Cómo utilizar la función WebRequest?
 Redes neuronales en el trading: Aprendizaje jerárquico de características en nubes de puntos
Redes neuronales en el trading: Aprendizaje jerárquico de características en nubes de puntos
 Aprendiendo MQL5 de principiante a profesional (Parte V): Operadores básicos para redirigir el flujo de comandos
Aprendiendo MQL5 de principiante a profesional (Parte V): Operadores básicos para redirigir el flujo de comandos
 Creación de un Panel de administración de operaciones en MQL5 (Parte II): Mejorar la capacidad de respuesta y la rapidez de los mensajes
Creación de un Panel de administración de operaciones en MQL5 (Parte II): Mejorar la capacidad de respuesta y la rapidez de los mensajes
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso