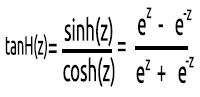
Scienza dei Dati e Apprendimento Automatico — Rete Neurale (Parte 01): Rete Neurale Feed Forward demistificata
"... stanco di sapere troppo e di capire troppo poco".
― Jan Karon, Home to Holly Springs
Introduzione
Le reti neurali suonano come questa cosa nuova di fantasia che sembra come un modo per costruire sistemi di trading del Sacro Graal, molti trader sono sbalorditi dai programmi realizzati con le reti neurali, perché sembrano essere bravi a prevedere i movimenti del mercato, in pratica sono bravi a svolgere qualsiasi compito. Anch'io credo che abbiano un enorme potenziale quando si tratta di prevedere o classificare sulla base di dati non addestrati o mai visti.
Per quanto possano essere validi, devono essere costruiti da qualcuno esperto e a volte devono essere ottimizzati per assicurarsi che non solo il percettrone Multistrato abbia l'architettura corretta, ma anche che il tipo di problema sia quello che richiede una rete neurale piuttosto che un modello di regressione lineare o logistica o qualsiasi altra tecnica di apprendimento automatico.
Le Reti Neurali sono un argomento più ampio, così come l'Apprendimento Automatico in generale; motivo per cui ho deciso di aggiungere una sottosezione per le reti neurali, mentre procederò con altri aspetti del ML nell'altra sottosezione della serie.
In questo articolo vedremo le basi di una rete neurale e risponderemo ad alcune delle domande fondamentali che ritengo siano importanti per un appassionato di ML per comprendere e padroneggiare questo argomento.
Che cos'è la Rete Neurale Artificiale?
Le Reti Neurali Artificiali (RNA), solitamente chiamate reti neurali, sono sistemi di calcolo ispirati alle reti neurali biologiche che costituiscono il cervello degli animali.
Percettrone Multistrato vs Rete Neurale Profonda
Quando si parla di reti neurali, si sente spesso pronunciare il termine Percettrone Multistrato (MLP). Questo non è altro che il tipo più comune di rete neurale. Una MLP è una rete composta da uno strato di input, uno strato nascosto e uno strato di output. Grazie alla loro semplicità, richiedono tempi di addestramento brevi per apprendere le relazioni nei dati e produrre un output.
Applicazioni:
Le MLP vengono solitamente utilizzate per dati non linearmente separabili, come nell'analisi di regressione. Grazie alla loro semplicità, sono più adatte a compiti di classificazione complessi e alla modellazione predittiva. Sono stati utilizzati per le traduzioni automatiche, le previsioni meteorologiche, il rilevamento delle frodi, le previsioni del mercato azionario, le previsioni della valutazione del credito e molti altri aspetti che si possono pensare.
Le Reti Neurali Profonde, invece, hanno una struttura comune, ma l'unica differenza è che comprendono molti strati nascosti. Se la rete ha più di tre (3) strati nascosti, la si considera una rete neurale profonda. A causa della loro natura complessa, richiedono lunghi periodi di addestramento sui dati di input, inoltre, richiedono computer potenti con unità di elaborazione specializzate, come le Tensor Processing Units (TPU) e le Neural Processing Units (NPU).
Applicazioni:
I DNN sono potenti algoritmi grazie ai loro strati profondi e per questo vengono solitamente utilizzati per gestire compiti computazionali complessi, tra cui la computer vision.
Tabella delle differenze:
| MLP | DNN |
|---|---|
| Numero ridotto di strati nascosti | Numero elevato di strati nascosti |
| Periodi di addestramento brevi | Molte ore di addestramento |
| È sufficiente un dispositivo dotato di GPU | Il dispositivo di attivazione TPU è sufficiente |
Vediamo ora i tipi di reti neurali.
Esistono molti tipi di reti neurali, ma grosso modo si suddividono in tre (3) classi principali;
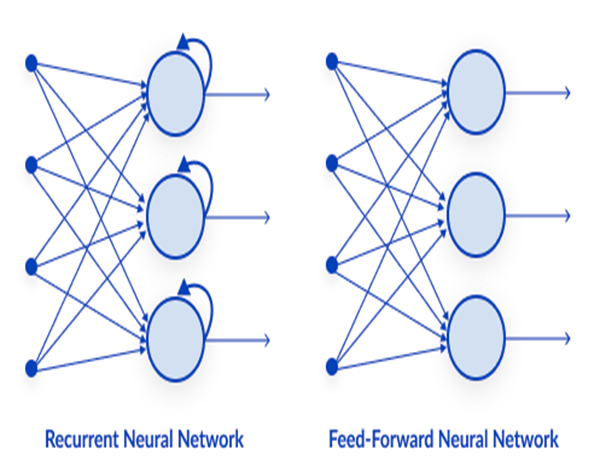
- Reti neurali feedforward
- Reti neurali convoluzionali
- Reti neurali ricorrenti
01: Rete Neurale Feedforward
È uno dei tipi più semplici di reti neurali. In una rete neurale feed-forward, i dati passano attraverso i diversi nodi di input fino a raggiungere un nodo di output. A differenza della retropropagazione, qui i dati si muovono in una sola direzione.
Semplicemente, la Retropropagazione esegue nella rete neurale gli stessi processi del feed-forward, in cui i dati vengono passati dallo strato di input a quello di output, ma nella retropropagazione, dopo che il risultato della rete ha raggiunto lo strato di uscita, si va a vedere il valore reale di una classe e lo si confronta con il valore che ha previsto, il modello vede quanto è sbagliata o corretta la sua previsione, se ha fatto una previsione sbagliata rimanda i dati indietro alla rete e aggiorna i suoi parametri in modo da fare previsioni corrette la volta successiva. Si tratta di un algoritmo di tipo autodidatta.
02: Rete Neurale Ricorrente
Una rete neurale ricorrente è un tipo di rete neurale artificiale in cui l’output di un particolare strato viene salvato e riportato allo strato di input. Questo aiuta a prevedere l'esito dello strato.
Le reti neurali ricorrenti sono utilizzate per risolvere problemi relativi a
- Dati delle serie temporali
- Dati di testo
- Dati audio
L'uso più comune dei dati testuali è quello di consigliare le parole successive da pronunciare a un'intelligenza artificiale, ad esempio: Come + stai +?
03: Rete neurale convoluzionale (CNN)
Le CNN sono di gran moda nella comunità dell'apprendimento profondo. Sono prevalenti nei progetti di elaborazione di immagini e video.
Ad esempio, per l’intelligenza artificiale il rilevamento e la classificazione delle immagini sono composte da reti neurali convoluzionali.
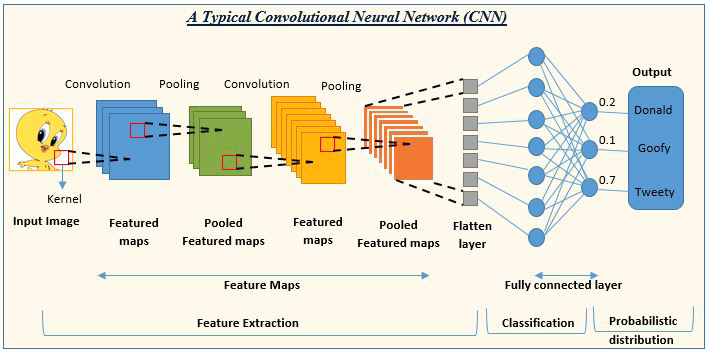
Fonte: analyticsvidhya.com
Ora che abbiamo visto i tipi di reti neurali, spostiamo l'attenzione sull'argomento principale di questo articolo, le Reti Neurali Feed Forward.
Reti Neurali Feed Forward
A differenza di altri tipi di reti neurali più complesse, in questo tipo di rete neurale non c'è la retropropagazione, cioè il flusso di dati va in una sola direzione. Una rete neurale feed-forward può avere un singolo strato nascosto o più strati nascosti.
Vediamo cosa fa funzionare questa rete
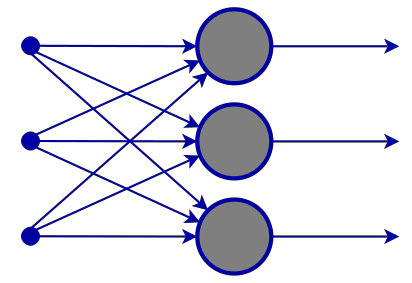
Strato di input
Dalle immagini di una rete neurale, sembra che ci sia uno strato di input, ma in realtà lo strato di input è solo una presentazione. Nello strato di input non vengono eseguiti calcoli.
Strato Nascosto
Lo strato nascosto è quello in cui viene svolta la maggior parte del lavoro della rete.
Per chiarire le cose, esaminiamo il nodo del secondo strato nascosto.
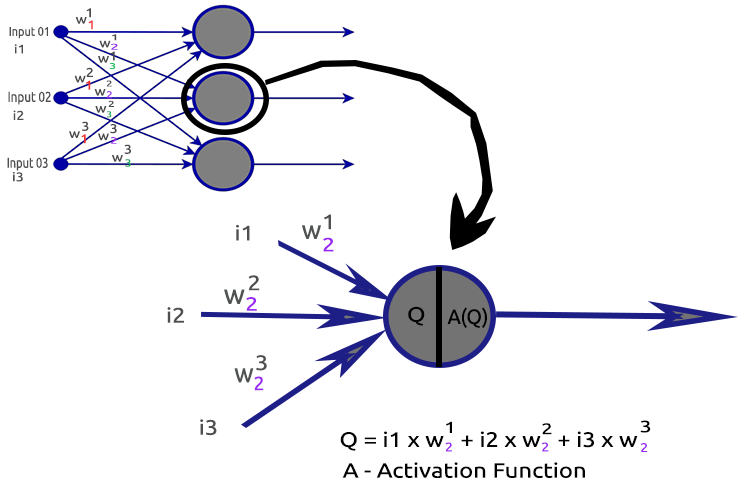
Processi coinvolti:
- Trovare il prodotto dei punti degli input e dei loro rispettivi pesi
- Aggiungere il prodotto dei punti ottenuto al bias
- Il risultato della seconda procedura viene passato alla funzione di attivazione
Che cos'è il Bias?
Il bias consente di spostare la regressione lineare verso l'alto e verso il basso per adattare meglio la linea di previsione ai dati. È la stessa intercetta di una retta nella regressione lineare.
Questo parametro è ben compreso nella sezione MLP con un singolo nodo in uno strato nascosto è un modello di Regressione Lineare.
L'importanza dei bias è ben spiegata in questo Stack.
Cosa sono i Pesi?
I pesi riflettono l'importanza degli input e sono i coefficienti dell'equazione che si sta cercando di risolvere. I pesi negativi riducono il valore di output e viceversa. Quando una rete neurale viene addestrata su un set di dati, viene inizializzata con un insieme di pesi. Questi pesi vengono poi ottimizzati durante il periodo di addestramento per ottenere il valore ottimale dei pesi.
Che cos'è una Funzione di Attivazione?
Una funzione di attivazione non è altro che una funzione matematica che prende un input e produce un output.
Tipi di Funzioni di Attivazione
Esistono molte funzioni di attivazione con le loro varianti, ma ecco quelle più comunemente utilizzate:
- Relu
- Sigmoide
- TanH
- Softmax
Sapere dove e quale funzione di attivazione utilizzare è molto importante, non so dirvi quante volte ho visto articoli online che suggerivano di utilizzare una funzione di attivazione in un punto in cui era irrilevante. Vediamolo in dettaglio.
01: RELU
RELU sta per Funzione di Attivazione Lineare Rettificata (Rectified Linear Activation Function).
È la funzione di attivazione più utilizzata nelle reti neurali. È la più semplice di tutti, facile da codificare e da interpretare, ecco perché è così popolare. Questa funzione emette direttamente l'input se è un numero positivo, altrimenti produce zero.
Ecco la logica
if x < 0 : return 0
else return x
Questa funzione è meglio utilizzarla per la risoluzione di problemi di regressione.
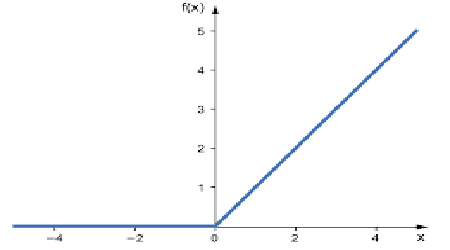
Il suo output va da zero a infinito positivo.
Il suo codice MQL5 è:
double CNeuralNets::Relu(double z) { if (z < 0) return(0); else return(z); }
RELU risolve il problema della scomparsa del gradiente che affligge la sigmoide e TanH (vedremo di cosa si tratta nell'articolo sulla retropropagazione).
02: Sigmoide
Suona familiare, vero? Ricordiamola dalla regressione logistica.
La sua formula è riportata di seguito.
![]()
Questa funzione è più adatta per i problemi di classificazione, in particolare per la classificazione di una o due classi.
Il suo output va da zero a uno (in termini di probabilità).
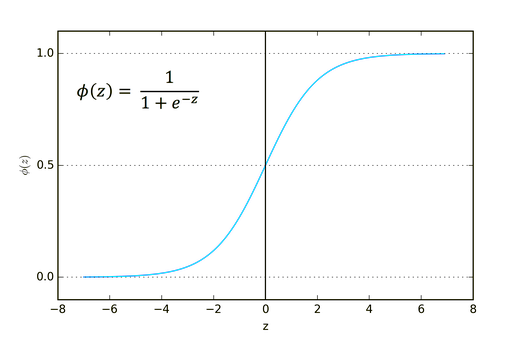
Ad esempio, la rete ha due nodi in uscita. Il primo nodo è per un gatto e l'altro per un cane. Si potrebbe scegliere l'output se l'uscita del primo nodo è maggiore di 0,5 per indicare che si tratta di un gatto e lo stesso ma al contrario per un cane.
Il suo codice MQL5 è:
double CNeuralNets::Sigmoid(double z) { return(1.0/(1.0+MathPow(e,-z))); }
03: TanH
La Funzione Tangente Iperbolica.
È data dalla formula:
Il suo grafico è simile a quello riportato di seguito:
Questa funzione di attivazione è simile alla sigmoide, ma migliore.
Il suo output varia da -1 a 1.
Questa funzione è meglio utilizzarla nelle reti neurali di classificazione multiclasse.
Il suo codice MQL5 è riportato di seguito:
double CNeuralNets::tanh(double z) { return((MathPow(e,z) - MathPow(e,-z))/(MathPow(e,z) + MathPow(e,-z))); }
04: SoftMax
Una volta qualcuno ha chiesto perché non esiste un grafico per la funzione SoftMax. A differenza di altre funzioni di attivazione, SoftMax non viene utilizzata negli strati nascosti ma solo nello strato di output e deve essere usata solo quando si vuole convertire l'output di una rete neurale multiclasse in termini di probabilità.
SoftMax prevede una distribuzione di probabilità multinomiale.
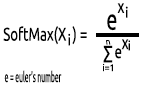
Ad esempio, gli output di una rete neurale di regressione sono [1,3,2], se si applica la funzione SoftMax a questo output, queste diventano [0.09003, 0.665240, 0.244728].
L'output di questa funzione è compresa tra 0 e 1.
Il suo codice MQL5 sarà:
void CNeuralNets::SoftMax(double &Nodes[]) { double TempArr[]; ArrayCopy(TempArr,Nodes); ArrayFree(Nodes); double proba = 0, sum=0; for (int j=0; j<ArraySize(TempArr); j++) sum += MathPow(e,TempArr[j]); for (int i=0; i<ArraySize(TempArr); i++) { proba = MathPow(e,TempArr[i])/sum; Nodes[i] = proba; } ArrayFree(TempArr); }
Ora che abbiamo capito come è composto un singolo neurone di uno strato nascosto, vediamo come codificarlo.
void CNeuralNets::Neuron(int HLnodes, double bias, double &Weights[], double &Inputs[], double &Outputs[] ) { ArrayResize(Outputs,HLnodes); for (int i=0, w=0; i<HLnodes; i++) { double dot_prod = 0; for(int j=0; j<ArraySize(Inputs); j++, w++) { if (m_debug) printf("i %d w %d = input %.2f x weight %.2f",i,w,Inputs[j],Weights[w]); dot_prod += Inputs[j]*Weights[w]; } Outputs[i] = ActivationFx(dot_prod+bias); } }
All'interno di ActivationFx(), abbiamo una selezione di quale funzione di attivazione è stata scelta quando si chiama il costruttore NeuralNets .
double CNeuralNets::ActivationFx(double Q) { switch(A_fx) { case SIGMOID: return(Sigmoid(Q)); break; case TANH: return(tanh(Q)); break; case RELU: return(Relu(Q)); break; default: Print("Unknown Activation Function"); break; } return(0); }
Ulteriori spiegazioni sul codice:
La funzione Neuron() non è solo un singolo nodo all'interno dello strato nascosto, ma tutte le operazioni di uno strato nascosto vengono eseguite all'interno di questa funzione. I nodi di tutti gli strati nascosti avranno la stessa dimensione del nodo di input fino al nodo di output finale. Ho scelto questa struttura perché sto per eseguire una classificazione con questa rete neurale su un set di dati generato in modo casuale.
La funzione FeedForwardMLP() sotto è una struttura NxN, il che significa che se si hanno 3 nodi di input e si sceglie di avere 3 strati nascosti, si avranno 3 nodi nascosti su ciascun strato nascosto, come si vede nell'immagine.
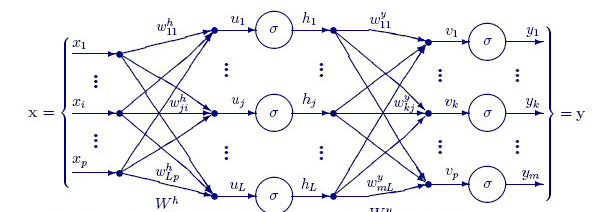
Ecco la Funzione FeedForwardMLP():
void CNeuralNets::FeedForwardMLP(int HiddenLayers, double &MLPInputs[], double &MLPWeights[], double &bias[], double &MLPOutput[]) { double L_weights[], L_inputs[], L_Out[]; ArrayCopy(L_inputs,MLPInputs); int HLnodes = ArraySize(MLPInputs); int no_weights = HLnodes*ArraySize(L_inputs); int weight_start = 0; for (int i=0; i<HiddenLayers; i++) { if (m_debug) printf("<< Hidden Layer %d >>",i+1); ArrayCopy(L_weights,MLPWeights,0,weight_start,no_weights); Neuron(HLnodes,bias[i],L_weights,L_inputs,L_Out); ArrayCopy(L_inputs,L_Out); ArrayFree(L_Out); ArrayFree(L_weights); weight_start += no_weights; } if (use_softmax) SoftMax(L_inputs); ArrayCopy(MLPOutput,L_inputs); if (m_debug) { Print("\nFinal MLP output(s)"); ArrayPrint(MLPOutput,5); } }
Le operazioni per trovare il prodotto dei punti in una rete neurale potrebbero essere gestite tramite operazioni matriciali, ma per mantenere le cose chiare e facili da capire per tutti in questo primo articolo, ho scelto il metodo a ciclo che utilizzeremo la prossima volta con la moltiplicazione matriciale.
Ora che avete visto l'architettura che ho scelto di default al fine di costruire la libreria, sorge una domanda sull'architettura delle reti neurali.
Se andate su Google e cercate le immagini di una rete neurale, sarete bombardati da migliaia, se non da decine di migliaia di immagini con diverse strutture di reti neurali, come ad esempio queste:
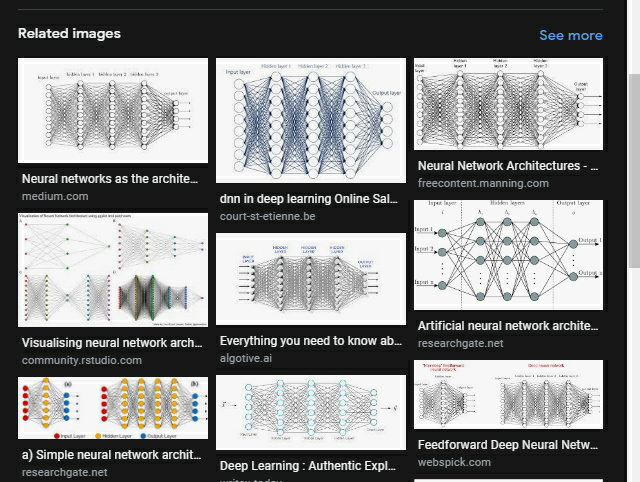
La domanda da un milione di dollari è: qual è la migliore architettura di rete neurale?
"Nessuno si sbaglia tanto quanto l'uomo che conosce tutte le risposte" - Thomas Merton.
Scomponiamo la cosa per capire cosa è necessario e cosa no.
Lo strato di InputIl numero di input compreso questo strato deve essere uguale al numero di caratteristiche (colonne del set di dati).
Lo strato di Output
La determinazione della dimensione (il numero di neuroni) è determinata dalle classi del dataset per una rete neurale di classificazione, mentre per un problema di regressione il numero di neuroni è determinato dalla configurazione del modello scelto. Uno strato di output per un regressore è spesso più che sufficiente.
Strati Nascosti
Se il problema non è abbastanza complesso, uno o due strati nascosti sono più che sufficienti, anzi due strati nascosti sono sufficienti per la maggior parte dei problemi. Ma, quanti nodi sono necessari in ogni strato nascosto? Non sono sicuro di questo, ma credo che dipenda dalle prestazioni, questo serve a voi come sviluppatori per esplorare e provare diversi nodi per vedere cosa funziona meglio per un particolare tipo di problema, inoltre prima di iniziare a giocare con questo dovreste conoscere altri tipi di reti neurali di cui abbiamo parlato in precedenza.
Su stats.stackexchange.com c'è un ottimo argomento su questo tema: qui.
Penso che avere lo stesso numero di nodi dello strato di input per tutti gli strati nascosti sia l'ideale per una rete neurale feed-forward; che è la configurazione che seguo la maggior parte delle volte.
L'MLP con un singolo Nodo e un singolo strato nascosto è un modello Lineare.
Se si presta attenzione alle operazioni svolte all'interno di un singolo nodo di uno strato nascosto di una rete neurale, si noterà questo:
Q = wi * Ii + b
Nel frattempo, l'equazione di regressione lineare è;
Y = mi * xi + c
Notate qualche somiglianza? Teoricamente sono la stessa cosa, questa operazione è il regressore lineare e questo ci riporta all'importanza del bias di uno strato nascosto. Il bias è una costante per il modello lineare con il ruolo di aggiungere la flessibilità al nostro modello per adattarsi al set di dati dato, senza di esso tutti i modelli passeranno tra gli assi x e y a zero (0).
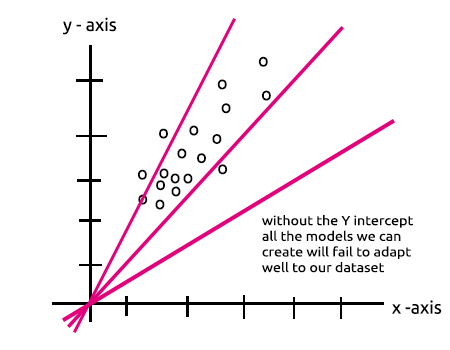
Durante l'addestramento della rete neurale verranno aggiornati i pesi e i bias. I parametri che producono meno errori per il nostro modello saranno conservati e ricordati nel dataset di test.
Ora, per chiarire meglio i punti, costruiamo una MLP per la classificazione di due classi. Prima di ciò, lasciatemi generare un set di dati casuali con campioni etichettati che vedremo attraverso la nostra rete neurale. La funzione seguente crea un insieme di dati casuali, il secondo campione viene moltiplicato per 5 e il primo viene moltiplicato per 2 solo per ottenere dati su scale diverse.
void MakeBlobs(int size=10) { ArrayResize(data_blobs,size); for (int i=0; i<size; i++) { data_blobs[i].sample_1 = (i+1)*(2); data_blobs[i].sample_2 = (i+1)*(5); data_blobs[i].class_ = (int)round(nn.MathRandom(0,1)); } }
Quando stampo il set di dati, ecco l'output:
QK 0 18:27:57.298 TestScript (EURUSD,M1) CNeural Nets Initialized activation = SIGMOID UseSoftMax = No IR 0 18:27:57.298 TestScript (EURUSD,M1) [sample_1] [sample_2] [class_] LH 0 18:27:57.298 TestScript (EURUSD,M1) [0] 2.0000 5.0000 0 GG 0 18:27:57.298 TestScript (EURUSD,M1) [1] 4.0000 10.0000 0 NL 0 18:27:57.298 TestScript (EURUSD,M1) [2] 6.0000 15.0000 1 HJ 0 18:27:57.298 TestScript (EURUSD,M1) [3] 8.0000 20.0000 0 HQ 0 18:27:57.298 TestScript (EURUSD,M1) [4] 10.0000 25.0000 1 OH 0 18:27:57.298 TestScript (EURUSD,M1) [5] 12.0000 30.0000 1 JF 0 18:27:57.298 TestScript (EURUSD,M1) [6] 14.0000 35.0000 0 DL 0 18:27:57.298 TestScript (EURUSD,M1) [7] 16.0000 40.0000 1 QK 0 18:27:57.298 TestScript (EURUSD,M1) [8] 18.0000 45.0000 0 QQ 0 18:27:57.298 TestScript (EURUSD,M1) [9] 20.0000 50.0000 0
La parte successiva consiste nel generare valori di peso casuali e il bias,
generate_weights(weights,ArraySize(Inputs));
generate_bias(biases); Ecco il risultato:
RG 0 18:27:57.298 TestScript (EURUSD,M1) weights QS 0 18:27:57.298 TestScript (EURUSD,M1) 0.7084 -0.3984 0.6182 0.6655 -0.3276 0.8846 0.5137 0.9371 NL 0 18:27:57.298 TestScript (EURUSD,M1) biases DD 0 18:27:57.298 TestScript (EURUSD,M1) -0.5902 0.7384
Ora vediamo l'intera operazione nella funzione principale del nostro script:
#include "NeuralNets.mqh"; CNeuralNets *nn; input int batch_size =10; input int hidden_layers =2; data data_blobs[]; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- nn = new CNeuralNets(SIGMOID); MakeBlobs(batch_size); ArrayPrint(data_blobs); double Inputs[],OutPuts[]; ArrayResize(Inputs,2); ArrayResize(OutPuts,2); double weights[], biases[]; generate_weights(weights,ArraySize(Inputs)); generate_bias(biases); Print("weights"); ArrayPrint(weights); Print("biases"); ArrayPrint(biases); for (int i=0; i<batch_size; i++) { Print("Dataset Iteration ",i); Inputs[0] = data_blobs[i].sample_1; Inputs[1]= data_blobs[i].sample_2; nn.FeedForwardMLP(hidden_layers,Inputs,weights,biases,OutPuts); } delete(nn); }
Cose da notare:
- Il numero di bias è uguale al numero di strati nascosti.
- Numero totale di pesi = numero di input al quadrato moltiplicato per il numero di strati nascosti. Ciò è stato reso possibile dal fatto che la nostra rete ha lo stesso numero di nodi dello strato di input/strato precedente della rete (tutti gli strati hanno lo stesso numero di nodi dall'ingresso all'uscita).
- Si seguirà lo stesso principio, diciamo che se si hanno 3 nodi di input, tutti gli strati nascosti avranno 3 nodi, eccetto l'ultimo strato di cui stiamo per vedere come trattarlo.
Guardando il dataset generato casualmente si noteranno due caratteristiche/colonne di input nel dataset e ho scelto di avere 2 strati nascosti, ecco la breve panoramica nei nostri log di come il nostro modello eseguirà i calcoli (escludere questi log impostando la modalità debug su false nel codice).
NL 0 18:27:57.298 TestScript (EURUSD,M1) Dataset Iteration 0 EJ 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 1 >> GO 0 18:27:57.298 TestScript (EURUSD,M1) NS 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 EI 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 2.00000 x weight 0.70837 FQ 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 5.00000 x weight -0.39838 QP 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product -0.57513 + bias -0.590 = -1.16534 RH 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.23770 CQ 0 18:27:57.298 TestScript (EURUSD,M1) OE 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 CO 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 2.00000 x weight 0.61823 FI 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 5.00000 x weight 0.66553 PN 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 4.56409 + bias -0.590 = 3.97388 GM 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.98155 DI 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 2 >> GL 0 18:27:57.298 TestScript (EURUSD,M1) NF 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 FH 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 0.23770 x weight -0.32764 ID 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 0.98155 x weight 0.88464 QO 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 0.79044 + bias 0.738 = 1.52884 RK 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.82184 QG 0 18:27:57.298 TestScript (EURUSD,M1) IH 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 DQ 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 0.23770 x weight 0.51367 CJ 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 0.98155 x weight 0.93713 QJ 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 1.04194 + bias 0.738 = 1.78034 JP 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.85574 EI 0 18:27:57.298 TestScript (EURUSD,M1) GS 0 18:27:57.298 TestScript (EURUSD,M1) Final MLP output(s) OF 0 18:27:57.298 TestScript (EURUSD,M1) 0.82184 0.85574 CN 0 18:27:57.298 TestScript (EURUSD,M1) Dataset Iteration 1 KH 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 1 >> EM 0 18:27:57.298 TestScript (EURUSD,M1) DQ 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 QH 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 4.00000 x weight 0.70837 PD 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 10.00000 x weight -0.39838 HR 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product -1.15027 + bias -0.590 = -1.74048 DJ 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.14925 OP 0 18:27:57.298 TestScript (EURUSD,M1) CK 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 MN 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 4.00000 x weight 0.61823 NH 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 10.00000 x weight 0.66553 HI 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 9.12817 + bias -0.590 = 8.53796 FO 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.99980 RG 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 2 >> IR 0 18:27:57.298 TestScript (EURUSD,M1) PD 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 RN 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 0.14925 x weight -0.32764 HF 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 0.99980 x weight 0.88464 EM 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 0.83557 + bias 0.738 = 1.57397 EL 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.82835 KE 0 18:27:57.298 TestScript (EURUSD,M1) GN 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 LS 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 0.14925 x weight 0.51367 FL 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 0.99980 x weight 0.93713 KH 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 1.01362 + bias 0.738 = 1.75202 IR 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.85221 OH 0 18:27:57.298 TestScript (EURUSD,M1) IM 0 18:27:57.298 TestScript (EURUSD,M1) Final MLP output(s) MH 0 18:27:57.298 TestScript (EURUSD,M1) 0.82835 0.85221
Ora prestate attenzione agli output finali di MLP per tutte le iterazioni e noterete uno strano comportamento: gli output tendono ad avere valori perfettamente uguali. Questo problema ha diverse cause, come discusso in questo Stack, una delle quali è l'utilizzo di una funzione di attivazione errata nello strato di output. È qui che entra in gioco la funzione di attivazione SoftMax.
Da quanto ho capito, la funzione sigmoide restituisce le probabilità solo quando c'è un singolo nodo nello strato di output, che deve classificare una sola classe. In questo caso è necessario che l'output della sigmoide dica se qualcosa appartiene o meno a una certa classe, ma è un'altra storia in caso di multiclasse. Se sommiamo gli output dei nostri nodi finali, il valore supera uno (1) la maggior parte delle volte, quindi ora sapete che non si tratta di probabilità, perché la probabilità non può superare il valore 1.
Se applichiamo SoftMax all'ultimo strato, gli output saranno.
Output della Prima Iterazione [0.4915 0.5085], Output della Seconda Iterazione [0.4940 0.5060].
è possibile interpretare i risultati come [Probabilità di appartenenza alla classe 0 Probabilità di appartenenza alla classe 1] in questo caso
Bene, almeno ora abbiamo delle probabilità su cui possiamo fare affidamento per interpretare qualcosa di significativo dalla nostra rete.
Riflessioni finali
Non abbiamo ancora finito con la rete neurale feed-forward, ma almeno per ora avete capito la teoria e le cose più importanti che vi saranno utili per padroneggiare le reti neurali in MQL5. La rete neurale Feedforward progettata è quella per scopi di classificazione, significa che le funzioni di Attivazione adatte sono sigmoide e tanh, a seconda dei campioni e delle classi che si desidera classificare nel set di dati. Non è possibile modificare lo strato di output in modo che restituisca qualsiasi cosa ci piaccia e nemmeno i nodi negli strati nascosti; l'introduzione delle matrici aiuterà tutte queste operazioni a diventare dinamiche in modo da poter costruire una rete neurale molto standard per qualsiasi compito, questo è l'obiettivo di questa serie di articoli, rimanete sintonizzati per saperne di più.
Anche sapere quando utilizzare la rete neurale è importante, perché non tutti i compiti necessitano di essere risolti con le reti neurali; se un compito può essere risolto con la regressione lineare, un modello lineare può superare la rete neurale. Questo è uno degli aspetti da tenere presente.
GitHub repo: https://github.com/MegaJoctan/NeuralNetworks-MQL5
Ulteriori Letture | Libri | Riferimenti
-
Neural Networks for Pattern Recognition (Advanced Texts in Econometrics)
-
Neural Networks: Tricks of the Trade (Lecture Notes in Computer Science, 7700)
-
Deep Learning (Adaptive Computation and Machine Learning series)
Articoli di Riferimento:
-
Scienza dei Dati e Apprendimento Automatico (Parte 01): Regressione Lineare
-
Scienza dei Dati e Apprendimento Automatico (Parte 02): Regressione Logistica
-
Scienza dei Dati e Apprendimento Automatico (Parte 03): Regressioni a Matrice
-
Scienza dei Dati e Apprendimento Automatico (Parte 06): Discesa del Gradiente
Tradotto dall’inglese da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/en/articles/11275
 MetaTrader 4 su Mac OS
MetaTrader 4 su Mac OS
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso