Características del Wizard MQL5 que debe conocer (Parte 11): Muros numéricos

Introducción

Para las series temporales múltiples, podemos derivar una fórmula para el siguiente valor de la secuencia basándonos en los valores anteriores que han aparecido en ella. Los muros numéricos lo consiguen creando primero un "muro numérico" en forma de matriz usando la llamada regla cruzada (cross-rule). Creando esta matriz, el objetivo principal será establecer si la secuencia considerada converge. El algoritmo de muro numérico de regla cruzada responde a esta pregunta si, tras unas filas de aplicación, las filas siguientes de la matriz son solo ceros.

En el artículo presentado, que demuestra estos conceptos, se utilizó la serie de potencias de Laurent (Laurent Power Series), también conocida como serie formal de Laurent (Formal Laurent Series, FLS), como base para representar estas secuencias con su aritmética en formato polinómico utilizando productos de Cauchy.

En general, las secuencias LFSR cumplen la relación de recurrencia de modo que la combinación lineal de términos sucesivos sea siempre cero, como se muestra en la ecuación siguiente:

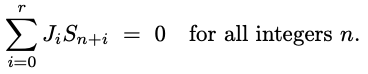
donde la secuencia Sn es un registro de desplazamiento lineal recurrente o de realimentación lineal (LFSR), y también existe un vector |Ji| (relación) distinto de cero de longitud r + 1.

Esto implica una relación vectorial en la que los coeficientes de x (las constantes son coeficientes con x de grado cero) constituyen sus elementos. Este vector tiene una magnitud de al menos 2 por definición.

Para ilustrarlo, podemos analizar un par de ejemplos sencillos, el primero de los cuales serás una secuencia de cubos de números. Sabemos que los números de un cubo se numeran de cero en adelante, siendo cada valor el cubo de su posición de índice. Si los pusiéramos en una matriz de muros numéricos, la representación original sería así:

Los ceros y unos dados como filas sobre la secuencia están siempre implícitos y ayudan a aplicar la regla cruzada para propagar todos los valores que faltan en la matriz. Al aplicar la regla cruzada a 5 valores cualesquiera de una matriz que tenga un formato de cruce simple, el producto de los valores verticales exteriores cuando se suma al producto de los valores horizontales exteriores deberá ser siempre equivalente al cuadrado del valor central.

Si aplicamos esta regla a la secuencia básica de números del cubo anterior, obtendremos la matriz siguiente:

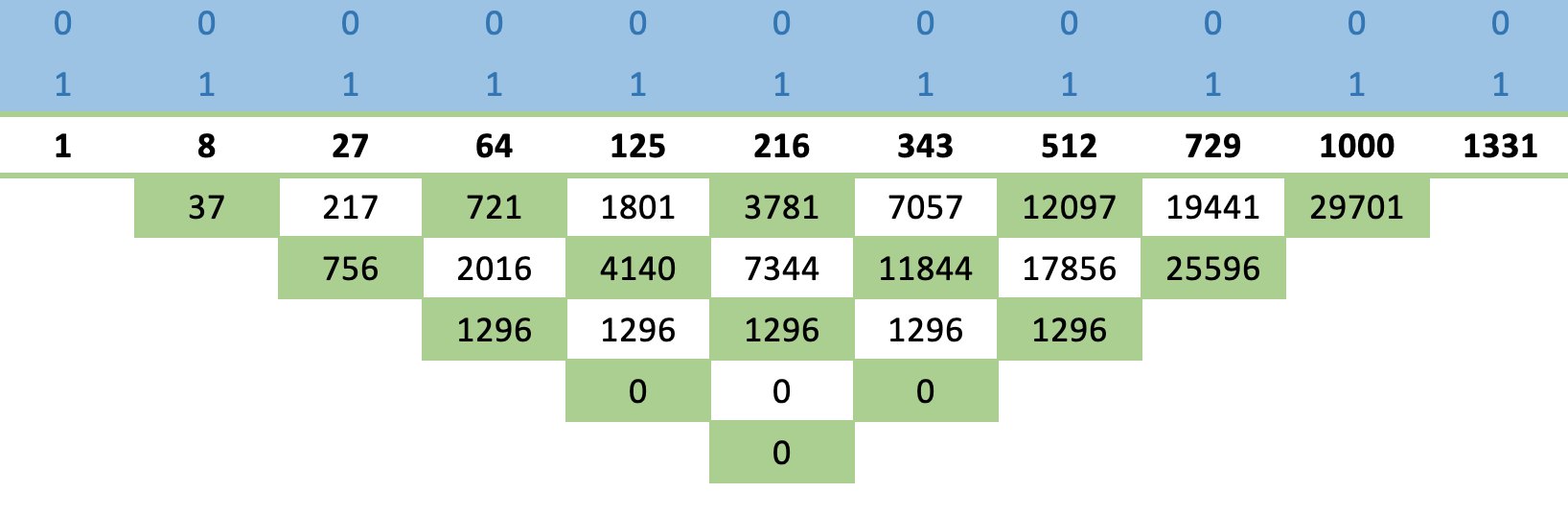
Vamos a ilustrar la regla cruzada: el número inferior a 216, es decir 3781, se obtiene de la diferencia del cuadrado de 216 y el producto de 125 y 343, que se divide por el número superior a 216, a saber. 1.

El hecho de que podamos obtener una serie de ceros tan rápidamente indica que esta secuencia sí converge, y podemos sacar fácilmente una fórmula para sus valores consecuentes.

Pero antes de ver las fórmulas, le proponemos echar un vistazo a otro ejemplo, la serie de Fibonacci. Si aplicamos esta secuencia a nuestra matriz y aplicamos la regla de cruz larga como vemos más arriba, ¡obtendremos filas de ceros aún más rápido!

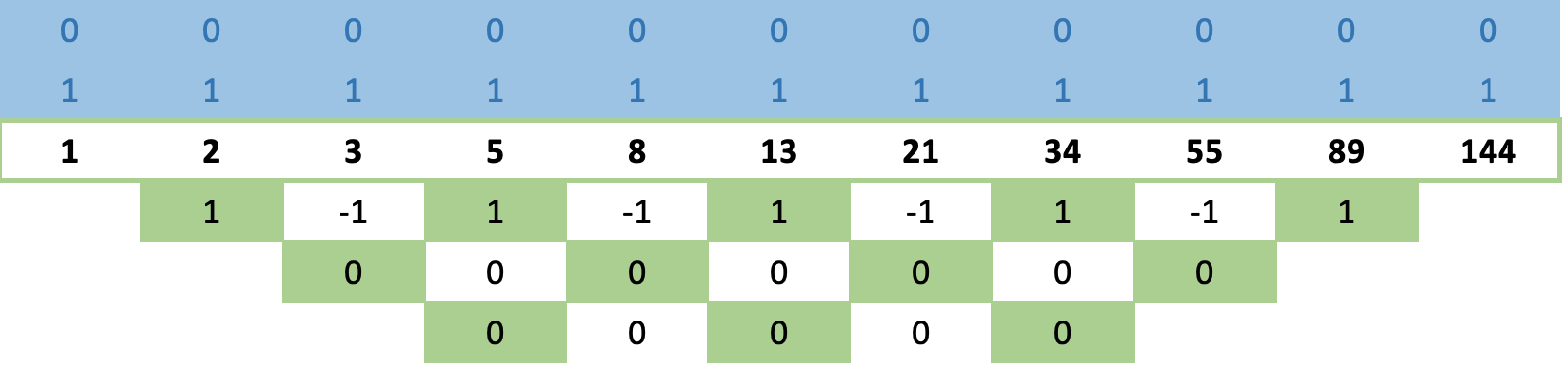
Esto parece extraño, ya que cabría esperar que la serie de Fibonacci fuera más compleja que los números del cubo y, por tanto, tardara más en converger, ¡pero no es así! Converge a la fila 2.

Para obtener una formulación de una serie convergente como la de los dos ejemplos anteriores, deberemos sustituir la secuencia en la matriz de muros numéricos por un formato de fórmula que sustituya cualquier valor de la secuencia por el mismo valor menos el valor anterior multiplicado por x. Debería parecerse a esto:

Aquí simplemente aplicaremos nuestra regla cruzada, como hemos hecho con las secuencias anteriores, y generaremos valores en formato polinómico para las siguientes filas. Sorprendentemente, si la secuencia converge, incluso con valores polinómicos podremos obtener una serie de ceros después de unas cuantas aplicaciones de la cruz larga. Esto se muestra a continuación para la secuencia de Fibonacci.

¿Qué haremos entonces con estos valores polinómicos? Si igualamos la última ecuación a 0 y encontramos el mayor grado de x, los coeficientes de x que nos queden en el lado opuesto serán múltiplos de los valores anteriores de la secuencia que se suman para dar el siguiente valor.

Así, usando la última ecuación de la sucesión de Fibonacci, si resolvemos x^2, el grado máximo que nos quedará: 1 + x;

Tenga en cuenta que 1 representa x^0 y es esencialmente el cociente del número ordinal antes del número ordinal cuyo cociente es x. En pocas palabras, esto nos dice que en la serie de Fibonacci, cualquier número es la suma de los dos números anteriores de la secuencia.

¿Y cómo es la ecuación polinómica de una sucesión cúbica? Se necesitan más líneas para la convergencia, como se muestra arriba, y por ello, dicha ecuación es más compleja.

¿Qué pasa con las filas no convergentes? ¿Qué tipo de matrices podrían crearse en estos casos? A título ilustrativo, podríamos proceder directamente a observar la secuencia de precios de un par de divisas ordinario, como el EURUSD. Si intentamos crear una matriz de muro numérico (sin fórmula) para probar la convergencia de la secuencia de precios de cierre diarios de EURUSD para los 5 primeros días de negociación de 2024, obtendremos un muro para las 5 primeras filas similar al siguiente.

Por supuesto, no lograremos la convergencia en la primera serie, de hecho no está nada claro si alguna vez alcanzaremos la convergencia estricta, aunque el muro numérico tiende a cero, lo cual resulta alentador. Esto debilitará la aplicabilidad de los muros numéricos para nuestros fines. Además, la comprobación previa también suele demandar muchos recursos informáticos, y aquí es donde entra en juego la matriz Toeplitz.

Si creamos una matriz en la que todas las filas están relacionadas entre sí de alguna forma, para lo cual utilizaremos una repetición deslizante de la fila de una secuencia; si la secuencia converge, entonces el determinante de esta matriz será cero. Esta es una forma computacionalmente más eficiente de comprobar la convergencia y, además, "cuantifica" la probabilidad de que la secuencia converja usando como base la magnitud del determinante.

Así, podríamos extender la regla cruzada a una matriz de fórmulas de cualquier secuencia y usar el tamaño del determinante para "descontar" el valor predicho de la fórmula. O podemos tener un valor umbral absoluto del determinante, superado el cual ignoraremos el resultado de nuestra fórmula.

Todas estas son posibles soluciones para las series financieras no convergentes y otras series temporales, y ciertamente no resultan ideales, pero vamos a ver qué potencial tienen cuando se implementan en MQL5.

Aplicación en MQL5

Para ilustrar estas ideas en MQL5, las implementaremos en un ejemplar de la clase Expert Trailing. Combinado con la clase Awesome Oscillator incorporada, crearemos un asesor sencillo. El ejemplar de la clase de trailing utilizará un muro numérico para determinar el tamaño del valor del trailing stop y el nivel de take profit.

Al implementar en MQL5, a menudo usaremos los tipos de datos de matriz y vector incorporados, teniendo en cuenta sus funciones adicionales y los requisitos mínimos de código. Podemos comprobar previamente la convergencia de la secuencia construyendo un muro numérico típico (no como fórmula) y comprobando si llegamos a una línea de ceros, pero dada la naturaleza y complejidad de las series temporales financieras, la matriz no convergerá. Así que es mejor calcular la fórmula para el siguiente valor de la secuencia obtenido a partir de la fila inferior de la última columna después de la propagación.

Para propagar el muro, utilizaremos vectores para almacenar los coeficientes de x. La multiplicación de dos vectores cualesquiera en el proceso de resolución de la fila desconocida será equivalente a la correlación mutua, ya que los valores resultantes de los vectores serán los coeficientes de x, donde un índice más alto indicará un índice de grado más alto para x. Esta función está integrada. Sin embargo, cuando hablamos de la división, necesitaremos redimensionar los dos vectores cociente (quotient vectors) para asegurarnos de que coinciden con cualquier diferencia de tamaño, lo cual implica simplemente que no coinciden en términos de los exponentes de x.

A la hora de determinar cuánto ajustar el TP y el SL de una posición abierta, los valores del indicador de media móvil serán nuestra secuencia de entrada para nuestro muro numérico. Podemos utilizar cualquier indicador, pero las Bandas de Bollinger o las envolventes son mejores para fijar un trailing stop.

Los vectores MQL5 copiarán y cargarán fácilmente los valores de los indicadores después de definir el manejador. Veamos un código típico para comprobar un trailing stop (podemos utilizarlo tanto para posiciones largas como cortas)

//+------------------------------------------------------------------+
//| Checking trailing stop and/or profit for long position.          |
//+------------------------------------------------------------------+
bool CTrailingLFSR::CheckTrailingStopLong(CPositionInfo *position, double &sl, double &tp)
{
//--- check

...

//---
   vector _t, _p;
   _p.Init(2);
   _t.CopyIndicatorBuffer(m_ma.Handle(), 0, 0, 2);
   double _s = 0.0;
   for(int i = 1; i >= 0; i--)
   {  _s = 0.0;
      _p[i] = GetOutput(i, _s);
   }
   double _o = SetOutput(_t, _p);
//---
  
...

}

Podemos ver que el proceso de toma de decisiones se desarrolla en torno a dos funciones, GetOutput y SetOutput. GetOutput es básico porque construye un muro numérico y da salida a los coeficientes polinómicos para la ecuación que encuentra el siguiente valor en la secuencia. A continuación le mostramos el listado de GetOutput:

//+------------------------------------------------------------------+
//| LFSR Output.                                                     |
//+------------------------------------------------------------------+
double CTrailingLFSR::GetOutput(int Index, double &Solution)
{  double _output = 0.0;
   vector _v;
   _v.CopyIndicatorBuffer(m_ma.Handle(), 0, Index, m_length);
   Solution = Solvability(_v);
   _v.Resize(m_length + 1);
   for(int i = 2; i < 2 + m_length; i++)
   {  for(int ii = 2; ii < 2 + m_length; ii++)
      {  if(i == 2)
         {  vector _vi;
            _vi.Init(1);
            _vi[0] = _v[m_length - ii + 1];
            m_numberwall.row[i].column[ii] = _vi;
         }
         else if(i == 3)
         {  vector _vi;
            _vi.Init(2);
            _vi[0] = m_numberwall.row[i - 1].column[ii][0];
            _vi[1] = -1.0 * m_numberwall.row[i - 1].column[ii - 1][0];
            m_numberwall.row[i].column[ii] = _vi;
         }
         else if(ii < m_length + 1)
         {  m_numberwall.row[i].column[ii] = Get(m_numberwall.row[i - 2].column[ii], m_numberwall.row[i - 1].column[ii - 1], m_numberwall.row[i - 1].column[ii + 1], m_numberwall.row[i - 1].column[ii]);
         }
      }
   }
   vector _u = Set();
   vector _x;
   _x.CopyIndicatorBuffer(m_ma.Handle(), 0, Index, m_length);
   _u.Resize(fmax(_u.Size(),_x.Size()));
   _x.Resize(fmax(_u.Size(),_x.Size()));
   vector _y = _u * _x;
   _output = _y.Sum();
   return(_output);
}

Nuestra lista general anterior consta básicamente de 2 partes. Construiremos el muro para obtener los coeficientes de la ecuación, y utilizaremos la ecuación con las lecturas de la secuencia actual para la proyección. En la primera parte, la función get realizará una multiplicación clave de las ecuaciones generadas y resolverá la ecuación de la línea siguiente. Encontrará el código a continuación:

//+------------------------------------------------------------------+
//| Get known Value                                                  |
//+------------------------------------------------------------------+
vector CTrailingLFSR::Get(vector &Top, vector &Left, vector &Right, vector &Center)
{  vector _cc, _lr, _cc_lr, _i_top;
   _cc = Center.Correlate(Center, VECTOR_CONVOLVE_FULL);
   _lr = Left.Correlate(Right, VECTOR_CONVOLVE_FULL);
   ulong _size = fmax(_cc.Size(), _lr.Size());
   _cc_lr.Init(_size);
   _cc.Resize(_size);
   _lr.Resize(_size);
   _cc_lr = _cc - _lr;
   _i_top = 1.0 / Top;
   vector _bottom = _cc_lr.Correlate(_i_top, VECTOR_CONVOLVE_FULL);
   return(_bottom);
}

Del mismo modo, la función set utilizará el vector inferior que tiene los últimos coeficientes comunes para resolver el siguiente valor de la secuencia. Le mostramos el código a continuación:

//+------------------------------------------------------------------+
//| Set Unknown Value                                                |
//+------------------------------------------------------------------+
vector CTrailingLFSR::Set()
{  vector _formula = m_numberwall.row[m_length + 1].column[m_length + 1];
   vector _right;
   _right.Copy(_formula);
   _right.Resize(ulong(fmax(_formula.Size() - 1, 1.0)));
   double _solver = -1.0 * _formula[int(_formula.Size() - 1)];
   if(_solver != 0.0)
   {  _right /= _solver;
   }
   return(_right);
}

Ahora, en la función de comprobación final, llamaremos a la función GetOutput dos veces porque necesitamos obtener no solo la previsión actual sino también las anteriores para ayudar a normalizar nuestros datos de salida. Como la mayoría de las secuencias, y especialmente las series temporales financieras, no convergen, el valor del pronóstico bruto de los datos de salida resultará seguramente muy ajeno en relación con los valores de la secuencia de entrada. No es infrecuente obtener valores dobles muy grandes, varias veces superiores a los valores típicos de la secuencia, o incluso un valor negativo cuando claramente solo se esperan valores positivos.

Por ello, al realizar la normalización, utilizaremos una función SetOutput muy corta y sencilla, que mostraremos a continuación:

//+------------------------------------------------------------------+
//| Normalising Output to match Indicator Value                      |
//+------------------------------------------------------------------+
double CTrailingLFSR::SetOutput(vector &True, vector &Predicted)
{  return(True[1] - ((True[0] - True[1]) * ((Predicted[0] - Predicted[1]) / fmax(m_symbol.Point(), fabs(Predicted[0]) + fabs(Predicted[1])))));
}

Simplemente normalizaremos el valor predicho para que su valor se encuentre dentro del rango de valores de secuencia, y lo conseguiremos utilizando cambios de secuencia tanto para los valores predichos como para los verdaderos.

Además, en una comprobación típica del trailing stop, medimos la resolubilidad dentro de la función GetOutput en su inicio. Esta métrica se usará como un filtro de umbral para determinar si debemos ignorar la predicción, ya que valores más altos del determinante (lo que llamamos resolubilidad) indicarán un mayor fracaso a la hora de converger. Baste decir que incluso una matriz con un determinante pequeño no convergerá, pero suponemos que lo hará con mayor probabilidad si tiene más filas para construir un muro numérico que una matriz con un determinante mayor.

Así, obtendremos el ejemplar de la clase finalizadora adjunta al final del artículo, y aunque las pruebas preliminares indican que requiere muchos recursos computacionales, en mi opinión esta idea podría mejorarse e incluso combinarse con diferentes estrategias para desarrollar un sistema comercial más robusto.

El código MQL5 adjunto a la clase de seguimiento se puede ensamblar fácilmente utilizando el Wizard para crear diferentes asesores dependiendo de la elección de la clase de señal y la gestión de capital. Como siempre, toda la información está en el artículo.

Notas adicionales

Los muros numéricos analizados hasta ahora en el código general y las ilustraciones anteriores utilizaban precios enteros que no incluían ceros. Si, por ejemplo, queremos predecir los cambios en el precio de un símbolo, no solo el precio inicial, lo ideal sería disponer de una serie de entrada de cambios en el precio. En cuanto empecemos a tratar con el cambio en lugar de con el precio absoluto, no solo nos encontraremos con valores negativos, sino que podremos tener múltiples ceros, y muy a menudo.

Los ceros pueden parecer inofensivos al principio, pero cuando construimos muros numéricos, generan problemas a la hora de determinar los valores de la fila siguiente. Consideremos el siguiente ejemplo:

Usando nuestra regla cruzada básica cuando buscamos un valor desconocido, nos encontraremos con un problema porque un valor conocido es cero, por lo que al multiplicarlo por nuestra incógnita nos quedaremos con las manos vacías. Para evitar este problema, resulta útil la regla de la cruz larga. Ampliemos nuestra imagen anterior:

Podemos evitar el cero sobre la fila actual con cierta confianza aplicando la fórmula siguiente:

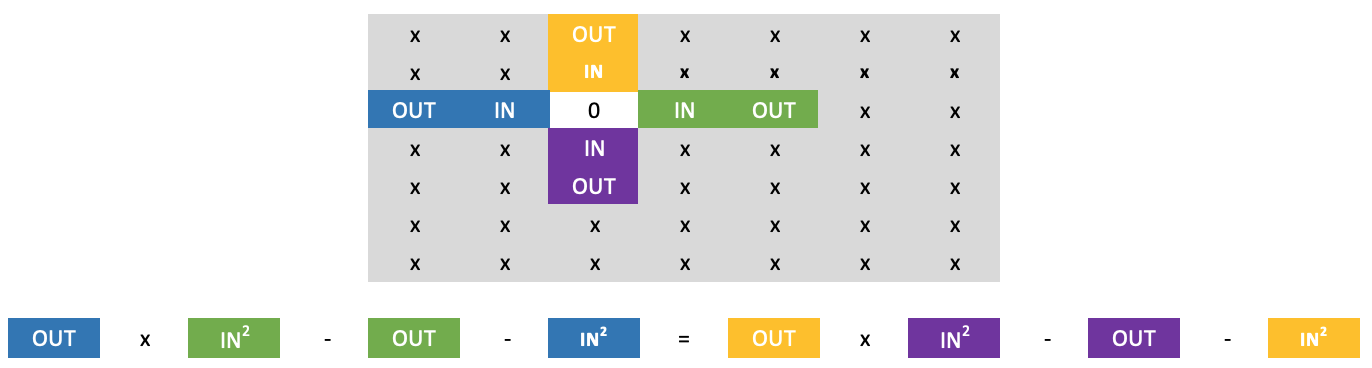
No he dicho "con cierta seguridad" porque sí, porque los muros numéricos tienen una propiedad única a la hora de incluir ceros. En cualquier número, si hay ceros, se encuentran de forma singular o al cuadrado, por lo que podría haber 1 x 1 (singular), o 2 x 2, o 3 x 3, y así sucesivamente. Esencialmente, esto significa que si encontramos un cero entre dos números en cualquier fila, el número situado debajo no será cero. Sin embargo, cuando aplicamos la regla de cruz larga, tenemos una incógnita adicional en forma del valor exterior más bajo en el muro. No obstante, esto no es un problema porque se multiplica por nuestro cero conocido, lo cual nos permitirá resolver la ecuación sin tener que introducir su valor.

El problema que resuelve la regla de cruz larga se aplica estrictamente a los muros numéricos convergentes y, como hemos visto en las ilustraciones anteriores, este rara vez será el caso de las series temporales financieras. Entonces, ¿deberíamos tener esto en cuenta? Deberemos determinar esto secuencialmente, en función de la serie temporal a la que se oriente el sistema comercial. Algunos podrían incluso aplicar esta característica a las series financieras si la "resolubilidad" o determinante de la matriz de Toeplitz alcanza un umbral necesario; otros podrían dejar de construir el muro y trabajar con los coeficientes vectoriales que tienen en ese momento (cuando llegan a cero) en la construcción de la ecuación de pronóstico polinómico. Puede haber otras opciones y la elección dependerá de cada tráder.

La regla de la cruz larga es bastante flexible si solo se encuentra un cero al propagar un muro numérico, pero si los ceros están en un cuadrado más grande (ya que los ceros siempre ocupan el formato nxn en la pared), entonces no tendrá mucho sentido. En estos casos, suele usarse la regla de la herradura. Según esta regla, si tenemos un cuadrado grande de ceros, las secuencias que bordean este cuadrado se escalarán por un factor determinado.

Estos cuatro factores, uno por cada lado del cuadrado, tendrán una propiedad única que puede demostrarse mediante la fórmula siguiente:

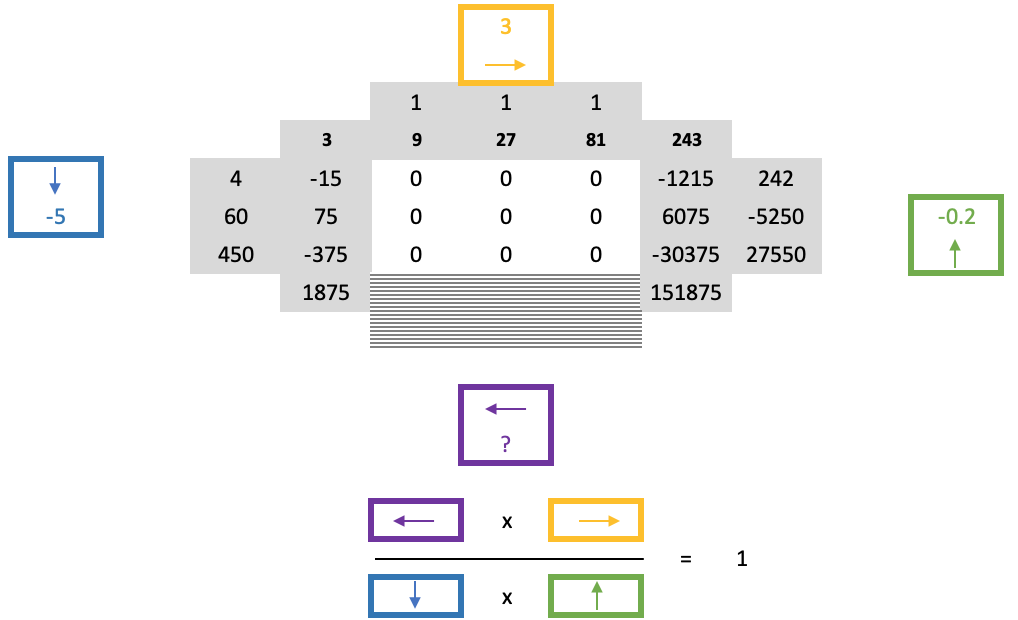
Así, al encontrar una gran porción de ceros, los números superiores y laterales que bordean estos ceros ya serán conocidos, y puesto que conocemos la anchura de los cuadrados de los ceros, conoceremos esencialmente sus alturas, es decir, sabremos dónde evaluar los valores límite desconocidos. Partiendo de la ecuación anterior, los valores límite inmediatos que se indican a continuación podrán obtenerse determinando el factor de escala inferior y calculando sus números, normalmente de izquierda a derecha.

No obstante, avanzar a partir de este punto utilizando la regla de cruzada habitual seguirá resultando difícil, ya que los ceros del cuadrado dificultarán su aplicación a la hora de determinar la línea situada por debajo de la línea límite que se acaba de resolver. La solución a este problema será la "segunda parte" de la regla de la herradura y se basará en la siguiente fórmula, bastante larga:

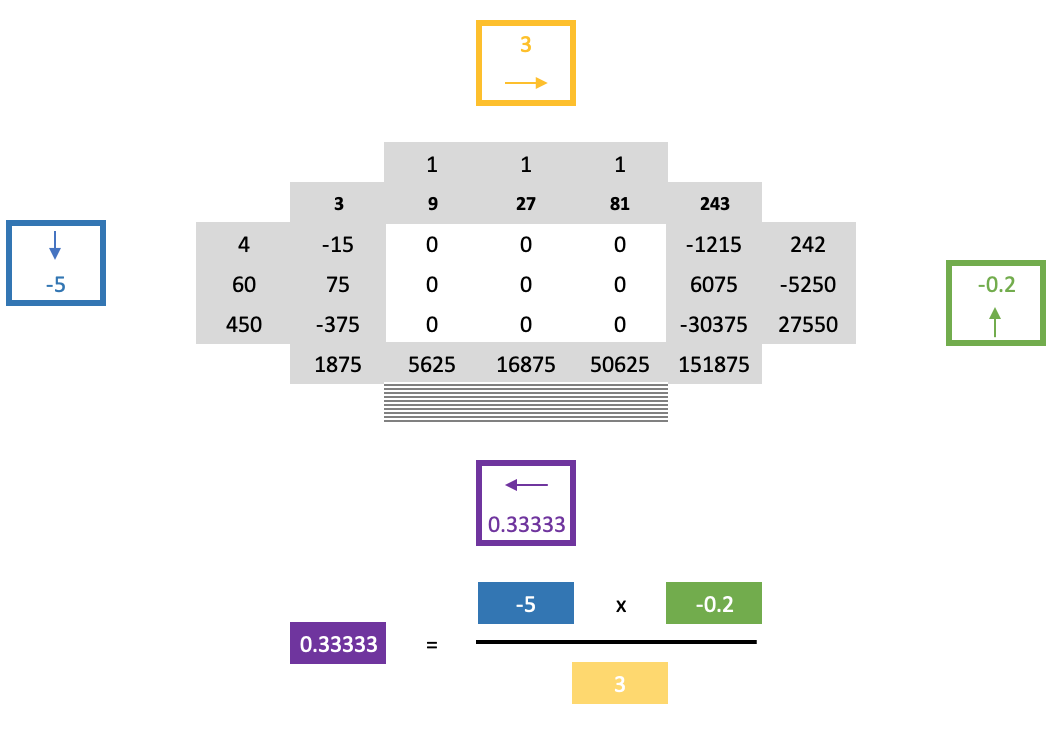
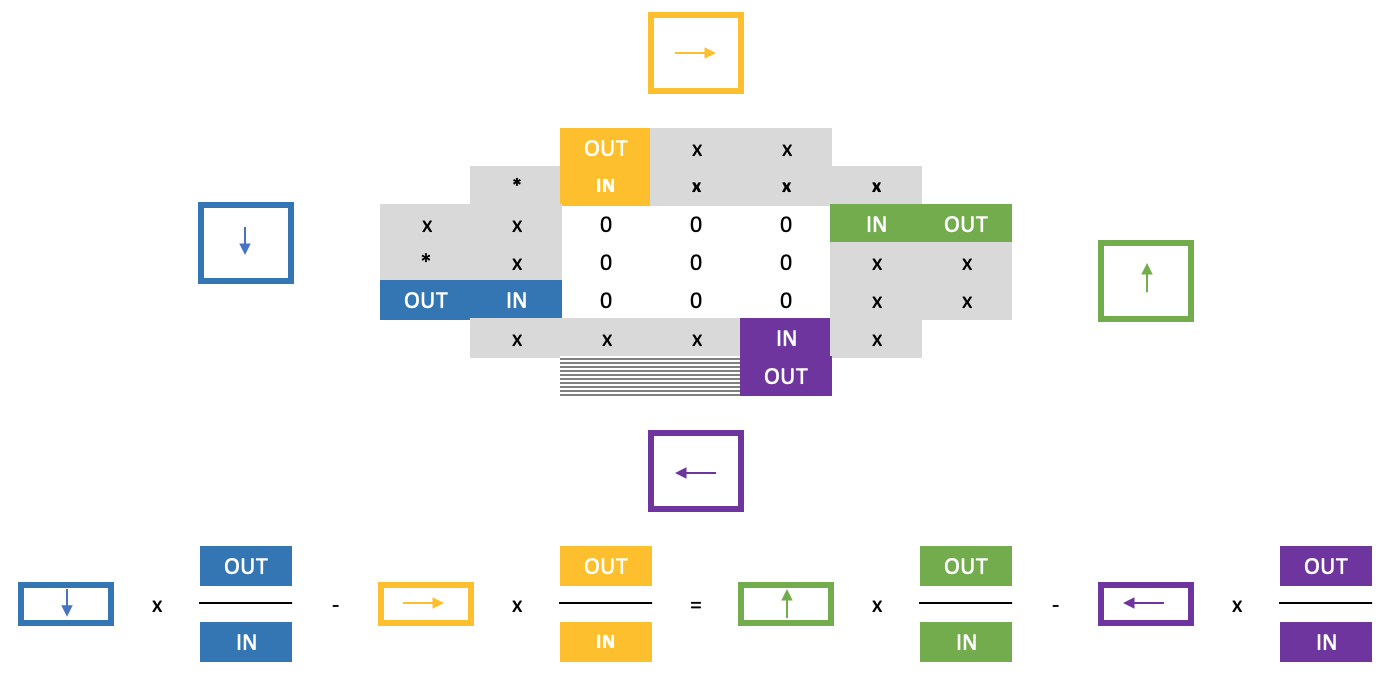
El artículo mencionado, además de tratar muchos de los puntos aquí expuestos, también menciona la conjetura de la pagoda (pagoda conjecture). En su forma más simple, es la suma de un grupo de conjuntos de números, cada uno de los cuales contiene un conjunto de igual tamaño, de forma que si cada uno de los conjuntos incluidos se considera como un polígono, cada vértice del cual representa uno de los números de su conjunto, entonces estos polígonos podrán pegarse para formar una red compleja mayor, siempre que en cualquier vértice conectado todos los vértices del polígono tengan el mismo número. Esto es, por supuesto, bajo el supuesto de que cada número de vértice de cualquier polígono sea único en este conjunto.

En primer lugar, esto tiene implicaciones interesantes para los conjuntos de tres números que forman la pagoda, pues resulta que cuando los números de cada conjunto se disponen en secuencia, pueden observarse patrones de repetición muy interesantes en el muro con los números extendidos, y en el artículo se presentan algunas de estas imágenes.

Sin embargo, a efectos de negociación, este "nuevo" enfoque de categorización representa otra forma de ver las series temporales financieras que requiere un artículo aparte. Baste decir que podríamos resumir varias formas de uso de las secuencias de pagodas para nuestros cometidos.

A la hora de utilizar la hipótesis, sería prudente ceñirse a las pagodas triangulares en lugar de a formas de mayor dimensión, pues estas tienden a abrir más posibilidades y, por tanto, complican las formas de conexión. Nuestra tarea consistiría, en primer lugar, en normalizar nuestras series financieras para considerar la repetición de valores, que es un requisito de la definición de las pagodas. El grado en que se realiza esta normalización es algo que habrá que investigar, ya que distintas iteraciones darán necesariamente resultados diferentes.

En segundo lugar, una vez nos sentamos cómodos con un determinado umbral de normalización, tendremos que fijar el número de triángulos de nuestra pagoda, es decir, el tamaño del grupo. Tenga en cuenta que, a medida que aumente el tamaño del grupo, disminuirá la necesidad de que todos los triángulos estén conectados directamente. En una pagoda de tres triángulos, todos los triángulos estarán conectados, pero a medida que este número aumente, para cualquier triángulo el mayor número de conexiones que puede tener será 3. Esto significa que, por ejemplo, en una pagoda con seis triángulos, solo el triángulo central inferior tendrá conexiones en todos los vértices, y todos los demás solo tendrán conexiones en dos vértices.

Este aumento de la complejidad al conectar triángulos con el aumento del tamaño del grupo puede indicar que la determinación del tamaño óptimo del grupo debe realizarse al mismo tiempo que establecemos el umbral de normalización, ya que este último nos proporcionará datos recurrentes que son clave para establecer conexiones entre triángulos.

Conclusión

Hoy hemos analizado los muros numéricos, una cuadrícula numérica generada a partir de la serie temporal secuencial que analizamos, y hemos visto cómo puede utilizarse en las previsiones estableciendo correctamente el TP y el SL de una posición abierta en el código. Además, hemos estudiado las hipótesis relacionadas con las pagodas que se analizan en el artículo sobre los muros numéricos y hemos propuesto algunas ideas sobre cómo podrían suponer otro medio de clasificación de las series temporales financieras.

Epílogo

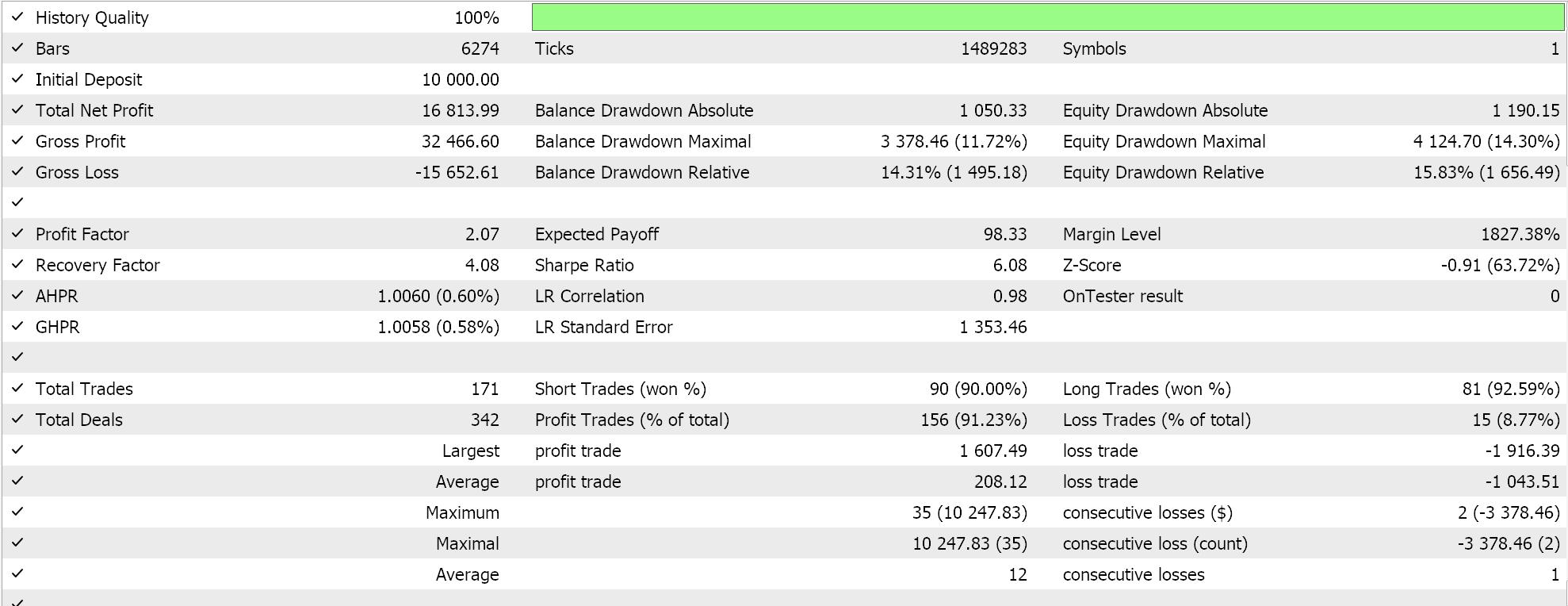
A continuación, le presentamos las pruebas comparativas de los asesores montados por el Wizard. Ambos utilizan las señales de Awesome Oscillator y tienen básicamente los mismos ajustes de entrada, que mostramos a continuación:

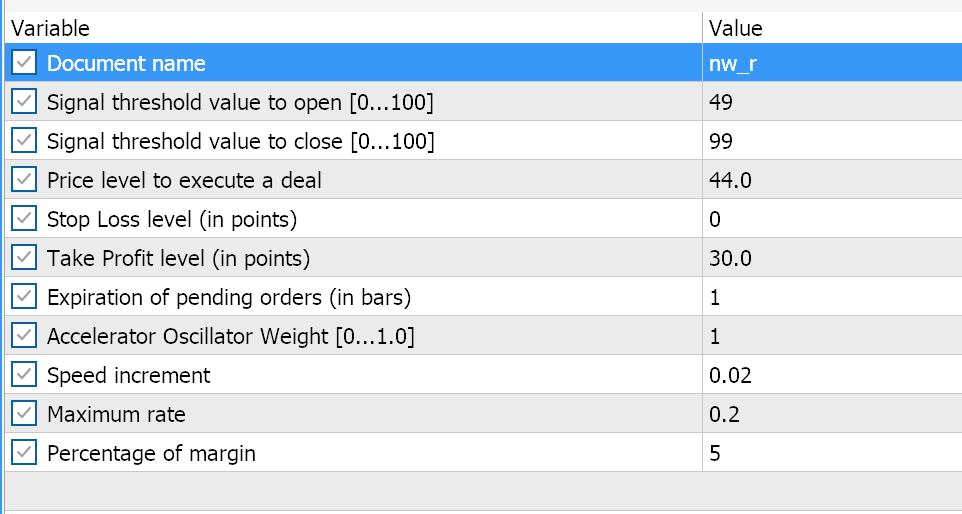
La diferencia entre los dos es que un asesor utiliza Parabolic SAR para rastrear y cerrar posiciones abiertas, mientras que el otro utiliza el algoritmo de muro numérico presentado en este artículo. Sin embargo, sus informes al realizar las pruebas con EURUSD durante el último año en el marco temporal de horas, a pesar de tener la misma señal, son diferentes. El primero es el informe del asesor basado en Parabolic SAR.

A continuación le mostramos los cálculos del asesor basado en el muro numérico:

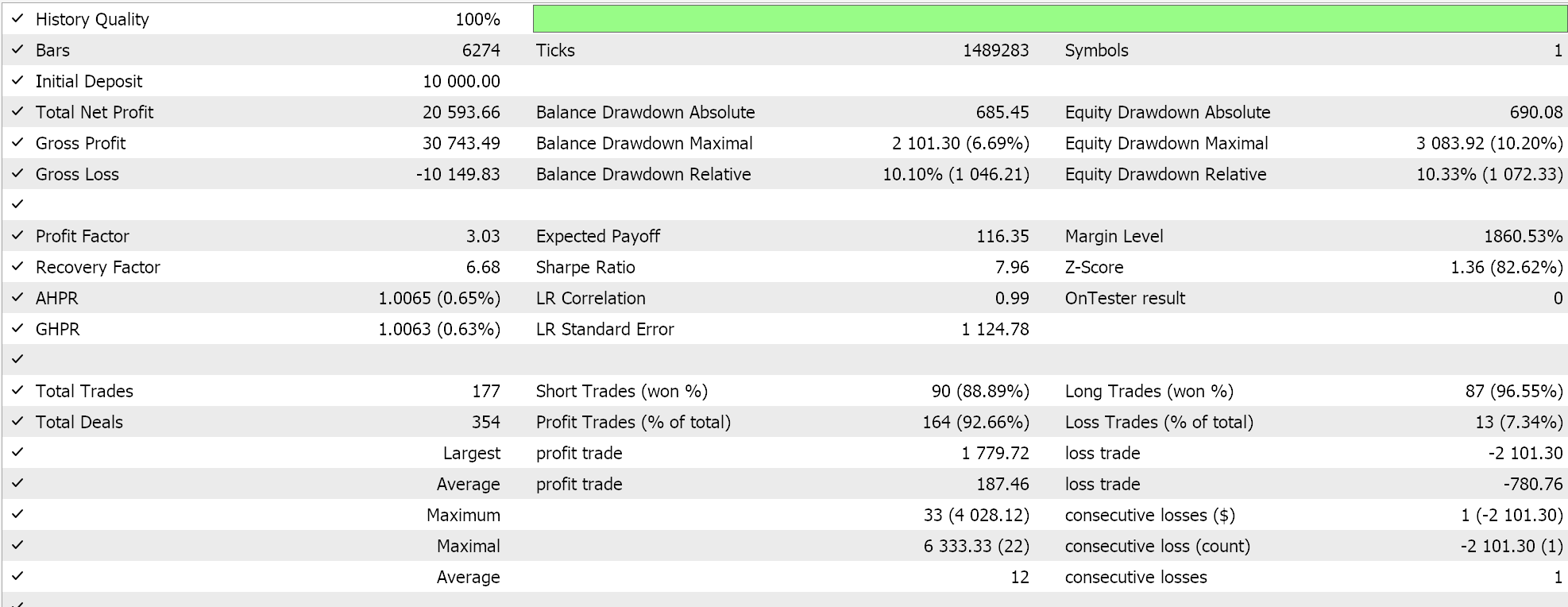
La diferencia global en los resultados es pequeña, pero puede resultar crucial al realizar pruebas no solo durante períodos más largos, sino también en diferentes clases de asesores, como la gestión de capital o incluso la generación de señales.