Características del Wizard MQL5 que debe conocer (Parte 18): Búsqueda de arquitectura neural con vectores propios

Introducción

Continuamos la serie sobre la implementación del asistente MQL5 analizandoBúsqueda de arquitectura neuronal mientras nos centramos específicamente en el papel que pueden desempeñar los vectores propios para hacer que este proceso de agilizar el entrenamiento de la red sea más eficiente. Se podría decir que las redes neuronales son el ajuste de una curva a un conjunto de datos, ya que ayudan a generar una expresión formulaica que, cuando se aplica a los datos de entrada (x), proporciona un valor objetivo (y), tal como lo hace una ecuación cuadrática con una curva. Sin embargo, los puntos de datos x e y pueden ser, y de hecho a menudo lo son, multidimensionales, razón por la cual las redes neuronales han ganado mucha popularidad. No obstante, el principio de llegar a una expresión formulaica sigue vigente, por lo que las redes neuronales son simplemente un medio para llegar a esto, pero no la única manera de hacerlo.

Introducción

Si elegimos utilizar redes neuronales para definir la relación entre un conjunto de datos de entrenamiento y su objetivo, como es el caso de este artículo, entonces tenemos que lidiar con la pregunta de ¿qué configuraciones utilizará esta red? Existen varios tipos de redes, y esto implica que los diseños y configuraciones aplicables también son muchos. Para este artículo, consideramos un caso muy básico que suele denominarse perceptrón multicapa. Con este tipo, los ajustes en los que nos detendremos serán únicamente el número de capas ocultas y el tamaño de cada capa oculta.

Normalmente, NAS puede ayudar a identificar estas 2 configuraciones y muchas más. Por ejemplo, incluso con MLP simples, la cuestión de qué tipo de activación utilizar, los pesos iniciales a utilizar y los sesgos iniciales son todos factores sensibles al rendimiento y la precisión de la red. Sin embargo, se omiten aquí porque el espacio de búsqueda es muy extenso y los recursos informáticos necesarios para la propagación hacia delante y hacia atrás, incluso en un conjunto de datos de tamaño moderado, serían prohibitivos.

Sin embargo, el enfoque que se va a adoptar aquí es un poco novedoso, ya que utiliza vectores y valores propios en un espacio de búsqueda matricial para identificar los ajustes ideales. Convencionalmente, el NAS se lleva a cabo mediante aprendizaje por refuerzo, o algoritmo evolutivos, u optimización bayesiana, o búsqueda aleatoria.

Cada uno de estos enfoques convencionales implica el entrenamiento y la validación cruzada de una red con su configuración seleccionada (también conocida como arquitectura) mediante la evaluación comparativa de cada rendimiento con respecto al objetivo, a efectos de comparación. Lo que los diferencia es lo exhaustivos que son, o su enfoque a la hora de ser eficientes sin ser exhaustivos dentro del espacio de búsqueda. El aprendizaje por refuerzo se basa en un algoritmo que evalúa previamente una red dentro del espacio de búsqueda en función de su configuración, y va mejorando este algoritmo con cada selección. Los algoritmos evolutivos cruzan o combinan redes dentro del espacio de búsqueda para llegar a nuevas redes que no tenían por qué haber estado en el espacio de búsqueda en un principio, de nuevo evaluando su rendimiento en función de un objetivo. La optimización bayesiana, como la búsqueda aleatoria, se basa en que el espacio de búsqueda esté ordenado en un formato de matriz o en que las diferentes configuraciones de la red puedan percibirse como coordenadas dentro del espacio de búsqueda. Por ejemplo, si un espacio de búsqueda es bidimensional con sólo 2 variables el tamaño estándar de una capa oculta, y el número de capas ocultas entonces estas opciones se extenderían por esta matriz en un orden ascendente (o descendente) a través de su diagonal en un formato similar al de la imagen inferior.

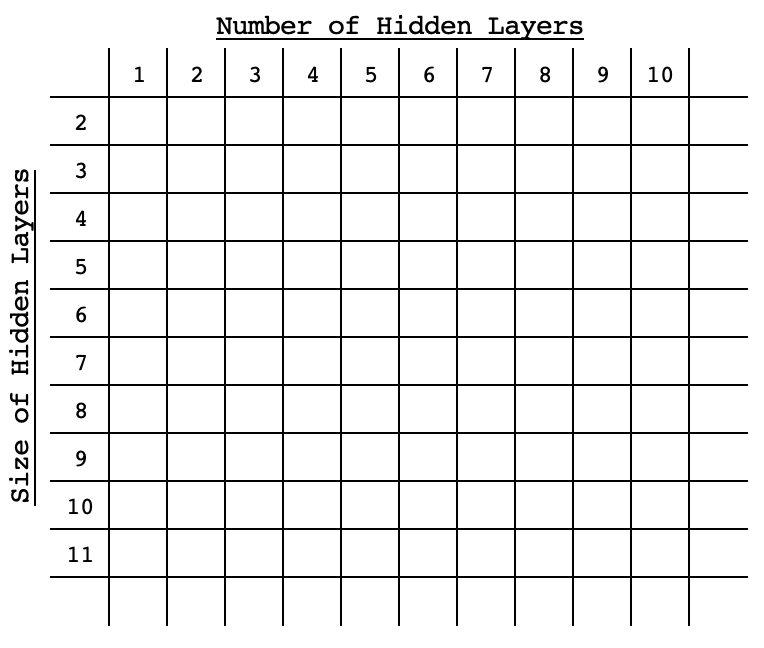
Con esta disposición, el rendimiento de cualquier red se vincularía a sus «coordenadas» dentro del espacio, por lo que se utilizarían métodos estadísticos con cada selección posterior para afinar la elección de la red que ofreciera el mejor rendimiento. Este artículo sobre vectores propios y PCA que se escribió hace unos días utilizaba un espacio de búsqueda matricial para seleccionar un día de la semana ideal y un precio aplicado del indicador, para operar con el EURUSD cuando se utiliza el marco temporal de 4 horas. Esto se obtuvo a partir de una matriz cruzada de cambios de precios para cada uno de los días de 5 semanas y en cada uno de los precios aplicados considerados.

Consideraremos un enfoque de búsqueda similar para este artículo. Dado que el entrenamiento exhaustivo de todas las redes es un problema que intentamos «resolver», nuestros puntos de referencia serán simplemente puntuaciones de paso adelante de los valores objetivo en redes inicializadas con pesos y sesgos estándar. Haremos sólo ejecuciones hacia adelante sobre una muestra de datos, y la puntuación media de cada ajuste servirá como su punto de referencia dentro de la matriz.

El papel de los vectores propios en el NAS

La matriz eigen que utilizaremos para la NAS será bidimensional por brevedad, como se ha aludido anteriormente. Si consideramos una MLP simple en la que todas las capas ocultas tienen el mismo tamaño, las 2 únicas preguntas que querremos responder serán cuántas capas ocultas debe tener la MLP y qué tamaño tiene cada capa oculta.

Las posibles respuestas a estas preguntas pueden presentarse fácilmente en una matriz, con el rendimiento por defecto de cada red registrado en cada combinación de tamaño de capa y número de capa. Las redes variarán en su configuración como se refleja en la tabla matriz, sin embargo sus capas de entrada y salida serán estándar. Para este artículo, tendremos una capa de entrada de tamaño 4, y una capa de salida de tamaño 1. Estamos ante un escenario ordinario en el que pronosticamos el próximo precio de cierre basándonos en los 4 últimos valores de precio de cierre.

El símbolo de prueba será EURJPY durante el año 2022 en el marco temporal de 4 horas. Esto significa que nuestros datos serán precios de cierre de 4 horas para el año 2022. Al «entrenar» este modelo, lo único que estamos haciendo es registrar la desviación media respecto a los valores objetivo a lo largo del año para todas las configuraciones de la red. Nuestra configuración abarcará desde una sola capa oculta hasta 10 capas ocultas a lo largo de las filas de la matriz, mientras que en las columnas figurarán los tamaños de las capas ocultas, que irán de 2 a 11. Estos ajustes de prueba son arbitrarios y, dado que al final de este artículo se adjunta el código fuente completo, el lector puede personalizarlo según sus preferencias.

Para reiterar, el «entrenamiento» del modelo implicará una única pasada hacia delante de cada una de las redes disponibles, todas con los pesos y sesgos estándar por defecto a lo largo del año 2022 con cada previsión de barra comparada con el precio de cierre real. No habrá retropropagación ni entrenamiento típico de redes durante este «entrenamiento».

Nos basamos en una clase de red que vimos en este artículo para implementar el MLP. Simplemente requiere una matriz de enteros cuyo tamaño defina el número total de capas, donde el valor entero en cada índice establece el tamaño de la capa.

Aunque en este artículo y en esta serie se está haciendo hincapié en el asistente MQL5, el «entrenamiento» mencionado anteriormente se realizará mediante un script, tal y como se hizo en el último artículo sobre vectores propios, y utilizaremos los resultados/recomendaciones del mismo para codificar una instancia de clase de señal para probarla con un asesor experto ensamblado por el asistente. Nuestra prueba del asesor experto montado tendrá el entrenamiento habitual de la red en cada barra o con cada nuevo punto de datos. El resultado del probador de estrategias de la red recomendada se comparará con la peor recomendación, como control, para poder evaluar la tesis de si los vectores y valores propios pueden ser ingeniosos en la NAS.

Sin embargo, si recapitulamos lo que tratamos en el último artículo sobre los vectores y valores propios, la reducción de la dimensionalidad utilizada nos proporcionó un único vector de una matriz analizada. Así, en nuestro caso, el rendimiento registrado de cada red que tenemos en una matriz se reducirá a un vector. En el último artículo, queríamos obtener el día de la semana y el precio aplicado que capturara la mayor parte de la varianza del par EURJPY a lo largo de un año en el marco temporal de 4 horas. Esto implicaba que nos centrábamos en los valores máximos de los vectores propios dentro de la matriz proyectada, ya que eran los que más correlacionaban positivamente con nuestro objetivo.

En este caso, sin embargo, nuestra matriz ha registrado desviaciones de los valores objetivo, lo que implica que lo que tenemos en nuestra matriz es el factor de error de cada red. Dado que para las pruebas queremos utilizar la red con el menor error, nuestras selecciones para la red por número de capas y tamaño de cada capa serán los mínimos en cada uno de los vectores propios tal y como se recuperan de la matriz de proyección. Este preprocesamiento, como se ha mencionado, se realiza en su totalidad mediante un script, y puede dividirse en 5 secciones, a saber: a) inicialización de las redes:

//initialise networks
   ArrayResize(__M.row, __SIZE);
   for(int r = 0; r < __SIZE; r++)
   {  for(int c = 0; c < __SIZE; c++)
      {  ArrayResize(__M.row[r].col, __SIZE);
         ArrayResize(__M.row[r].col[c].settings, 2 + __LEAST_LAYERS + r);
         ArrayFill(__M.row[r].col[c].settings, 0, __LEAST_LAYERS + r + 2, __LEAST_SIZE + c);
         __M.row[r].col[c].settings[0] = __INPUTS;
         __M.row[r].col[c].settings[__LEAST_LAYERS + r + 1] = __OUTPUTS;
         __M.row[r].col[c].n = new Cnetwork(__M.row[r].col[c].settings, __initial_weight, __initial_bias);
      }
   }

B) Evaluación comparativa de las redes:

//benchmark networks
   int _buffer_size = (52*PeriodSeconds(PERIOD_W1))/PeriodSeconds(Period());
   PrintFormat(__FUNCSIG__ + " buffered: %i", _buffer_size);
   if(_buffer_size >= __INPUTS)
   {  for(int i = _buffer_size - 1; i >= 0; i--)
      {  for(int r = 0; r < __SIZE; r++)
         {  for(int c = 0; c < __SIZE; c++)
            {  vector _in,_out;
               vector _in_new,_out_new,_in_old,_out_old;
               _in_new.CopyRates(Symbol(), Period(), 8, i + 1, __INPUTS);
               _in_old.CopyRates(Symbol(), Period(), 8, i + 1 + 1, __INPUTS);
               _out_new.CopyRates(Symbol(), Period(), 8, i, __OUTPUTS);
               _out_old.CopyRates(Symbol(), Period(), 8, i + 1, __OUTPUTS);
               _in = Norm(_in_new, _in_old);
               _out = Norm(_out_new, _out_old);
               __M.row[r].col[c].n.Set(_in);
               __M.row[r].col[c].n.Forward();
               __M.row[r].col[c].benchmark += fabs(__M.row[r].col[c].n.output[0]-_out[0]);
            }
         }
      }
   }

C) Copiar los puntos de referencia en la matriz de análisis:

//copy benchmarks to analysis matrix
   matrix _m;
   _m.Init(__SIZE, __SIZE);
   _m.Fill(0.0);
   for(int r = 0; r < __SIZE; r++)
   {  for(int c = 0; c < __SIZE; c++)
      {  _m[r][c] = __M.row[r].col[c].benchmark;
      }
   }

D) Normalizar la matriz y generar los vectores y valores propios:

//generating eigens
   PrintFormat(" for: %s, with: %s", Symbol(), EnumToString(Period()));
   matrix _z = ZNorm(_m);
   matrix _cov_col = _z.Cov(false);
   matrix _e_vectors;
   vector _e_values;
   _cov_col.Eig(_e_vectors, _e_values);

E) Y, por último, interpretando los vectores propios para recuperar los números de capa de red ideal y peor y los tamaños de capa a partir de la matriz de proyección:

//interpreting the eigens from projection
   matrix _t = _e_vectors.Transpose();
   matrix _p = _m * _t;
   vector _max_row = _p.Max(0);
   vector _max_col = _p.Max(1);
   string _layers[__SIZE];
   for(int i=0;i<__SIZE;i++)
   {  _layers[i] = IntegerToString(i + __LEAST_LAYERS)+" layer";
   }
   double _nr_layers[];
   _max_row.Swap(_nr_layers);
   //since network performance inversely relates to network deviation from target
   PrintFormat(" est. ideal nr. of layers is: %s", _layers[ArrayMinimum(_nr_layers)]);
   PrintFormat(" est. worst nr. of layers is: %s", _layers[ArrayMaximum(_nr_layers)]);
   string _sizes[__SIZE];
   for(int i=0;i<__SIZE;i++)
   {  _sizes[i] = "size "+IntegerToString(i + __LEAST_SIZE);
   }
   double _size_nr[];
   _max_col.Swap(_size_nr);
   PrintFormat(" est. ideal size of layers is: %s", _sizes[ArrayMinimum(_size_nr)]);
   PrintFormat(" est. worst size of layers is: %s", _sizes[ArrayMaximum(_size_nr)]);

La ejecución del script anterior en un espacio de búsqueda de 100 se ejecuta durante unos segundos, lo que es una buena señal. Sin embargo, se podría argumentar que el espacio no es lo suficientemente amplio y ese es un argumento válido, por lo que el script adjunto tiene los atributos de tamaño del espacio como una variable global que el usuario puede modificar para crear algo más diligente. Además, necesitábamos una estructura para manejar las instancias de red y sus puntos de referencia. Esto se define en la cabecera de la siguiente manera:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
struct Scol
{  int   settings[];
   Cnetwork *n;
   double benchmark;
   
   Scol()
   {  ArrayFree(settings);
      benchmark = 0.0;
   }
   ~Scol(){ delete n; };
};
struct Srow
{  Scol  col[];

   Srow(){};
   ~Srow(){};
};
struct Smatrix
{  Srow  row[];
   
   Smatrix(){};
   ~Smatrix(){};
};
Smatrix __M;   //matrix of networks

Probar el Asesor Experto

Si ejecutamos el script anterior que ayuda a buscar la configuración ideal de la red, obtendremos los siguientes registros, cuando se adjunta a EURJPY en el marco de tiempo de 4 horas:

2024.05.03 18:22:39.336 nas_1_changes (EURJPY.ln,H4) void OnStart() buffered: 2184

2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) for: EURJPY.ln, with: PERIOD_H4

2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) est. ideal nr. of layers is: 6 layer

2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) est. worst nr. of layers is: 9 layer

2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) est. ideal size of layers is: size 2

2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) est. worst size of layers is: size 4

La configuración de red recomendada es para una red de 6 capas, donde el tamaño de cada una es de ¡2! Como nota al margen, los datos objetivo (valores y) utilizados para comparar la matriz se normalizaron para que estuvieran en el intervalo de 0,0 a 1,0, donde una lectura de 0,5 implica que el cambio de precio resultante fue 0, mientras que cualquier valor inferior a 0,5 indicaría una caída del precio resultante y un valor superior a 0,5 apuntaría a una subida del precio. El código de la función que realiza esta normalización figura a continuación:

//+------------------------------------------------------------------+
//| Normalization (0.0 - 1.0, with 0.5 for 0                         |
//+------------------------------------------------------------------+
vector Norm(vector &A, vector &B)
{  vector _n;
   _n.Init(A.Size());
   if(A.Size() > 0 && B.Size() > 0 && A.Size() == B.Size() && A.Min() > 0.0 && B.Min() > 0.0)
   {  int _size = int(A.Size());
      _n.Fill(0.5);
      for(int i = 0; i < _size; i++)
      {  if(A[i] > B[i])
         {  _n[i] += (0.5*((A[i] - B[i])/A[i]));
         }
         else if(A[i] < B[i])
         {  _n[i] -= (0.5*((B[i] - A[i])/B[i]));
         }
      }
   }
   return(_n);
}

Esta normalización era necesaria porque, dado el pequeño conjunto de datos que estamos considerando, entrenar una red para desarrollar pesos y sesgos capaces de manejar valores negativos y positivos como salidas requeriría conjuntos de datos extensamente grandes, configuraciones de red más complejas y, sin duda, más recursos informáticos. Ninguno de estos escenarios se explora en este artículo, pero pueden aventurarse si se consideran factibles. Así, con nuestra normalización, podemos obtener resultados sensibles de nuestra red con conjuntos de datos y entrenamiento modestos.

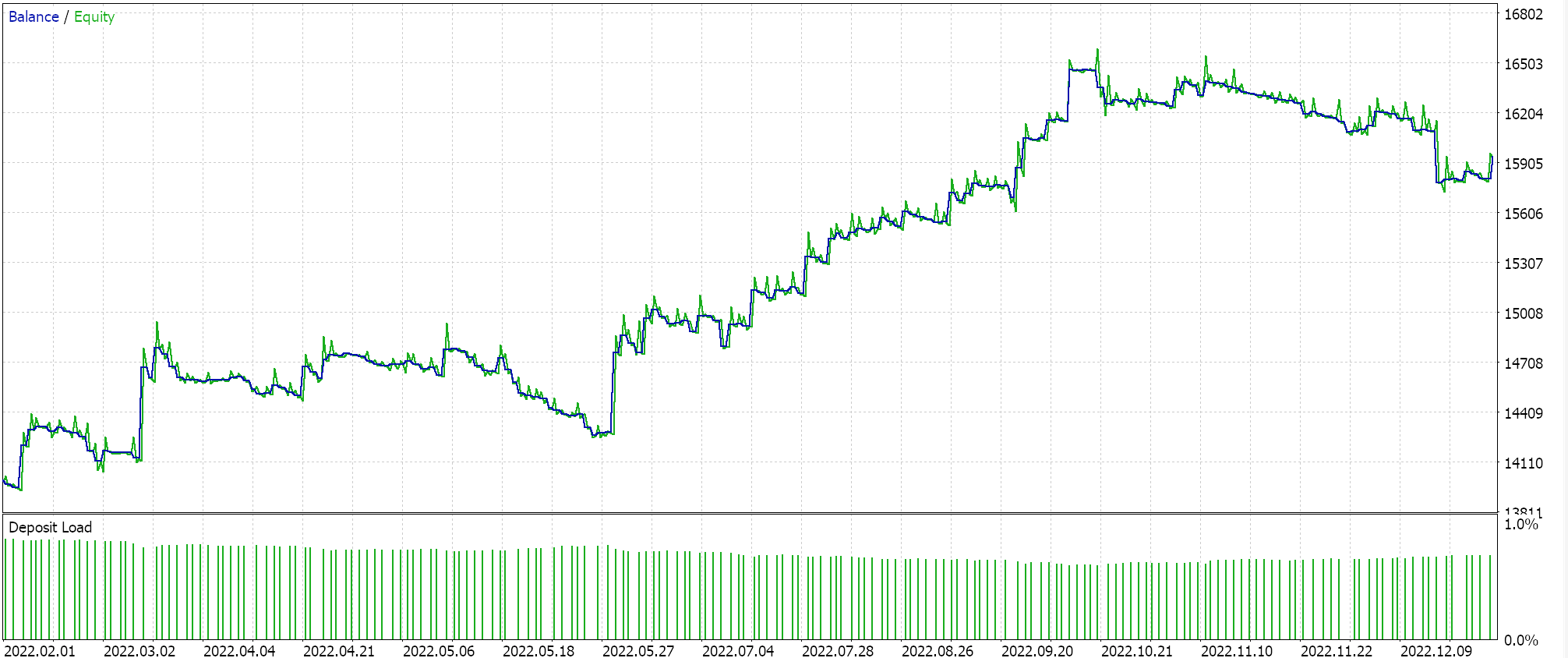
Si realizamos las pruebas con la configuración de red recomendada de 6 capas a un tamaño de 2, obtendremos el informe y la curva de equidad que se presentan a continuación:

También se marcó en los resultados del registro del script la configuración de red de 9 capas, dimensionadas a 4. Si realizamos pruebas con ajustes de entrada de expertos idénticos para esta configuración de red, obtendremos los siguientes resultados:

Sorprendentemente, ¡los resultados son casi idénticos! ¿Por qué? Bueno, hay algunas razones teóricas que podrían explicar esto:

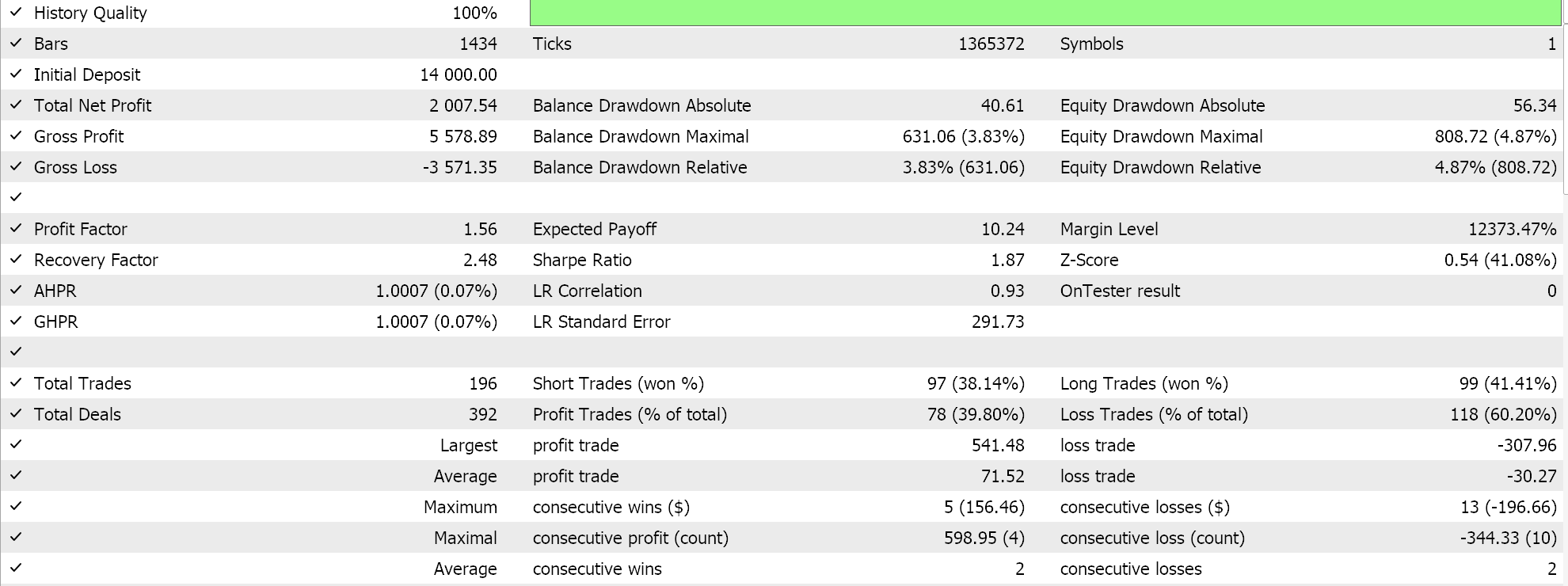
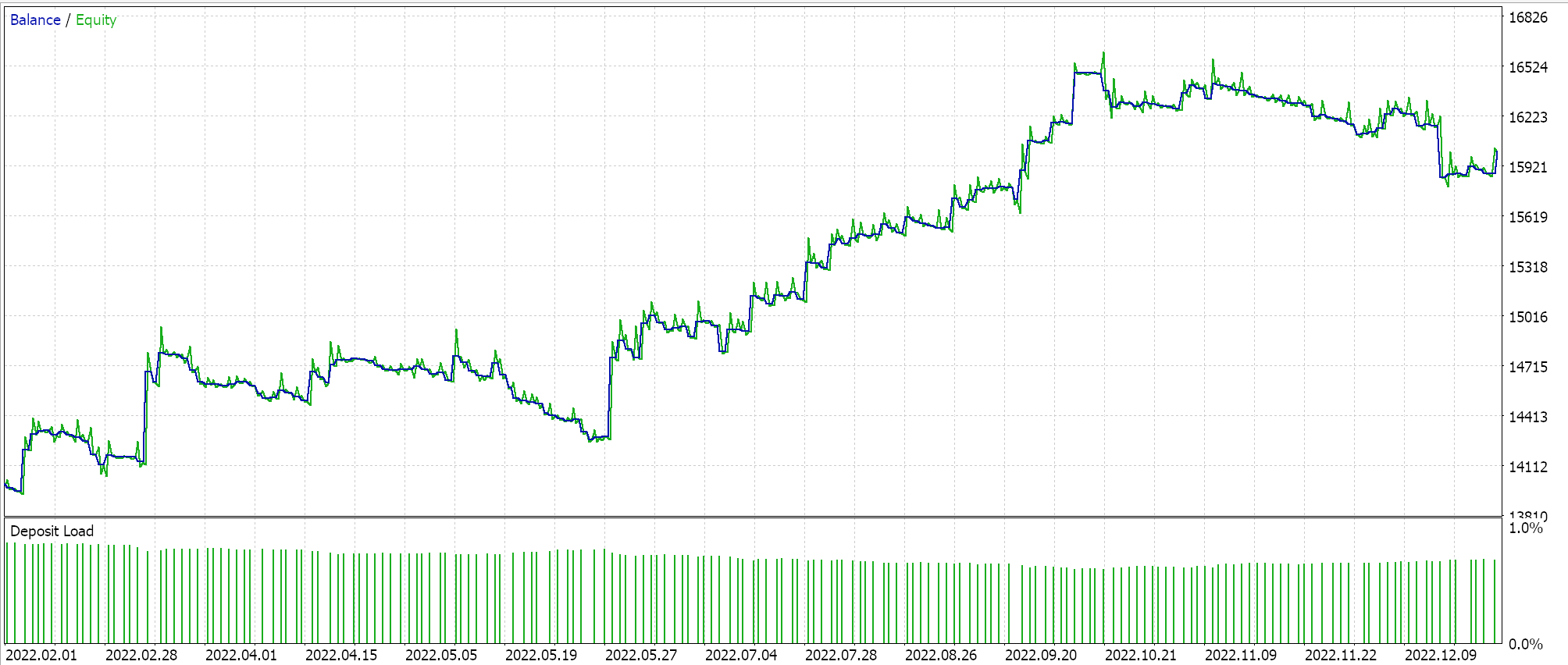
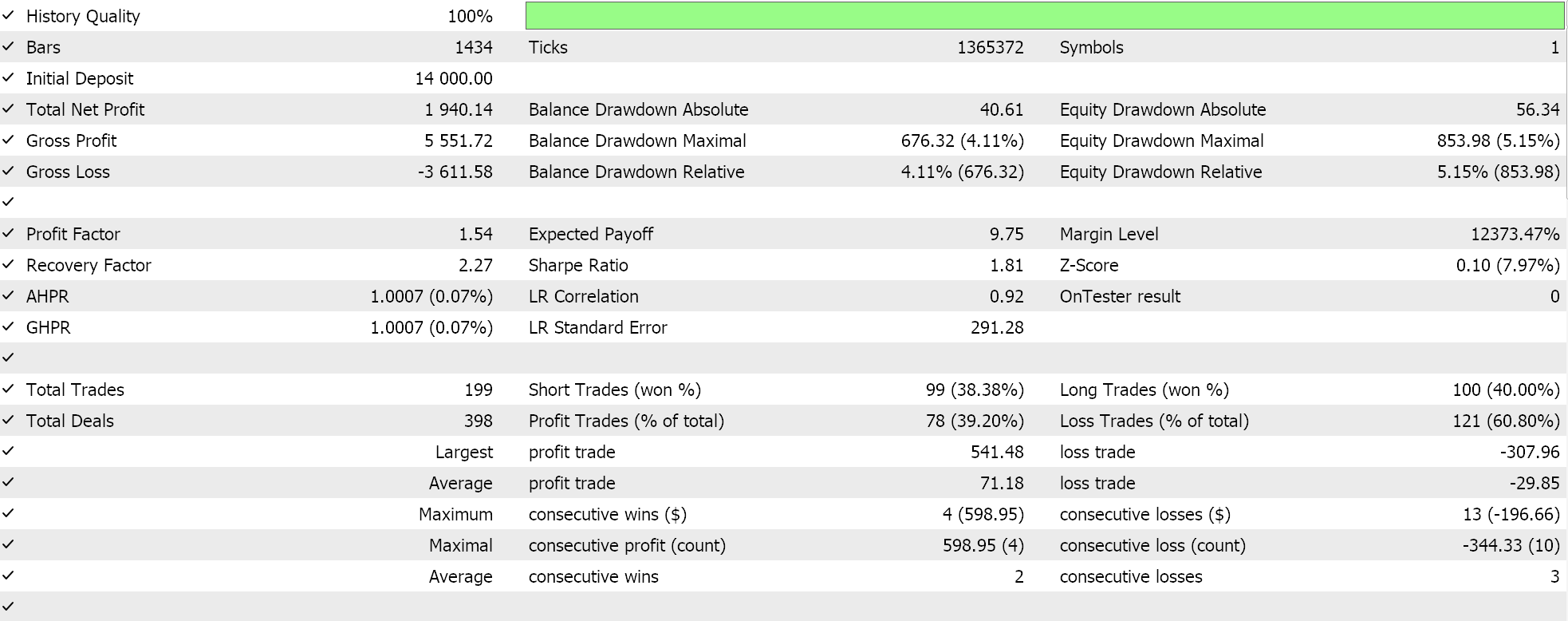
Las redes neuronales pueden sufrir de redundancia en su capacidad, donde diferentes configuraciones (o arquitecturas) aprenden las mismas relaciones subyacentes en los datos aunque tengan estructuras diferentes. Recordemos que en ambas pasadas las redes se estaban entrenando, por lo que tanto los pesos como los sesgos se estaban mejorando. Así, mientras que los vectores propios con mayor varianza captan un conjunto más amplio de características y los de menor varianza se centran en los detalles, cualquiera de las dos configuraciones de red puede aprender lo básico para obtener un buen rendimiento.

Aunque el número de capas ocultas y su tamaño son factores cruciales para determinar el rendimiento de la red en esta situación, podría haber otros factores dominantes en juego, como nuestra elección de la función de activación (utilizamos soft plus) o la cotización de aprendizaje utilizada. Cada uno de ellos o todos ellos podrían haber tenido una influencia desproporcionada en el rendimiento de las redes.

Otra posible explicación podría tener que ver con las limitaciones del espacio de búsqueda. Consideramos 10 tamaños de capa diferentes y 10 opciones distintas de capa oculta, todas ellas con una forma rectangular. Esto podría haber restringido intrínsecamente las posibles combinaciones de redes al cartografiar este conjunto de datos concreto, de modo que cualquiera de estas pocas opciones podría llegar fácilmente a la solución deseada.

Conclusión

Hemos visto cómo se puede hacer NAS de forma poco ortodoxa con los vectores y valores propios cuando nos enfrentamos a un ámbito modesto de configuraciones de redes neuronales entre las que elegir. Este proceso puede escalarse y quizá incluso ampliarse para incluir o considerar otros factores que no formaban parte de la matriz de análisis añadiendo la forma de la capa oculta (nosotros sólo nos fijamos en los rectángulos) o incluso los tipos de activación. Esto último es lo más fácil de añadir a una matriz como la analizada en este artículo, ya que sólo hay 2 ó 3 tipos principales de activación y esto podría significar simplemente triplicar el número de columnas y ampliar al mismo tiempo el número de filas para garantizar que se mantiene una matriz cuadrada, un requisito previo para el análisis de vectores propios. La adición de la forma de la capa oculta también podría hacerse de forma similar si las distintas formas que deben considerarse se enumeran en tipos claros. 

Notas:

Los archivos adjuntos se pueden utilizar siguiendo las guías del ensamblaje del Asistente del Asesor Experto que se encuentran aquí y aquí.