知っておくべきMQL5ウィザードのテクニック（第11回）：ナンバーウォール

はじめに

2、3の時系列については、その中に現れた過去の値に基づいて、数列の次の値の計算式を考案することが可能です。ナンバーウォールは、「クロスルール」と呼ばれるものを介して行列の形で「数値の壁」を事前に生成することによって、これを達成することができます。この行列を生成する際の第一の目的は、問題の数列が収束しているかどうかを確認することです。数列を適用した後、行列の後続の行が0だけであれば、数列のナンバーウォールのクロスルールアルゴリズムはこの問いに喜んで答えます。

この論文では、これらの概念を示すために、ローラン冪級数（別名フォーマルローラン級数、FLS）を、コーシー積を用いながら、多項式形式で演算してこれらの数列を表現する枠組みとして用いています。

一般に、LFSR数列は、下式で示されるように、連続する項の線形結合が常に0になるような再帰関係を満たします。

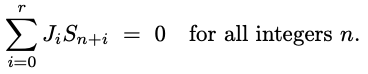
ここで、数列Snは線形再帰または線形帰還シフトレジスタ(LFSR)であり、長さr+1の非0ベクトル｜Ji｜（関係）が存在します。

これは、xの係数（定数はxの0乗の係数）がその要素を構成するベクトル関係を意味します。このベクトルは定義上、少なくとも2の長さを持ちます。

これを説明するために、簡単な例をいくつか考えてみましょう。最初の例は3の冪の数列です。3の冪が0から上向きに列挙され、各値がそのインデックスの3乗であることは皆が知っています。これをナンバーウォール行列に入力すると、初期表現は次のようになります。

列の上に行として示されている0と1は常に暗黙的なものであり、行列内のすべての欠損値を伝播するようにクロスルールを適用するのに役立ちます。クロスルールを適用する際、行列内の5つの値が単純な十字形である場合、外側の垂直方向の値の積と外側の水平方向の値の積を足すと、常に中央の値の2乗と等しくなります。

この規則を上記の基本的な3の冪の数列に適用すると、以下のような行列が得られます。

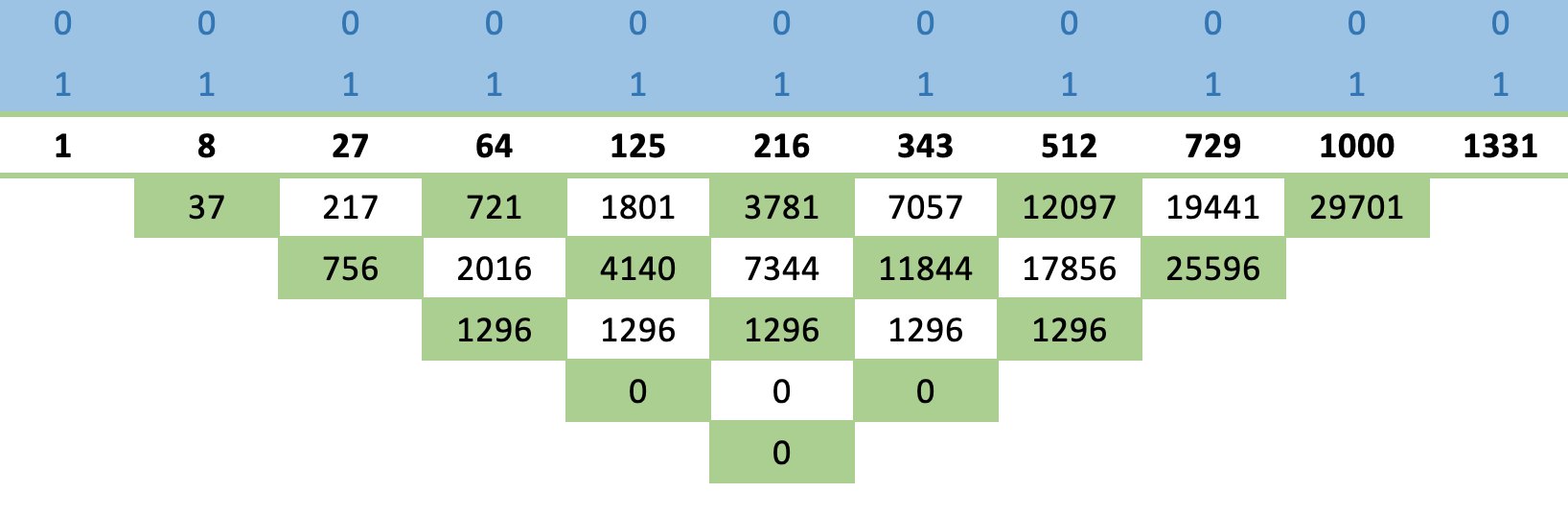
ここでクロスルールを説明してみます。数列の上部の216を見てください。その前(125)と後(343)の積と、その上(1)と下(3781)の積を足すと、216の2乗になります。

0の列をこれほど早く得ることができるという事実は、この数列が確かに収束していることを示し、その後の値の式を簡単に導くことができます。

しかし、式を見る前に、もう1つの例であるフィボナッチ級数を考えてみましょう。この数列を行列に当てはめ、上記のようにロングクロスルールを適用すれば、0の行をより早く得ることができます。

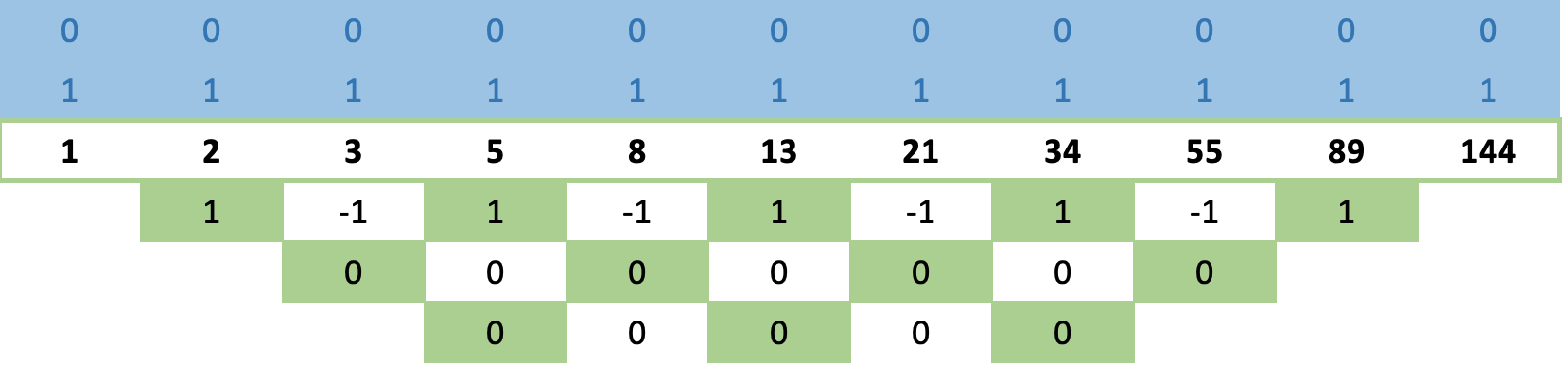
フィボナッチ数列は3の冪よりも複雑であるため、収束するまでに時間がかかることが予想されるため、これは確かに奇妙に思えますが、実は 2行目までに収束します。

上記の2つの例のような収束級数の定式化を導き出すには、数列の中のどの値も、同じ値からxを掛けた前の値を差し引いた値に置き換える数式形式に、ナンバーウォール行列の中で置き換えることになります。これは次のような形になります。

ここからは、上の数列と同じようにクロスルールを適用し、それに続く行に多項式形式の値を生成するだけです。興味深いことに、数列が収束していれば、たとえ多項式の値であっても、ロングクロスルールを数回伝播させると、0の列ができます。これは、フィボナッチ数列について以下に図解されています。

では、この多項式の値をどうするのでしょうか。最後の方程式を0に等しくし、xの最大冪乗を解くと、反対側に残るxの係数は、次の値までの和をとる数列の前の値の倍数であることがわかりました。

つまり、フィボナッチ数列の最後の式で、x^2の最大冪乗を求めると、1 + xになります。

1はx^0を表し、事実上、係数がxである数列番号の前の数列番号に対する係数でもあることにご注意ください。つまり、フィボナッチ級数では、どの数字も2つ前の数字の和になるということです。

立方数列の多項式はどのようなものでしょうか。上記のように収束するのに多くの行を必要とするため、方程式を立方体として表現するよりも複雑です。

収束しない系列についてはどうでしょうか。このようなシナリオでは、どのような行列が生成されるのでしょうか。これを説明するために、EURUSDを例に、通常のFXペアの価格推移を見てみましょう。2024年の最初の5取引日のEURUSD日足終値の列で収束をテストするために（計算式なしで）ナンバーウォール行列を生成しようとすると、最初の5行でこのような壁ができます。

自明のことですが、最初の行で収束することはありません。実際、厳密に収束するのかどうか、はっきりしません。とはいえ、壁の傾向は0に向かっており、これは良いことです。これは、私たちの目的に対するナンバーウォールの適用性を弱めます。実際、この予備的な確認プロセスも一般的に計算量が多く、テプリッツ行列の出番となります。

すべての行が何らかの方法で互いに関連している行列を作成し、その行列の行をスライディング反復すると、もしその行列が収束していれば、この行列の行列式は0になります。これは、収束をテストするための計算効率のより高い方法であり、それ以上に、行列式の大きさに基づいて数列が収束する可能性がどの程度あるかを「定量化」するものです。

つまり、数式行列のクロスルールを任意の数列に伝播させ、行列式の大きさを使用して数式の予測値を「割り引く」ことができるのです。あるいは、絶対的な閾値決定値を設定し、それを超えると計算式の結果を無視することになります。

これらはすべて、金融やその他の時系列が収束しない場合の回避策であり、完璧なものではありませんが、MQL5に実装した場合にどのような可能性があるのかを検証してみましょう。

MQL5の実装

これらのアイデアを説明するための単純なEAをMQL5で作成するために、内蔵のAwesome OscillatorクラスとペアになっているExpertTrailingクラスのインスタンスに実装します。トレーリングクラスのインスタンスは、トレーリングストップロスとテイクプロフィットレベルの大きさを決定するために、ナンバーウォールを使用します。

MQL5で実装する場合、追加の機能と最小限のコード要件を考慮して、行列とベクトルの組み込みデータ型を多く利用します。典型的な（定型的でない）ナンバーウォールを構築し、0の行に到達するかどうかを確認することで、収束する数列を事前にスクリーニングできますが、金融時系列の性質と複雑さを考慮すると、行列が収束しないことは明らかです。したがって、伝播後の最後の列の最下行から取得した数列内の次の値の式を計算する方がよいでしょう。

壁を伝搬させるために、ベクトルを使用して係数をxに格納します。未知の行を解く過程で、このような2つのベクトルを掛け合わせることは、結果として得られるベクトル値がx係数となるため、相互相関と等価です。ここで、より高いインデックスの配置はxのより高い指数を示します。この関数はビルトインですが、除算に関しては、2つの商ベクトルのサイズを変更してサイズの違いに一致するようにする必要があります。つまり、単にx指数が一致しないことを意味します。

未決済ポジションのTPとSLをどの程度調整するかを決定する際、ナンバーウォールの入力数列は移動平均の指標値となります。トレール注文の調整には、この指標やボリンジャーバンド、エンベロープスタイルの指標が適しているかもしれませんが、どのような指標でも使用できます。

MQL5ベクトルは、ハンドルが定義されると、指標値を簡単にコピーして読み込みます。典型的なトレール注文確認コード（ロングとショートの両方で使用可能）を以下のソースで見てみましょう。

//+------------------------------------------------------------------+
//| Checking trailing stop and/or profit for long position.          |
//+------------------------------------------------------------------+
bool CTrailingLFSR::CheckTrailingStopLong(CPositionInfo *position, double &sl, double &tp)
{
//--- check

...

//---
   vector _t, _p;
   _p.Init(2);
   _t.CopyIndicatorBuffer(m_ma.Handle(), 0, 0, 2);
   double _s = 0.0;
   for(int i = 1; i >= 0; i--)
   {  _s = 0.0;
      _p[i] = GetOutput(i, _s);
   }
   double _o = SetOutput(_t, _p);
//---
  
...

}

GetOutputとSetOutputという2つの関数を中心に、意思決定が進化していることがわかります。GetOutputは、ナンバーウォールを構築し、数列内の次の値を解く方程式の多項式係数を計算するための主要な関数です。GetOutputのコードは次の通りです。

//+------------------------------------------------------------------+
//| LFSR Output.                                                     |
//+------------------------------------------------------------------+
double CTrailingLFSR::GetOutput(int Index, double &Solution)
{  double _output = 0.0;
   vector _v;
   _v.CopyIndicatorBuffer(m_ma.Handle(), 0, Index, m_length);
   Solution = Solvability(_v);
   _v.Resize(m_length + 1);
   for(int i = 2; i < 2 + m_length; i++)
   {  for(int ii = 2; ii < 2 + m_length; ii++)
      {  if(i == 2)
         {  vector _vi;
            _vi.Init(1);
            _vi[0] = _v[m_length - ii + 1];
            m_numberwall.row[i].column[ii] = _vi;
         }
         else if(i == 3)
         {  vector _vi;
            _vi.Init(2);
            _vi[0] = m_numberwall.row[i - 1].column[ii][0];
            _vi[1] = -1.0 * m_numberwall.row[i - 1].column[ii - 1][0];
            m_numberwall.row[i].column[ii] = _vi;
         }
         else if(ii < m_length + 1)
         {  m_numberwall.row[i].column[ii] = Get(m_numberwall.row[i - 2].column[ii], m_numberwall.row[i - 1].column[ii - 1], m_numberwall.row[i - 1].column[ii + 1], m_numberwall.row[i - 1].column[ii]);
         }
      }
   }
   vector _u = Set();
   vector _x;
   _x.CopyIndicatorBuffer(m_ma.Handle(), 0, Index, m_length);
   _u.Resize(fmax(_u.Size(),_x.Size()));
   _x.Resize(fmax(_u.Size(),_x.Size()));
   vector _y = _u * _x;
   _output = _y.Sum();
   return(_output);
}

上記の共有リストは基本的に2部構成になっています。方程式係数を得るために壁を作り、方程式と現在の数列の測定値を用いて投影します。最初の部分では、Get関数がキーとなり、生成された方程式を掛け合わせ、次の行の方程式を解きます。コードは以下の通りです。

//+------------------------------------------------------------------+
//| Get known Value                                                  |
//+------------------------------------------------------------------+
vector CTrailingLFSR::Get(vector &Top, vector &Left, vector &Right, vector &Center)
{  vector _cc, _lr, _cc_lr, _i_top;
   _cc = Center.Correlate(Center, VECTOR_CONVOLVE_FULL);
   _lr = Left.Correlate(Right, VECTOR_CONVOLVE_FULL);
   ulong _size = fmax(_cc.Size(), _lr.Size());
   _cc_lr.Init(_size);
   _cc.Resize(_size);
   _lr.Resize(_size);
   _cc_lr = _cc - _lr;
   _i_top = 1.0 / Top;
   vector _bottom = _cc_lr.Correlate(_i_top, VECTOR_CONVOLVE_FULL);
   return(_bottom);
}

同様に、Set関数は、最後に伝搬された係数を持つ一番下のベクトルを使用して次の数列値を解きます。そのコードは次の通りです。

//+------------------------------------------------------------------+
//| Set Unknown Value                                                |
//+------------------------------------------------------------------+
vector CTrailingLFSR::Set()
{  vector _formula = m_numberwall.row[m_length + 1].column[m_length + 1];
   vector _right;
   _right.Copy(_formula);
   _right.Resize(ulong(fmax(_formula.Size() - 1, 1.0)));
   double _solver = -1.0 * _formula[int(_formula.Size() - 1)];
   if(_solver != 0.0)
   {  _right /= _solver;
   }
   return(_right);
}

次に、CheｃｋTrailing関数内で、GetOutput関数を2回呼び出します。これは、現在の予測だけでなく、出力の正規化を支援するために以前の予測も取得する必要があるためです。前述したように、ほとんどの数列、特に金融時系列が収束しないためです。冒頭で述べたように、生の出力予測は入力数列値とは非常に異質な数値になるはずです。典型的な数列の値の数倍という非常に大きなdouble値や、明らかに正の値しか期待できないのに負の値が出ることさえ珍しくありません。

そこで、正規化する際には、以下に示す非常に簡単でシンプルなSetOutput関数を使用します。

//+------------------------------------------------------------------+
//| Normalising Output to match Indicator Value                      |
//+------------------------------------------------------------------+
double CTrailingLFSR::SetOutput(vector &True, vector &Predicted)
{  return(True[1] - ((True[0] - True[1]) * ((Predicted[0] - Predicted[1]) / fmax(m_symbol.Point(), fabs(Predicted[0]) + fabs(Predicted[1])))));
}

ここでおこなっているのは、単に予測値を正規化して、その大きさが配列値の範囲内に収まるようにすることだけです。これは、予測値と真の値の両方について配列の変化を利用することで実現します。

また、典型的なトレール注文確認では、その開始時にGetOutput関数内で可解性を測定します。このメトリックは、予測を無視すべきかどうかを判断するための閾値フィルターとして使用され、より大きな行列式値（私たちが解決可能性と呼んでいるもの）は、より高い収束不能性を示しています。行列式が小さい行列でも収束しないことは言うまでもありませんが、より大きな行列式を持つ行列よりも、ナンバーウォールを構築するためにより多くの行が提供された場合の方が、収束する可能性が高いと仮定します。

そして、予備テストでは計算負荷が高いことがわかりましたが、私の意見では、より強固な取引システムを開発するために、もっと磨きをかけ、さらに別の戦略と組み合わせることができるアイデアを提示しています。

MQL5のトレーリングクラスに添付されているコードは、ウィザードを使用して簡単に組み立てることができ、シグナルクラスや資金管理の選択によって、さまざまなEAを作成することができます。いつものように、どうすればいいかのガイドとしてヘルプがこちらにあります。

追記

共有コードおよび上記の図でここまで考慮されたナンバーウォールは、0を含まない証券価格全体を使用しました。例えば、生の価格だけでなく、証券価格の変化を予測したい場合、理想的には価格変化の入力系列を持つことになります。絶対的な価格ではなく、変化を扱い始めると、負の値にぶつかるだけでなく、0がいくつか発生することもあります。

最初は0は無害に思えるかもしれませんが、ナンバーウォールを作るときには、次の行の値を決定する際に課題となります。次の例を考えてください。

基本的なクロスルールで未知の値を解くと、既知の値の1つが0であるため、未知の値と掛け合わせると何も得られないという問題にぶつかります。これを回避するには、対数クロスルールが便利です。そして、上の画像を拡大するとこうなります。

以下の公式を使えば、現在の行の上にある0を回避することができます。

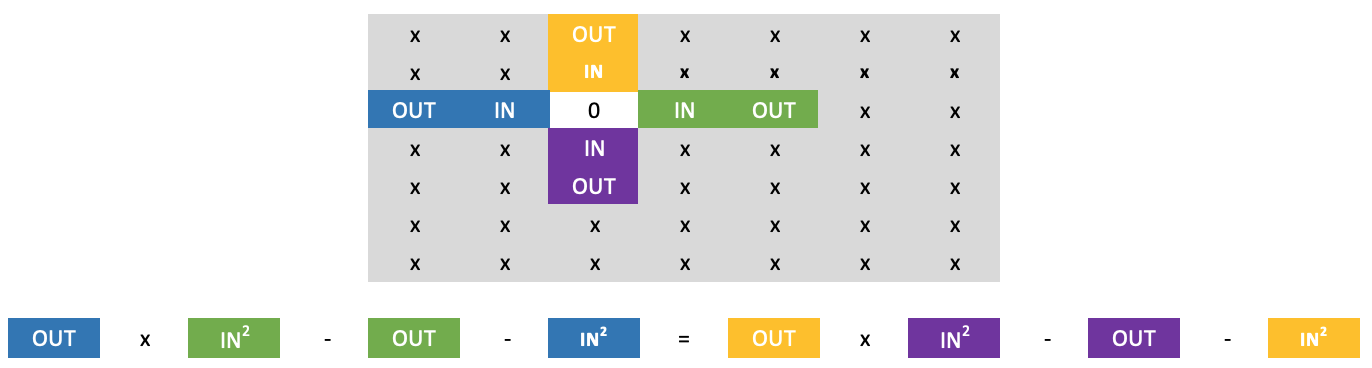
私が「ある程度の自信をもって」と言ったのは、ナンバーウォールには0を含むという非常にユニークな性質があるからです。どのような数でも、0がある場合、それは単数か正方形で、つまり1×1（単数）、2×2、3×3などの形になることがわかりました。これは基本的に、どの行でも2つの数字の間に0があれば、その下の数字は0ではないということです。しかし、ロングクロスルールを適用すると、壁の外側の最低値という形で未知数が増えることは誰にでもわかります。しかし、既知の0を掛けることで、その値を入力することなく方程式を解くことができるので、これは問題ではありません。

ロングクロスルールが対処する問題は、収束するナンバーウォールに厳密に適用されるものであり、上記の図解で見てきたように、金融時系列ではこのようなケースはめったにありません。では、これを考慮すべきなのでしょうか。この素直さは、取引システムが対象とする時系列に応じて、数列ごとに決定されるべきです。また、「可解性」やテプリッツ行列の行列式が必要な閾値を満たしていれば、金融系列であってもこれを適用することを選択することもできるし、壁の構築を終了し、予測多項式を構築する際に、その時点（0にぶつかった時点）で持っているベクトル係数を用いて作業することもできます。この他にもいくつかの選択肢があり、その選択はトレーダーによって異なるでしょう。

ロングクロスルールは、ナンバーウォールを伝播するときに0が1つだけある場合には便利ですが、0がより大きな正方形内にある場合 (0は常に壁内で n x n 形式をとるため)、あまり役に立ちません。 このような場合によく考慮されるのは、蹄鉄ルールです。このルールでは、通常、0の大きな正方形ができると、その正方形に接する配列は、その値が特定の係数でスケーリングされます。

これらの4つの要素は、正方形の各辺に1つずつ、以下の式で合計できるユニークな性質を共有しています。

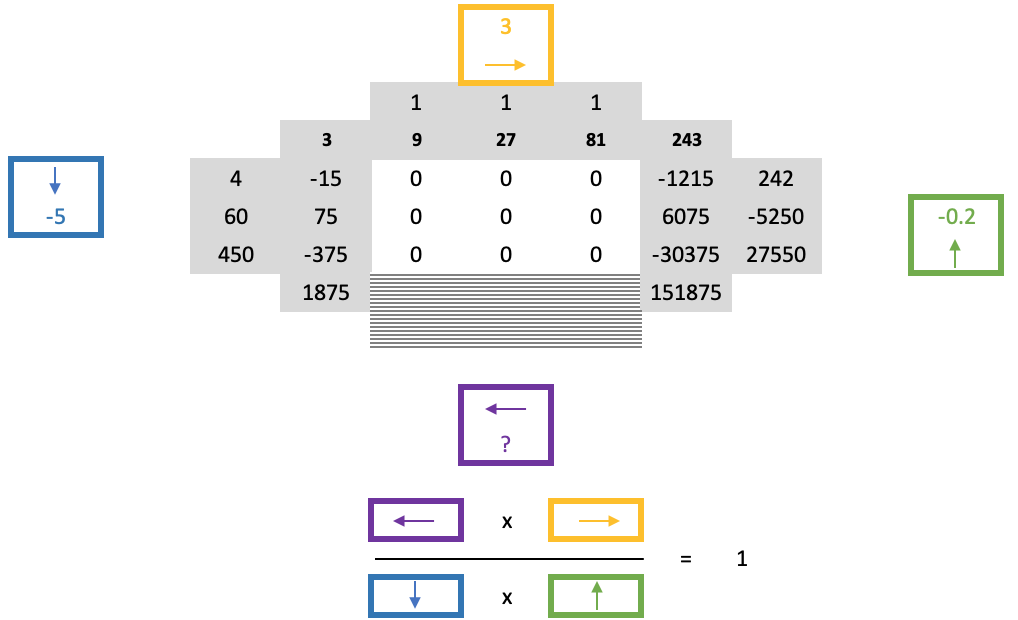
つまり、0の大きな塊に遭遇した場合、その0の境界となる上部と側部の数字はすでに分かっているはずで、0の正方形の幅が分かっている以上、その高さも分かっていることになります。つまり、未知の境界値をどこで評価すべきかが分かっているということです。上記の式から、一番下のスケールファクターを計算し、その数値を一般的に左から右に計算することで、境界のすぐ下の値を得ることができます。

しかし、この時点から通常のクロスルールで進めても、正方形に0があるため、解いたばかりの境界列の下の列を決定するのは難しくなります。これを解決するのが、蹄鉄ルールの「第2部」であり、次のようなやや長い数式に頼ることになります。

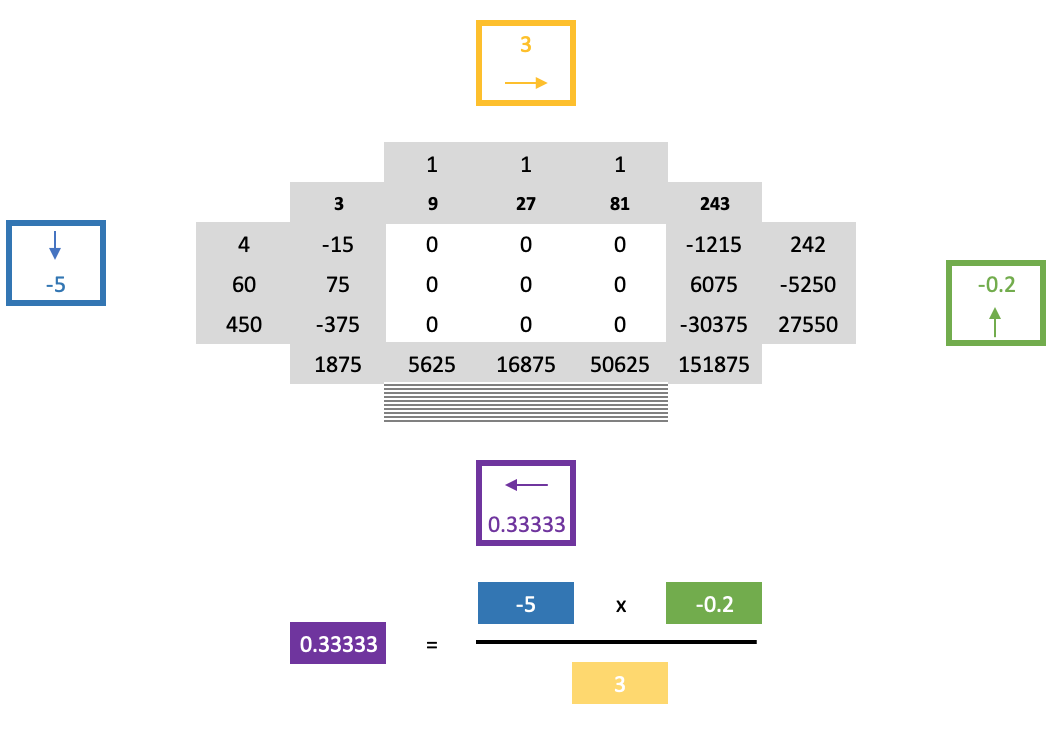
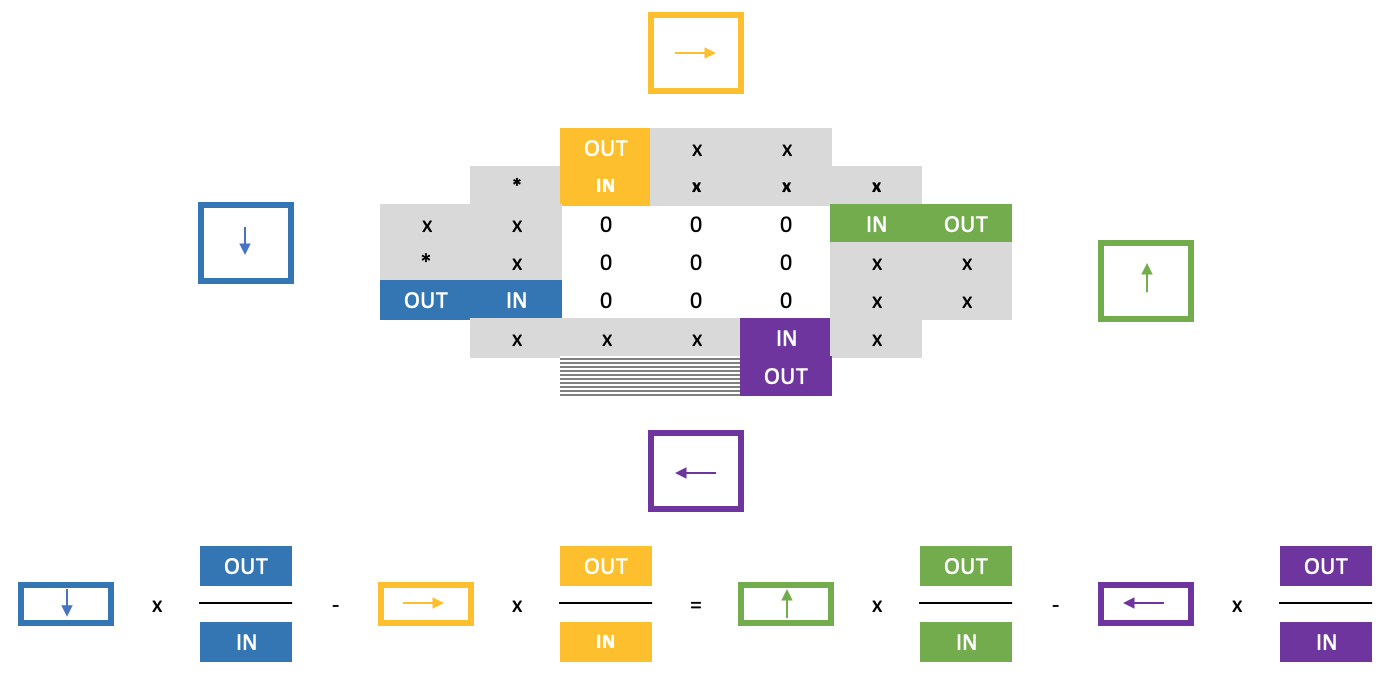
前述の、この件に関する論文は、ここで共有されたポイントの多くを強調しているほか、パゴダ予想についても少し触れています。最も単純な形では、これは数値のセットのグループの合計であり、含まれる各セットが等しいサイズであるため、含まれるセットのそれぞれがそのセット内の数値の1つを表す各頂点を持つ多角形として解釈されます。次に、つながった頂点ですべての多角形の頂点が同じ番号を持つという条件で、これらの多角形をまとめて、より大きな複雑な格子を形成できます。これはもちろん、多角形の各頂点番号がその集合内で一意であるという条件付きで起こります。

これはまず、パゴダを形成する3つの数集合に対して、絵的に興味深い結果をもたらします。各数集合の数字を連続して並べると、そこから伝播するナンバーウォールに非常に興味深い反復パターンが観察されるからです。この論文にはこれらの画像のいくつかが紹介されています。

ただし、取引目的の場合、分類におけるこの「斬新な」アプローチは、金融時系列を見るさらに別の方法を示しています。正直に言うと、独立した記事が必要ですが、 パゴダシーケンスを私たちの用途に合わせて適用できるいくつかの方法を一般化できると言えば十分です。

もし、これをぶっつけ本番で適用するのであれば、より高い次元の形とは対照的に、三角形のパゴダにこだわるのが賢明でしょう。前者はより多くの可能性を引き起こす傾向があり、そのため結合方法が複雑になるためです。これを受け入れることができれば、私たちの仕事はまず、値の繰り返しに対応するために金融系列を正規化することです。これは、すでに強調したようにパゴダを定義する際の要件であり、この正規化がどの程度おこなわれるかは、調整する必要があるものになります。反復が異なれば必ず異なる結果が得られるためです。

次に、ある正規化閾値に満足したら、パゴダ内の三角形の数、つまりグループサイズを設定する必要があります。グループのサイズが大きくなるにつれて、すべての三角形が直接つながる必要性は減少していきます。3つの三角形のパゴダではすべての三角形がつながっていますが、この数が増えるにつれて、どの三角形でもリンクできる最大数は3つになります。つまり、6つの三角形の塔の場合、一番下の中央の三角形だけがそのすべての頂点でつながり、他のすべての三角形は2つの頂点でのみつながります。

グループサイズが大きくなるにつれて三角形の結合の複雑さが増すことから、最適なグループサイズの決定は、正規化の閾値の設定と同時におこなうべきであることが示唆されます。後者は、三角形間のつながりを確立する際の鍵となる繰り返しデータを提供するためです。

結論

ナンバーウォール（検討中の一連の時系列から生成された数字のグリッド）を見てきました。コード例を共有し、未決済ポジションのTPとSLを適切に設定することによって、予測にどのように使用できるかを見ました。さらに、ナンバーウォールに関する論文のハイライトであったパゴダ予想に関連する概念に注目し、それが金融時系列を分類する際の別の手段となり得るかについて、いくつかのアイデアを提示しました。

おわりに

ウィザードで組み立てたEAの比較テストを以下に示します。どちらもAwesome Oscillatorシグナルを使用し、ここに示されているように、基本的には同じような入力を持っています。

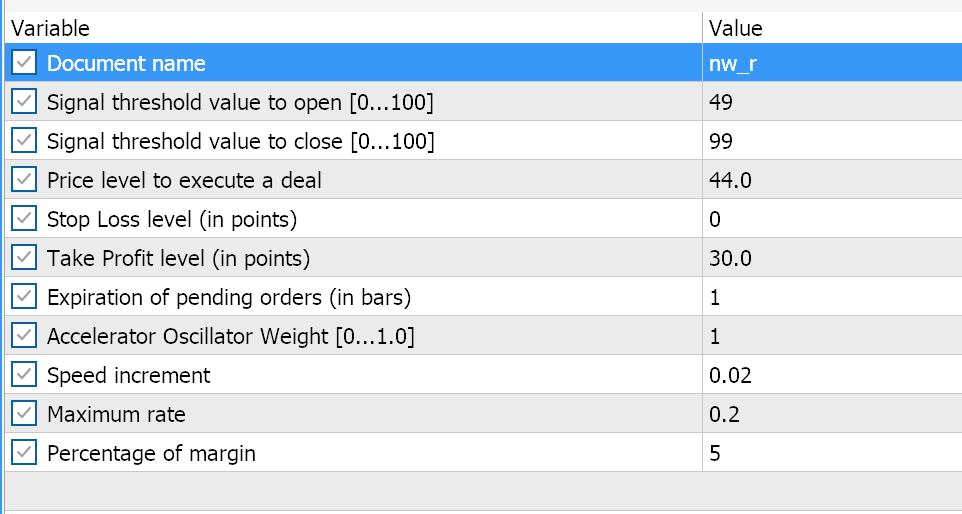
両者の違いは、一方のEAがParabolic SARを使用して未決済ポジションをトレールしクローズするのに対し、もう一方はこの記事で紹介したナンバーウォールアルゴリズムを使用していることです。過去1年間のEURUSDを1時間足で検証した場合、同じシグナルにもかかわらず、両者のレポートは異なっています。まず、Parabolic SARのトレール注文のEAです。

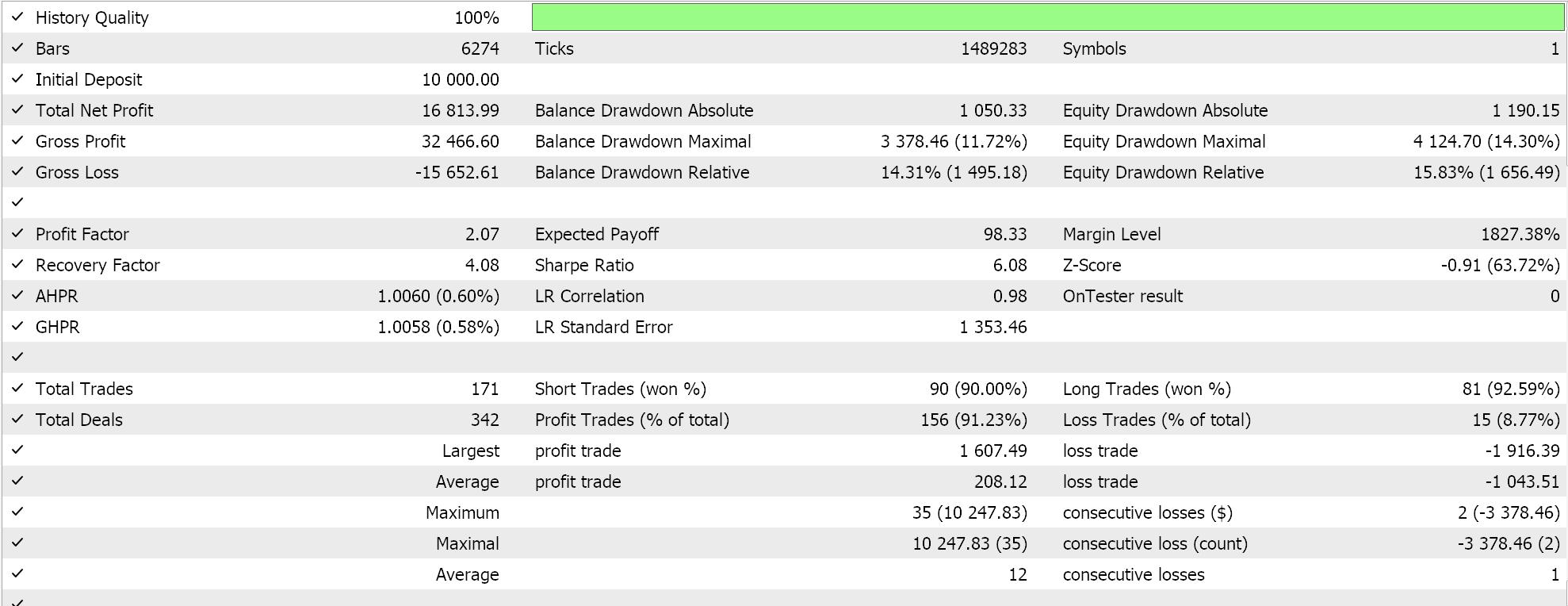
ナンバーウォールレポートは以下の通りです。

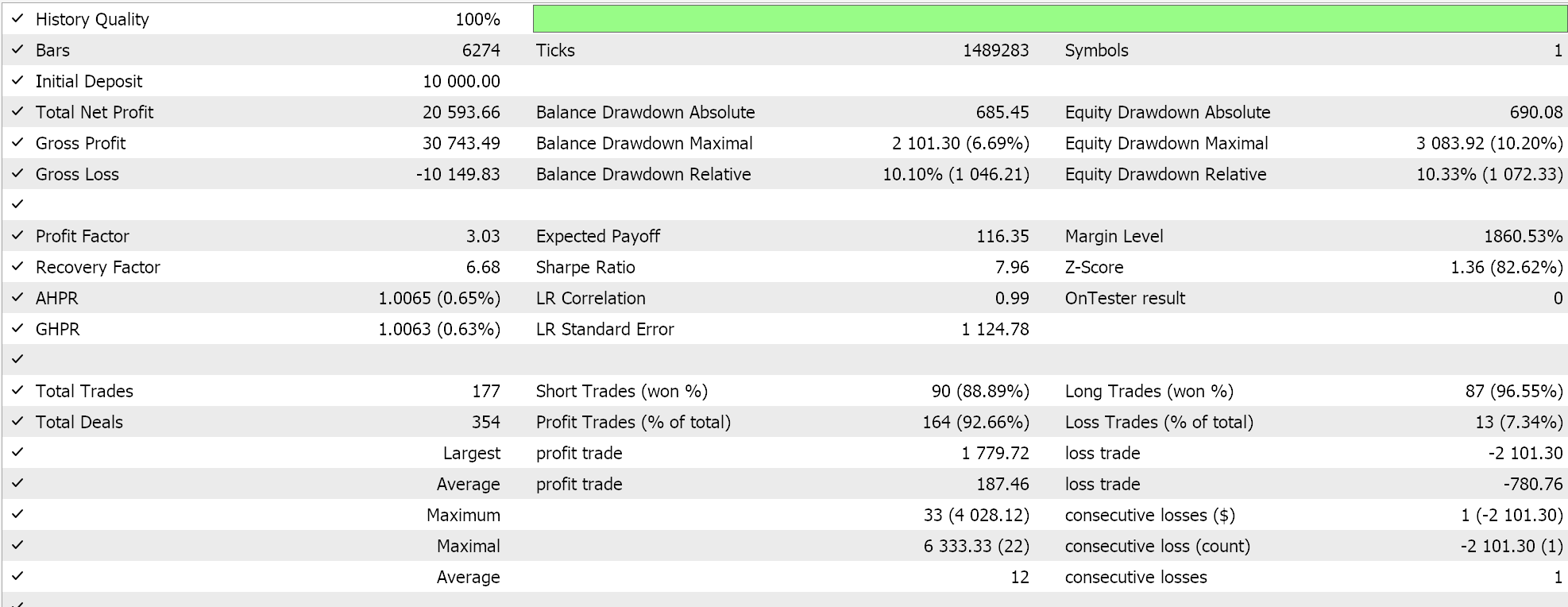
全体的な結果の差はそれほど大きくありませんが、より長い期間だけでなく、資金管理やシグナル生成のような異なるEAクラスでもテストして試してみれば、決定的な差が出る可能性があります。