Возможности Мастера MQL5, которые вам нужно знать (Часть 11): Числовые стены

Введение

Для нескольких временных рядов можно вывести формулу для следующего значения в последовательности на основе предыдущих значений, которые появлялись в ней. Числовые стены позволяют добиться этого путем предварительного создания "стены чисел" в форме матрицы с помощью так называемого перекрестного правила (cross-rule). При создании этой матрицы основная цель состоит в том, чтобы установить, сходится ли рассматриваемая последовательность. Алгоритм перекрестного правила числовой стены отвечает на этот вопрос, если после нескольких строк применения последующие строки в матрице являются только нулями.

В представленной статье, который демонстрирует эти концепции, степенной ряд Лорана (Laurent Power Series), также известный как формальный ряд Лорана (Formal Laurent Series, FLS), использовался в качестве основы для представления этих последовательностей с их арифметикой в полиномиальном формате при использовании произведений Коши.

В целом, последовательности LFSR удовлетворяют рекуррентному соотношению, так что линейная комбинация последовательных членов всегда равна нулю, как показано в уравнении ниже:

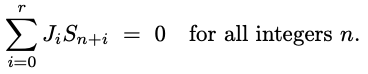
где последовательность Sn - линейный регистр сдвига с рекуррентной или линейной обратной связью (linear feedback shift register, LFSR), а также существует ненулевой вектор |Ji| (отношение) длины r + 1.

Это подразумевает векторное отношение, в котором коэффициенты x (константы - это коэффициенты при x в нулевой степени) составляют его элементы. Этот вектор по определению имеет величину не менее 2.

Чтобы проиллюстрировать это, мы можем рассмотреть пару простых примеров, первым из которых является последовательность кубов чисел. Мы знаем, что числа в кубе нумеруются от нуля вверх, причем каждое значение является кубом его индексной позиции. Если бы мы поместили их в матрицу числовых стен, исходное представление выглядело бы следующим образом:

Нули и единицы, указанные в виде строк над последовательностью, всегда неявны и помогают применить перекрестное правило для распространения всех недостающих значений в матрице. При применении перекрестного правила для любых 5 значений в матрице, которые имеют простой перекрестный формат, произведение внешних вертикальных значений при добавлении к произведению внешних горизонтальных значений всегда должно быть эквивалентно квадрату центрального значения.

Если мы применим это правило к базовой последовательности чисел в кубе, приведенной выше, мы получим матрицу, представленную ниже:

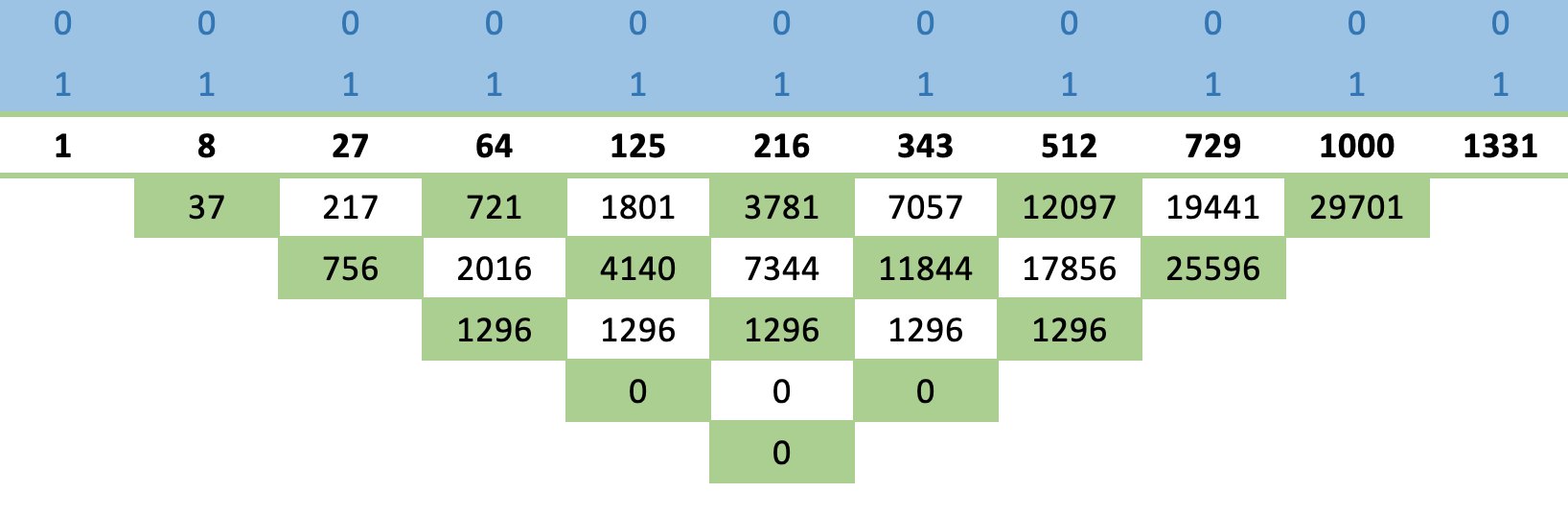
Проиллюстрируем перекрестное правило: число ниже 216, т. е. 3781, получается из разности квадрата 216 и произведения 125 и 343, которое делится на число выше 216, т. е. 1.

Тот факт, что мы можем так быстро получить ряды нулей, свидетельствует о том, что эта последовательность действительно сходится, и можно легко вывести формулу для ее последующих значений.

Но прежде чем мы рассмотрим формулы, давайте рассмотрим еще один пример — ряд Фибоначчи. Если мы применим эту последовательность в нашей матрице и применим правило длинного перекрестия, как указано выше, мы получим строки нулей еще быстрее!

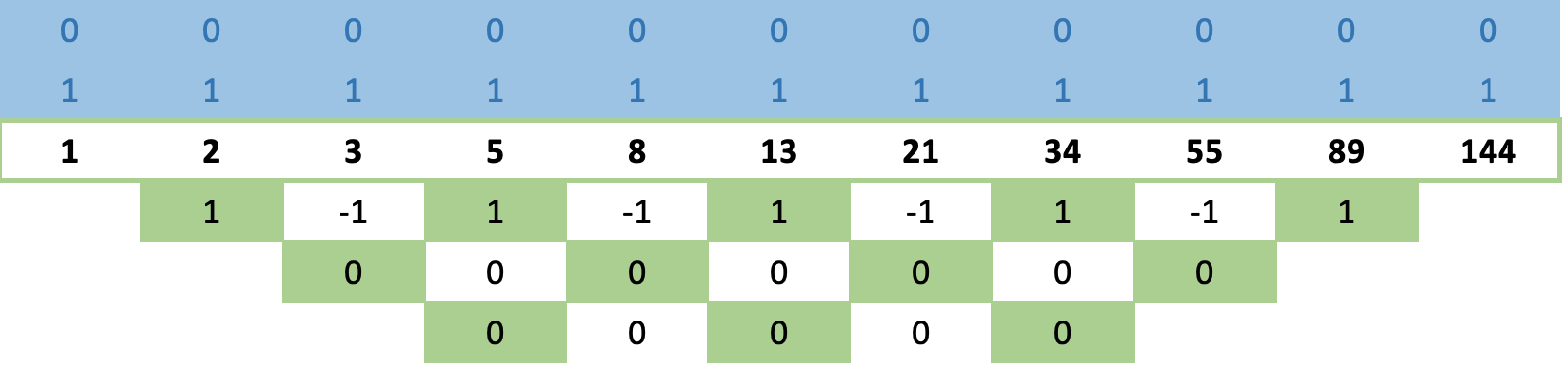
Это, конечно, кажется странным, поскольку можно было бы ожидать, что ряд Фибоначчи будет более сложным, чем числа в кубе, и поэтому для его сходимости потребуется больше времени, но нет! Он сходится ко 2-й строке.

Чтобы получить формулировку сходящегося ряда, такого как два примера, рассмотренные выше, мы должны в матрице числовых стен заменить последовательность формульным форматом, который заменяет любое значение в последовательности тем же значением за вычетом предыдущего значения, умноженного на x. Это выглядит так:

Здесь мы просто применяем наше перекрестное правило, как мы это делали с последовательностями выше, и генерируем значения в полиномиальном формате для следующих строк. Примечательно, что если последовательность сходится, даже с полиномиальными значениями мы все равно можем получить ряды нулей после нескольких применений длинного перекрестного креста. Это показано ниже для последовательности Фибоначчи.

Что же тогда нам делать с этими полиномиальными значениями? Если мы приравняем последнее уравнение к 0 и найдем наибольшую степень x, коэффициенты x, которые у нас останутся на противоположной стороне, будут кратными предыдущим значениям в последовательности, которые в сумме дают следующее значение.

Итак, с помощью последнего уравнения для последовательности Фибоначчи, если мы решим x^2, максимальная степень, которая у нас останется: 1 + x;

Имейте в виду, что 1 представляет собой x^0 и, по сути, является коэффициентом порядкового номера перед порядковым номером, коэффициент которого равен x. Проще говоря, это говорит о том, что в ряду Фибоначчи любое число представляет собой сумму двух предыдущих чисел в последовательности.

Как выглядит полиномиальное уравнение для кубической последовательности? Для сходимости требуется больше строк, как показано выше, и, следовательно, такое уравнение является более сложным.

Как насчет несходящихся рядов? Какие матрицы можно было бы создать в этих сценариях? Для иллюстрации мы могли бы сразу перейти к рассмотрению ценовой последовательности обычной Форекс-пары, например EURUSD. Если мы попытаемся создать матрицу числовых стен (без формулы), чтобы проверить сходимость последовательности дневных цен закрытия EURUSD за первые 5 торговых дней 2024 года, мы получим стену для первых 5 строк, похожую на следующую.

Разумеется, мы не получаем сходимости в пределах первых рядов, на самом деле далеко не ясно, добьемся ли мы когда-нибудь строгой сходимости, хотя числовая стена стремится к нулю, что обнадеживает. Это ослабляет применимость числовых стен для наших целей. Кроме того, предварительная проверка также обычно требует больших вычислительных ресурсов, и именно здесь в игру вступает матрица Тёплица.

Если мы создадим матрицу, в которой все строки каким-то образом связаны друг с другом, посредством чего мы используем скользящее повторение строки последовательности, если последовательность сходится, то определитель этой матрицы будет равен нулю. Это более эффективный в вычислениях способ проверки сходимости, и более того, он "количественно" определяет, насколько вероятно, что последовательность сойдется, на основе величины определителя.

Таким образом, мы могли бы распространить перекрестное правило на формульную матрицу любой последовательности и использовать размер определителя, чтобы "дисконтировать" прогнозируемое значение формулы. Либо мы можем иметь абсолютное пороговое значение определяющего фактора, превышение которого означает, что мы игнорируем результат нашей формулы.

Все это возможные обходные пути для неконвергентных финансовых и других временных рядов, и они, конечно, не идеальны, но давайте посмотрим, какой потенциал у них есть при реализации в MQL5.

Реализация в MQL5

Чтобы проиллюстрировать эти идеи в MQL5, мы реализуем их в экземпляре класса Expert Trailing. В сочетании со встроенным классом Awesome Oscillator мы создадим простой советник. Экземпляр трейлинг-класса будет использовать числовую стену для определения размера величины трейлинг-стопа и уровня тейк-профита.

При реализации на MQL5 мы будем часто использовать встроенные типы данных матрицы и вектора, учитывая их дополнительные функции и минимальные требования к коду. Мы можем предварительно проверить последовательность на сходимость, построив типичную (неформульную) числовую стену и проверив, приходим ли мы к строке нулей, но, учитывая природу и сложность финансовых временных рядов, матрица не будет сходиться. Поэтому нам лучше вычислить формулу для следующего значения в последовательности, полученную из нижней строки последнего столбца после распространения.

Чтобы распространить стену, мы используем векторы для хранения коэффициентов для x. Умножение любых двух таких векторов в процессе решения неизвестной строки будет эквивалентно взаимной корреляции, поскольку результирующие значения векторов будут коэффициентами x, где более высокий индекс указывает на более высокий показатель степени для x. Эта функция встроена. Однако, когда дело доходит до деления, нам необходимо изменить размер двух векторов частных (quotient vectors), чтобы гарантировать, что они совпадают с любой разницей в размере, просто подразумевая, что они не совпадают по экспонентам x.

При определении того, насколько корректировать TP и SL открытой позиции, нашей входной последовательностью для нашей числовой стены будут значения индикатора скользящей средней. Можно использовать любой индикатор, но для настройки трейлинг-стопа лучше подойдут полосы Боллинджера или конверты.

Векторы MQL5 легко копируют и загружают значения индикатора после определения хэндла. Посмотрим на типичный код проверки трейлинг-стопа (может использоваться как для длинных, так и для коротких позиций)

//+------------------------------------------------------------------+
//| Checking trailing stop and/or profit for long position.          |
//+------------------------------------------------------------------+
bool CTrailingLFSR::CheckTrailingStopLong(CPositionInfo *position, double &sl, double &tp)
{
//--- check

...

//---
   vector _t, _p;
   _p.Init(2);
   _t.CopyIndicatorBuffer(m_ma.Handle(), 0, 0, 2);
   double _s = 0.0;
   for(int i = 1; i >= 0; i--)
   {  _s = 0.0;
      _p[i] = GetOutput(i, _s);
   }
   double _o = SetOutput(_t, _p);
//---
  
...

}

Мы видим, что процесс принятия решений развивается вокруг двух функций - GetOutput и SetOutput. GetOutput является основной, поскольку она строит числовую стену и выдает полиномиальные коэффициенты для уравнения, которое находит следующее значение в последовательности. Ниже представлен листинг GetOutput:

//+------------------------------------------------------------------+
//| LFSR Output.                                                     |
//+------------------------------------------------------------------+
double CTrailingLFSR::GetOutput(int Index, double &Solution)
{  double _output = 0.0;
   vector _v;
   _v.CopyIndicatorBuffer(m_ma.Handle(), 0, Index, m_length);
   Solution = Solvability(_v);
   _v.Resize(m_length + 1);
   for(int i = 2; i < 2 + m_length; i++)
   {  for(int ii = 2; ii < 2 + m_length; ii++)
      {  if(i == 2)
         {  vector _vi;
            _vi.Init(1);
            _vi[0] = _v[m_length - ii + 1];
            m_numberwall.row[i].column[ii] = _vi;
         }
         else if(i == 3)
         {  vector _vi;
            _vi.Init(2);
            _vi[0] = m_numberwall.row[i - 1].column[ii][0];
            _vi[1] = -1.0 * m_numberwall.row[i - 1].column[ii - 1][0];
            m_numberwall.row[i].column[ii] = _vi;
         }
         else if(ii < m_length + 1)
         {  m_numberwall.row[i].column[ii] = Get(m_numberwall.row[i - 2].column[ii], m_numberwall.row[i - 1].column[ii - 1], m_numberwall.row[i - 1].column[ii + 1], m_numberwall.row[i - 1].column[ii]);
         }
      }
   }
   vector _u = Set();
   vector _x;
   _x.CopyIndicatorBuffer(m_ma.Handle(), 0, Index, m_length);
   _u.Resize(fmax(_u.Size(),_x.Size()));
   _x.Resize(fmax(_u.Size(),_x.Size()));
   vector _y = _u * _x;
   _output = _y.Sum();
   return(_output);
}

Наш общий список выше в основном состоит из 2 частей. Построим стену, чтобы получить коэффициенты уравнения, и используем уравнение с текущими показаниями последовательности для проецирования. В первой части функция get выполняет ключевое умножение сгенерированных уравнений и решает уравнение для следующей строки. Код приведен ниже:

//+------------------------------------------------------------------+
//| Get known Value                                                  |
//+------------------------------------------------------------------+
vector CTrailingLFSR::Get(vector &Top, vector &Left, vector &Right, vector &Center)
{  vector _cc, _lr, _cc_lr, _i_top;
   _cc = Center.Correlate(Center, VECTOR_CONVOLVE_FULL);
   _lr = Left.Correlate(Right, VECTOR_CONVOLVE_FULL);
   ulong _size = fmax(_cc.Size(), _lr.Size());
   _cc_lr.Init(_size);
   _cc.Resize(_size);
   _lr.Resize(_size);
   _cc_lr = _cc - _lr;
   _i_top = 1.0 / Top;
   vector _bottom = _cc_lr.Correlate(_i_top, VECTOR_CONVOLVE_FULL);
   return(_bottom);
}

Аналогично, функция set использует нижний вектор, который имеет последние распространенные коэффициенты для решения следующего значения последовательности. Код представлен ниже:

//+------------------------------------------------------------------+
//| Set Unknown Value                                                |
//+------------------------------------------------------------------+
vector CTrailingLFSR::Set()
{  vector _formula = m_numberwall.row[m_length + 1].column[m_length + 1];
   vector _right;
   _right.Copy(_formula);
   _right.Resize(ulong(fmax(_formula.Size() - 1, 1.0)));
   double _solver = -1.0 * _formula[int(_formula.Size() - 1)];
   if(_solver != 0.0)
   {  _right /= _solver;
   }
   return(_right);
}

Теперь в функции проверки трейлинга мы дважды вызываем функцию GetOutput, потому что нам нужно получить не только текущий прогноз, но и предыдущие, чтобы помочь в нормализации наших выходных данных. Поскольку большинство последовательностей и особенно финансовых временных рядов не сходятся, необработанный прогноз выходных данных обязательно будет очень чуждым по значению по отношению к значениям входной последовательности. Получение очень больших двойных значений, в несколько раз превышающих типичные значения последовательности, или даже отрицательного значения, когда явно ожидаются только положительные значения, не является редкостью.

Итак, при нормализации мы используем очень краткую и простую функцию SetOutput, которая представлена ниже:

//+------------------------------------------------------------------+
//| Normalising Output to match Indicator Value                      |
//+------------------------------------------------------------------+
double CTrailingLFSR::SetOutput(vector &True, vector &Predicted)
{  return(True[1] - ((True[0] - True[1]) * ((Predicted[0] - Predicted[1]) / fmax(m_symbol.Point(), fabs(Predicted[0]) + fabs(Predicted[1])))));
}

Мы просто нормализуем прогнозируемое значение, чтобы его величина находилась в пределах диапазона значений последовательности, и мы достигаем этого, используя изменения последовательности как для прогнозируемых, так и для истинных значений.

Кроме того, в типичной проверке трейлинг-стопа мы измеряем разрешимость внутри функции GetOutput в ее начале. Эта метрика используется в качестве порогового фильтра, чтобы определить, следует ли нам игнорировать прогноз, поскольку более высокие значения определителя (то, что мы называем разрешимостью) указывают на более высокую неспособность сходиться. Достаточно сказать, что даже матрица с маленьким определителем не сходится, однако мы предполагаем, что она сойдется с большей вероятностью, если у нее больше строк для построения числовой стены, чем у матрицы с более высоким определителем.

Итак, мы получаем экземпляр завершающего класса, прикрепленный в конце статьи, и хотя предварительное тестирование действительно указывает на то, что он требует больших вычислительных ресурсов, на мой взгляд, эту идею можно было бы улучшить и даже объединить с различными стратегиями для развития более надежной торговой системы.

Прилагаемый к трейлинг-классу MQL5-код можно легко собрать с помощью Мастера для создания различных советников в зависимости от выбора класса сигнала и управления капиталом. Как обычно, вся информация есть в статье.

Дополнительные примечания

В числовых стенах, рассмотренных до сих пор в общем коде и на иллюстрациях выше, использовались целые цены, не включающие нулей. Если мы, например, хотим спрогнозировать изменения в цене символа, а не только в исходной цене, в идеале мы должны иметь входной ряд изменений цен. Как только мы начинаем иметь дело с изменениями, а не с абсолютной ценой, мы не только сталкиваемся с отрицательными значениями, но также можем и довольно часто должны иметь несколько нулей.

Поначалу нули могут показаться безобидными, но когда мы строим числовые стены, они создают проблемы при определении значений в следующей строке. Рассмотрим следующий пример:

Используя наше основное перекрестное правило при поиске неизвестного значения, мы сталкиваемся с проблемой, поскольку одно известное значение равно нулю, и поэтому при умножении на наше неизвестное мы остаемся с пустыми руками. Чтобы обойти эту проблему, пригодится длинное перекрестное правило. Расширим наше предыдущее изображение:

Мы можем с некоторой уверенностью обойти ноль над текущей строкой, применив приведенную ниже формулу:

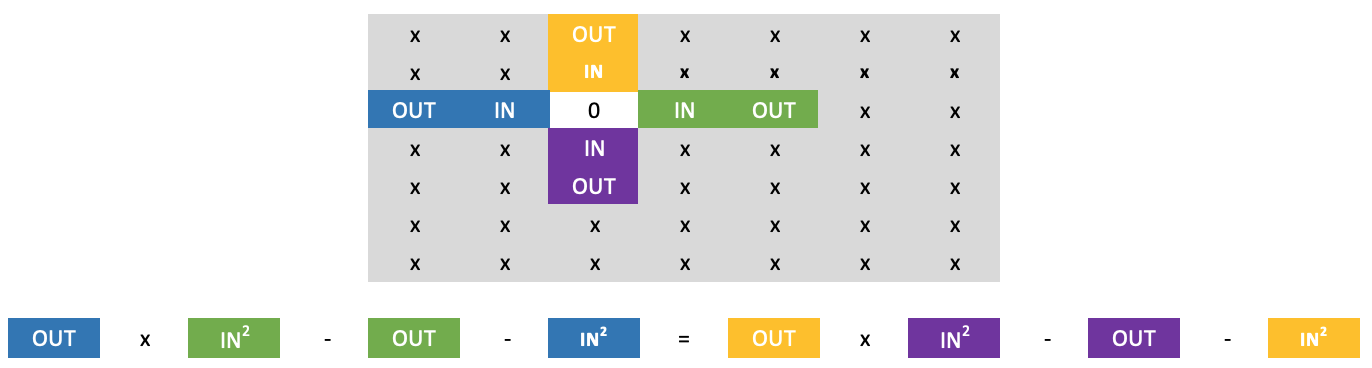
Я не зря сказал "с некоторой уверенностью", потому что числовые стены обладают уникальным свойством, когда дело доходит до включения нулей. В любом числе, если есть нули, то они встречаются в единственном числе или в квадрате, то есть могут быть 1 х 1 (единственное число), или 2 х 2, или 3 х 3 и так далее. По сути, это означает, что если мы встретим ноль между двумя числами в любой строке, то число под ним не будет нулем. Однако, когда мы применяем длинное перекрестное правило, у нас есть дополнительное неизвестное в виде самого низкого внешнего значения в стене. Однако это не проблема, поскольку оно умножается на наш известный ноль, что позволяет нам решить уравнение без необходимости ввода его значения.

Проблема, решаемая правилом длинного перекрестия, применима строго к сходящимся стенам чисел, и, как мы видели на иллюстрациях выше, это редко случается с финансовыми временными рядами. Итак, следует ли это учитывать? Это следует определять последовательно, в зависимости от временного ряда, на который ориентирована торговая система. Некоторые могли бы применить эту особенность даже к финансовым рядам, если "разрешимость" или определитель матрицы Тёплица достигает необходимого порога, другие могли бы прекратить построение стены и работать с векторными коэффициентами, которые у них есть в этой точке (когда они достигают нулей) при построении полиномиального уравнения прогноза. Возможно есть и другие варианты, и выбор будет зависеть от конкретного трейдера.

Правило длинного перекрестия является довольно гибким, если при распространении числовой стены встречается только один ноль, однако если нули находятся в большем квадрате (поскольку нули всегда занимают формат nxn в стене), тогда оно не будет иметь большого смысла. В этих случаях часто применяют правило подковы (horse shoe rule). Согласно этому правилу, если у нас есть большой квадрат нулей, последовательности, граничащие с этим квадратом, масштабируются с определенным коэффициентом.

Эти четыре фактора, по одному на каждую сторону квадрата, обладают уникальным свойством, которое можно показать формулой ниже:

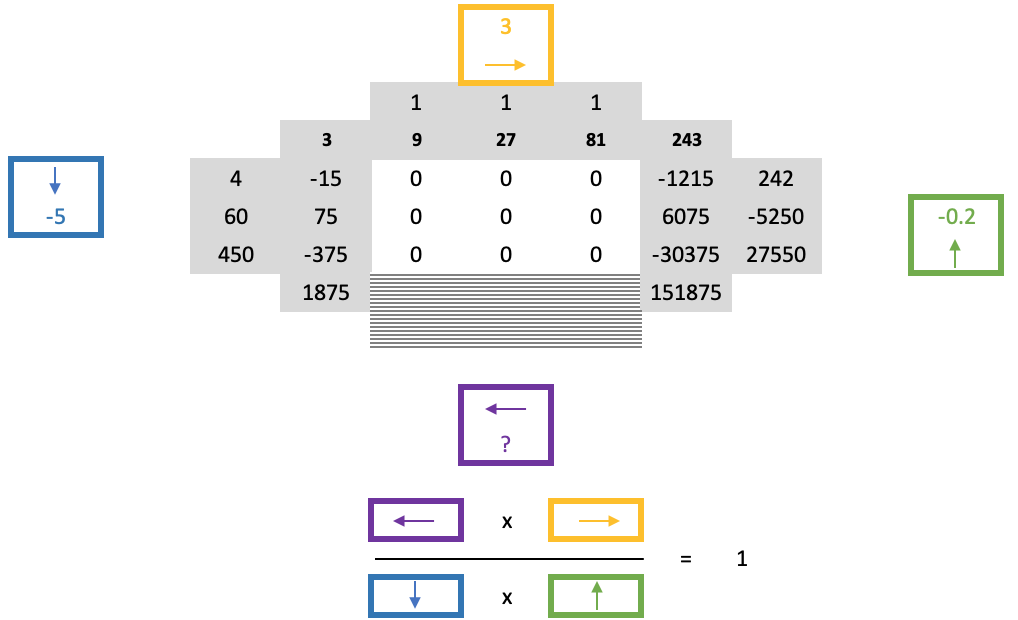
Таким образом, когда встречается большая порция нулей, верхние и боковые числа, граничащие с этими нулями, уже будут известны, и поскольку мы знаем ширину квадратов нулей, мы, по сути, знаем их высоту, то есть мы знаем, где оценивать неизвестные граничные значения. Из приведенного выше уравнения можно получить непосредственные граничные значения, приведенные ниже, путем определения нижнего масштабного коэффициента и вычисления его чисел, обычно слева направо.

Однако продвижение от этой точки с помощью обычного перекрестного правила по-прежнему будет затруднительно, поскольку нули в квадрате затрудняют его применение при определении строки ниже только что решенной граничной строки. Решение этой проблемы представляет собой "вторую часть" правила подковы и основано на следующей довольно длинной формуле:

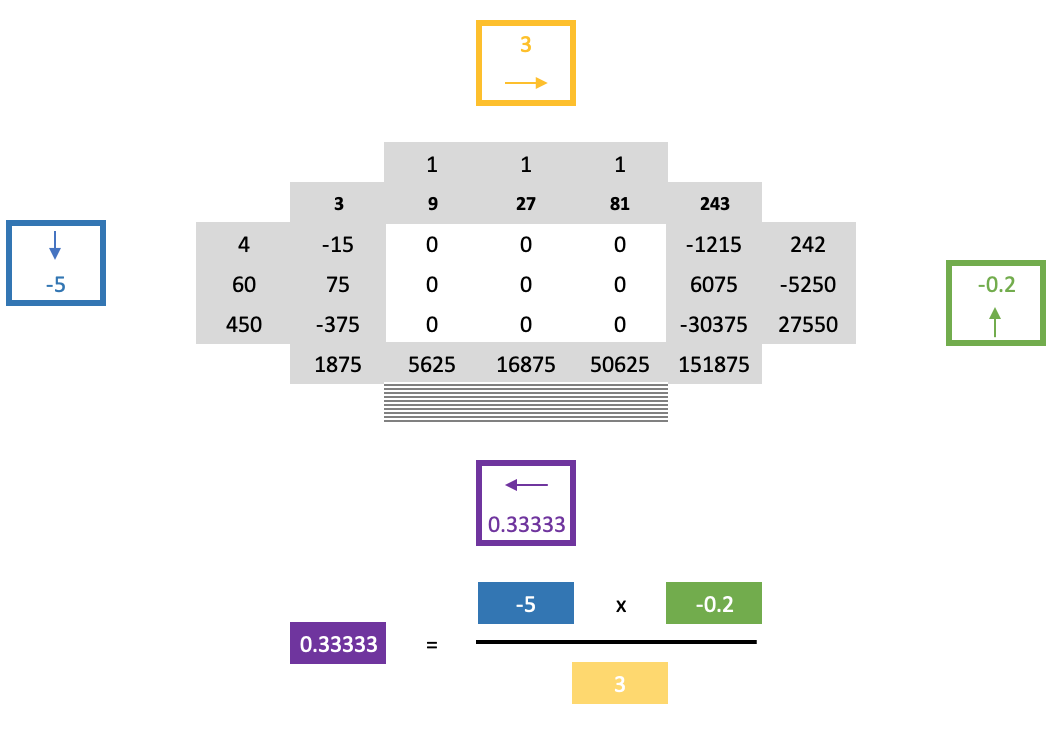
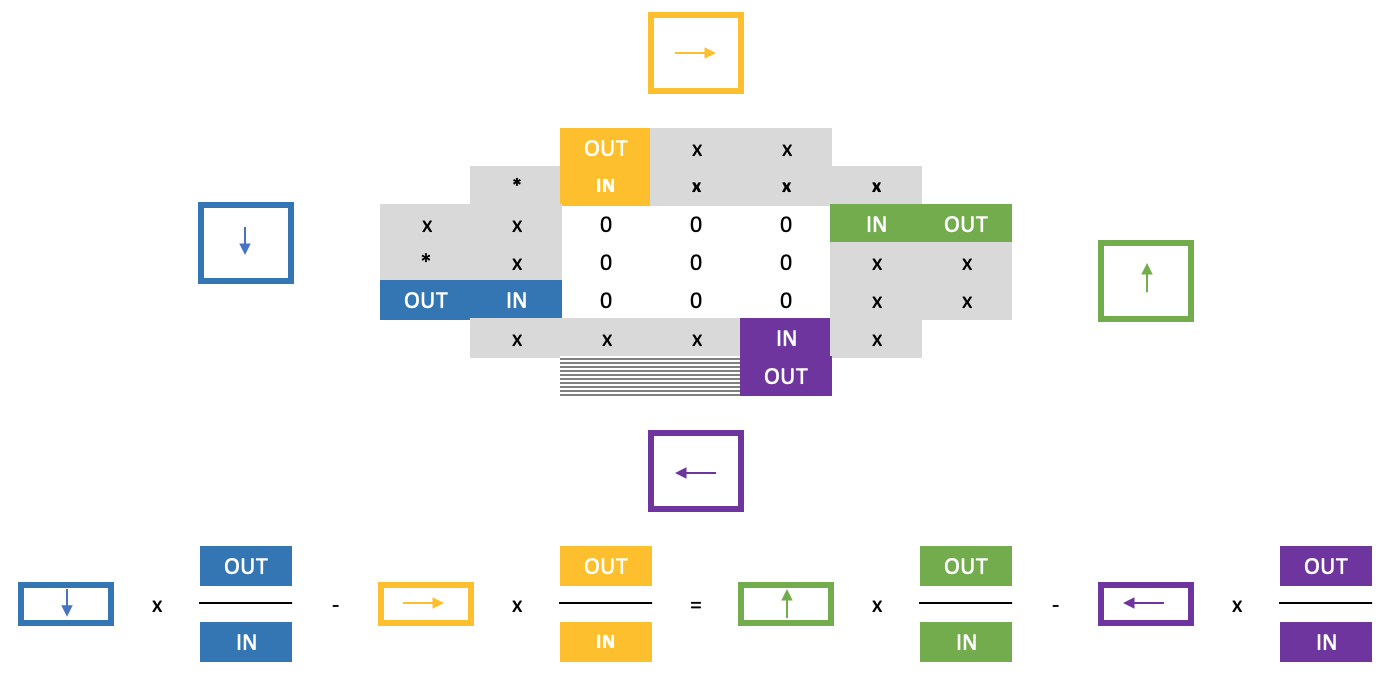
В уже упомянутой статье по этой теме, помимо освещения многих из изложенных здесь моментов, также упоминается гипотеза о пагоде (pagoda conjecture). В своей простейшей форме это суммирование группы наборов чисел, каждый из которых содержит набор одинакового размера, так что если каждый из включенных наборов рассматривать как многоугольник, каждая вершина которого представляет одно из чисел в его наборе, то эти многоугольники можно склеить вместе, чтобы сформировать более крупную комплексную решетку при условии, что в любой связанной вершине все вершины многоугольника имеют одинаковое количество. Это, конечно, происходит при условии, что каждый номер вершин любого многоугольника уникален в этом наборе.

Во-первых, это имеет интересные последствия для наборов из трех чисел, которые образуют пагоду, поскольку оказывается, что когда числа каждого набора расположены в последовательности, на стене с распространяемыми числами можно наблюдать очень интересные повторяющиеся узоры, и в статье представлены некоторые из этих изображений.

Однако для торговых целей этот "новый" подход к классификации действительно представляет собой еще один способ рассмотрения финансовых временных рядов, который требует отдельной статьи. Достаточно сказать, что мы могли бы обобщить несколько способов применения последовательностей пагод в наших целях.

При использовании гипотезы было бы разумно придерживаться треугольных пагод, а не форм более высоких измерений, поскольку они, как правило, открывают больше возможностей и, следовательно, усложняют способы соединения. Нашей задачей было бы, во-первых, нормализовать наши финансовые ряды, чтобы учесть повторение значений, что является требованием при определении пагод. Степень, в которой выполняется эта нормализация, - это то, что необходимо будет изучить, поскольку разные итерации обязательно дадут разные результаты.

Во-вторых, как только мы освоимся с определенным порогом нормализации, нам нужно будет установить количество треугольников в нашей пагоде, то есть размер группы. Имейте в виду, что по мере увеличения размера группы потребность в том, чтобы все треугольники были напрямую связаны, уменьшается. В пагоде из трех треугольников все треугольники связаны, но по мере увеличения этого числа для любого треугольника наибольшее количество связей, которые он может иметь, равно 3. Это означает, что, скажем, в пагоде с шестью треугольниками, только нижний центральный треугольник имеет связи во всех вершинах, а все остальные имеют связи только в двух вершинах.

Эта возрастающая сложность соединения треугольников с увеличением размера группы может указывать на то, что определение оптимального размера группы должно выполняться одновременно с установкой порога нормализации, поскольку последний дает нам повторяющиеся данные, которые являются ключевыми в установлении связей между треугольниками.

Заключение

Мы рассмотрели стены чисел - числовую сетку, сгенерированную на основе исследуемого временного ряда последовательности, и увидели, как ее можно использовать в прогнозировании, правильно установив TP и SL открытой позиции в коде. Кроме того, мы рассмотрели связанную с этим гипотезу о пагодах, рассмотренную в статье о числовых стенах, и выдвинули некоторые идеи о том, как они могут стать еще одним средством классификации финансовых временных рядов.

Эпилог

Ниже приведены сравнительные тесты советников, собранных Мастером. Они оба используют сигналы Awesome Oscillator в принципе имеют одинаковые входные настройки, как показано ниже:

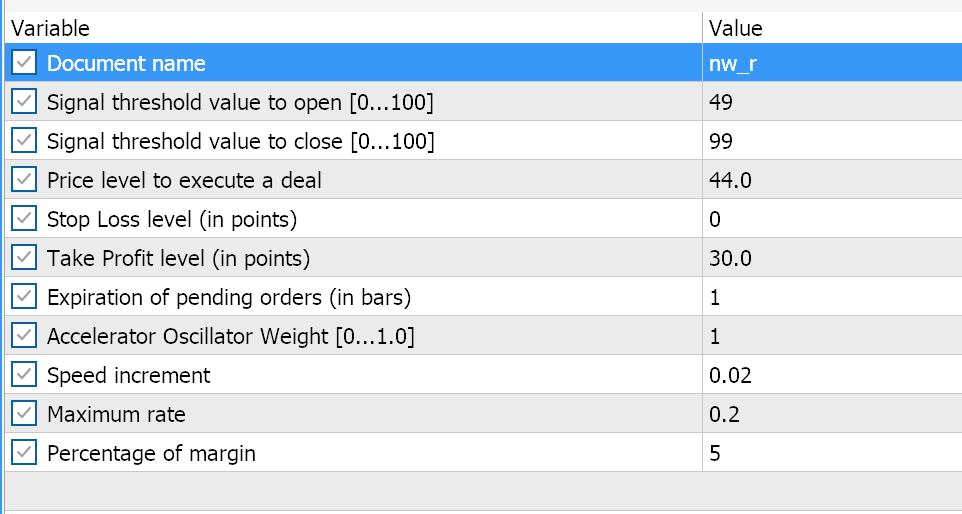
Разница между ними заключается в том, что один советник использует Parabolic SAR для отслеживания и закрытия открытых позиций, а другой использует алгоритм числовой стены, представленный в этой статье. Однако их отчеты при тестировании на EURUSD за последний год на часовом таймфрейме, несмотря на один и тот же сигнал, различаются. Первым идет отчет советника на основе Parabolic SAR.

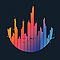
Ниже представлен отсчет советника на основе числовой стены:

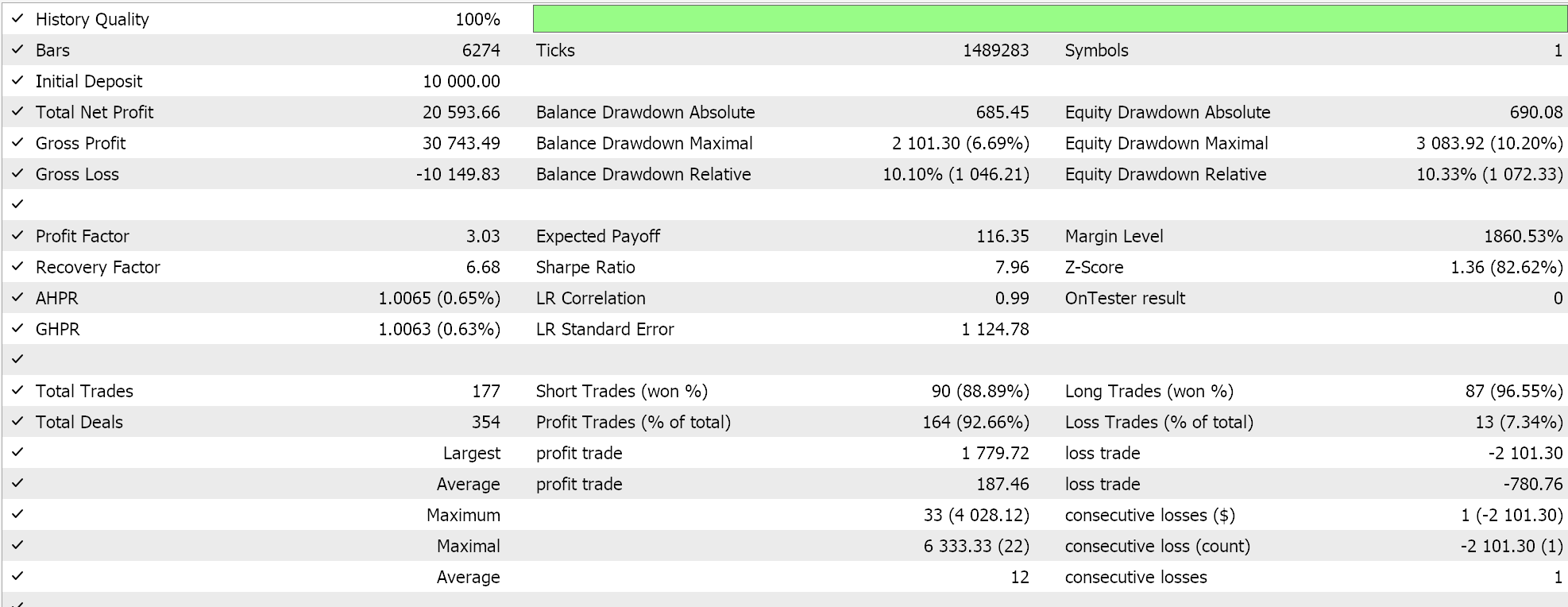
Общая разница в результатах незначительна, но может иметь решающее значение, если тестироваться не только на более длительных периодах, но и в различных классах советников, таких как управление капиталом или даже генерация сигналов.