Funcionalidades do assistente MQL5 que você precisa conhecer (Parte 11): Paredes numéricas

Introdução

Para várias séries temporais, é possível derivar uma fórmula para o próximo valor na sequência com base nos valores anteriores que apareceram nela. As paredes numéricas permitem alcançar isso criando previamente uma "parede de números" na forma de uma matriz usando a chamada regra cruzada (cross-rule). Ao criar esta matriz, o objetivo principal é determinar se a sequência em questão converge. O algoritmo da regra cruzada da parede numérica responde a esta pergunta se, após várias linhas de aplicação, as linhas subsequentes na matriz consistirem apenas em zeros.

No artigo apresentado, que demonstra esses conceitos, a série de Laurent (Laurent Power Series), também conhecida como série formal de Laurent (Formal Laurent Series, FLS), foi usada como base para representar essas sequências com sua aritmética em formato polinomial usando produtos de Cauchy.

No geral, sequências LFSR satisfazem uma relação recorrente, de forma que a combinação linear dos termos subsequentes é sempre igual a zero, conforme mostrado na equação abaixo:

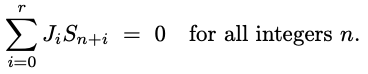
onde a sequência Sn é um registrador de deslocamento com feedback linear (linear feedback shift register, LFSR), e existe um vetor não nulo |Ji| (relação) de comprimento r + 1.

Isso implica uma relação vetorial, na qual os coeficientes x (as constantes são os coeficientes em x na potência zero) compõem seus elementos. Por definição, este vetor tem magnitude de pelo menos 2.

Para ilustrar isso, podemos considerar alguns exemplos simples, sendo o primeiro uma sequência de cubos de números. Sabemos que os números em cubo são numerados de zero para cima, sendo que cada valor é o cubo de sua posição de índice. Se os colocássemos em uma matriz de paredes numéricas, a representação inicial seria a seguinte:

Zeros e uns, indicados como linhas acima da sequência, são sempre implícitos e ajudam a aplicar a regra cruzada para preencher todos os valores ausentes na matriz. Ao aplicar a regra cruzada para quaisquer 5 valores na matriz que tenham um formato cruzado simples, o produto dos valores verticais externos ao ser adicionado ao produto dos valores horizontais externos deve ser sempre equivalente ao quadrado do valor central.

Se aplicarmos essa regra à sequência base de números em cubo mencionada acima, obteremos a matriz apresentada abaixo:

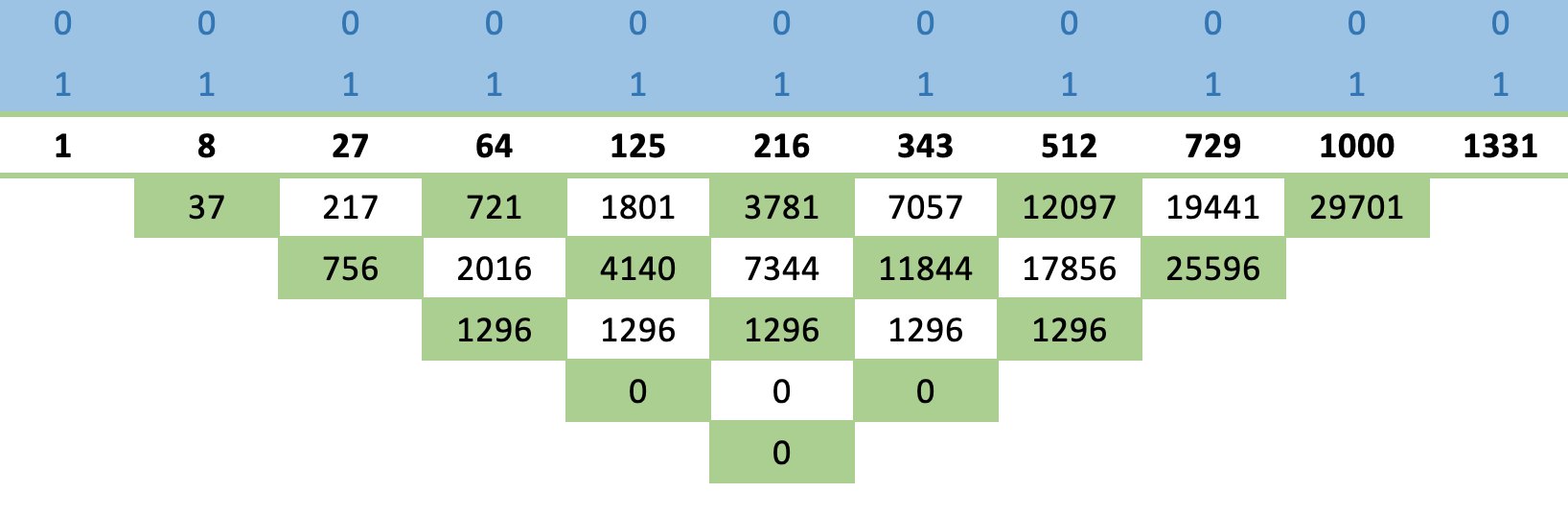
Para ilustrar a regra cruzada: o número abaixo de 216, ou seja, 3781, é obtido pela diferença entre o quadrado de 216 e o produto de 125 e 343, que é dividido pelo número acima de 216, ou seja, 1.

O fato de podermos obter rapidamente linhas de zeros indica que essa sequência realmente converge, e podemos facilmente derivar a fórmula para seus valores subsequentes.

Mas antes de considerarmos as fórmulas, vamos ver outro exemplo, a série de Fibonacci. Se aplicarmos essa sequência na nossa matriz e aplicarmos a regra do cruzamento longo, como indicado acima, obteremos linhas de zeros ainda mais rapidamente!

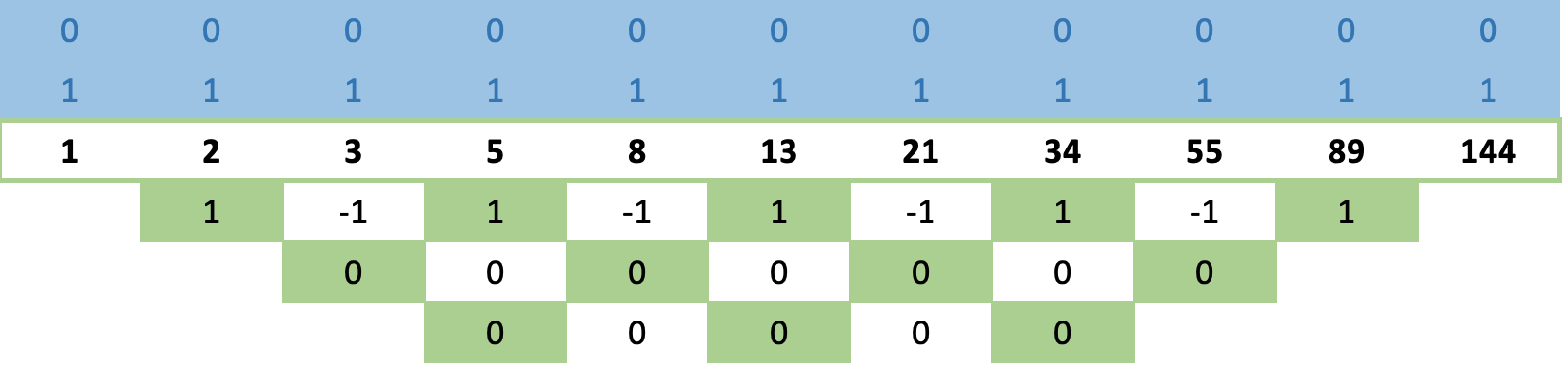
Isso parece estranho, pois seria esperado que a série de Fibonacci fosse mais complexa do que os números em cubo e, portanto, demorasse mais para convergir, mas não! Ela converge na 2ª linha.

Para obter a formulação de uma série convergente, como os dois exemplos mencionados acima, devemos substituir a sequência na matriz de paredes numéricas por um formato de fórmula, que substitui qualquer valor na sequência pelo mesmo valor menos o valor anterior multiplicado por x. Isso se apresenta assim:

Aqui, simplesmente aplicamos nossa regra cruzada, como fizemos com as sequências acima, e geramos valores em formato polinomial para as linhas subsequentes. Notavelmente, se a sequência convergir, mesmo com valores polinomiais, ainda poderemos obter linhas de zeros após algumas aplicações da cruz longa. Isso é mostrado abaixo para a sequência de Fibonacci.

O que fazemos então com esses valores polinomiais? Se igualarmos a última equação a 0 e encontrarmos o maior grau de x, os coeficientes de x que restarem do outro lado serão múltiplos dos valores anteriores na sequência, que somam o valor seguinte.

Assim, com a última equação para a sequência de Fibonacci, se resolvermos x^2, o grau máximo que restar é: 1 + x;

Lembre-se de que 1 representa x^0 e, essencialmente, é o coeficiente do número ordinal antes do número ordinal, cujo coeficiente é x. Simplificando, isso indica que na sequência de Fibonacci qualquer número é a soma dos dois números anteriores na sequência.

Como seria a equação polinomial para a sequência cúbica? Para a convergência, são necessárias mais linhas, como mostrado acima, e, portanto, tal equação é mais complexa.

E as séries não convergentes? Que matrizes poderiam ser criadas nesses cenários? Para ilustrar, poderíamos considerar a sequência de preços de um par de Forex comum, como EURUSD. Se tentarmos criar uma matriz de paredes numéricas (sem fórmula) para verificar a convergência da sequência de preços de fechamento diários do EURUSD nos primeiros 5 dias de negociação de 2024, obteremos uma parede para as primeiras 5 linhas, semelhante ao seguinte.

Claro, não obtemos convergência nas primeiras linhas, na verdade, não está claro se conseguiremos uma convergência estrita, embora a parede numérica tenda a zero, o que é encorajador. Isso enfraquece a aplicabilidade das paredes numéricas para nossos objetivos. Além disso, a verificação preliminar geralmente também exige muitos recursos computacionais, e é aqui que entra a matriz de Toeplitz.

Se criarmos uma matriz onde todas as linhas estejam de alguma forma conectadas entre si, usando uma repetição deslizante da linha da sequência, se a sequência convergir, o determinante dessa matriz será igual a zero. Essa é uma maneira mais eficiente de verificar a convergência em termos computacionais e, além disso, ela "quantifica" a probabilidade de a sequência convergir, com base na magnitude do determinante.

Assim, poderíamos aplicar a regra cruzada na matriz de fórmula de qualquer sequência e usar o tamanho do determinante para "descontar" o valor previsto da fórmula. Alternativamente, podemos ter um valor limiar absoluto do fator determinante, excedendo o qual significa que ignoramos o resultado da nossa fórmula.

Esses são possíveis caminhos alternativos para séries temporais financeiras e outras não convergentes, e eles certamente não são ideais, mas vamos ver que potencial eles têm na implementação no MQL5.

Implementação no MQL5

Para ilustrar essas ideias no MQL5, vamos implementá-las em uma instância da classe Expert Trailing. Em combinação com a classe embutida Awesome Oscillator, criaremos um EA simples. A instância da classe trailing usará a parede numérica para determinar o tamanho do trailing stop e o nível de take profit.

Ao implementar no MQL5, utilizaremos frequentemente os tipos de dados embutidos de matriz e vetor, considerando suas funcionalidades adicionais e requisitos mínimos de código. Podemos verificar previamente a sequência quanto à convergência, construindo uma parede numérica típica (não formal) e verificando se chegamos a uma linha de zeros, mas, considerando a natureza e a complexidade das séries temporais financeiras, a matriz não convergirá. Portanto, é melhor calcular a fórmula para o próximo valor na sequência, obtida da última linha da última coluna após a propagação.

Para propagar a parede, usaremos vetores para armazenar os coeficientes de x. A multiplicação de quaisquer dois desses vetores no processo de solução da linha desconhecida será equivalente à correlação mútua, pois os valores resultantes dos vetores serão os coeficientes de x, onde um índice mais alto indica um expoente mais alto para x. Essa função está embutida. No entanto, quando se trata de divisão, precisamos redimensionar os dois vetores quocientes para garantir que coincidam com qualquer diferença de tamanho, apenas implicando que eles não correspondem aos expoentes de x.

Ao determinar o quanto ajustar o TP e o SL da posição aberta, nossa sequência de entrada para nossa parede numérica será os valores do indicador de média móvel. Qualquer indicador pode ser usado, mas para ajustar o trailing stop, bandas de Bollinger ou envelopes são mais adequados.

Os vetores MQL5 copiam e carregam facilmente os valores do indicador após a definição do handle. Vamos ver um código típico de verificação do trailing stop (que pode ser usado tanto para posições longas quanto curtas).

//+------------------------------------------------------------------+
//| Checking trailing stop and/or profit for long position.          |
//+------------------------------------------------------------------+
bool CTrailingLFSR::CheckTrailingStopLong(CPositionInfo *position, double &sl, double &tp)
{
//--- check

...

//---
   vector _t, _p;
   _p.Init(2);
   _t.CopyIndicatorBuffer(m_ma.Handle(), 0, 0, 2);
   double _s = 0.0;
   for(int i = 1; i >= 0; i--)
   {  _s = 0.0;
      _p[i] = GetOutput(i, _s);
   }
   double _o = SetOutput(_t, _p);
//---
  
...

}

Vemos que o processo de tomada de decisão se desenvolve em torno de duas funções - GetOutput e SetOutput. GetOutput é a principal, pois constrói a parede numérica e fornece os coeficientes polinomiais para a equação que encontra o próximo valor na sequência. Abaixo está o código da GetOutput:

//+------------------------------------------------------------------+
//| LFSR Output.                                                     |
//+------------------------------------------------------------------+
double CTrailingLFSR::GetOutput(int Index, double &Solution)
{  double _output = 0.0;
   vector _v;
   _v.CopyIndicatorBuffer(m_ma.Handle(), 0, Index, m_length);
   Solution = Solvability(_v);
   _v.Resize(m_length + 1);
   for(int i = 2; i < 2 + m_length; i++)
   {  for(int ii = 2; ii < 2 + m_length; ii++)
      {  if(i == 2)
         {  vector _vi;
            _vi.Init(1);
            _vi[0] = _v[m_length - ii + 1];
            m_numberwall.row[i].column[ii] = _vi;
         }
         else if(i == 3)
         {  vector _vi;
            _vi.Init(2);
            _vi[0] = m_numberwall.row[i - 1].column[ii][0];
            _vi[1] = -1.0 * m_numberwall.row[i - 1].column[ii - 1][0];
            m_numberwall.row[i].column[ii] = _vi;
         }
         else if(ii < m_length + 1)
         {  m_numberwall.row[i].column[ii] = Get(m_numberwall.row[i - 2].column[ii], m_numberwall.row[i - 1].column[ii - 1], m_numberwall.row[i - 1].column[ii + 1], m_numberwall.row[i - 1].column[ii]);
         }
      }
   }
   vector _u = Set();
   vector _x;
   _x.CopyIndicatorBuffer(m_ma.Handle(), 0, Index, m_length);
   _u.Resize(fmax(_u.Size(),_x.Size()));
   _x.Resize(fmax(_u.Size(),_x.Size()));
   vector _y = _u * _x;
   _output = _y.Sum();
   return(_output);
}

Nossa lista geral acima consiste basicamente de 2 partes. Construímos a parede para obter os coeficientes da equação e usamos a equação com as leituras atuais da sequência para projeção. Na primeira parte, a função get realiza a multiplicação chave das equações geradas e resolve a equação para a próxima linha. O código está abaixo:

//+------------------------------------------------------------------+
//| Get known Value                                                  |
//+------------------------------------------------------------------+
vector CTrailingLFSR::Get(vector &Top, vector &Left, vector &Right, vector &Center)
{  vector _cc, _lr, _cc_lr, _i_top;
   _cc = Center.Correlate(Center, VECTOR_CONVOLVE_FULL);
   _lr = Left.Correlate(Right, VECTOR_CONVOLVE_FULL);
   ulong _size = fmax(_cc.Size(), _lr.Size());
   _cc_lr.Init(_size);
   _cc.Resize(_size);
   _lr.Resize(_size);
   _cc_lr = _cc - _lr;
   _i_top = 1.0 / Top;
   vector _bottom = _cc_lr.Correlate(_i_top, VECTOR_CONVOLVE_FULL);
   return(_bottom);
}

Da mesma forma, a função set utiliza o vetor inferior, que possui os coeficientes propagados mais recentes para resolver o próximo valor da sequência. O código está abaixo:

//+------------------------------------------------------------------+
//| Set Unknown Value                                                |
//+------------------------------------------------------------------+
vector CTrailingLFSR::Set()
{  vector _formula = m_numberwall.row[m_length + 1].column[m_length + 1];
   vector _right;
   _right.Copy(_formula);
   _right.Resize(ulong(fmax(_formula.Size() - 1, 1.0)));
   double _solver = -1.0 * _formula[int(_formula.Size() - 1)];
   if(_solver != 0.0)
   {  _right /= _solver;
   }
   return(_right);
}

Agora, na função de verificação do trailing, chamamos a função GetOutput duas vezes, porque precisamos obter não apenas a previsão atual, mas também as anteriores para ajudar na normalização de nossos dados de saída. Como a maioria das sequências, e especialmente as séries temporais financeiras, não convergem, a previsão bruta dos dados de saída será necessariamente muito diferente dos valores da sequência de entrada. Obter valores duplos muito grandes, várias vezes maiores que os valores típicos da sequência, ou mesmo valores negativos quando claramente são esperados apenas valores positivos, não é raro.

Portanto, ao normalizar, usamos uma função muito breve e simples chamada SetOutput, que está abaixo:

//+------------------------------------------------------------------+
//| Normalising Output to match Indicator Value                      |
//+------------------------------------------------------------------+
double CTrailingLFSR::SetOutput(vector &True, vector &Predicted)
{  return(True[1] - ((True[0] - True[1]) * ((Predicted[0] - Predicted[1]) / fmax(m_symbol.Point(), fabs(Predicted[0]) + fabs(Predicted[1])))));
}

Nós simplesmente normalizamos o valor previsto para que sua magnitude esteja dentro da faixa dos valores da sequência, e alcançamos isso utilizando as mudanças na sequência tanto para os valores previstos quanto para os reais.

Além disso, na verificação típica do trailing stop, medimos a resolubilidade dentro da função GetOutput em seu início. Essa métrica é usada como um filtro de limiar para determinar se devemos ignorar a previsão, pois valores mais altos do determinante (o que chamamos de resolubilidade) indicam uma maior incapacidade de convergir. Basta dizer que mesmo uma matriz com um determinante pequeno não converge, no entanto, presumimos que ela terá mais probabilidade de convergir se tiver mais linhas para construir a parede numérica do que uma matriz com um determinante mais alto.

Então, obtemos uma instância da classe final, anexada ao final do artigo, e embora os testes preliminares realmente indiquem que ela exige muitos recursos computacionais, na minha opinião, essa ideia poderia ser aprimorada e até mesmo combinada com várias estratégias para desenvolver um sistema de negociação mais robusto.

O código MQL5 anexado à classe trailing pode ser facilmente montado usando o Assistente para criar vários EAs, dependendo da escolha da classe de sinal e da gestão de capital. Como de costume, todas as informações estão no artigo.

Notas adicionais

Nas paredes numéricas consideradas até agora no código geral e nas ilustrações acima, foram usados preços inteiros, sem incluir zeros. Se quisermos, por exemplo, prever mudanças no preço do símbolo, e não apenas no preço original, idealmente deveríamos ter uma série de entradas com mudanças de preço. Assim que começamos a lidar com mudanças, em vez do preço absoluto, não só nos deparamos com valores negativos, mas também podemos e frequentemente devemos ter vários zeros.

A princípio, os zeros podem parecer inofensivos, mas quando construímos paredes numéricas, eles criam problemas na determinação dos valores na linha seguinte. Considere o exemplo a seguir:

Usando nossa regra cruzada básica ao procurar um valor desconhecido, encontramos um problema, pois um valor conhecido é zero e, portanto, ao multiplicar pelo nosso valor desconhecido, ficamos sem nada. Para contornar esse problema, a regra do cruzamento longo é útil. Expandamos nossa imagem anterior:

Podemos contornar o zero na linha atual com alguma confiança, aplicando a fórmula abaixo:

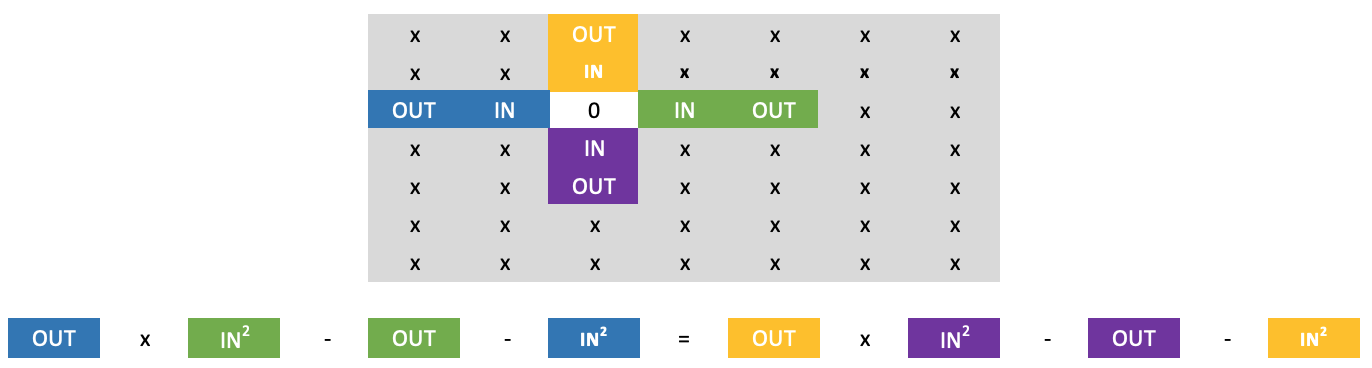
Não é à toa que disse "com alguma confiança", porque as paredes numéricas têm uma propriedade única quando se trata de incluir zeros. Em qualquer número, se houver zeros, eles aparecem em número único ou em quadrado, ou seja, podem ser 1 x 1 (número único), ou 2 x 2, ou 3 x 3 e assim por diante. Essencialmente, isso significa que se encontrarmos um zero entre dois números em qualquer linha, o número abaixo dele não será zero. No entanto, quando aplicamos a regra do cruzamento longo, temos um desconhecido adicional na forma do valor externo mais baixo na parede. No entanto, isso não é problema, pois ele é multiplicado pelo nosso zero conhecido, permitindo-nos resolver a equação sem a necessidade de inserir seu valor.

O problema resolvido pela regra do cruzamento longo aplica-se estritamente às paredes numéricas convergentes e, como vimos nas ilustrações acima, isso raramente acontece com séries temporais financeiras. Então, isso deve ser levado em conta? Isso deve ser determinado de forma consistente, dependendo da série temporal a que o sistema de negociação está direcionado. Alguns poderiam aplicar essa característica até mesmo a séries financeiras, se a "resolubilidade" ou determinante da matriz de Toeplitz atingir o limiar necessário, outros poderiam parar a construção da parede e trabalhar com os coeficientes vetoriais que possuem nesse ponto (quando atingem os zeros) ao construir a equação polinomial de previsão. Talvez haja outras opções, e a escolha dependerá do trader específico.

A regra do cruzamento longo é bastante flexível se encontrarmos apenas um zero ao propagar a parede numérica, no entanto, se os zeros estiverem em um quadrado maior (pois os zeros sempre ocupam um formato nxn na parede), então não fará muito sentido. Nesses casos, a regra da ferradura (horse shoe rule) é frequentemente aplicada. De acordo com essa regra, se tivermos um grande quadrado de zeros, as sequências que cercam esse quadrado são escaladas com um determinado coeficiente.

Esses quatro fatores, um para cada lado do quadrado, possuem uma propriedade única que pode ser mostrada na fórmula abaixo:

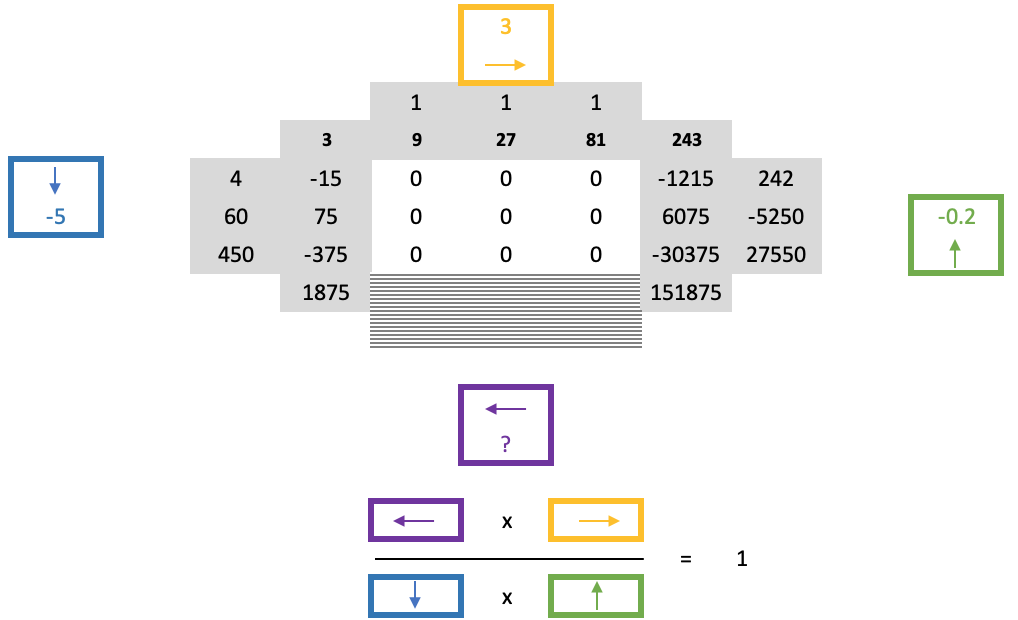
Assim, quando encontramos uma grande porção de zeros, os números superiores e laterais, que fazem fronteira com esses zeros, já serão conhecidos, e como sabemos a largura dos quadrados de zeros, essencialmente sabemos sua altura, ou seja, sabemos onde avaliar os valores desconhecidos de fronteira. A partir da equação acima, podemos obter diretamente os valores de fronteira indicados abaixo, determinando o coeficiente de escala inferior e calculando seus números, geralmente da esquerda para a direita.

No entanto, avançar a partir desse ponto usando a regra cruzada usual ainda será difícil, pois os zeros no quadrado dificultam sua aplicação ao determinar a linha abaixo da linha de fronteira recém-resolvida. A solução para esse problema é representada pela "segunda parte" da regra da ferradura e baseia-se na seguinte fórmula bastante longa:

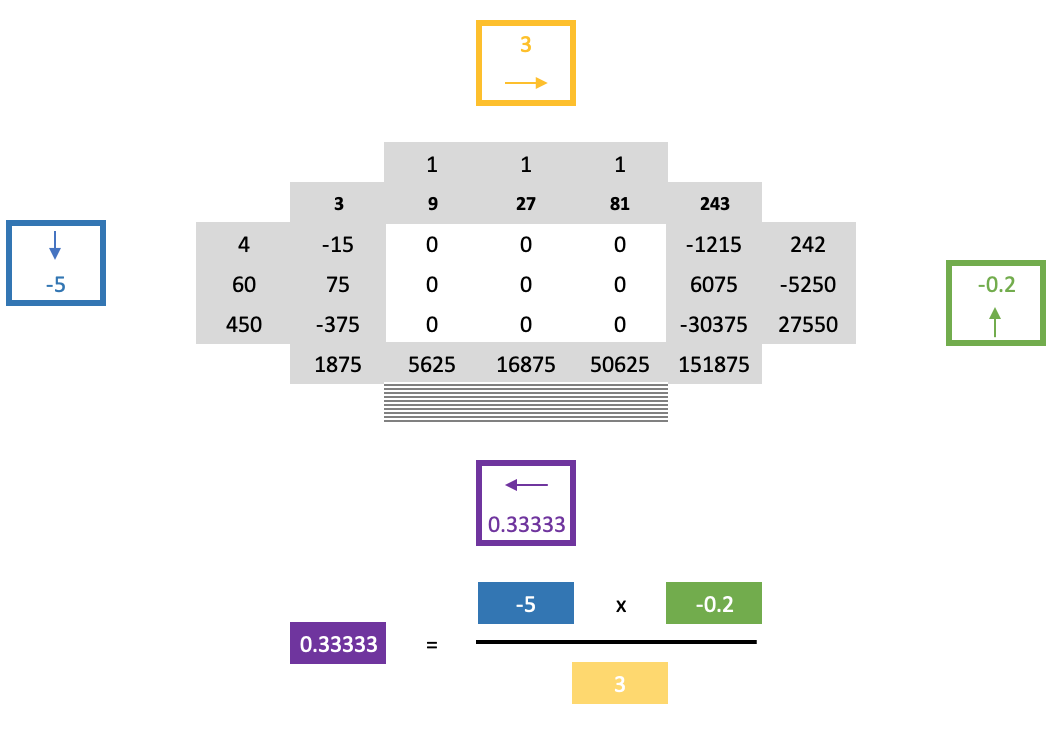
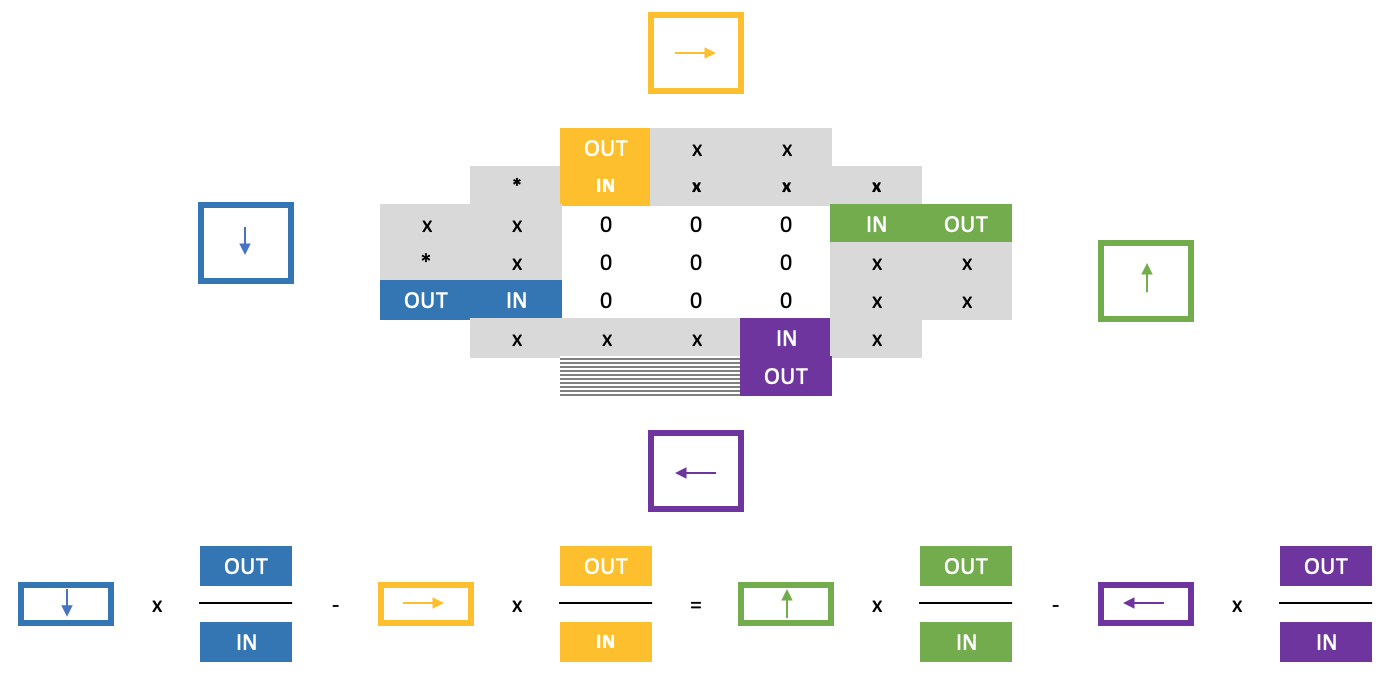
No já mencionado artigo sobre este tópico, além de abordar muitos dos pontos discutidos aqui, também é mencionada a conjectura da pagoda (pagoda conjecture). Em sua forma mais simples, trata-se de somar um grupo de conjuntos de números, cada um contendo um conjunto de tamanho igual, de modo que se cada um dos conjuntos incluídos for considerado um polígono, com cada vértice representando um dos números em seu conjunto, esses polígonos podem ser colados juntos para formar uma grade complexa maior, desde que em qualquer vértice conectado todos os vértices do polígono tenham a mesma quantidade. Isso, é claro, ocorre sob a condição de que cada número dos vértices de qualquer polígono seja único nesse conjunto.

Primeiramente, isso tem implicações interessantes para conjuntos de três números, que formam uma pagoda, pois verifica-se que quando os números de cada conjunto são dispostos em sequência, na parede com números propagados é possível observar padrões repetitivos muito interessantes, e o artigo apresenta algumas dessas imagens.

No entanto, para fins de negociação, essa "nova" abordagem de classificação representa, na verdade, mais uma maneira de considerar séries temporais financeiras, que requer um artigo separado. Basta dizer que poderíamos generalizar várias maneiras de aplicar sequências de pagoda para nossos propósitos.

Ao usar a conjectura, seria razoável aderir a pagodas triangulares, em vez de formas de dimensões mais altas, pois estas tendem a abrir mais possibilidades e, portanto, a complicar as maneiras de conexão. Nossa tarefa seria, em primeiro lugar, normalizar nossas séries financeiras para levar em conta a repetição de valores, o que é um requisito ao determinar as pagodas. O grau em que essa normalização é realizada é algo que precisará ser estudado, pois diferentes iterações certamente darão resultados diferentes.

Em segundo lugar, assim que nos familiarizarmos com um determinado limite de normalização, precisaremos estabelecer a quantidade de triângulos em nossa pagoda, ou seja, o tamanho do grupo. Lembre-se de que, à medida que o tamanho do grupo aumenta, a necessidade de que todos os triângulos estejam diretamente conectados diminui. Em uma pagoda de três triângulos, todos os triângulos estão conectados, mas conforme esse número aumenta, para qualquer triângulo, o número máximo de conexões que ele pode ter é 3. Isso significa que, por exemplo, em uma pagoda com seis triângulos, apenas o triângulo central inferior tem conexões em todos os vértices, enquanto todos os outros têm conexões em apenas dois vértices.

Essa complexidade crescente de conectar triângulos com o aumento do tamanho do grupo pode indicar que a determinação do tamanho ideal do grupo deve ser realizada simultaneamente com o estabelecimento do limite de normalização, pois este nos fornece dados repetitivos que são fundamentais para estabelecer conexões entre os triângulos.

Considerações finais

Examinamos as paredes numéricas, que são uma grade numérica gerada com base na série temporal da sequência em estudo, e vimos como ela pode ser usada na previsão, configurando corretamente o TP e o SL da posição aberta no código. Além disso, discutimos a conjectura da pagoda associada, abordada no artigo sobre paredes numéricas, e apresentamos algumas ideias sobre como ela pode se tornar mais um meio de classificar séries temporais financeiras.

Epílogo

Abaixo estão os testes comparativos dos EAs montados com o Assistente. Ambos usam sinais do Awesome Oscillator e têm as mesmas configurações de entrada, conforme mostrado abaixo:

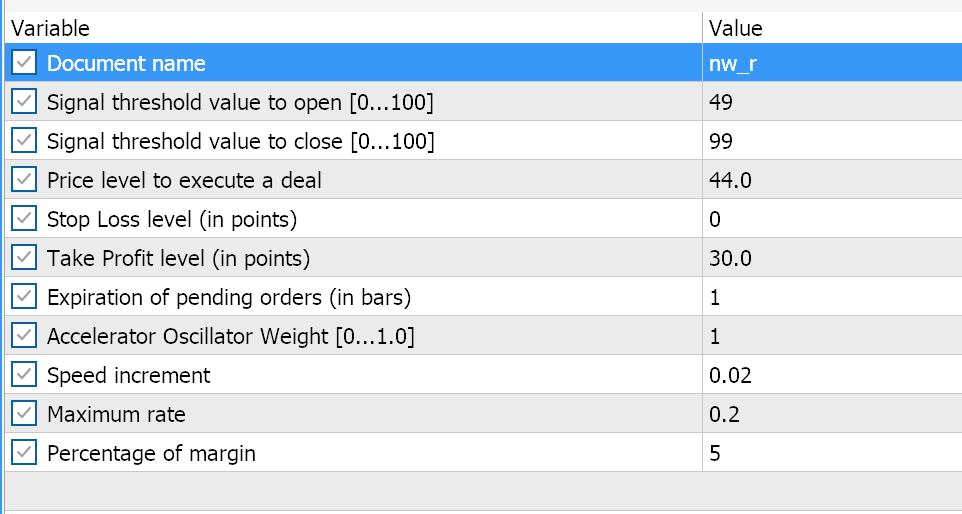
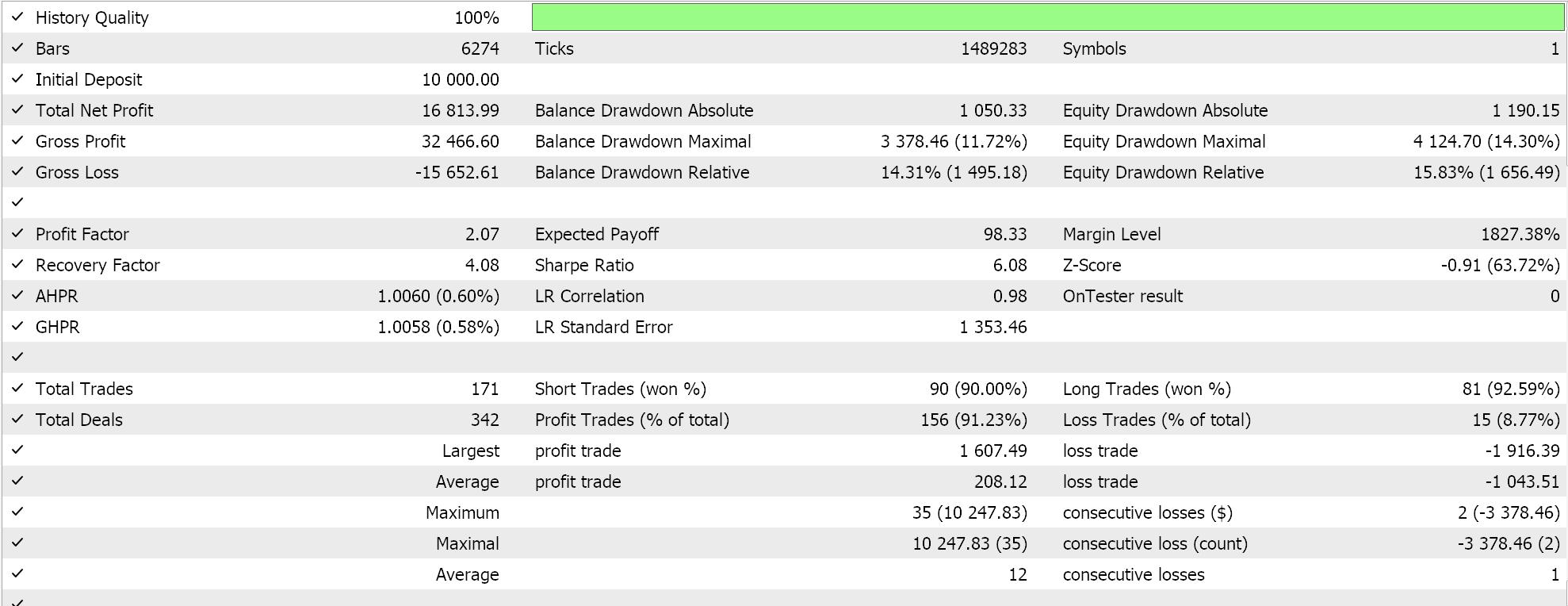
A diferença entre eles é que um EA usa o Parabolic SAR para rastrear e fechar posições abertas, enquanto o outro usa o algoritmo da parede numérica apresentado neste artigo. No entanto, seus relatórios de teste no EURUSD no último ano, em um timeframe de uma hora, apesar de usar o mesmo sinal, diferem. Primeiro, o relatório do EA baseado no Parabolic SAR.

Abaixo está o relatório do EA baseado na parede numérica:

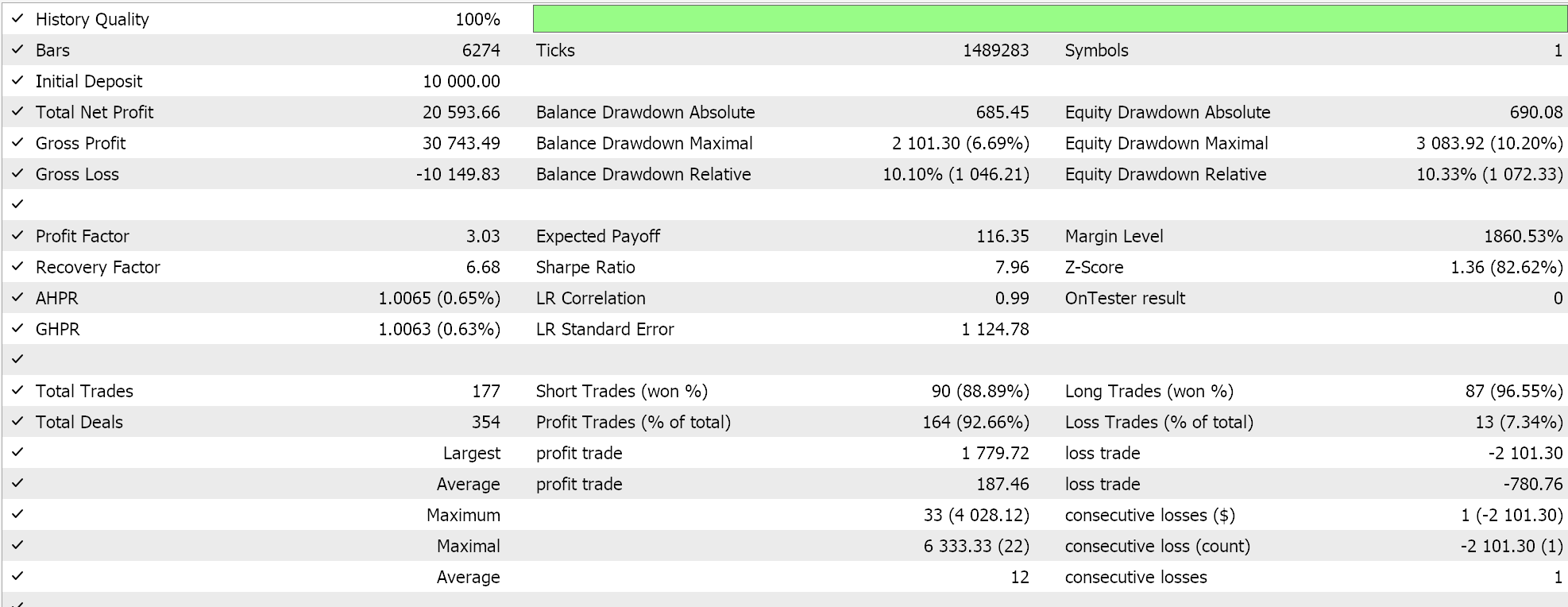
A diferença geral nos resultados é pequena, mas pode ser crucial se testada em períodos mais longos e em diferentes classes de EAs, como gestão de capital ou até mesmo geração de sinais.