Características del Wizard MQL5 que debe conocer (Parte 14): Previsión multiobjetivo de series temporales con STF

Introducción

Este artículo sobre Fusión espacio-temporal (STF) despertó mi interés en el tema gracias a su enfoque bidireccional para la predicción.. Para refrescar la memoria, el artículo está inspirado en resolver un problema de pronóstico basado en probabilidades que es colaborativo tanto para la oferta como para la demanda en plataformas de transporte bajo demanda de dos caras, como Uber y Didi. Las relaciones colaborativas de oferta y demanda son comunes en varios mercados de dos caras, como Amazon, Airbnb y eBay, donde, en esencia, la empresa no solo atiende al ‘cliente’ o comprador tradicional, sino que también satisface a los proveedores del cliente.

Por lo tanto, el pronóstico bidireccional en un caso donde la oferta depende en parte de la demanda puede ser importante para estas empresas de manera frecuente. Sin embargo, esta proyección dual de la demanda y la oferta ciertamente se apartó del enfoque convencional de pronosticar un valor específico en una serie temporal o conjunto de datos. El artículo también presentó lo que denominó un marco de causaltrans, donde la relación causal "colaborativa" entre la oferta y la demanda se capturaba mediante una matriz G, y todas las predicciones se realizaban a través de una red de transformadores, con resultados destacables.

Tomando ejemplo de ello, tratamos de prever la oferta y la demanda de valores negociados utilizando la tendencia bajista y alcista como indicadores sustitutivos de estos dos parámetros. Estrictamente hablando, sin embargo, la típica clase Expert-Signal calcula ambos valores como enteros en el rango 0-100 como se puede ver en los archivos de la librería MQL5 o en los archivos que hemos codificado en estas series hasta ahora. Lo que sería nuevo, sin embargo, es la adición de una matriz espacial y un parámetro temporal para hacer nuestras predicciones (los 2 inputs adicionales que citamos del artículo).

La cuantización espacial de los valores comerciales es subjetiva, al igual que la elección de la métrica temporal. Utilizando las series de precios altos y bajos de la seguridad como anclas de la demanda y la oferta, empleamos los valores de autocorrelación entre estos topes como coordenadas de una matriz espacial, así como el índice del día de la semana como indicador temporal. Este enfoque rudimentario, que puede personalizarse y mejorarse, sirve a nuestros propósitos para este artículo.

En el artículo se utilizó redes de transformadores, que nosotros no usaremos ya que son ineficientes para nuestros propósitos; sin embargo, todas las predicciones se realizarán a través de un perceptrón multicapa personalizado y codificado a mano. Con tantas librerías y ejemplos de código sobre el tema, parece una pérdida de tiempo intentar codificar un perceptrón multicapa propio. Sin embargo, la clase de red utilizada tiene menos de 300 líneas y es razonablemente escalable en cuanto a la personalización del número de capas y el tamaño de cada una, algo de lo que aún carecen la mayoría de las librerías disponibles.

Por lo tanto, al utilizar una red neuronal singular y no transformadores, la implementación del marco causaltrans del artículo no se realizará aquí. Sin embargo, todavía tenemos mucho trabajo por delante con lo que vamos a utilizar, ya que seguiremos haciendo pronósticos duales para la demanda y la oferta, y también emplearemos una matriz espacial y el tiempo en el proceso. Y, como siempre, existen riesgos inherentes en cualquier sistema de comercio, por lo que invitamos al lector a realizar su propia diligencia antes de utilizar cualquier material compartido aquí.

Ilustración STF

El STF se utiliza sobre todo en actividades de Teledetección y centradas en lo visual, en las que las métricas de espacio y tiempo pueden casarse de forma tangible.

Si no estás muy interesado en explorar el potencial del STF fuera del trading, entonces puedes saltarte esta sección y continuar con la implementación en MQL5.

Si nos fijamos en la teledetección, por ejemplo, las imágenes captadas por satélite captan el componente espacial de los datos y la región que se examina, mientras que el tiempo se refiere al momento en que se toman las imágenes. Esta información no sólo puede formar una serie temporal, sino que también es importante para hacer previsiones sobre cambios meteorológicos, de la vida vegetal o incluso del hábitat animal en la zona estudiada, todo ello gracias al STF.

Consideremos, paso a paso, cómo la Fusión Espacio-Temporal (STF) podría ayudar a resolver problemas relacionados con la deforestación y la vegetación. El primer paso, como suele ocurrir con los problemas de aprendizaje automático, es la recopilación de datos. Los satélites de teledetección captarían imágenes multiespectrales de la zona de estudio durante un periodo de tiempo. Dado que los satélites pueden ser multiespectrales pueden captar información de longitud de onda reflejada y absorbida no visible a simple vista pero que se encuentra en bandas de longitud de onda asociadas a la vegetación, o masas de agua, etc. Todo ello añade riqueza (y complejidad) al tipo de datos que pueden modelizarse en una serie, ya que estas imágenes se capturarían a lo largo de cierto tiempo.

La integración de datos espaciales es lo que podría seguir, puesto que cada imagen ya lleva un sello de tiempo, se podría utilizar un sistema de coordenadas GPS adecuado para cartografiar cada imagen garantizando la coherencia de la información espacial en todas las imágenes para todos los puntos temporales en los que fueron capturadas.

Lo siguiente sería normalizar nuestros «datos» para asegurarnos de que están en un formato pertinente para la vegetación y la deforestación. Una de las formas de conseguirlo es registrando las firmas espectrales de cada imagen en diferentes puntos temporales mediante indexación, de modo que los datos no sólo sean más fáciles de manejar por los modelos de entrenamiento, sino que también se centren en el tema en cuestión.

Esta normalización también implicaría la detección de cambios en las imágenes capturadas a lo largo del tiempo, de modo que puedan extraerse o definirse características importantes para la vegetación, como las cotizaciones de crecimiento, las variaciones estacionales, los patrones de distribución, etc. Cada una de estas características podría constituir una dimensión de los datos.

La elección del modelo puede variar, pero cabe esperar que una red neuronal sea la mejor candidata. Para ello se utilizaría una buena parte de las imágenes, que ahora son datos normalizados, y se reservaría un conjunto de datos más pequeño para las pruebas, como suele ser el caso.

Así pues, la previsión con el modelo se realizaría a partir de los resultados satisfactorios del entrenamiento y las pruebas, y lo más importante a tener en cuenta sería la interpretación, puesto que ya se ha realizado una gran normalización, por lo que habría que hacer lo contrario con cuidado para los resultados del modelo.

En nuestro artículo citado, que fue aceptado recientemente por ACM, las ecuaciones para la demanda y la oferta futuras se representan de la siguiente manera:

x v (t+δt) = f x (x v (t), G v (t), δt),

y v (t+δt) = f y (x v (t), y v (t), G v (t), δt),

Donde:

• x v es la función de demanda con respecto al tiempo.
• y v es la función de oferta con respecto al tiempo.
• G v es también un vector o matriz de información espacial.
• δt es el incremento de tiempo al que se realiza una previsión.
• t es el tiempo.

Así, en nuestro caso, las funciones f x y f y serán redes neuronales con los vectores o matrices de parámetros que contienen los datos que se introducen en sus respectivas capas de entrada.

Implementación de STF en MQL5

Para implementar STF en MQL5 seguiríamos las ecuaciones compartidas anteriores para establecer cómo estructuramos los datos de entrada a nuestro modelo. A partir de las dos ecuaciones, está claro que los datos de entrada de cada una de ellas adoptarían normalmente un formato vectorial o matricial, lo que, por supuesto, presenta innumerables posibilidades y retos. Las entradas potenciales de cada función f en las 2 ecuaciones son buffers similares, con la única diferencia entre las 2 ecuaciones de que la ecuación de la oferta depende no sólo de sus valores anteriores, sino también de los de la demanda. Esto sigue la tesis del autor del documento de que la oferta depende de la demanda y no al revés.

Por tanto, el número total de búferes, dado el solapamiento entre ambas ecuaciones, es de 4. Todos ellos están presentes en la ecuación de la oferta y, para enumerarlos, son la demanda previa, la oferta previa, los valores espaciales y el incremento temporal.

El buffer de demanda se interpreta como un buffer de series temporales de puntos de precio «alcistas» para este artículo. Podría decirse que un buffer más conciso sería el volumen real de contratos largos, pero esta información rara vez la comparten los intermediarios y, aunque lo hicieran, no sería una representación exacta del volumen, dada la naturaleza díscola de la información sobre el volumen en los mercados de divisas. Por lo tanto, los precios altos menos los precios abiertos se eligen como un buffer alternativo a los contratos reales de volumen largo. Otros posibles buffers que podrían desempeñar esta función podrían ser parámetros específicos de cada moneda, como los tipos de interés, la inflación o incluso los índices de oferta monetaria de los bancos centrales. La elección de los precios máximos menos los precios abiertos como buffer tiene por objeto medir la volatilidad al alza y, puesto que se puede entender que se correlaciona positivamente con los contratos de volumen largo, se utiliza como la siguiente mejor aproximación. Estos valores sólo pueden ser positivos o cero, con una lectura de cero indicando un hombre colgado o una barra de precios plana.

El buffer de oferta, al igual que su predecesor, también se aproximará tomando los precios abiertos menos los precios bajos. Esto también puede tomarse como una lectura de la volatilidad a la baja, que se correlaciona positivamente con los contratos de volumen bajista. Al igual que en el caso anterior, los valores de este buffer sólo serán positivos, y un valor cero indicará una estrella Doji 'Lápida' o una barra plana. La ecuación de la oferta se diferencia de la demanda en que toma más inputs lo que implica que además su modelo también será similar al de la demanda pero diferente. Por lo tanto, habrá dos instancias del modelo de previsión, una para la demanda y otra para la oferta. Dado que nuestro resultado final es obtener una única señal, ésta se determinará restando la previsión de oferta de la previsión de demanda. Recordemos que todas las inputs del modelo de oferta y demanda son positivas o nulas, por lo que, con toda probabilidad, también lo deberían ser las salidas. Por lo tanto, al restar la salida del modelo de oferta de la salida de la demanda, obtenemos un número doble cuyo valor positivo indicaría una tendencia alcista y cuyo valor negativo significaría una tendencia bajista.

La elección del margen temporal es simplemente un índice para el día de la semana. Las pruebas, que se cubren en la siguiente sección, se realizarán en el marco de tiempo diario, por lo que el índice del día de la semana se relaciona fácilmente con esto. Sin embargo, si se considerara un marco de tiempo alternativo, por ejemplo, uno más pequeño que el marco de tiempo diario, se podría considerar un índice que abarque dentro de un día o incluso una semana. Por ejemplo, en un marco de tiempo de 8 horas, hay quince barras de 8 horas en una semana de trading, lo que proporciona quince posibles índices de tiempo dentro de la semana. Podrías elegir la hora del día, la sesión de trading del día, etc. Las opciones aquí son abundantes, y realizar pruebas preliminares para determinar qué funciona mejor para tu sistema de trading podría ser un mejor enfoque. Nuestra función simple que devuelve el índice de días de la semana es la siguiente:

//+------------------------------------------------------------------+
//| Temporal (Time) Indexing function                                |
//+------------------------------------------------------------------+
int CSignalNetwork::T(datetime Time)
{  MqlDateTime _dt;
   if(TimeToStruct(Time,_dt))
   {  if(_dt.day_of_week==TUESDAY)
      {  return(1);
      }
      else if(_dt.day_of_week==WEDNESDAY)
      {  return(2);
      }
      else if(_dt.day_of_week==THURSDAY)
      {  return(3);
      }
      else if(_dt.day_of_week==FRIDAY||_dt.day_of_week==SATURDAY)
      {  return(4);
      }
   }
   return(0);
}

La matriz G recoge nuestros datos espaciales para este modelo y su definición puede resultar complicada. ¿Cómo definir el espacio en un entorno de comercio de valores? Si consideramos nuestro artículo de referencia, por ejemplo, una tabla cruzada de metadatos entre la oferta y la demanda se "normaliza" alimentándola a través de lo que el artículo denomina Graph Attention Transformers (GAT). Funcionan en dos capas: la primera captura las relaciones complejas entre nodos y la segunda agrega la información de los vecinos para las predicciones finales de los nodos. Las lecturas de GAT son luego parte de lo que se alimenta a través de las respectivas redes neuronales para pronosticar la demanda o la oferta. En nuestro caso, los metadatos para nuestros buffers de precios alcistas y bajistas se obtendrán de las lecturas de correlación compartidas por estos buffers. Estas correlaciones se capturan como se muestra en el código siguiente:

//+------------------------------------------------------------------+
//| Spatial (Space) Indexing function. Returns Matrix Determinant    |
//| This however can be customised to return all matrix values as    |
//| a vector, depending on the detail required.                      |
//+------------------------------------------------------------------+
double CSignalNetwork::G(vector &X,vector &Y)
{  matrix _m;
   if(X.Size()!=2*m_train_set||Y.Size()!=2*m_train_set)
   {  return(0.0);
   }
   _m.Init(2,2);
   vector _x1,_x2,_y1,_y2;
   _x1.Init(m_train_set);_x1.Fill(0.0);
   _x2.Init(m_train_set);_x2.Fill(0.0);
   _y1.Init(m_train_set);_y1.Fill(0.0);
   _y2.Init(m_train_set);_y2.Fill(0.0);
   for(int i=0;i<m_train_set;i++)
   {  _x1[i] = X[i];
      _x2[i] = X[i+m_train_set];
      _y1[i] = Y[i];
      _y2[i] = Y[i+m_train_set];
   }
   _m[0][0] = _x1.CorrCoef(_x2);
   _m[0][1] = _x1.CorrCoef(_y2);
   _m[1][0] = _y1.CorrCoef(_x2);
   _m[1][1] = _y1.CorrCoef(_y2);
   return(_m.Det());
}

Nótese que devolvemos un único valor que representa la matriz y no sus lecturas individuales ya que utilizamos su determinante. Las lecturas individuales también podrían utilizarse alternativamente, ya que los valores de correlación siempre se normalizan de -1,0 a +1,0 y esto podría conducir a resultados más precisos para el modelo en general. Para nuestros propósitos, sin embargo, nos quedamos con el determinante, ya que la eficiencia es un poco más importante, al menos para las pruebas preliminares.

Con los 4 búferes de datos mencionados puede ser útil hablar también de nuestro modelo muy rudimentario que es una red neuronal simple que está codificada sin usar ninguna librería. Descomponemos una red en sus componentes básicos: entradas, pesos, sesgos, salidas ocultas, salidas y objetivo, y sólo los utilizamos para realizar la alimentación hacia delante y la retropropagación. Nuestra interfaz de red es la siguiente:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cnetwork
{
protected:
   matrix            weights[];
   vector            biases[];

   vector            inputs;
   vector            hidden_outputs[];
   vector            target;

   int               hidden_layers;
   double            Softplus(double X);
   double            SoftplusDerivative(double X);

public:
   vector            output;

   void              Get(vector &Target)
   {                 target.Copy(Target);
   }

   void              Set(vector &Inputs)
   {                 inputs.Copy(Inputs);
   }
   
   bool              Get(string File, double &Criteria, datetime &Version);
   bool              Set(string File, double Criteria);

   void              Forward();
   void              Backward(double LearningRate);

   void              Cnetwork(int &Settings[],double InitialWeight,double InitialBias)
   {                 
                        
                        ...
                        ...

   };
   void              ~Cnetwork(void) { };
};

Además de las funciones comunes para establecer y obtener entradas y objetivos, también se incluyen algunas funciones de exportación para pesos y sesgos después del entrenamiento. El algoritmo de avance es ordinario y utiliza soft-plus para la activación en cada capa, y la función de retropropagación también es de la vieja escuela y se basa en la regla de la cadena y los métodos de descenso de gradiente para ajustar los pesos y los sesgos de la red. La inicialización de la red, sin embargo, requiere algunas entradas y éstas pasan por una «validación» antes de que la instancia de la clase pueda ser utilizada con seguridad. Las entradas para crear la red son la matriz de ajustes, el valor de los pesos iniciales (en toda la red) y los valores iniciales de sesgo. El array settings determina el número de capas ocultas que tendrá la red por su propio tamaño y cada entero en sus índices establece el tamaño de la capa respectiva.

   void              Cnetwork(int &Settings[],double InitialWeight,double InitialBias)
   {                 int _size =    ArraySize(Settings);
                     if(_size >= 2 && _size <= USHORT_MAX && Settings[ArrayMinimum(Settings)] > 0 && Settings[ArrayMaximum(Settings)] < USHORT_MAX)
                     {  ArrayResize(weights, _size - 1);
                        ArrayResize(biases, _size - 1);
                        ArrayResize(hidden_outputs, _size - 2);
                        hidden_layers = _size - 2;
                        for(int i = 0; i < _size - 1; i++)
                        {  weights[i].Init(Settings[i + 1], Settings[i]);
                           weights[i].Fill(InitialWeight);
                           biases[i].Init(Settings[i + 1]);
                           biases[i].Fill(InitialBias);
                           if(i < _size - 2)
                           {  hidden_outputs[i].Init(Settings[i + 1]);
                              hidden_outputs[i].Fill(0.0);
                           }
                        }
                        output.Init(Settings[_size - 1]);
                        target.Init(Settings[_size - 1]);
                     }
                     else
                     {  printf(__FUNCSIG__ + " invalid network settings. ");
                        //~Cnetwork(void);
                     }
   };

Dado que prevemos tanto la demanda como la oferta, necesitaremos dos instancias distintas de nuestra red, una para cada tarea. Nuestra función de obtención de salida, que actúa como una fuente para las funciones Check Open Long y Check Open Short, llenará las capas de entrada respectivas de cada red con los márgenes de datos ya mencionados anteriormente. Para la demanda, ya que la demanda sólo depende de sus valores previos, además de los parámetros de espacio y tiempo, su capa de entrada tiene un tamaño de 3. Sin embargo, la oferta, además de depender de sus valores previos, puede verse influida por la demanda anterior, por lo que su capa de entrada tiene un tamaño de 4 si se tienen en cuenta las entradas de espacio y tiempo similares. El llenado de estas capas se maneja dentro de la función GetOutput() en cada nueva barra de la siguiente manera:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalNetwork::GetOutput()
{  

        ...
        ...

   for(int i = 0; i < m_train_set; i++)
   {  for(int ii = 0; ii < __LONGS_INPUTS; ii++)
      {  if(ii==0)//time
         {  m_model_longs.x[i][ii] = T(m_time.GetData(i));
         }
         else if(ii==1)//spatial matrix
         {  vector _x,_y;
            _x.CopyRates(m_symbol.Name(),m_period,2,StartIndex() + ii + i,2*m_train_set);
            _y.CopyRates(m_symbol.Name(),m_period,4,StartIndex() + ii + i,2*m_train_set);
            m_model_longs.x[i][ii] = G(_x,_y);
         }
         else if(ii==2)//demand
         {  m_model_longs.x[i][ii] = (m_high.GetData(StartIndex() + ii + i) - m_open.GetData(StartIndex() + ii + i));
         }
      }
      if(i > 0) //assign classifier 
      {  m_model_longs.y[i - 1] = (m_high.GetData(StartIndex() + i - 1) - m_open.GetData(StartIndex() + i - 1));
      }
   }
   for(int i = 0; i < m_train_set; i++)
   {  for(int ii = 0; ii < __SHORTS_INPUTS; ii++)
      {  if(ii==0)//time
         {  m_model_shorts.x[i][ii] = T(m_time.GetData(i));
         }
         else if(ii==1)//spatial matrix
         {  vector _x,_y;
            _x.CopyRates(m_symbol.Name(),m_period,4,StartIndex() + ii + i,2*m_train_set);
            _y.CopyRates(m_symbol.Name(),m_period,2,StartIndex() + ii + i,2*m_train_set);
            m_model_shorts.x[i][ii] = G(_x,_y);
         }  
         else if(ii==2)//demand
         {  m_model_shorts.x[i][ii] = (m_high.GetData(StartIndex() + ii + i) - m_open.GetData(StartIndex() + ii + i));
         }  
         else if(ii==3)//supply
         {  m_model_shorts.x[i][ii] = (m_open.GetData(StartIndex() + ii + i) - m_low.GetData(StartIndex() + ii + i));
         }
      }
      if(i > 0) //assign classifier
      {  m_model_shorts.y[i - 1] = (m_open.GetData(StartIndex() + i - 1) - m_low.GetData(StartIndex() + i - 1));
      }
   }

        ...
        ...

}

Después de esto, asignamos los valores de entrada y objetivo para las dos redes recuperando esta información de la estructura del modelo dentro de los bucles de entrenamiento, donde cada bucle itera a través de las redes durante un número determinado de épocas. A partir de las pruebas preliminares, se determinó que el número ideal de épocas era de aproximadamente 10.000, con una cotización de 0,5 por bucle de entrenamiento. Se trata, sin duda, de un proceso de cálculo intensivo, por lo que los resultados de las pruebas que se presentan en la siguiente sección utilizan valores muy conservadores de unas 250 épocas.

La función de salida establecida nos permite registrar los pesos y sesgos de la red en cada pasada siempre que los resultados de la pasada superen los criterios establecidos por los pesos utilizados en la inicialización. Al inicializar existe la opción de leer pesos y los criterios establecidos por esos pesos sirven de referencia para la prueba en curso.

Ejecuciones de prueba

Realizamos ejecuciones de prueba en EURUSD en el marco temporal diario para el año 2023 con configuraciones de red muy sencillas. La red de previsión de la demanda tiene 3 capas en total con una oculta y sus tamaños son 3, 5 y 1. La red de previsión de suministro también tiene 3 capas, pero como se ha indicado anteriormente, la capa de entrada tiene un tamaño diferente, por lo que sus tamaños son 4, 5 y 1. El 1 al final de ambas redes almacena las salidas de cada red.

Como siempre, ensamblar el código adjunto al final de este artículo en un asesor experto se logra a través del asistente de MQL5, así que si eres nuevo o no estás familiarizado, consulta los artículos aquí y aquí para obtener orientación.

Estas dos configuraciones son muy básicas y podría decirse que son las más sencillas que se pueden plantear dado que la clase de red referenciada puede generar hasta UCHAR_MAX capas cada una con un tamaño también de UCHAR_MAX si la configuración de inicialización así lo define. A medida que se utilizan más capas e incluso capas de mayor tamaño, los recursos informáticos aumentan. No obstante, cabe señalar que el tamaño de las capas en el rango de 100 unidades suele considerarse suficiente, incluso cuando se configuran con pocas capas.

Realizamos ejecuciones como siempre sin objetivos de precio de salida en las que las posiciones se mantienen hasta que la señal se invierte, ya que este enfoque tiende a ser más a largo plazo y evalúa mejor las principales tendencias de los precios. Una prueba con ticks reales y algunas de las configuraciones ideales nos proporciona el siguiente informe:

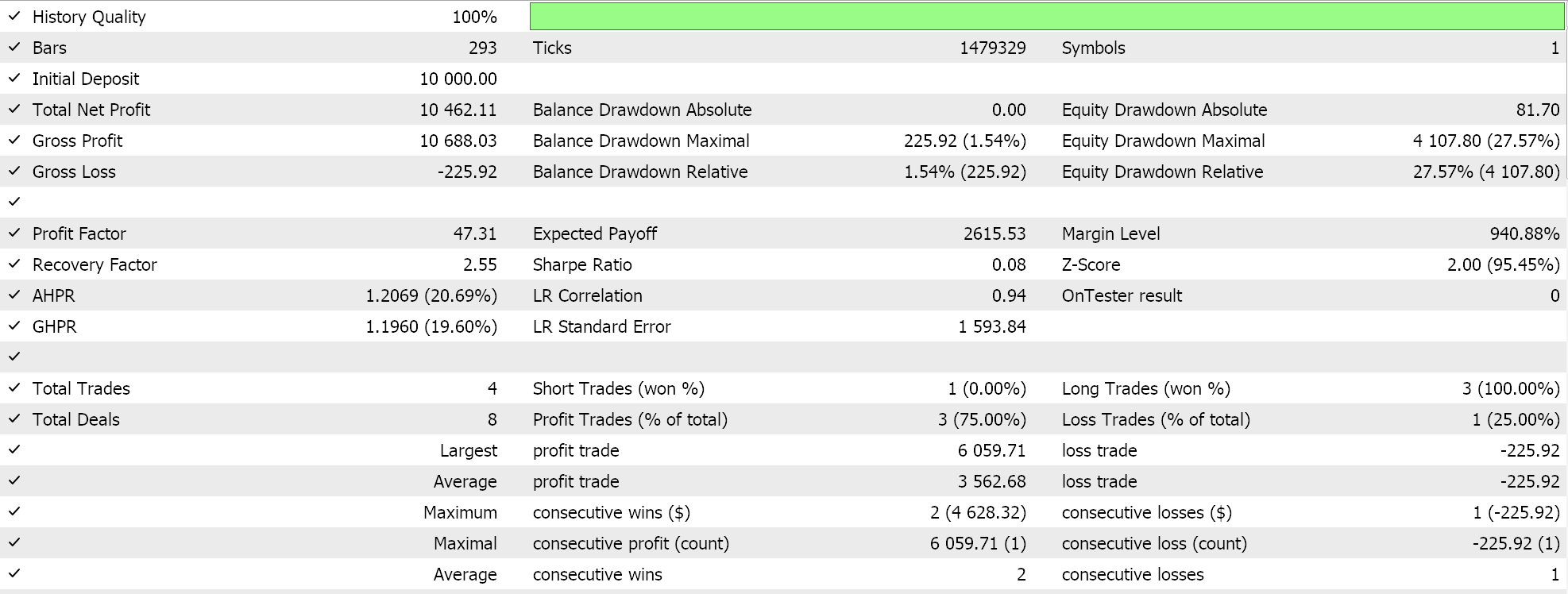
Y la curva de equidad que se muestra a continuación:

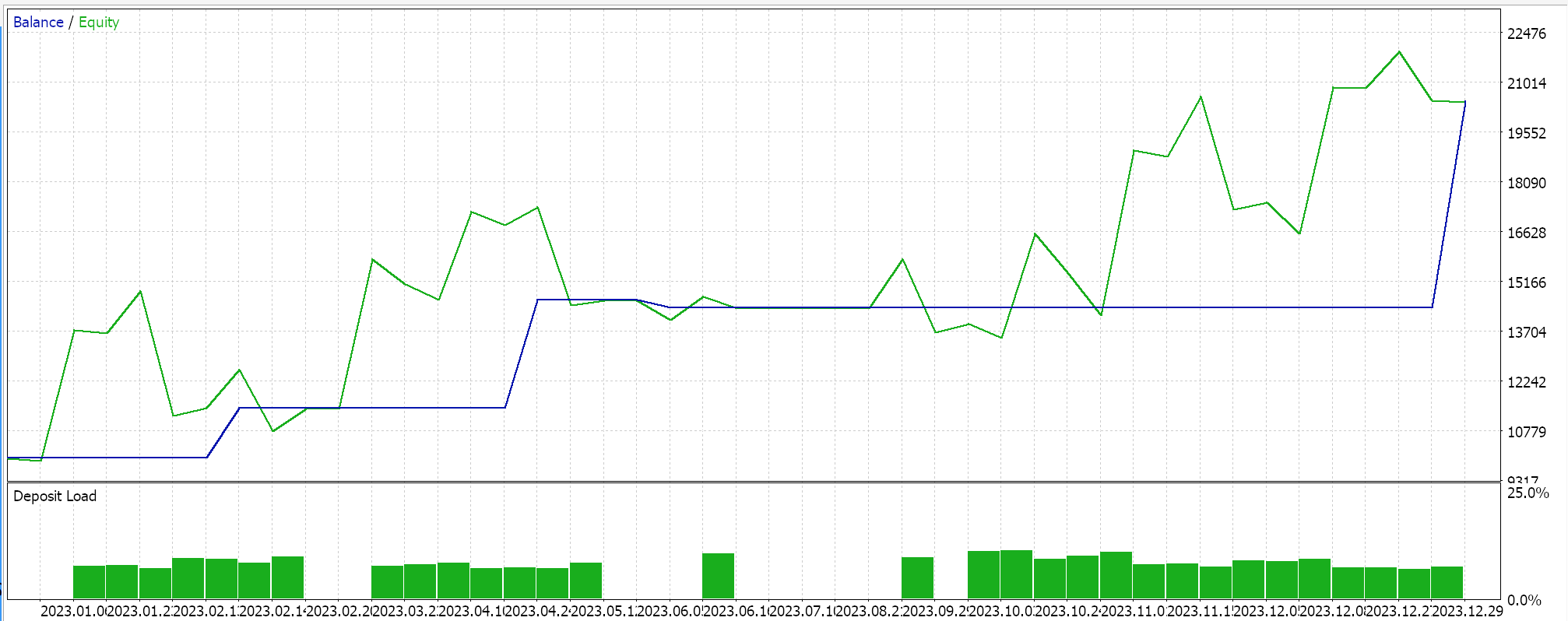
Si profundizamos en este informe, queda claro que se realizaron muy pocas operaciones a lo largo del año, lo que en primer lugar no es malo porque su calidad era sólida, ya que se mantuvieron durante periodos prolongados hasta que se activaron las inversiones de señal y durante este periodo probado sufrieron detracciones mínimas. Sin embargo, en los mercados planos o con fluctuaciones, suele ser prudente, especialmente en los casos en los que existe apalancamiento, ser más sensible a los micromovimientos de los precios. En el sistema que probamos estábamos usando el marco de tiempo diario y esto está bien, ya que tiende a centrarse en el panorama general, pero si fuéramos a hacer esto un poco más pragmático tendríamos que considerar marcos de tiempo más pequeños, probablemente de 4 horas o incluso de 1 hora. Cuando hagamos esto, nuestros recursos informáticos sólo para pruebas aumentarán en una magnitud considerable, de hecho, decir que esta relación es exponencial no es una exageración. Y ten en cuenta que se trataba de una red muy rudimentaria de 3 capas con una capa oculta de 5 puntos y la matriz espacial reducida a un determinante. Todos estos factores son importantes porque, a medida que se empieza a trabajar con plazos más cortos, la necesidad de cribar el ruido se hace aún más importante y una de las mejores formas de hacerlo es siendo un poco pedante. 

Además, dentro de la clase de red referenciada hay funciones que ayudan a importar y exportar los ajustes de peso y sesgo de la red al principio y al final de cada pasada. No los utilicé para estas pruebas porque también ralentizaban un poco el proceso, pero habría que utilizarlos cuando se realicen pruebas durante periodos prolongados (sólo hemos considerado un año para esta prueba). Cuando se utilizan, hay que sopesar cuidadosamente los criterios para los que se realizan las pruebas, ya que por defecto, en la clase de red, cuanto más grande, mejor. Por lo tanto, si uno está más preocupado por las reducciones (drawdowns), por ejemplo, entonces el código adjunto en la clase de la red debe modificarse en consecuencia para reflejar esto, de modo que en cada ejecución, los pesos escritos en el archivo solo se actualicen si el valor del criterio de esa ejecución es MENOR que el valor anterior. Esto implica también que el valor inicial o por defecto en cada ejecución debe ser DBL_MAX o un valor suficientemente alto para evitar errores innecesarios.

Conclusión

La capacidad de la Fusión Espacio-Temporal (STF) para manejar pronósticos duales ciertamente presenta un enfoque intrigante que no es muy común y, sin duda, tiene potencial para ser refinado y mejorado. Por ejemplo, la matriz G para información espacial utilizada en nuestras pruebas puede expandirse a una matriz de n x n al dividir los vectores de datos de entrada en partes más pequeñas, e incluso cada uno de sus valores podría ser puntos de datos de entrada para una red, así como muchos otros ajustes. Sin embargo, estos cambios tienen un costo en términos de recursos de computación.

De hecho, en general, implementar la Fusión Espacio-Temporal (STF) mediante redes neuronales es esencialmente un esfuerzo que consume muchos recursos de computación y requiere pruebas con cantidades bastante grandes de datos para obtener una validación cruzada confiable. Y esto presenta su principal limitación, que es aún más evidente cuando se implementa en el artículo citado anteriormente, donde se utilizaron transformadores de red.

Sin embargo, es un aspecto de este campo que está siendo aceptado lentamente por la industria, ya que vemos que NVIDIA se vuelve cada vez más relevante en este panorama. Se podrían explorar modelos alternativos más eficientes, como los bosques aleatorios, siempre que sus configuraciones asociadas no sean excesivamente complejas. Sin embargo, a medida que los costos de computación comiencen a disminuir, los beneficios en relación con el costo de estos modelos podrían no ser factibles.

El asistente de MQL5, sin embargo, sigue siendo una herramienta para la creación rápida de prototipos y pruebas de ideas, y este artículo sobre la Fusión Espacio-Temporal (STF) presenta otra ilustración de esto.