Características del Wizard MQL5 que debe conocer (Parte 15): Máquinas de vectores de soporte utilizando el polinomio de Newton

Introducción

Support Vector Machines (SVM) es un algoritmo de clasificación de aprendizaje automático. La clasificación es diferente de la agrupación, que hemos considerado en artículos anteriores aquí y aquí, siendo la principal diferencia entre ambas que la clasificación separa los datos en conjuntos predefinidos, con supervisión, mientras que la agrupación busca determinar qué y cuántos de estos conjuntos existen, sin supervisión.

En pocas palabras, la SVM clasifica los datos teniendo en cuenta la relación que tendrá cada punto de datos con todos los demás si se añadiera una dimensión a los datos. La clasificación se consigue si se puede definir un hiperplano, que diseccione limpiamente los conjuntos de datos predefinidos.

A menudo, los conjuntos de datos considerados tienen múltiples dimensiones, y es precisamente este atributo el que convierte a la SVM en una herramienta muy potente para clasificar dichos conjuntos de datos, especialmente si los números de cada conjunto son pequeños o la proporción relativa de los conjuntos de datos está sesgada. El código fuente de la implementación de las SVMs que tienen más de dos dimensiones es muy complejo, y a menudo los casos de uso en Python o C# siempre utilizan bibliotecas, lo que deja al usuario con una mínima entrada de código para obtener un resultado.

Los datos de alta dimensión tienen tendencia a ajustarse a los datos de entrenamiento, lo que los hace menos fiables en datos fuera de muestra, y éste es uno de los principales inconvenientes de la SVM. Por otro lado, los datos de menor dimensión se validan de forma cruzada mucho mejor y tienen casos de uso más comunes.

Para este artículo consideraremos un caso muy básico de SVM que maneja datos bidimensionales (también conocido como SVM lineal), ya que el código fuente completo de la implementación debe ser compartido sin referencia a ninguna biblioteca de terceros. Normalmente, el hiperplano de separación se deriva de uno de estos dos métodos: un kernel polinómico o un kernel radial. Este último es más complejo y no se tratará aquí, ya que sólo nos ocuparemos del primero, el núcleo polinómico.

Por lo general, cuando se utiliza el núcleo polinómico, que se define formalmente por la ecuación siguiente:

Determinar los valores ideales de `c` y `d`, que establecen la ecuación del hiperplano, es un proceso iterativo que tiene como objetivo que los vectores de soporte estén lo más separados posible, ya que miden la distancia entre los dos conjuntos de datos.

Para este artículo, sin embargo, como se indica en el título, utilizaremos el polinomio de Newton para derivar la ecuación del hiperplano en conjuntos de datos bidimensionales. Habíamos visto el polinomio de Newton en un artículo reciente, por lo que se omitirá parte de su implementación.

Aplicamos el polinomio de Newton en tres escenarios. En primer lugar, interpolamos los puntos medios entre dos conjuntos de datos predefinidos para obtener un conjunto de puntos límite y estos puntos se utilizan para derivar una ecuación de línea/curva que define nuestro hiperplano. Con este hiperplano definido, lo tratamos como un clasificador en la ejecución de decisiones comerciales para una clase de señal experta de prueba, que se utilizará. En el segundo escenario, añadimos una función de regresión para que la clase de señal experta no solo produzca salidas de 0 o 100 (como en el ^primero), sino que también proporcione valores dentro del rango. Calculamos el valor de regresión a partir de lo cerca que está el vector no clasificado de los puntos del vector conocido. En tercer lugar, nos basamos en el segundo escenario interpolando sólo un pequeño número de puntos al definir el hiperplano. El pequeño número de puntos, también conocidos como vectores de soporte, son los que están más cerca del otro conjunto de datos, con lo que se «refina» la ecuación del hiperplano mientras se adopta todo lo demás.

Antecedentes del kernel polinómico

Para esta pieza estamos considerando SVMs lineales dado que la implementación completa del código fuente va a ser compartida, y queremos evitar el uso de librerías ofreciendo total transparencia en todo el código fuente. En las aplicaciones reales de SVM, sin embargo, los tipos no lineales se utilizan mucho, dada la complejidad inherente y la multidimensionalidad de muchos conjuntos de datos. Hacer frente a estos desafíos en SVMs ha demostrado ser manejable gracias al truco del kernel. Se trata de un método que permite estudiar un conjunto de datos en una dimensión superior manteniendo su estructura original. El truco del kernel utiliza el producto punto de los vectores para preservar los valores de los vectores de dimensión inferior. Al apuntar el conjunto de datos a dimensiones más altas, se consigue fácilmente la separación de los conjuntos de datos y esto se hace también con menos recursos informáticos.

Como se ha indicado anteriormente, nuestra función kernel se define formalmente como:

Donde `x` e `y` sirven como puntos de datos a través de dos puntos de datos comparados cualesquiera en cada conjunto, `c` es una constante (cuyo valor suele fijarse inicialmente en 1) y `d` es el grado polinómico. A medida que `d` aumenta, puede definirse una ecuación de hiperplano más precisa, pero esto tiende a conducir a un ajuste excesivo, por lo que es necesario establecer un equilibrio. Los puntos de datos `x` e `y` están en muchos casos en formato vectorial o incluso matricial, por lo que la potencia `T` representa la transposición de `x`.

La implementación de un kernel polinómico en MQL5, a título ilustrativo, podría adoptar la siguiente forma:

//+------------------------------------------------------------------+
//| Define a data point structure                                    |
//+------------------------------------------------------------------+
struct Sdatapoint
{  double      features[2];
   int               label;
                     Sdatapoint()
   {                 ArrayInitialize(features, 0.0);
      label = 0;
   };
                    ~Sdatapoint() {};

};

//+------------------------------------------------------------------+
//| Function to calculate the polynomial kernel value                |
//+------------------------------------------------------------------+
double PolynomialKernel(Sdatapoint &A, Sdatapoint &B, double Constant, int Degree)
{  double _kernel_sum = 0.0;
   for (int i = 0; i < 2; i++)
   {  _kernel_sum += (A.features[i] * B.features[i]);
   }
   _kernel_sum += Constant; // Add constant term
   return(pow(_kernel_sum, Degree));
}

Las ponderaciones de las relaciones entre los puntos de datos que se encuentran en conjuntos separados se calculan y almacenan en una matriz kernel. Esta matriz kernel cuantifica el espaciado de los puntos de datos y, por tanto, filtra para los vectores de soporte los puntos de datos que se encuentran en el borde de cada conjunto de datos y están más cerca del conjunto vecino.

Fuente.

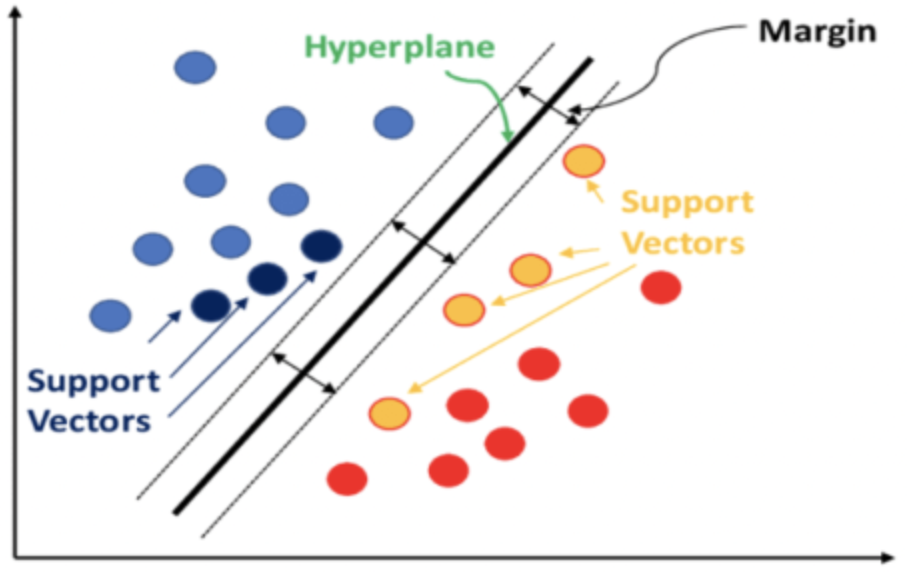
Estos vectores de soporte sirven de entrada para calcular la ecuación del hiperplano. Todo esto se maneja en funciones de biblioteca como: PyLIBSVM, o shogun para Python; o kernlab o SVMlight en R. Son funciones de biblioteca como éstas, dada la naturaleza compleja de derivar la ecuación del hiperplano, las que computan y dan salida al hiperplano.

A la hora de determinar la matriz kernel, se pueden considerar varios valores constantes y de grado polinómico para llegar a una solución óptima. Sin embargo, dado que esto complica aún más el ya de por sí complejo proceso de obtener un hiperplano a partir de una sola matriz al hacerlo sobre múltiples matrices, es más prudente seleccionar siempre una constante y un grado polinómico definitivos (o subóptimos según los conocimientos) una vez al principio y utilizarlos para llegar al hiperplano. Para ello, el valor de la constante también suele fijarse en 1. Y como cabría esperar, cuanto mayor sea el grado polinómico mejor será la clasificación, pero esto tiene riesgos de sobreajuste ya mencionados anteriormente.

Además, los grados polinómicos más altos tienden a ser más intensos desde el punto de vista computacional, por lo que es necesario establecer desde el principio un valor intuitivo que no sea demasiado alto.

Los kernels polinomiales que se consideran aquí son relativamente fáciles de entender, pero no son el núcleo más utilizado o preferido en muchas implementaciones de SVM, ya que esos derechos de presunción pertenecen al kernel de función de base radial.

El kernel de función de base radial es más comúnmente elegido porque la ventaja de SVM está en el manejo de datos multidimensionales y sobresale en esto mejor que el kernel polinómico. Una vez elegido el kernel, se emprendería el problema de optimización dual, en el que, como se ha mencionado anteriormente, los conjuntos de datos se trasladan a un espacio de dimensión superior y, gracias a las reglas del producto punto que se recogen en lo que se denomina el truco del kernel, esta optimización (de ida y vuelta) puede realizarse de forma más eficiente, al tiempo que se expresa de forma más sencilla. La naturaleza compleja de las ecuaciones de hiperplano para conjuntos de datos con más de 2 dimensiones lo hace indispensable. Al final, la ecuación del hiperplano adopta la forma siguiente:

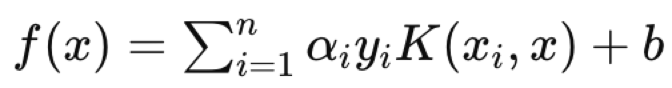
Donde:

• f(x)​ es la función de decisión.
• αi​ son los coeficientes obtenidos del proceso de optimización.
• yi​ son las etiquetas de clase.
• K(xi​,x) es la función kernel.
• b es el término de sesgo.

La ecuación del hiperplano define cómo se separan los dos conjuntos de datos mediante la función de decisión que asigna una etiqueta de clase que define a qué lado pertenece cualquier punto de consulta. Así, un punto de datos de consulta sería la `x` de la ecuación, siendo `xi` e `yi` los datos de entrenamiento y sus clasificadores, respectivamente.

Por otra parte, las aplicaciones de SVM son muy variadas y pueden ir desde el filtrado de spam, si se pueden incrustar las cabeceras y el contenido del correo electrónico en un formato estructurado, hasta la selección de solicitantes de préstamos para evitar impagos, etc. Lo que haría que SVM fuera ideal frente a otras alternativas de aprendizaje automático es la robustez para desarrollar modelos a partir de conjuntos de datos pequeños o muy sesgados.

Implementación en MQL5

La estructura del modelo que utilizamos para almacenar los valores `x` e `y` es muy similar a la de nuestras implementaciones recientes, con la diferencia de que aquí se añade un contador para cada tipo de clasificador. SVM es inherentemente un clasificador, y vamos a ver ejemplos de esto en acción donde estos contadores serán útiles.

Así, los valores del vector `x` son 2 en cada índice, ya que estamos restringiendo la multidimensionalidad de nuestros conjuntos de datos a 2 para poder utilizar el polinomio de Newton. El aumento de la dimensionalidad también entraña el riesgo de sobreajuste. La primera dimensión o valor de `x` son los cambios en el buffer de precios altos, mientras que la segunda serán los cambios en el buffer de precios bajos, como cabría esperar. La elección de los datos de entrada es ahora un aspecto crucial en el aprendizaje automático. Aunque los transformadores, las CNN y las RNN son muy ingeniosos, la decisión sobre los datos de entrada y cómo incrustarlos o normalizarlos puede ser más crítica.

Hemos elegido un conjunto de datos muy sencillo, pero el lector debe ser consciente de que su elección de los datos de entrada no se limita a los datos brutos de los precios o incluso a los valores de los indicadores, sino que podría incluir los valores de los indicadores económicos de las noticias. Y, de nuevo, la forma en que decidas normalizarlo puede marcar la diferencia.

//+------------------------------------------------------------------+
//| Function to get and prepare data.                                |
//+------------------------------------------------------------------+
double CSignalSVM::GetOutput(int Index)
{  double _get = 0.0;
   

        ....
        ....

   int _x = StartIndex() + Index;
   for(int i = 0; i < m_length; i++)
   {  for(int ii = 0; ii < Dimensions(); ii++)
      {  if(ii == 0) //dim-1
         {  m_model.x[i][ii] = m_high.GetData(StartIndex() + i + _x) - m_high.GetData(StartIndex() + i + _x + 1);
         }
         else if(ii == 1) //dim-2
         {  m_model.x[i][ii] = m_low.GetData(StartIndex() + i + _x) - m_low.GetData(StartIndex() + i + _x + 1);
         }
      }
      if(i > 0) //assign classifier
      {  if(m_close.GetData(StartIndex() + i + _x - 1) - m_close.GetData(StartIndex() + i + _x) > 0.0)
         {  m_model.y[i - 1] = 1;
            m_model.y1s++;
         }
         else if(m_close.GetData(StartIndex() + i + _x - 1) - m_close.GetData(StartIndex() + i + _x) < 0.0)
         {  m_model.y[i - 1] = 0;
            m_model.y0s++;
         }
      }
   }
//
   _get = SetOutput();
   return(_get);
}

Nuestro conjunto de datos `y` se basará en las variaciones del precio de cierre retardadas, como se ha hecho anteriormente. Introducimos contadores para las dos clases que se etiquetan como `y0` e `y1`. Estos simplemente registran, para cada barra procesada cuyos dos valores `x` se establecen, si el cambio posterior en el precio de cierre fue alcista (en cuyo caso se registra un 0) o fue bajista (donde se registraría un 1).

Dado que y es un vector, podríamos haber obtenido, como una nota al margen, estos conteos de 0 y 1 comparando sus valores actuales con vectores llenos de 0s y vectores llenos de 1s, ya que los valores devueltos serían efectivamente un conteo de los 0s y 1s presentes en el vector y, respectivamente.

La función 'set-output' es otra adición a las funciones que hemos tenido, en el procesamiento de la información de nuestro modelo. Toma los valores del vector x para cada clase e interpola un punto medio entre los dos conjuntos que podría servir como hiperplano de los dos conjuntos. Este no es el enfoque SVM como ya se ha mencionado, pero lo que esto hace por nosotros, ya que queremos definir un hiperplano por el polinomio de Newton, es darnos un conjunto de puntos con los que podemos trabajar para derivar una ecuación de hiperplano.

//+------------------------------------------------------------------+
//| Function to set and train data                                   |
//+------------------------------------------------------------------+
double CSignalSVM::SetOutput(void)
{  double _set = 0.0;
   matrix _a,_b;
   Classifier(_a,_b);
   if(_a.Rows() * _b.Rows() > 0)
   {  matrix _interpolate;
      _interpolate.Init(_a.Rows() * _b.Rows(), Dimensions());
      for(int i = 0; i < int(_a.Rows()); i++)
      {  for(int ii = 0; ii < int(_b.Rows()); ii++)
         {  _interpolate[(i*_b.Rows())+ii][0] = 0.5 * (_a[i][0] + _b[ii][0]);
            _interpolate[(i*_b.Rows())+ii][1] = 0.5 * (_a[i][1] + _b[ii][1]);
         }
      }
      vector _w;
      vector _x = _interpolate.Col(0);
      vector _y = _interpolate.Col(1);
      _w.Init(m_model.y0s * m_model.y1s);
      _w[0] = _y[0];
      m_newton.Set(_w, _x, _y);
      double _xx = m_model.x[0][0], _yy = m_model.x[0][1], _zz = 0.0;
      m_newton.Get(_w, _xx, _zz);
      if(_yy < _zz)
      {  _set = 100.0;
      }
      else if(_yy > _zz)
      {  _set = -100.0;
      }
      _set *= Regressor(_x, _y, _xx, _yy);
   }
   return(_set);
}

Consideramos 3 enfoques para derivar el hiperplano dentro de este método. El primer enfoque tiene en cuenta todos los puntos de cada conjunto para obtener los puntos del hiperplano interpolando la media de cada punto de un conjunto con cada punto del conjunto alternativo. Es evidente que no se consideran vectores de soporte, pero se presentan aquí a efectos de estudio y comparación con los demás enfoques.

El segundo método es similar al primero, con la única diferencia de que el valor pronosticado de `y` es regresivo, lo que significa que en lugar de tenerlo como un 0 o 1, utilizamos una función "reguladora" para transformar o normalizar los pronósticos de salida como un valor de punto flotante en el rango de 0,0 a 1,0. De este modo se obtiene un sistema que, en principio, se aleja aún más de las SVM, pero que sigue utilizando un hiperplano para diferenciar puntos de datos bidimensionales.

//+------------------------------------------------------------------+
//| Regressor for the model                                          |
//+------------------------------------------------------------------+
double CSignalSVM::Regressor(vector &X, vector &Y, double XX, double YY)
{  double _x_max = fmax(X.Max(), XX);
   double _x_min = fmin(X.Min(), XX);
   double _y_max = fmax(Y.Max(), YY);
   double _y_min = fmin(Y.Min(), YY);
   return(0.5 * ((1.0 - ((_x_max - XX) / fmax(m_symbol.Point(), _x_max - _x_min))) + (1.0 - ((_y_max - YY) / fmax(m_symbol.Point(), _y_max - _y_min)))));
}

Podemos obtener un valor regresivo aproximado comparando el valor previsto con el valor máximo y mínimo de su conjunto, de forma que si coincide con el mínimo se devuelve 0 frente al 1 que se devolvería si coincidiera con el valor máximo.

En tercer y último lugar, mejoramos el método de la parte 2 añadiendo una función "clasificadora" que filtra los puntos de cada uno de los conjuntos que se utilizan para derivar el hiperplano. Al considerar los puntos que están más lejos del centroide de su propio conjunto y más cerca del centroide del conjunto opuesto, obtenemos 2 subconjuntos de puntos, uno de cada clase, que pueden utilizarse para interpolar el límite del hiperplano entre los dos conjuntos.

//+------------------------------------------------------------------+
//| 'Classifier' for the model that identifies Support Vector points |
//|  for each set.                                                   |
//+------------------------------------------------------------------+
void CSignalSVM::Classifier(matrix &A, matrix &B)
{  if(m_model.y0s * m_model.y1s > 0)
   {  matrix _a_centroid, _b_centroid;
      _a_centroid.Init(1, Dimensions());
      _b_centroid.Init(1, Dimensions());
      for(int i = 0; i < m_length; i++)
      {  if(m_model.y[i] == 0)
         {  _a_centroid[0][0] += m_model.x[i][0];
            _a_centroid[0][1] += m_model.x[i][1];
         }
         else if(m_model.y[i] == 1)
         {  _b_centroid[0][0] += m_model.x[i][0];
            _b_centroid[0][1] += m_model.x[i][1];
         }
      }
      _a_centroid[0][0] /= m_model.y0s;
      _a_centroid[0][1] /= m_model.y0s;
      _b_centroid[0][0] /= m_model.y1s;
      _b_centroid[0][1] /= m_model.y1s;
      double _a_sd = 0.0, _b_sd = 0.0;
      double _ab_sd = 0.0, _ba_sd = 0.0;
      for(int i = 0; i < m_length; i++)
      {  if(m_model.y[i] == 0)
         {  double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            _a_sd += sqrt(_0);
            double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            _ab_sd += sqrt(_1);
         }
         else if(m_model.y[i] == 1)
         {  double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            _b_sd += sqrt(_1);
            double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            _ba_sd += sqrt(_0);
         }
      }
      _a_sd /= m_model.y0s;
      _ab_sd /= m_model.y0s;
      _b_sd /= m_model.y1s;
      _ba_sd /= m_model.y1s;
      for(int i = 0; i < m_length; i++)
      {  if(m_model.y[i] == 0)
         {  double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            if(sqrt(_0) >= _a_sd && _ab_sd <= sqrt(_1))
            {  A.Resize(A.Rows()+1,Dimensions());
               A[A.Rows()-1][0] = m_model.x[i][0];
               A[A.Rows()-1][1] = m_model.x[i][1];
            }
         }
         else if(m_model.y[i] == 1)
         {  double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            if(sqrt(_1) >= _b_sd && _ba_sd <= sqrt(_0))
            {  B.Resize(B.Rows()+1,Dimensions());
               B[B.Rows()-1][0] = m_model.x[i][0];
               B[B.Rows()-1][1] = m_model.x[i][1];
            }
         }
      }
   }
}

El código compartido anteriormente que realiza esta tarea es un poco extenso, y estoy seguro de que se pueden hacer implementaciones más eficientes, especialmente si se utilizan las funciones integradas de los tipos de datos vector y matriz que se introdujeron recientemente en MQL5. Pero lo que estamos haciendo es encontrar primero el centroide (o media) de cada conjunto de datos. Una vez definido esto, procedemos a calcular la desviación típica de cada conjunto de datos, que se obtiene mediante las variables que llevan el sufijo `_sd`. Una vez que disponemos de las coordenadas del centroide y de la magnitud de la desviación típica, podemos medir y comparar para cada punto la distancia que lo separa de su centroide, así como la distancia que lo separa del centroide del conjunto de datos opuesto, sirviendo las desviaciones típicas calculadas como umbral para determinar si está demasiado lejos o demasiado cerca.

Los puntos interpolados son todo lo que necesitamos para definir una ecuación con el polinomio de Newton. Como vimos aquí, cuantos más puntos se aporten, mayor será el exponente de la ecuación. El número máximo de puntos interpolados que podemos utilizar con el polinomio de Newton está controlado por el tamaño de los conjuntos de datos y esto es directamente proporcional al parámetro `m_length`, una variable que establece cuántos puntos de datos en la historia necesitamos mirar hacia atrás cuando definimos los dos conjuntos de datos en el modelo.

De los tres métodos utilizados para derivar un hiperplano, sólo el último se parece a los métodos típicos de SVM. Al seleccionar los puntos de cada conjunto que están más cerca del límite del conjunto y que, por tanto, son más relevantes para el hiperplano, definimos los vectores de soporte. Estos puntos del vector de soporte sirven de entrada a nuestra clase de polinomios de Newton para derivar la ecuación del hiperplano. Por el contrario, si fuéramos a hacer una SVM estricta, añadiríamos una dimensión extra a nuestros puntos de datos para una diferenciación extra mientras iteramos a través de las constantes en la ecuación del kernel polinómico que permite esto. Incluso con sólo datos bidimensionales es claramente un orden de magnitud más complicado, por no hablar de los recursos informáticos implicados. De hecho, por simplicidad o mejor práctica, se supone que una de estas constantes (la `c`) es siempre 1, mientras que sólo se optimiza la variable del grado del polinomio (la `d` en las ecuaciones anteriores). Y como puedes imaginar, con conjuntos de datos que tienen más de 2 dimensiones, esto claramente requeriría una biblioteca de ^terceros porque la ecuación del exponente 4, 5 o `n` que se busca será varios órdenes de magnitud más compleja.

La implementación del polinomio de Newton es muy similar a lo que cubrimos en el anterior artículo relacionado, salvo por algunas depuraciones en la función "Get" que ejecuta la ecuación construida para determinar el siguiente valor de `y`. Se adjunta a continuación.

Resultados de las pruebas.

Los 3 archivos de clase de señal adjuntos al final de este artículo se pueden ensamblar en un asesor experto mediante el asistente MQL5 Wizard. Hay ejemplos de cómo hacerlo en los artículos aquí y aquí.

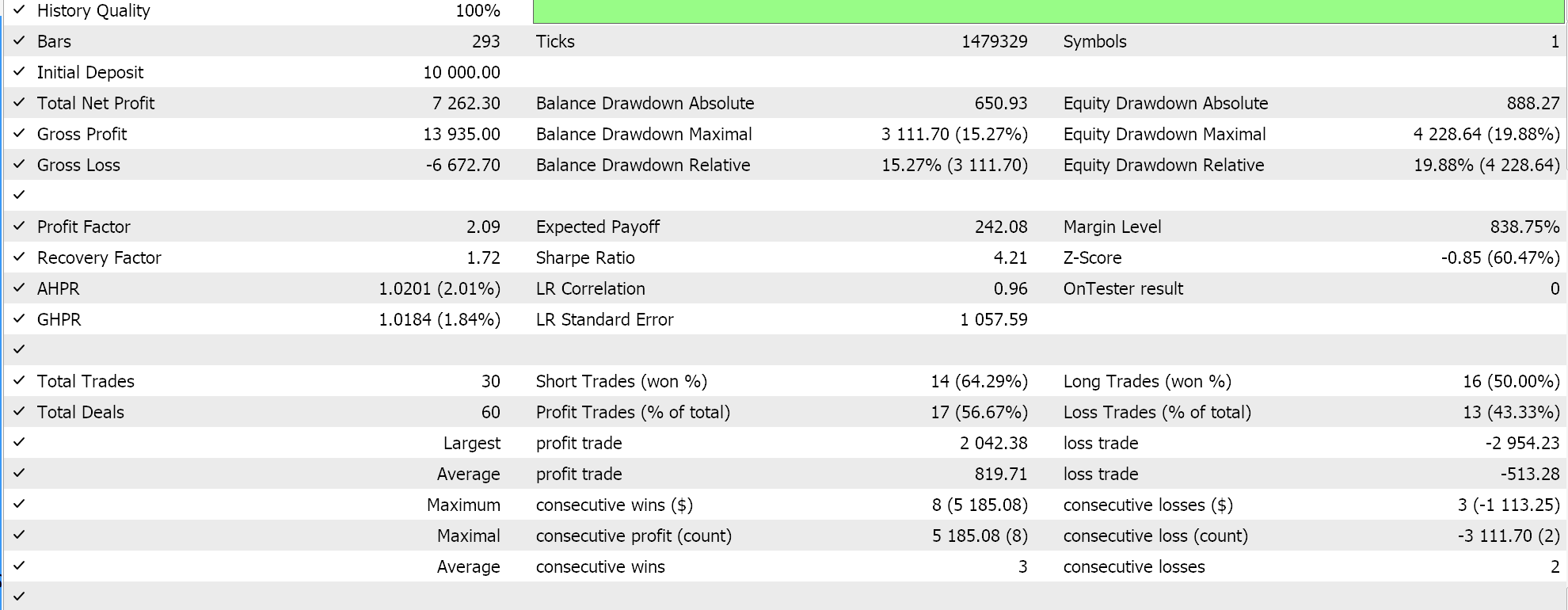
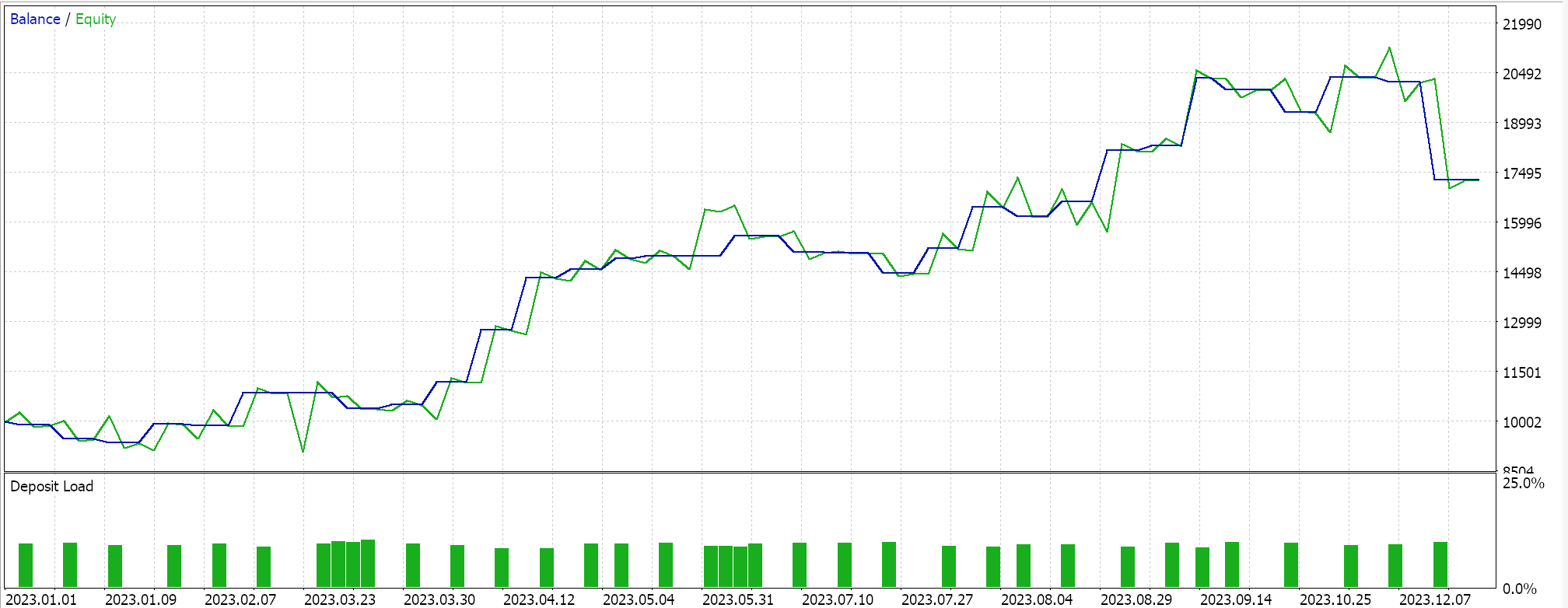
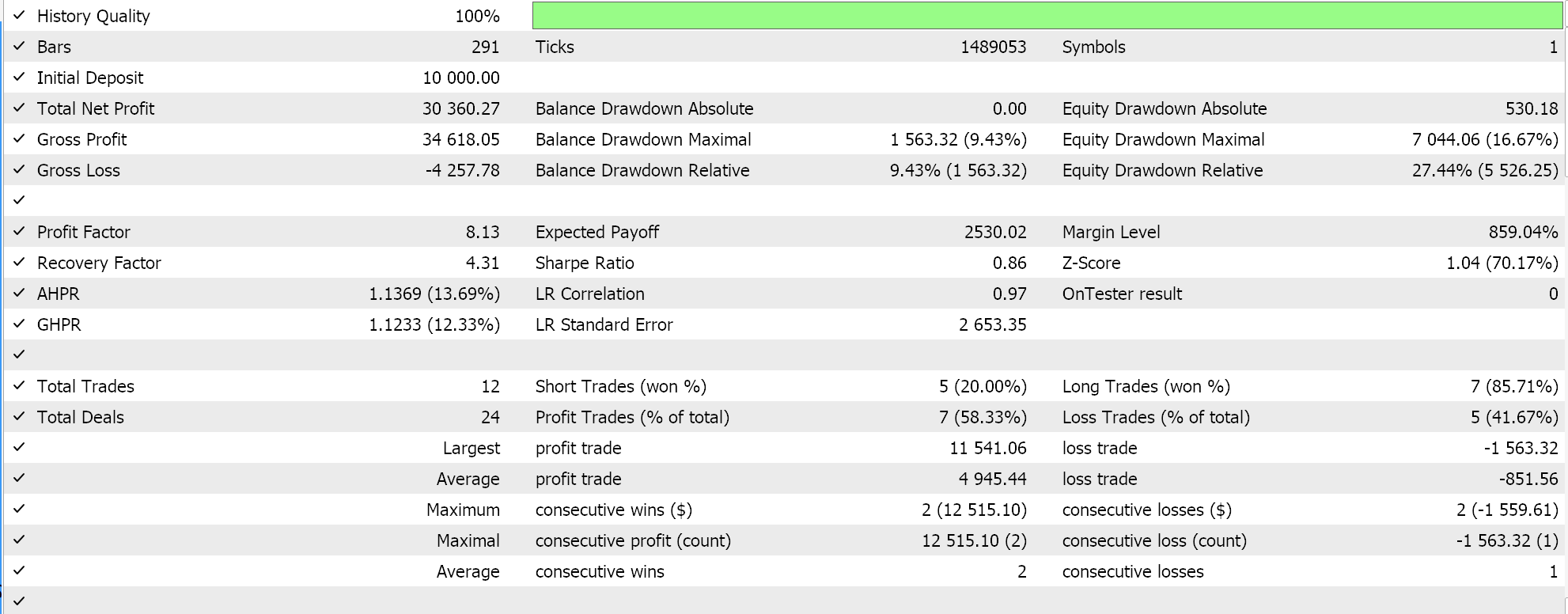
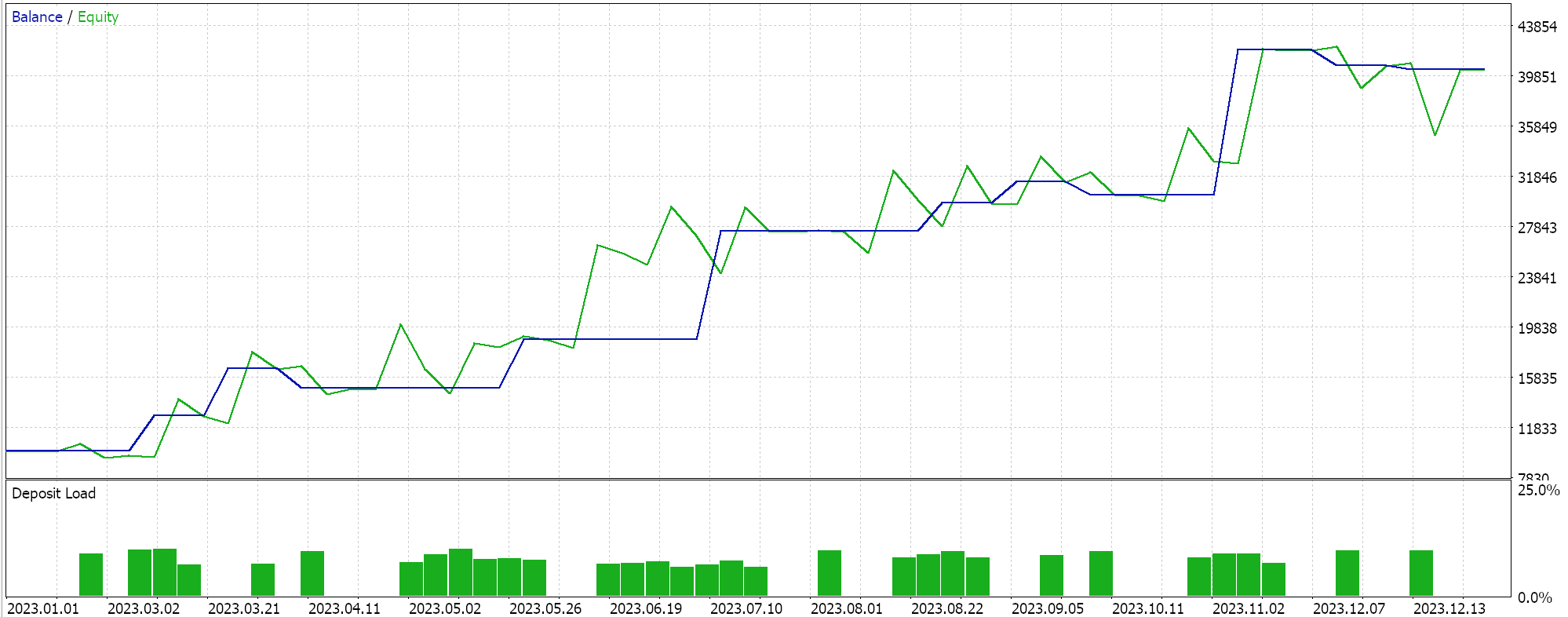
Así, al realizar las pruebas de la primera implementación en la que el hiperplano se obtiene interpolando todos los puntos de ambos conjuntos sin buscar vectores de soporte, obtenemos los siguientes resultados:

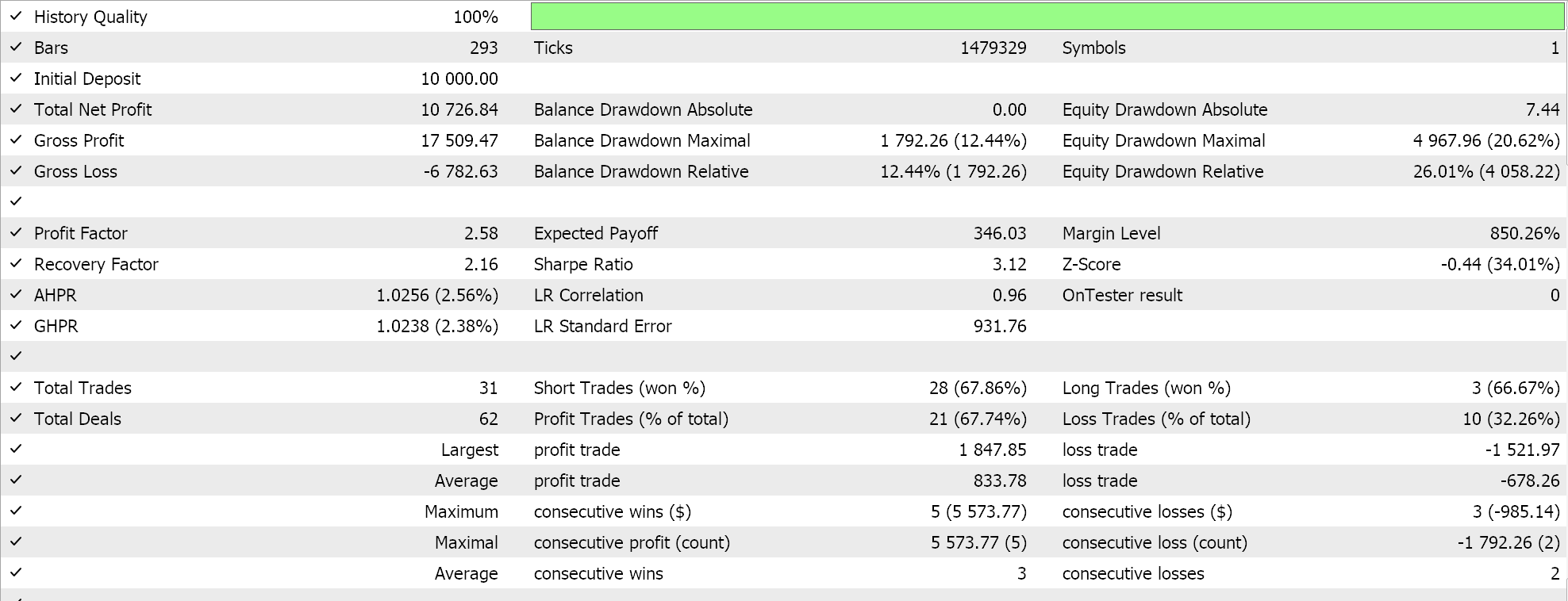
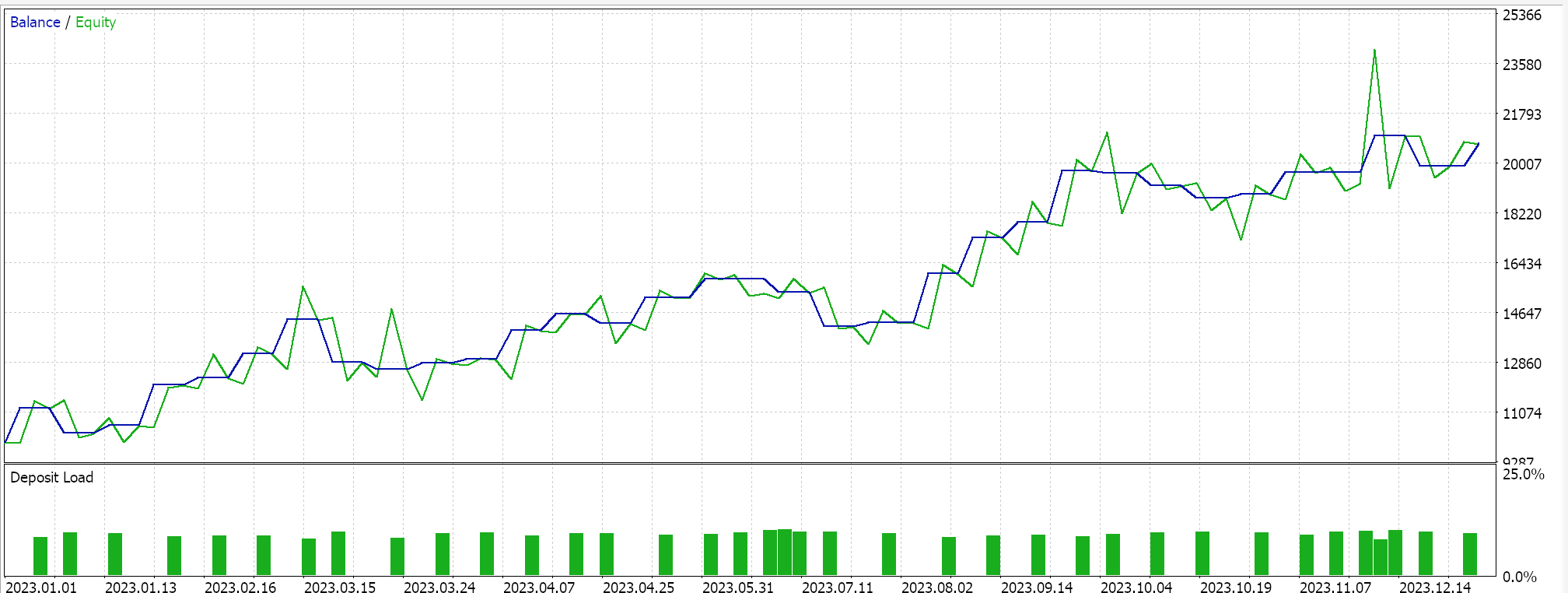
Si realizamos pruebas similares, como las anteriores, donde nuestro símbolo de prueba es EURJPY en el marco temporal diario para el año 2023, para el segundo método, que solo añade regresión al método anterior, tenemos lo siguiente:

Por último, el enfoque que más se parece a la SVM, que examina cualquiera de los conjuntos de datos en busca de puntos de vectores de soporte antes de derivar su hiperplano, cuando se prueba nos da los siguientes resultados:

De nuestros informes anteriores se puede deducir que el método que utiliza vectores de soporte es el más prometedor, lo que no debería sorprender dado el ajuste adicional que implica (aunque el número de parámetros es idéntico en los tres métodos).

Como nota al margen, esta prueba se realiza en ticks reales con órdenes limitadas y no se utiliza Take Profit ni Stop Loss. Como siempre, es necesario realizar más pruebas antes de sacar conclusiones más significativas. Sin embargo, es interesante observar que, con el mismo número de parámetros de entrada, el método del vector de soporte obtiene mejores resultados. Hizo menos operaciones y eso le dio un rendimiento drásticamente mejor que los otros dos enfoques.

La adición de la regresión en el segundo enfoque sólo mejoró marginalmente el rendimiento, como puede verse en los resultados. El número de operaciones también fue casi el mismo, aunque la preselección de los puntos del conjunto de datos en busca de vectores de soporte antes de definir el hiperplano supuso claramente un cambio de juego. Los informes de MetaTrader son muy subjetivos, y muchos debaten cuál sería la estadística más crítica en la que confiar como un indicador de si el sistema de comercio puede avanzar, y yo tampoco tengo una respuesta definitiva sobre ese tema. Sin embargo, creo que una comparación entre la ganancia promedio y la pérdida promedio (por operación), teniendo en cuenta también la relación entre las victorias consecutivas promedio y las pérdidas consecutivas promedio, podría ser reveladora. Todos estos valores suelen combinarse para calcular un coeficiente denominado "expectativa". Esto es muy diferente de la ganancia esperada, que es simplemente el beneficio dividido por todas las operaciones. Si comparamos la expectativa de todos los informes, el método que utilizó vectores de soporte es mejor por un orden de magnitud de casi 10 en comparación con los otros 2 enfoques.

Conclusión

Entonces, para resumir, hemos examinado otro ejemplo de desarrollo y prueba rápida de una posible idea de comercio para evaluar si es una mejora o si encaja dentro de la estrategia existente.

SVM es un algoritmo bastante complicado que rara vez, si es que alguna vez, se implementa sin la ayuda de una biblioteca de ^terceros, ya sea PyLIBSVM para Python o SVMlight para R, y más allá de eso, uno de los parámetros optimizables a menudo se toma como igual a 1 para simplificar este proceso. Para recapitular, este proceso consiste en aumentar las dimensiones de una copia del conjunto de datos estudiado mediante una fórmula reversible específica denominada kernel polinómico. La relativa sencillez y reversibilidad de este kernel polinómico es lo que le ha valido el nombre de "truco del kernel". Esta simplicidad y reversibilidad, que es posible gracias a los productos punto, es muy necesaria en casos donde el conjunto de datos tiene más de 2 dimensiones, porque, como se puede imaginar, en casos de conjuntos de datos con una dimensionalidad muy alta, la ecuación del hiperplano que clasifica correctamente tales conjuntos de datos tiende a ser muy compleja.

Entonces, al introducir una forma alternativa de derivar el hiperplano a través del polinomio de Newton, que en primer lugar no es tan intensiva en cálculos, pero que también es mucho más fácil de entender y presentar, las variantes de implementaciones de SVM no solo pueden ser probadas, sino que también podrían considerarse como alternativas a la estrategia existente o como complementarias. El IDE de MQL5 permite ambos escenarios, en el primero de los cuales desarrollarías un sistema de comercio completamente nuevo basado en el código de la clase de señal compartido aquí. Pero quizás lo que a menudo se pasa por alto es el potencial acumulativo que presenta el asistente MQL5 Wizard, que permite ensamblar y probar múltiples estrategias simultáneamente. Esto también se puede hacer de manera rápida y con un mínimo de codificación al evaluar ideas y estrategias en la etapa preliminar. Y como siempre, además de observar la clase de señal de las clases ensambladas del asistente, también se pueden explorar la clase `trailing`y las clases de gestión monetaria.