Aprendizaje automático y ciencia de datos (Parte 15): SVM, una herramienta útil en el arsenal de los tráders
307
0
Contenido:
- Introducción
- ¿Qué es un hiperplano?
- Método lineal de vectores soporte
- SVM dual
- Separación rígida
- Separación suave
- Entrenamiento del modelo del método lineal de vectores de soporte
- Obtención de previsiones a partir de un modelo lineal de vectores de soporte
- Entrenamiento y prueba del modelo lineal de vectores de soporte
- Recogida y normalización de datos
- Ejemplar de la clase DualSVMONNX. Inicialización de clases
- Entrenamiento del modelo SVM dual en Python
- Conversión del modelo de vectores de soporte de sklearn a ONNX
- Conclusiones finales
Introducción
El método de la máquina de vectores soporte (SVM) es una forma de aprendizaje automático supervisado que se utiliza en tareas de clasificación y regresión lineal y no lineal, y ocasionalmente para tareas de detección de valores atípicos.
A diferencia de los métodos de clasificación bayesiana y regresión logística, que usan modelos matemáticos sencillos para clasificar la información, la SVM utiliza sofisticadas funciones matemáticas de aprendizaje destinadas a encontrar el hiperplano óptimo que separa los datos en un espacio N-dimensional.
El algoritmo SVM se usa más comúnmente para tareas de clasificación. Estos son los tipos de tareas que abordaremos en este artículo.
¿Qué es un hiperplano?
Un hiperplano es una línea que se utiliza para separar puntos de datos de clases diferentes.
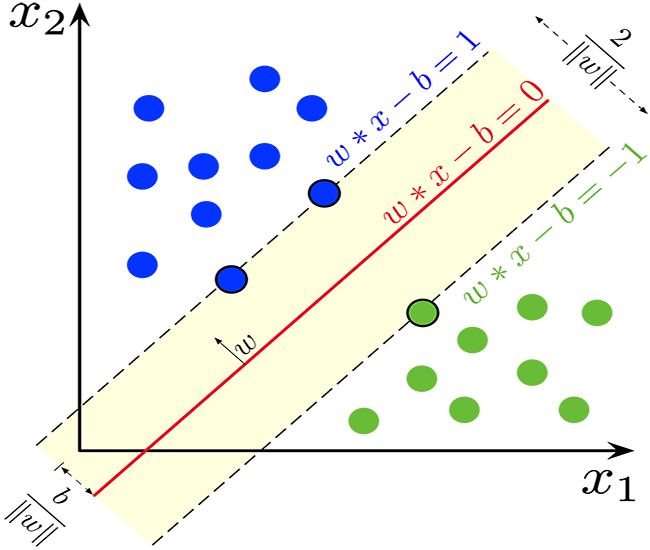
El hiperplano posee las siguientes propiedades:
Dimensionalidad. En tareas de clasificación binaria, un hiperplano es un subespacio (d-1)-dimensional, donde d será la dimensionalidad del espacio de características. Por ejemplo, en un espacio de características bidimensional, un hiperplano será una línea unidimensional.
Matemáticamente, el hiperplano puede representarse usando una ecuación lineal de la forma:
- vector ortogonal al hiperplano, y que determina su orientación.
- vector de características.
b — término de desplazamiento escalar que aleja el hiperplano del inicio de las coordenadas.
Separación. El hiperplano divide el espacio de características en dos semiespacios:
El área donde 
corresponde a una clase.
El área donde 
corresponde a otra clase.
Separación. En la SVM, el objetivo consiste en encontrar un hiperplano que maximice la distancia entre el hiperplano y los puntos de datos más cercanos de cualquier clase. Estos puntos de datos más próximos se denominan "vectores de soporte". La SVM trata de encontrar un hiperplano que maximice la separación y minimice el error de clasificación.
Clasificación. El hiperplano óptimo encontrado puede usarse para clasificar los nuevos puntos de datos. Calculando 
, podremos determinar en qué lado del hiperplano se encuentra el punto de datos y asignarlo así a una de las dos clases.
El concepto de hiperplano supone un elemento clave de los vectores de soporte, ya que constituye la base del clasificador con la separación máxima. El objetivo del método de vectores soporte es encontrar el hiperplano que mejor separe los datos manteniendo la máxima separación entre clases, lo que a su vez aumentará el carácter general del modelo y su robustez ante datos no vistos.
double CLinearSVM::hyperplane(vector &x) { return x.MatMul(W) - B; }
y 
son equivalentes y describen el mismo hiperplano. La selección de una concreta es una cuestión de preferencia personal, pero ambas son equivalentes algebraicamente. En mi código, no he transpuesto la matriz x porque decidí usar W como vector, por lo que no será necesario.Como hemos mencionado antes, el término de desplazamiento, denotado como b, será un término escalar, por lo que hemos tendido que declarar una variable double para él.
class CLinearSVM { protected: CMatrixutils matrix_utils; CMetrics metrics; CPreprocessing<vector, matrix> *normalize_x; vector W; //Weights vector double B; //bias term bool is_fitted_already; struct svm_config { uint batch_size; double alpha; double lambda; uint epochs; }; private: svm_config config;
Aquí utilizaremos la clase CLinearSVM. En general, en este documento consideraremos dos variantes del método de vectores de soporte: la lineal y la dual.
Método lineal de vectores soporte
La SVM lineal es un tipo de vectores de soportes que utiliza un núcleo lineal, lo cual significa que utilizará un límite de decisión lineal para separar los puntos de datos. En la SVM lineal, se trabaja directamente con el espacio de características, y el problema de optimización se expresa con frecuencia en su forma más simple. El objetivo principal de la SVM lineal será encontrar el hiperplano lineal que mejor separe los datos.
Este tipo funcionará mejor con datos linealmente separables.
SVM dual
La forma dual no supone un tipo aparte del método de vectores de soporte, sino más bien una representación del problema de optimización SVM. La forma SVM dual es una reformulación matemática del problema de optimización original que permite métodos de solución más eficaces. Los multiplicadores de Lagrange se introducirán en la fórmula para maximizar la función objetivo dual, que será equivalente al problema principal. La resolución del problema dual conducirá a la definición de los vectores de soporte que sean cruciales para la clasificación.
Este tipo es el más adecuado para los datos que no son linealmente separables.
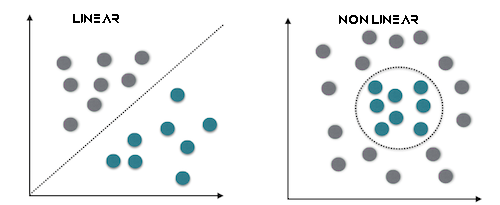
Además, las separaciones duras o blandas pueden usarse para tomar decisiones en el clasificador SVM usando un hiperplano.
Separación rígida
Si los datos de entrenamiento son linealmente separables, podemos seleccionar dos hiperplanos paralelos que separen las dos clases de datos de forma que la distancia entre ellos sea lo mayor posible. El área delimitada por estos dos hiperplanos se denomina separación, y el hiperplano con una separación máxima será el que se encuentre a medio camino entre ellos. Utilizando un conjunto de datos normalizado o estandarizado, estos hiperplanos pueden describirse usando las ecuaciones
(todo lo que se encuentre en este límite o por encima de él pertenecerá a la misma clase etiquetada como 1)
y
(todo lo que esté por encima o por debajo de este límite pertenecerá a otra clase denominada -1).
La distancia entre ellos será 2/||w||, mientras que para maximizar la distancia, ||w|| deberá minimizarse. Para evitar que cualquier punto de datos caiga dentro del campo, añadiremos una restricción: yi(wTXi -b) >= 1, donde yi = será la fila i-ésima del objetivo, mientras que Xi = será la fila i-ésima de X.
Separación suave
Para utilizar SVM en casos en los que los datos no son linealmente separables, se ha introducido una función de pérdida bisagra.
.
Aquí 
es el i-ésimo objetivo (es decir, en este caso 1 o -1), mientras que 
es la i-ésima muestra.
Si el punto de datos tiene una clase = 1 entonces la pérdida será 0, en caso contrario será la distancia entre el límite y el punto de datos. Nuestro objetivo es minimizar
donde λ supone la compensación entre el tamaño de la separación, mientras que xi se encuentra a la derecha de esa separación. Si el valor de λ es demasiado bajo, la ecuación se convierte en una separación rígida.
Utilizaremos la separación rígida para la clase SVM lineal. Esto resulta posible gracias a la función de signo, que devuelve el signo de un número real en notación matemática. Se expresa como:
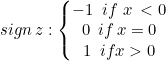
int CLinearSVM::sign(double var) { if (var == 0) return (0); else if (var < 0) return -1; else return 1; }
Entrenamiento del modelo del método lineal de vectores de soporte
El proceso de entrenamiento del método de vectores de soporte SVM consiste en hallar el hiperplano óptimo que separa los datos maximizando la brecha. La brecha, o separación, será la distancia entre el hiperplano y los puntos de datos más cercanos de cualquier clase. El objetivo es hallar un hiperplano que maximice la brecha y minimice los errores de clasificación.
Actualizamos los pesos (w):
а. Primer miembro. El primer término de la función de pérdida se corresponde con la pérdida bisagra, que mide el error de clasificación. Para cada ejemplo de entrenamiento icalcularemos la derivada de la función de pérdida con respecto a los pesos w:
- Si
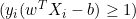, esto significará que el punto de datos está correctamente clasificado y fuera del campo la derivada será 0. - Si
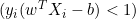, significará que el punto de datos se encuentra dentro del campo o mal clasificado, y la derivada será 
.
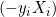b. Segundo miembro:
El segundo término representará la regularización. De este modo se conseguirá un pequeño intervalo y se evitará el sobreentrenamiento. La derivada de este término con respecto a los pesos w será 2λw, donde λ será el parámetro de regularización.
c. Combinamos las derivadas del primer y el segundo de los sumandos,
Actualización de los pesos w:
-Si 
, actualizaremos los pesos así: 
, y si 
, actualizaremos así: 
. Aquí α será la tasa de aprendizaje.
Actualización del punto de intersección (b):
а. Primer miembro:
La derivada de la función de pérdida bisagra con respecto al punto de intersección b se calculará de forma similar a los pesos:
- Si
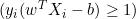, la derivada será cero. - Si
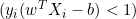, la derivada será 
.
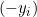b. Segundo miembro:
El segundo miembro no dependerá del punto de intersección, por lo que su derivada en b será igual a cero. c. Actualizamos el punto de intersección b:
- Si
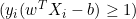, actualizaremos 
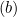así: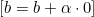 
- Si
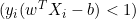, actualizaremos 
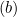así: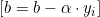 
Variable de desajuste (ξ):
La variable de desajuste (ξ) permite que algunos puntos de datos estén dentro de una separación, lo cual significa que estarán mal clasificados o se encontrarán dentro de esa separación. La condición 
significa que el límite de la solución deberá estar al menos en la zona 
unidades separada del punto de datos i.
Por consiguiente, el proceso de aprendizaje de SVM implicará la actualización de los pesos y la intersección basada en la pérdida bisagra y el término de regularización. El objetivo consistirá en encontrar el hiperplano óptimo que maximice la brecha considerando los posibles errores de clasificación dentro del límite permitido por la variable de desajuste. Este proceso suele resolverse usando técnicas de optimización. En este caso, los vectores de soporte se identificarán durante el entrenamiento. Su finalidad es definir el límite de decisión.
void CLinearSVM::fit(matrix &x, vector &y) { matrix X = x; vector Y = y; ulong rows = X.Rows(), cols = X.Cols(); if (X.Rows() != Y.Size()) { Print("Support vector machine Failed | FATAL | X m_rows not same as yvector size"); return; } W.Resize(cols); B = 0; normalize_x = new CPreprocessing<vector, matrix>(X, NORM_STANDARDIZATION); //Normalizing independent variables //--- if (rows < config.batch_size) { Print("The number of samples/rows in the dataset should be less than the batch size"); return; } matrix temp_x; vector temp_y; matrix w, b; vector preds = {}; vector loss(config.epochs); during_training = true; for (uint epoch=0; epoch for (uint batch=0; batch<=(uint)MathFloor(rows/config.batch_size); batch+=config.batch_size) { temp_x = matrix_utils.Get(X, batch, (config.batch_size+batch)-1); temp_y = matrix_utils.Get(Y, batch, (config.batch_size+batch)-1); #ifdef DEBUG_MODE: Print("X\n",temp_x,"\ny\n",temp_y); #endif for (uint sample=0; sample // yixiw-b≥1 if (temp_y[sample] * hyperplane(temp_x.Row(sample)) >= 1) { this.W -= config.alpha * (2 * config.lambda * this.W); // w = w + α* (2λw - yixi) } else { this.W -= config.alpha * (2 * config.lambda * this.W - ( temp_x.Row(sample) * temp_y[sample] )); // w = w + α* (2λw - yixi) this.B -= config.alpha * temp_y[sample]; // b = b - α* (yi) } } } //--- Print the loss at the end of an epoch is_fitted_already = true; preds = this.predict(X); loss[epoch] = preds.Loss(Y, LOSS_BCE); printf("---> epoch [%d/%d] Loss = %f Accuracy = %f",epoch+1,config.epochs,loss[epoch],metrics.confusion_matrix(Y, preds, false)); #ifdef DEBUG_MODE: Print("W\n",W," B = ",B); #endif } during_training = false; return; }
Obtención de previsiones a partir de un modelo lineal de vectores de soporte
Para obtener predicciones de nuestro modelo, necesitaremos pasar los datos a la función de signo después de que el hiperplano haya dado resultados.
int CLinearSVM::predict(vector &x) { if (!is_fitted_already) { Print("Err | The model is not trained, call the fit method to train the model before you can use it"); return 1000; } vector temp_x = x; if (!during_training) normalize_x.Normalization(temp_x); //Normalize a new input data when we are not running the model in training return sign(hyperplane(temp_x)); }
Entrenamiento y prueba del modelo lineal de vectores de soporte
Deberemos probar un modelo antes de implantarlo para hacer predicciones significativas sobre los datos del mercado. Comenzaremos inicializando un ejemplar de la clase SVM Lineal.
#include CLinearSVM *svm; input uint bars = 1000; input uint epochs_ = 1000; input uint batch_size_ = 64; input double alpha__ =0.1; input double lambda_ = 0.01; bool train_once; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- svm = new CLinearSVM(batch_size_, alpha__, epochs_, lambda_); train_once = false; //--- return(INIT_SUCCEEDED); }
Continuaremos recopilando datos. Para ello, utilizaremos 4 variables independientes: RSI, HIGH BANDS BOLLINGER, LOW y MID.
vec_.CopyIndicatorBuffer(rsi_handle, 0, 0, bars); dataset.Col(vec_, 0); vec_.CopyIndicatorBuffer(bb_handle, 0, 0, bars); dataset.Col(vec_, 1); vec_.CopyIndicatorBuffer(bb_handle, 1, 0, bars); dataset.Col(vec_, 2); vec_.CopyIndicatorBuffer(bb_handle, 2, 0, bars); dataset.Col(vec_, 3); open.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_OPEN, 0, bars); close.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_CLOSE, 0, bars); for (ulong i=0; i //preparing the independent variable dataset[i][4] = close[i] > open[i] ? 1 : -1; // if price closed above its opening thats bullish else bearish
Finalizaremos el proceso de recogida de datos dividiéndolos en muestras de entrenamiento y de prueba.
matrix_utils.TrainTestSplitMatrices(dataset,train_x,train_y,test_x,test_y,0.7,42); //split the data into training and testing samples
Entrenamiento/Selección de modelos
svm.fit(train_x, train_y);
Resultado
0 15:15:42.394 svm test (EURUSD,H1) ---> epoch [1/1000] Loss = 7.539322 Accuracy = 0.489000 IK 0 15:15:42.395 svm test (EURUSD,H1) ---> epoch [2/1000] Loss = 7.499849 Accuracy = 0.491000 EG 0 15:15:42.395 svm test (EURUSD,H1) ---> epoch [3/1000] Loss = 7.499849 Accuracy = 0.494000 .... .... GG 0 15:15:42.537 svm test (EURUSD,H1) ---> epoch [998/1000] Loss = 6.907756 Accuracy = 0.523000 DS 0 15:15:42.537 svm test (EURUSD,H1) ---> epoch [999/1000] Loss = 7.006438 Accuracy = 0.521000 IM 0 15:15:42.537 svm test (EURUSD,H1) ---> epoch [1000/1000] Loss = 6.769601 Accuracy = 0.516000
Observamos la precisión del modelo tanto en el entrenamiento como en las pruebas.
vector train_pred = svm.predict(train_x), test_pred = svm.predict(test_x); printf("Train accuracy = %f",metrics.confusion_matrix(train_y, train_pred, true)); printf("Test accuracy = %f ",metrics.confusion_matrix(test_y, test_pred, true));
Resultado
CH 0 15:15:42.538 svm test (EURUSD,H1) Confusion Matrix IQ 0 15:15:42.538 svm test (EURUSD,H1) [[171,175] HE 0 15:15:42.538 svm test (EURUSD,H1) [164,190]] DQ 0 15:15:42.538 svm test (EURUSD,H1) NO 0 15:15:42.538 svm test (EURUSD,H1) Classification Report JD 0 15:15:42.538 svm test (EURUSD,H1) LO 0 15:15:42.538 svm test (EURUSD,H1) _ Precision Recall Specificity F1 score Support JQ 0 15:15:42.538 svm test (EURUSD,H1) -1.0 0.51 0.49 0.54 0.50 346.0 DH 0 15:15:42.538 svm test (EURUSD,H1) 1.0 0.52 0.54 0.49 0.53 354.0 HL 0 15:15:42.538 svm test (EURUSD,H1) FG 0 15:15:42.538 svm test (EURUSD,H1) Accuracy 0.52 PP 0 15:15:42.538 svm test (EURUSD,H1) Average 0.52 0.52 0.52 0.52 700.0 PS 0 15:15:42.538 svm test (EURUSD,H1) W Avg 0.52 0.52 0.52 0.52 700.0 FK 0 15:15:42.538 svm test (EURUSD,H1) Train accuracy = 0.516000 MS 0 15:15:42.538 svm test (EURUSD,H1) Confusion Matrix LI 0 15:15:42.538 svm test (EURUSD,H1) [[79,74] CM 0 15:15:42.538 svm test (EURUSD,H1) [68,79]] FJ 0 15:15:42.538 svm test (EURUSD,H1) HF 0 15:15:42.538 svm test (EURUSD,H1) Classification Report DM 0 15:15:42.538 svm test (EURUSD,H1) NH 0 15:15:42.538 svm test (EURUSD,H1) _ Precision Recall Specificity F1 score Support NN 0 15:15:42.538 svm test (EURUSD,H1) -1.0 0.54 0.52 0.54 0.53 153.0 PQ 0 15:15:42.538 svm test (EURUSD,H1) 1.0 0.52 0.54 0.52 0.53 147.0 JE 0 15:15:42.538 svm test (EURUSD,H1) GP 0 15:15:42.538 svm test (EURUSD,H1) Accuracy 0.53 RI 0 15:15:42.538 svm test (EURUSD,H1) Average 0.53 0.53 0.53 0.53 300.0 JH 0 15:15:42.538 svm test (EURUSD,H1) W Avg 0.53 0.53 0.53 0.53 300.0 DO 0 15:15:42.538 svm test (EURUSD,H1) Test accuracy = 0.527000
El modelo ha mostrado una precisión del 53% en las predicciones fuera de muestra. Algunos dirán que es un mal modelo, pero yo diría que es normal. Estos resultados pueden atribuirse a muchos factores, tales como errores en el modelo, mala normalización, criterios de convergencia, etc. Usted mismo puede experimentar con los parámetros e intentar mejorar el resultado. Sin embargo, lo más probable es que los datos resulten demasiado complejos para un modelo lineal. Estoy bastante seguro de ello, así que probaremos el método SVM dual y veremos si muestra mejores resultados.
Estudiaremos el método SVM dual en ONXX Python. No he sido capaz de conseguir un modelo en MQL5 que se acerque lo suficiente al rendimiento y precisión del modelo python sklearn. Por eso vamos a seguir trabajando en el método SVM dual en Python. Sin embargo, he adjuntado la biblioteca Dual SVM en MQL5 en el archivo principal svm.mqh: se adjunta a este artículo y también estará disponible en mi GitHub vinculado al final del presente trabajo.
Para ejecutar el método SVM dual en Python, necesitaremos recopilar datos y normalizarlos utilizando MQL5. Necesitaremos crear una nueva clase llamada CDualSVMONNX dentro del archivo svm.mqh. Esta clase se encargará de gestionar el modelo ONNX derivado de Python.
class CDualSVMONNX { private: CPreprocessing<vectorf, matrixf> *normalize_x; CMatrixutils matrix_utils; struct data_struct { ulong rows, cols; } df; public: CDualSVMONNX(void); ~CDualSVMONNX(void); long onnx_handle; void SendDataToONNX(matrixf &data, string csv_name = "DualSVMONNX-data.csv", string csv_header=""); bool LoadONNX(const uchar &onnx_buff[], ENUM_ONNX_FLAGS flags=ONNX_NO_CONVERSION); int Predict(vectorf &inputs); vector Predict(matrixf &inputs); };
Esta es una visión general de la clase.
Recopilación y normalización de datos
Para nuestro modelo, necesitaremos datos de los que podamos aprender. Deberemos limpiar estos datos para que se ajusten a nuestro modelo SVM:
void CDualSVMONNX::SendDataToONNX(matrixf &data, string csv_name = "DualSVMONNX-data.csv", string csv_header="") { df.cols = data.Cols(); df.rows = data.Rows(); if (df.cols == 0 || df.rows == 0) { Print(__FUNCTION__," data matrix invalid size "); return; } matrixf split_x; vectorf split_y; matrix_utils.XandYSplitMatrices(data, split_x, split_y); //since we are going to be normalizing the independent variable only we need to split the data into two normalize_x = new CPreprocessing<vectorf,matrixf>(split_x, NORM_MIN_MAX_SCALER); //Normalizing Independent variable only matrixf new_data = split_x; new_data.Resize(data.Rows(), data.Cols()); new_data.Col(split_y, data.Cols()-1); if (csv_header == "") { for (ulong i=0; i "COLUMN " +string(i+1) + (i==df.cols-1 ? "" : ","); //do not put delimiter on the last column } //--- Save the Normalization parameters also matrixf params = {}; string sep=","; ushort u_sep; string result[]; u_sep=StringGetCharacter(sep,0); int k=StringSplit(csv_header,u_sep,result); ArrayRemove(result, k-1, 1); //remove the last column header since we do not have normalization parameters for the target variable as it is not normalized normalize_x.min_max_scaler.min.Swap(params); matrix_utils.WriteCsv("min_max_scaler.min.csv",params,result,false,8); normalize_x.min_max_scaler.max.Swap(params); matrix_utils.WriteCsv("min_max_scaler.max.csv",params,result,false,8); //--- matrix_utils.WriteCsv(csv_name, new_data, csv_header, false, 8); //Save dataset to a csv file }
Como la recogida de datos para el entrenamiento debe hacerse una sola vez, utilizaremos un script para este fin.
Script GetDataforONNX.mq5
#include CDualSVMONNX dual_svm; input uint bars = 1000; input uint epochs_ = 1000; input uint batch_size_ = 64; input double alpha__ =0.1; input double lambda_ = 0.01; input int rsi_period = 13; input int bb_period = 20; input double bb_deviation = 2.0; int rsi_handle, bb_handle; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { rsi_handle = iRSI(Symbol(),PERIOD_CURRENT,rsi_period, PRICE_CLOSE); bb_handle = iBands(Symbol(), PERIOD_CURRENT, bb_period,0, bb_deviation, PRICE_CLOSE); //--- matrixf data = GetTrainTestData<float>(); dual_svm.SendDataToONNX(data,"DualSVMONNX-data.csv","rsi,bb-high,bb-low,bb-mid,target"); } //+------------------------------------------------------------------+ //| Getting data for Training and Testing the model | //+------------------------------------------------------------------+ template <typename T> matrix GetTrainTestData() { matrix data(bars, 5); vector v; //Temporary vector for storing Indicator buffers v.CopyIndicatorBuffer(rsi_handle, 0, 0, bars); data.Col(v, 0); v.CopyIndicatorBuffer(bb_handle, 0, 0, bars); data.Col(v, 1); v.CopyIndicatorBuffer(bb_handle, 1, 0, bars); data.Col(v, 2); v.CopyIndicatorBuffer(bb_handle, 2, 0, bars); data.Col(v, 3); vector open, close; open.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_OPEN, 0, bars); close.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_CLOSE, 0, bars); for (ulong i=0; i //preparing the independent variable data[i][4] = close[i] > open[i] ? 1 : -1; // if price closed above its opening thats bullish else bearish return data; }
Resultado
Hemos creado un archivo llamado DualSVMONNX-data.csv en la carpeta Files del directorio MQL5.
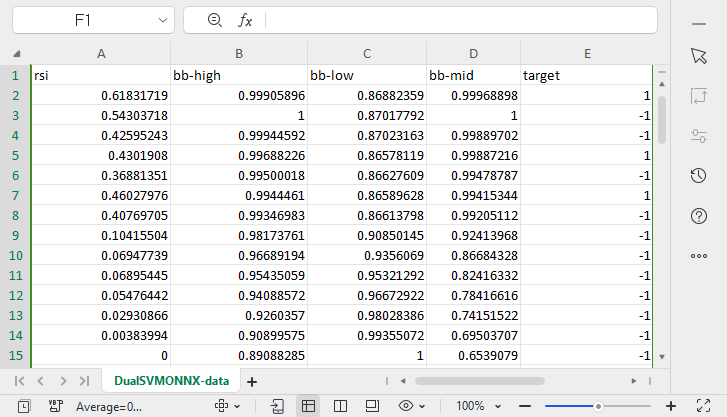
Preste atención al final de la función SendDataToONNX .
También hemos guardado los parámetros de normalización.
normalize_x.min_max_scaler.min.Swap(params); matrix_utils.WriteCsv("min_max_scaler.min.csv",params,result,false,8); normalize_x.min_max_scaler.max.Swap(params); matrix_utils.WriteCsv("min_max_scaler.max.csv",params,result,false,8);
Los parámetros de normalización utilizados los volveremos a utilizar para obtener las mejores predicciones del modelo. Por lo tanto, guardar los datos nos ayudará a no perder de vista los valores de los parámetros de normalización. Los archivos CSV se encontrarán en la misma carpeta que el conjunto de datos. También mantendremos ahí el modelo ONNX.
Ejemplar de la clase DualSVMONNX. Inicialización de clases
class DualSVMONNX: def __init__(self, dataset, c=1.0, kernel='rbf'): data = pd.read_csv(dataset) # reading a csv file np.random.seed(42) self.X = data.drop(columns=['target']).astype(np.float32) # dropping the target column from independent variable self.y = data["target"].astype(int) # storing the target variable in its own vector self.X = self.X.to_numpy() self.y = self.y.to_numpy() # Split the data into training and testing sets self.X_train, self.X_test, self.y_train, self.y_test = train_test_split(self.X, self.y, test_size=0.2, random_state=42) self.onnx_model_name = "DualSVMONNX" #our final onnx model file name for saving purposes really # Create a dual SVM model with a kernel self.svm_model = SVC(kernel=kernel, C=c)
Entrenamiento del modelo SVM dual en Python
def fit(self): self.svm_model.fit(self.X_train, self.y_train) # fitting/training the model y_preds = self.svm_model.predict(self.X_train) print("accuracy = ",accuracy_score(self.y_train, y_preds))
Después de entrenar el modelo, vamos a ver cuál será la precisión tras ejecutar este fragmento de código.
Resultado
Hemos obtenido una precisión del 63%, lo cual indica que el modelo SVM para clasificar este problema concreto será mediocre en el mejor de los casos. No obstante, hemos realizado una comprobación cruzada para ver si la precisión es la que debería ser:
scores = cross_val_score(self.svm_model, self.X_train, self.y_train, cv=5) mean_cv_accuracy = np.mean(scores) print(f"\nscores {scores} mean_cv_accuracy {mean_cv_accuracy}")
Resultado
¿Qué significa este resultado de validación cruzada?
Al ejecutar el modelo con distintos parámetros, no existe mucha diferencia entre los resultados. Esto nos indica que nuestro modelo va por buen camino. La precisión media que hemos logrado obtener es de 59,875, lo cual no está lejos de los 63,3 que obtuvimos.
Conversión del modelo de vectores de soporte de sklearn a ONNX
def saveONNX(self):
initial_type = [('float_input', FloatTensorType(shape=[None, 4]))] # None means we don't know the rows but we know the columns for sure, Remember !! we have 4 independent variables
onnx_model = convert_sklearn(self.svm_model, initial_types=initial_type) # Convert the scikit-learn model to ONNX format
onnx.save_model(onnx_model, dataset_path + f"\\{self.onnx_model_name}.onnx") #saving the onnx model
El modelo se ha guardado en el catálogo MQL5/Archivos.
Abajo podrá ver del aspecto del archivo ONNX abierto en el MetaEditor. Observe la explicación del proceso: es importante.
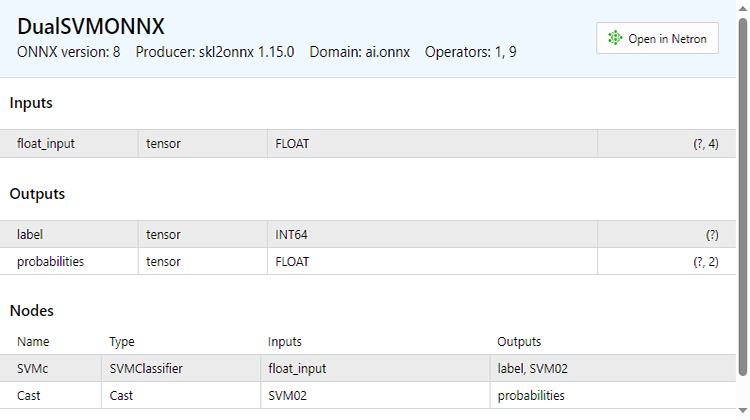
En la sección de parámetros de entrada, tendremos float_input, un parámetro de tipo float. Además, "tensor" significa que tenemos que pasar una matriz o un vector a la entrada de la función OnnxRun, ya que ambos son tensores. Al final se indica (?, 4); el tamaño de las entradas, en este caso, es ?, denotando que el número de filas es desconocido; el número de columnas es 4. A continuación viene la parte Outputs.
En él tenemos dos nodos, uno da las etiquetas predichas -1 o 1, que en este caso serán de tipo INT64 o INT en mql5.
El segundo nodo con probabilidades, será un tensor de tipos float, tiene 2 columnas y un número desconocido de filas. Puede utilizar una matriz nx2 o simplemente un vector de tamaño >= 2 para extraer los valores.
Como hay dos nodos en los datos de salida, podemos extraer los resultados dos veces:
long outputs_0[] = {1}; if (!OnnxSetOutputShape(onnx_handle, 0, outputs_0)) //giving the onnx handle first node output shape { Print(__FUNCTION__," Failed to set the output shape Err=",GetLastError()); return false; } long outputs_1[] = {1,2}; if (!OnnxSetOutputShape(onnx_handle, 1, outputs_1)) //giving the onnx handle second node output shape { Print(__FUNCTION__," Failed to set the output shape Err=",GetLastError()); return false; }
Por otra parte, podemos extraer un único nodo de entrada.
const long inputs[] = {1,4}; if (!OnnxSetInputShape(onnx_handle, 0, inputs)) //Giving the Onnx handle the input shape { Print(__FUNCTION__," Failed to set the input shape Err=",GetLastError()); return false; }
Este código ONNX se ha obtenido a partir de la función LoadONNX, que se muestra a continuación:
bool CDualSVMONNX::LoadONNX(const uchar &onnx_buff[], ENUM_ONNX_FLAGS flags=ONNX_NO_CONVERSION) { onnx_handle = OnnxCreateFromBuffer(onnx_buff, flags); //creating onnx handle buffer if (onnx_handle == INVALID_HANDLE) { Print(__FUNCTION__," OnnxCreateFromBuffer Error = ",GetLastError()); return false; } //--- const long inputs[] = {1,4}; if (!OnnxSetInputShape(onnx_handle, 0, inputs)) //Giving the Onnx handle the input shape { Print(__FUNCTION__," Failed to set the input shape Err=",GetLastError()); return false; } long outputs_0[] = {1}; if (!OnnxSetOutputShape(onnx_handle, 0, outputs_0)) //giving the onnx handle first node output shape { Print(__FUNCTION__," Failed to set the output shape Err=",GetLastError()); return false; } long outputs_1[] = {1,2}; if (!OnnxSetOutputShape(onnx_handle, 1, outputs_1)) //giving the onnx handle second node output shape { Print(__FUNCTION__," Failed to set the output shape Err=",GetLastError()); return false; } return true; }
Fíjese bien en la función que habrá adivinado que nos falta al cargar los parámetros de normalización. Estos parámetros resultan muy importantes para normalizar los nuevos datos de entrada de modo que coincidan con las dimensiones de los datos entrenados con los que el modelo ya está familiarizado.
Puede cargar los parámetros desde un archivo CSV: esto funcionará sin problemas durante la duración de la operación real. Sin embargo, este método puede resultar complicado y no siempre funcionará bien en el simulador de estrategias. Así que por ahora, copiaremos los parámetros de normalización en nuestro código del asesor manualmente. Como resultado, obtendremos los parámetros de normalización dentro de nuestro asesor. En primer lugar, modificaremos la función LoadONNX para aceptar los vectores de entrada max y min que se utilizan en el Min Max Scaler.
bool CDualSVMONNX::LoadONNX(const uchar &onnx_buff[], ENUM_ONNX_FLAGS flags, vectorf &norm_max, vectorf &norm_min)
Final de esta función.
normalize_x = new CPreprocessing<vectorf,matrixf>(norm_max, norm_min); //Load min max scaler with parameters
Copiado y pegado de parámetros de normalización de archivos CSV a asesores.
Vamos a entrenar e intentar probar el modelo de la misma manera que hemos hecho con Python. Nuestro objetivo será asegurarnos de que vamos por el mismo camino en ambos lenguajes.
Función OnInit en el asesor de prueba test.mq5
vector min_v = {14.32424641,1.04674852,1.04799891,1.04392886}; vector max_v = {86.28263092,1.07385755,1.07907069,1.07267821}; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- rsi_handle = iRSI(Symbol(),PERIOD_CURRENT, rsi_period, PRICE_CLOSE); bb_handle = iBands(Symbol(), PERIOD_CURRENT, bb_period, 0 , bb_deviation, PRICE_CLOSE); vector y_train, y_test; // float values matrixf datasetf = GetTrainTestData<float>(); matrixf x_trainf, x_testf; vectorf y_trainf, y_testf; //--- matrix_utils.TrainTestSplitMatrices(datasetf,x_trainf,y_trainf,x_testf,y_testf,0.8,42); //split the data into training and testing samples vectorf max_vf = {}, min_vf = {}; //convertin the parameters into float type max_vf.Assign(max_v); min_vf.Assign(min_v); dual_svm.LoadONNX(SVMModel, ONNX_DEFAULT, max_vf, min_vf); y_train.Assign(y_trainf); y_test.Assign(y_testf); vector train_preds = dual_svm.Predict(x_trainf); vector test_preds = dual_svm.Predict(x_testf); Print("\n<<<<< Train Classification Report >>>>\n"); metrics.confusion_matrix(y_train, train_preds); Print("\n<<<<< Test Classification Report >>>>\n"); metrics.confusion_matrix(y_test, test_preds); return(INIT_SUCCEEDED); }Resultado
RP 0 17:08:53.068 svm test (EURUSD,H1) <<<<< Train Classification Report >>>> HE 0 17:08:53.068 svm test (EURUSD,H1) MR 0 17:08:53.068 svm test (EURUSD,H1) Confusion Matrix IG 0 17:08:53.068 svm test (EURUSD,H1) [[245,148] CO 0 17:08:53.068 svm test (EURUSD,H1) [150,257]] NK 0 17:08:53.068 svm test (EURUSD,H1) DE 0 17:08:53.068 svm test (EURUSD,H1) Classification Report HO 0 17:08:53.068 svm test (EURUSD,H1) FI 0 17:08:53.068 svm test (EURUSD,H1) _ Precision Recall Specificity F1 score Support ON 0 17:08:53.068 svm test (EURUSD,H1) 1.0 0.62 0.62 0.63 0.62 393.0 DP 0 17:08:53.068 svm test (EURUSD,H1) -1.0 0.63 0.63 0.62 0.63 407.0 JG 0 17:08:53.068 svm test (EURUSD,H1) FR 0 17:08:53.068 svm test (EURUSD,H1) Accuracy 0.63 CK 0 17:08:53.068 svm test (EURUSD,H1) Average 0.63 0.63 0.63 0.63 800.0 KI 0 17:08:53.068 svm test (EURUSD,H1) W Avg 0.63 0.63 0.63 0.63 800.0 PP 0 17:08:53.068 svm test (EURUSD,H1) DH 0 17:08:53.068 svm test (EURUSD,H1) <<<<< Test Classification Report >>>> PQ 0 17:08:53.068 svm test (EURUSD,H1) EQ 0 17:08:53.068 svm test (EURUSD,H1) Confusion Matrix HJ 0 17:08:53.068 svm test (EURUSD,H1) [[61,31] MR 0 17:08:53.068 svm test (EURUSD,H1) [40,68]] NH 0 17:08:53.068 svm test (EURUSD,H1) DP 0 17:08:53.068 svm test (EURUSD,H1) Classification Report HL 0 17:08:53.068 svm test (EURUSD,H1) FF 0 17:08:53.068 svm test (EURUSD,H1) _ Precision Recall Specificity F1 score Support GJ 0 17:08:53.068 svm test (EURUSD,H1) -1.0 0.60 0.66 0.63 0.63 92.0 PO 0 17:08:53.068 svm test (EURUSD,H1) 1.0 0.69 0.63 0.66 0.66 108.0 DD 0 17:08:53.068 svm test (EURUSD,H1) JO 0 17:08:53.068 svm test (EURUSD,H1) Accuracy 0.65 LH 0 17:08:53.068 svm test (EURUSD,H1) Average 0.65 0.65 0.65 0.64 200.0 CJ 0 17:08:53.068 svm test (EURUSD,H1) W Avg 0.65 0.65 0.65 0.65 200.0
Hemos obtenido la misma precisión que con el script de Python, el 63%. ¿No es maravilloso?
Este será el aspecto de la función de previsión desde dentro:
int CDualSVMONNX::Predict(vectorf &inputs) { vectorf outputs(1); //label outputs vectorf x_output(2); //probabilities vectorf temp_inputs = inputs; normalize_x.Normalization(temp_inputs); //Normalize the input features if (!OnnxRun(onnx_handle, ONNX_DEFAULT, temp_inputs, outputs, x_output)) { Print("Failed to get predictions from onnx Err=",GetLastError()); return (int)outputs[0]; } return (int)outputs[0]; }
Esta ejecutará el archivo ONNX para recuperar las predicciones y retornará un número entero para la marca predicha.
A continuación, implementaremos una estrategia sencilla para probar ambos modelos del método de vectores de soporte en el simulador de estrategias. La estrategia será simple: si la clase SVM predicha == 1, abriremos una operación de compra; de lo contrario, si la clase predicha == -1, abriremos una operación de venta.
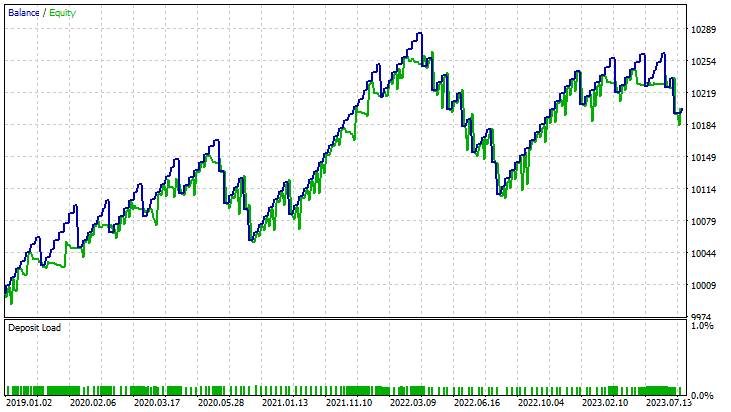
Resultados en el simulador de estrategias:
Para el método lineal de vectores de soporte:
Para la fórmula dual del método de vectores de soporte:
Mantendremos los mismos datos de entrada excepto svm_type.
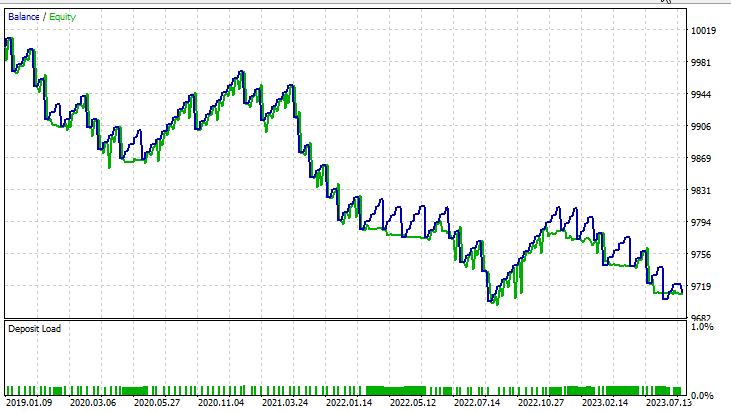
La SVM dual no ha funcionado bien con entradas que sí funcionaron para la SVM lineal. Puede que sea necesario seguir optimizando e investigando por qué el modelo ONNX no converge, pero ese es un tema para otro artículo.
Conclusiones finales
Ventajas de los modelos de vectores de soporte SVM
- Trabajo eficiente en espacios multidimensionales, es decir, el método de vectores de soporte es adecuado para trabajar con muestras de datos financieros con múltiples funciones, indicadores comerciales y variables de mercado.
- Los vectores de soporte resultan menos propensos al sobreajuste, lo cual da lugar a una solución más generalizada que puede adaptarse mejor a las condiciones imprevistas del mercado.
- Los modelos SVM ofrecen versatilidad a través de diferentes características básicas, lo cual permite a los tráders experimentar con diferentes estrategias y adaptar el modelo a patrones de mercado específicos.
- Los métodos SVM son buenos para captar las relaciones no lineales dentro de los datos, un aspecto crucial al trabajar con mercados financieros complejos.
Desventajas
- Las SVM pueden resultar sensibles a los datos ruidosos, lo que afecta a sus resultados y las hace más susceptibles al comportamiento volátil del mercado.
- El entrenamiento de modelos SVM puede ser costoso en cuanto a recursos computacionales, especialmente cuando hablamos de grandes conjuntos de datos, lo cual limita su escalabilidad en determinados escenarios comerciales en tiempo real.
- Los vectores de soporte dependen en gran medida del diseño de las características, lo cual requiere conocimientos especializados para seleccionar los indicadores adecuados y un preprocesamiento eficaz de los datos.
- Como hemos visto, los modelos en SVM han mostrado precisiones medias de hasta el 63% para la forma dual y del 59% para la forma lineal. Aunque puede que estos modelos no superen a algunas técnicas avanzadas de aprendizaje automático, siguen ofreciendo un punto de partida razonable para los tráders de MQL5.
Descenso de la popularidad
A pesar de su éxito en el pasado, la popularidad de las SVM ha descendido en los últimos años. Esto puede tener que ver con lo siguiente:
- El desarrollo de técnicas de aprendizaje profundo (especialmente las redes neuronales) ha superado a los algoritmos tradicionales de aprendizaje automático gracias a su capacidad para extraer automáticamente características jerárquicas.
- Cada vez se dispone de más conjuntos de datos financieros extensos, por lo que los modelos de aprendizaje profundo que gestionan con éxito grandes cantidades de datos se han vuelto más atractivos.
- La llegada de hardware potente y recursos informáticos distribuidos ha hecho más factible entrenar y desplegar modelos complejos de aprendizaje profundo.
En conclusión, aunque los modelos SVM no sean una solución avanzada, su uso en entornos comerciales MQL5 está justificado. Su sencillez, fiabilidad y adaptabilidad los convierten en una herramienta valiosa, especialmente para los tráders con datos o recursos informáticos limitados. Los vectores de soporte pueden considerarse parte de un conjunto más amplio de herramientas, potencialmente ampliadas con nuevos enfoques de aprendizaje automático a medida que evoluciona la dinámica del mercado.
Gracias por su atención.
| Archivo | Descripción | Aplicación |
|---|---|
| dual_svm.py | python script | Implementación de SVM dual en Python. |
| GetDataforONNX.mq5 | mql5 script | Puede usarlo para recopilar, normalizar y almacenar datos en un archivo csv ubicado en la carpeta MQL5/Files. |
| preprocessing.mqh | mql5 include file | Contiene una clase y funciones para normalizar y estandarizar los datos de entrada. |
| matrix_utils.mqh | mql5 include file | Biblioteca con operaciones matriciales adicionales. |
| metrics.mqh | mql5 include file | Biblioteca que contiene funciones adicionales para analizar el rendimiento de los modelos de aprendizaje automático. |
| svm test.mq5 | EA | Asesor para probar todo el código que aparece en el artículo. |
El código usado en este artículo también se podrá encontrar en mi repositorio en GitHub.
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/13395
Desarrollo de un sistema de repetición (Parte 38): Pavimentando el terreno (II)
Cómo desarrollar un agente de aprendizaje por refuerzo en MQL5 con Integración RestAPI (Parte 2): Funciones MQL5 para interacción HTTP con API REST del juego de tres en raya
Redes neuronales: así de sencillo (Parte 64): Método de clonación conductual ponderada conservadora (CWBC)
Desarrollo de un sistema de repetición (Parte 37): Pavimentando el terreno (I)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso