Datenwissenschaft und maschinelles Lernen (Teil 15): SVM, ein Muss im Werkzeugkasten jedes Händlers
166
0
Inhalt:
- Einführung
- Was ist eine Hyperebene?
- Lineare SVM
- Zweifache SVM
- Harte Grenze
- Weiche Grenze
- Training des Modells einer linearen Support-Vektor-Maschin
- Gewinnen der Vorhersagen von einer linearen Support-Vektor-Modells
- Trainieren und Testen des linearen SVM-Modells
- Sammeln und Normalisieren von Daten
- Die Klasseninstanz von DualSVMONNX | Initialisierung einer Klasse
- Training des Dual-SVM-Modells in Python
- Konvertierung des SVC-Modells sklearn nach ONNX und Speichern
- Abschließende Überlegungen
Einführung
Support Vector Machine (SVM) ist ein leistungsfähiger überwachter Algorithmus für maschinelles Lernen, der für lineare oder nichtlineare Klassifizierungs- und Regressionsaufgaben und manchmal auch für die Erkennung von Ausreißern verwendet wird.
Im Gegensatz zu Bayes'schen Klassifizierungstechniken und logistischer Regression, die einfache mathematische Modelle zur Klassifizierung von Informationen einsetzen, verfügt die SVM über einige komplexe mathematische Lernfunktionen, die darauf abzielen, die optimale Hyperebene zu finden, die die Daten in einem N-dimensionalen Raum trennt.
Support Vector Machine wird normalerweise für Klassifizierungsaufgaben verwendet, was wir auch in diesem Artikel tun werden
Was ist eine Hyperebene?
Eine Hyperebene ist eine Linie, die zur Trennung von Datenpunkten verschiedener Klassen verwendet wird.
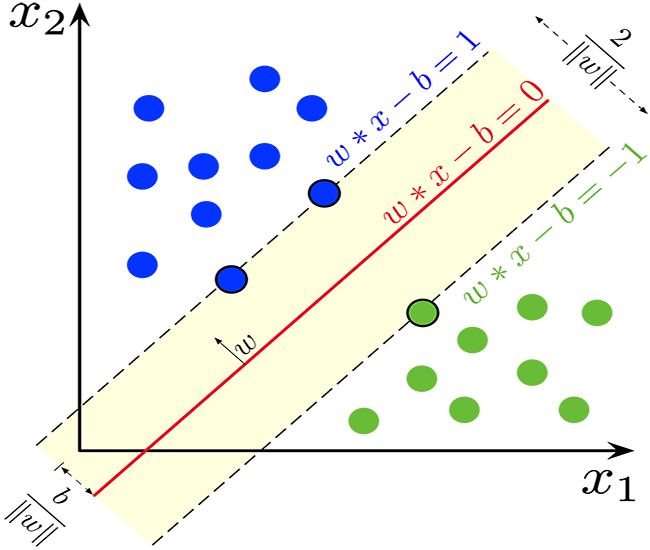
Die Hyperebene hat die folgenden Eigenschaften:
Dimensionalität: Bei einem binären Klassifikationsproblem ist die Hyperebene ein (d-1)-dimensionaler Unterraum, wobei „d“ die Dimension des Merkmalsraums ist. In einem zweidimensionalen Merkmalsraum ist die Hyperebene zum Beispiel eine eindimensionale Linie.
Gleichung: Mathematisch lässt sich eine Hyperebene durch eine lineare Gleichung der Form darstellen:
ist ein Vektor, der orthogonal zur Hyperebene ist und ihre Ausrichtung bestimmt.
ist ein Merkmalsvektor.
b ist ein skalarer Bias-Term, der die Hyperebene vom Ursprung wegschiebt.
Abtrennung: Die Hyperebene unterteilt den Merkmalsraum in zwei Halbräume:
Der Bereich 
, der einer Klasse entspricht.
Der Bereich 
, der der anderen Klasse entspricht.
Grenze: Bei SVM besteht das Ziel darin, die Hyperebene zu finden, die die Grenze maximiert, d. h. den Abstand zwischen der Hyperebene und den nächstgelegenen Datenpunkten der beiden Klassen. Diese nächstgelegenen Datenpunkte werden als „Support-Vektoren“ bezeichnet. Die SVM zielt darauf ab, die Hyperebene zu finden, die die maximale Grenze bei gleichzeitiger Minimierung des Klassifikationsfehlers erreicht.
Einstufung: Sobald die optimale Hyperebene gefunden ist, kann sie zur Klassifizierung neuer Datenpunkte verwendet werden. Durch die Auswertung von 
können wir feststellen, auf welche Seite der Hyperebene ein Datenpunkt fällt, und ihn so in eine der beiden Klassen einordnen.
Das Konzept der Hyperebene ist ein Schlüsselelement der SVM, da es die Grundlage für den Maximum-Grenz-Klassifikator bildet. SVMs zielen darauf ab, die Hyperebene zu finden, die die Daten am besten trennt und gleichzeitig eine maximale Spanne zwischen den Klassen beibehält, was wiederum die Generalisierung des Modells und seine Robustheit gegenüber ungesehenen Daten verbessert.
double CLinearSVM::hyperplane(vector &x) { return x.MatMul(W) - B; }
und die Gleichung 
sind gleichwertig und beschreiben die gleiche Hyperebene. Die Wahl der zu verwendenden Form ist eine Frage der Konvention und der persönlichen Vorliebe, aber die beiden Formen sind algebraisch gleichwertig. In meinem Code habe ich die x-Matrix nicht transponiert, weil ich mich für W als Vektor entschieden habe, sodass dies nicht notwendig ist.Wie bereits erwähnt, der ist der Bias-Term mit b bezeichnet, einem skalarer Term, sodass für ihn eine Double-Variable deklariert werden musste.
class CLinearSVM { protected: CMatrixutils matrix_utils; CMetrics metrics; CPreprocessing<vector, matrix> *normalize_x; vector W; //Weights vector double B; //bias term bool is_fitted_already; struct svm_config { uint batch_size; double alpha; double lambda; uint epochs; }; private: svm_config config;
Wir haben den Klassennamen CLinearSVM gesehen, der selbst erklärt, dass es sich um eine lineare Support Vector Machine handelt. Dies bringt uns zu den Aspekten der SVM, wo wir lineare und duale Support Vector Machine haben
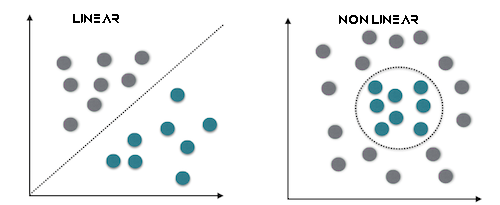
Lineare SVM
Eine lineare SVM ist eine Art von SVM, die einen linearen Kernel verwendet, d. h. sie nutzt eine lineare Entscheidungsgrenze, um Datenpunkte zu trennen. Bei einer linearen SVM arbeiten Sie direkt mit dem Merkmalsraum, und das Optimierungsproblem wird oft in seiner primären Form ausgedrückt. Das primäre Ziel einer linearen SVM ist es, eine lineare Hyperebene zu finden, die die Daten am besten trennt.
Dies funktioniert am besten bei linear trennbaren Daten.
Zweifache SVM
Die duale SVM ist keine eigene Art von SVM, sondern eine Darstellung des SVM-Optimierungsproblems. Die duale Form einer SVM ist eine mathematische Umformulierung des ursprünglichen Optimierungsproblems, die effizientere Lösungsmethoden ermöglicht. Es führt Lagrange-Multiplikatoren ein, um eine duale Zielfunktion zu maximieren, die dem primären Problem gleichwertig ist. Die Lösung des dualen Problems führt zur Bestimmung von Support-Vektoren, die für die Klassifizierung entscheidend sind.
Dies eignet sich am besten für Daten, die nicht linear trennbar sind.
Es ist auch wichtig zu wissen, dass wir entweder harte oder weiche Ränder verwenden können, um SVM-Klassifizierungsentscheidungen mithilfe der Hyperebene zu treffen.
Harte Grenze
Wenn die Trainingsdaten linear trennbar sind, können wir zwei parallele Hyperebenen auswählen, die die beiden Datenklassen trennen, sodass der Abstand zwischen ihnen so groß wie möglich ist. Der Bereich, der von diesen beiden Hyperebenen begrenzt wird, wird als Grenze (Margin) bezeichnet, und die Hyperebene mit der maximalen Grenze ist die Hyperebene, die in der Mitte zwischen ihnen liegt. Bei einem normalisierten oder standardisierten Datensatz können diese Hyperebenen durch die folgenden Gleichungen beschrieben werden
(alles, was auf oder über dieser Grenze liegt, gehört zu einer Klasse mit der Kennzeichnung 1)
und
(alles, was auf oder unter dieser Grenze liegt, gehört zu der anderen Klasse und hat die Kennzeichnung -1).
Der Abstand zwischen ihnen ist 2/||w|| und um den Abstand zu maximieren, sollte ||w|| minimal sein. Um zu verhindern, dass ein Datenpunkt in den Grenzbereich fällt, fügen wir die Einschränkung yi(wTXi -b) >= 1 hinzu, wobei yi = i-te Zeile im Ziel und Xi = i-te Zeile in der X
Weiche Grenze
Um SVM auf Fälle zu erweitern, in denen die Daten nicht linear trennbar sind, ist die Scharnierverlustfunktion hilfreich
.
Beachten Sie, dass 
das i-te Ziel (d.h., im Falle von 1 oder −1), und 
ist die i-te Ausgabe.
Wenn der Datenpunkt die Klasse = 1 hat, ist der Verlust 0, andernfalls ist er der Abstand zwischen der Grenze und dem Datenpunkt.
wobei λ ein Kompromiss zwischen der Größe der Grenze und der Tatsache ist, dass xi auf der richtigen Seite der Grenze liegt. Wenn λ zu niedrig ist, wird die Gleichung zu einer harten Grenze.
Wir werden die harte Grenze für die Klasse Linear SVM verwenden. Dies wird durch die Vorzeichenfunktion ermöglicht, eine Funktion, die das Vorzeichen einer reellen Zahl in mathematischer Notation zurückgibt. Ausgedrückt als:
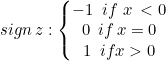
int CLinearSVM::sign(double var) { if (var == 0) return (0); else if (var < 0) return -1; else return 1; }
Training des Modells einer linearen Support-Vektor-Maschin
Beim Trainingsprozess einer Support Vector Machine (SVM) geht es darum, die optimale Hyperebene zu finden, die die Daten trennt und gleichzeitig die Grenze maximiert. Die Grenze ist der Abstand zwischen der Hyperebene und den nächstgelegenen Datenpunkten der beiden Klassen. Ziel ist es, die Hyperebene zu finden, die die Grenze maximiert und gleichzeitig die Klassifikationsfehler minimiert.
Aktualisierung der Gewichte (w):
a. Erste Amtszeit: Der erste Term in der Verlustfunktion entspricht dem Scharnierverlust, der den Klassifikationsfehler misst. Für jedes Trainingsbeispiel i berechnen wir die Ableitung des Verlustes nach den Gewichten w wie folgt:
- Wenn
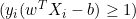, was bedeutet, dass der Datenpunkt korrekt klassifiziert ist und außerhalb der Grenze liegt, ist die Ableitung 0. - Wenn
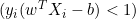, was bedeutet, dass der Datenpunkt innerhalb der Grenze liegt oder falsch klassifiziert wurde, lautet die Ableitung 
.
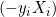b. Zweite Amtszeit:
Der zweite Term ist der Regularisierungsterm. Sie fördert eine kleine Grenze und hilft, eine Überanpassung zu verhindern. Die Ableitung dieses Terms in Bezug auf die Gewichte w ist 2λw, wobei λ der Regularisierungsparameter ist.
c. Kombination der Ableitungen des ersten und zweiten Terms,
Die Aktualisierung für die Gewichte w erfolgt wie folgt:
Wenn 
, aktualisieren wir die Gewichte wie folgt: 
und wenn 
, aktualisieren wir die Gewichte wie folgt: 
, hier ist α die Lernrate.
Aktualisierung des Abschnitts (b):
a. Erster Term:
Die Ableitung des Scharnierverlustes nach dem Achsenabschnitt b wird in ähnlicher Weise berechnet wie die Gewichte:
- Wenn
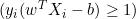, ist die Ableitung 0. - Wenn
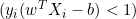, ist die Ableitung 
.
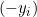b. Zweiter Term:
Der zweite Term hängt nicht vom Achsenabschnitt ab, sodass seine Ableitung nach b 0 ist. c. Die Aktualisierung für den Intercept b ist wie folgt:
- Wenn
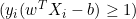, aktualisieren wir 
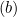wie folgt: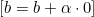 
- Wenn
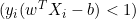, aktualisieren wir 
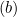wie folgt: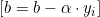 
Schlupfvariable (ξ):
Die Schlupfvariable (ξ) lässt zu, dass einige Datenpunkte innerhalb der Grenze liegen, was bedeutet, dass sie falsch klassifiziert sind oder innerhalb der Grenze liegen. Die Bedingung 
besagt, dass die Entscheidungsgrenze mindestens so groß sein sollte wie 
Einheiten vom Datenpunkt i entfernt.
Zusammenfassend lässt sich sagen, dass der Trainingsprozess einer SVM die Aktualisierung der Gewichte und des Intercepts auf der Grundlage des Scharnierverlusts und des Regularisierungsterms beinhaltet. Ziel ist es, die optimale Hyperebene zu finden, die die Grenze maximiert und gleichzeitig mögliche Fehlklassifikationen innerhalb des durch die Schlupfvariable erlaubten Grenze berücksichtigt. Dieser Prozess wird in der Regel mit Hilfe von Optimierungstechniken gelöst, und während des Trainingsprozesses werden Unterstützungsvektoren identifiziert, um die Entscheidungsgrenze zu definieren.
void CLinearSVM::fit(matrix &x, vector &y) { matrix X = x; vector Y = y; ulong rows = X.Rows(), cols = X.Cols(); if (X.Rows() != Y.Size()) { Print("Support vector machine Failed | FATAL | X m_rows not same as yvector size"); return; } W.Resize(cols); B = 0; normalize_x = new CPreprocessing<vector, matrix>(X, NORM_STANDARDIZATION); //Normalizing independent variables //--- if (rows < config.batch_size) { Print("The number of samples/rows in the dataset should be less than the batch size"); return; } matrix temp_x; vector temp_y; matrix w, b; vector preds = {}; vector loss(config.epochs); during_training = true; for (uint epoch=0; epoch<config.epochs; epoch++) { for (uint batch=0; batch<=(uint)MathFloor(rows/config.batch_size); batch+=config.batch_size) { temp_x = matrix_utils.Get(X, batch, (config.batch_size+batch)-1); temp_y = matrix_utils.Get(Y, batch, (config.batch_size+batch)-1); #ifdef DEBUG_MODE: Print("X\n",temp_x,"\ny\n",temp_y); #endif for (uint sample=0; sample<temp_x.Rows(); sample++) { // yixiw-b≥1 if (temp_y[sample] * hyperplane(temp_x.Row(sample)) >= 1) { this.W -= config.alpha * (2 * config.lambda * this.W); // w = w + α* (2λw - yixi) } else { this.W -= config.alpha * (2 * config.lambda * this.W - ( temp_x.Row(sample) * temp_y[sample] )); // w = w + α* (2λw - yixi) this.B -= config.alpha * temp_y[sample]; // b = b - α* (yi) } } } //--- Print the loss at the end of an epoch is_fitted_already = true; preds = this.predict(X); loss[epoch] = preds.Loss(Y, LOSS_BCE); printf("---> epoch [%d/%d] Loss = %f Accuracy = %f",epoch+1,config.epochs,loss[epoch],metrics.confusion_matrix(Y, preds, false)); #ifdef DEBUG_MODE: Print("W\n",W," B = ",B); #endif } during_training = false; return; }
Gewinnen der Vorhersagen von einer linearen Support-Vektor-Modells
Um die Vorhersagen aus dem Modell zu erhalten, müssen die Daten an die Vorzeichenfunktion übergeben werden, nachdem die Hyperebene eine Ausgabe geliefert hat.
int CLinearSVM::predict(vector &x) { if (!is_fitted_already) { Print("Err | The model is not trained, call the fit method to train the model before you can use it"); return 1000; } vector temp_x = x; if (!during_training) normalize_x.Normalization(temp_x); //Normalize a new input data when we are not running the model in training return sign(hyperplane(temp_x)); }
Trainieren und Testen des linearen SVM-Modells
Es ist üblich, das Modell zu testen, bevor es eingesetzt wird, um aussagekräftige Vorhersagen über Marktdaten zu treffen. Wir beginnen mit der Initialisierung der Klasseninstanz Linear SVM.
#include <MALE5\Support Vector Machine(SVM)\svm.mqh> CLinearSVM *svm; input uint bars = 1000; input uint epochs_ = 1000; input uint batch_size_ = 64; input double alpha__ =0.1; input double lambda_ = 0.01; bool train_once; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- svm = new CLinearSVM(batch_size_, alpha__, epochs_, lambda_); train_once = false; //--- return(INIT_SUCCEEDED); }
Wir werden die Datenerfassung fortsetzen und die 4 unabhängigen Variablen RSI, BOLLINGER BANDS HIGH, LOW und MID verwenden.
vec_.CopyIndicatorBuffer(rsi_handle, 0, 0, bars); dataset.Col(vec_, 0); vec_.CopyIndicatorBuffer(bb_handle, 0, 0, bars); dataset.Col(vec_, 1); vec_.CopyIndicatorBuffer(bb_handle, 1, 0, bars); dataset.Col(vec_, 2); vec_.CopyIndicatorBuffer(bb_handle, 2, 0, bars); dataset.Col(vec_, 3); open.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_OPEN, 0, bars); close.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_CLOSE, 0, bars); for (ulong i=0; i<vec_.Size(); i++) //preparing the independent variable dataset[i][4] = close[i] > open[i] ? 1 : -1; // if price closed above its opening thats bullish else bearish
Wir beenden die Datenerfassung, indem wir die Daten in Trainings- und Teststichproben aufteilen.
matrix_utils.TrainTestSplitMatrices(dataset,train_x,train_y,test_x,test_y,0.7,42); //split the data into training and testing samples
Training / Anpassen des Modells
svm.fit(train_x, train_y);
Ausdruck:
0 15:15:42.394 svm test (EURUSD,H1) ---> epoch [1/1000] Loss = 7.539322 Accuracy = 0.489000 IK 0 15:15:42.395 svm test (EURUSD,H1) ---> epoch [2/1000] Loss = 7.499849 Accuracy = 0.491000 EG 0 15:15:42.395 svm test (EURUSD,H1) ---> epoch [3/1000] Loss = 7.499849 Accuracy = 0.494000 .... .... GG 0 15:15:42.537 svm test (EURUSD,H1) ---> epoch [998/1000] Loss = 6.907756 Accuracy = 0.523000 DS 0 15:15:42.537 svm test (EURUSD,H1) ---> epoch [999/1000] Loss = 7.006438 Accuracy = 0.521000 IM 0 15:15:42.537 svm test (EURUSD,H1) ---> epoch [1000/1000] Loss = 6.769601 Accuracy = 0.516000
Beobachtung der Genauigkeit des Modells sowohl beim Training als auch beim Test.
vector train_pred = svm.predict(train_x), test_pred = svm.predict(test_x); printf("Train accuracy = %f",metrics.confusion_matrix(train_y, train_pred, true)); printf("Test accuracy = %f ",metrics.confusion_matrix(test_y, test_pred, true));
Ausdruck:
CH 0 15:15:42.538 svm test (EURUSD,H1) Confusion Matrix IQ 0 15:15:42.538 svm test (EURUSD,H1) [[171,175] HE 0 15:15:42.538 svm test (EURUSD,H1) [164,190]] DQ 0 15:15:42.538 svm test (EURUSD,H1) NO 0 15:15:42.538 svm test (EURUSD,H1) Classification Report JD 0 15:15:42.538 svm test (EURUSD,H1) LO 0 15:15:42.538 svm test (EURUSD,H1) _ Precision Recall Specificity F1 score Support JQ 0 15:15:42.538 svm test (EURUSD,H1) -1.0 0.51 0.49 0.54 0.50 346.0 DH 0 15:15:42.538 svm test (EURUSD,H1) 1.0 0.52 0.54 0.49 0.53 354.0 HL 0 15:15:42.538 svm test (EURUSD,H1) FG 0 15:15:42.538 svm test (EURUSD,H1) Accuracy 0.52 PP 0 15:15:42.538 svm test (EURUSD,H1) Average 0.52 0.52 0.52 0.52 700.0 PS 0 15:15:42.538 svm test (EURUSD,H1) W Avg 0.52 0.52 0.52 0.52 700.0 FK 0 15:15:42.538 svm test (EURUSD,H1) Train accuracy = 0.516000 MS 0 15:15:42.538 svm test (EURUSD,H1) Confusion Matrix LI 0 15:15:42.538 svm test (EURUSD,H1) [[79,74] CM 0 15:15:42.538 svm test (EURUSD,H1) [68,79]] FJ 0 15:15:42.538 svm test (EURUSD,H1) HF 0 15:15:42.538 svm test (EURUSD,H1) Classification Report DM 0 15:15:42.538 svm test (EURUSD,H1) NH 0 15:15:42.538 svm test (EURUSD,H1) _ Precision Recall Specificity F1 score Support NN 0 15:15:42.538 svm test (EURUSD,H1) -1.0 0.54 0.52 0.54 0.53 153.0 PQ 0 15:15:42.538 svm test (EURUSD,H1) 1.0 0.52 0.54 0.52 0.53 147.0 JE 0 15:15:42.538 svm test (EURUSD,H1) GP 0 15:15:42.538 svm test (EURUSD,H1) Accuracy 0.53 RI 0 15:15:42.538 svm test (EURUSD,H1) Average 0.53 0.53 0.53 0.53 300.0 JH 0 15:15:42.538 svm test (EURUSD,H1) W Avg 0.53 0.53 0.53 0.53 300.0 DO 0 15:15:42.538 svm test (EURUSD,H1) Test accuracy = 0.527000
Unser Modell war bei den Vorhersagen außerhalb der Stichprobe zu 53 % genau, manche würden sagen, ein schlechtes Modell, aber ich würde sagen, ein durchschnittliches Modell. Es kann viele Faktoren geben, die dazu führen, einschließlich Fehler im Modell, schlechte Normalisierung, Konvergenzkriterien und vieles mehr. Sie können versuchen, die Parameter anzupassen, um zu sehen, was zu einem besseren Ergebnis führt. Es könnte aber auch sein, dass die Daten zu komplex für ein lineares Modell sind, da bin ich mir sicher.
Für die Dual-SVM, die wir im ONXX Python-Format untersuchen werden, konnte ich das mql5-codierte Modell nicht annähernd an die Leistung und Genauigkeit des Python-Sklearn-Dual-SVM-Modells heranbringen. Daher denke ich, dass es sich lohnt, Dual-SVM in Python zu untersuchen. Jetzt ist die duale SVM-Bibliothek in MQL5 immer noch in der Hauptdatei svm.mqh zu finden, die in diesem Artikel bereitgestellt wird, und auf meinem GitHub, der am Ende dieses Artikels verlinkt ist.
Um die duale SVM in Python zu starten, müssen wir Daten sammeln und mit mql5 normalisieren. Möglicherweise müssen wir eine neue Klasse mit dem Namen CDualSVMONNX in der Datei svm.mqh erstellen. Diese Klasse wird für den Umgang mit dem ONNX-Modell aus dem Python-Code verantwortlich sein.
class CDualSVMONNX { private: CPreprocessing<vectorf, matrixf> *normalize_x; CMatrixutils matrix_utils; struct data_struct { ulong rows, cols; } df; public: CDualSVMONNX(void); ~CDualSVMONNX(void); long onnx_handle; void SendDataToONNX(matrixf &data, string csv_name = "DualSVMONNX-data.csv", string csv_header=""); bool LoadONNX(const uchar &onnx_buff[], ENUM_ONNX_FLAGS flags=ONNX_NO_CONVERSION); int Predict(vectorf &inputs); vector Predict(matrixf &inputs); };
So würde die Klasse auf den ersten Blick aussehen,
Sammeln und Normalisieren von Daten
Wir brauchen Daten, aus denen unser Modell lernen kann, und wir müssen diese Daten auch bereinigen, um sie für unser SVM-Modell geeignet zu machen, das sei gesagt:
void CDualSVMONNX::SendDataToONNX(matrixf &data, string csv_name = "DualSVMONNX-data.csv", string csv_header="") { df.cols = data.Cols(); df.rows = data.Rows(); if (df.cols == 0 || df.rows == 0) { Print(__FUNCTION__," data matrix invalid size "); return; } matrixf split_x; vectorf split_y; matrix_utils.XandYSplitMatrices(data, split_x, split_y); //since we are going to be normalizing the independent variable only we need to split the data into two normalize_x = new CPreprocessing<vectorf,matrixf>(split_x, NORM_MIN_MAX_SCALER); //Normalizing Independent variable only matrixf new_data = split_x; new_data.Resize(data.Rows(), data.Cols()); new_data.Col(split_y, data.Cols()-1); if (csv_header == "") { for (ulong i=0; i<df.cols; i++) csv_header += "COLUMN "+string(i+1) + (i==df.cols-1 ? "" : ","); //do not put delimiter on the last column } //--- Save the Normalization parameters also matrixf params = {}; string sep=","; ushort u_sep; string result[]; u_sep=StringGetCharacter(sep,0); int k=StringSplit(csv_header,u_sep,result); ArrayRemove(result, k-1, 1); //remove the last column header since we do not have normalization parameters for the target variable as it is not normalized normalize_x.min_max_scaler.min.Swap(params); matrix_utils.WriteCsv("min_max_scaler.min.csv",params,result,false,8); normalize_x.min_max_scaler.max.Swap(params); matrix_utils.WriteCsv("min_max_scaler.max.csv",params,result,false,8); //--- matrix_utils.WriteCsv(csv_name, new_data, csv_header, false, 8); //Save dataset to a csv file }
Da die Datenerfassung für das Training einmalig erfolgen muss, gibt es keinen besseren Weg für die Datenerfassung als ein Skript.
Im Skript GetDataforONNX.mq5
#include <MALE5\Support Vector Machine(SVM)\svm.mqh> CDualSVMONNX dual_svm; input uint bars = 1000; input uint epochs_ = 1000; input uint batch_size_ = 64; input double alpha__ =0.1; input double lambda_ = 0.01; input int rsi_period = 13; input int bb_period = 20; input double bb_deviation = 2.0; int rsi_handle, bb_handle; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { rsi_handle = iRSI(Symbol(),PERIOD_CURRENT,rsi_period, PRICE_CLOSE); bb_handle = iBands(Symbol(), PERIOD_CURRENT, bb_period,0, bb_deviation, PRICE_CLOSE); //--- matrixf data = GetTrainTestData<float>(); dual_svm.SendDataToONNX(data,"DualSVMONNX-data.csv","rsi,bb-high,bb-low,bb-mid,target"); } //+------------------------------------------------------------------+ //| Getting data for Training and Testing the model | //+------------------------------------------------------------------+ template <typename T> matrix<T> GetTrainTestData() { matrix<T> data(bars, 5); vector<T> v; //Temporary vector for storing Inidcator buffers v.CopyIndicatorBuffer(rsi_handle, 0, 0, bars); data.Col(v, 0); v.CopyIndicatorBuffer(bb_handle, 0, 0, bars); data.Col(v, 1); v.CopyIndicatorBuffer(bb_handle, 1, 0, bars); data.Col(v, 2); v.CopyIndicatorBuffer(bb_handle, 2, 0, bars); data.Col(v, 3); vector open, close; open.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_OPEN, 0, bars); close.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_CLOSE, 0, bars); for (ulong i=0; i<v.Size(); i++) //preparing the independent variable data[i][4] = close[i] > open[i] ? 1 : -1; // if price closed above its opening thats bullish else bearish return data; }
Ausdruck:
Eine csv-Datei mit dem Namen DualSVMONNX-data.csv wurde unter dem MQL5-Verzeichnis Files erstellt.
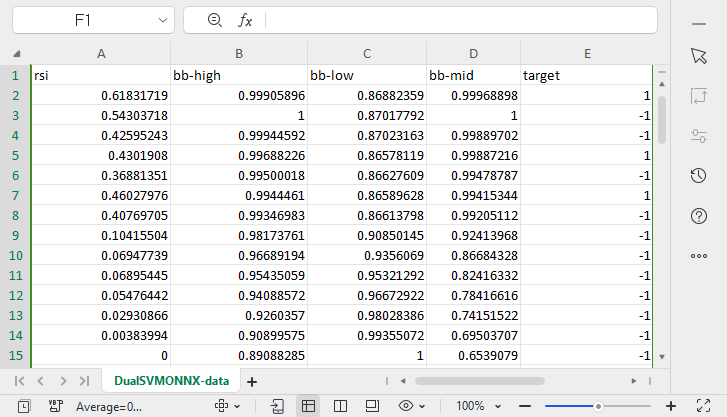
Beachten Sie am Ende der Funktion SendDataToONNX!!
Ich habe auch die Normalisierungsparameter gespeichert,
normalize_x.min_max_scaler.min.Swap(params); matrix_utils.WriteCsv("min_max_scaler.min.csv",params,result,false,8); normalize_x.min_max_scaler.max.Swap(params); matrix_utils.WriteCsv("min_max_scaler.max.csv",params,result,false,8);
Der Grund dafür ist, dass die Normalisierungsparameter, die einmal verwendet wurden, immer wieder verwendet werden müssen, um die besten Vorhersagen aus dem Modell zu erhalten. Das Speichern dieser Parameter würde uns helfen, den Überblick über die Werte unserer Datennormalisierungsparameter zu behalten. Die CSV-Dateien befinden sich im selben Ordner wie der Datensatz und wir werden auch das ONNX-Modell dort aufbewahren.
Die Klasseninstanz DualSVMONNX | Initialisierung einer Klasse:
class DualSVMONNX: def __init__(self, dataset, c=1.0, kernel='rbf'): data = pd.read_csv(dataset) # reading a csv file np.random.seed(42) self.X = data.drop(columns=['target']).astype(np.float32) # dropping the target column from independent variable self.y = data["target"].astype(int) # storing the target variable in its own vector self.X = self.X.to_numpy() self.y = self.y.to_numpy() # Split the data into training and testing sets self.X_train, self.X_test, self.y_train, self.y_test = train_test_split(self.X, self.y, test_size=0.2, random_state=42) self.onnx_model_name = "DualSVMONNX" #our final onnx model file name for saving purposes really # Create a dual SVM model with a kernel self.svm_model = SVC(kernel=kernel, C=c)
Training des Dual-SVM-Modells in Python
def fit(self): self.svm_model.fit(self.X_train, self.y_train) # fitting/training the model y_preds = self.svm_model.predict(self.X_train) print("accuracy = ",accuracy_score(self.y_train, y_preds))
Nachdem das Modell trainiert wurde, wollen wir sehen, wie die Genauigkeit nach der Ausführung dieses Codeschnipsels aussieht.
Ausdruck:
Wir haben eine Genauigkeit von 63 % erreicht, was uns sagt, dass das SVM-Modell für die Klassifizierung dieses speziellen Problems bestenfalls durchschnittlich ist. Ich bin jedoch misstrauisch und möchte eine Kreuzvalidierung durchführen, um zu prüfen, ob die Genauigkeit das ist, was sie sein soll:
scores = cross_val_score(self.svm_model, self.X_train, self.y_train, cv=5) mean_cv_accuracy = np.mean(scores) print(f"\nscores {scores} mean_cv_accuracy {mean_cv_accuracy}")
Ausdruck:
Was bedeutet dieses Ergebnis der Kreuzvalidierung?
Es gibt keine großen Unterschiede zwischen den Ergebnissen, wenn das Modell mit verschiedenen Parametern ausgeführt wird. Dies zeigt uns, dass unser Modell auf dem richtigen Weg ist: Die durchschnittliche Genauigkeit, die wir erreichen konnten, liegt bei 59,875, was nicht weit von den 63,3 entfernt ist, die wir erhalten haben.
Konvertierung des SVC-Modells von sklearn nach ONNX und Speicherung.
def saveONNX(self):
initial_type = [('float_input', FloatTensorType(shape=[None, 4]))] # None means we don't know the rows but we know the columns for sure, Remember !! we have 4 independent variables
onnx_model = convert_sklearn(self.svm_model, initial_types=initial_type) # Convert the scikit-learn model to ONNX format
onnx.save_model(onnx_model, dataset_path + f"\\{self.onnx_model_name}.onnx") #saving the onnx model Ausdruck: NB: Das Modell wurde im Verzeichnis MQL5/Files gespeichert
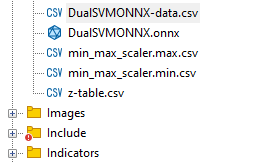
Nachfolgend sehen Sie, wie die ONNX-Datei aussieht, wenn sie in MetaEditor geöffnet wird. Es ist wichtig, dass Sie aufmerksam zuhören, was ich Ihnen jetzt erklären werde.
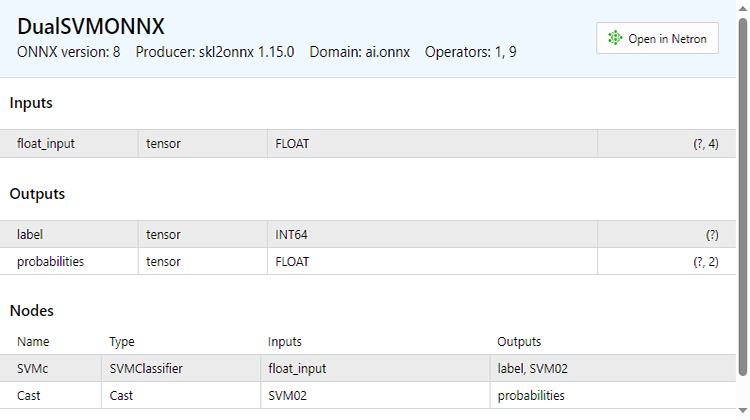
Sehen Sie sich den Abschnitt Eingaben an. Wir haben float_input, der erklärt, dass es sich um eine Eingabe des Typs float handelt, daneben steht tensor, was uns sagt, dass wir die OnnxRun-Funktion mit einer Matrix oder einem Vektor füttern müssen, da beides Tensoren sind. Am Ende steht (?, 4). Dies ist die Eingabegröße, ein Fragezeichen steht für die unbekannte Anzahl der Zeilen, während die Anzahl der Spalten 4 ist. Dies gilt für den Rest der Abschnitte, aber wir sehen den Abschnitt Output.
Sie hat zwei Knoten, von denen einer die vorausgesagten Kennzeichnung -1 oder 1 enthält. In diesem Fall sind sie vom Typ INT64 oder einfach INT in mql5.
Der andere Knoten, der uns die Wahrscheinlichkeiten gibt, ist ein Tensor von Float-Typen, der unbekannte Zeilen, aber 2 Spalten hat, sodass eine nx2-Matrix verwendet werden kann, um die Werte hier zu extrahieren, oder einfach ein Vektor mit einer Größe >= 2
Da es zwei Knoten in der Ausgabe gibt, können wir die Ausgaben zweimal extrahieren:
long outputs_0[] = {1}; if (!OnnxSetOutputShape(onnx_handle, 0, outputs_0)) //giving the onnx handle first node output shape { Print(__FUNCTION__," Failed to set the output shape Err=",GetLastError()); return false; } long outputs_1[] = {1,2}; if (!OnnxSetOutputShape(onnx_handle, 1, outputs_1)) //giving the onnx handle second node output shape { Print(__FUNCTION__," Failed to set the output shape Err=",GetLastError()); return false; }
Andererseits können wir einen einzelnen Eingabeknoten extrahieren, den wir haben.
const long inputs[] = {1,4}; if (!OnnxSetInputShape(onnx_handle, 0, inputs)) //Giving the Onnx handle the input shape { Print(__FUNCTION__," Failed to set the input shape Err=",GetLastError()); return false; }
Dieser ONNX-Code wurde aus der unten angegebenen LoadONNX-Funktion extrahiert:
bool CDualSVMONNX::LoadONNX(const uchar &onnx_buff[], ENUM_ONNX_FLAGS flags=ONNX_NO_CONVERSION) { onnx_handle = OnnxCreateFromBuffer(onnx_buff, flags); //creating onnx handle buffer if (onnx_handle == INVALID_HANDLE) { Print(__FUNCTION__," OnnxCreateFromBuffer Error = ",GetLastError()); return false; } //--- const long inputs[] = {1,4}; if (!OnnxSetInputShape(onnx_handle, 0, inputs)) //Giving the Onnx handle the input shape { Print(__FUNCTION__," Failed to set the input shape Err=",GetLastError()); return false; } long outputs_0[] = {1}; if (!OnnxSetOutputShape(onnx_handle, 0, outputs_0)) //giving the onnx handle first node output shape { Print(__FUNCTION__," Failed to set the output shape Err=",GetLastError()); return false; } long outputs_1[] = {1,2}; if (!OnnxSetOutputShape(onnx_handle, 1, outputs_1)) //giving the onnx handle second node output shape { Print(__FUNCTION__," Failed to set the output shape Err=",GetLastError()); return false; } return true; }
Wenn Sie sich die Funktion genauer ansehen, werden Sie feststellen, dass die Normalisierungsparameter nicht geladen werden. Sie sind entscheidend für die Standardisierung der neuen Eingabedaten, damit sie mit den Dimensionen der trainierten Daten übereinstimmen, mit denen das Modell bereits vertraut ist.
Wir können die Parameter aus einer CSV-Datei laden, was während des Live-Handels reibungslos funktioniert. Allerdings könnte diese Methode kompliziert werden und für den Strategietester nicht immer so effektiv funktionieren, daher sollten wir die Normalisierungsparameter zumindest vorerst manuell in unseren EA-Code kopieren, damit wir am Ende die Normalisierungsparameter in unserem EA haben. Ändern wir zunächst die Funktion LoadONNX so, dass sie die Eingangsvektoren max und min übernimmt, die bei Min Max Scaler eine große Rolle spielen.
bool CDualSVMONNX::LoadONNX(const uchar &onnx_buff[], ENUM_ONNX_FLAGS flags, vectorf &norm_max, vectorf &norm_min)
Am Ende der Funktion habe ich sie eingeführt.
normalize_x = new CPreprocessing<vectorf,matrixf>(norm_max, norm_min); //Load min max scaler with parameters
Kopieren und Einfügen der Normalisierungsparameter aus CSV-Dateien in EA's.
Lassen Sie uns das Modell auf die gleiche Weise trainieren und testen wie in Python, um sicherzustellen, dass wir in beiden Sprachen auf dem gleichen Weg sind.
Innerhalb von OnInit von svm test.mq5
vector min_v = {14.32424641,1.04674852,1.04799891,1.04392886}; vector max_v = {86.28263092,1.07385755,1.07907069,1.07267821}; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- rsi_handle = iRSI(Symbol(),PERIOD_CURRENT, rsi_period, PRICE_CLOSE); bb_handle = iBands(Symbol(), PERIOD_CURRENT, bb_period, 0 , bb_deviation, PRICE_CLOSE); vector y_train, y_test; // float values matrixf datasetf = GetTrainTestData<float>(); matrixf x_trainf, x_testf; vectorf y_trainf, y_testf; //--- matrix_utils.TrainTestSplitMatrices(datasetf,x_trainf,y_trainf,x_testf,y_testf,0.8,42); //split the data into training and testing samples vectorf max_vf = {}, min_vf = {}; //convertin the parameters into float type max_vf.Assign(max_v); min_vf.Assign(min_v); dual_svm.LoadONNX(SVMModel, ONNX_DEFAULT, max_vf, min_vf); y_train.Assign(y_trainf); y_test.Assign(y_testf); vector train_preds = dual_svm.Predict(x_trainf); vector test_preds = dual_svm.Predict(x_testf); Print("\n<<<<< Train Classification Report >>>>\n"); metrics.confusion_matrix(y_train, train_preds); Print("\n<<<<< Test Classification Report >>>>\n"); metrics.confusion_matrix(y_test, test_preds); return(INIT_SUCCEEDED); }Ausdruck:
RP 0 17:08:53.068 svm test (EURUSD,H1) <<<<< Train Classification Report >>>> HE 0 17:08:53.068 svm test (EURUSD,H1) MR 0 17:08:53.068 svm test (EURUSD,H1) Confusion Matrix IG 0 17:08:53.068 svm test (EURUSD,H1) [[245,148] CO 0 17:08:53.068 svm test (EURUSD,H1) [150,257]] NK 0 17:08:53.068 svm test (EURUSD,H1) DE 0 17:08:53.068 svm test (EURUSD,H1) Classification Report HO 0 17:08:53.068 svm test (EURUSD,H1) FI 0 17:08:53.068 svm test (EURUSD,H1) _ Precision Recall Specificity F1 score Support ON 0 17:08:53.068 svm test (EURUSD,H1) 1.0 0.62 0.62 0.63 0.62 393.0 DP 0 17:08:53.068 svm test (EURUSD,H1) -1.0 0.63 0.63 0.62 0.63 407.0 JG 0 17:08:53.068 svm test (EURUSD,H1) FR 0 17:08:53.068 svm test (EURUSD,H1) Accuracy 0.63 CK 0 17:08:53.068 svm test (EURUSD,H1) Average 0.63 0.63 0.63 0.63 800.0 KI 0 17:08:53.068 svm test (EURUSD,H1) W Avg 0.63 0.63 0.63 0.63 800.0 PP 0 17:08:53.068 svm test (EURUSD,H1) DH 0 17:08:53.068 svm test (EURUSD,H1) <<<<< Test Classification Report >>>> PQ 0 17:08:53.068 svm test (EURUSD,H1) EQ 0 17:08:53.068 svm test (EURUSD,H1) Confusion Matrix HJ 0 17:08:53.068 svm test (EURUSD,H1) [[61,31] MR 0 17:08:53.068 svm test (EURUSD,H1) [40,68]] NH 0 17:08:53.068 svm test (EURUSD,H1) DP 0 17:08:53.068 svm test (EURUSD,H1) Classification Report HL 0 17:08:53.068 svm test (EURUSD,H1) FF 0 17:08:53.068 svm test (EURUSD,H1) _ Precision Recall Specificity F1 score Support GJ 0 17:08:53.068 svm test (EURUSD,H1) -1.0 0.60 0.66 0.63 0.63 92.0 PO 0 17:08:53.068 svm test (EURUSD,H1) 1.0 0.69 0.63 0.66 0.66 108.0 DD 0 17:08:53.068 svm test (EURUSD,H1) JO 0 17:08:53.068 svm test (EURUSD,H1) Accuracy 0.65 LH 0 17:08:53.068 svm test (EURUSD,H1) Average 0.65 0.65 0.65 0.64 200.0 CJ 0 17:08:53.068 svm test (EURUSD,H1) W Avg 0.65 0.65 0.65 0.65 200.0
Wir haben mit 63 % den gleichen Genauigkeitswert wie bei unserem Python-Skript erhalten. Ist das nicht wunderbar!!!
So sieht die Vorhersagefunktion von innen aus:
int CDualSVMONNX::Predict(vectorf &inputs) { vectorf outputs(1); //label outputs vectorf x_output(2); //probabilities vectorf temp_inputs = inputs; normalize_x.Normalization(temp_inputs); //Normalize the input features if (!OnnxRun(onnx_handle, ONNX_DEFAULT, temp_inputs, outputs, x_output)) { Print("Failed to get predictions from onnx Err=",GetLastError()); return (int)outputs[0]; } return (int)outputs[0]; }
Sie führt die ONNX-Datei aus, um die Vorhersagen zu erhalten, und gibt eine ganze Zahl für die vorhergesagte Kennzeichnung zurück.
Schließlich musste ich eine einfache Strategie implementieren, die es uns ermöglicht, beide Support Vector Machine-Modelle im Strategietester zu testen. Die Strategie ist einfach: Wenn die vom SVM vorhergesagte Klasse == 1 ist, soll eine Kaufposition eröffnet werden, wenn die vorhergesagte Klasse == -1 ist, soll eine Verkaufsposition eröffnet werden.
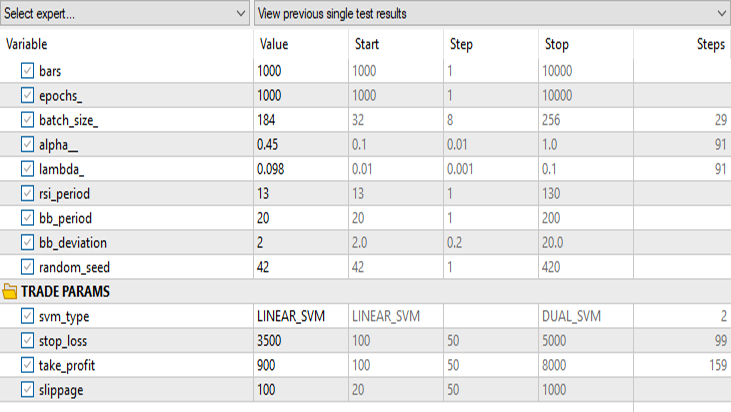
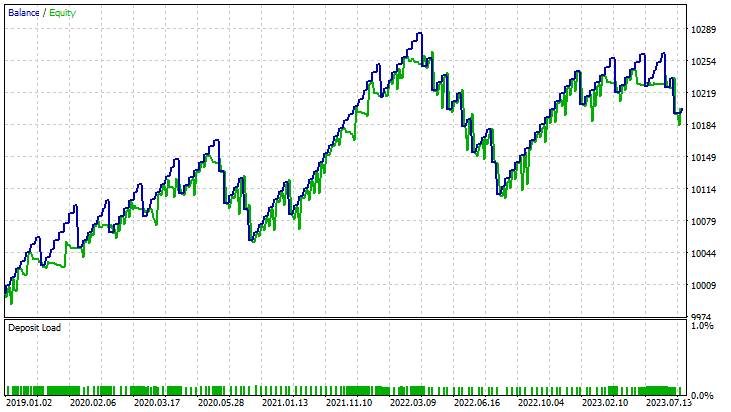
Ergebnisse im Strategietester:
für lineare Support-Vektor-Maschinen:
für Dual Support Vector Machine:
Alle Eingaben mit Ausnahme des svm_type bleiben gleich.
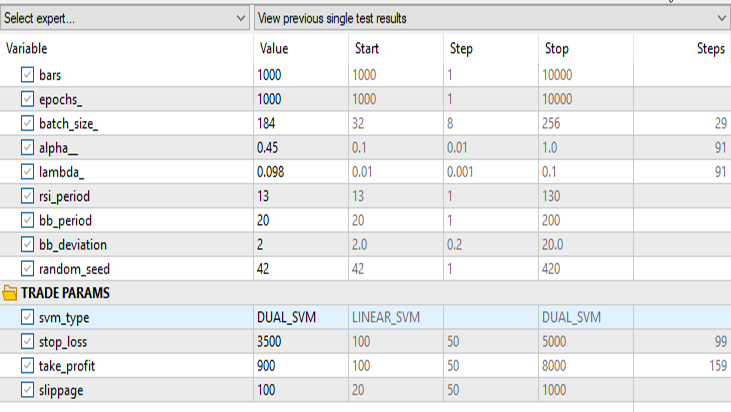
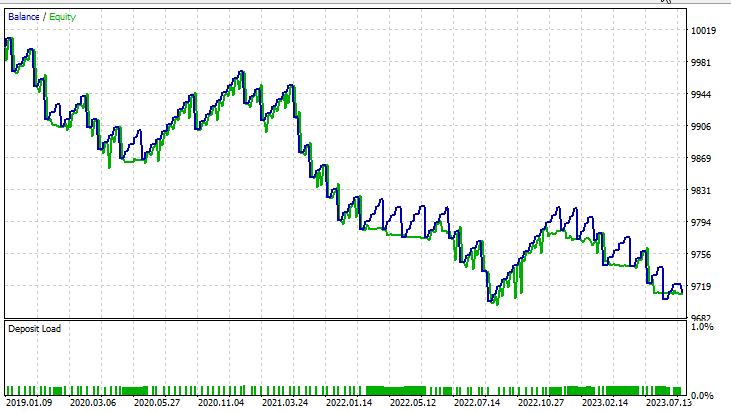
Die duale SVM schnitt mit den Eingaben, die bei der linearen SVM funktionierten, nicht gut ab. Möglicherweise müssen wir weiter optimieren und untersuchen, warum das ONNX-Modell nicht konvergiert, aber das ist ein Thema für einen anderen Artikel.
Abschließende Überlegungen
Vorteile von SVM-Modellen:
- Effektiv in vieldimensionalen Räumen: SVMs funktionieren gut in vieldimensionalen Räumen, was sie für Finanzdatensätze mit zahlreichen Merkmalen, wie Handelsindikatoren und Marktvariablen, geeignet macht.
- Robust gegen Überanpassung: SVMs sind weniger anfällig für eine Überanpassung und bieten eine allgemeinere Lösung, die sich besser an unvorhergesehene Marktbedingungen anpassen kann.
- Vielseitigkeit der Kernel: SVMs bieten Vielseitigkeit durch verschiedene Kernel-Funktionen, die es Händlern ermöglichen, mit verschiedenen Strategien zu experimentieren und das Modell an spezifische Marktmuster anzupassen.
- Starke Leistung in nichtlinearen Szenarien: SVMs zeichnen sich durch die Erfassung nichtlinearer Beziehungen innerhalb von Daten aus, ein entscheidender Aspekt beim Umgang mit komplexen Finanzmärkten.
Nachteile
- Empfindlichkeit gegenüber Rauschen: SVMs können empfindlich auf verrauschte Daten reagieren, was ihre Leistung beeinträchtigt und sie anfälliger für erratisches Marktverhalten macht.
- Computerkomplexität: Das Training von SVM-Modellen kann rechenintensiv sein, insbesondere bei großen Datensätzen, was ihre Skalierbarkeit in bestimmten Echtzeithandelsszenarien einschränkt.
- Bedarf an Quality Feature Engineering: SVMs stützen sich in hohem Maße auf das Feature-Engineering und erfordern Fachwissen, um relevante Indikatoren auszuwählen und Daten effektiv vorzuverarbeiten.
- Durchschnittliche Leistung: Wie wir gesehen haben, erreichten die SVM-Modelle eine durchschnittliche Genauigkeit von 63 % für die duale SVM und 59 % für die lineare SVM. Auch wenn diese Modelle einige fortgeschrittene Techniken des maschinellen Lernens nicht übertreffen, bieten sie dennoch einen vernünftigen Ausgangspunkt für MQL5-Händler.
Der Rückgang der Popularität:
Trotz ihres historischen Erfolgs haben SVMs in den letzten Jahren an Popularität eingebüßt. Dies ist zurückzuführen auf:
- Die Entstehung von Deep Learning: Der Aufstieg der Deep-Learning-Techniken, insbesondere der neuronalen Netze, hat die traditionellen Algorithmen des maschinellen Lernens wie SVMs in den Schatten gestellt, da sie in der Lage sind, automatisch hierarchische Merkmale zu extrahieren.
- Verbesserte Verfügbarkeit von Daten: Mit der zunehmenden Verfügbarkeit großer Finanzdatensätze werden Deep-Learning-Modelle, die mit großen Datenmengen arbeiten, immer interessanter.
- Fortschritte bei der Datenverarbeitung: Die Verfügbarkeit von leistungsfähiger Hardware und verteilten Rechenressourcen hat das Trainieren und Bereitstellen komplexer Deep-Learning-Modelle erleichtert.
Zusammenfassend lässt sich sagen, dass SVM-Modelle zwar nicht die modernste Lösung darstellen, ihre Verwendung in MQL5-Handelsumgebungen jedoch gerechtfertigt ist. Ihre Einfachheit, Robustheit und Anpassungsfähigkeit machen sie zu einem wertvollen Instrument, insbesondere für Händler mit begrenzten Daten- oder Rechenressourcen. Für Händler ist es wichtig, SVMs als Teil eines breiteren Instrumentariums zu betrachten und sie möglicherweise mit neueren Machine-Learning-Ansätzen zu ergänzen, wenn sich die Marktdynamik weiterentwickelt.
Mit freundlichen Grüßen, Peace out.
| Datei | Beschreibung | Verwendung |
|---|---|
| dual_svm.py | Python Skript | Es hat Dual SVM Implementierung in Python |
| GetDataforONNX.mq5 | mql5-Skript | Kann verwendet werden, um die Daten zu sammeln, zu normalisieren und in einer csv-Datei zu speichern, die sich unter MQL5/Files befindet |
| preprocessing.mqh | mql5 include-Datei | Enthält Klasse und Funktionen zur Normalisierung und Standardisierung der Eingabedaten |
| matrix_utils.mqh | mql5 include-Datei | Eine Bibliothek mit zusätzlichen Matrixoperationen |
| metrics.mqh | mql5 Include-Datei | Eine Bibliothek mit zusätzlichen Funktionen zur Analyse der Leistung von ML-Modellen |
| svm test.mq5 | EA | Ein Experten Advisor zum Testen des gesamten Codes, den wir im Artikel vorgestellt haben |
Der Code, der in diesem Artikel verwendet wird, befindet sich auch auf meinem GitHub-Repositorium.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/13395
Entwicklung eines MQTT-Clients für Metatrader 5: ein TDD-Ansatz — Teil 4
Entwurfsmuster in der Softwareentwicklung und MQL5 (Teil I): Erzeugungsmuster
Wie man einen einfachen Multi-Currency Expert Advisor mit MQL5 erstellt (Teil 3): Hinzufügen von Symbolpräfixen und/oder -suffixen und der Handelszeiten
Die visuelle Programmiersprache DRAKON - Kommunikationswerkzeug für MQL-Entwickler und Kunden
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.