Population optimization algorithms: Evolution of Social Groups (ESG)

Contents

1. Introduction
2. Algorithm
3. Test results

1. Introduction

In the field of optimization, there is a wide range of population algorithms designed to find optimal solutions in various problems. However, despite their importance, multi-population and multi-swarm algorithms have not previously been sufficiently covered in my articles. In this regard, I feel the need for a more detailed consideration of this fascinating and promising topic.

Multi-population algorithms are based on the idea of using multiple independent populations to solve optimization problems. Populations work logically in parallel and can exchange information about optimal solutions, which makes it possible to simultaneously explore different regions of the parameter space and find different optima. On the other hand, multi-swarm algorithms use social groups (swarms) of many interacting particles that can also cooperate with each other and exchange information to achieve optimal solutions.

In this article, we will consider the multi-population ESG algorithm that I created specifically for this article. We will look at the basic principles of such algorithms. In addition, we will consider the results of comparative studies that will allow us to evaluate the effectiveness of these algorithms in comparison with mono-population optimization methods.

2. Algorithm

The multi-population algorithm can be based on the following principles in various combinations:

1. Social groups. The algorithm does not operate with individual particles, but with social groups united by cooperation and exchange of experience. Each group has its own decision center and a set of particles as optimization agents. Groups interact, share experiences, and use information about best solutions to improve their results.

2. Collective movement. Particles within social groups interact and move together in parameter space. This allows groups to explore different regions of the parameter space and share information about the best solutions found.

3. Local and global experience. Each social group stores information about the best solution within it (local experience). There is also an overall best score among all groups (global experience). Groups retain the best solutions, share experiences, and use them to improve results.

4. Evolution and exchange of experience. The algorithm goes through iterations, during which social groups update and share experiences. There is an iterative improvement of solutions and a search for the optimal result.

5. Adaptability and diversity. Through interaction and exchange of experience, groups can adapt to changing conditions and find a variety of optimal solutions. The algorithm has the property of adaptability, which allows it to effectively respond to changing conditions and requirements of the optimization problem. Groups can adapt to new conditions, change their strategy for moving through parameter space, and update their decisions based on experience. This allows the algorithm to efficiently search for optimal solutions, especially in cases where the problem conditions change over time.

Above we talked about the basic principles of multi-population algorithms. Now let's look at the specifics of the ESG search strategy.

Suppose that we have a society of particles, which we call a "social group". In this group, a certain behavior model (the "center") prevails, and the particles of the group follow this model with some deviation, which can be described by a certain distribution law. Most particles deviate slightly from the center, but some deviate greatly within the zone of influence of the group, the boundaries of which are determined by the distribution. When a more adapted behavior pattern appears among particles, it becomes the new center of the group. Thus, the group moves in search of the most stable model of particle behavior.

There can be several such groups, and they are independent, so it can be called a multi-population algorithm, simulating the behavior of individual members in social groups at a low level and the general behavior of groups at a high level.

Given this concept, situations are possible when some individual groups or even all groups simultaneously stop in their development and get stuck in local extremes. To avoid this, we introduce the concept of "expanding the sphere of influence of a social group". If there is no progress at each iteration, the group boundaries are expanded, allowing new search areas to be opened and the group population to be diversified. If the group finds a solution that is superior to the previous one, the group boundary radius is reduced again to the default minimum value. This helps the algorithm avoid getting stuck in local traps and, if necessary, enhances the exploration of new areas. Increasing the radius also contributes to the diversity of social groups. Different groups will explore different regions of the parameter space.

This concept of a multi-population algorithm for the evolution of social groups looks promising. However, not everything is as simple as it might seem at first glance. The current position of the group's center may be in an unfortunate position on the corresponding coordinates, and even expanding the zone of influence may not be effective. In such cases, we can say that a "diagonal expansion" occurs (as in the ACO algorithm, where the ants run only along their paths without deviating to the side), when in fact a "perpendicular expansion" is required, or the exact opposite situation is also possible.

To overcome the above problem, it is important to ensure that successful experiences are transferred between groups. For this purpose, some particles can be allowed to borrow ideas from the centers of "alien" groups. Thus, the central behavior pattern will influence individual particles of other groups. By the way, the impact cannot and will not necessarily be positive. The behavior model of social groups is shown schematically in Figure 1.

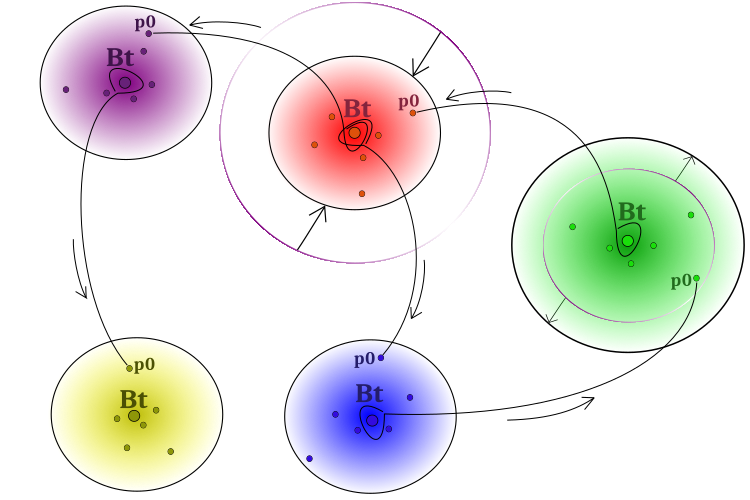
Figure 1. Algorithm operation. Separate groups, expansion in case of lack of progress, narrowing in case of the solution improvement,

borrowing the "best ideas" (coordinates) from neighboring "Bt" (best of team) groups by "p0" particles (particle at the conditional 0 th group index)

The pseudocode of the ESG algorithm can be represented as follows:

1. Randomly place the centers of the groups in the search space.
2. Place the particles of the groups around the corresponding centers with a given distribution*.
3. Calculate the particle fitness values.
4. Update the global solution.
5. Update the center of each group.
6. Expand the boundaries of the groups if there is no improvement in the position of the center and reduce it if we managed to improve the position.
7. Place the particles of the groups around the corresponding centers with a given distribution.
8. Add information from the centers of "alien groups" to one particle of each group (the particle receives a set of coordinates from alien groups selected at random).
9. Calculate the particle fitness values.
   
10. Repeat from step 4 until the stop criterion is met.

* - In ESG, I used distribution power law for the distribution of group particles relative to the center. However, other distribution laws can be used, including their combinations for individual parts of the strategy logic. The topic is open for experimentation.

Let's move on to reviewing the code. To describe a social group, we will write the S_Group structure, which contains several member variables:

• "cB" - array of values to store the "center" coordinates.
• "fB" - center fitness function initialized by "-DBL_MAX".
• "sSize" - group size.
• "sRadius" - group radius.
  

The Init method in the structure takes two arguments: "coords" - the number of coordinates and "groupSize" - the size of the group.

//——————————————————————————————————————————————————————————————————————————————
struct S_Group
{
  void Init (int coords, int groupSize)
  {
    ArrayResize (cB, coords);
    fB          = -DBL_MAX;
    sSize       = groupSize;
  }

  double cB [];
  double fB;
  int    sSize;
  double sRadius;
};
//——————————————————————————————————————————————————————————————————————————————

A simple structure describing the search agent is suitable For the logic of the ESG algorithm. I decided not to include the structure of agent particles in the group description fields. Each group will have access to its particles as part of the general population, which will allow maintaining the usual access to agents from outside the algorithm and at the same time avoiding unnecessary copying of group particles into agents.

The definition of the S_Agent structure contains two variables:

• "c" - array of agent coordinate values.
• "f" - agent fitness value initialized by "-DBL_MAX".
  

The Init method takes the "coords" argument to resize the "c" array.

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (const int coords)
  {
    ArrayResize (c, coords);
    f = -DBL_MAX;
  }

  double c []; //coordinates
  double f;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

Define the C_AO_ESG class, which contains several fields and methods:

1. Public fields:

• "cB" - array of values for the best coordinates of the global solution.
• "fB" - fitness value of the best coordinates.
• "a" - array of S_Agent type objects representing agents.
• "rangeMax" - array of maximum search range values.
• "rangeMin" - array of minimum search range values.
•  "rangeStep" - array of search step values.

2. Methods:

• "Init" - function used to initialize class member variables. Accepts arguments: number of coordinates, population size, number of groups, initial group radius, group expansion factor and degree of distribution.
  
• "Moving" - the method is responsible for moving agents.
• "Revision" - the method is responsible for the revision of agents.
• "SeInDiSp" - method for calculating values in a range with a given step.
• "RNDfromCI" - method for generating random numbers in a given interval.
• "Scale" - method for scaling values from one range to another.
• "PowerDistribution" - method for generating values according to a power distribution.

3. Private fields:

• "coords" - number of coordinates.
• "popSize" - population size.
• "gr" - array of S_Group type objects representing groups.
• "groups" - number of groups.
• "groupRadius" - group radius.
• "expansionRatio" - expansion ratio.
• "power" - power.
•  "revision" - flag indicating the need for revision.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ESG
{
  //----------------------------------------------------------------------------
  public: double  cB [];       //best coordinates
  public: double  fB;          //FF of the best coordinates
  public: S_Agent a  [];       //agents

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    groupsP,              //number of groups
                     const double groupRadiusP,         //group radius
                     const double expansionRatioP,      //expansion ratio
                     const double powerP);              //power

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int     coords;
  private: int     popSize;          //population size
  private: S_Group gr [];            //group

  private: int    groups;            //number of groups
  private: double groupRadius;       //group radius
  private: double expansionRatio;    //expansion ratio
  private: double power;             //power

  private: bool   revision;

  private: double SeInDiSp          (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI         (double min, double max);
  private: double Scale             (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
  private: double PowerDistribution (const double In, const double outMin, const double outMax, const double power);
};
//——————————————————————————————————————————————————————————————————————————————

The Init method of the class is used to initialize class variables based on the passed parameters. In addition to the primary initialization of variables and setting the sizes of arrays, the method calculates the number of particles in each group if the number of groups is not a multiple of the population size.

The "partInSwarms" array is resized to "groups", where "groups" is the number of groups. The variable "particles" is then set to the result of dividing "popSize" by "groups", where "popSize" is the population size. The values of the "partInSwarms" array are filled with the value "particles", that is, the quantity without a remainder. The number of lost elements is then calculated by subtracting the product of "particles" and "groups" from "popSize". If there are lost elements ("lost > 0"), then they are evenly distributed among the groups in the 'while' loop.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ESG::Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    groupsP,              //number of groups
                     const double groupRadiusP,         //group radius
                     const double expansionRatioP,      //expansion ratio
                     const double powerP)
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords         = coordinatesNumberP;
  popSize        = populationSizeP;
  groups         = groupsP;
  groupRadius    = groupRadiusP;
  expansionRatio = expansionRatioP;
  power          = powerP;

  //----------------------------------------------------------------------------
  int partInSwarms [];
  ArrayResize (partInSwarms, groups);

  int particles = popSize / groups;
  ArrayInitialize (partInSwarms, particles);

  int lost = popSize - particles * groups;

  if (lost > 0)
  {
    int pos = 0;

    while (true)
    {
      partInSwarms [pos]++;
      lost--;
      pos++;
      if (pos >= groups) pos = 0;
      if (lost == 0) break;
    }
  }

  //----------------------------------------------------------------------------
  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);

  ArrayResize (gr,        groups);
  for (int s = 0; s < groups; s++) gr [s].Init (coords, partInSwarms [s]);

  ArrayResize (a, popSize);
  for (int i = 0; i < popSize; i++) a [i].Init (coords);
}
//——————————————————————————————————————————————————————————————————————————————

The Moving method is used to generate group centers and individuals at the beginning of optimization. The method does the following:

• Generating centers for each "s" group in the outer "for" loop. To do this, a nested "for" loop generates a "coordinate" random value in a given range for each "c" coordinate. The "coordinate" value is then converted to the desired range and stored in the "gr[s].cB[c]" array.

• Generate individuals for each "s" group and each "p" individual in the outer "for" loop. The value of "radius" is calculated based on the given parameters and the current state of the group in the nested "for" loops. The "min" and "max" values are then calculated by adjusting the "radius" relative to the range bounds. A random "coordinate" value within the given range is then generated using the "PowerDistribution" function. The resulting "coordinate" value is converted and stored in the "a[cnt].c[c]" array.

• Setting the "revision" flag to "true" to indicate that the generation of centers and individuals is in progress.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ESG::Moving ()
{
  if (!revision)
  {
    int    cnt        = 0;
    double coordinate = 0.0;
    double radius     = 0.0;
    double min        = 0.0;
    double max        = 0.0;

    //generate centers----------------------------------------------------------
    for (int s = 0; s < groups; s++)
    {
      gr [s].sRadius = groupRadius;

      for (int c = 0; c < coords; c++)
      {
        coordinate    = RNDfromCI (rangeMin [c], rangeMax [c]);
        gr [s].cB [c] = SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    //generate individuals of groups--------------------------------------------
    for (int s = 0; s < groups; s++)
    {
      for (int p = 0; p < gr [s].sSize; p++)
      {
        for (int c = 0; c < coords; c++)
        {
          radius = (rangeMax [c] - rangeMin [c]) * gr [s].sRadius;
          min    = gr [s].cB [c] - radius;
          max    = gr [s].cB [c] + radius;

          if (min < rangeMin [c]) min = rangeMin [c];
          if (max > rangeMax [c]) max = rangeMax [c];

          coordinate    = PowerDistribution (gr [s].cB [c], min, max, power);
          a [cnt].c [c] = SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]);
        }

        cnt++;
      }
    }

    revision = true;
  }
}
//——————————————————————————————————————————————————————————————————————————————

The main actions for generating new particles occur in the "Revision" method, which updates the best global solution, generates new individuals of groups and exchanges experience between groups by transferring information from the centers of "alien" groups to one particle. Thus, only one particle in a group is allowed to borrow experience from other groups. The method does the following:

• Updating the global solution. In the "for" loop, go through all individuals and check if the value of the fitness function of the current individual exceeds the current best value of the fitness function. Then the best value is updated and the array of coordinates of the current individual is copied to the array of coordinates of the best solution.

• Generating new group individuals. In the "for" loop, go through all groups and their individuals. The radius, as well as minimum and maximum coordinate values for each group are calculated in nested loops. Random coordinate values are then generated using the "PowerDistribution" function and the result is stored in an array of individuals' coordinates.

• Exchange of experience between groups. In the "for" loop, go through all the groups. In the nested "for" loop, a random value is generated that determines which group the experience will be exchanged with. The coordinate values of the individuals in the current group are then updated with the coordinate values of the selected group.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ESG::Revision ()
{
  //----------------------------------------------------------------------------
  //update the best global solution
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  int cnt = 0;
  bool impr = false;

  for (int s = 0; s < groups; s++)
  {
    impr = false;

    for (int p = 0; p < gr [s].sSize; p++)
    {
      if (a [cnt].f > gr [s].fB)
      {
        gr [s].fB = a [cnt].f;
        ArrayCopy (gr [s].cB, a [cnt].c, 0, 0, WHOLE_ARRAY);
        impr = true;
      }

      cnt++;
    }

    if (!impr) gr [s].sRadius *= expansionRatio;
    else       gr [s].sRadius  = groupRadius;

    if (gr [s].sRadius > 0.5) gr [s].sRadius = 0.5;
  }

  //generate individuals of groups----------------------------------------------
  double coordinate = 0.0;
  double radius     = 0.0;
  double min        = 0.0;
  double max        = 0.0;
  cnt = 0;

  for (int s = 0; s < groups; s++)
  {
    for (int p = 0; p < gr [s].sSize; p++)
    {
      for (int c = 0; c < coords; c++)
      {
        if (RNDfromCI (0.0, 1.0) < 1.0)
        {
        radius = (rangeMax [c] - rangeMin [c]) * gr [s].sRadius;
        min    = gr [s].cB [c] - radius;
        max    = gr [s].cB [c] + radius;

        if (min < rangeMin [c]) min = rangeMin [c];
        if (max > rangeMax [c]) max = rangeMax [c];

        coordinate    = PowerDistribution (gr [s].cB [c], min, max, power);
        a [cnt].c [c] = SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }

      cnt++;
    }
  }

  //exchange of experience----------------------------------------------------------------
  cnt = 0;

  for (int s = 0; s < groups; s++)
  {
    for (int c = 0; c < coords; c++)
    {
      int posSw = (int)RNDfromCI (0, groups);
      if (posSw >= groups) posSw = groups - 1;

      //if (sw [posSw].fB > sw [s].fB)
      {
        a [cnt].c [c] = gr [posSw].cB [c];
      }
    }

    cnt += gr [s].sSize;
  }
}
//——————————————————————————————————————————————————————————————————————————————

After writing the main ESG algorithm presented above, I decided to make changes and allow particles of different groups to exchange information in order to improve the combinatorial qualities of the algorithm. To do this, we have to make changes to the agent structure. We will need additional fields: "cMain" - main coordinates and "fMain" - main experience.

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (const int coords)
  {
    ArrayResize (c,     coords);
    ArrayResize (cMain, coords);
    f     = -DBL_MAX;
    fMain = -DBL_MAX;
  }

  double c     []; //coordinates
  double cMain []; //coordinates
  double f;        //fitness
  double fMain;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

the difference between the two options lies in the changes made to the "Revision" method:

1. In the main version, the exchange of experience between agents is carried out at the group level. In the inner "for" loop, a random group is selected and the current agent's coordinate value is replaced with the center coordinate value in the selected group. Thus, groups exchange experience by transferring experience to only one particle in the corresponding group.

2. In the second option, the exchange of experience between agents is carried out at the level of the entire population, that is, between particles of groups if the particle chosen for exchange has a higher fitness. Thus, only the best particles can transfer experience to the worst particles between groups. In the inner "for" loop, a random agent is selected, and with a certain probability (determined by the "copyProb" value), the coordinate value of the current agent is replaced with the coordinate value of the selected agent in the population.

Additionally, the second option has an additional block of code that updates the agents. If the current agent's fitness function value is greater than its previous best value (f > fMain), then the current agent's coordinate values are updated with the values of its current best solution (cMain). This allows agents to save and use their best decisions later.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ESG::Revision ()
{
  //----------------------------------------------------------------------------
  //Update the best global solution
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  //update agents
  for (int p = 0; p < popSize; p++)
  {
    if (a [p].f > a [p].fMain)
    {
      a [p].fMain = a [p].f;
      ArrayCopy (a [p].cMain, a [p].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  int cnt = 0;
  bool impr = false;

  for (int s = 0; s < groups; s++)
  {
    impr = false;

    for (int p = 0; p < gr [s].sSize; p++)
    {
      if (a [cnt].f > gr [s].fB)
      {
        gr [s].fB = a [cnt].f;
        ArrayCopy (gr [s].cB, a [cnt].c, 0, 0, WHOLE_ARRAY);
        impr = true;
      }

      cnt++;
    }

    if (!impr) gr [s].sRadius *= expansionRatio;
    else       gr [s].sRadius  = groupRadius;

    if (gr [s].sRadius > 0.5) gr [s].sRadius = 0.5;
  }

  //generate individuals of groups----------------------------------------------
  double coordinate = 0.0;
  double radius     = 0.0;
  double min        = 0.0;
  double max        = 0.0;
  cnt = 0;

  for (int s = 0; s < groups; s++)
  {
    for (int p = 0; p < gr [s].sSize; p++)
    {
      for (int c = 0; c < coords; c++)
      {
        if (RNDfromCI (0.0, 1.0) < 0.6)
        {
        radius        = (rangeMax [c] - rangeMin [c]) * gr [s].sRadius;
        min           = gr [s].cB [c] - radius;
        max           = gr [s].cB [c] + radius;

        if (min < rangeMin [c]) min = rangeMin [c];
        if (max > rangeMax [c]) max = rangeMax [c];

        coordinate    = PowerDistribution (gr [s].cB [c], min, max, power);
        a [cnt].c [c] = SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }

      cnt++;
    }
  }

  //exchange of experience----------------------------------------------------------------
  cnt = 0;

  for (int p = 0; p < popSize; p++)
  {
    for (int c = 0; c < coords; c++)
    {
      int pos = (int)RNDfromCI (0, popSize);
      if (pos >= popSize) pos = popSize - 1;

      if (RNDfromCI(0.0, 1.0) < copyProb)
      {
        if (a [pos].fMain > a [p].fMain)
        {
          a [p].c [c] = a [pos].cMain [c];
        }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

As a result of experiments and testing of the second version of the algorithm, the overall result did not bring the expected progress and deteriorated slightly. This can be explained by the fact that it is important to keep the experience of particles within the boundaries of their own groups and not allow complete mixing of ideas between groups. The unique experience of each individual group should be preserved and only partial exchange of experience should be ensured.

The failure of the experiment is not final and does not mean that improvement of the algorithm is impossible. This is just one attempt that allows us to understand what aspects are worth paying attention to and what strategies are best to apply. With further research and development, the knowledge gained can be used to create new variants of the algorithm that can lead to significant improvements in search capabilities. It is important to remain optimistic and persistent in achieving set goals. The test results are presented below.

3. Test results

ESG main version test stand results:

C_AO_ESG|200|100|0.1|2.0|10.0
=============================
5 Hilly's; Func runs: 10000; result: 0.9990564816911227
25 Hilly's; Func runs: 10000; result: 0.7965424362150277
500 Hilly's; Func runs: 10000; result: 0.35055904999599663
=============================
5 Forest's; Func runs: 10000; result: 1.0
25 Forest's; Func runs: 10000; result: 0.8286255415345216
500 Forest's; Func runs: 10000; result: 0.13102081222227177
=============================
5 Megacity's; Func runs: 10000; result: 0.8233333333333333
25 Megacity's; Func runs: 10000; result: 0.5529999999999999
500 Megacity's; Func runs: 10000; result: 0.04724999999999998
=============================
All score: 5.52939 (61.44%)

Slightly modified ESG version test stand results:

C_AO_MPSO|200|100|0.1|1.1|10.0|1.0
=============================
5 Hilly's; Func runs: 10000; result: 0.9986983861349696
25 Hilly's; Func runs: 10000; result: 0.7971379560351051
500 Hilly's; Func runs: 10000; result: 0.3351159723676586
=============================
5 Forest's; Func runs: 10000; result: 1.0
25 Forest's; Func runs: 10000; result: 0.8288612676775615
500 Forest's; Func runs: 10000; result: 0.11374411604788078
=============================
5 Megacity's; Func runs: 10000; result: 0.8333333333333333
25 Megacity's; Func runs: 10000; result: 0.5116666666666667
500 Megacity's; Func runs: 10000; result: 0.049316666666666654
=============================
All score: 5.46787 (60.75%)

We can see good convergence of the main version of the algorithm. On the test functions Hilly and Forest, a slight scatter in the trajectories is noticeable on the convergence graph. However, on the Megacity function, this scatter is quite large, although most algorithms on this test function also show a wide scatter of convergence. Unlike of most algorithms presented earlier, the algorithm "prefers" a much larger population size - 200 (usually 50 is used), despite the fact that the number of epochs is proportionally reduced. ESG works well at local extremes. This property is influenced by the multi-population "nature" of the algorithm.

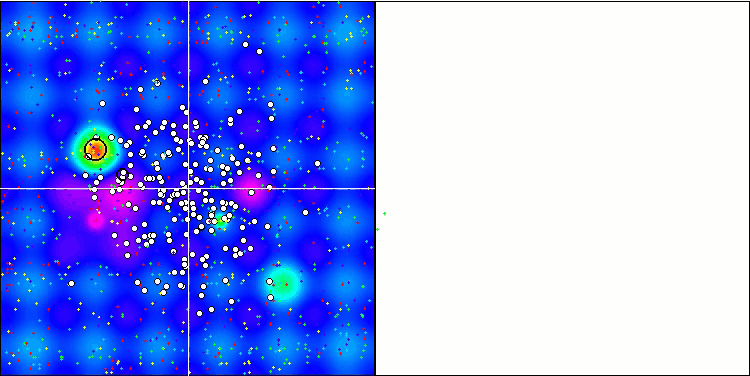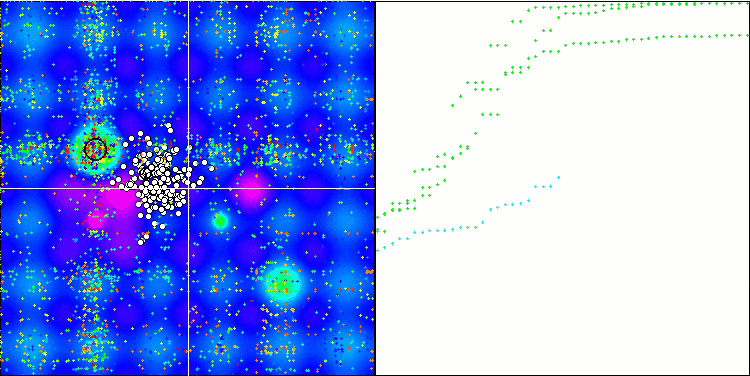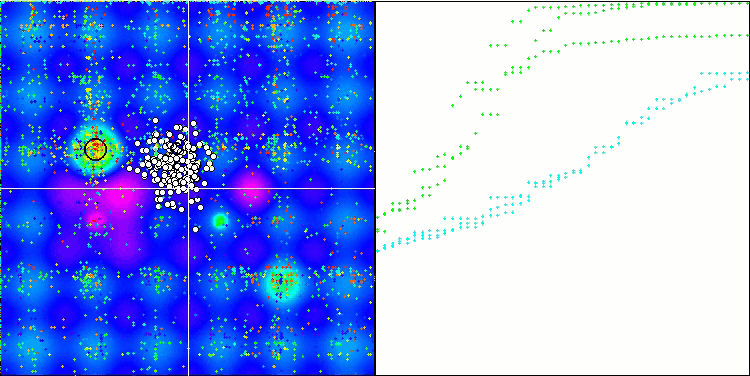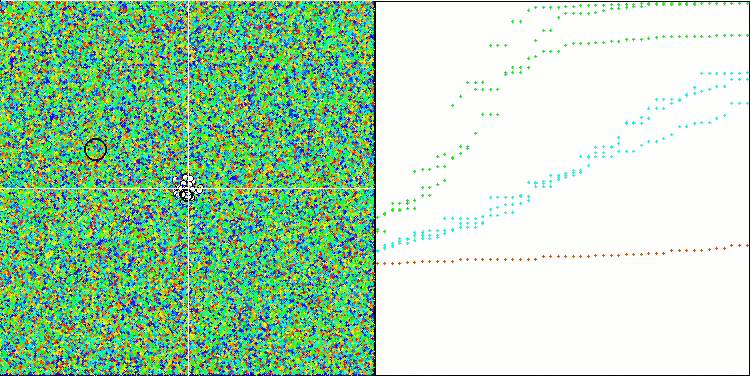
  ESG on the Hilly test function

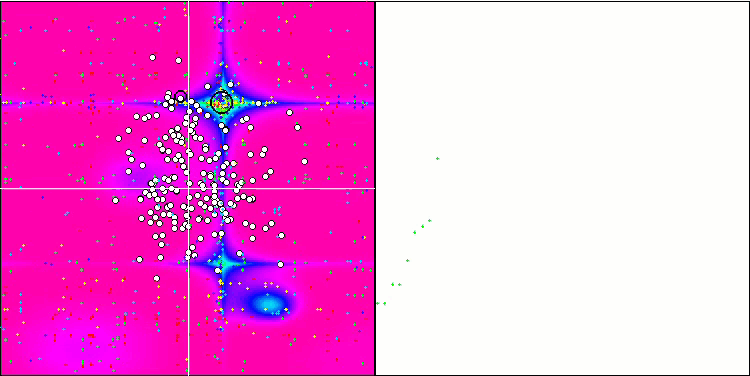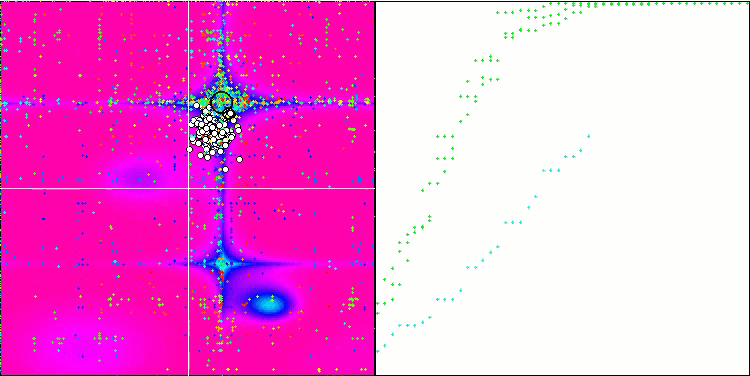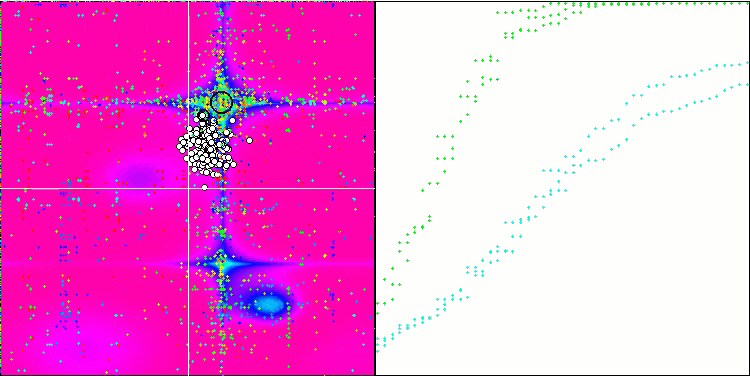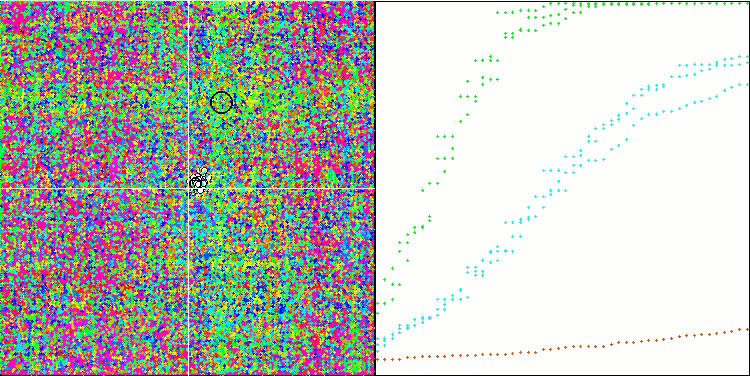
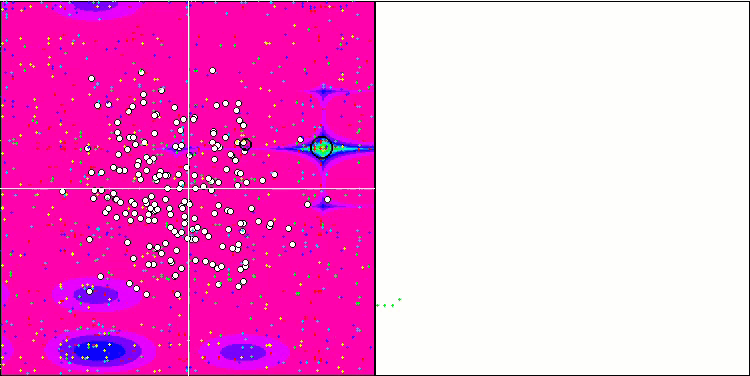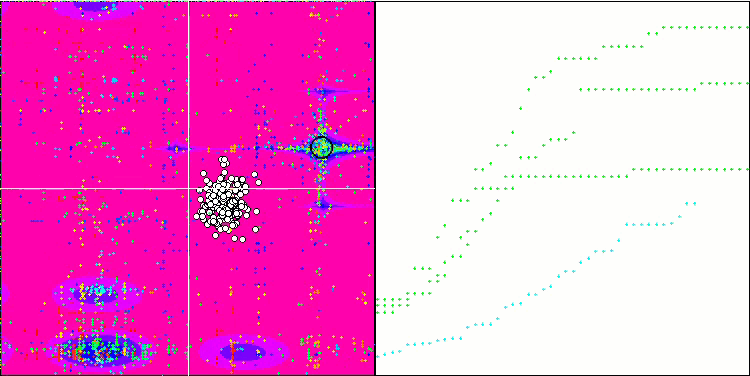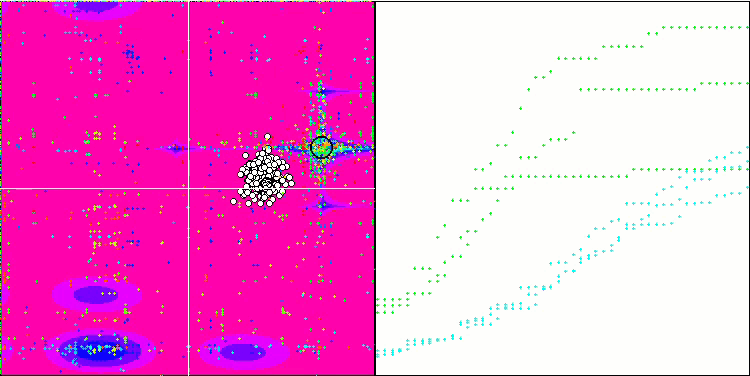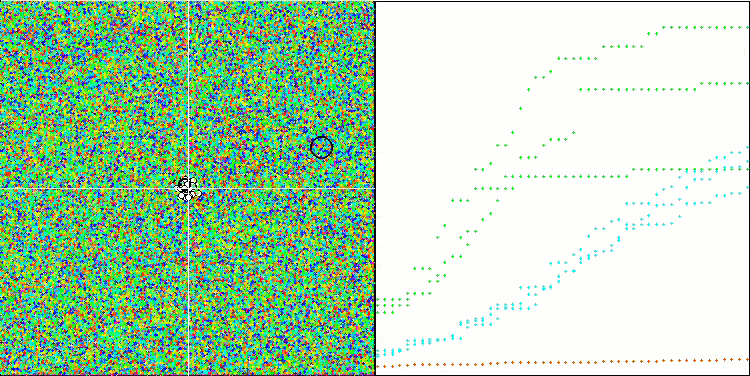
  ESG on the Forest test function

  ESG on the Megacity test function

The ESG algorithm showed decent results and was among the leaders in the rating table. One can note 100% convergence for the Forest function with 10 parameters and almost complete, 99.9% convergence for the Hilly function with 10 parameters. The table contains the results of the main version of the algorithm, while the experimental version is located in the "variant2" folder.

#	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	BGA	binary genetic algorithm	0.99992	0.99484	0.50483	2.49959	1.00000	0.99975	0.32054	2.32029	0.90667	0.96400	0.23035	2.10102	6.921	76.90
2	(P+O)ES	(P+O) evolution strategies	0.99934	0.91895	0.56297	2.48127	1.00000	0.93522	0.39179	2.32701	0.83167	0.64433	0.21155	1.68755	6.496	72.18
3	SDSm	stochastic diffusion search M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
4	ESG	evolution of social groups	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
5	SIA	simulated isotropic annealing	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
6	DE	differential evolution	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
7	HS	harmony search	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
8	SSG	saplings sowing and growing	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
9	(PO)ES	(PO) evolution strategies	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
10	ACOm	ant colony optimization M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
11	BFO-GA	bacterial foraging optimization - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
12	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
13	IWO	invasive weed optimization	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
14	Micro-AIS	micro artificial immune system	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
15	COAm	cuckoo optimization algorithm M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
16	SDOm	spiral dynamics optimization M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
17	NMm	Nelder-Mead method M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
18	FAm	firefly algorithm M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
19	GSA	gravitational search algorithm	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
20	BFO	bacterial foraging optimization	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
21	ABC	artificial bee colony	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
22	BA	bat algorithm	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
23	SA	simulated annealing	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
24	IWDm	intelligent water drops M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
25	PSO	particle swarm optimisation	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
26	MA	monkey algorithm	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
27	SFL	shuffled frog-leaping	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
28	FSS	fish school search	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
29	RND	random	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
30	GWO	grey wolf optimizer	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32
31	CSS	charged system search	0.44252	0.35454	0.35201	1.14907	0.24140	0.11345	0.06814	0.42299	0.18333	0.06300	0.02322	0.26955	1.842	20.46
32	EM	electroMagnetism-like algorithm	0.46250	0.34594	0.32285	1.13129	0.21245	0.09783	0.10057	0.41085	0.15667	0.06033	0.02712	0.24412	1.786	19.85

Summary

In conclusion, the social group evolution algorithm is an effective optimization method based on cooperation and sharing of experiences between groups. It has the properties of adaptability, diversity and is able to find optimal solutions in various optimization problems.

I can recommend the ESG algorithm for use in various areas where optimization of parameters is required. For example, it can be used to tune hyperparameters in machine learning, optimize functions in optimal control problems, solve combinatorial optimization problems, and other problems where finding optimal parameter values is required.

The presented algorithm can be considered as a kind of template, which can be supplemented with various individual techniques and search strategies described in previous articles. In addition, each group can use separate optimization algorithms, such as PSO, ABC, ACO, etc. Thus, the architecture of the ESG algorithm makes it easy to implement such optimization methods and use them together, combining the advantages of each algorithm separately.

It is important to emphasize that ESG is a standalone solution with good results and is an extremely flexible approach to solving complex problems. Its full potential can be unlocked through experimentation and development of the core idea, and opportunities for such experimentation are open to everyone.

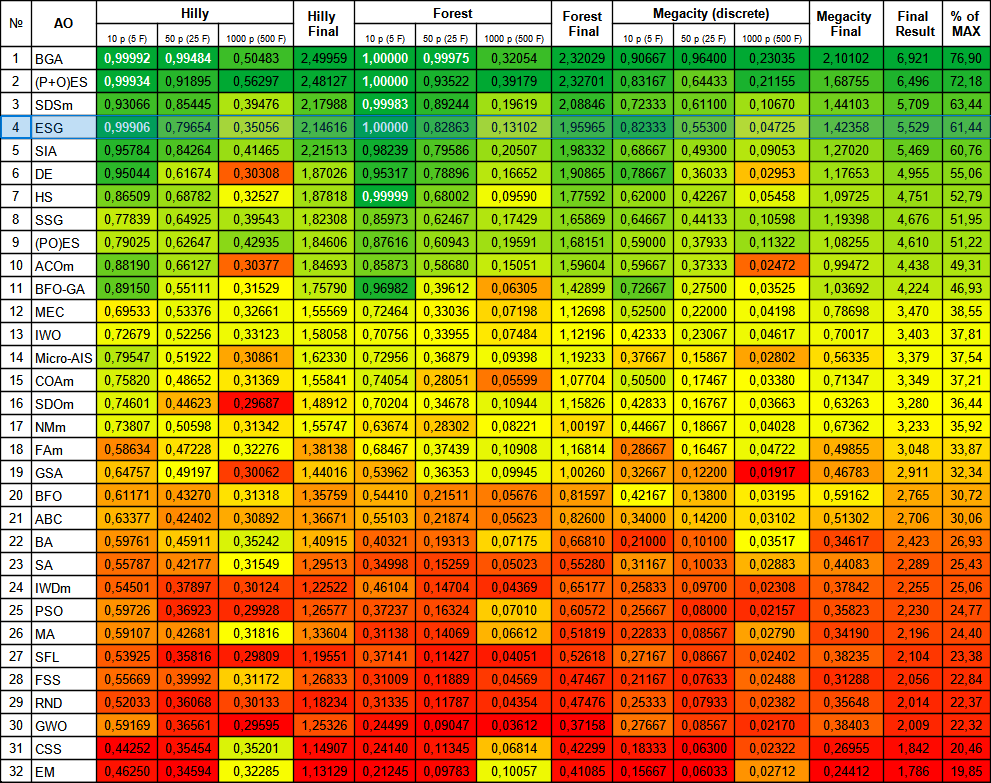
Figure 2. Color gradation of algorithms according to relevant tests Results greater than or equal to 0.99 are highlighted in white

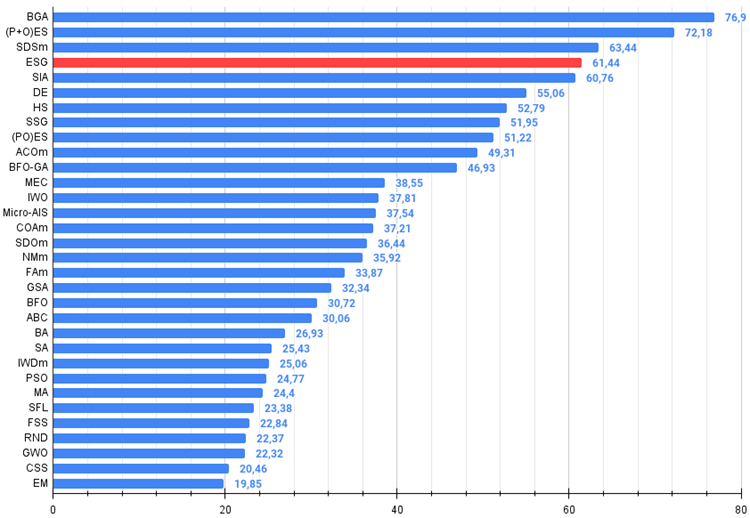
Figure 3. The histogram of algorithm test results (on a scale from 0 to 100, the more the better,

where 100 is the maximum possible theoretical result, the archive features a script for calculating the rating table)

ESG pros and cons:

Advantages:

1. Simple architecture.
   
2. High convergence.
3. Not demanding on computing resources.

Disadvantages:

1. Poor results on functions with a large number of parameters.
   

The article is accompanied by an archive with updated current versions of the algorithm codes described in previous articles. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.