Algoritmos de otimização populacionais: evolução de grupos sociais (Evolution of Social Groups, ESG)

Conteúdo:

1. Introdução
2. Descrição do algoritmo
3. Resultados dos testes

1. Introdução

No campo da otimização, existe uma ampla gama de algoritmos populacionais destinados à busca de soluções ótimas em diversas tarefas. Contudo, apesar de sua importância, algoritmos multipopulacionais e de enxames não foram suficientemente abordados em meus artigos e pesquisas anteriores. Por isso, decidi abordar mais detalhadamente este tema fascinante e promissor.

Os algoritmos multipopulacionais são baseados na ideia de usar várias populações independentes para resolver problemas de otimização. As populações operam logicamente em paralelo e podem trocar informações sobre soluções ótimas, o que permite explorar simultaneamente diferentes regiões do espaço de parâmetros e encontrar diversos ótimos. Por outro lado, os algoritmos de enxames utilizam grupos sociais (enxames) compostos por múltiplas partículas interagentes, que também podem cooperar entre si e trocar informações para alcançar soluções ótimas.

Neste artigo, preencheremos essa lacuna e consideraremos como exemplo o algoritmo multipopulacional ESG, criado por mim especificamente para este artigo. Examinaremos os princípios básicos de funcionamento desses algoritmos. Além disso, discutiremos os resultados de estudos comparativos que permitirão avaliar a eficácia desses algoritmos em comparação com métodos de otimização monopopulacionais.

2. Descrição do algoritmo

A base do algoritmo multipopulacional pode ser formada por diversas variantes e combinações dos princípios a seguir:

1. Grupos sociais. O algoritmo opera não com partículas individuais, mas com grupos sociais, unidos pela cooperação e troca de experiências. Cada grupo tem seu próprio centro de tomada de decisões e um conjunto de partículas como agentes de otimização. Os grupos interagem, trocam experiências e utilizam informações sobre as melhores soluções para melhorar seus resultados.

2. Movimento Coletivo. As partículas dentro dos grupos sociais interagem e se movem conjuntamente no espaço de parâmetros. Isso permite que os grupos explorem diferentes regiões do espaço de parâmetros e troquem informações sobre as melhores soluções encontradas.

3. Experiência Local e Global. Cada grupo social armazena informações sobre a melhor solução dentro dele (experiência local). Também existe o melhor resultado geral entre todos os grupos (experiência global). Os grupos guardam as melhores soluções, trocam experiências e utilizam-nas para melhorar os resultados.

4. Evolução e Troca de Experiências. O algoritmo passa por iterações, em que os grupos sociais são atualizados e trocam experiências. Ocorre a melhoria iterativa das soluções e a busca pelo resultado ótimo.

5. Adaptabilidade e Diversidade. Graças à interação e troca de experiências, os grupos podem se adaptar às condições mutáveis e encontrar diversas soluções ótimas. O algoritmo possui a propriedade de adaptabilidade, o que lhe permite reagir eficientemente às condições e requisitos variáveis da tarefa de otimização. Os grupos podem se adaptar às novas condições, alterar sua estratégia de movimentação no espaço de parâmetros e atualizar suas soluções com base na experiência adquirida. Isso permite que o algoritmo busque eficientemente soluções ótimas, especialmente nos casos em que as condições da tarefa mudam ao longo do tempo.

Acima, falamos sobre os princípios básicos dos algoritmos multipopulacionais. Agora, vamos considerar as características da estratégia de busca ESG.

Suponhamos que temos uma sociedade de partículas, que chamaremos de "grupo social". Nesse grupo, predomina um determinado modelo de comportamento - "centro", e as partículas do grupo seguem esse modelo com alguma variação, que pode ser descrita por uma determinada lei de distribuição. A maioria das partículas difere ligeiramente do centro, mas algumas se desviam significativamente dentro da zona de influência do grupo, cujos limites são determinados pela distribuição. Quando aparece um modelo de comportamento mais adaptável entre as partículas, ele se torna o novo centro do grupo. Dessa forma, o grupo busca o modelo de comportamento das partículas que seja mais estável.

Pode haver vários desses grupos, e eles são independentes, por isso isso pode ser chamado de algoritmo multipopulacional, que imita o comportamento de membros individuais em grupos sociais em um nível baixo e o comportamento geral dos grupos em um nível alto.

Considerando esse conceito, podem ocorrer situações em que alguns grupos individuais ou até mesmo todos os grupos simultaneamente param de se desenvolver e ficam presos em extremos locais. Para evitar isso, introduzimos o conceito de "expansão da esfera de influência do grupo social". Na ausência de progresso em cada iteração, os limites do grupo são expandidos, o que permite abrir novas áreas de busca e diversificar a população de grupos. Se o grupo encontrar uma solução que supere a anterior, o raio dos limites do grupo é novamente reduzido ao valor mínimo padrão. Isso ajuda o algoritmo a evitar ficar preso em armadilhas locais e, se necessário, intensifica a exploração de novas áreas. O aumento do raio também contribui para a diversidade dos grupos sociais. Grupos diferentes explorarão diferentes áreas do espaço de parâmetros.

Essa concepção de um algoritmo multipopulacional de evolução de grupos sociais parece promissora. No entanto, nem tudo é tão simples quanto pode parecer à primeira vista. A posição atual do centro do grupo pode estar em uma posição desfavorável nas coordenadas correspondentes, e até mesmo a expansão da zona de influência pode não surtir o efeito desejado. Nesses casos, pode-se dizer que ocorre uma "expansão diagonal" (como no algoritmo ACO, onde as formigas correm apenas em suas trilhas sem desviar), quando na verdade é necessária uma "expansão perpendicular", ou também é possível uma situação exatamente oposta.

Para superar o problema mencionado anteriormente, é importante garantir a transferência de experiências bem-sucedidas entre os grupos. Para esse fim, pode-se permitir que algumas partículas emprestem ideias dos centros de grupos "estrangeiros". Assim, o modelo central de comportamento influenciará partículas individuais de outros grupos. A influência, a propósito, não necessariamente será positiva. Esquematicamente, o modelo de comportamento dos grupos sociais é apresentado na Figura 1.

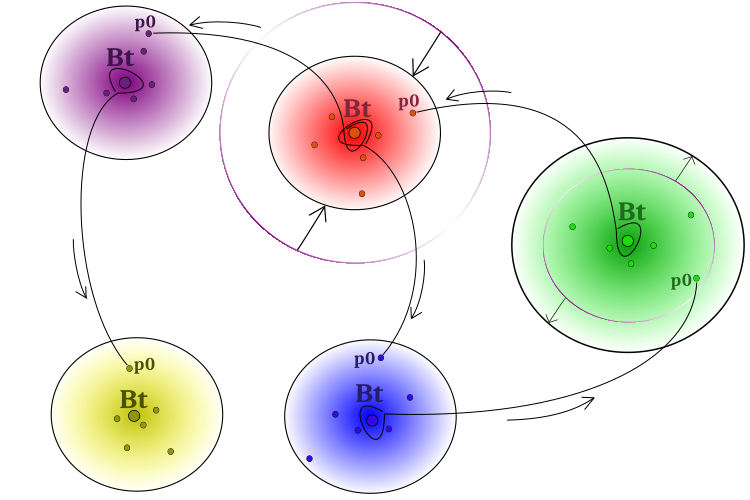
Figura 1. Esquema de funcionamento do algoritmo. Grupos individuais, expansão em caso de ausência de progresso, contração em caso de melhoria da solução,

empréstimo das "melhores ideias" (coordenadas) de grupos vizinhos "Bt" (best of team) pelas partículas "p0" (partícula no índice 0 do grupo).

O pseudocódigo do algoritmo ESG pode ser representado da seguinte forma:

1. Distribuir aleatoriamente os centros dos grupos no espaço de busca.
2. Distribuir as partículas dos grupos ao redor dos centros correspondentes com uma distribuição definida*.
3. Calcular os valores de adaptabilidade das partículas.
4. Atualizar a solução global.
5. Atualizar o centro de cada grupo.
6. Expandir os limites dos grupos na ausência de melhoria da posição do centro e reduzir, se houver melhora na posição.
7. Distribuir as partículas dos grupos ao redor dos centros correspondentes com uma distribuição definida.
8. Adicionar informações dos centros de "grupos estrangeiros" a uma partícula de cada grupo (a partícula recebe um conjunto de coordenadas de grupos estrangeiros selecionados aleatoriamente).
9. Calcular os valores de adaptabilidade das partículas.
   
10. Repetir a partir do passo 4 até a execução do critério de parada.

* - No ESG, usei a lei de distribuição de potência para a distribuição das partículas do grupo em relação ao centro, mas, em princípio, podem ser usadas outras leis de distribuição, incluindo suas combinações para partes específicas da lógica da estratégia. O campo está aberto para experimentação.

Vamos agora para a análise do código. Para descrever o grupo social, escreveremos a estrutura "S_Group", que contém várias variáveis-membro:

• "cB" - array de valores para armazenar as coordenadas do "centro".
• "fB" - valor da função de adaptabilidade do centro, inicializado com o valor "-DBL_MAX".
• "sSize" - tamanho do grupo.
• "sRadius" - raio do grupo.
  

O método "Init" na estrutura aceita dois argumentos: "coords" - número de coordenadas e "groupSize" - tamanho do grupo.

//——————————————————————————————————————————————————————————————————————————————
struct S_Group
{
  void Init (int coords, int groupSize)
  {
    ArrayResize (cB, coords);
    fB          = -DBL_MAX;
    sSize       = groupSize;
  }

  double cB [];
  double fB;
  int    sSize;
  double sRadius;
};
//——————————————————————————————————————————————————————————————————————————————

Para a lógica do algoritmo ESG, uma estrutura simples que descreva o agente de busca é suficiente. Decidi não incluir a estrutura das partículas-agentes nos campos de descrição do grupo, cada grupo terá acesso às suas partículas como parte da população geral, o que permitirá manter o acesso habitual aos agentes de fora do algoritmo e, ao mesmo tempo, evitará a cópia excessiva das partículas do grupo para os agentes.

A definição da estrutura "S_Agent" contém duas variáveis:

• "c" - array de valores das coordenadas do agente.
• "f" - valor da adaptabilidade do agente, inicializado com o valor "-DBL_MAX".
  

O método "Init" aceita o argumento "coords" para redimensionar o array "c".

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (const int coords)
  {
    ArrayResize (c, coords);
    f = -DBL_MAX;
  }

  double c []; //coordinates
  double f;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

Definiremos a classe "C_AO_ESG", que contém vários campos e métodos:

1. Campos públicos:

• "cB" - array de valores das melhores coordenadas da solução global.
• "fB" - valor da adaptabilidade (fitness) das melhores coordenadas.
• "a" - array de objetos do tipo "S_Agent", representando os agentes.
• "rangeMax" - array de valores máximos do intervalo de busca.
• "rangeMin" - array de valores mínimos do intervalo de busca.
•  "rangeStep" - array de valores dos passos de busca.

2. Métodos:

• "Init" - função usada para inicializar as variáveis-membro da classe. Aceita os argumentos: número de coordenadas, tamanho da população, número de grupos, raio inicial do grupo, coeficiente de expansão do grupo e grau de distribuição.
  
• "Moving" - método responsável pelo movimento dos agentes.
• "Revision" - método responsável pela revisão dos agentes.
• "SeInDiSp" - método para calcular valores no intervalo com um passo definido.
• "RNDfromCI" - método de geração de números aleatórios em um intervalo definido.
• "Scale" - método para escalar valores de um intervalo para outro.
• "PowerDistribution" - método para gerar valores de acordo com a distribuição de potência.

3. Campos privados:

• "coords" - número de coordenadas.
• "popSize" - tamanho da população.
• "gr" - array de objetos do tipo "S_Group", representando os grupos.
• "groups" - número de grupos.
• "groupRadius" - raio do grupo.
• "expansionRatio" - coeficiente de expansão.
• "power" - grau.
•  "revision" - flag indicando a necessidade de revisão.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ESG
{
  //----------------------------------------------------------------------------
  public: double  cB [];       //best coordinates
  public: double  fB;          //FF of the best coordinates
  public: S_Agent a  [];       //agents

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    groupsP,              //number of groups
                     const double groupRadiusP,         //group radius
                     const double expansionRatioP,      //expansion ratio
                     const double powerP);              //power

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int     coords;
  private: int     popSize;          //population size
  private: S_Group gr [];            //group

  private: int    groups;            //number of groups
  private: double groupRadius;       //group radius
  private: double expansionRatio;    //expansion ratio
  private: double power;             //power

  private: bool   revision;

  private: double SeInDiSp          (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI         (double min, double max);
  private: double Scale             (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
  private: double PowerDistribution (const double In, const double outMin, const double outMax, const double power);
};
//——————————————————————————————————————————————————————————————————————————————

O método "Init" da classe é usado para inicializar as variáveis da classe com base nos parâmetros fornecidos. Além da inicialização inicial das variáveis e definição dos tamanhos dos arrays, o método calcula o número de partículas em cada grupo no caso de o número de grupos não ser múltiplo do tamanho da população.

O array "partInSwarms" é redimensionado para "groups", onde "groups" é o número de grupos. Em seguida, a variável "particles" é atribuída ao resultado da divisão de "popSize" por "groups", onde "popSize" é o tamanho da população. Os valores do array "partInSwarms" são preenchidos com o valor "particles", ou seja, o número sem resto. Em seguida, é calculado o número de elementos perdidos ("lost") subtraindo o produto de "particles" e "groups" de "popSize". Se houver elementos perdidos ("lost > 0"), eles são distribuídos uniformemente entre os grupos em um loop while.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ESG::Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    groupsP,              //number of groups
                     const double groupRadiusP,         //group radius
                     const double expansionRatioP,      //expansion ratio
                     const double powerP)
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords         = coordinatesNumberP;
  popSize        = populationSizeP;
  groups         = groupsP;
  groupRadius    = groupRadiusP;
  expansionRatio = expansionRatioP;
  power          = powerP;

  //----------------------------------------------------------------------------
  int partInSwarms [];
  ArrayResize (partInSwarms, groups);

  int particles = popSize / groups;
  ArrayInitialize (partInSwarms, particles);

  int lost = popSize - particles * groups;

  if (lost > 0)
  {
    int pos = 0;

    while (true)
    {
      partInSwarms [pos]++;
      lost--;
      pos++;
      if (pos >= groups) pos = 0;
      if (lost == 0) break;
    }
  }

  //----------------------------------------------------------------------------
  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);

  ArrayResize (gr,        groups);
  for (int s = 0; s < groups; s++) gr [s].Init (coords, partInSwarms [s]);

  ArrayResize (a, popSize);
  for (int i = 0; i < popSize; i++) a [i].Init (coords);
}
//——————————————————————————————————————————————————————————————————————————————

O método "Moving" é usado para gerar os centros e os indivíduos dos grupos no início da otimização. O método realiza as seguintes ações:

• Geração dos centros para cada grupo "s" no loop externo "for". Para isso, no loop interno "for", um valor aleatório "coordinate" é gerado no intervalo definido para cada coordenada "c". Em seguida, o valor "coordinate" é convertido para o intervalo necessário e armazenado no array "gr[s].cB[c]".

• Geração dos indivíduos para cada grupo "s" e cada indivíduo "p" no loop externo "for". Nos loops internos "for", o valor "radius" é calculado com base nos parâmetros definidos e no estado atual do grupo. Em seguida, os valores "min" e "max" são calculados ajustando o "radius" em relação aos limites do intervalo. Em seguida, um valor aleatório "coordinate" é gerado no intervalo definido usando a função "PowerDistribution". O valor "coordinate" obtido é convertido e armazenado no array "a[cnt].c[c]".

• Definição do flag "revision" para "true" para indicar a realização da geração dos centros e indivíduos.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ESG::Moving ()
{
  if (!revision)
  {
    int    cnt        = 0;
    double coordinate = 0.0;
    double radius     = 0.0;
    double min        = 0.0;
    double max        = 0.0;

    //generate centers----------------------------------------------------------
    for (int s = 0; s < groups; s++)
    {
      gr [s].sRadius = groupRadius;

      for (int c = 0; c < coords; c++)
      {
        coordinate    = RNDfromCI (rangeMin [c], rangeMax [c]);
        gr [s].cB [c] = SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    //generate individuals of groups--------------------------------------------
    for (int s = 0; s < groups; s++)
    {
      for (int p = 0; p < gr [s].sSize; p++)
      {
        for (int c = 0; c < coords; c++)
        {
          radius = (rangeMax [c] - rangeMin [c]) * gr [s].sRadius;
          min    = gr [s].cB [c] - radius;
          max    = gr [s].cB [c] + radius;

          if (min < rangeMin [c]) min = rangeMin [c];
          if (max > rangeMax [c]) max = rangeMax [c];

          coordinate    = PowerDistribution (gr [s].cB [c], min, max, power);
          a [cnt].c [c] = SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]);
        }

        cnt++;
      }
    }

    revision = true;
  }
}
//——————————————————————————————————————————————————————————————————————————————

As principais ações para a geração de novas partículas ocorrem no método "Revision", que realiza a atualização da melhor solução global, a geração de novos indivíduos nos grupos e a troca de experiências entre os grupos por meio da transferência de informações dos centros de grupos "estrangeiros" para uma partícula. Assim, apenas uma partícula no grupo pode aproveitar a experiência de outros grupos. O método realiza as seguintes ações:

• Atualização da melhor solução global. No loop "for", percorremos todos os indivíduos e verificamos se o valor da função de adaptabilidade do indivíduo atual excede o valor atual da melhor função de adaptabilidade. Se sim, o melhor valor é atualizado e o array de coordenadas do indivíduo atual é copiado para o array de coordenadas da melhor solução.

• Geração de novos indivíduos nos grupos. No loop "for", percorremos todos os grupos e seus indivíduos. Nos loops internos, são calculados os valores do raio, dos valores mínimo e máximo das coordenadas para cada grupo. Em seguida, são gerados valores aleatórios de coordenadas usando a função "PowerDistribution", e o resultado é armazenado no array de coordenadas dos indivíduos.

• Troca de experiências entre os grupos. No loop "for", percorremos todos os grupos. No loop interno "for", é gerado um valor aleatório que determina com qual grupo a troca de experiências será realizada. Em seguida, os valores das coordenadas dos indivíduos do grupo atual são atualizados com os valores das coordenadas do grupo selecionado.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ESG::Revision ()
{
  //----------------------------------------------------------------------------
  //update the best global solution
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  int cnt = 0;
  bool impr = false;

  for (int s = 0; s < groups; s++)
  {
    impr = false;

    for (int p = 0; p < gr [s].sSize; p++)
    {
      if (a [cnt].f > gr [s].fB)
      {
        gr [s].fB = a [cnt].f;
        ArrayCopy (gr [s].cB, a [cnt].c, 0, 0, WHOLE_ARRAY);
        impr = true;
      }

      cnt++;
    }

    if (!impr) gr [s].sRadius *= expansionRatio;
    else       gr [s].sRadius  = groupRadius;

    if (gr [s].sRadius > 0.5) gr [s].sRadius = 0.5;
  }

  //generate individuals of groups----------------------------------------------
  double coordinate = 0.0;
  double radius     = 0.0;
  double min        = 0.0;
  double max        = 0.0;
  cnt = 0;

  for (int s = 0; s < groups; s++)
  {
    for (int p = 0; p < gr [s].sSize; p++)
    {
      for (int c = 0; c < coords; c++)
      {
        if (RNDfromCI (0.0, 1.0) < 1.0)
        {
        radius = (rangeMax [c] - rangeMin [c]) * gr [s].sRadius;
        min    = gr [s].cB [c] - radius;
        max    = gr [s].cB [c] + radius;

        if (min < rangeMin [c]) min = rangeMin [c];
        if (max > rangeMax [c]) max = rangeMax [c];

        coordinate    = PowerDistribution (gr [s].cB [c], min, max, power);
        a [cnt].c [c] = SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }

      cnt++;
    }
  }

  //exchange of experience----------------------------------------------------------------
  cnt = 0;

  for (int s = 0; s < groups; s++)
  {
    for (int c = 0; c < coords; c++)
    {
      int posSw = (int)RNDfromCI (0, groups);
      if (posSw >= groups) posSw = groups - 1;

      //if (sw [posSw].fB > sw [s].fB)
      {
        a [cnt].c [c] = gr [posSw].cB [c];
      }
    }

    cnt += gr [s].sSize;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Após a escrita do algoritmo principal ESG, cujo código é apresentado acima, surgiu a ideia de fazer modificações e permitir que partículas de diferentes grupos troquem informações para aumentar as qualidades combinatórias do algoritmo. Para isso, faremos alterações na estrutura do agente. Precisaremos de campos adicionais "cMain" - coordenadas principais e "fMain" - experiência principal.

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (const int coords)
  {
    ArrayResize (c,     coords);
    ArrayResize (cMain, coords);
    f     = -DBL_MAX;
    fMain = -DBL_MAX;
  }

  double c     []; //coordinates
  double cMain []; //coordinates
  double f;        //fitness
  double fMain;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

A diferença entre as duas versões reside nas alterações feitas no método "Revision":

1. Na versão principal, a troca de experiências entre os agentes ocorre no nível dos grupos. No loop interno "for", é selecionado um grupo aleatório, e o valor da coordenada do agente atual é substituído pelo valor da coordenada do centro do grupo selecionado. Assim, os grupos trocam experiências por meio da transferência de experiência apenas para uma partícula no grupo correspondente.

2. Na segunda versão, a troca de experiências entre os agentes ocorre no nível de toda a população, ou seja, entre as partículas dos grupos no caso de a partícula selecionada para troca ter uma adaptabilidade mais alta. Assim, apenas as melhores partículas podem transferir suas melhores experiências para as piores partículas entre os grupos. No loop interno "for", é selecionado um agente aleatório, e com certa probabilidade (determinada pelo valor "copyProb"), o valor da coordenada do agente atual é substituído pelo valor da coordenada do agente selecionado na população.

Além disso, na segunda versão, há um bloco de código adicional que atualiza os agentes. Se o valor da função de adaptabilidade do agente atual exceder seu valor anterior de melhor função (f > fMain), os valores das coordenadas do agente atual são atualizados com os valores de sua melhor solução atual (cMain). Isso permite que os agentes preservem e utilizem suas melhores soluções no futuro.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ESG::Revision ()
{
  //----------------------------------------------------------------------------
  //Update the best global solution
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  //update agents
  for (int p = 0; p < popSize; p++)
  {
    if (a [p].f > a [p].fMain)
    {
      a [p].fMain = a [p].f;
      ArrayCopy (a [p].cMain, a [p].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  int cnt = 0;
  bool impr = false;

  for (int s = 0; s < groups; s++)
  {
    impr = false;

    for (int p = 0; p < gr [s].sSize; p++)
    {
      if (a [cnt].f > gr [s].fB)
      {
        gr [s].fB = a [cnt].f;
        ArrayCopy (gr [s].cB, a [cnt].c, 0, 0, WHOLE_ARRAY);
        impr = true;
      }

      cnt++;
    }

    if (!impr) gr [s].sRadius *= expansionRatio;
    else       gr [s].sRadius  = groupRadius;

    if (gr [s].sRadius > 0.5) gr [s].sRadius = 0.5;
  }

  //generate individuals of groups----------------------------------------------
  double coordinate = 0.0;
  double radius     = 0.0;
  double min        = 0.0;
  double max        = 0.0;
  cnt = 0;

  for (int s = 0; s < groups; s++)
  {
    for (int p = 0; p < gr [s].sSize; p++)
    {
      for (int c = 0; c < coords; c++)
      {
        if (RNDfromCI (0.0, 1.0) < 0.6)
        {
        radius        = (rangeMax [c] - rangeMin [c]) * gr [s].sRadius;
        min           = gr [s].cB [c] - radius;
        max           = gr [s].cB [c] + radius;

        if (min < rangeMin [c]) min = rangeMin [c];
        if (max > rangeMax [c]) max = rangeMax [c];

        coordinate    = PowerDistribution (gr [s].cB [c], min, max, power);
        a [cnt].c [c] = SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }

      cnt++;
    }
  }

  //exchange of experience----------------------------------------------------------------
  cnt = 0;

  for (int p = 0; p < popSize; p++)
  {
    for (int c = 0; c < coords; c++)
    {
      int pos = (int)RNDfromCI (0, popSize);
      if (pos >= popSize) pos = popSize - 1;

      if (RNDfromCI(0.0, 1.0) < copyProb)
      {
        if (a [pos].fMain > a [p].fMain)
        {
          a [p].c [c] = a [pos].cMain [c];
        }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Como resultado dos experimentos e testes da segunda versão do algoritmo, o resultado geral não trouxe o progresso esperado e piorou ligeiramente. Isso pode ser explicado pelo fato de que é importante preservar a experiência das partículas dentro das fronteiras dos próprios grupos e evitar a mistura completa de ideias entre os grupos. Deve-se manter a experiência única em cada grupo individual, ao mesmo tempo que se garante apenas uma troca parcial de experiências.

É importante notar que o resultado desfavorável do experimento não é definitivo e não significa que a melhoria do algoritmo seja impossível. É apenas uma tentativa que nos permite entender em quais aspectos devemos focar e quais estratégias são mais eficazes. Nas pesquisas e desenvolvimentos futuros, pode-se usar o conhecimento adquirido para criar novas versões do algoritmo que possam levar a melhorias significativas nas capacidades de busca. É essencial manter o otimismo e a perseverança na busca dos objetivos estabelecidos. Os resultados dos testes são apresentados abaixo.

3. Resultados dos testes

Impressão do funcionamento da versão principal do algoritmo de evolução de grupos sociais ESG no ambiente de teste:

C_AO_ESG|200|100|0.1|2.0|10.0
=============================
5 Hilly's; Func runs: 10000; result: 0.9990564816911227
25 Hilly's; Func runs: 10000; result: 0.7965424362150277
500 Hilly's; Func runs: 10000; result: 0.35055904999599663
=============================
5 Forest's; Func runs: 10000; result: 1.0
25 Forest's; Func runs: 10000; result: 0.8286255415345216
500 Forest's; Func runs: 10000; result: 0.13102081222227177
=============================
5 Megacity's; Func runs: 10000; result: 0.8233333333333333
25 Megacity's; Func runs: 10000; result: 0.5529999999999999
500 Megacity's; Func runs: 10000; result: 0.04724999999999998
=============================
All score: 5.52939 (61.44%)

Impressão do funcionamento da versão modificada do algoritmo de evolução de grupos sociais ESG no ambiente de teste:

C_AO_MPSO|200|100|0.1|1.1|10.0|1.0
=============================
5 Hilly's; Func runs: 10000; result: 0.9986983861349696
25 Hilly's; Func runs: 10000; result: 0.7971379560351051
500 Hilly's; Func runs: 10000; result: 0.3351159723676586
=============================
5 Forest's; Func runs: 10000; result: 1.0
25 Forest's; Func runs: 10000; result: 0.8288612676775615
500 Forest's; Func runs: 10000; result: 0.11374411604788078
=============================
5 Megacity's; Func runs: 10000; result: 0.8333333333333333
25 Megacity's; Func runs: 10000; result: 0.5116666666666667
500 Megacity's; Func runs: 10000; result: 0.049316666666666654
=============================
All score: 5.46787 (60.75%)

Na visualização do ambiente de teste, pode-se observar uma boa convergência da versão principal do algoritmo. Nas funções de teste "Hilly" e "Forest", nota-se uma pequena dispersão nas trajetórias no gráfico de convergência. No entanto, na função "Megacity", essa dispersão é bastante grande, embora a maioria dos algoritmos também mostre uma ampla dispersão de convergência nessa função de teste. O algoritmo "prefere", ao contrário da maioria dos apresentados anteriormente, um tamanho de população significativamente maior - 200 (normalmente usa-se 50), apesar de o número de épocas ser proporcionalmente reduzido. ESG trabalha bem os extremos locais, característica influenciada pela "natureza" multipopulacional do algoritmo.

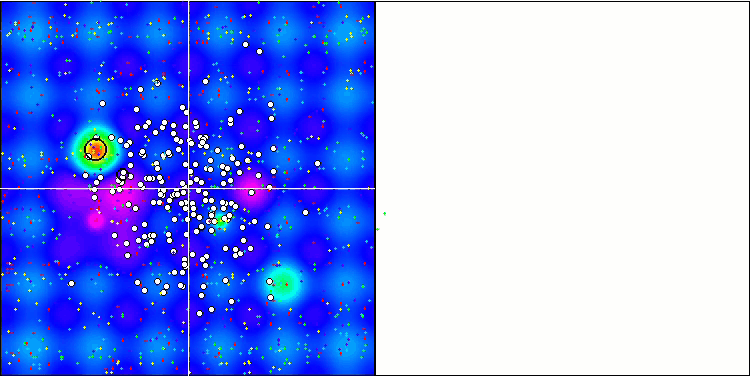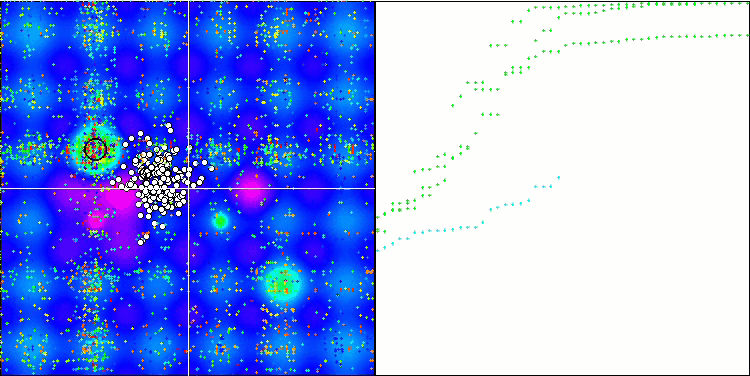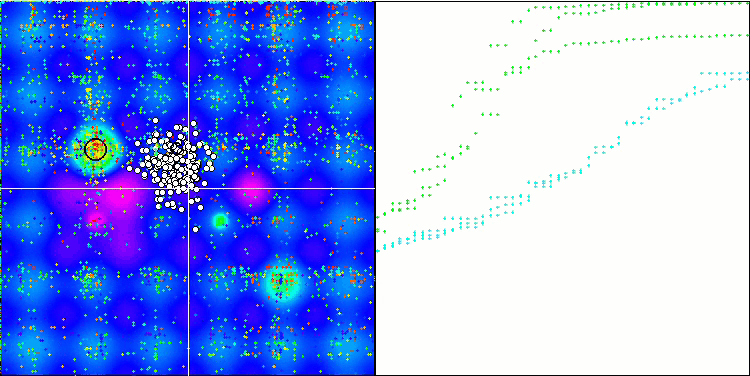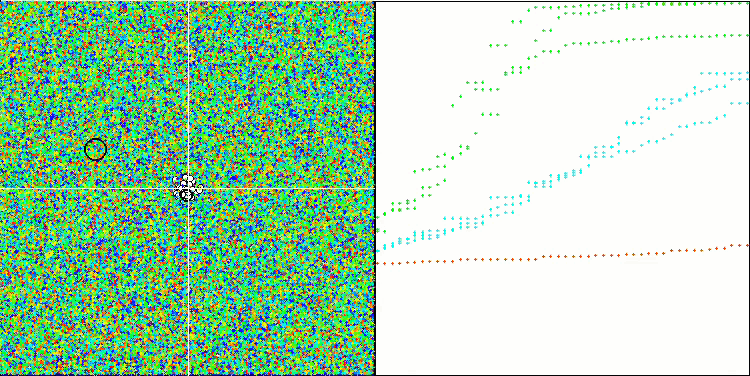
  ESG na função de teste Hilly.

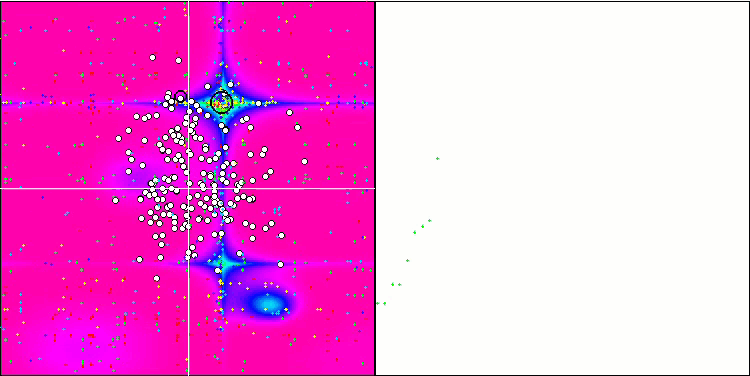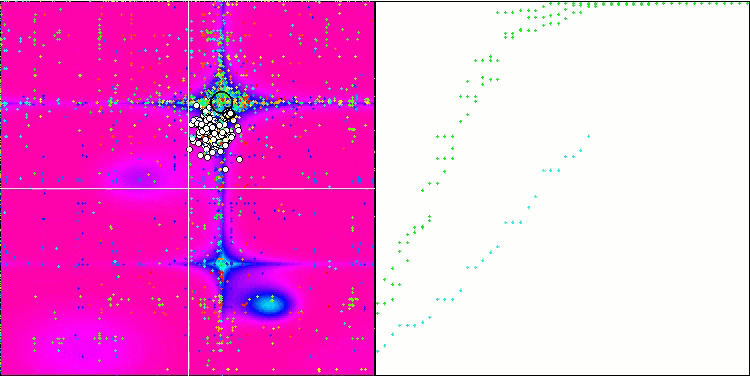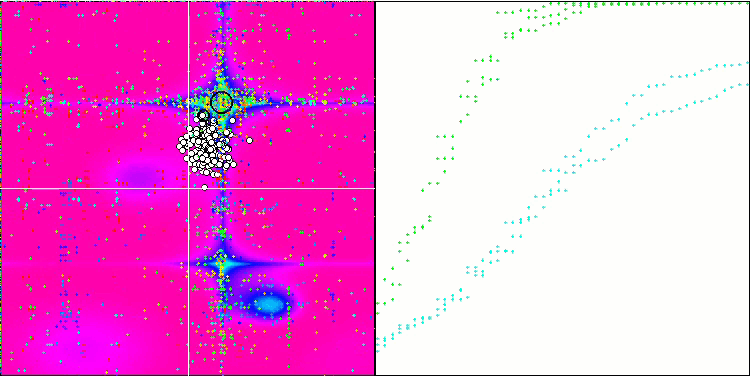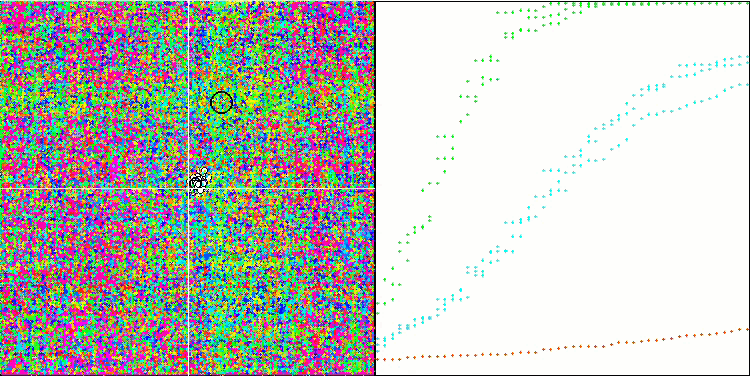
  ESG na função de teste Forest.

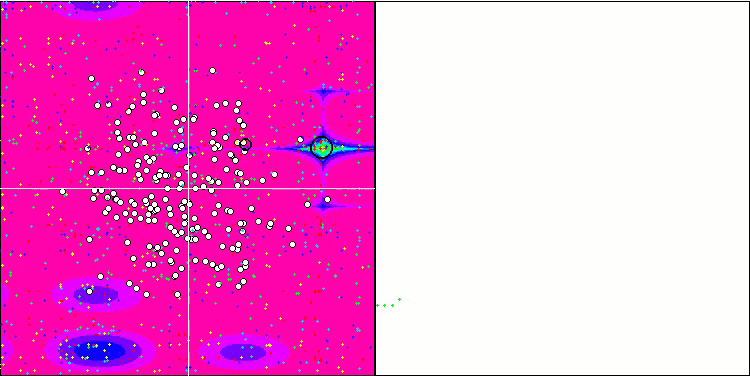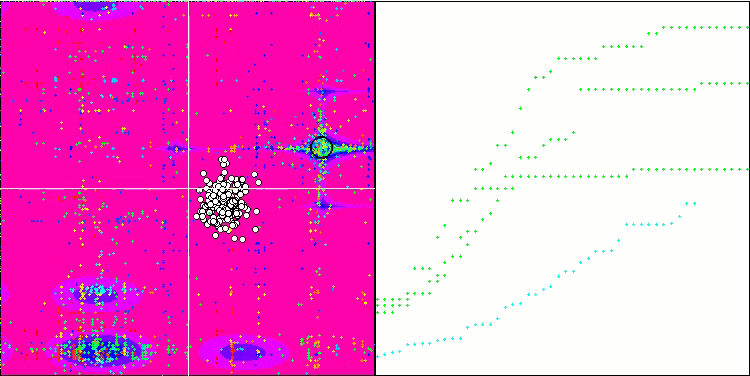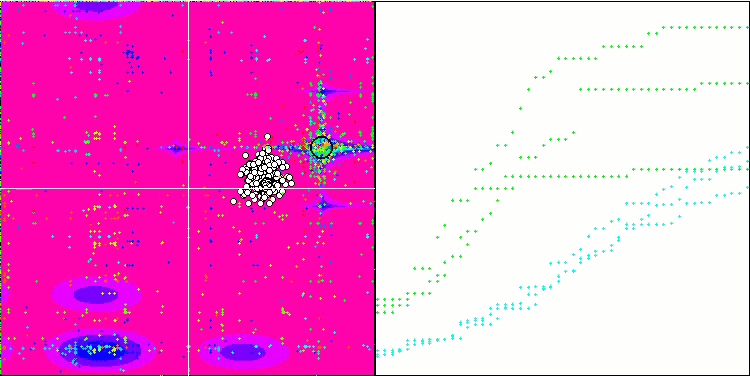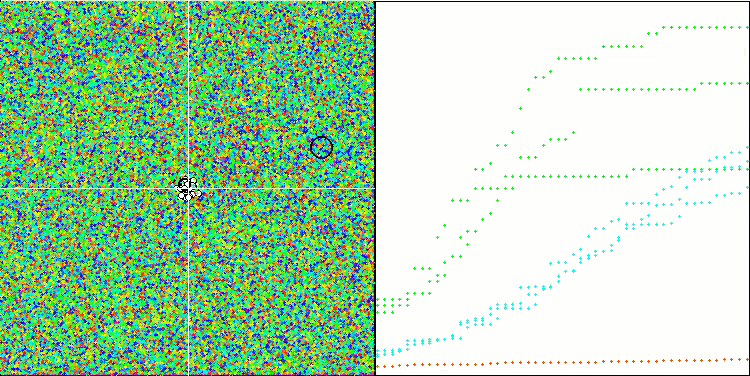
  ESG na função de teste Megacity.

O algoritmo ESG mostrou resultados dignos e ficou entre os líderes na tabela de classificação. Pode-se notar 100% de convergência na função "Forest" com 10 parâmetros e quase total, 99.9% de convergência na função "Hilly" com 10 parâmetros. A tabela contém os resultados da versão principal do algoritmo, e a versão experimental está na pasta "variant2".

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	BGA	binary genetic algorithm	0,99992	0,99484	0,50483	2,49959	1,00000	0,99975	0,32054	2,32029	0,90667	0,96400	0,23035	2,10102	6,921	76,90
2	(P+O)ES	(P+O) evolution strategies	0,99934	0,91895	0,56297	2,48127	1,00000	0,93522	0,39179	2,32701	0,83167	0,64433	0,21155	1,68755	6,496	72,18
3	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
4	ESG	evolution of social groups	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
5	SIA	simulated isotropic annealing	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
6	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
7	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
8	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
9	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
10	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
11	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
12	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
13	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
14	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
15	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
16	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
17	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
18	FAm	firefly algorithm M	0,58634	0,47228	0,32276	1,38138	0,68467	0,37439	0,10908	1,16814	0,28667	0,16467	0,04722	0,49855	3,048	33,87
19	GSA	gravitational search algorithm	0,64757	0,49197	0,30062	1,44016	0,53962	0,36353	0,09945	1,00260	0,32667	0,12200	0,01917	0,46783	2,911	32,34
20	BFO	bacterial foraging optimization	0,61171	0,43270	0,31318	1,35759	0,54410	0,21511	0,05676	0,81597	0,42167	0,13800	0,03195	0,59162	2,765	30,72
21	ABC	artificial bee colony	0,63377	0,42402	0,30892	1,36671	0,55103	0,21874	0,05623	0,82600	0,34000	0,14200	0,03102	0,51302	2,706	30,06
22	BA	bat algorithm	0,59761	0,45911	0,35242	1,40915	0,40321	0,19313	0,07175	0,66810	0,21000	0,10100	0,03517	0,34617	2,423	26,93
23	SA	simulated annealing	0,55787	0,42177	0,31549	1,29513	0,34998	0,15259	0,05023	0,55280	0,31167	0,10033	0,02883	0,44083	2,289	25,43
24	IWDm	intelligent water drops M	0,54501	0,37897	0,30124	1,22522	0,46104	0,14704	0,04369	0,65177	0,25833	0,09700	0,02308	0,37842	2,255	25,06
25	PSO	particle swarm optimisation	0,59726	0,36923	0,29928	1,26577	0,37237	0,16324	0,07010	0,60572	0,25667	0,08000	0,02157	0,35823	2,230	24,77
26	MA	monkey algorithm	0,59107	0,42681	0,31816	1,33604	0,31138	0,14069	0,06612	0,51819	0,22833	0,08567	0,02790	0,34190	2,196	24,40
27	SFL	shuffled frog-leaping	0,53925	0,35816	0,29809	1,19551	0,37141	0,11427	0,04051	0,52618	0,27167	0,08667	0,02402	0,38235	2,104	23,38
28	FSS	fish school search	0,55669	0,39992	0,31172	1,26833	0,31009	0,11889	0,04569	0,47467	0,21167	0,07633	0,02488	0,31288	2,056	22,84
29	RND	random	0,52033	0,36068	0,30133	1,18234	0,31335	0,11787	0,04354	0,47476	0,25333	0,07933	0,02382	0,35648	2,014	22,37
30	GWO	grey wolf optimizer	0,59169	0,36561	0,29595	1,25326	0,24499	0,09047	0,03612	0,37158	0,27667	0,08567	0,02170	0,38403	2,009	22,32
31	CSS	charged system search	0,44252	0,35454	0,35201	1,14907	0,24140	0,11345	0,06814	0,42299	0,18333	0,06300	0,02322	0,26955	1,842	20,46
32	EM	electroMagnetism-like algorithm	0,46250	0,34594	0,32285	1,13129	0,21245	0,09783	0,10057	0,41085	0,15667	0,06033	0,02712	0,24412	1,786	19,85

Considerações finais

Em conclusão, o algoritmo de evolução de grupos sociais representa um método de otimização eficaz, baseado na cooperação e troca de experiências entre grupos. Ele possui propriedades de adaptabilidade, diversidade e é capaz de encontrar soluções ótimas em várias tarefas de otimização.

O algoritmo ESG pode ser recomendado para aplicação em diversas áreas onde a otimização de parâmetros é necessária. Por exemplo, ele pode ser usado para ajuste de hiperparâmetros em aprendizado de máquina, otimização de funções em problemas de controle ótimo, resolução de problemas de otimização combinatória e outras tarefas onde a busca por valores ótimos de parâmetros é essencial.

O algoritmo apresentado pode ser visto como uma espécie de modelo que pode ser complementado com várias técnicas e estratégias de busca descritas em artigos anteriores. Além disso, cada grupo pode usar algoritmos de otimização separados, como PSO, ABC, ACO, entre outros. Dessa forma, a arquitetura do algoritmo ESG proporciona facilidade na implementação desses métodos de otimização e seu uso conjunto, combinando as vantagens de cada algoritmo individualmente.

É importante ressaltar que o ESG é uma solução autônoma e independente com bons resultados e representa uma abordagem extremamente flexível para resolver problemas complexos. Seu potencial pode ser totalmente explorado por meio de experimentos e desenvolvimento da ideia principal, e a possibilidade de realizar tais experimentos está aberta a todos os interessados.

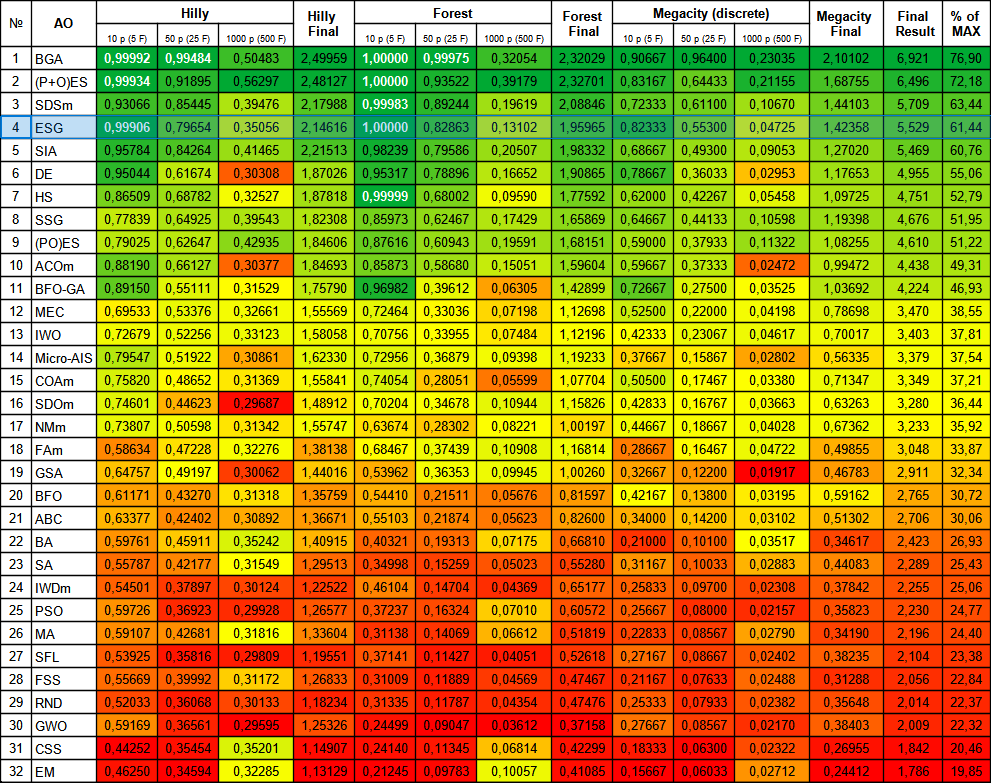
Figura 2. Graduação de cores dos algoritmos nos testes correspondentes. Os resultados maiores ou iguais a 0.99 estão destacados em branco.

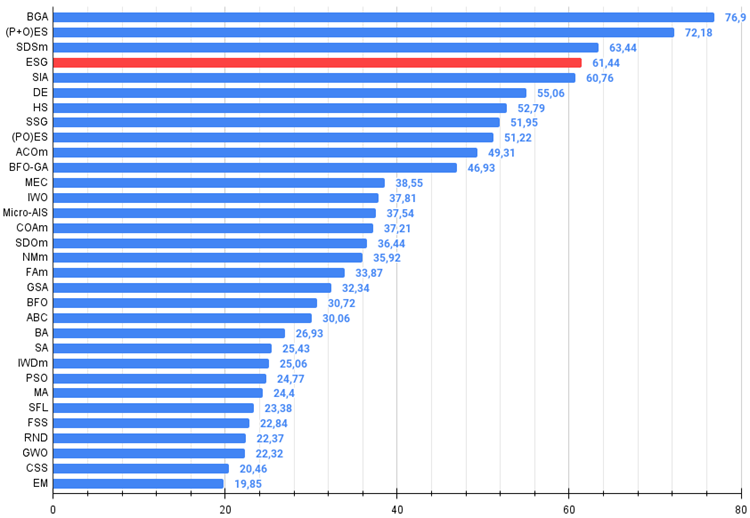
Figura 3. Histograma dos resultados dos testes dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor,

onde 100 é o resultado teórico máximo possível; o arquivo contém o script para cálculo da tabela de classificações).

Prós e contras do algoritmo de evolução de grupos sociais (ESG):

Prós:

1. Arquitetura simples.
   
2. Alta convergência.
3. Pouca exigência de recursos computacionais.

Contras:

1. Resultados baixos em funções com grande número de parâmetros.
   

Está anexado ao artigo um arquivo com as versões atualizadas dos códigos dos algoritmos descritos em artigos anteriores. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar as capacidades de busca. As conclusões e juízos apresentados nos artigos são baseados nos resultados dos experimentos realizados.