Population optimization algorithms: Charged System Search (CSS) algorithm

Contents

1. Introduction
2. Algorithm
3. Test results

1. Introduction

In physics, the space surrounding an electric charge has a property known as an electric field. This field exerts a force on other electrically charged objects. The electric field surrounding a point charge is determined by Coulomb's law. Coulomb confirmed that the electric force between any two small charged spheres is inversely proportional to the square of the distance between the particles along the line connecting them, and proportional to the product of the charges of the two particles. Additionally, the magnitude of the electric field at a point inside a charged sphere can be obtained using Gauss law, which states that it is proportional to the distance between particles. Using these principles, CSS defines a set of possible solutions called charged particles. Each particle is considered as a charged sphere (in contrast to the electromagnetic algorithm - EM, where the particle is a one-dimensional point) and can have an electrical effect on other agents (charged particles).

On the other hand, Newton's second law explains that the acceleration of an object is directly proportional to the net force acting on that object. Thus, the resulting electrical force acting on the particle causes it to accelerate. According to Newtonian mechanics, the position of a particle, considered as a point mass of infinitesimal size, is completely known at any time if its position, velocity and acceleration in space are known at the previous time. CSS uses the governing laws of motion from Newtonian mechanics to determine the position of particles. The application of these laws should, in theory, provide a good balance between exploration and exploitation of the algorithm.

Charged System Search (CSS) was first proposed by A. Kaveh and S. Talatahari in 2010.

Optimization is an important and integral part of solving problems of mathematical modeling and machine learning. Metaheuristic algorithms are an effective and popular class of optimization methods. Metaheuristics can be understood as an algorithm that stochastically searches for possible solutions to a problem that are close to optimal until a certain condition is met or a given number of iterations is reached.

In the scientific literature, metaheuristics are considered to combine basic heuristic methods into higher-level algorithmic schemes that allow more efficient exploration of search spaces and decision making. This usually requires less work than developing new specialized heuristics. The challenge is to adapt general metaheuristic schemes to solve difficult optimization problems. In addition, an effective implementation of metaheuristics can ensure that a solution close to the optimal one is found in an acceptable time. Various approaches to understanding metaheuristics make it possible to formulate some fundamental properties that characterize them. In recent years, the use of metaheuristic methods has increased, and efforts have been made to increase the power of algorithms and reduce optimization time.

2. Algorithm

CSS algorithm operates charged particles in the form of a sphere. The minimum size of the sphere is determined by an external parameter (it is a part of the maximum possible Euclidean distance along all coordinates of the search space), when particles approach at a distance less than the radius of the sphere, repulsive forces act on the particles. At the same time, the direction of forces between particles is also affected by their mutual difference in charges. The algorithm takes into account the coordinate values at the previous iteration, thereby simulating the particle speed. Acceleration (a component of particle motion) is influenced by charges and their mutual distance.

Taking into account the above, let's write down the pseudocode steps of the algorithm:

1. Initialize the particles with an initial random position in the search space and also set a random position in space for the previous iteration (we make the assumption that there was a previous iteration).

2. Calculate the fitness function value.

3. Calculate the next position of the particles using the equations.

4. Determine the best and worst values of the fitness function among all particles.

5. Repeat the steps from step 2 until the stop condition is met.

Let's look at the equations for calculating the mutual motion of particles. The main characteristic of a charged particle is its charge:

q = (φp - φw) / (φb - φw)

where:

• q - current particle charge
• φp - particle fitness function value
• φb - best value of the fitness function among all particles
• φw - worst value of the fitness function among all particles

To determine the distance between particles, we will use the equation:

r(i,j) = (|Xi - Xj|) / (|(Xi - Xj) * 0.5 - Xb|)

where:

• || - Euclidean distance
• r(i,j) - distance between particles i and j
• Xi and Xj - corresponding coordinates of i and j particles
• Xb - corresponding coordinate of the best position found over all iterations.

Here, apparently, the authors' idea was to take into account the position of the particles relative to the best global coordinates. This may have been a good idea, but my experiments suggested that the best solution for this algorithm would be to just calculate the numerator in the equation.

As in the electromagnetic EM algorithm, interaction forces can be either attractive or repulsive. Let's denote the sign of the direction of the variable c. Use the following condition expression to take into account the direction of forces:

c = -1 if φi < φj, otherwise c = 1

where:

• c - sign of the interaction forces direction
• φi and φj - fitness function values of i and j particles

The sign of the force direction can be interpreted in such a way that a particle with a smaller value of the fitness function repels, and a particle with a larger value attracts.

Since we agreed that, unlike the EM algorithm, the particle is a sphere whose radius is greater than 0 (an external parameter of the algorithm), then the force on the particle is collinear to the corresponding coordinate (in our algorithm, the total force on the particle is a set of vectors) and can be presented as an equation:

F = qi * Q * c * (Xj - Xi)

where:

• F - action force affecting the particle
• qi - particle the action force is calculated for
• Q - component that takes into account the relative position of the two particles under consideration depending on the penetration of their spheres into each other, the equation for Q:

Q = ((qj * r(i,j) * b1) / a^3) + (qj * b2) / r(i,j)^2

where:

• qj - charge of the particle affecting the considered
• b1 and b2 for "enabling/disabling" the corresponding expression term. b1 = 0 and b2 = 1 for r >= particle radius. Otherwise, b1 = 1 and b2 = 0.

Finally, we can calculate the new coordinate of particle movement using the equation:

Xn = X + λ1 * U * V + λ2 * U * coordinatesNumber * (F / qi)

where:

• Xn - new coordinate
• λ1 - weight coefficient (external parameter) determines the degree of influence of the second term - speed
• λ2 - weight coefficient (external parameter) determines the degree of influence of the third term - acceleration
• U - random number in the range [0;1]
• V - difference between the coordinate at the current iteration and at the previous one
• coordinatesNumber - number of coordinates. This "ratio" is not included into the original equation. I introduced it since as the dimension of the search space increases, the λ2 ratio has to be increased (therefore, it was introduced to avoid the effect of "freezing" particles)

The relative values of λ1 and λ2 determine the balance between diversification and search intensification. Increasing the values of the λ1 parameter enhances the influence of the previous position of the particle, increasing the research properties of the algorithm. Large values of λ2 lead to a strong influence of attractive forces and can cause premature convergence of the algorithm. On the contrary, small values slow down the convergence rate of the algorithm providing a wider exploration of the search area.

Let's start analyzing the CSS algorithm code. The search agent of the algorithm is a particle, which can be conveniently represented as the S_Particle structure.

The particle structure includes the following fields:

• -c: array of particle coordinates. This array contains the current coordinates of the particle in space.
• -cPrev: array of previous particle coordinates. This array contains the previous coordinates of the particle in space.
• -cNew: array of new particle coordinates. This array contains the new particle coordinates that will be used in the next iteration of the algorithm.
• -q: particle charge. This value represents the charge assigned to that particle. Charge can only take positive values other than 0.
• -f: particle fitness function value.

The presence of an array of new coordinates in the structure of the particle and its charge made it possible to simplify the algorithm due to its features although these quantities could be kept in the form of variables for general use by all particles (at first glance, this seems logical). 

//——————————————————————————————————————————————————————————————————————————————
struct S_Particle
{
  double c     [];  //coordinates
  double cPrev [];  //coordinates
  double cNew  [];  //coordinates
  double q;         //particle charge
  double f;         //fitness
};
//——————————————————————————————————————————————————————————————————————————————

Declare the C_AO_CSS class, which includes:

Class properties:

• - p: particle array
• - rangeMax: array with maximum search range values for each coordinate
• - rangeMin: array with minimum search range values for each coordinate
• - rangeStep: array with search step sizes for each coordinate
• - cB: array with the best coordinates found
• - fB: fitness function value for the best coordinates
• - fW: fitness function value for the worst coordinates

Class methods:

• - Init: initializes the algorithm parameters (number of coordinates, number of particles, radius size, velocity and acceleration ratios)
• - Moving: performs particle movement
• - Revision: performs an update of the best coordinates

Private class properties:

• - coordinatesNumber: number of coordinates
• - particlesNumber: number of particles
• - radius: radius size
• - speedCo: speed ratio
• - accelCo: acceleration ratio
• - F: force vector
• - revision: flag indicating the need for revision

Private class methods:

• - SeInDiSp: calculates a new coordinate value in a given range with a given step
• - RNDfromCI: generates a random number in a given interval

//——————————————————————————————————————————————————————————————————————————————
class C_AO_CSS
{
  //----------------------------------------------------------------------------
  public: S_Particle p     []; //particles
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates
  public: double fW;           //FF of the worst coordinates

  public: void Init (const int    coordinatesNumberP, //coordinates number
                     const int    particlesNumberP,   //particles number
                     const double radiusSizeP,        //radius size
                     const double speedCoP,           //speed coefficient
                     const double accelCoP);          //acceleration coefficient

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber; //coordinates number
  private: int    particlesNumber;   //particles number
  private: double radius;            //radius size
  private: double speedCo;           //speed coefficient
  private: double accelCo;           //acceleration coefficient
  private: double F       [];        //force vector
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

The C_AO_CSS method initializes the parameters of the class object. It takes the number of coordinates, number of particles, radius size, velocity and acceleration ratios as arguments.

Inside the method, the random number generator is reset and the initial values for the fB and revision variables are set. The argument values are then assigned to the corresponding object variables.
Next, the sizes of the rangeMax, rangeMin, rangeStep, F, p and cB arrays change in accordance with the number of coordinates and particles.
Then the arrays for each particle are resized in a loop and the initial value of the variable f is set for each particle.
At the end of the method, the size of the cB array changes in accordance with the number of coordinates.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CSS::Init (const int    coordinatesNumberP, //coordinates number
                     const int    particlesNumberP,   //particles number
                     const double radiusSizeP,        //radius size
                     const double speedCoP,           //speed coefficient
                     const double accelCoP)           //acceleration coefficient
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber = coordinatesNumberP;
  particlesNumber   = particlesNumberP;
  radius            = radiusSizeP;
  speedCo           = speedCoP;
  accelCo           = accelCoP;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);
  ArrayResize (F,         coordinatesNumber);

  ArrayResize (p,  particlesNumber);

  for (int i = 0; i < particlesNumber; i++)
  {
    ArrayResize (p [i].c,     coordinatesNumber);
    ArrayResize (p [i].cPrev, coordinatesNumber);
    ArrayResize (p [i].cNew,  coordinatesNumber);
    p [i].f  = -DBL_MAX;
  }

  ArrayResize (cB, coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

The main logic for moving particles (search agents) is implemented in the Moving() method.

At the very first iteration, initialize the initial values of the particle coordinates with a random number in the range from rangeMin to rangeMax and take the particle fitness value equal to the value `-DBL_MAX`.

The external parameter of the RadiusSize_P algorithm determines the particle size in parts of the maximum possible Euclidean distance for all coordinates, which is the root of the sum of squared differences between the maximum and minimum allowable values for each coordinate.
At the end of the code, the `revision` variable is set to `true`.

//----------------------------------------------------------------------------
if (!revision)
{
  fB = -DBL_MAX;

  for (int obj = 0; obj < particlesNumber; obj++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      p [obj].c     [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      p [obj].cPrev [c] = RNDfromCI (rangeMin [c], rangeMax [c]);

      p [obj].c     [c] = SeInDiSp (p [obj].c     [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      p [obj].cPrev [c] = SeInDiSp (p [obj].cPrev [c], rangeMin [c], rangeMax [c], rangeStep [c]);

      p [obj].f         = -DBL_MAX;
    }
  }

  double r = 0.0;
  double t = 0.0;

  for (int c = 0; c < coordinatesNumber; c++)
  {
    t = rangeMax [c] - rangeMin [c];
    r += t * t;
  }

  radius *= sqrt (r);
  revision = true;
}

The remaining part of the Moving() method code is executed in the second and subsequent iterations and is responsible for moving particles in the search space.

The difference between the fB and fW values of the fitness function is calculated first (for the best coordinates found over all iterations and the worst coordinates among particles at the current iteration) and stored in the 'difference' variable. If 'difference' is 0.0, then it is assigned the value of 1.0.

This is followed by the loop, in which a new value is calculated for each particle. For each particle i, a new value of charge q is calculated.

Next, the variables summ1, summ2, q, e, c, b1, b2, X, Q, U, V, t1 and t2 are declared and initialized for use in the equations described above.

In the loop, for each particle, we calculate the total force F acting on the part of all other particles in the population. For each i particle, a loop occurs, in which the sum of summ1 and summ2 is calculated. Then the r distance between i and j particles is calculated. If r is 0.0, then it is assigned the value of 0.01 to avoid dividing by 0. The values of b1 and b2 are then calculated depending on the value of r and 'radius'. The value of the direction of the force c is then calculated depending on the fitness values of the two particles in question. Next, we calculate the Q value. Then, the force value F[k] is calculated for each k coordinate.

Having the values of the vector of forces acting on the particle, we can calculate the values of the new coordinates for its movement. Then a cycle occurs, in which the values of the previous coordinates and the current coordinates of particle i are updated.

The code preserves parts of the original equations as commented out elements to show how it was done by the CSS authors.

double difference = fB - fW;
if (difference == 0.0) difference = 1.0;

for (int i = 0; i < particlesNumber; i++)
{
  p [i].q = ((p [i].f - fW) / difference) + 0.1;
}

double summ1 = 0.0;
double summ2 = 0.0;
double q     = 0.1;
double e     = 0.001;
double c     = 0.0;
double b1    = 0.0;
double b2    = 0.0;
double X     = 0.0;
double Q     = 0.0;
double U     = 0.0;
double V     = 0.0;
double t1    = 0.0;
double t2    = 0.0;

for (int i = 0; i < particlesNumber && !IsStopped (); i++)
{
  ArrayInitialize (F, 0.0);

for (int j = 0; j < particlesNumber && !IsStopped (); j++)
{
  if (i == j) continue;

  summ1 = 0.0;
  summ2 = 0.0;

  for (int k = 0; k < coordinatesNumber && !IsStopped (); k++)
  {
    t1 = p [i].c [k] - p [j].c [k];
    summ1 += t1 * t1;

    //t2 = t1 * 0.5 - cB [k];
    //summ2 += t2 * t2;
  }

  //r = sqrt (summ1) / (sqrt (summ2) + e);
  r = sqrt (summ1);
        
  if (r == 0.0) r = 0.01;

  if (r >= radius)
  {
    b1 = 0.0;
    b2 = 1.0;
  }
  else
  {
    b1 = 1.0;
    b2 = 0.0;
  }

  c = p [i].f < p [j].f ? -1.0 : 1.0;

  q = p [j].q;

  Q = ((q * r * b1 / (radius * radius * radius)) + (q * b2 / (r * r))) * c;

  for (int k = 0; k < coordinatesNumber && !IsStopped (); k++)
  {
    F [k] += /*p [i].q */ Q * (p [j].c [k] - p [i].c [k]);
  }
}

  for (int k = 0; k < coordinatesNumber && !IsStopped (); k++)
  {
    V = p [i].c [k] - p [i].cPrev [k];
    U = RNDfromCI (0.0, 1.0);

    X = p [i].c [k] + speedCo * U * V + accelCo * U * coordinatesNumber * (F [k] / p [i].q);
        
    p [i].cNew [k] = SeInDiSp (X, rangeMin [k], rangeMax [k], rangeStep [k]);
  }
}

for (int i = 0; i < particlesNumber && !IsStopped (); i++)
{
  for (int k = 0; k < coordinatesNumber && !IsStopped (); k++)
  {
    p [i].cPrev [k] = p [i].c [k];
    p [i].c [k] = p [i].cNew [k];
  }
}

Finally comes the Revision() method.
At the beginning of the method, the variable fW is assigned the maximum value of type double (DBL_MAX), so that we can subsequently determine the worst particle with the minimum value of the fitness function.
Then a cycle occurs through all system particles. The following actions are performed for each particle:
- If the current particle's f value is greater than fB (the best fitness function of all particles), then the fB value is updated with the current particle's f value, and the cB array (best position) is copied from the current particle's position.
- If the current particle's f value is less than the fW value (the smallest fitness function of all particles), then the fW value is updated with the current particle's f value.

So this code finds the best and worst fitness functions among all particles and updates the corresponding values.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CSS::Revision ()
{
  fW  = DBL_MAX;

  for (int i = 0; i < particlesNumber; i++)
  {
    if (p [i].f > fB)
    {
      fB = p [i].f;
      ArrayCopy (cB, p [i].c, 0, 0, WHOLE_ARRAY);
    }

    if (p [i].f < fW)
    {
      fW = p [i].f;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Test results

Printout of the Charged System Search algorithm on the test bench:

C_AO_CSS:50;0.1;0.7;0.01
=============================
5 Rastrigin's; Func runs 10000 result: 70.43726076935499
Score: 0.87276
25 Rastrigin's; Func runs 10000 result: 68.88569793414477
Score: 0.85353
500 Rastrigin's; Func runs 10000 result: 66.01225385184436
Score: 0.81793
=============================
5 Forest's; Func runs 10000 result: 0.4891262437640296
Score: 0.27667
25 Forest's; Func runs 10000 result: 0.1494549763925046
Score: 0.08454
500 Forest's; Func runs 10000 result: 0.07829232143185726
Score: 0.04429
=============================
5 Megacity's; Func runs 10000 result: 2.04
Score: 0.17000
25 Megacity's; Func runs 10000 result: 0.744
Score: 0.06200
500 Megacity's; Func runs 10000 result: 0.26880000000000004
Score: 0.02240
=============================
All score: 3.20412

The print of the algorithm operation results indicates a low overall result. Attention is drawn to the fact that for the Rastrigin functions for 10, 50 and 1000 variables, the results of the fitness function values are not much different. Below we will try to figure out what this means.

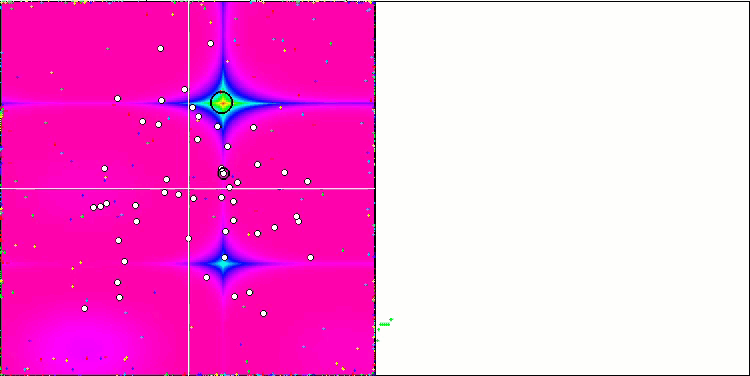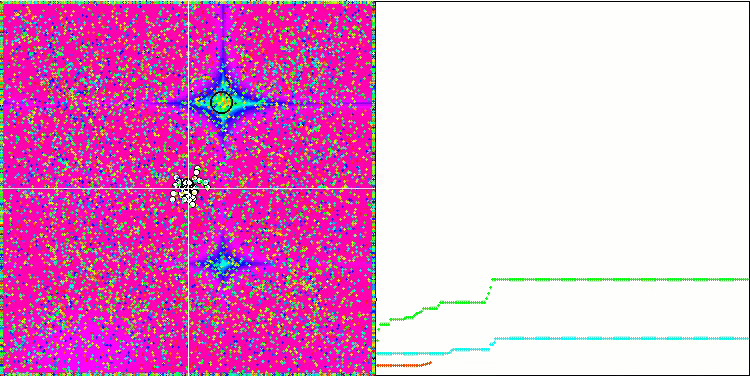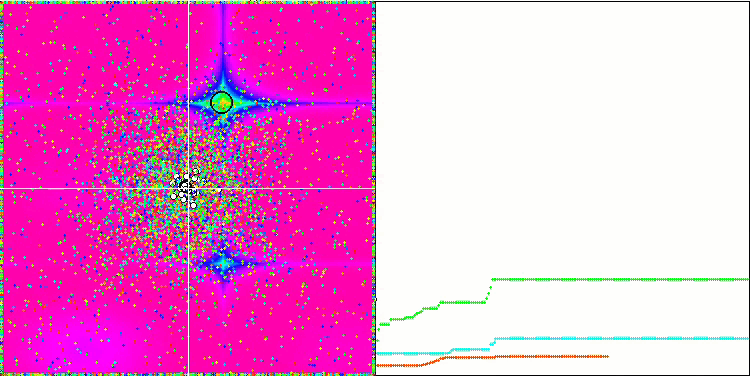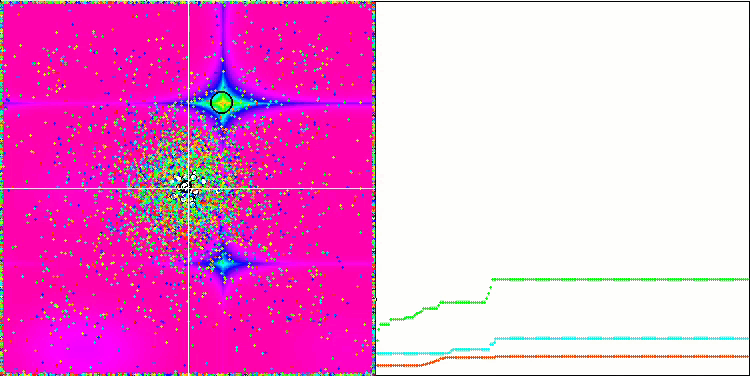
Visualization of the Rastrigin test function shows a clearly visible division of the particle population along significant local extrema, which means a good study of local areas, but similar behavior is not observed in the Forest and Megacity functions, where the population behaves like a shapeless cloud. Long horizontal sections of the convergence graph indicate the tendency of the algorithm to get stuck in local extrema, although this considerable drawback is somewhat compensated by its excellent scalability on the smooth Rastrigin function.

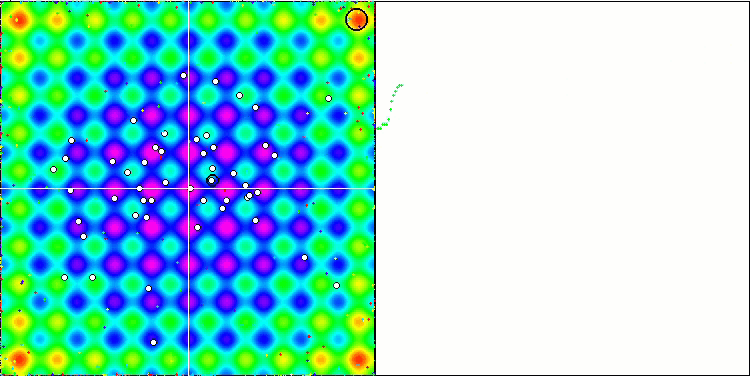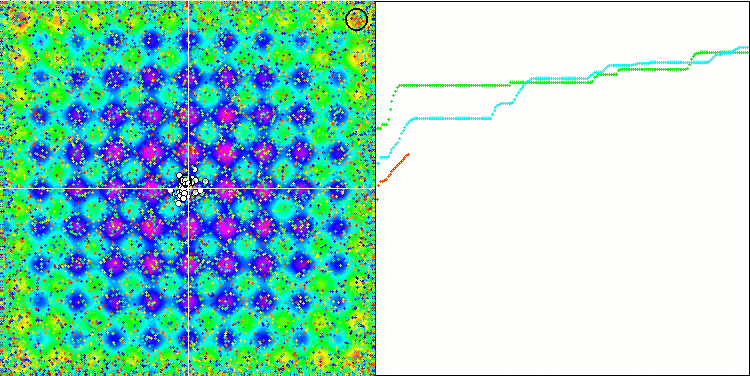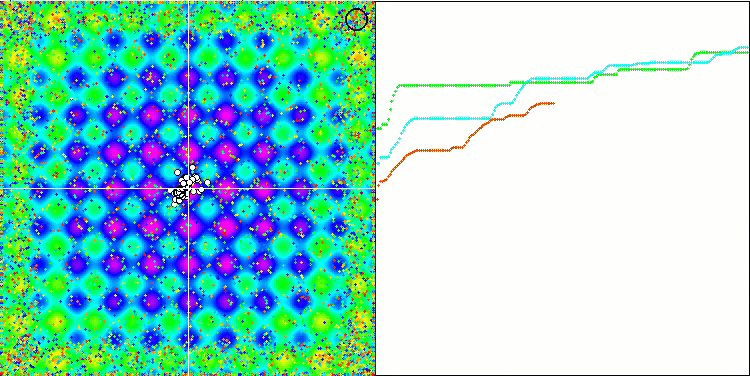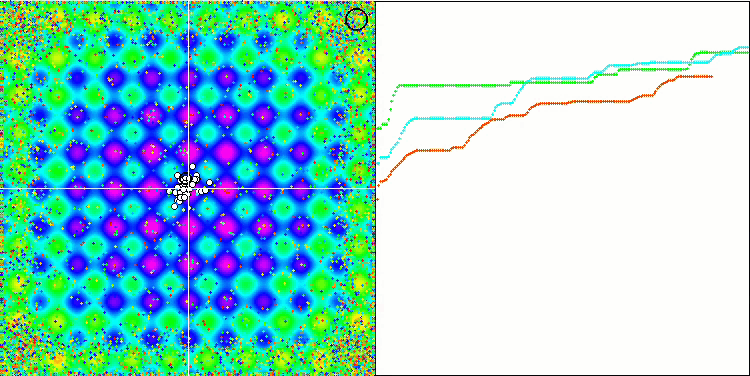
  CSS on the Rastrigin test function.

  CSS on the Forest test function.

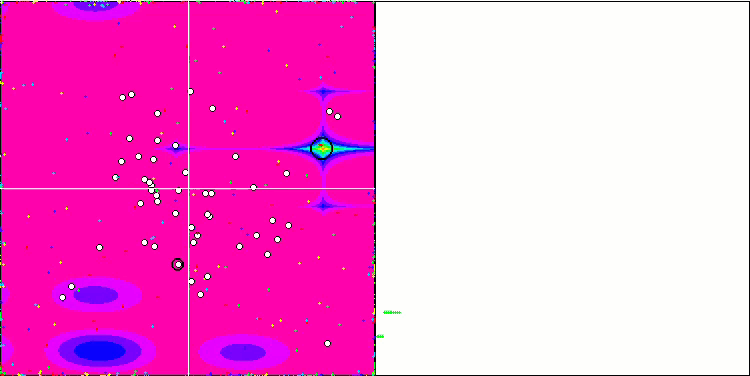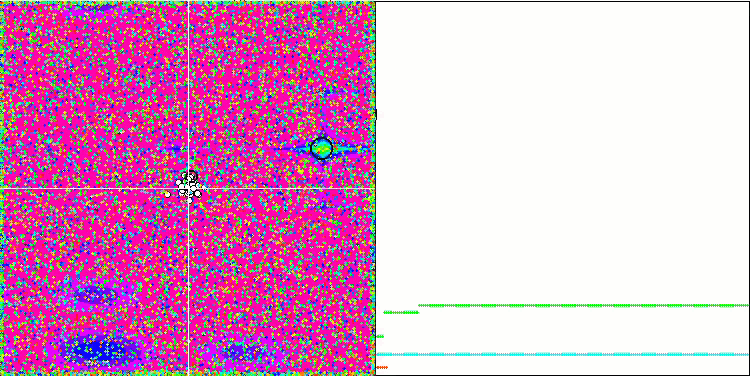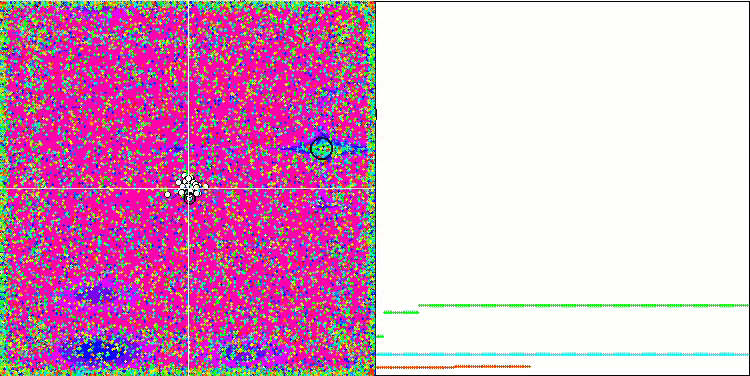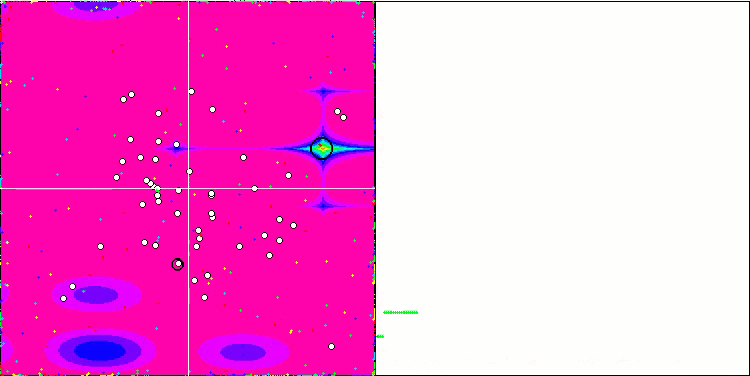
  CSS on the Megacity test function.

Testing of the CSS algorithm has identified a new leader for optimizing smooth functions. The previous leader for the Rastrigin function was also an algorithm inspired by inanimate nature - electromagnetic search (EM). This time the new record exceeds the previous one by almost 10%. Unfortunately, the algorithm demonstrates some of the worst results on the Forest function with a sharp global extremum and on the discrete Megacity function. Thanks to the impressive results on Rastrigin with 1000 variables, the algorithm was able to get into 13th place out of 20 based on total parameters. During the 10,000 runs of the CSS algorithm allotted by the test regulations, CSS was unable to get closer than 90% to the global extremum (see prints of the test bench shown above).   

#	AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	SDS	stochastic Diffusion Search	0.99737	1.00000	0.58904	2.58641	0.96893	1.00000	0.95092	2.91985	1.00000	1.00000	0.72149	2.72149	100000
2	SSG	saplings sowing and growing	1.00000	0.95313	0.51630	2.46944	0.72740	0.69680	1.00000	2.42421	0.69612	0.65918	1.00000	2.35531	87.506
3	HS	harmony search	0.99676	0.90817	0.44686	2.35179	1.00000	0.72930	0.44806	2.17736	0.91159	0.76578	0.41537	2.09274	79.501
4	ACOm	ant colony optimization M	0.34611	0.17142	0.15808	0.67562	0.86888	0.73719	0.77362	2.37968	0.91159	0.68163	0.05606	1.64929	55.026
5	IWO	invasive weed optimization	0.95828	0.63939	0.27647	1.87415	0.70773	0.34168	0.31773	1.36714	0.72927	0.32539	0.33289	1.38756	54.060
6	MEC	mind evolutionary computation	0.99270	0.48648	0.21148	1.69066	0.60762	0.29973	0.25459	1.16194	0.85083	0.31978	0.26170	1.43231	49.669
7	COAm	cuckoo optimization algorithm M	0.92400	0.44601	0.24120	1.61121	0.58378	0.25090	0.16526	0.99994	0.66298	0.25666	0.17083	1.09047	42.223
8	FAm	firefly algorithm M	0.59825	0.32387	0.15893	1.08106	0.51073	0.31182	0.49790	1.32045	0.31491	0.21880	0.35258	0.88629	36.941
9	ABC	artificial bee colony	0.78170	0.31182	0.19313	1.28664	0.53837	0.15816	0.13344	0.82998	0.51381	0.20758	0.13926	0.86064	32.977
10	BA	bat algorithm	0.40526	0.60773	0.78330	1.79629	0.20841	0.12884	0.25989	0.59714	0.27073	0.08135	0.17371	0.52579	32.236
11	GSA	gravitational search algorithm	0.70167	0.43098	0.00000	1.13265	0.31660	0.26845	0.33204	0.91710	0.54144	0.27208	0.00000	0.81352	31.522
12	BFO	bacterial foraging optimization	0.67203	0.29511	0.10957	1.07671	0.39702	0.19626	0.20652	0.79980	0.47514	0.25807	0.18932	0.92253	30.702
13	CSS	charged system search	0.56605	0.70573	1.00000	2.27178	0.14081	0.01980	0.16282	0.32343	0.09393	0.00000	0.03481	0.12874	29.743
14	EM	electroMagnetism-like algorithm	0.12235	0.44109	0.92752	1.49096	0.00000	0.02578	0.34880	0.37458	0.00000	0.00562	0.10924	0.11486	20.252
15	SFL	shuffled frog-leaping	0.40072	0.22627	0.24624	0.87323	0.20153	0.03057	0.02652	0.25862	0.24862	0.04769	0.06639	0.36270	14.050
16	MA	monkey algorithm	0.33192	0.31883	0.13582	0.78658	0.10012	0.05817	0.08932	0.24762	0.19889	0.03787	0.10720	0.34396	12.564
17	FSS	fish school search	0.46812	0.24149	0.10483	0.81445	0.12840	0.03696	0.06516	0.23052	0.15471	0.04208	0.08283	0.27961	11.880
18	PSO	particle swarm optimisation	0.20449	0.07816	0.06641	0.34906	0.18895	0.07730	0.21738	0.48363	0.21547	0.05049	0.01957	0.28553	9.246
19	RND	random	0.16826	0.09287	0.07438	0.33551	0.13496	0.03546	0.04715	0.21757	0.15471	0.03507	0.04922	0.23900	5.083
20	GWO	grey wolf optimizer	0.00000	0.00000	0.02093	0.02093	0.06570	0.00000	0.00000	0.06570	0.29834	0.06170	0.02557	0.38561	1.000

Summary

I had to conduct a lot of experiments and code edits in order to force particles to move across the field without them "sticking together" and "freezing". The algorithm authors did not take into account the influence of the number of optimized parameters on the quality of optimization (with increasing dimension of the problem, the convergence deteriorated disproportionately quickly). Adding more coordinates into the equation made it possible to enhance the effect of acceleration and improve the performance of CSS (without these changes, the algorithm showed very poor results). The inherent laws of particle movement are too capricious to any changes for research purposes, and therefore complicate attempts to improve the performance of this interesting optimization algorithm.

The algorithm is an effective method for optimizing smooth functions. It applies a cloud of charged particles interconnected by Coulomb forces. When using this interesting algorithm, one should take into account its low suitability for problems with a discrete search space field. However, this is the best optimization algorithm for smooth functions with multiple variables among previously considered ones. CSS can be used in all areas of optimization with a large number of variables. It does not need either gradient information or search space continuity.

For a more visual representation of the advantages and disadvantages of individual algorithms, the table above can be represented using the color scale in Figure 1. The color gradation of the table allows for a clearer representation of the possibility of using each individual algorithm, depending on the specific optimization problem. For now, I was unable to find a perfectly universal algorithm for the best solution to any problem (perhaps I will be able to find one in subsequent research).

For example, if we consider the very first algorithm in the rating (SDS), then it is not the best on individual test problems (smooth functions with multiple variables for it are given as average in the table). As for the ACOm algorithm, its individual results are far below the average in the table (it solves smooth functions surprisingly poorly), but it copes very well with Forest and discrete Megacity (it was originally designed to solve discrete problems - such as the Traveling Salesman problem), although scalability leaves much to be desired.

The last algorithm presented (CSS) works well on the Rastrigin function with 1000 variables (it might be a good choice for training neural networks with many parameters) showing the best result among all previously considered optimization algorithms, although based on the total results, it does not look like the best in the table. Therefore, the correct choice of algorithm depending on the specifics of the problem is very important.

Large-scale testing of optimization algorithms with a variety of search strategies revealed an unexpected fact - the strategy may turn out to be even worse than when using a simple random search with the selection of the best result - RND takes second place from the bottom instead of the last expected one, GWO turned out to be worse than random search with the exception of discrete Megacity with 10 parameters.

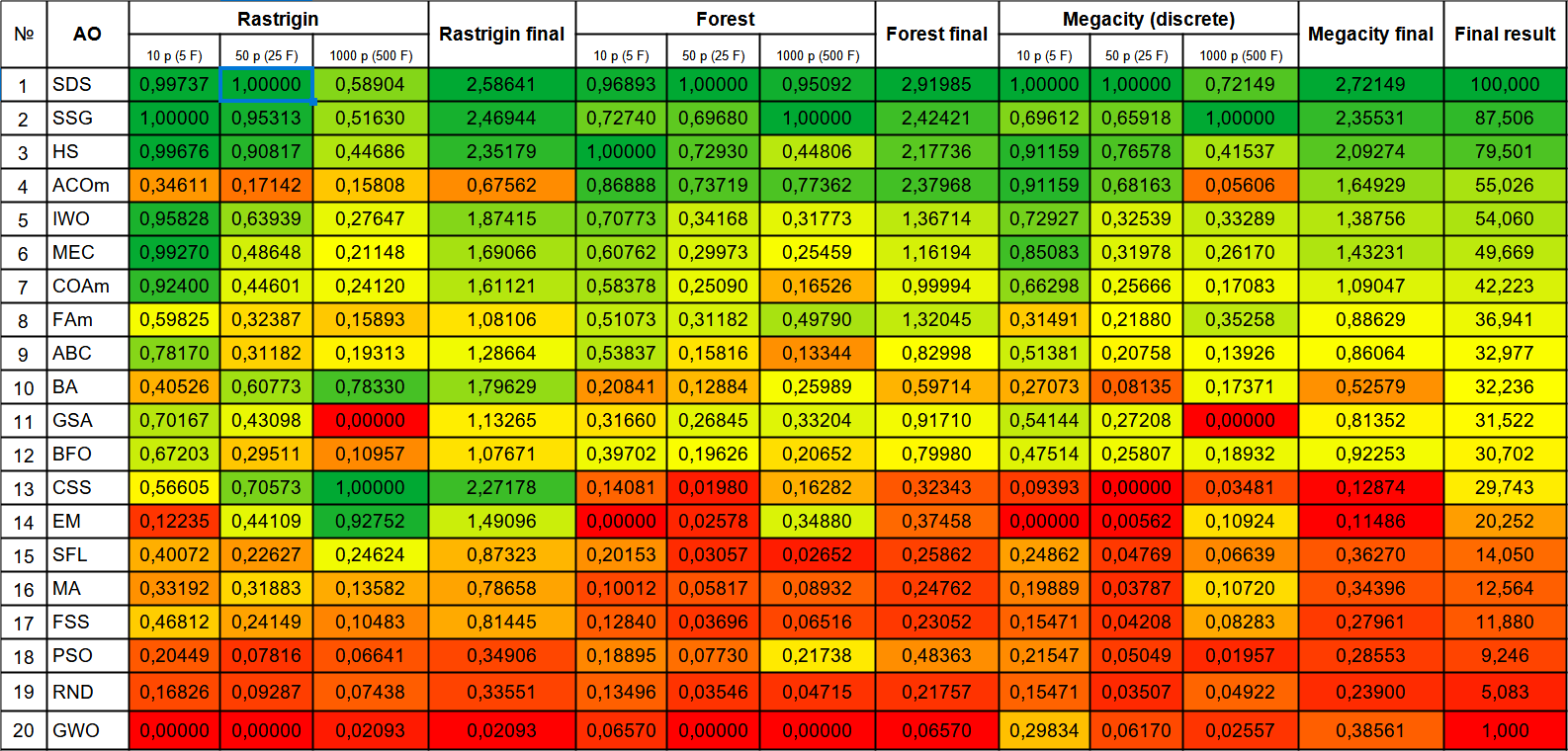
Figure 1. Color gradation of algorithms according to relevant tests

The histogram of the algorithm test results is provided below (on a scale from 0 to 100, the more the better, in the archive there is a script for calculating the rating table using the method described in this article):

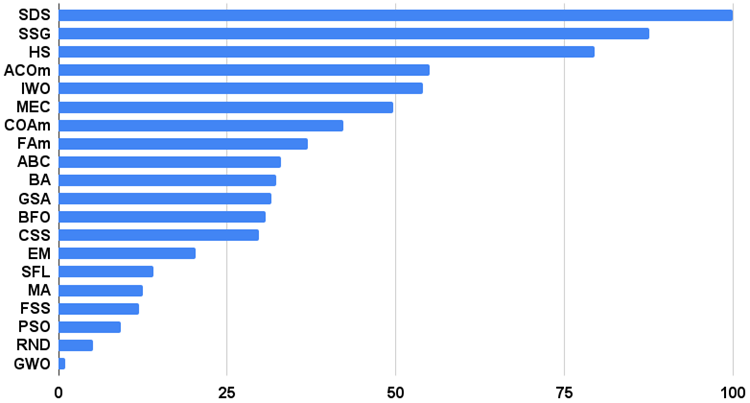
Figure 2. Histogram of the final results of testing algorithms

Pros and cons of the Charged System Search (CSS) algorithm:

Pros:
1. High scalability on smooth functions.
2. A small number of external parameters.

Cons:
1. Low results on discrete functions.
2. Low convergence.
3. Tendency to get stuck in local extremes.

Each article is accompanied by an archive with updated current versions of the algorithm codes described in previous articles. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.