MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português
preview
母集団最適化アルゴリズム：社会集団の進化(ESG)

母集団最適化アルゴリズム：社会集団の進化(ESG)

MetaTrader 5 — 例 | 25 6月 2024, 11:26
149 0
Andrey Dik
Andrey Dik

内容

1.はじめに
2.アルゴリズム
3.テスト結果


1.はじめに

最適化の分野では、さまざまな問題で最適解を見つけるために設計された幅広い集団アルゴリズムが存在します。しかし、その重要性にもかかわらず、多母集団アルゴリズムやマルチスウォームアルゴリズムは、これまで記事で十分に取り上げられてきませんでした。この点で、私はこの魅力的で有望なトピックについて、より詳細な考察の必要性を感じています。

多母集団アルゴリズムは、複数の独立した母集団を使用して最適化問題を解くという考えに基づいています。集団は論理的に並行して動作し、最適解に関する情報を交換することができるため、パラメータ空間の異なる領域を同時に探索し、異なる最適解を見つけることが可能になります。一方、マルチスウォームアルゴリズムは、最適解を得るために、互いに協力し情報を交換することもできる、相互作用する多数の粒子からなる社会集団（スウォーム）を使用します。

この記事では、この記事のために特別に作成した多母集団ESGアルゴリズムについて考察します。そのようなアルゴリズムの基本原理を見ていきます。さらに、これらのアルゴリズムの有効性を単個体最適化手法と比較して評価できるような比較研究の結果についても検討します。

2.アルゴリズム

多母集団アルゴリズムは、様々な組み合わせで以下の原則に基づくことができます。

1.社会的集団：このアルゴリズムは、個々の粒子ではなく、協力と経験の交換によって結ばれた社会的集団によって作動します。各集団には意思決定の中心があり、最適化エージェントとして粒子の集合を持ちます。集団は交流し、経験を共有し、最適解に関する情報を利用して成果を向上させます。

2.集団的な動き：社会的集団内の粒子は相互作用し、パラメータ空間で一緒に動きます。これにより、各集団はパラメータ空間の異なる領域を探索し、見つかった最適解に関する情報を共有することができます。

3.局所的経験および大域的経験：各社会的集団は、その中で最適解に関する情報（局所的経験）を保存しています。また、全集団の中で総合的なベストスコアもあります（大域的経験）。集団は最適解を保持し、経験を共有し、結果を改善するためにそれらを利用します。

4.進化と経験の交換：アルゴリズムは反復を繰り返し、その間に社会的集団は更新し、経験を共有します。解を繰り返し改善し、最適な結果を探します。

5.適応性と多様性：交流と経験の交換を通じて、集団は状況の変化に適応し、さまざまな最適解を見出すことができます。このアルゴリズムには適応性があり、最適化問題の条件や要件の変化に効果的に対応することができます。集団は新しい状況に適応し、パラメータ空間を移動する戦略を変更し、経験に基づいて決定を更新することができます。これにより、特に問題の条件が時間と共に変化するような場合に、アルゴリズムが効率的に最適解を探索できるようになります。

上記では、多母集団アルゴリズムの基本原理について話しました。では、ESG検索戦略の具体的な内容を見てみましょう。

社会集団と呼ぶ粒子の社会があるとします。この集団では、ある種の行動モデル（「中心」）が優勢であり、集団の粒子は、ある種の分布法則で記述することができ、多少のずれはあるものの、このモデルに従います。ほとんどの粒子は中心からわずかに逸脱していますが、一部の粒子は集団の影響範囲内で大きく逸脱しており、その境界は分布によって決定されます。粒子間でより適応した行動パターンが現れると、それが集団の新たな中心となります。こうして、集団は粒子挙動の最も安定したモデルを求めて動き出します。

このような集団は複数存在する可能性があり、独立しているため、低レベルでは社会集団内の個々のメンバーの行動を、高レベルでは集団の一般的な行動をシミュレートする、多母集団アルゴリズムと呼ぶことができます。

この概念からすると、ある個々の集団、あるいはすべての集団が同時に発達を止め、極限から抜け出せなくなる状況もあり得ます。これを避けるために、「社会集団の影響範囲の拡大」という概念を導入しています。各反復で進展がない場合、集団の境界が拡大され、新しい探索領域が開かれ、集団集団が多様化されます。集団が前のものより優れた解を見つけた場合、集団の境界半径はデフォルトの最小値まで再び縮小されます。これは、アルゴリズムが局所的な罠にはまるのを避け、必要であれば新しいエリアの探索を強化するのに役立ちます。半径を広げることは、社会集団の多様性にも貢献します。集団によってパラメータ空間の異なる領域を探索します。

この社会集団の進化のための多母集団アルゴリズムという概念には、将来性がありそうです。しかし、すべてが一見したところほど単純ではありません。集団の中心の現在位置が、対応する座標上で不運な位置にある可能性があり、影響範囲を広げても効果がない場合があります。このような場合、実際には「垂直方向の展開」が必要であるにもかかわらず、「斜め方向の展開」（ACOアルゴリズムのように、蟻が横に逸れることなく経路に沿ってのみ走る）が起こると言うことができます。または、まったく逆の状況も考えられます。

上記の問題を克服するためには、成功した経験を集団間で確実に伝達することが重要です。この目的のために、いくつかの粒子は「異質な」集団の中心からアイデアを借りることが許されます。したがって、中心的な行動パターンは、他の集団の個々の粒子に影響を与えます。ところで、その影響が必ずしもプラスになることはできないし、なることはありません。社会集団の行動モデルを図1に模式的に示します。



ESG

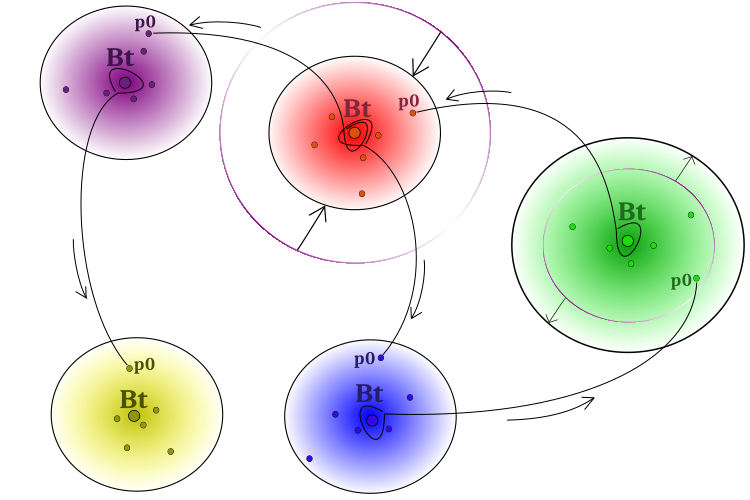
図1：アルゴリズム操作。集団を分け、進展がない場合は拡大し、解が改善された場合は縮小する

隣接するBt（ベストオブチーム）集団から、p0粒子（条件0番目の集団インデックスの粒子）により、最適のアイデア（座標）を借用します。

ESGアルゴリズムの擬似コードは以下のように表されます。

  1. 集団の中心を探索空間にランダムに配置します。
  2. 各集団の粒子を、対応する中心の周りに、与えられた分布で配置します。*。
  3. 粒子の適応度値を計算します。
  4. 大域的な解を更新します。
  5. 各集団の中心を更新します。
  6. 中心の位置に改善が見られない場合は集団の境界を広げ、位置を改善できた場合は集団の境界を狭めます。
  7. 集団の粒子を、対応する中心の周りに、与えられた分布で配置します。
  8. 「エイリアン集団」の中心からの情報を、各集団の1つの粒子に加えます（粒子はランダムに選ばれたエイリアン集団の座標セットを受け取る）。
  9. 粒子の適応度値を計算します。
  10. 停止基準が満たされるまで、ステップ4から繰り返します。

* ESGでは、中心に対する集団粒子の分布に分布冪乗則を使用しました。しかし、戦略ロジックの個々の部分について、それらの組み合わせを含め、他の分配法則を使用することもできます。このトピックには試行錯誤が必要です。

コードの見直しに移りましょう。社会集団を記述するために、いくつかのメンバー変数を含むS_Group構造体を記述します。

  • cB：中心座標を格納する値の配列
  • fB：-DBL_MAXによって初期化された中心適応度関数
  • sSize：集団のサイズ
  • sRadius：集団半径

構造体のInitメソッドは、coords：座標の数、groupSize：集団のサイズの、2つの引数を取ります。

//——————————————————————————————————————————————————————————————————————————————
struct S_Group
{
  void Init (int coords, int groupSize)
  {
    ArrayResize (cB, coords);
    fB          = -DBL_MAX;
    sSize       = groupSize;
  }

  double cB [];
  double fB;
  int    sSize;
  double sRadius;
};
//——————————————————————————————————————————————————————————————————————————————

検索エージェントを記述するシンプルな構造体は、ESGアルゴリズムのロジックに適しています。エージェント粒子の構造体は集団の説明フィールドに含めないことにしました。各集団は、一般的な集団の一部としてその粒子にアクセスすることができ、アルゴリズム外部からのエージェントへの通常のアクセスを維持すると同時に、エージェントへの集団粒子の不必要なコピーを避けることができます。

S_Agent構造体の定義には、2つの変数が含まれています。

  • c：エージェント座標値の配列
  • f：-DBL_MAXによって初期化されたエージェントの適応度値

Initメソッドは、c配列のサイズを変更するためにcoords引数を取ります。

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (const int coords)
  {
    ArrayResize (c, coords);
    f = -DBL_MAX;
  }

  double c []; //coordinates
  double f;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_ESGクラスを定義します。このクラスにはいくつかのフィールドとメソッドがあります。

1.publicフィールド：

  • cB：大域解の最適座標の値の配列
  • fB：最適座標の適応度値
  • a：エージェントを表すS_Agent型オブジェクトの配列
  • rangeMax：検索範囲の最大値の配列
  • rangeMin：検索範囲の最小値の配列
  •  rangeStep：検索ステップ値の配列

2.メソッド

  • Init：クラスのメンバー変数を初期化するための関数。座標数、母集団サイズ、集団数、初期集団半径、集団拡大係数、分布度の引数を受け取ります。
  • Moving：エージェントの移動を担当するメソッド
  • Revision：エージェントの改訂を担当するメソッド
  • SeInDiSp：指定されたステップで範囲内の値を計算するメソッド
  • RNDfromCI：与えられた間隔で乱数を生成するメソッド
  • Scale：ある範囲から別の範囲に値をスケーリングするメソッド
  • PowerDistribution：電力分布に従って値を生成するメソッド

3.privateフィールド

  • coords：座標の数
  • popSize：母集団のサイズ
  • gr：集団を表す S_Group 型オブジェクトの配列
  • groups：集団の数
  • groupRadius：集団半径
  • expansionRatio：拡張率
  • power：パワー
  •  revision：改訂の必要性を示すフラグ
//——————————————————————————————————————————————————————————————————————————————
class C_AO_ESG
{
  //----------------------------------------------------------------------------
  public: double  cB [];       //best coordinates
  public: double  fB;          //FF of the best coordinates
  public: S_Agent a  [];       //agents

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    groupsP,              //number of groups
                     const double groupRadiusP,         //group radius
                     const double expansionRatioP,      //expansion ratio
                     const double powerP);              //power

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int     coords;
  private: int     popSize;          //population size
  private: S_Group gr [];            //group

  private: int    groups;            //number of groups
  private: double groupRadius;       //group radius
  private: double expansionRatio;    //expansion ratio
  private: double power;             //power

  private: bool   revision;

  private: double SeInDiSp          (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI         (double min, double max);
  private: double Scale             (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
  private: double PowerDistribution (const double In, const double outMin, const double outMax, const double power);
};
//——————————————————————————————————————————————————————————————————————————————

クラスのInitメソッドは、渡されたパラメータに基づいてクラス変数を初期化するために使用されます。変数の初期化と配列のサイズの設定に加え、集団数が母集団サイズの倍数でない場合、このメソッドは各集団の粒子数を計算します。

partInSwarms配列はgroupsにリサイズされます。groupsは集団の数です。そして変数 particlesには、popSize（母集団のサイズ）をgroupsで割った結果が設定されます。partInSwarms配列の値はparticles、つまり余りのない量で満たされます。そして、失われた要素の数は、popSizeからparticlesとgroupsの積を引くことで計算されます。失われた要素がある場合（lost > 0）、それらはwhileループの集団間で均等に分配されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ESG::Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    groupsP,              //number of groups
                     const double groupRadiusP,         //group radius
                     const double expansionRatioP,      //expansion ratio
                     const double powerP)
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords         = coordinatesNumberP;
  popSize        = populationSizeP;
  groups         = groupsP;
  groupRadius    = groupRadiusP;
  expansionRatio = expansionRatioP;
  power          = powerP;

  //----------------------------------------------------------------------------
  int partInSwarms [];
  ArrayResize (partInSwarms, groups);

  int particles = popSize / groups;
  ArrayInitialize (partInSwarms, particles);

  int lost = popSize - particles * groups;

  if (lost > 0)
  {
    int pos = 0;

    while (true)
    {
      partInSwarms [pos]++;
      lost--;
      pos++;
      if (pos >= groups) pos = 0;
      if (lost == 0) break;
    }
  }

  //----------------------------------------------------------------------------
  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);

  ArrayResize (gr,        groups);
  for (int s = 0; s < groups; s++) gr [s].Init (coords, partInSwarms [s]);

  ArrayResize (a, popSize);
  for (int i = 0; i < popSize; i++) a [i].Init (coords);
}
//——————————————————————————————————————————————————————————————————————————————

Movingメソッドは、最適化の最初に集団中央と個体を生成するために使用されます。このメソッドは次のようなものです。

  • 外側のforループで各s集団の中央を生成します。そのために、入れ子になったforループが、各c座標に対して与えられた範囲のcoordinate乱数値を生成します。次に、coordinate値が目的の範囲に変換され、gr[s].cB[c]配列に格納されます。
  • 各s集団と各p個体について、外側のforループで個体を生成します。半径の値は、与えられたパラメータと、ネストされたforループ内の集団の現在の状態に基づいて計算されます。そして、minとmaxの値は、radiusを範囲境界に相対的に調整することによって計算されます。そして、PowerDistribution関数を使用して、与えられた範囲内のランダムなcoordinate値が生成されます。結果のcoordinate値は変換され、a[cnt].c[c]配列に格納されます。
  • revisionフラグをtrueに設定し、中央と個体の生成が進行中であることを示します。
//——————————————————————————————————————————————————————————————————————————————
void C_AO_ESG::Moving ()
{
  if (!revision)
  {
    int    cnt        = 0;
    double coordinate = 0.0;
    double radius     = 0.0;
    double min        = 0.0;
    double max        = 0.0;

    //generate centers----------------------------------------------------------
    for (int s = 0; s < groups; s++)
    {
      gr [s].sRadius = groupRadius;

      for (int c = 0; c < coords; c++)
      {
        coordinate    = RNDfromCI (rangeMin [c], rangeMax [c]);
        gr [s].cB [c] = SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    //generate individuals of groups--------------------------------------------
    for (int s = 0; s < groups; s++)
    {
      for (int p = 0; p < gr [s].sSize; p++)
      {
        for (int c = 0; c < coords; c++)
        {
          radius = (rangeMax [c] - rangeMin [c]) * gr [s].sRadius;
          min    = gr [s].cB [c] - radius;
          max    = gr [s].cB [c] + radius;

          if (min < rangeMin [c]) min = rangeMin [c];
          if (max > rangeMax [c]) max = rangeMax [c];

          coordinate    = PowerDistribution (gr [s].cB [c], min, max, power);
          a [cnt].c [c] = SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]);
        }

        cnt++;
      }
    }

    revision = true;
  }
}
//——————————————————————————————————————————————————————————————————————————————

新しい粒子を生成するための主なアクションはRevisionメソッドで発生します。このメソッドは、最適なグローバル解を更新し、集団の新しい個体を生成し、「エイリアン」集団の中心から1つの粒子に情報を転送することによって集団間の経験を交換します。したがって、集団内の1つの粒子だけが、他の集団から経験を借りることが許されます。このメソッドは次のようなものです。

  • 大域的な解を更新する：forループの中で、すべての個体を通して、現在の個体の適合度関数の値が現在の適合度関数の最適値を超えているかどうかを確認します。その後、最適値が更新され、現在の個体の座標の配列が最適解の座標の配列にコピーされます。
  • 集団の新しい個体を生成する：forループで、すべての集団とその個体を調べます。半径、各集団の最小最大座標値は、ネストされたループの中で計算されます。その後、PowerDistribution関数を使用してランダムな座標値を生成し、その結果を個体の座標の配列に格納します。
  • 集団間の経験交換：forループの中で、すべての集団を調べます。ネストされたforループの中で、どの集団と経験値を交換するかを決めるランダムな値が生成されます。そして、現在の集団の個体の座標値が、選択された集団の座標値で更新されます。
//——————————————————————————————————————————————————————————————————————————————
void C_AO_ESG::Revision ()
{
  //----------------------------------------------------------------------------
  //update the best global solution
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  int cnt = 0;
  bool impr = false;

  for (int s = 0; s < groups; s++)
  {
    impr = false;

    for (int p = 0; p < gr [s].sSize; p++)
    {
      if (a [cnt].f > gr [s].fB)
      {
        gr [s].fB = a [cnt].f;
        ArrayCopy (gr [s].cB, a [cnt].c, 0, 0, WHOLE_ARRAY);
        impr = true;
      }

      cnt++;
    }

    if (!impr) gr [s].sRadius *= expansionRatio;
    else       gr [s].sRadius  = groupRadius;

    if (gr [s].sRadius > 0.5) gr [s].sRadius = 0.5;
  }

  //generate individuals of groups----------------------------------------------
  double coordinate = 0.0;
  double radius     = 0.0;
  double min        = 0.0;
  double max        = 0.0;
  cnt = 0;

  for (int s = 0; s < groups; s++)
  {
    for (int p = 0; p < gr [s].sSize; p++)
    {
      for (int c = 0; c < coords; c++)
      {
        if (RNDfromCI (0.0, 1.0) < 1.0)
        {
        radius = (rangeMax [c] - rangeMin [c]) * gr [s].sRadius;
        min    = gr [s].cB [c] - radius;
        max    = gr [s].cB [c] + radius;

        if (min < rangeMin [c]) min = rangeMin [c];
        if (max > rangeMax [c]) max = rangeMax [c];

        coordinate    = PowerDistribution (gr [s].cB [c], min, max, power);
        a [cnt].c [c] = SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }

      cnt++;
    }
  }

  //exchange of experience----------------------------------------------------------------
  cnt = 0;

  for (int s = 0; s < groups; s++)
  {
    for (int c = 0; c < coords; c++)
    {
      int posSw = (int)RNDfromCI (0, groups);
      if (posSw >= groups) posSw = groups - 1;

      //if (sw [posSw].fB > sw [s].fB)
      {
        a [cnt].c [c] = gr [posSw].cB [c];
      }
    }

    cnt += gr [s].sSize;
  }
}
//——————————————————————————————————————————————————————————————————————————————

上で紹介した主なESGアルゴリズムを書いた後、アルゴリズムの組み合わせの質を向上させるため、変更を加え、異なる集団の粒子が情報を交換できるようにすることにしました。そのためには、エージェントの構造に変更を加えなければなりません。cMainはメインの座標、fMainはメインの経験です。

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (const int coords)
  {
    ArrayResize (c,     coords);
    ArrayResize (cMain, coords);
    f     = -DBL_MAX;
    fMain = -DBL_MAX;
  }

  double c     []; //coordinates
  double cMain []; //coordinates
  double f;        //fitness
  double fMain;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

この2つのオプションの違いは、Revisionメソッドに加えられた変更にあります。

1.メインバージョンでは、エージェント間の経験交換は集団レベルでおこなわれます。内側のforループでは、ランダムな集団が選択され、現在のエージェントの座標値が選択された集団の中心座標値に置き換えられます。このように、集団は、対応する集団内のただ1つの粒子に経験を伝達することによって、経験を交換します。

2.第2のオプションでは、エージェント間の経験交換は集団全体のレベルでおこなわれます。つまり、交換対象として選択された粒子の適応度がより高い場合、グループの粒子間で交換がおこなわれます。従って、集団間で最悪の粒子に経験を伝えられるのは、最高の粒子のみです。内側のforループでは、ランダムなエージェントが選択され、ある確率（copyProb値によって決定される）で、現在のエージェントの座標値が、母集団で選択されたエージェントの座標値に置き換えられます。

さらに、2番目のオプションには、エージェントを更新するコードのブロックが追加されています。もし現在のエージェントの適合度関数の値がその前の最適値よりも大きければ(f > fMain)、現在のエージェントの座標値はその現在の最適解の値(cMain)で更新されます。これにより、エージェントは最善の判断を保存し、後で利用することができます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ESG::Revision ()
{
  //----------------------------------------------------------------------------
  //Update the best global solution
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  //update agents
  for (int p = 0; p < popSize; p++)
  {
    if (a [p].f > a [p].fMain)
    {
      a [p].fMain = a [p].f;
      ArrayCopy (a [p].cMain, a [p].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  int cnt = 0;
  bool impr = false;

  for (int s = 0; s < groups; s++)
  {
    impr = false;

    for (int p = 0; p < gr [s].sSize; p++)
    {
      if (a [cnt].f > gr [s].fB)
      {
        gr [s].fB = a [cnt].f;
        ArrayCopy (gr [s].cB, a [cnt].c, 0, 0, WHOLE_ARRAY);
        impr = true;
      }

      cnt++;
    }

    if (!impr) gr [s].sRadius *= expansionRatio;
    else       gr [s].sRadius  = groupRadius;

    if (gr [s].sRadius > 0.5) gr [s].sRadius = 0.5;
  }

  //generate individuals of groups----------------------------------------------
  double coordinate = 0.0;
  double radius     = 0.0;
  double min        = 0.0;
  double max        = 0.0;
  cnt = 0;

  for (int s = 0; s < groups; s++)
  {
    for (int p = 0; p < gr [s].sSize; p++)
    {
      for (int c = 0; c < coords; c++)
      {
        if (RNDfromCI (0.0, 1.0) < 0.6)
        {
        radius        = (rangeMax [c] - rangeMin [c]) * gr [s].sRadius;
        min           = gr [s].cB [c] - radius;
        max           = gr [s].cB [c] + radius;

        if (min < rangeMin [c]) min = rangeMin [c];
        if (max > rangeMax [c]) max = rangeMax [c];

        coordinate    = PowerDistribution (gr [s].cB [c], min, max, power);
        a [cnt].c [c] = SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }

      cnt++;
    }
  }

  //exchange of experience----------------------------------------------------------------
  cnt = 0;

  for (int p = 0; p < popSize; p++)
  {
    for (int c = 0; c < coords; c++)
    {
      int pos = (int)RNDfromCI (0, popSize);
      if (pos >= popSize) pos = popSize - 1;

      if (RNDfromCI(0.0, 1.0) < copyProb)
      {
        if (a [pos].fMain > a [p].fMain)
        {
          a [p].c [c] = a [pos].cMain [c];
        }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

アルゴリズムの第2バージョンの実験とテストの結果、全体的な結果は期待された進展をもたらさず、わずかに悪化しました。これは、粒子の経験をそれぞれの集団の枠内にとどめ、集団間での完全な混同を許さないことが重要であるという事実から説明できます。各集団のユニークな経験は守られるべきであり、経験の交換は部分的なものにとどめるべきです。

実験の失敗は最終的なものではなく、アルゴリズムの改善が不可能であることを意味するものでもありません。これは、どのような点に注意を払う価値があり、どのような戦略を適用するのが最善なのかを理解するためのひとつの試みにすぎません。さらに研究開発を進めれば、得られた知識をもとに、検索能力の大幅な向上につながるアルゴリズムの新たなバリエーションを生み出すことができます。設定した目標を達成するためには、楽観的でありつづけることが重要です。テスト結果を以下に示します。


3.テスト結果

ESGメインバージョンのテストスタンド結果

C_AO_ESG|200|100|0.1|2.0|10.0
=============================
5 Hilly's; Func runs:10000; result:0.9990564816911227
25 Hilly's; Func runs:10000; result:0.7965424362150277
500 Hilly's; Func runs:10000; result:0.35055904999599663
=============================
5 Forest's; Func runs:10000; result:1.0
25 Forest's; Func runs:10000; result:0.8286255415345216
500 Forest's; Func runs:10000; result:0.13102081222227177
=============================
5 Megacity's; Func runs:10000; result:0.8233333333333333
25 Megacity's; Func runs:10000; result:0.5529999999999999
500 Megacity's; Func runs:10000; result:0.04724999999999998
=============================
All score:5.52939 (61.44%)

ESGバージョンのテストスタンドの結果を若干修正すると、次のようになります。


C_AO_MPSO|200|100|0.1|1.1|10.0|1.0
=============================
5 Hilly's; Func runs:10000; result:0.9986983861349696
25 Hilly's; Func runs:10000; result:0.7971379560351051
500 Hilly's; Func runs:10000; result:0.3351159723676586
=============================
5 Forest's; Func runs:10000; result:1.0
25 Forest's; Func runs:10000; result:0.8288612676775615
500 Forest's; Func runs:10000; result:0.11374411604788078
=============================
5 Megacity's; Func runs:10000; result:0.8333333333333333
25 Megacity's; Func runs:10000; result:0.5116666666666667
500 Megacity's; Func runs:10000; result:0.049316666666666654
=============================
All score:5.46787 (60.75%)

主要バージョンのアルゴリズムがうまく収束しているのがわかります。テスト関数のHillyとForestでは、収束グラフで軌跡のわずかなばらつきが目立ちます。ただし、Megacity関数では、このばらつきはかなり大きいですが、このテスト関数では、ほとんどのアルゴリズムが収束のばらつきも大きいです。先に紹介したほとんどのアルゴリズムとは異なり、このアルゴリズムは、エポック数が比例して減少するという事実にもかかわらず、200（通常は50が使用される）というはるかに大きな母集団サイズを「好みます」。ESGは極値でもうまく機能します。この性質は、アルゴリズムの多母集団性に影響されます。

Hilly

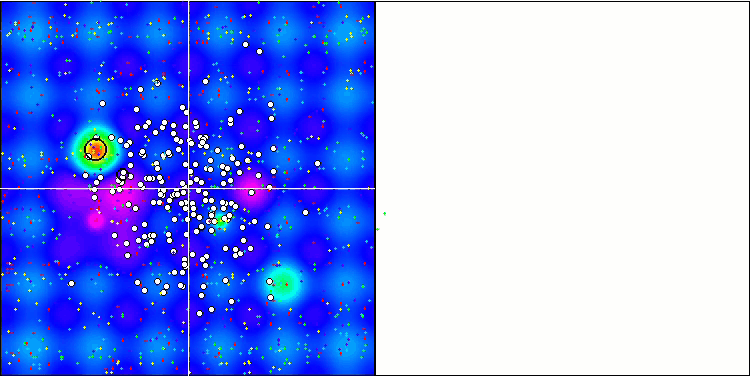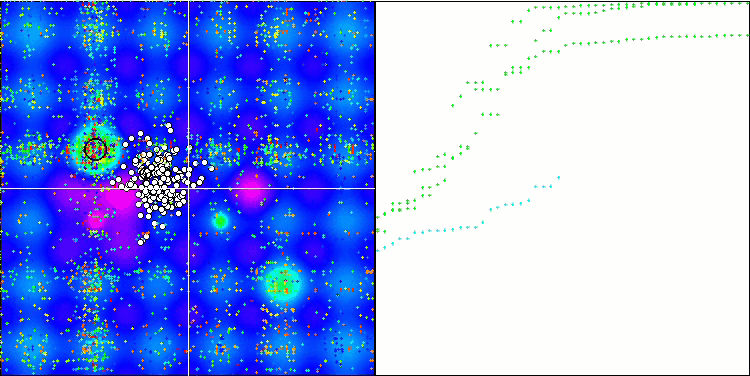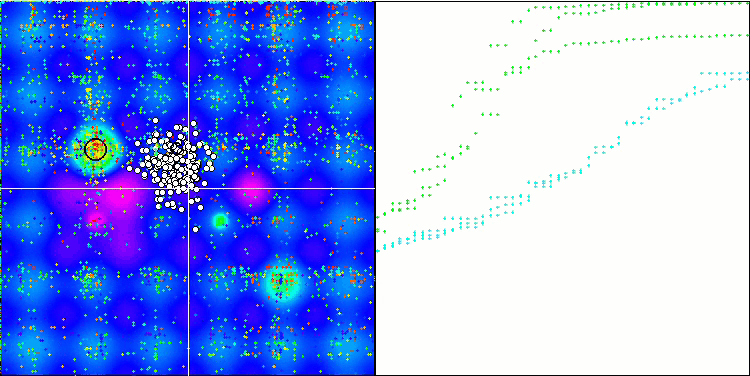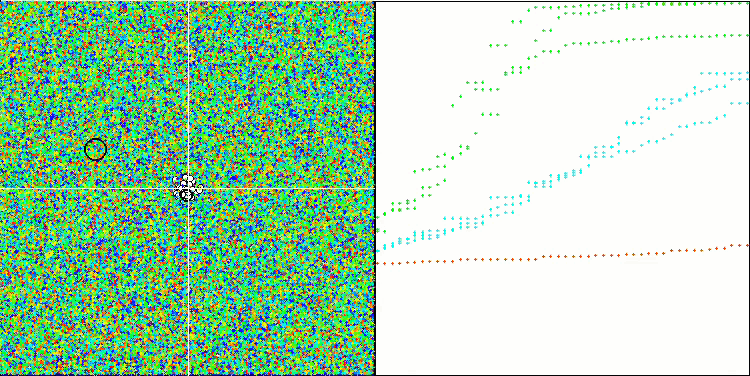
  Hillyテスト関数のESG

Forest

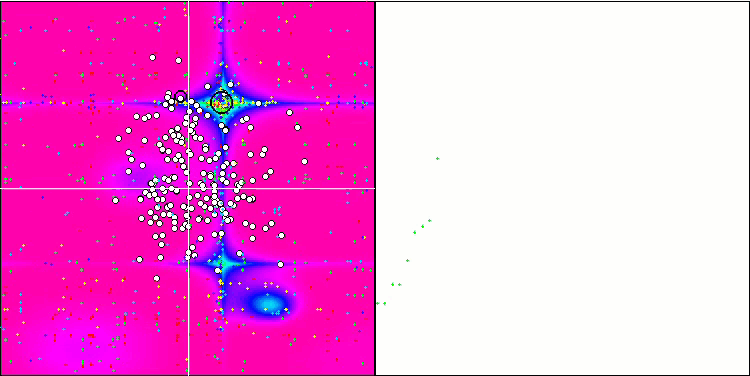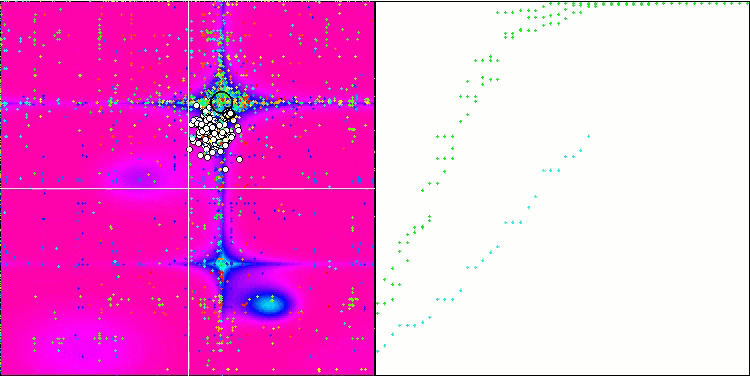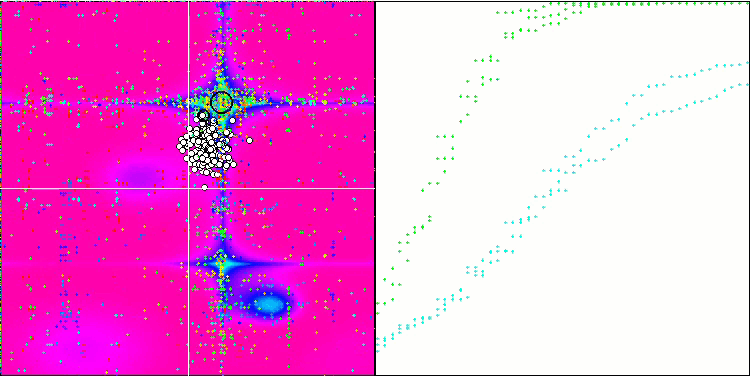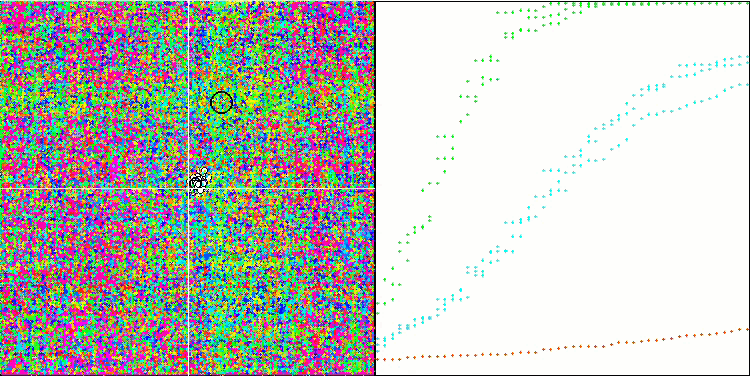
  Forestテスト関数のESG

Megacity

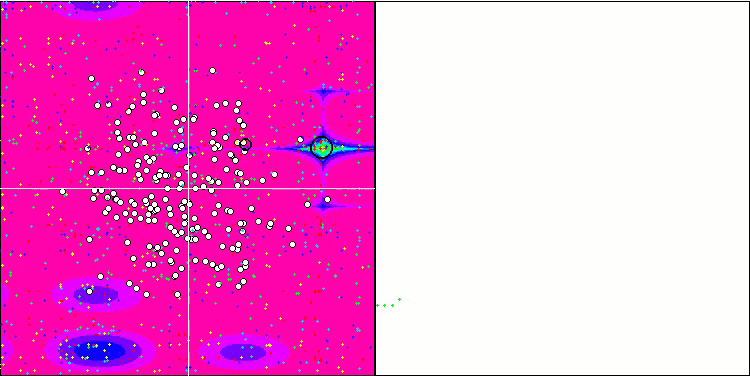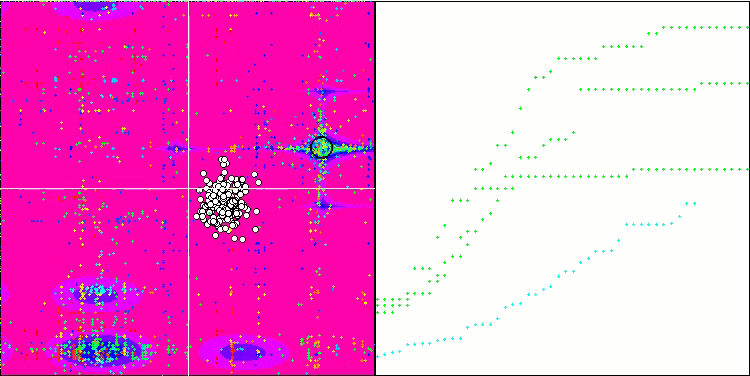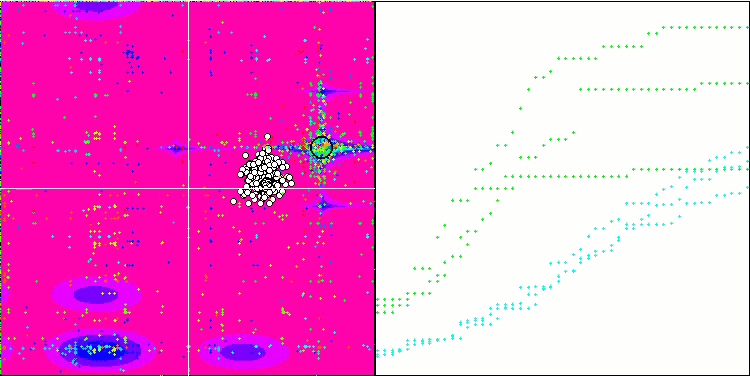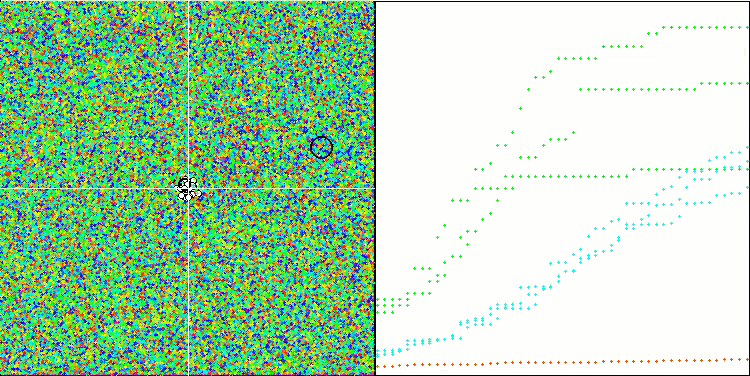
  Megacityテスト関数のESG


ESGアルゴリズムはまずまずの結果を示し、格付け表の上位に入りました。10個のパラメータを持つForest関数では100％収束し、10個のパラメータを持つHilly関数では99.9％とほぼ完全に収束していることがわかります。表はアルゴリズムのメインバージョンの結果を含み、実験バージョンはvariant2フォルダにあります。

# AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 BGA バイナリ遺伝的アルゴリズム 0.99992 0.99484 0.50483 2.49959 1.00000 0.99975 0.32054 2.32029 0.90667 0.96400 0.23035 2.10102 6.921 76.90
2 (P+O)ES (P+O）進化戦略 0.99934 0.91895 0.56297 2.48127 1.00000 0.93522 0.39179 2.32701 0.83167 0.64433 0.21155 1.68755 6.496 72.18
3 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
4 ESG 社会集団の進化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
5 SIA 等方的焼きなまし 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
6 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
7 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
8 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
9 (PO)ES (PO）進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
10 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
11 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
12 MEC Mind Evolutionary Computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
13 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
14 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
15 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
16 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
17 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
18 FAm ホタルアルゴリズムM 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
19 GSA 重力探索法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
20 BFO 細菌採餌の最適化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
21 ABC 人工蜂コロニー 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
22 BA コウモリアルゴリズム 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
23 SA 焼きなまし 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
24 IWDm インテリジェント水滴M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
25 PSO 粒子群最適化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
26 MA モンキーアルゴリズム 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
27 SFL Shuffled Frog-Leaping 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
28 FSS 魚群検索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
29 RND 無作為 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
30 GWO 灰色オオカミオプティマイザ 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32
31 CSS 荷電系探索 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46
32 EM 電磁気学的アルゴリズム 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85


まとめ

結論として、社会的集団進化アルゴリズムは、集団間の協力と経験の共有に基づく効果的な最適化手法です。適応性、多様性という特性を持ち、様々な最適化問題において最適解を見つけることができます。

ESGアルゴリズムは、パラメータの最適化が必要とされる様々な分野での使用にお勧めできます。例えば、機械学習におけるハイパーパラメータの調整、最適制御問題における関数の最適化、組合せ最適化問題の解法、その他最適なパラメータ値を求める必要のある問題に使用できます。

提示されたアルゴリズムは一種のテンプレートと考えることができ、以前の記事で説明した様々な個別のテクニックや検索戦略で補うことができます。さらに、PSO、ABC、ACOなど、各集団が別々の最適化アルゴリズムを使用することもできます。したがって、ESGアルゴリズムのアーキテクチャは、このような最適化手法を容易に実装し、各アルゴリズムの長所を組み合わせて併用することができます。

重要なのは、ESGが独立した解であり、良い結果をもたらしていること、そして複雑な問題を解決するための極めて柔軟なアプローチであることを強調することです。その可能性を最大限に引き出すことができるのは、核となるアイデアを実験的に発展させることであり、そのような実験の機会は誰にでも開かれています。

格付け表

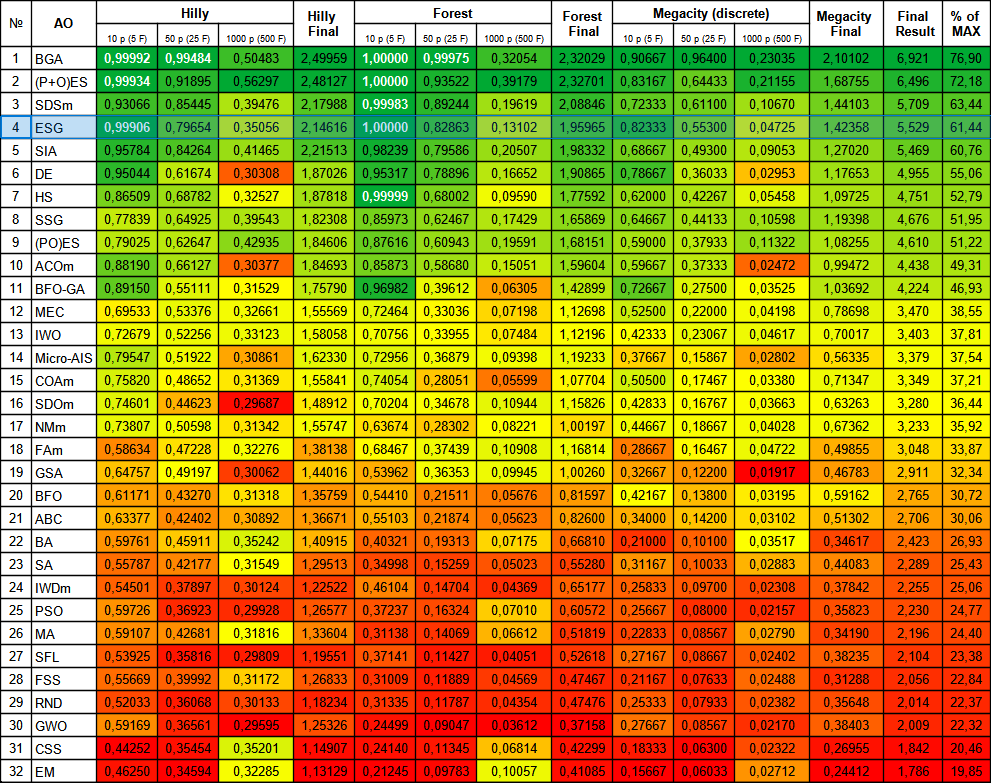
図2：関連テストに応じたアルゴリズムのカラーグラデーション0.99以上の結果は白で強調表示

チャート

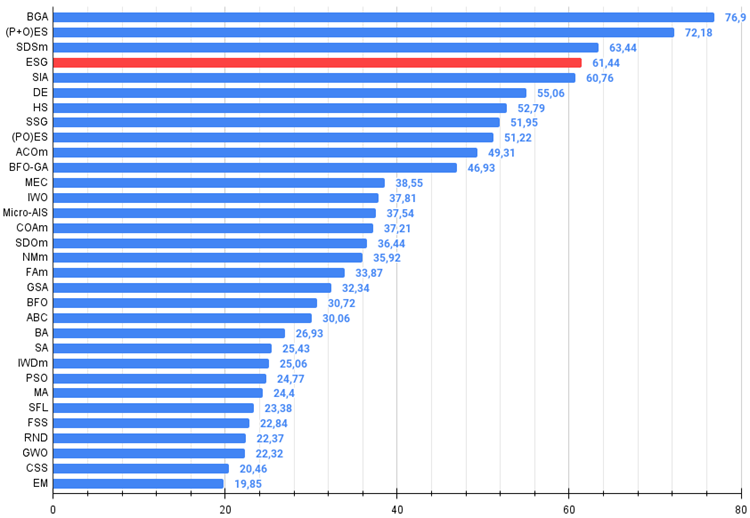
図3：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良いです。

ここで、100は理論的に可能な最大の結果であり、アーカイブにはレーティングテーブルを計算するスクリプトが含まれている)


ESGの長所と短所

長所

  1. シンプルな構造
  2. 収束性が高い
  3. コンピューティングリソースに負荷をかけない

短所

  1. パラメータ数の多い関数での結果が悪い

この記事には、過去の記事で説明したアルゴリズムコードの最新版を更新したアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/14136

添付されたファイル |
ZIPをダウンロード
32_The_world_of_AO_ESG.zip (592.48 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
母集団最適化アルゴリズム：人工多社会的検索オブジェクト（MSO） 母集団最適化アルゴリズム：人工多社会的検索オブジェクト（MSO）
前回に引き続き、社会的集団について考えてみたいと思います。この記事では、移動と記憶のアルゴリズムを用いて社会集団の進化を探求しています。その結果は、社会システムの進化を理解し、最適化や解の探索に応用するのに役立つでしょう。
最適化アルゴリズムを使用してEAパラメータをオンザフライで設定する 最適化アルゴリズムを使用してEAパラメータをオンザフライで設定する
この記事では、最適化アルゴリズムを使用して最適なEAパラメータをオンザフライで見つけることや、取引操作とEAロジックの仮想化について、実践的な側面から論じています。この記事は、最適化アルゴリズムをEAに実装するためのインストラクションとして使用できます。
ニューラルネットワークが簡単に（第75回）：軌道予測モデルのパフォーマンス向上 ニューラルネットワークが簡単に（第75回）：軌道予測モデルのパフォーマンス向上
私たちが作成するモデルはより大きく、より複雑になっています。そのため、訓練だけでなく、運用にもコストがかかります。しかし、決断に要する時間はしばしば重要です。この観点から、品質を損なうことなくモデルのパフォーマンスを最適化する手法を考えてみましょう。
多通貨エキスパートアドバイザーの開発（第3回）：アーキテクチャの改訂 多通貨エキスパートアドバイザーの開発（第3回）：アーキテクチャの改訂
複数の戦略が並行して動作する多通貨EAの開発はすでにある程度進んでいます。蓄積された経験を考慮し、先に進みすぎる前に、ソリューションのアーキテクチャを見直し、改善を試みましょう。