MetaTrader 5 / Tester
Русский Português
preview
Atmosphere Clouds Model Optimization (ACMO): Practice

Atmosphere Clouds Model Optimization (ACMO): Practice

MetaTrader 5 — Tester | 24 April 2025, 12:35
528 1
Andrey Dik
Andrey Dik

Contents

  1. Introduction
  2. Implementation of the algorithm
  3. Test results


Introduction

In the world of science, where technology and nature intersect, a unique idea of a metaheuristic ACMO (Atmospheric Cloud Model Optimization) algorithm for optimizing complex problems has emerged. In the previous article, we have technically analyzed the implementation of an algorithm that models the process of formation and movement of clouds in the atmosphere based on various meteorological parameters. In the first part, we created a class to manage cloud simulation, containing methods for initialization, cloud movement, updating region properties, and other processes.

We have divided the search space into regions. The initial humidity and pressure values in these regions were determined. We set the parameters of the model, such as: initial entropy, hyperentropy, threshold humidity value for cloud formation, and others. The next step was to generate clouds by selecting an area with high humidity. The cloud center, entropy and hyperentropy were calculated. We updated meteorological parameters of humidity and pressure in regions after cloud generation. Besides, we implemented the movement of clouds into low-pressure areas and subsequent updating of cloud characteristics depending on their movement between regions, as well as cloud dispersal. 

What else remains to be done? We need to implement functions for random placement of droplets and their distribution among clouds, complete the rain process and update the global solution, as well as test the model on our test functions with different parameters to evaluate its performance and accuracy. We will make changes to the process of rain and droplet formation to implement a more complete exchange of information about promising regions in the population.


Implementation of the algorithm

Let's describe the entire meteorological process in the form of a pseudocode, which will allow us to assemble the final version of the algorithm based on it:

1. In the first epoch, the clouds are placed randomly:
   EnCk = EnM0;
   HeCk = HeM0;
//------------------------------------------------------------------------------
1.1 Movement of clouds towards regions with lower pressure:
   β = deltaP / normP
   d = Tck.x - Cck.c
   VC = β * d;
   Ck = Ck + VC

   change in the number of droplets after movement:
   nk = nk × (1 - γ)

   change in entropy and hyperentropy:
   α = ΔP / ΔPmax;
   EnCk = EnCk * (1 + α)
   HeCk = HeCk * (1 - α)
//------------------------------------------------------------------------------
2. The process of rain, the falling of drops:
   the distribution of droplets between clouds is proportional to the humidity of the region
   increase in the number of droplets to those existing in the clouds
//------------------------------------------------------------------------------
3. Calculating the fitness function for droplets
//------------------------------------------------------------------------------
4. Update of global solution and minimum pressure in regions where drops fell
//------------------------------------------------------------------------------
5. Check for cloud decay and creation of new ones to replace those that have decayed in regions above the threshold:
   rule of disintegration due to expansion greater than the permissible value (cloud break):
   En > 5 * EnM0_t
   rule of decay at moisture content below critical value (cloud drying):
   dCk < dMin

   threshold value above which regions may form clouds:
   HT = H_min + λ * (H_max - H_min);
//------------------------------------------------------------------------------
6. Calculate entropy and hyperentropy for new clouds:
   En = EnM0 / (1 + 2.72 ^ (-(8 - 16 * (t / maxT))))
   He = HeM0 / (1 + 2.72 ^ ((8 - 16 * (t / maxT))))

Let's continue. Let's look at the Moving method of the C_AO_ACMO class. The method performs two operations: MoveClouds (revision) is responsible for clouds movement, RainProcess (revision) handles rain, which depends on the state of the clouds and the revision parameter. The Moving method performs two main actions related to cloud dynamics and rain. It encapsulates the logic of how clouds move and interact with the rain process. Thus, the Moving method is used to update the state of clouds and rain as part of the weather simulation.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::Moving ()
{
  MoveClouds       (revision);
  RainProcess      (revision);
}
//——————————————————————————————————————————————————————————————————————————————

Let's take a closer look at the MoveClouds method of the C_AO_ACMO class:

1. The first block (if rev is false): the method creates clouds with random centers. For each cloud and each coordinate:

  • A random value of the cloud center is generated in the given ranges (the RNDfromCI function).
  • The center is adjusted using SeInDiSp to normalize the values.
  • The index of the region the cloud is located in is determined using GetRegionIndex.
  • The entropy and initial entropy values for the cloud are set.
  • The initial value of hyperentropy is set to hyperEntropy.
The method terminates execution.

2. The second block (if rev is equal to true):

  • If rev is equal to true, the method begins to search for regions with the lowest pressure.
  • Arrays are created to store indices of regions with the lowest humidity lHind and to normalize pressure normP.

3. Loop to find the region with the lowest pressure:

  • For each c cooridnate, the minimum and maximum pressure among all regions is determined.
  • The index of the region with the lowest pressure is stored in the lHind array.
  • The normalized pressure for each coordinate is stored in normP.

4. Cloud movement for each of them and each coordinate:

  • If the cloud is already in the region with the lowest pressure, the iteration is skipped.
  • A random target region with less pressure is selected.
  • The pressure difference between the current and target region is calculated.
  • The pressure value is normalized and the VC cloud movement speed is calculated.
  • The cloud center is updated based on the speed of movement.
  • The region index is being updated.
  • The cloud entropy is updated taking into account the change in pressure.
  • The amount of moisture in the cloud decreases and the hyperentropy is updated, limiting its value to a maximum of 8.

The MoveClouds method is responsible for moving clouds to regions of lower pressure, updating their parameters such as entropy and hyperentropy. The method implements a dynamic model, reflecting changes in the atmosphere.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::MoveClouds (bool &rev)
{
  //----------------------------------------------------------------------------
  if (!rev)
  {
    //creating clouds with random centers---------------------------------------
    for (int i = 0; i < cloudsNumber; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        clouds [i].center [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        clouds [i].center [c] = u.SeInDiSp  (clouds [i].center [c], rangeMin [c], rangeMax [c], rangeStep [c]);

        clouds [i].regionIndex [c] = GetRegionIndex (clouds [i].center [c], c);

        clouds [i].entropy      [c] = entropy [c] * EnM0;
        clouds [i].entropyStart [c] = clouds [i].entropy [c];
      }

      clouds [i].hyperEntropy = HeM0;
    }

    return;
  }

  //search for the region with the lowest pressure------------------------------
  int targetRegion = 0;

  int lHind []; //lowest humidity index
  ArrayResize     (lHind, coords);
  ArrayInitialize (lHind, 0);

  double normP [];
  ArrayResize (normP, coords);
  double minP;
  double maxP;

  for (int c = 0; c < coords; c++)
  {
    minP =  DBL_MAX;
    maxP = -DBL_MAX;

    for (int r = 0; r < regionsNumber; r++)
    {
      if (areas [c].regions [r].pressure < areas [c].regions [lHind [c]].pressure)
      {
        lHind [c] = r;
      }

      if (areas [c].regions [r].pressure < minP) minP = areas [c].regions [r].pressure;
      if (areas [c].regions [r].pressure > maxP) maxP = areas [c].regions [r].pressure;
    }

    normP [c] = maxP - minP;
  }

  //moving the cloud to a region with less pressure-----------------------------
  int    clRegIND = 0;
  double deltaP   = 0.0;
  double α        = 0.0; // Entropy factor
  double β        = 0.0; // Atmospheric pressure factor
  double VC       = 0.0; // Cloud velocity
  double d        = 0.0; // Cloud direction

  for (int i = 0; i < cloudsNumber; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      //find a region with lower pressure---------------------------------------
      if (clouds [i].regionIndex [c] == lHind [c]) continue;

      clRegIND = clouds [i].regionIndex [c];

      do targetRegion = u.RNDminusOne (regionsNumber);
      while (areas [c].regions [clRegIND].pressure < areas [c].regions [targetRegion].pressure);

      //------------------------------------------------------------------------
      deltaP = areas [c].regions [clRegIND].pressure - areas [c].regions [targetRegion].pressure;

      β = deltaP / normP [c];
      d = areas [c].regions [targetRegion].x - areas [c].regions [clRegIND].centre;

      VC = β * d;

      clouds [i].center      [c] += VC;
      clouds [i].center      [c] = u.SeInDiSp (clouds [i].center [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      clouds [i].regionIndex [c] = GetRegionIndex (clouds [i].center [c], c);

      α = β;
      clouds [i].entropy [c] *=(1 + α);
    }

    clouds [i].droplets     *=(1 - γ);
    clouds [i].hyperEntropy *=(1 + α);
    if (clouds [i].hyperEntropy > 8) clouds [i].hyperEntropy = 8;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Next, let's analyze the GetRegionIndex method of the C_AO_ACMO class. Method description:

1. Calculating the position of a region. The regPos region index with the specified point is calculated and the floor function is used to round down to the nearest integer number.
2. Checking boundaries. This block checks if the regPos calculated index exceeds permissible values (it cannot exceed the permissible number of regions).
3. The method returns the index of the region the point is located in.

The GetRegionIndex method is intended to determine the index of the region, in which a given point is located within a certain range. It takes into account the number of regions and correctly handles cases where the point is on the boundary of the range. 

//——————————————————————————————————————————————————————————————————————————————
int C_AO_ACMO::GetRegionIndex (double point, int ind)
{
  int regPos = (int)floor ((point - rangeMin [ind]) / ((rangeMax [ind] - rangeMin [ind]) / regionsNumber));

  if (regPos >= regionsNumber) regPos = regionsNumber - 1;

  return regPos;
}
//——————————————————————————————————————————————————————————————————————————————

Describe the next method RainProcess of the C_AO_ACMO class:

2. Initializing arrays:

  • Create two arrays: cloud for storing cloud values and drops for storing the number of raindrops for each cloud.
  • Both arrays vary in size depending on the amount of clouds (cloudsNumber).

3. Initializing the cloud array:

  • If rev is equal to false, all cloud array elements are initialized using the value of 1.0.
  • Otherwise, the cloud array is initialized using the value of 0.0 and then the humidity is calculated for each cloud.

4. Humidity calculation:

  • For each cloud and each coordinate, humidity is calculated depending on the regions.
  • If the humidity is not equal to -DBL_MAX, it is added to the corresponding element of the cloud array. Otherwise, the minGp minimum drop value is added.

5. Droplet distribution:

  • Calling the DropletsDistribution method to distribute drops based on values in the cloud array.

6. The main droplet handling loop, for each cloud and each droplet:

  • The values of dist, centre, xMin and xMax are calculated.
  • The x value is generated using normal (Gaussian) distribution.
  • If x is out of range, it is corrected using the RNDfromCI method.
  • The x value is normalized using the SeInDiSp method and saved in the a array.

After all droplets for a cloud have been handled, the total number of droplets in the cloud is updated. Thus, the RainProcess method simulates a rain falling from clouds, taking into account the humidity and distribution of drops. It initializes the arrays, calculates the humidity for each cloud, distributes the raindrops, and generates values for each drop assuming a normal distribution. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::RainProcess (bool &rev)
{
  //to shed drops from every cloud----------------------------------------------
  double cloud [];
  int    drops [];
  ArrayResize (cloud, cloudsNumber);
  ArrayResize (drops, cloudsNumber);

  if (!rev)
  {
    ArrayInitialize (cloud, 1.0);
  }
  else
  {
    ArrayInitialize (cloud, 0.0);

    double humidity;

    for (int i = 0; i < cloudsNumber; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        for (int r = 0; r < regionsNumber; r++)
        {
          humidity = areas [c].regions [clouds [i].regionIndex [r]].humidity;
          if (humidity != -DBL_MAX) cloud [i] += humidity;
          else                      cloud [i] += minGp;
        }
      }
    }
  }

  DropletsDistribution (cloud, drops);

  double dist   = 0.0;
  double centre = 0.0;
  double xMin   = 0.0;
  double xMax   = 0.0;
  double x      = 0.0;
  int    dCNT   = 0;

  for (int i = 0; i < cloudsNumber; i++)
  {
    for (int dr = 0; dr < drops [i]; dr++)
    {
      for (int c = 0; c < coords; c++)
      {
        dist   = clouds [i].entropy [c];
        centre = clouds [i].center  [c];
        xMin   = centre - dist;
        xMax   = centre + dist;

        x = u.GaussDistribution (centre, xMin, xMax, clouds [i].hyperEntropy);

        if (x < rangeMin [c]) x = u.RNDfromCI (rangeMin [c], centre);
        if (x > rangeMax [c]) x = u.RNDfromCI (centre, rangeMax [c]);

        x = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);

        a [dCNT].c [c] = x;
      }

      dCNT++;
    }

    clouds [i].droplets += drops [i];
  }
}
//——————————————————————————————————————————————————————————————————————————————

The next method DropletsDistribution of the C_AO_ACMO class is designed to distribute raindrops between clouds based on their humidity. Let's have a thorough look at it.

2. Initialization of variables:

  • minHumidity is initialized to the maximum value so that the minimum humidity can be found.
  • indMinHumidity stores the cloud index with minimum humidity.
  • totalHumidity is used to store the sum of the humidity of all clouds.

3. Humidity summation sums the humidity of all clouds and determines the cloud with the lowest humidity.

4. Proportional distribution of drops - for each cloud, the number of drops is calculated proportionally to its humidity in relation to the total humidity. This value is stored in the droplets array.

5. Distribution of remaining drops:

  • First, the total number of distributed droplets totalDrops is calculated.
  • The number of remaining drops (remainingDrops) is then calculated.
  • If there are any remaining droplets, they are added to the cloud with minimal humidity.

The DropletsDistribution method effectively distributes raindrops between clouds based on their moisture content. It first distributes the droplets proportionally and then adjusts the distribution by adding the remaining droplets to the cloud with the lowest humidity. This allows for a more realistic simulation of the rainfall, while maintaining a constant number of drops, which corresponds to the population size in the external parameters of the algorithm.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::DropletsDistribution (double &cloud [], int &droplets [])
{
  double minHumidity    = DBL_MAX;
  int    indMinHumidity = -1;
  double totalHumidity  = 0; //total amount of humidity in all clouds

  for (int i = 0; i < ArraySize (cloud); i++)
  {
    totalHumidity += cloud [i];

    if (cloud [i] < minHumidity)
    {
      minHumidity = cloud [i];
      indMinHumidity = i;
    }
  }

  // Filling the droplets array in proportion to the value in clouds
  for (int i = 0; i < ArraySize (clouds); i++)
  {
    droplets [i] = int((cloud [i] / totalHumidity)*popSize); //proportional distribution of droplets
  }

  // Distribute the remaining drops, if any
  int totalDrops = 0;

  for (int i = 0; i < ArraySize (droplets); i++)
  {
    totalDrops += droplets [i];
  }

  // If not all drops are distributed, add the remaining drops to the element with the lowest humidity
  int remainingDrops = popSize - totalDrops;

  if (remainingDrops > 0)
  {
    droplets [indMinHumidity] += remainingDrops; //add the remaining drops to the lightest cloud
  }
}
//——————————————————————————————————————————————————————————————————————————————

The Revision method of the C_AO_ACMO class performs a system state update. Let's look at it in more detail:

1. Loop through a array elements (population of optimization agents). This loop iterates through all the elements of the a array of popSize size:

  • If the f fitness value of the current element is greater than the current fB maximum fitness value, fB is updated, while the ind index is set to the current index.
  • The search for the minimum f fitness value is also carried out among all elements of the array, and if the current value is less than minGp, then minGp is updated.

2. Copying data: if an element with the maximum f fitness value was found (ind is not -1), the data (namely, a [ind]) is copied from the c array to the cB array.

3. Updating region properties: UpdateRegionProperties method is called. It updates humidity and pressure parameters in different regions.

4. Cloud generation: the GenerateClouds method, which is responsible for the disappearance of old clouds and the creation of new ones, is called.

5. Status update:

  • The revision flag is set to true, which indicates that the initial state of the system has been passed.
  • The epochNow counter is increased to track the number of epochs.

The Revision method is responsible for updating the state of the system related to clouds. It finds the maximum f fitness value, updates the relevant parameters, initializes new clouds and updates the region properties. The method is key to keeping the data in the model up-to-date, allowing the system to adapt to changes.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }

    if (a [i].f < minGp) minGp = a [i].f;
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  UpdateRegionProperties (); //updating humidity and pressure in the regions
  GenerateClouds         (); //disappearance of clouds and the creation of new ones

  revision = true;
  epochNow++;
}
//——————————————————————————————————————————————————————————————————————————————

The GenerateClouds method of the C_AO_ACMO class is responsible for creating clouds and managing their state depending on various factors, such as humidity and entropy. Method description:

1. Humidity threshold calculation: the CalculateHumidityThreshold function is called, which returns the humidity threshold value required for clouds to form.

2. Structure for storing region indices:

  • The S_Areas structure is defined. The structure contains an array of indices of regions capable of forming clouds. 
  • The ar method is initialized with a size equal to the coords number of coordinates.

3. Region information collection: This double loop tests each region to see if it meets its humidity threshold. If the humidity of a region is greater than the threshold, the index of that region is added to the regsIND array of the appropriate S_Areas structure.

4. Checking cloud decay conditions:

  • For each cloud, it is checked whether its entropy exceeds a certain limit (5 times the initial entropy). If this is the case, the cloud is considered to have disintegrated.
  • Then it is checked if the amount of moisture in the cloud is less than the minimum value of dMin, which may also lead to the cloud disintegration.

5. Creating a new cloud in the wettest regions:

  • If the cloud disintegrates, a new cloud is created in one of the wettest regions. For each coordinate, a region index is randomly selected, and the cloud receives new center coordinates and a region index.
  • The CalculateNewEntropy function is then called. The function recalculates the entropy for a new cloud depending on the current epoch.

The GenerateClouds method manages cloud creation and disintegration based on humidity and entropy. It collects information about regions capable of forming clouds, checks existing clouds for decay, and creates new clouds in suitable regions. This method is key to dynamically controlling the state of clouds in the model.                                                                                                                                                    

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::GenerateClouds ()
{
  //Collecting statistics of regions capable of creating clouds-----------------
  double Ht = CalculateHumidityThreshold ();

  struct S_Areas
  {
      int regsIND []; //index of the potential region
  };

  S_Areas ar [];
  ArrayResize (ar, coords);

  int sizePr = 0;

  for (int i = 0; i < coords; i++)
  {
    for (int r = 0; r < regionsNumber; r++)
    {
      if (areas [i].regions [r].humidity > Ht)
      {
        sizePr = ArraySize (ar [i].regsIND);
        sizePr++;
        ArrayResize (ar [i].regsIND, sizePr, coords);
        ar [i].regsIND [sizePr - 1] = r;
      }
    }
  }

  //Check the conditions for cloud decay----------------------------------------
  bool   cloudDecay = false;

  for (int i = 0; i < cloudsNumber; i++)
  {
    cloudDecay = false;

    //checking the cloud for too much entropy-----------------------------------
    for (int c = 0; c < coords; c++)
    {
      if (clouds [i].entropy [c] > 5.0 * clouds [i].entropyStart [c])
      {
        //Print ("Disintegration of cloud #", i, " - tore at epoch ", epochNow);
        cloudDecay = true;
        break;
      }
    }

    //checking the cloud for decay----------------------------------------------
    if (!cloudDecay)
    {
      if (clouds [i].droplets < dMin)
      {
        //Print ("Disintegration of cloud #", i, " - dried up at epoch ", epochNow);
        cloudDecay = true;
      }
    }

    //if the cloud has decayed--------------------------------------------------
    int regIND = 0;

    if (cloudDecay)
    {
      //creating a cloud in a very humid region---------------------------------
      for (int c = 0; c < coords; c++)
      {
        regIND = u.RNDminusOne (ArraySize (ar [c].regsIND));
        regIND = ar [c].regsIND [regIND];

        clouds [i].center      [c] = areas [c].regions [regIND].x;
        clouds [i].regionIndex [c] = regIND;
      }

      CalculateNewEntropy (clouds [i], epochNow);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

The CalculateHumidityThreshold method of the C_AO_ACMO class is responsible for calculating the humidity threshold required for cloud formation. Here are the steps in detail:

1. Double cycle to find minimum humidity. The outer loop goes through all coords coordinates, while the inner loop iterates through all regions (regionsNumber) in each coordinate. If the humidity of the region is not equal to -DBL_MAX, a check is performed: if the current humidity is less than the current H_min, H_min is updated.

2. The method returns H_min increased by the product of λ and the difference of H_max and H_min, which represents the moisture threshold required for clouds to form.

The CalculateHumidityThreshold method calculates the humidity threshold based on the minimum humidity among all regions and adjusts it based on the maximum humidity and the λ ratio. This makes it possible to determine under what conditions clouds can form, based on the state of the environment.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_ACMO::CalculateHumidityThreshold ()
{
  double H_max = fB;
  double H_min = DBL_MAX;

  for (int c = 0; c < coords; c++)
  {
    for (int r = 0; r < regionsNumber; r++)
    {
      if (areas [c].regions [r].humidity != -DBL_MAX)
      {
        if (areas [c].regions [r].humidity < H_min)
        {
          H_min = areas [c].regions [r].humidity;
        }
      }
    }
  }

  return H_min + λ * (H_max - H_min);
}
//——————————————————————————————————————————————————————————————————————————————

The CalculateNewEntropy method of the C_AO_ACMO class is responsible for calculating the new entropy and hyperentropy for clouds represented by the S_ACMO_Cloud structure. Let's take a detailed look at it:

1. Calculating entropy:

  • The cycle goes through all coords coordinates.
  • For each coordinate, a new entropy value is calculated "cl.entropy [c]", using the equation: En = (entropy [c] * EnM0) / (1 + e ^ (-(8 - 16 * (t / epochs)))).
  • cl.entropyStart [c] and cl.entropy [c] are initialized with the value of entropy [c], which serves to preserve the initial value of entropy.

2. Calculating hyperentropy: He = 1 / (1 + e ^ (8 - 16 * (t / epochs))).

3. Hyperentropy is scaled using the Scale method of the u object, which allows us to scale the hyperentropy value to a given range (from 0 to 8) using the HeM0 parameters and 8.0.

The CalculateNewEntropy method updates entropy and hyperentropy values for clouds based on the current time t and the specified parameters. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::CalculateNewEntropy (S_ACMO_Cloud &cl, int t)
{
  //----------------------------------------------------------------------------
  //En: 1/(1+2.72^(-(8-16*(t/maxT))))
  for (int c = 0; c < coords; c++)
  {
    cl.entropy      [c] = entropy [c] * EnM0 / (1.0 + pow (M_E, (-(8.0 - 16.0 * (t / epochs)))));
    cl.entropyStart [c] = cl.entropy [c] = entropy [c];
  }

  //----------------------------------------------------------------------------
  //He: 1/(1+2.72^((8-16*(t/maxT))))
  cl.hyperEntropy = 1.0 / (1.0 + pow (M_E, ((8.0 - 16.0 * (t / epochs)))));

  cl.hyperEntropy = u.Scale (cl.hyperEntropy, 0.0, 8.0, HeM0, 8.0);
}
//——————————————————————————————————————————————————————————————————————————————

En and He 2

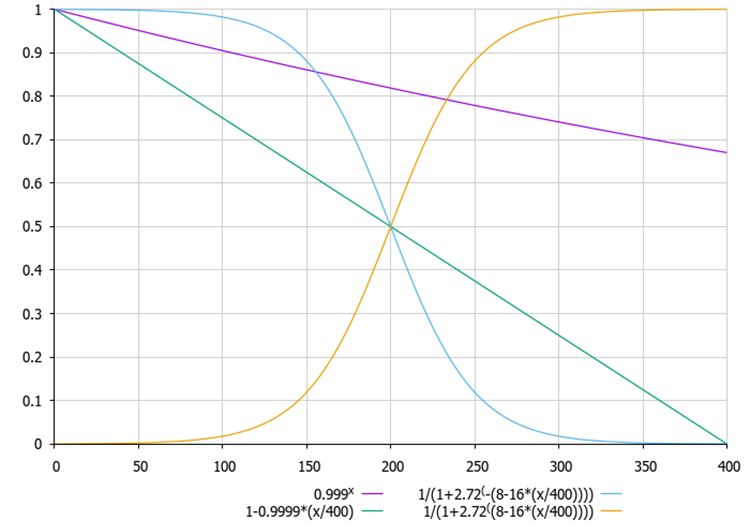
Figure 1. Variants of equations for calculating the ζ ratio depending on the current epoch. We can select an equation and try out the algorithm with each of them (the code strings are commented out)


Test results

Let's move on to testing the algorithm. The meteorological model of cloud formation, as conceived by the authors, works as follows:

//original version
ACMO|Atmospheric Cloud Model Optimization|50.0|5.0|10.0|0.2|5.0|5.0|0.9|0.2|
=============================
5 Hilly's; Func runs: 10000; result: 0.6017884495404766
25 Hilly's; Func runs: 10000; result: 0.3426222382089618
500 Hilly's; Func runs: 10000; result: 0.2526410178225118
=============================
5 Forest's; Func runs: 10000; result: 0.4780554376190664
25 Forest's; Func runs: 10000; result: 0.261057831391174
500 Forest's; Func runs: 10000; result: 0.17318135866144563
=============================
5 Megacity's; Func runs: 10000; result: 0.3507692307692307
25 Megacity's; Func runs: 10000; result: 0.16153846153846158
500 Megacity's; Func runs: 10000; result: 0.09632307692307775
=============================
All score: 2.71798 (30.20%)

Unfortunately, the results are much lower than expected. I think that despite the beautiful model of the cloud formation principle with a large number of different equations and logical actions aimed at avoiding getting stuck in extremes, the convergence of the algorithm is low. The algorithm lacks direct interaction and exchange of information between agents about the best solutions, the presence of which usually leads to an improvement in the search qualities of any algorithm. As a result, I decided to add information exchange through probabilistic transmission of information from the best drops to the worst ones. Now let's see what came out of this:

ACMOm|Atmospheric Cloud Model Optimization|50.0|4.0|10.0|0.2|0.2|2.0|0.9|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.9032099148349984
25 Hilly's; Func runs: 10000; result: 0.48545807643133143
500 Hilly's; Func runs: 10000; result: 0.30403284557071203
=============================
5 Forest's; Func runs: 10000; result: 0.8026793420899985
25 Forest's; Func runs: 10000; result: 0.3785708322859447
500 Forest's; Func runs: 10000; result: 0.1917777390119122
=============================
5 Megacity's; Func runs: 10000; result: 0.6230769230769231
25 Megacity's; Func runs: 10000; result: 0.244
500 Megacity's; Func runs: 10000; result: 0.10795384615384714
=============================
All score: 4.04076 (44.90%)

The results have improved significantly. The idea was successful. The idea is to transmit information about the best solution with some probability to cloud drops from other drops if they have higher humidity (in the context of the algorithm, this is fitness). 

At the end, for each cloud, the total number of drops (for a cloud, this is an indicator of humidity) dropped from it is updated by adding the corresponding value from the drops array. The RainProcess method implements a mechanism that models the rain, taking into account humidity, droplet distribution, and interaction with the population. The location where changes were made to the code is highlighted in green.

For each generated x value, a random p index from the population is selected. Depending on the probability (95%), the values in the a array are updated. The value represents a population or a set of solutions. At the end, the total number of drops dropped from the cloud is updated for each cloud by adding the corresponding value from the drops array.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::RainProcess (bool &rev)
{
  //to shed drops from every cloud----------------------------------------------
  double cloud [];
  int    drops [];
  ArrayResize (cloud, cloudsNumber);
  ArrayResize (drops, cloudsNumber);

  if (!rev)
  {
    ArrayInitialize (cloud, 1.0);
  }
  else
  {
    ArrayInitialize (cloud, 0.0);

    double humidity;

    for (int i = 0; i < cloudsNumber; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        humidity = areas [c].regions [clouds [i].regionIndex [c]].humidity;
       
        if (humidity != -DBL_MAX) cloud [i] += humidity;

        else                      cloud [i] += minGp;
      }
    }
  }

  DropletsDistribution (cloud, drops);
  //ArrayPrint (drops);

  double dist   = 0.0;
  double centre = 0.0;
  double xMin   = 0.0;
  double xMax   = 0.0;
  double x      = 0.0;

  int    dCNT   = 0;


  for (int i = 0; i < cloudsNumber; i++)
  {
    for (int dr = 0; dr < drops [i]; dr++)
    {
      for (int c = 0; c < coords; c++)
      {
        dist   = clouds [i].entropy [c];
        centre = clouds [i].center  [c];
        xMin   = centre - dist;
        xMax   = centre + dist;

        x = u.GaussDistribution (centre, xMin, xMax, clouds [i].hyperEntropy);

        if (x < rangeMin [c]) x = u.RNDfromCI (rangeMin [c], centre);
        
        if (x > rangeMax [c]) x = u.RNDfromCI (centre, rangeMax [c]);

        x = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);

        int p = u.RNDminusOne (popSize);

        if (a [p].f > a [dCNT].f)
        {
          if (u.RNDprobab () < 0.95) a [dCNT].c [c] = a [p].c [c];
        }

        else
        {
          a [dCNT].c [c] = x;
        }
      }
      dCNT++;
    }

    clouds [i].droplets += drops [i];
  }
}
//——————————————————————————————————————————————————————————————————————————————

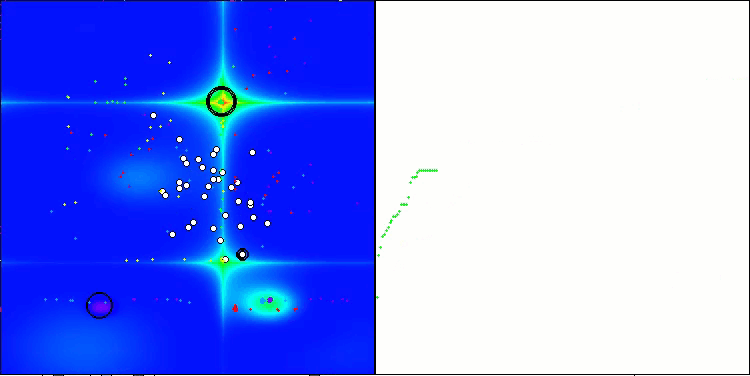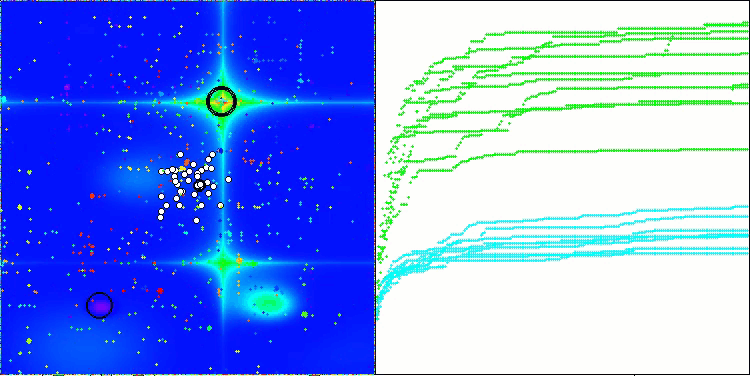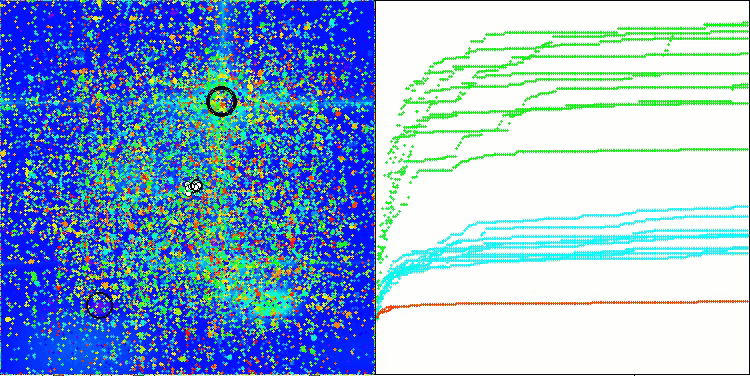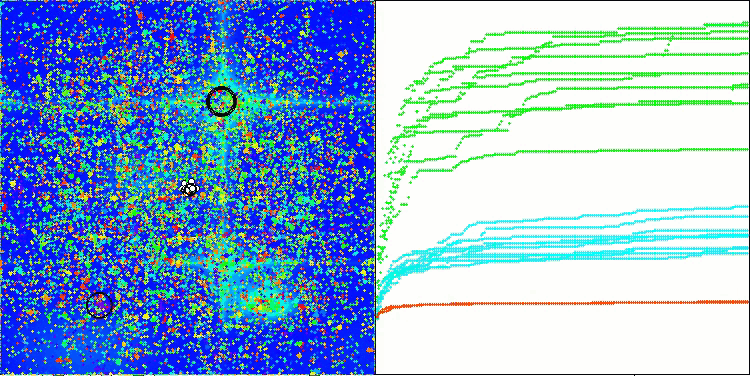
The visualization of the algorithm's operation shows the following: good convergence of the algorithm, long flat sections on the convergence graph with a small number of optimized parameters indicate some tendency for the algorithm to get stuck in local extremes, and with an increase in the number of parameters, this disadvantage disappears.

The clouds in the visualization appear as dense clusters, but by choosing different settings for external parameters (number of regions, clouds, initial entropy, and drying threshold), they can simulate the appearance of floating clouds in the sky, as in nature.

Hilly

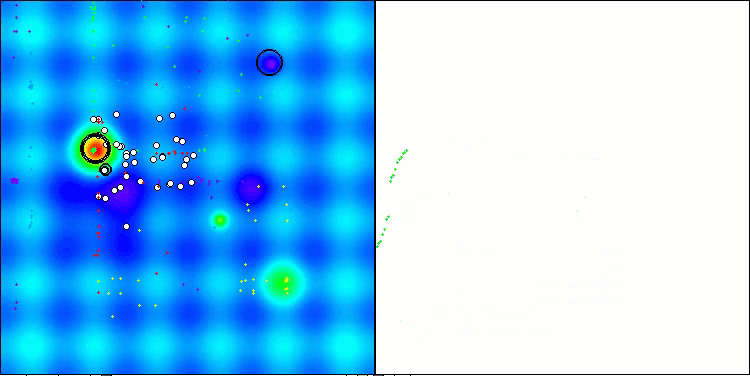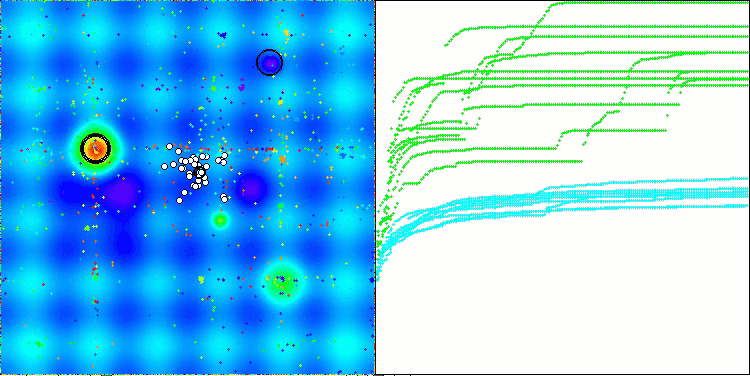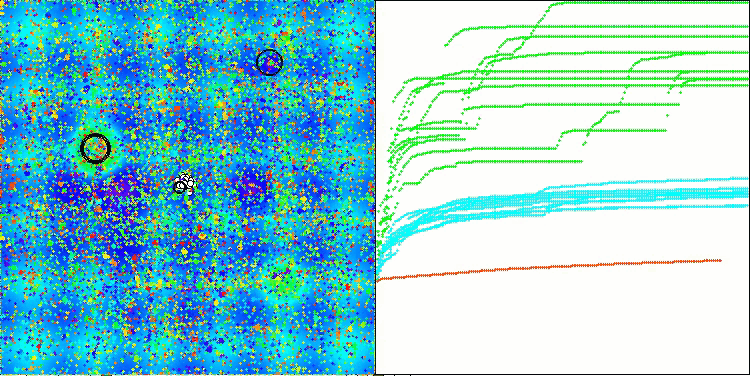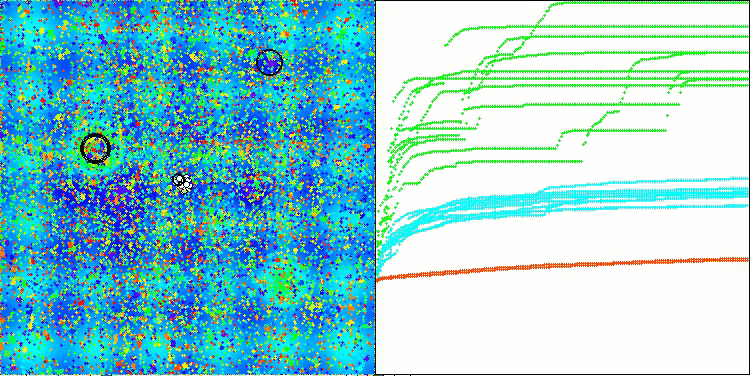
AСMO on the Hilly test function

Forest

ACMO on the Forest test function

Megacity

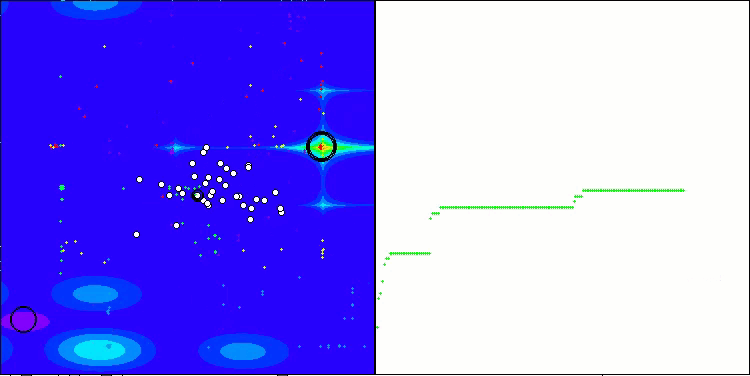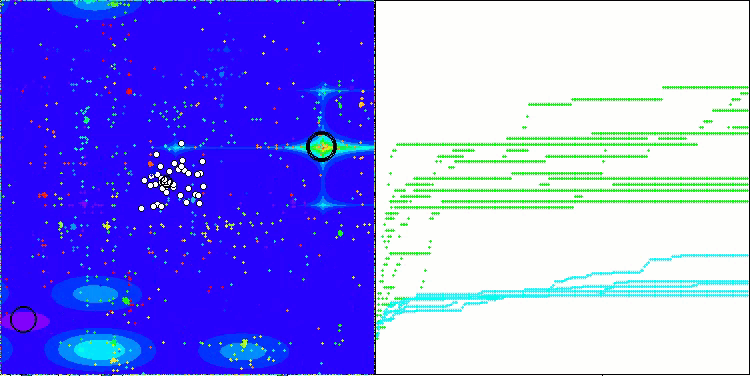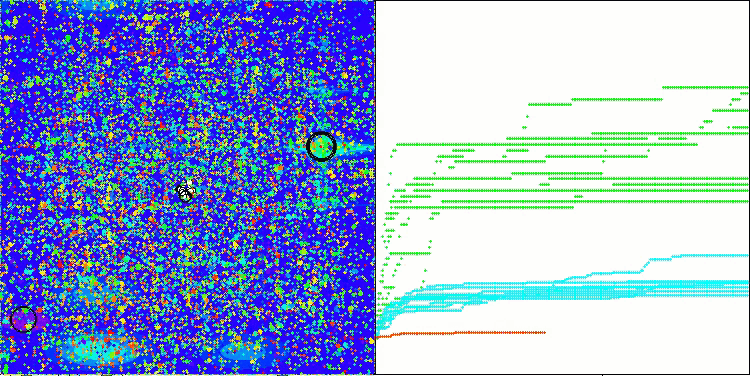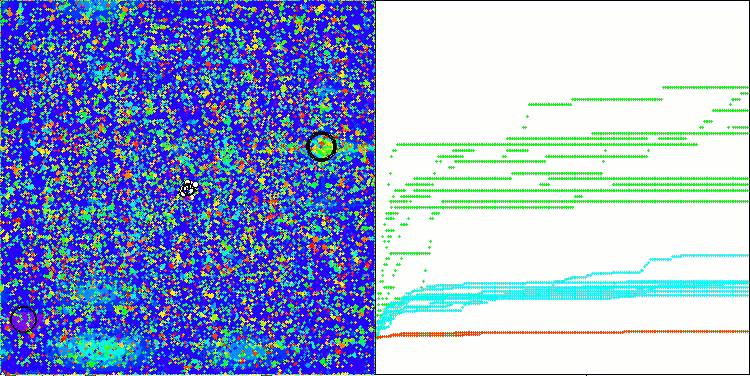
ACMO on the Megacity test function

According to the results of testing the modified version, the algorithm ranks 27 th, which is a fairly stable indicator. I would like to emphasize that the table now always contains 45 algorithms and, in fact, with each new algorithm the difference between the previous and subsequent ones will gradually decrease, thus, we can say that the table represents the top known algorithms. 

# AO Description Hilly Hilly final Forest Forest final Megacity (discrete) Megacity final Final result % of MAX
10 p (5 F)50 p (25 F)1000 p (500 F)10 p (5 F)50 p (25 F)1000 p (500 F)10 p (5 F)50 p (25 F)1000 p (500 F)
1ANSacross neighbourhood search0.949480.847760.438572.235811.000000.923340.399882.323230.709230.634770.230911.574916.13468.15
2CLAcode lock algorithm0.953450.871070.375902.200420.989420.917090.316422.222940.796920.693850.193031.683806.10767.86
3AMOmanimal migration ptimization M0.903580.843170.462842.209590.990010.924360.465982.380340.567690.591320.237731.396755.98766.52
4(P+O)ES(P+O) evolution strategies0.922560.881010.400212.203790.977500.874900.319452.171850.673850.629850.186341.490035.86665.17
5CTAcomet tail algorithm0.953460.863190.277702.094350.997940.857400.339492.194840.887690.564310.105121.557125.84664.96
6SDSmstochastic diffusion search M0.930660.854450.394762.179880.999830.892440.196192.088460.723330.611000.106701.441035.70963.44
7AAmarchery algorithm M0.917440.708760.421602.047800.925270.758020.353282.036570.673850.552000.237381.463235.54861.64
8ESGevolution of social groups0.999060.796540.350562.146161.000000.828630.131021.959650.823330.553000.047251.423585.52961.44
9SIAsimulated isotropic annealing0.957840.842640.414652.215130.982390.795860.205071.983320.686670.493000.090531.270205.46960.76
10ACSartificial cooperative search0.755470.747440.304071.806981.000000.888610.224132.112740.690770.481850.133221.305835.22658.06
11ASOanarchy society optimization0.848720.746460.314651.909830.961480.791500.238031.991010.570770.540620.166141.277525.17857.54
12TSEAturtle shell evolution algorithm0.967980.644800.296721.909490.994490.619810.227081.841390.690770.426460.135981.253225.00455.60
13DEdifferential evolution0.950440.616740.303081.870260.953170.788960.166521.908650.786670.360330.029531.176534.95555.06
14CROchemical reaction optimization0.946290.661120.298531.905930.879060.584220.211461.674730.758460.426460.126861.311784.89254.36
15BSAbird swarm algorithm0.893060.649000.262501.804550.924200.711210.249391.884790.693850.326150.100121.120124.80953.44
16HSharmony search0.865090.687820.325271.878180.999990.680020.095901.775920.620000.422670.054581.097254.75152.79
17SSGsaplings sowing and growing0.778390.649250.395431.823080.859730.624670.174291.658690.646670.441330.105981.193984.67651.95
18BCOmbacterial chemotaxis optimization M0.759530.622680.314831.697040.893780.613390.225421.732590.653850.420920.144351.219124.64951.65
19(PO)ES(PO) evolution strategies0.790250.626470.429351.846060.876160.609430.195911.681510.590000.379330.113221.082554.61051.22
20TSmtabu search M0.877950.614310.291041.783300.928850.518440.190541.637830.610770.382150.121571.114494.53650.40
21BSObrain storm optimization0.937360.576160.296881.810410.931310.558660.235371.725340.552310.290770.119140.962224.49849.98
22WOAmwale optimization algorithm M0.845210.562980.262631.670810.931000.522780.163651.617430.663080.411380.113571.188034.47649.74
23AEFAartificial electric field algorithm0.877000.617530.252351.746880.927290.726980.180641.834900.666150.116310.095080.877544.45949.55
24ACOmant colony optimization M0.881900.661270.303771.846930.858730.586800.150511.596040.596670.373330.024720.994724.43849.31
25BFO-GAbacterial foraging optimization - ga0.891500.551110.315291.757900.969820.396120.063051.428990.726670.275000.035251.036924.22446.93
26ABHAartificial bee hive algorithm0.841310.542270.263041.646630.878580.477790.171811.528180.509230.338770.103970.951974.12745.85
27ACMOatmospheric cloud model optimization0.903210.485460.304031.692700.802680.378570.191781.373030.623080.244000.107950.975034.04144.90
28ASBOadaptive social behavior optimization0.763310.492530.326191.582020.795460.400350.260971.456770.264620.171690.182000.618313.65740.63
29MECmind evolutionary computation0.695330.533760.326611.555690.724640.330360.071981.126980.525000.220000.041980.786983.47038.55
30IWOinvasive weed optimization0.726790.522560.331231.580580.707560.339550.074841.121960.423330.230670.046170.700173.40337.81
31Micro-AISmicro artificial immune system0.795470.519220.308611.623300.729560.368790.093981.192330.376670.158670.028020.563353.37937.54
32COAmcuckoo optimization algorithm M0.758200.486520.313691.558410.740540.280510.055991.077040.505000.174670.033800.713473.34937.21
33SDOmspiral dynamics optimization M0.746010.446230.296871.489120.702040.346780.109441.158260.428330.167670.036630.632633.28036.44
34NMmNelder-Mead method M0.738070.505980.313421.557470.636740.283020.082211.001970.446670.186670.040280.673623.23335.92
35FAmfirefly algorithm M0.586340.472280.322761.381380.684670.374390.109081.168140.286670.164670.047220.498553.04833.87
36GSAgravitational search algorithm0.647570.491970.300621.440160.539620.363530.099451.002600.326670.122000.019170.467832.91132.34
37BFObacterial foraging optimization0.611710.432700.313181.357590.544100.215110.056760.815970.421670.138000.031950.591622.76530.72
38ABCartificial bee colony0.633770.424020.308921.366710.551030.218740.056230.826000.340000.142000.031020.513022.70630.06
39BAbat algorithm0.597610.459110.352421.409150.403210.193130.071750.668100.210000.101000.035170.346172.42326.93
40AAAalgae adaptive algorithm0.500070.320400.255251.075720.370210.222840.167850.760890.278460.148000.097550.524022.36126.23
41SAsimulated annealing0.557870.421770.315491.295130.349980.152590.050230.552800.311670.100330.028830.440832.28925.43
42IWDmintelligent water drops M0.545010.378970.301241.225220.461040.147040.043690.651770.258330.097000.023080.378422.25525.06
43PSOparticle swarm optimisation0.597260.369230.299281.265770.372370.163240.070100.605720.256670.080000.021570.358232.23024.77
44Boidsboids algorithm0.433400.305810.254250.993460.357180.201600.157080.715860.278460.142770.098340.519572.22924.77
45MAmonkey algorithm0.591070.426810.318161.336040.311380.140690.066120.518190.228330.085670.027900.341902.19624.40


Summary

Two versions of the algorithm are presented: original and modified. The latter involves small changes but significantly increases performance due to the exchange of information within the population. This demonstrates that even minor adjustments to the algorithm's logic can lead to significant increases in efficiency across a variety of tasks.

I really liked the idea of the algorithm, as it is aimed at avoiding getting stuck in extremes. The algorithm uses complex multi-stage logic of moving clouds from high pressure zones to low pressure zones and precipitation. However, this was not sufficient to achieve high convergence. As a result, I attempted a modification by introducing information exchange in the population, which helped improve convergence, which is one of the key aspects of any optimization algorithm.

The peculiarity of the algorithm is that no cloud stays in one place for too long. The ever-increasing pressure in the region inevitably pushes the cloud into a new, unexplored area. This mechanism was conceived by the authors as a means of counteracting getting stuck in local extremes. However, trying to improve the convergence of the algorithm increased the probability of getting stuck, which, unfortunately, partially negated the key feature that inspired me to apply this approach to other optimization algorithms. The design of any optimization algorithm is always associated with finding a compromise between resistance to getting stuck and finding an exact solution. If desired, the probability of information exchange can be reduced in the code. At the moment it is 95%, which will increase the stability.

The algorithm is a wonderful base and a set of interesting techniques (rules for the formation of humidity in regions and the distribution of pressure between them, and additionally physical laws of acceleration and inertia, depending on the mass of clouds and many other ideas can be applied) and is a real boon for researchers.

Tab

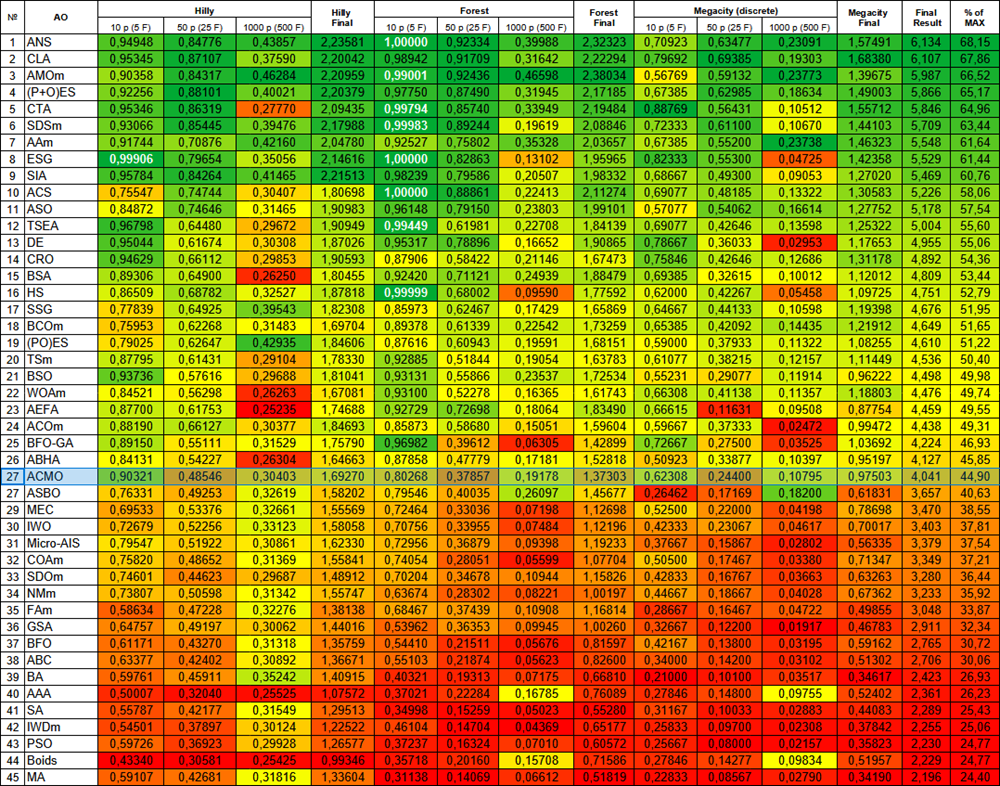
Figure 2. Histogram of algorithm testing results (scale from 0 to 100, the higher the better, where 100 is the maximum possible theoretical result, in the archive there is a script for calculating the rating table)

chart

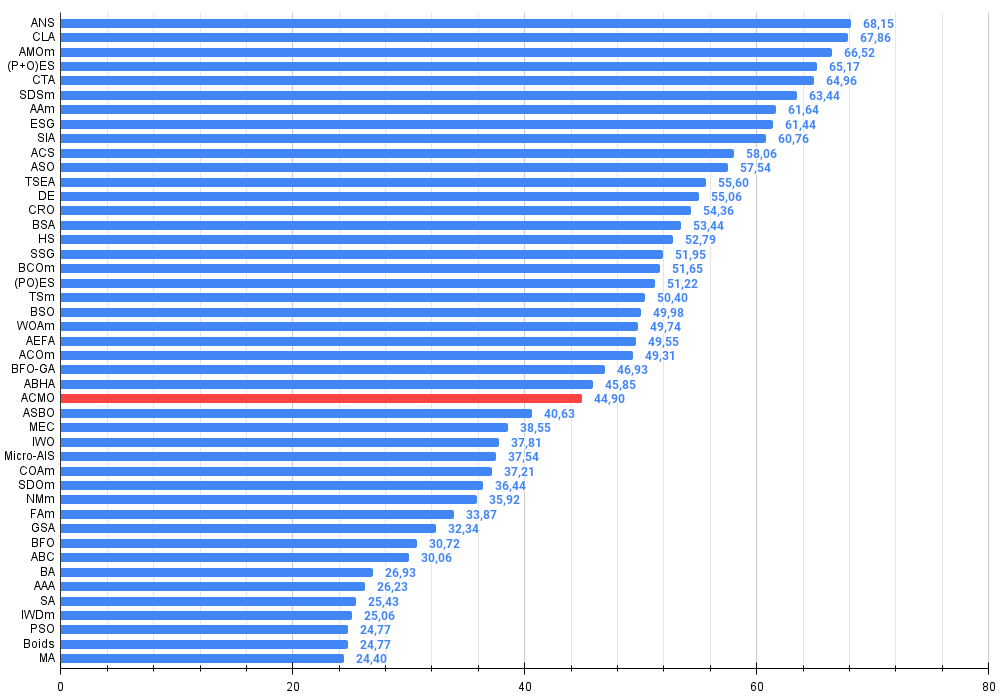
Figure 3. Color gradation of algorithms according to relevant tests Results greater than or equal to 0.99 are highlighted in white

ACMO pros and cons:

Pros:

  1. Built-in mechanisms against getting stuck.
  2. Relatively good convergence.
  3. Relatively good scalability.

Cons:

  1. A huge number of external parameters.
  2. Complex implementation.
  3. Difficulty in finding the right balance between getting stuck and converging.

The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.

Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/15921

Attached files |
Download ZIP
ACMO.zip (39.7 KB)
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.

Other articles by this author

Last comments | Go to discussion (1)
Arda Kaya
Arda Kaya | 24 Apr 2025 at 16:13
Really interesting topic!
Automating Trading Strategies in MQL5 (Part 15): Price Action Harmonic Cypher Pattern with Visualization Automating Trading Strategies in MQL5 (Part 15): Price Action Harmonic Cypher Pattern with Visualization
In this article, we explore the automation of the Cypher harmonic pattern in MQL5, detailing its detection and visualization on MetaTrader 5 charts. We implement an Expert Advisor that identifies swing points, validates Fibonacci-based patterns, and executes trades with clear graphical annotations. The article concludes with guidance on backtesting and optimizing the program for effective trading.
Neural Networks in Trading: Exploring the Local Structure of Data Neural Networks in Trading: Exploring the Local Structure of Data
Effective identification and preservation of the local structure of market data in noisy conditions is a critical task in trading. The use of the Self-Attention mechanism has shown promising results in processing such data; however, the classical approach does not account for the local characteristics of the underlying structure. In this article, I introduce an algorithm capable of incorporating these structural dependencies.
Websockets for MetaTrader 5: Asynchronous client connections with the Windows API Websockets for MetaTrader 5: Asynchronous client connections with the Windows API
This article details the development of a custom dynamically linked library designed to facilitate asynchronous websocket client connections for MetaTrader programs.
Data Science and ML (Part 36): Dealing with Biased Financial Markets Data Science and ML (Part 36): Dealing with Biased Financial Markets
Financial markets are not perfectly balanced. Some markets are bullish, some are bearish, and some exhibit some ranging behaviors indicating uncertainty in either direction, this unbalanced information when used to train machine learning models can be misleading as the markets change frequently. In this article, we are going to discuss several ways to tackle this issue.