Популяционные алгоритмы оптимизации: Эволюция социальных групп (Evolution of Social Groups, ESG)

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов

1. Введение

В области оптимизации существует широкий спектр популяционных алгоритмов, предназначенных для поиска оптимальных решений в различных задачах. Однако, несмотря на их важность, многопопуляционные и многороевые алгоритмы ранее не были достаточно освещены в моих статьях и исследованиях. В связи с этим я пришел к мысли о необходимости более подробного рассмотрения этой увлекательной и перспективной темы.

Многопопуляционные алгоритмы основаны на идее использования нескольких независимых популяций для решения задач оптимизации. Популяции работают логически параллельно и могут обмениваться информацией об оптимальных решениях, что позволяет исследовать одновременно разные области пространства параметров и находить различные оптимумы. С другой стороны, многороевые алгоритмы используют социальные группы (рои) из множества взаимодействующих частиц, которые могут так же сотрудничать друг с другом и обмениваться информацией для достижения оптимальных решений.

В данной статье заполним этот пробел и рассмотрим в качестве примера многопопуляционный алгоритм ESG, созданный мной специально для этой статьи. Мы рассмотрим основные принципы работы подобных алгоритмов. Кроме того, мы рассмотрим результаты сравнительных исследований, которые позволят оценить эффективность этих алгоритмов по сравнению с моно-популяционными методами оптимизации.

2. Описание алгоритма

В основе многопопуляционного алгоритма могут быть заложены в различных вариантах и комбинациях следующие принципы:

1. Социальные группы. Алгоритм оперирует не отдельными частицами, а социальными группами, объединенными сотрудничеством и обменом опытом. Каждая группа имеет свой центр принятия решений и набор частиц в качестве агентов оптимизации. Группы взаимодействуют, обмениваются опытом и используют информацию о лучших решениях для улучшения своих результатов.

2. Коллективное движение. Частицы внутри социальных групп взаимодействуют и совместно перемещаются в пространстве параметров. Это позволяет группам исследовать различные регионы пространства параметров и обмениваться информацией о лучших найденных решениях.

3. Локальный и глобальный опыт. Каждая социальная группа хранит информацию о лучшем решении внутри нее (локальный опыт). Существует также общий лучший результат среди всех групп (глобальный опыт). Группы сохраняют лучшие решения, обмениваются опытом и используют его для улучшения результатов.

4. Эволюция и обмен опытом. Алгоритм проходит через итерации, в ходе которых социальные группы обновляются и обмениваются опытом. Происходит итерационное улучшение решений и поиск оптимального результата.

5. Адаптивность и разнообразие. Благодаря взаимодействию и обмену опытом, группы могут адаптироваться к изменяющимся условиям и находить разнообразные оптимальные решения. Алгоритм обладает свойством адаптивности, что позволяет ему эффективно реагировать на изменяющиеся условия и требования задачи оптимизации. Группы могут адаптироваться к новым условиям, изменять свою стратегию перемещения в пространстве параметров и обновлять свои решения на основе полученного опыта. Это позволяет алгоритму эффективно искать оптимальные решения, особенно в случаях, когда условия задачи изменяются со временем.

Выше мы поговорили об основных принципах многопопуляционных алгоритмов. Теперь рассмотрим особенности поисковой стратегии ESG.

Допустим, у нас есть общество частиц, которое мы назовем "социальной группой". В этой группе преобладает определенная модель поведения - "центр", и частицы группы следуют этой модели с некоторым отклонением, которое можно описать определенным законом распределения. Большинство частиц незначительно отличаются от центра, но некоторые сильно отклоняются в пределах зоны влияния группы, границы которой определяются распределением. Когда появляется более приспособленная модель поведения среди частиц, она становится новым центром группы. Таким образом, группа перемещается в поисках наиболее стабильной модели поведения частиц.

Таких групп может быть несколько, и они независимы, поэтому это можно назвать многопопуляционным алгоритмом, имитирующим поведение отдельных членов в социальных группах на низком уровне и общее поведение групп на высоком уровне.

Учитывая такую концепцию, возможны ситуации, когда некоторые отдельные группы или даже все группы одновременно останавливаются в своем развитии и застревают в локальных экстремумах. Чтобы избежать этого, мы вводим понятие "расширения сферы влияния социальной группы". В случае отсутствия прогресса на каждой итерации границы группы расширяются, что позволяет открывать новые области поиска и разнообразить популяцию групп. Если группа находит решение, превосходящее предыдущее, радиус границ группы снова сокращается до минимального значения по умолчанию. Это помогает алгоритму избегать застревания в локальных ловушках и, при необходимости, усиливает исследование новых областей. Увеличение радиуса также способствует разнообразию социальных групп. Разные группы будут исследовать разные области пространства параметров.

Такая концепция многопопуляционного алгоритма эволюции социальных групп выглядит многообещающей. Однако не все так просто, как может показаться на первый взгляд. Текущее положение центра группы может находиться в неудачном положении на соответствующих координатах, и даже расширение зоны влияния может оказаться неэффективным. В таких случаях, можно сказать, происходит "расширение по диагонали" (как в алгоритме ACO, где муравьи бегают только по своим дорожкам не отклоняясь в сторону), когда на самом деле требуется "перпендикулярное расширение", или так же возможна ситуация в точности до наоборот.

Для преодоления вышеупомянутой проблемы важно обеспечить передачу успешного опыта между группами. Для этой цели можно позволить некоторым частицам заимствовать идеи у центров "чужих" групп. Таким образом, центральная модель поведения будет влиять на отдельные частицы других групп. Влияние, кстати, необязательно может быть и будет положительным. Схематично модель поведения социальных групп представлена на рисунке 1.

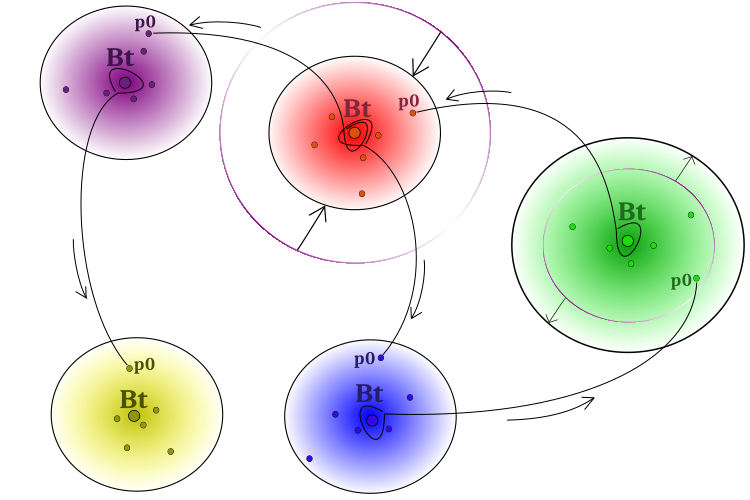
Рисунок 1. Схема работы алгоритма. Отдельные группы, расширение в случае отсутствия прогресса, сужение в случае улучшения решения,

заимствование "лучших идей" (координат) от соседних групп "Bt" (best of team) частицами "p0" (particle на условном 0-м индексе группы).

Псевдокод алгоритма ESG можно представить в следующем виде:

1. Разместим случайным образом центры групп в пространстве поиска.
2. Разместим частицы групп вокруг соответствующих центров с заданным распределением*.
3. Рассчитаем значения приспособленности частиц.
4. Обновим глобальное решение.
5. Обновим центр каждой группы.
6. Расширим границы групп в случае отсутствия улучшения положения центра и уменьшим, если удалось улучшить положение.
7. Разместим частицы групп вокруг соответствующих центров с заданным распределением.
8. Добавим информацию из центров "чужих групп" в одну частицу каждой группы (частица получает набор координат из чужих групп, выбранных случайным образом).
9. Рассчитаем значения приспособленности частиц.
   
10. Повторим с п.4 до выполнения критерия останова.

* - В ESG я использовал степенной закон распределения для распространения частиц группы относительно центра, но в принципе, могут быть использованы и другие законы распределения, в том числе и их комбинации для отдельных частей логики стратегии. Поле открыто для экспериментов.

Переходим к рассмотрению кода. Для описания социальной группы напишем структуру "S_Group", которая содержит несколько переменных-членов:

• "cB" - это массив значений для хранения координат "центра".
• "fB" - значение фитнес-функции центра, инициализируется значением "-DBL_MAX".
• "sSize" - размер группы.
• "sRadius" - радиус группы.
  

Метод "Init" в структуре принимает два аргумента: "coords" - количество координат и "groupSize" - размер группы.

//——————————————————————————————————————————————————————————————————————————————
struct S_Group
{
  void Init (int coords, int groupSize)
  {
    ArrayResize (cB, coords);
    fB          = -DBL_MAX;
    sSize       = groupSize;
  }

  double cB [];
  double fB;
  int    sSize;
  double sRadius;
};
//——————————————————————————————————————————————————————————————————————————————

Для логики алгоритма ESG подойдёт простая структура, описывающая поискового агента. Я решил не включать структуру частиц-агентов в поля описания группы, каждая группа получит доступ к своим частицам в составе общей популяции, что позволит сохранить привычный уже доступ к агентам извне алгоритма и при этом позволит избежать излишнего копирования частиц групп в агенты.

Определение структуры "S_Agent" содержит две переменные:

• "c" - это массив значений координат агента.
• "f" - значение приспособленности агента, инициализируется значением "-DBL_MAX".
  

Метод "Init" принимает аргумент "coords" для изменения размера массива "c".

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (const int coords)
  {
    ArrayResize (c, coords);
    f = -DBL_MAX;
  }

  double c []; //coordinates
  double f;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

Определим класс "C_AO_ESG", который содержит несколько полей и методов:

1. Публичные поля:

• "cB" - массив значений лучших координат глобального решения.
• "fB" - значение пригодности (fitness) лучших координат.
• "a" - массив объектов типа "S_Agent", представляющих агентов.
• "rangeMax" - массив максимальных значений диапазона поиска.
• "rangeMin" - массив минимальных значений диапазона поиска.
•  "rangeStep" - массив значений шагов поиска.

2. Методы:

• "Init" - функция, используемая для инициализации переменных-членов класса. Принимает аргументы: количество координат, размер популяции, количество групп, начальный радиус группы, коэффициент расширения группы и степень распределения.
  
• "Moving" - метод отвечает за перемещение агентов.
• "Revision" - метод отвечает за ревизию агентов.
• "SeInDiSp" - метод для вычисления значений в диапазоне с заданным шагом.
• "RNDfromCI" - метод генерации случайных чисел в заданном интервале.
• "Scale" - метод для масштабирования значений из одного диапазона в другой.
• "PowerDistribution" - метод для генерации значений согласно степенному распределению.

3. Приватные поля:

• "coords" - количество координат.
• "popSize" - размер популяции.
• "gr" - массив объектов типа "S_Group", представляющих группы.
• "groups" - количество групп.
• "groupRadius" - радиус группы.
• "expansionRatio" - коэффициент расширения.
• "power" - степень.
•  "revision" - флаг, указывающий на необходимость ревизии.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ESG
{
  //----------------------------------------------------------------------------
  public: double  cB [];       //best coordinates
  public: double  fB;          //FF of the best coordinates
  public: S_Agent a  [];       //agents

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    groupsP,              //number of groups
                     const double groupRadiusP,         //group radius
                     const double expansionRatioP,      //expansion ratio
                     const double powerP);              //power

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int     coords;
  private: int     popSize;          //population size
  private: S_Group gr [];            //group

  private: int    groups;            //number of groups
  private: double groupRadius;       //group radius
  private: double expansionRatio;    //expansion ratio
  private: double power;             //power

  private: bool   revision;

  private: double SeInDiSp          (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI         (double min, double max);
  private: double Scale             (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
  private: double PowerDistribution (const double In, const double outMin, const double outMax, const double power);
};
//——————————————————————————————————————————————————————————————————————————————

Метод "Init" класса используется для инициализации переменных класса на основе переданных параметров. Помимо первоначальной инициализации переменных и задания размеров массивов метод вычисляет количество частиц в каждой группе в случае некратного значения количества групп размеру популяции.

Массив "partInSwarms" изменяется размером до "groups", где "groups" - количество групп. Затем переменной "particles" присваивается результат деления "popSize" на "groups", где "popSize" - размер популяции. Значения массива "partInSwarms" заполняются значением "particles", то есть количество без остатка. Затем вычисляется количество потерянных элементов ("lost") путем вычитания произведения "particles" и "groups" из "popSize". Если есть потерянные элементы ("lost > 0"), то они равномерно распределяются по группам в цикле while.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ESG::Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const int    groupsP,              //number of groups
                     const double groupRadiusP,         //group radius
                     const double expansionRatioP,      //expansion ratio
                     const double powerP)
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords         = coordinatesNumberP;
  popSize        = populationSizeP;
  groups         = groupsP;
  groupRadius    = groupRadiusP;
  expansionRatio = expansionRatioP;
  power          = powerP;

  //----------------------------------------------------------------------------
  int partInSwarms [];
  ArrayResize (partInSwarms, groups);

  int particles = popSize / groups;
  ArrayInitialize (partInSwarms, particles);

  int lost = popSize - particles * groups;

  if (lost > 0)
  {
    int pos = 0;

    while (true)
    {
      partInSwarms [pos]++;
      lost--;
      pos++;
      if (pos >= groups) pos = 0;
      if (lost == 0) break;
    }
  }

  //----------------------------------------------------------------------------
  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);

  ArrayResize (gr,        groups);
  for (int s = 0; s < groups; s++) gr [s].Init (coords, partInSwarms [s]);

  ArrayResize (a, popSize);
  for (int i = 0; i < popSize; i++) a [i].Init (coords);
}
//——————————————————————————————————————————————————————————————————————————————

Метод "Moving" используется для генерации центров и индивидуумов групп вначале оптимизации. Метод выполняет следующие действия:

• Генерация центров для каждой группы "s" во внешнем цикле "for". Для этого во вложенном цикле "for" генерируется случайное значение "coordinate" в заданном диапазоне для каждой координаты "c". Затем значение "coordinate" преобразуется в нужный диапазон и сохраняется в массиве "gr[s].cB[c]".

• Генерация индивидуумов для каждой группы "s" и каждого индивидуума "p" во внешнем цикле "for". Во вложенных циклах "for" вычисляется значение "radius" на основе заданных параметров и текущего состояния группы. Затем вычисляются значения "min" и "max" путем корректировки "radius" относительно границ диапазона. Затем генерируется случайное значение "coordinate" в заданном диапазоне с использованием функции "PowerDistribution". Полученное значение "coordinate" преобразуется и сохраняется в массиве "a[cnt].c[c]".

• Установка флага "revision" в значение "true" для обозначения выполнения генерации центров и индивидуумов.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ESG::Moving ()
{
  if (!revision)
  {
    int    cnt        = 0;
    double coordinate = 0.0;
    double radius     = 0.0;
    double min        = 0.0;
    double max        = 0.0;

    //generate centers----------------------------------------------------------
    for (int s = 0; s < groups; s++)
    {
      gr [s].sRadius = groupRadius;

      for (int c = 0; c < coords; c++)
      {
        coordinate    = RNDfromCI (rangeMin [c], rangeMax [c]);
        gr [s].cB [c] = SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    //generate individuals of groups--------------------------------------------
    for (int s = 0; s < groups; s++)
    {
      for (int p = 0; p < gr [s].sSize; p++)
      {
        for (int c = 0; c < coords; c++)
        {
          radius = (rangeMax [c] - rangeMin [c]) * gr [s].sRadius;
          min    = gr [s].cB [c] - radius;
          max    = gr [s].cB [c] + radius;

          if (min < rangeMin [c]) min = rangeMin [c];
          if (max > rangeMax [c]) max = rangeMax [c];

          coordinate    = PowerDistribution (gr [s].cB [c], min, max, power);
          a [cnt].c [c] = SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]);
        }

        cnt++;
      }
    }

    revision = true;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Основные действия по генерации новых частиц происходят в методе "Revision", который выполняет обновление лучшего глобального решения, генерацию новых индивидуумов групп и обмен опытом между группами посредством передачи информации от центров "чужих" групп одной частице. Таким образом только одной частице в группе позволено заимствовать опыт из других групп. Метод выполняет следующие действия:

• Обновление лучшего глобального решения. В цикле "for" проходим по всем индивидуумам и проверяем, если значение функции приспособленности текущего индивидуума превышает текущее лучшее значение функции приспособленности, то обновляется лучшее значение и копируется массив координат текущего индивидуума в массив координат лучшего решения.

• Генерация новых индивидуумов групп. В цикле "for" проходим по всем группам и их индивидуумам. Во вложенных циклах вычисляются значения радиуса, минимального и максимального значения координат для каждой группы. Затем генерируются случайные значения координат с использованием функции "PowerDistribution", и результат сохраняется в массиве координат индивидуумов.

• Обмен опытом между группами. В цикле "for" проходим по всем группам. Во вложенном цикле "for" генерируется случайное значение, которое определяет с какой группой будет производиться обмен опытом. Затем значения координат индивидуумов текущей группы обновляются значениями координат выбранной группы.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ESG::Revision ()
{
  //----------------------------------------------------------------------------
  //update the best global solution
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  int cnt = 0;
  bool impr = false;

  for (int s = 0; s < groups; s++)
  {
    impr = false;

    for (int p = 0; p < gr [s].sSize; p++)
    {
      if (a [cnt].f > gr [s].fB)
      {
        gr [s].fB = a [cnt].f;
        ArrayCopy (gr [s].cB, a [cnt].c, 0, 0, WHOLE_ARRAY);
        impr = true;
      }

      cnt++;
    }

    if (!impr) gr [s].sRadius *= expansionRatio;
    else       gr [s].sRadius  = groupRadius;

    if (gr [s].sRadius > 0.5) gr [s].sRadius = 0.5;
  }

  //generate individuals of groups----------------------------------------------
  double coordinate = 0.0;
  double radius     = 0.0;
  double min        = 0.0;
  double max        = 0.0;
  cnt = 0;

  for (int s = 0; s < groups; s++)
  {
    for (int p = 0; p < gr [s].sSize; p++)
    {
      for (int c = 0; c < coords; c++)
      {
        if (RNDfromCI (0.0, 1.0) < 1.0)
        {
        radius = (rangeMax [c] - rangeMin [c]) * gr [s].sRadius;
        min    = gr [s].cB [c] - radius;
        max    = gr [s].cB [c] + radius;

        if (min < rangeMin [c]) min = rangeMin [c];
        if (max > rangeMax [c]) max = rangeMax [c];

        coordinate    = PowerDistribution (gr [s].cB [c], min, max, power);
        a [cnt].c [c] = SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }

      cnt++;
    }
  }

  //exchange of experience----------------------------------------------------------------
  cnt = 0;

  for (int s = 0; s < groups; s++)
  {
    for (int c = 0; c < coords; c++)
    {
      int posSw = (int)RNDfromCI (0, groups);
      if (posSw >= groups) posSw = groups - 1;

      //if (sw [posSw].fB > sw [s].fB)
      {
        a [cnt].c [c] = gr [posSw].cB [c];
      }
    }

    cnt += gr [s].sSize;
  }
}
//——————————————————————————————————————————————————————————————————————————————

После написания основного алгоритма ESG, код которого представлен выше, возникла идея внести изменения и позволить частицам разных групп обмениваться информацией, чтобы повысить комбинаторные качества алгоритма. Для этого внесём изменения в структуру агента. Нам понадобятся дополнительные поля "cMain" - главные координаты и "fMain" - главный опыт.

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (const int coords)
  {
    ArrayResize (c,     coords);
    ArrayResize (cMain, coords);
    f     = -DBL_MAX;
    fMain = -DBL_MAX;
  }

  double c     []; //coordinates
  double cMain []; //coordinates
  double f;        //fitness
  double fMain;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

Далее, разница между двумя вариантами заключается в внесённых изменениях в метод "Revision"следующем:

1. В главной версии обмен опытом между агентами осуществляется на уровне групп. Во внутреннем цикле "for" выбирается случайная группа, и значение координаты текущего агента заменяется на значение координаты центра в выбранной группе. Таким образом, группы обмениваются опытом посредством передачи опыта только одной частице в соответствующей группе.

2. Во втором варианте обмен опытом между агентами осуществляется на уровне всей популяции, то есть, между частицами групп в случае, если выбранная для обмена частица имеет более высокую приспособленность. Таким образом опыт передать могут только лучшие худшим частицам между группами, причем лучший опыт, имеющийся у частицы. Во внутреннем цикле "for" выбирается случайный агент, и с некоторой вероятностью (определяемой значением "copyProb" значение координаты текущего агента заменяется на значение координаты выбранного агента в популяции.

Кроме того, во втором варианте есть дополнительный блок кода, который обновляет агентов. Если значение функции приспособленности текущего агента превышает его предыдущее лучшее значение (f > fMain), то значения координат текущего агента обновляются значениями его текущего лучшего решения (cMain). Это позволяет агентам сохранять и использовать свои лучшие решения в дальнейшем.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ESG::Revision ()
{
  //----------------------------------------------------------------------------
  //Update the best global solution
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  //update agents
  for (int p = 0; p < popSize; p++)
  {
    if (a [p].f > a [p].fMain)
    {
      a [p].fMain = a [p].f;
      ArrayCopy (a [p].cMain, a [p].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  int cnt = 0;
  bool impr = false;

  for (int s = 0; s < groups; s++)
  {
    impr = false;

    for (int p = 0; p < gr [s].sSize; p++)
    {
      if (a [cnt].f > gr [s].fB)
      {
        gr [s].fB = a [cnt].f;
        ArrayCopy (gr [s].cB, a [cnt].c, 0, 0, WHOLE_ARRAY);
        impr = true;
      }

      cnt++;
    }

    if (!impr) gr [s].sRadius *= expansionRatio;
    else       gr [s].sRadius  = groupRadius;

    if (gr [s].sRadius > 0.5) gr [s].sRadius = 0.5;
  }

  //generate individuals of groups----------------------------------------------
  double coordinate = 0.0;
  double radius     = 0.0;
  double min        = 0.0;
  double max        = 0.0;
  cnt = 0;

  for (int s = 0; s < groups; s++)
  {
    for (int p = 0; p < gr [s].sSize; p++)
    {
      for (int c = 0; c < coords; c++)
      {
        if (RNDfromCI (0.0, 1.0) < 0.6)
        {
        radius        = (rangeMax [c] - rangeMin [c]) * gr [s].sRadius;
        min           = gr [s].cB [c] - radius;
        max           = gr [s].cB [c] + radius;

        if (min < rangeMin [c]) min = rangeMin [c];
        if (max > rangeMax [c]) max = rangeMax [c];

        coordinate    = PowerDistribution (gr [s].cB [c], min, max, power);
        a [cnt].c [c] = SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }

      cnt++;
    }
  }

  //exchange of experience----------------------------------------------------------------
  cnt = 0;

  for (int p = 0; p < popSize; p++)
  {
    for (int c = 0; c < coords; c++)
    {
      int pos = (int)RNDfromCI (0, popSize);
      if (pos >= popSize) pos = popSize - 1;

      if (RNDfromCI(0.0, 1.0) < copyProb)
      {
        if (a [pos].fMain > a [p].fMain)
        {
          a [p].c [c] = a [pos].cMain [c];
        }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

В результате экспериментов и тестирования второй версии алгоритма, общий результат не принес ожидаемого прогресса и незначительно ухудшился. Это можно объяснить тем, что важно сохранять опыт частиц именно в границах собственных групп и не допускать полного смешивания идей между группами. Должен сохраняться уникальный опыт в каждой отдельной группе и при этом должно быть обеспечен только частичный обмен опытом.

Важно отметить, что неудачный результат эксперимента не является окончательным и не означает, что улучшение алгоритма невозможно. Это всего лишь одна из попыток, которая позволяет нам понять, на какие аспекты стоит обратить внимание и какие стратегии лучше применять. При дальнейшем исследовании и разработке можно использовать полученные знания для создания новых вариантов алгоритма, которые могут привести к значительному улучшению поисковых возможностей. Важно сохранять оптимизм и настойчивость в достижении поставленных целей. Результаты тестов представлены ниже.

3. Результаты тестов

Распечатка работы основного варианта алгоритма эволюции социальных групп ESG на тестовом стенде:

C_AO_ESG|200|100|0.1|2.0|10.0
=============================
5 Hilly's; Func runs: 10000; result: 0.9990564816911227
25 Hilly's; Func runs: 10000; result: 0.7965424362150277
500 Hilly's; Func runs: 10000; result: 0.35055904999599663
=============================
5 Forest's; Func runs: 10000; result: 1.0
25 Forest's; Func runs: 10000; result: 0.8286255415345216
500 Forest's; Func runs: 10000; result: 0.13102081222227177
=============================
5 Megacity's; Func runs: 10000; result: 0.8233333333333333
25 Megacity's; Func runs: 10000; result: 0.5529999999999999
500 Megacity's; Func runs: 10000; result: 0.04724999999999998
=============================
All score: 5.52939 (61.44%)

Распечатка работы варианта алгоритма эволюции социальных групп ESG с небольшой модификацией на тестовом стенде:

C_AO_MPSO|200|100|0.1|1.1|10.0|1.0
=============================
5 Hilly's; Func runs: 10000; result: 0.9986983861349696
25 Hilly's; Func runs: 10000; result: 0.7971379560351051
500 Hilly's; Func runs: 10000; result: 0.3351159723676586
=============================
5 Forest's; Func runs: 10000; result: 1.0
25 Forest's; Func runs: 10000; result: 0.8288612676775615
500 Forest's; Func runs: 10000; result: 0.11374411604788078
=============================
5 Megacity's; Func runs: 10000; result: 0.8333333333333333
25 Megacity's; Func runs: 10000; result: 0.5116666666666667
500 Megacity's; Func runs: 10000; result: 0.049316666666666654
=============================
All score: 5.46787 (60.75%)

На визуализации работы тестового стенда можно заметить хорошую сходимость основной версии алгоритма. На тестовых функциях "Hilly" и "Forest" заметен небольшой разброс в траекториях на графике сходимости. Однако на функции "Megacity" этот разброс является достаточно большим, хотя большинство алгоритмов на этой тестовой функции также показывают широкий разброс сходимости. Алгоритм "предпочитает", в отличие от большинства представленных ранее, размер популяции значительно больший - 200 (обычно используется 50), несмотря на то, что количество эпох при этом пропорционально сокращается. ESG хорошо прорабатывает локальные экстремумы, на это свойство оказывает влияние многопопуляционная "природа" алгоритма.

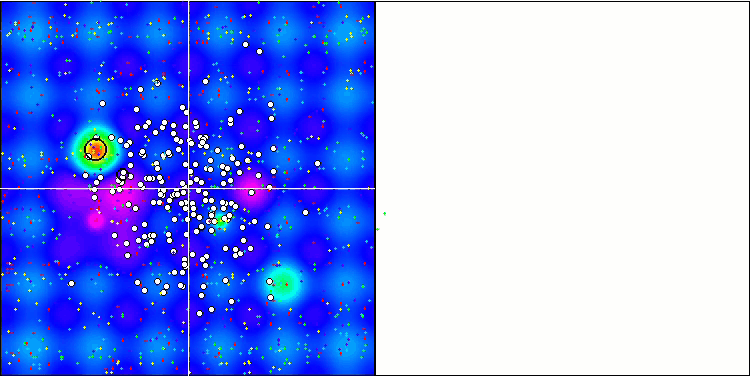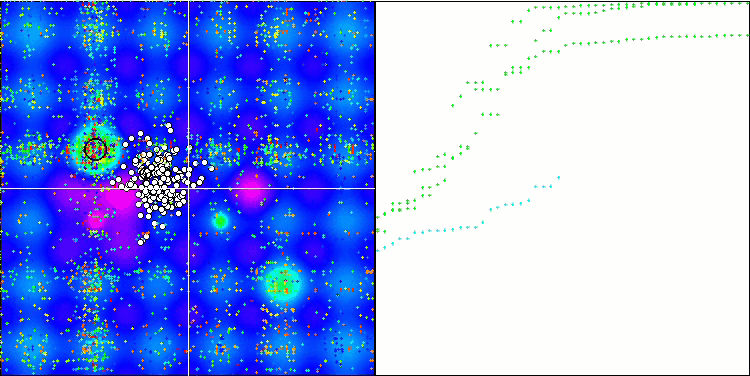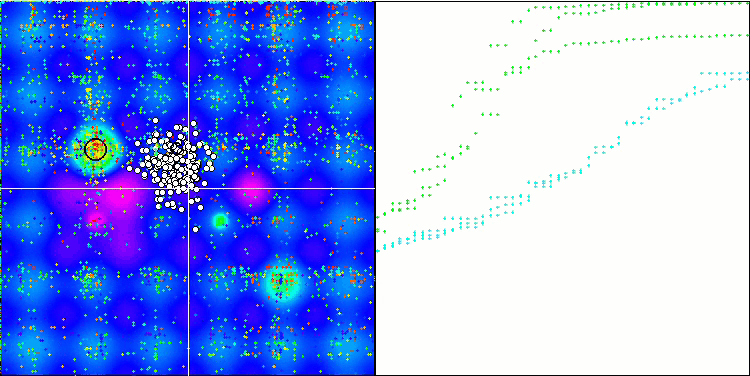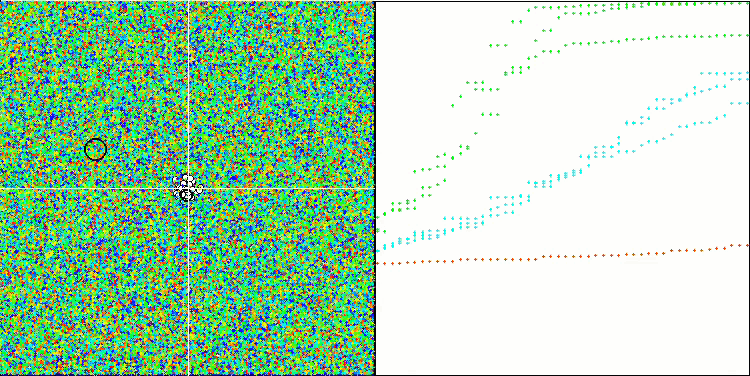
  ESG на тестовой функции Hilly.

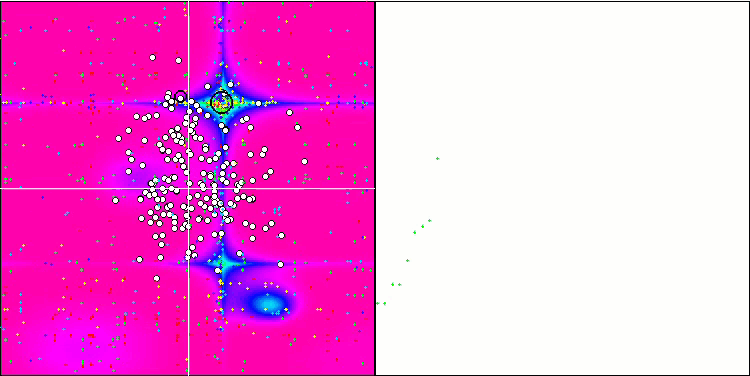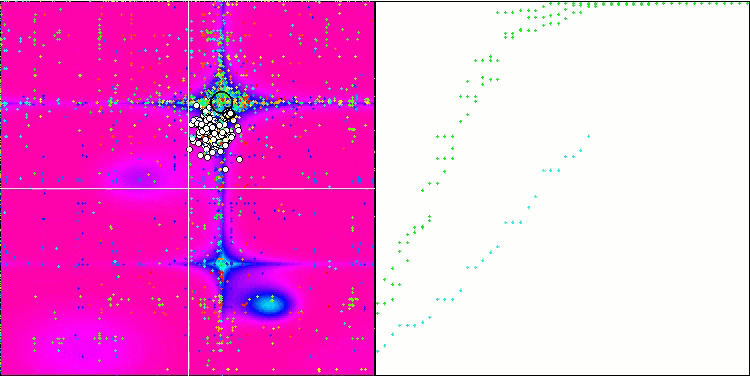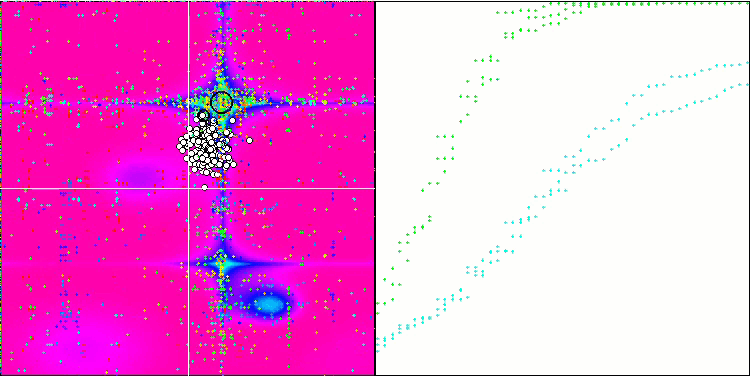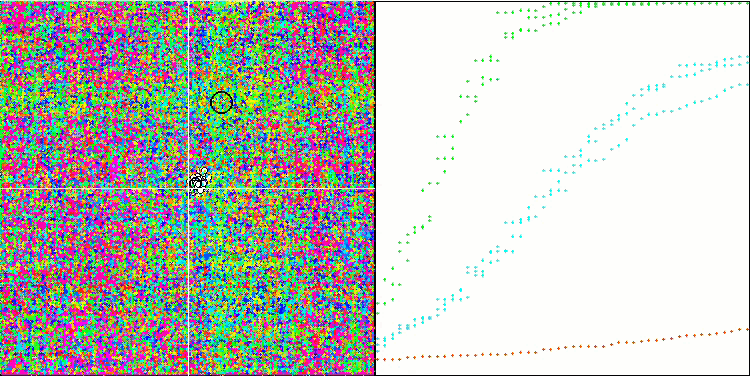
  ESG на тестовой функции Forest.

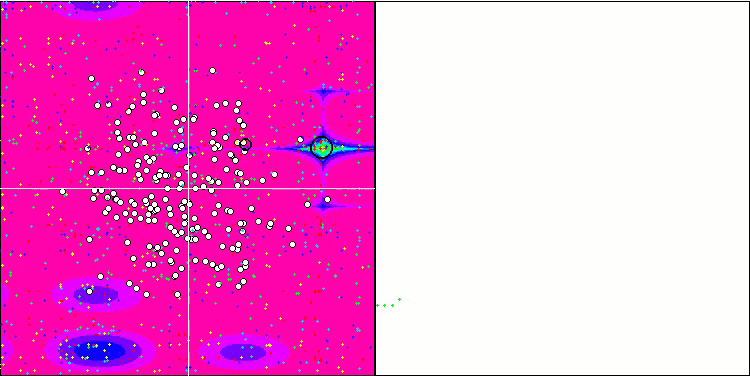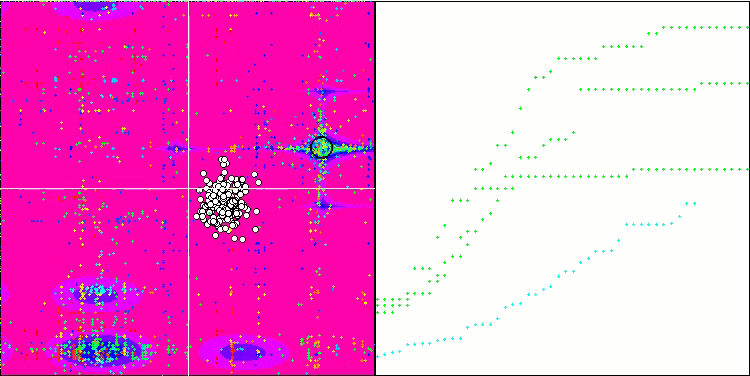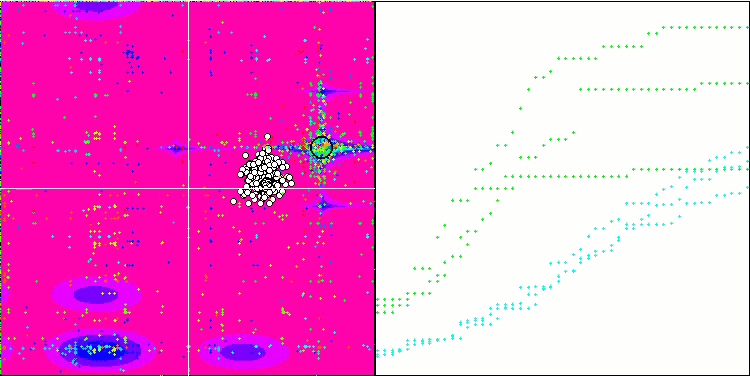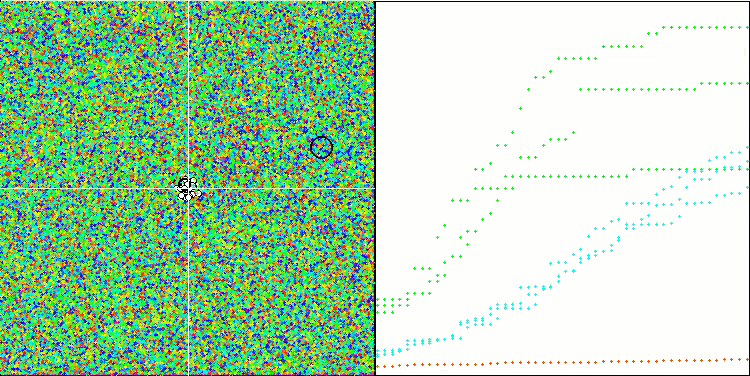
  ESG на тестовой функции Megacity.

Алгоритм ESG показал достойные результаты и оказался в числе лидеров рейтинговой таблицы. Можно отметить 100% сходимость на функции "Forest" с 10 параметрами и практически полную, 99.9% сходимость на функции "Hilly" с 10 параметрами. В таблицу внесены результаты основной версии алгоритма, а экспериментальная версия находится в папке "variant2".

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	BGA	binary genetic algorithm	0,99992	0,99484	0,50483	2,49959	1,00000	0,99975	0,32054	2,32029	0,90667	0,96400	0,23035	2,10102	6,921	76,90
2	(P+O)ES	(P+O) evolution strategies	0,99934	0,91895	0,56297	2,48127	1,00000	0,93522	0,39179	2,32701	0,83167	0,64433	0,21155	1,68755	6,496	72,18
3	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
4	ESG	evolution of social groups	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
5	SIA	simulated isotropic annealing	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
6	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
7	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
8	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
9	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
10	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
11	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
12	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
13	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
14	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
15	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
16	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
17	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
18	FAm	firefly algorithm M	0,58634	0,47228	0,32276	1,38138	0,68467	0,37439	0,10908	1,16814	0,28667	0,16467	0,04722	0,49855	3,048	33,87
19	GSA	gravitational search algorithm	0,64757	0,49197	0,30062	1,44016	0,53962	0,36353	0,09945	1,00260	0,32667	0,12200	0,01917	0,46783	2,911	32,34
20	BFO	bacterial foraging optimization	0,61171	0,43270	0,31318	1,35759	0,54410	0,21511	0,05676	0,81597	0,42167	0,13800	0,03195	0,59162	2,765	30,72
21	ABC	artificial bee colony	0,63377	0,42402	0,30892	1,36671	0,55103	0,21874	0,05623	0,82600	0,34000	0,14200	0,03102	0,51302	2,706	30,06
22	BA	bat algorithm	0,59761	0,45911	0,35242	1,40915	0,40321	0,19313	0,07175	0,66810	0,21000	0,10100	0,03517	0,34617	2,423	26,93
23	SA	simulated annealing	0,55787	0,42177	0,31549	1,29513	0,34998	0,15259	0,05023	0,55280	0,31167	0,10033	0,02883	0,44083	2,289	25,43
24	IWDm	intelligent water drops M	0,54501	0,37897	0,30124	1,22522	0,46104	0,14704	0,04369	0,65177	0,25833	0,09700	0,02308	0,37842	2,255	25,06
25	PSO	particle swarm optimisation	0,59726	0,36923	0,29928	1,26577	0,37237	0,16324	0,07010	0,60572	0,25667	0,08000	0,02157	0,35823	2,230	24,77
26	MA	monkey algorithm	0,59107	0,42681	0,31816	1,33604	0,31138	0,14069	0,06612	0,51819	0,22833	0,08567	0,02790	0,34190	2,196	24,40
27	SFL	shuffled frog-leaping	0,53925	0,35816	0,29809	1,19551	0,37141	0,11427	0,04051	0,52618	0,27167	0,08667	0,02402	0,38235	2,104	23,38
28	FSS	fish school search	0,55669	0,39992	0,31172	1,26833	0,31009	0,11889	0,04569	0,47467	0,21167	0,07633	0,02488	0,31288	2,056	22,84
29	RND	random	0,52033	0,36068	0,30133	1,18234	0,31335	0,11787	0,04354	0,47476	0,25333	0,07933	0,02382	0,35648	2,014	22,37
30	GWO	grey wolf optimizer	0,59169	0,36561	0,29595	1,25326	0,24499	0,09047	0,03612	0,37158	0,27667	0,08567	0,02170	0,38403	2,009	22,32
31	CSS	charged system search	0,44252	0,35454	0,35201	1,14907	0,24140	0,11345	0,06814	0,42299	0,18333	0,06300	0,02322	0,26955	1,842	20,46
32	EM	electroMagnetism-like algorithm	0,46250	0,34594	0,32285	1,13129	0,21245	0,09783	0,10057	0,41085	0,15667	0,06033	0,02712	0,24412	1,786	19,85

Выводы

В заключение, алгоритм эволюции социальных групп представляет собой эффективный метод оптимизации, основанный на сотрудничестве и обмене опытом между группами. Он обладает свойствами адаптивности, разнообразия и способен находить оптимальные решения в различных задачах оптимизации.

Алгоритм ESG могу рекомендовать для применения в различных областях, где требуется оптимизация параметров. Например, он может использоваться для настройки гиперпараметров в машинном обучении, оптимизации функций в задачах оптимального управления, решении задач комбинаторной оптимизации и других задач, где требуется нахождение оптимальных значений параметров.

Представленный алгоритм можно рассматривать как своеобразный шаблон, который может быть дополнен различными отдельными приемами и стратегиями поиска, описанными в предыдущих статьях. Кроме того, каждая группа может использовать отдельные алгоритмы оптимизации, такие как PSO, ABC, ACO и др. Таким образом, архитектура алгоритма ESG обеспечивает простоту внедрения таких методов оптимизации и совместное их использование, объединяя преимущества каждого алгоритма в отдельности.

Важно подчеркнуть, что ESG является самостоятельным самодостаточным решением с хорошими результатами и представляет собой чрезвычайно гибкий подход к решению сложных задач. Его потенциал может быть полностью раскрыт с помощью экспериментов и развития основной идеи и возможности для проведения таких экспериментов открыты для всех желающих.

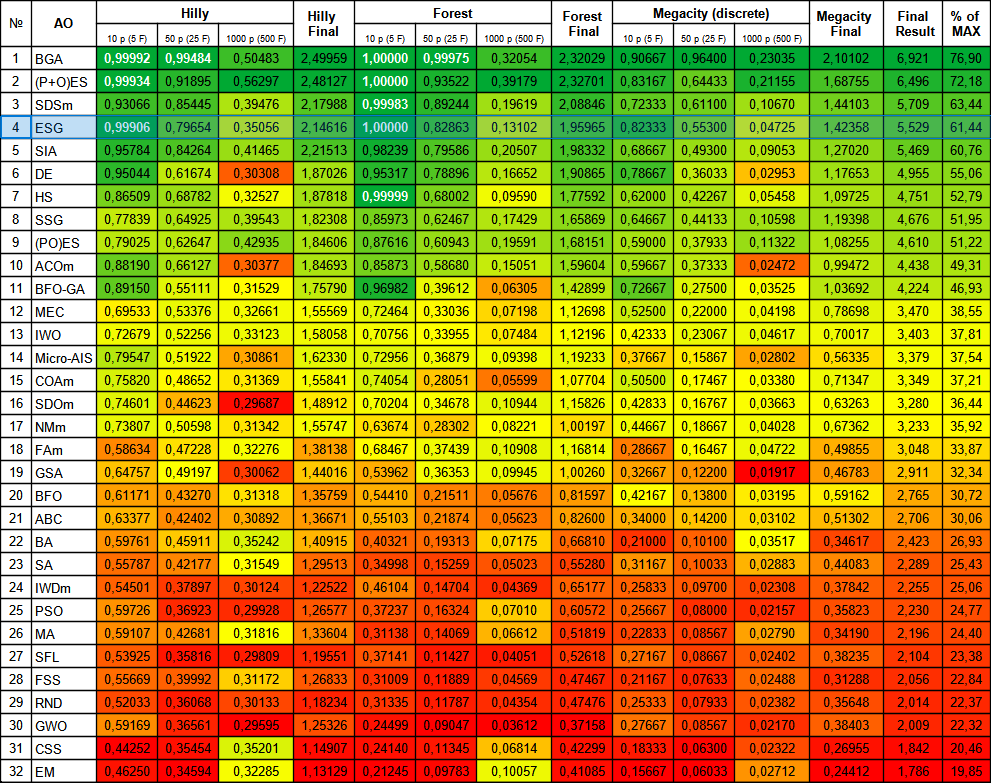
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам. Белым цветом подсвечены результаты больше или равные 0.99.

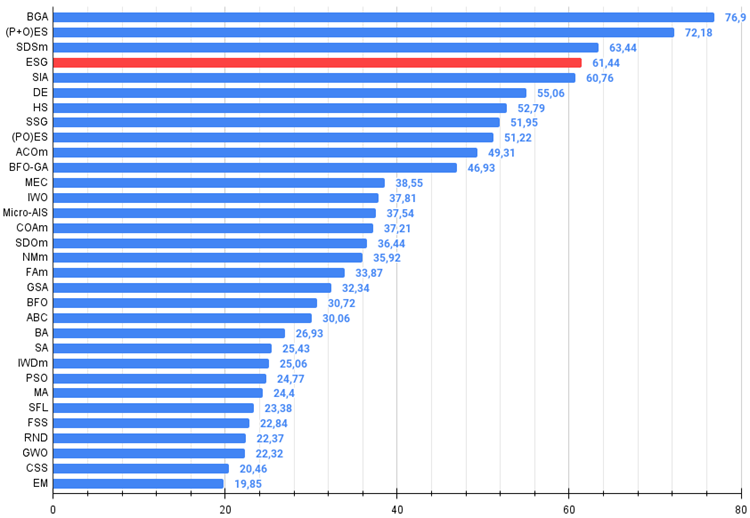
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше,

где 100 - максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы).

Плюсы и минусы алгоритма эволюции социальных групп (ESG):

Плюсы:

1. Простая архитектура.
   
2. Высокая сходимость.
3. Не требователен к вычислительным ресурсам.

Минусы:

1. Невысокие результаты на функциях с большим количеством параметров.
   

К статье прикреплен архив с обновленными актуальными версиями кодов алгоритмов, описанных в предыдущих статьях. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.