
Neuronale Netzwerke leicht gemacht (Teil 13): Batch-Normalisierung
Inhalt
- Einführung
- 1. Theoretische Voraussetzungen für die Normalisierung
- 2. Umsetzung
- 2.1. Erstellen einer neuen Klasse für unser Modell
- 2.2. Vorwärtsdurchlauf
- 2.3. Rückwärtsdurchlauf
- 2.4. Änderungen in den Basisklassen des neuronalen Netzwerks
- 3. Tests
- Schlussfolgerung
- Referenzen
- Die Programme dieses Artikels
Einführung
Im vorigen Artikel haben wir begonnen, Methoden zur Erhöhung der Konvergenz von neuronalen Netzen zu betrachten und haben die Dropout-Methode kennengelernt, die zur Reduzierung der Koadaptation von Features verwendet wird. Lassen Sie uns dieses Thema fortsetzen und sich mit den Methoden der Normalisierung vertraut machen.
1. Theoretische Voraussetzungen für die Normalisierung
In der Anwendungspraxis von neuronalen Netzwerken werden verschiedene Ansätze zur Normalisierung von Daten verwendet. Sie zielen jedoch alle darauf ab, die Daten der Trainingsstichprobe und die Ausgabe der versteckten Schichten des neuronalen Netzes innerhalb eines bestimmten Bereichs und mit bestimmten statistischen Merkmalen der Stichprobe, wie z. B. Varianz und Median, zu halten. Dies ist wichtig, weil die Neuronen des Netzes lineare Transformationen verwenden, die im Laufe des Trainings die Stichprobe in Richtung des Antigradienten verschieben.
Betrachten Sie ein vollständig verbundenes Perzeptron mit zwei versteckten Schichten. Während eines Vorwärtsdurchlaufs (feed-forward) erzeugt jede Schicht einen bestimmten Datensatz, der als Trainingsmuster für die nächste Schicht dient. Das Ergebnis der Ausgabeschicht wird mit den Referenzdaten verglichen. Dann wird während des Rückwärtsdurchlaufs (feed-backward) der Fehlergradient von der Ausgabeschicht durch die versteckten Schichten in Richtung der Ausgangsdaten propagiert. Nachdem wir an jedem Neuron einen Fehlergradienten erhalten haben, aktualisieren wir die Gewichtskoeffizienten und passen das neuronale Netz an die Trainingsmuster des letzten Vorwärtsdurchlaufs an. Hier entsteht ein Konflikt: die zweite versteckte Schicht (H2 in der Abbildung unten) wird an die Datenprobe am Ausgang der ersten versteckten Schicht (H1 in der Abbildung) angepasst, während wir durch die Änderung der Parameter der ersten versteckten Schicht bereits das Datenfeld geändert haben. Mit anderen Worten, wir passen die zweite versteckte Schicht an die Datenprobe an, die nicht mehr existiert. Ähnlich verhält es sich mit der Ausgabeschicht, die sich an die bereits geänderte Ausgabe der zweiten versteckten Schicht anpasst. Die Fehlerskala wird noch größer, wenn wir die Verzerrung zwischen der ersten und der zweiten versteckten Schicht berücksichtigen. Je tiefer das neuronale Netz ist, desto stärker ist der Effekt. Dieses Phänomen wird als interne Kovariatenverschiebung bezeichnet.
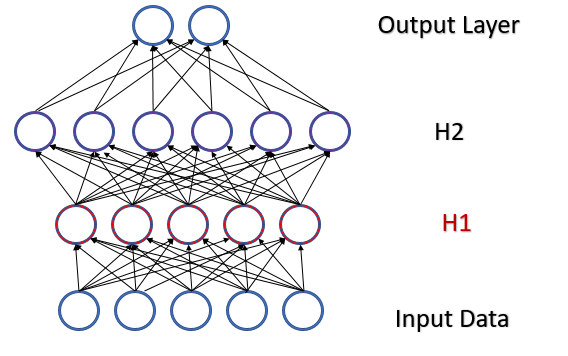
Klassische neuronale Netze lösen dieses Problem teilweise, indem sie die Lernrate reduzieren. Geringfügige Änderungen in den Gewichten haben keine signifikanten Änderungen in der Probenverteilung am Ausgang der neuronalen Schicht zur Folge. Aber dieser Ansatz löst nicht das Skalierungsproblem, das mit zunehmender Anzahl von Schichten des neuronalen Netzes auftritt, und er verringert auch die Lerngeschwindigkeit. Ein weiteres Problem einer kleinen Lernrate ist, dass der Prozess an lokalen Minima hängen bleiben kann, was wir bereits in Artikel 6 diskutiert haben.
Im Februar 2015 haben Sergey Ioffe und Christian Szegedy die Batch-Normalisierung als Lösung für das Problem der internen Kovarianzverschiebung vorgeschlagen [13]. Die Idee der Methode ist es, jedes einzelne Neuron in einem bestimmten Zeitintervall mit einer Verschiebung des Medians der Stichprobe (Batch) gegen Null zu normalisieren und die Stichprobenvarianz auf 1 zu bringen.
Der Algorithmus zur Normalisierung sieht wie folgt aus. Zunächst wird der Durchschnittswert für die Datenstichprobe berechnet.
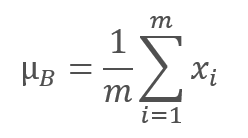
dabei ist m die Stichprobengröße.
Dann wird die Varianz der ursprünglichen Stichprobe berechnet.
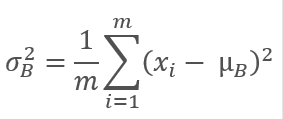
Die Daten der Stichprobe werden normalisiert, um die Stichprobe auf den Mittelwert von Null und die Varianz von 1 zu bringen.
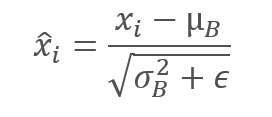
Beachten Sie, dass die Konstante ϵ, eine kleine positive Zahl, zur Varianz der Stichprobe im Nenner addiert wird, um eine Division durch Null zu vermeiden.
Es stellte sich jedoch heraus, dass eine solche Normalisierung den Einfluss der Originaldaten verfälschen kann. Daher haben die Autoren der Methode einen weiteren Schritt hinzugefügt: Skalierung und Verschiebung. Sie haben zwei Variablen, γ und β, eingeführt, die zusammen mit dem neuronalen Netz durch die Gradientenabstiegsmethode trainiert werden.
![]()
Die Anwendung dieser Methode ermöglicht es, einen Datenstapel mit der gleichen Verteilung bei jedem Trainingsschritt zu erhalten, was das Training des neuronalen Netzes stabiler macht und eine Erhöhung der Lernrate ermöglicht. Im Allgemeinen trägt diese Methode dazu bei, die Qualität des Trainings zu verbessern und gleichzeitig die Zeit für das Training des neuronalen Netzwerks zu reduzieren.
Dies erhöht jedoch die Kosten für die Speicherung zusätzlicher Koeffizienten. Außerdem sollten für die Berechnung des Mittelwerts und der Streuung historische Daten jedes Neurons für die gesamte Losgröße gespeichert werden. Hier können wir die Anwendung des exponentiellen Mittelwerts überprüfen. Die folgende Abbildung zeigt die Graphen des gleitenden Mittelwerts und der gleitenden Varianz für 100 Elemente im Vergleich mit dem exponentiellen gleitenden Mittelwert und der exponentiellen gleitenden Varianz für die gleichen 100 Elemente. Das Diagramm ist für 1000 Zufallselemente im Bereich zwischen -1,0 und 1,0 erstellt.
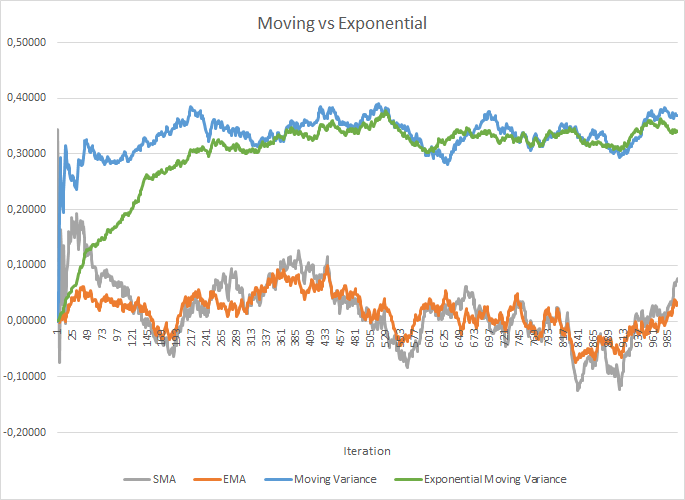
In diesem Diagramm nähern sich der gleitende Durchschnitt und der exponentiell gleitende Durchschnitt nach 120-130 Iterationen an und dann ist die Abweichung minimal (so dass sie vernachlässigt werden kann). Außerdem ist der Graph des exponentiellen gleitenden Durchschnitts glatter. Der EMA kann berechnet werden, wenn man den vorherigen Wert der Funktion und das aktuelle Element der Sequenz kennt. Sehen wir uns die Formel für den exponentiellen gleitenden Durchschnitt an:
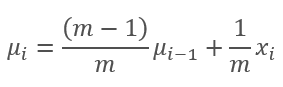 ,
,
wobei
- m ist die Losgröße,
- i ist eine Iteration.
Es waren etwas mehr Iterationen nötig (310-320), um die Graphen der gleitenden Varianz und der exponentiell gleitenden Varianz einander anzunähern, aber das Gesamtbild ist ähnlich. Im Fall der Varianz spart die Verwendung des exponentiellen Algorithmus nicht nur Speicher, sondern reduziert auch die Anzahl der Berechnungen erheblich, da bei der gleitenden Varianz die Abweichung vom Durchschnitt für die gesamte Charge berechnet würde.
Die von den Autoren der Methode durchgeführten Experimente zeigen, dass die Verwendung der Batch-Normalisierungsmethode auch als Regularisierung dient. Dies reduziert den Bedarf an anderen Regularisierungsmethoden, einschließlich des zuvor betrachteten Dropouts. Darüber hinaus zeigen nachfolgende Untersuchungen, dass die kombinierte Verwendung von Dropout und Batch-Normalisierung einen negativen Effekt auf die Lernergebnisse des neuronalen Netzes hat.
Der vorgeschlagene Algorithmus zur Normalisierung ist in verschiedenen Variationen in modernen neuronalen Netzwerkarchitekturen zu finden. Die Autoren schlagen vor, die Batch-Normalisierung unmittelbar vor der Nichtlinearität (Aktivierungsformel) zu verwenden. Die im Juli 2016 vorgestellte Methode der Layer-Normalisierung kann als eine der Variationen dieses Algorithmus besprochen werden. Wir haben diese Methode bereits bei der Untersuchung des Aufmerksamkeitsmechanismus berücksichtigt (Artikel 9).
2. Umsetzung
2.1 Erstellen einer neuen Klasse für unser Modell
Nachdem wir nun die theoretischen Aspekte betrachtet haben, wollen wir ihn in unserer Bibliothek implementieren. Erstellen wir eine neue Klasse CNeuronBatchNormOCL, um den Algorithmus zu implementieren.
class CNeuronBatchNormOCL : public CNeuronBaseOCL { protected: CNeuronBaseOCL *PrevLayer; ///< Pointer to the object of the previous layer uint iBatchSize; ///< Batch size CBufferDouble *BatchOptions; ///< Container of method parameters ///\ingroup neuron_base_ff virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); ///< \brief Feed Forward method of calling kernel ::BatchFeedForward().@param NeuronOCL Pointer to previous layer. ///\ingroup neuron_base_opt virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); ///< Method for updating weights.\details Calling one of kernels ::UpdateBatchOptionsMomentum() or ::UpdateBatchOptionsAdam() in depends on optimization type (#ENUM_OPTIMIZATION).@param NeuronOCL Pointer to previous layer. public: /** Constructor */CNeuronBatchNormOCL(void); /** Destructor */~CNeuronBatchNormOCL(void); //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, uint batchSize, ENUM_OPTIMIZATION optimization_type); ///< Method of initialization class.@param[in] numOutputs Number of connections to next layer.@param[in] myIndex Index of neuron in layer.@param[in] open_cl Pointer to #COpenCLMy object. #param[in] numNeurons Number of neurons in layer @param optimization_type Optimization type (#ENUM_OPTIMIZATION)@return Boolen result of operations. //--- virtual int getOutputIndex(void) { return (iBatchSize>1 ? Output.GetIndex() : PrevLayer.getOutputIndex()); } ///< Get index of output buffer @return Index virtual int getGradientIndex(void) { return (iBatchSize>1 ? Gradient.GetIndex() : PrevLayer.getGradientIndex()); } ///< Get index of gradient buffer @return Index //--- virtual int getOutputVal(double &values[]) { return (iBatchSize>1 ? Output.GetData(values) : PrevLayer.getOutputVal(values)); } ///< Get values of output buffer @param[out] values Array of data @return number of items virtual int getOutputVal(CArrayDouble *values) { return (iBatchSize>1 ? Output.GetData(values) : PrevLayer.getOutputVal(values)); } ///< Get values of output buffer @param[out] values Array of data @return number of items virtual int getGradient(double &values[]) { return (iBatchSize>1 ? Gradient.GetData(values) : PrevLayer.getGradient(values)); } ///< Get values of gradient buffer @param[out] values Array of data @return number of items virtual CBufferDouble *getOutput(void) { return (iBatchSize>1 ? Output : PrevLayer.getOutput()); } ///< Get pointer of output buffer @return Pointer to object virtual CBufferDouble *getGradient(void) { return (iBatchSize>1 ? Gradient : PrevLayer.getGradient()); } ///< Get pointer of gradient buffer @return Pointer to object //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); ///< Method to transfer gradient to previous layer by calling kernel ::CalcHiddenGradientBatch(). @param NeuronOCL Pointer to next layer. //--- virtual bool Save(int const file_handle);///< Save method @param[in] file_handle handle of file @return logical result of operation virtual bool Load(int const file_handle);///< Load method @param[in] file_handle handle of file @return logical result of operation //--- virtual int Type(void) const { return defNeuronBatchNormOCL; }///< Identificator of class.@return Type of class };
Die neue Klasse wird von der Basisklasse CNeuronBaseOCL abgeleitet. In Analogie zur Klasse CNeuronDropoutOCL fügen wir die Variable PrevLayer hinzu. Die im vorherigen Artikel demonstrierte Methode zur Ersetzung des Datenpuffers wird angewendet, wenn die Stichprobengröße kleiner als "2" ist, was in der Variablen iBatchSize gespeichert wird.
Der Algorithmus der Batch-Normalisierung erfordert die Speicherung einiger Parameter, die für jedes Neuron der normalisierten Schicht individuell sind. Um nicht viele separate Puffer für jeden einzelnen Parameter zu erzeugen, wird ein einziger BatchOptions-Puffer mit Parametern der folgenden Struktur erstellt.

Aus der vorgestellten Struktur ist ersichtlich, dass die Größe des Parameterpuffers von der angewandten Methode der Parameteroptimierung abhängt und daher in der Klasseninitialisierungsmethode erstellt wird.
Eine Reihe von Klassenmethoden ist bereits Standard. Schauen wir sie uns an. Im Klassenkonstruktor setzen wir die Zeiger auf Objekte zurück und setzen die Stichprobengröße auf eins, was die Schicht bis zur Initialisierung praktisch vom Netzbetrieb ausschließt.
CNeuronBatchNormOCL::CNeuronBatchNormOCL(void) : iBatchSize(1) { PrevLayer=NULL; BatchOptions=NULL; }
Wir löschen im Destruktor der Klasse das Objekt des Parameterpuffers und setzen den Zeiger auf die vorherige Ebene auf Null. Bitte beachten Sie, dass wir nicht das Objekt der vorherigen Ebene löschen, sondern nur den Zeiger auf Null setzen. Das Objekt wird dort gelöscht, wo es erzeugt wurde.
CNeuronBatchNormOCL::~CNeuronBatchNormOCL(void) { if(CheckPointer(PrevLayer)!=POINTER_INVALID) PrevLayer=NULL; if(CheckPointer(BatchOptions)!=POINTER_INVALID) delete BatchOptions; }
Betrachten wir nun die Klasseninitialisierungsmethode CNeuronBatchNormOCL::Init. Wir übergeben der Klasse in den Parametern die Anzahl der Neuronen der nächsten Schicht, einen Index zur Identifikation des Neurons, einen Zeiger auf das OpenCL-Objekt, die Anzahl der Neuronen in der Normalisierungsschicht, die Stichprobe und die Methode der Parameteroptimierung.
Am Anfang der Methode rufen wir dann die entsprechende Methode der Elternklasse auf, in der die Basisvariablen und Datenpuffer initialisiert werden. Dann speichern wir die Stichprobe und setzen die Aktivierungsfunktion der Schicht auf None.
Achten Sie bitte auf die Aktivierungsfunktion. Die Verwendung dieser Funktion hängt von der Architektur des neuronalen Netzes ab. Wenn die Architektur des neuronalen Netzes die Einbeziehung der Normalisierung vor der Aktivierungsfunktion erfordert, wie von den Autoren der Methode empfohlen, dann muss die Aktivierungsfunktion auf der vorhergehenden Schicht deaktiviert und die gewünschte Funktion in der Normalisierungsschicht angegeben werden. Technisch gesehen wird die Aktivierungsfunktion durch den Aufruf der Methode SetActivationFunction der Elternklasse, nach der Initialisierung einer Klasseninstanz, festgelegt. Wenn die Normalisierung entsprechend der Netzarchitektur nach der Aktivierungsfunktion verwendet werden soll, sollte die Aktivierungsmethode in der vorherigen Schicht angegeben werden und es wird keine Aktivierungsfunktion in der Normalisierungsschicht vorhanden sein.
bool CNeuronBatchNormOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint numNeurons,uint batchSize,ENUM_OPTIMIZATION optimization_type) { if(!CNeuronBaseOCL::Init(numOutputs,myIndex,open_cl,numNeurons,optimization_type)) return false; activation=None; iBatchSize=batchSize; //--- if(CheckPointer(BatchOptions)!=POINTER_INVALID) delete BatchOptions; int count=(int)numNeurons*(optimization_type==SGD ? 7 : 9); BatchOptions=new CBufferDouble(); if(CheckPointer(BatchOptions)==POINTER_INVALID || !BatchOptions.BufferInit(count,0)) return false; //--- return true; }
Am Ende der Methode legen wir einen Puffer mit Parametern an. Wie oben erwähnt, hängt die Puffergröße von der Anzahl der Neuronen in der Schicht und der Methode der Parameteroptimierung ab. Bei der Verwendung von SGD reservieren wir 7 Elemente für jedes Neuron; bei der Optimierung nach der Adam-Methode benötigen wir 9 Pufferelemente für jedes Neuron. Nach erfolgreichem Anlegen aller Puffer verlassen Sie die Methode mit true.
Der gesamte Code aller Klassen und Methoden befindet sich in der Anlage.
2.2. Vorwärtsdurchlauf
Als nächsten Schritt wollen wir den Vorwärtsdurchlauf betrachten. Beginnen wir mit der Betrachtung des direkten Durchgangs BatchFeedForward. Der Kernel-Algorithmus wird für jedes einzelne Neuron gestartet.
Der Kernel erhält in Parametern Zeiger auf 3 Puffer: Anfangsdaten, Puffer der Parameter und einen Puffer zum Schreiben der Ergebnisse. Zusätzlich werden in Parametern die Stichprobe, die Optimierungsmethode und der Neuronenaktivierungsalgorithmus übergeben.
Überprüfen wir zu Beginn des Kernels die angegebene Größe des Fensters für die Normalisierung. Wenn die Normalisierung für ein Neuron durchgeführt wurde, beenden wir die Methode ohne weitere Operationen.
Nach erfolgreicher Überprüfung erhalten wir den Stream-Identifier, der die Position des normalisierten Wertes im Eingangsdatentensor angibt. Anhand des Bezeichners können wir die Verschiebung für den ersten Parameter im Tensor der Normalisierungsparameter bestimmen. In diesem Schritt wird die Optimierungsmethode die Struktur des Parameterpuffers vorschlagen.
Als Nächstes berechnen wir in diesem Schritt den exponentiellen Mittelwert und die Varianz. Anhand dieser Daten berechnen wir den normalisierten Wert für unser Element.
Der nächste Schritt des Algorithmus der Stichprobennormalisierung ist die Verschiebung und Skalierung. Zuvor haben wir bei der Initialisierung den Parameterpuffer mit Nullen gefüllt, so dass wir, wenn wir diese Operation "in Reinform" im ersten Schritt durchführen, "0" erhalten. Um dies zu vermeiden, prüfen wir den aktuellen Wert des γ-Parameters und, ändern wenn er gleich "0" ist, ändern seinen Wert auf "1". Belassen wir die Verschiebung bei Null. Wir führen die Verschiebung und Skalierung in dieser Form durch.
__kernel void BatchFeedForward(__global double *inputs, __global double *options, __global double *output, int batch int optimization, int activation) { if(batch<=1) return; int n=get_global_id(0); int shift=n*(optimization==0 ? 7 : 9); //--- for(int i=0;i<(optimization==0 ? 7 : 9);i++) if(isnan(options[shift+i])) options[shift+i]=0; //--- double mean=(options[shift]*((double)batch-1)+inputs[n])/((double)batch); double delt=inputs[n]-mean; double variance=options[shift+1]*((double)batch-1.0)+pow(delt,2); if(options[shift+1]>0) variance/=(double)batch; double nx=delt/sqrt(variance+1e-6); //--- if(options[shift+3]==0) options[shift+3]=1; //--- double res=options[shift+3]*nx+options[shift+4]; switch(activation) { case 0: res=tanh(clamp(res,-20.0,20.0)); break; case 1: res=1/(1+exp(-clamp(res,-20.0,20.0))); break; case 2: if(res<0) res*=0.01; break; default: break; } //--- options[shift]=mean; options[shift+1]=variance; options[shift+2]=nx; output[n]=res; }
Nachdem wir den normalisierten Wert erhalten haben, prüfen wir, ob wir die Aktivierungsfunktion auf dieser Schicht ausführen müssen und führen die notwendigen Aktionen durch.
Speichern wir nun einfach die neuen Werte in den Datenpuffern und verlassen den Kernel.
Der Algorithmus zur Erstellung des BatchFeedForward-Kernels ist recht einfach und so können wir dazu übergehen, eine Methode zum Aufruf des Kernels aus dem Hauptprogramm zu erstellen. Diese Funktionsweise wird durch die Methode CNeuronBatchNormOCL::feedForward implementiert. Der Algorithmus der Methode ist ähnlich wie bei den entsprechenden Methoden der anderen Klassen. Die Methode erhält als Parameter einen Zeiger auf die vorherige Schicht des neuronalen Netzes.
Am Anfang der Methode wird die Gültigkeit des empfangenen Zeigers und des Zeigers auf das OpenCL-Objekt geprüft (wie Sie sich vielleicht erinnern, handelt es sich um eine Kopie einer Klasse der Standardbibliothek für die Arbeit mit dem OpenCL-Programm).
Im nächsten Schritt speichern wir den Zeiger auf die vorherige Schicht des neuronalen Netzes und überprüfen die Stichprobe. Wenn die Größe des Normalisierungsfensters nicht größer als "1" ist, kopieren wir den Typ der Aktivierungsfunktion der vorherigen Schicht und verlassen die Methode mit dem Ergebnis true. Auf diese Weise liefern wir Daten zum Ersetzen von Puffern und schließen unnötige Iterationen des Algorithmus aus.
bool CNeuronBatchNormOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- PrevLayer=NeuronOCL; if(iBatchSize<=1) { activation=(ENUM_ACTIVATION)NeuronOCL.Activation(); return true; } //--- if(CheckPointer(BatchOptions)==POINTER_INVALID) { int count=Neurons()*(optimization==SGD ? 7 : 9); BatchOptions=new CBufferDouble(); if(!BatchOptions.BufferInit(count,0)) return false; } if(!BatchOptions.BufferCreate(OpenCL)) return false; //--- uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=Neurons(); if(!OpenCL.SetArgumentBuffer(def_k_BatchFeedForward,def_k_bff_inputs,NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_BatchFeedForward,def_k_bff_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_BatchFeedForward,def_k_bff_output,Output.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_BatchFeedForward,def_k_bff_batch,iBatchSize)) return false; if(!OpenCL.SetArgument(def_k_BatchFeedForward,def_k_bff_optimization,(int)optimization)) return false; if(!OpenCL.SetArgument(def_k_BatchFeedForward,def_k_bff_activation,(int)activation)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_BatchFeedForward,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Batch Feed Forward: %d",GetLastError()); return false; } if(!Output.BufferRead() || !BatchOptions.BufferRead()) return false; BatchOptions.BufferFree(); //--- return true; }
Wenn wir nach allen Prüfungen den Start des Direktpass-Kerns erreicht haben, müssen wir die Anfangsdaten für den Start vorbereiten. Überprüfen wir zunächst die Gültigkeit des Zeigers auf den Parameterpuffer des Normalisierungsalgorithmus. Dann erzeugen und initialisieren wir ggf. einen neuen Puffer und erstellen anschließend einen Puffer im Speicher der Videokarte und laden den Pufferinhalt.
Setzen Sie die Anzahl der gestarteten Threads gleich der Anzahl der Neuronen in der Schicht und übergeben Sie die Zeiger auf die Datenpuffer zusammen mit den erforderlichen Parametern an den Kernel.
Nach den Vorarbeiten lassen wir den Kernel arbeiten und lesen die aktualisierten Pufferdaten aus dem Speicher der Grafikkarte zurück. Beachten Sie, dass von der Videokarte Daten aus zwei Puffern empfangen werden: Informationen aus der Algorithmusausgabe und ein Parameterpuffer, in dem wir den aktualisierten Mittelwert, die Varianz und den normalisierten Wert gespeichert haben. Diese Daten werden in weiteren Iterationen verwendet.
Nach Beendigung des Algorithmus löschen wir den Parameterpuffer aus dem Speicher der Videokarte, um Speicher für Puffer weiterer Schichten des neuronalen Netzes freizugeben. Anschließend beenden wir die Methode mit true.
Der vollständige Code aller Klassen und ihrer Methoden aus der Bibliothek ist im Anhang verfügbar.
2.3. Rückwärtsdurchlauf
Der Rückwärtsdurchlauf besteht wiederum aus zwei Stufen: Fehler-Rückpropagierung und die Aktualisierung der Gewichte. Anstelle der üblichen Gewichte werden wir die Parameter γ und β der Skalierungs- und Verschiebungsfunktion trainieren.
Beginnen wir mit der Gradientenabstiegsfunktion. Erstellen wir den Kernel CalcHiddenGradientBatch, um dessen Funktionalität zu implementieren. Der Kernel empfängt in Parametern Zeiger auf Tensoren von Normalisierungsparametern, die von der nächsten Schicht von Gradienten empfangen werden, Ausgangsdaten der vorherigen Schicht (die während des letzten Vorwärtsdurchlaufs erhalten wurden) und Tensoren von Gradienten der vorherigen Schicht, in die die Ergebnisse des Algorithmus geschrieben werden sollen. Der Kernel erhält als Parameter auch die Stichprobe, den Typ der Aktivierungsfunktion und die Methode zur Optimierung der Parameter.
Wie beim direkten Durchlauf wird zu Beginn des Kerns der Stichprobenumfang überprüft; wenn sie kleiner oder gleich 1 ist, wird der Kern ohne weitere Iterationen verlassen.
Der nächste Schritt besteht darin, die Seriennummer des Threads zu ermitteln und die Verschiebung im Parameter-Tensor zu bestimmen. Diese Aktionen ähneln denen, die zuvor im Vorwärtsdurchlauf beschrieben wurden.
__kernel void CalcHiddenGradientBatch(__global double *options, ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer __global double *matrix_g, ///<[in] Tensor of gradients at current layer __global double *matrix_i, ///<[in] Tensor of previous layer output __global double *matrix_ig, ///<[out] Tensor of gradients at previous layer uint activation, ///< Activation type (#ENUM_ACTIVATION) int batch, ///< Batch size int optimization ///< Optimization type ) { if(batch<=1) return; //--- int n=get_global_id(0); int shift=n*(optimization==0 ? 7 : 9); //--- double inp=matrix_i[n]; double gnx=matrix_g[n]*options[shift+3]; double temp=1/sqrt(options[shift+1]+1e-6); double gmu=(-temp)*gnx; double gvar=(options[shift]*inp)/(2*pow(options[shift+1]+1.0e-6,3/2))*gnx; double gx=temp*gnx+gmu/batch+gvar*2*inp/batch*pow((double)(batch-1)/batch,2.0); //--- if(isnan(gx)) gx=0; switch(activation) { case 0: gx=clamp(gx+inp,-1.0,1.0)-inp; gx=gx*(1-pow(inp==1 || inp==-1 ? 0.99999999 : inp,2)); break; case 1: gx=clamp(gx+inp,0.0,1.0)-inp; gx=gx*(inp==0 || inp==1 ? 0.00000001 : (inp*(1-inp))); break; case 2: if(inp<0) gx*=0.01; break; default: break; } matrix_ig[n]=clamp(gx,-MAX_GRADIENT,MAX_GRADIENT); }
Anschließend berechnen wir nacheinander die Gradienten für alle Funktionen des Algorithmus.

Und schließlich propagieren wir den Gradienten durch die Aktivierungsfunktion der vorherigen Schicht. Wir speichern den resultierenden Wert in den Gradiententensor der vorherigen Schicht.
Betrachten wir im Anschluss an den Kernel CalcHiddenGradientBatсh die Methode CNeuronBatchNormOCL::calcInputGradients, die den Kernel vom Hauptprogramm aus ausführen lässt. Ähnlich wie die entsprechenden Methoden anderer Klassen erhält die Methode als Parameter einen Zeiger auf das Objekt der vorherigen Schicht des neuronalen Netzes.
Zu Beginn der Methode wird die Gültigkeit des empfangenen Zeigers und des Zeigers auf das OpenCL-Objekt überprüft. Danach prüfen wir die Stichprobengröße. Wenn sie kleiner oder gleich 1 ist, dann wird die Methode verlassen. Das von der Methode zurückgegebene Ergebnis hängt von der Gültigkeit des Zeigers auf die vorherige Schicht ab, der während des Vorwärtsdurchlaufs gespeichert wurde.
Wenn wir uns weiter im Algorithmus bewegen, überprüfen wir die Gültigkeit des Parameterpuffers. Tritt ein Fehler auf, verlassen wir die Methode mit dem Ergebnis false.
Bitte beachten Sie, dass der propagierte Gradient zum letzten Vorwärtsdurchlauf gehört. Deshalb haben wir an den letzten beiden Kontrollpunkten die am Vorwärtsdurchlauf beteiligten Objekte überprüft.
bool CNeuronBatchNormOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- if(iBatchSize<=1) return (CheckPointer(PrevLayer)!=POINTER_INVALID); //--- if(CheckPointer(BatchOptions)==POINTER_INVALID || !BatchOptions.BufferCreate(OpenCL)) return false; //--- uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=Neurons(); if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_matrix_i,NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_matrix_g,Gradient.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_matrix_ig,NeuronOCL.getGradientIndex())) return false; if(!OpenCL.SetArgument(def_k_CalcHiddenGradientBatch,def_k_bchg_activation,NeuronOCL.Activation())) return false; if(!OpenCL.SetArgument(def_k_CalcHiddenGradientBatch,def_k_bchg_batch,iBatchSize)) return false; if(!OpenCL.SetArgument(def_k_CalcHiddenGradientBatch,def_k_bchg_optimization,(int)optimization)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_CalcHiddenGradientBatch,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Batch CalcHiddenGradient: %d",GetLastError()); return false; } if(!NeuronOCL.getGradient().BufferRead()) return false; BatchOptions.BufferFree(); //--- return true; }
Wie beim Vorwärtsdurchlauf ist die Anzahl der gestarteten Kernel-Threads gleich der Anzahl der Neuronen in der Schicht. Wir senden den Inhalt des Puffers für die Normalisierungsparameter an den Videokartenspeicher und übergeben die erforderlichen Tensor- und Parameterzeiger an den Kernel.
Nachdem wir alle oben genannten Operationen durchgeführt haben, führen wir den Kernel aus und berechnen die resultierenden Gradienten aus dem Videokartenspeicher in den entsprechenden Puffer.
Am Ende der Methode entfernen wir den Tensor der Normalisierungsparameter aus dem Videokartenspeicher und beenden die Methode mit dem Ergebnis true.
Nach der Propagierung des Gradienten ist es an der Zeit, die Verschiebungs- und Skalierungsparameter zu aktualisieren. Um diese Iterationen zu implementieren, erstellen wir 2 Kernel, entsprechend der Anzahl der zuvor beschriebenen Optimierungsmethoden UpdateBatchOptionsMomentum und UpdateBatchOptionsAdam.
Beginnen wir mit der Methode UpdateBatchOptionsMomentum. Die Methode erhält in Parametern Zeiger auf zwei Tensoren: von Normalisierungsparametern und oder Gradienten. Außerdem übergeben wir in den Methodenparametern die Konstanten der Optimierungsmethode: die Lernrate und das Momentum.
Am Anfang des Kerns erhalten Sie die Thread-Nummer und bestimmen die Verschiebung im Tensor der Normalisierungsparameter.
Mit Hilfe der Quelldaten berechnen wir das Delta für γ und β. Für diese Operation habe ich Vektorberechnungen mit dem 2-Element-Doppelvektor verwendet. Diese Methode erlaubt die Parallelisierung der Berechnungen.
Passen wir die Parameter γ, β an und speichern die Ergebnisse in den entsprechenden Elementen des Tensors der Normalisierungsparameter.
__kernel void UpdateBatchOptionsMomentum(__global double *options, ///<[in,out] Options matrix m*7, where m - Number of neurons in previous layer __global double *matrix_g, ///<[in] Tensor of gradients at current layer double learning_rates, ///< Learning rates double momentum ///< Momentum multiplier ) { const int n=get_global_id(0); const int shift=n*7; double grad=matrix_g[n]; //--- double2 delta=learning_rates*grad*(double2)(options[shift+2],1) + momentum*(double2)(options[shift+5],options[shift+6]); if(!isnan(delta.s0) && !isnan(delta.s1)) { options[shift+5]=delta.s0; options[shift+3]=clamp(options[shift+3]+delta.s0,-MAX_WEIGHT,MAX_WEIGHT); options[shift+6]=delta.s1; options[shift+4]=clamp(options[shift+4]+delta.s1,-MAX_WEIGHT,MAX_WEIGHT); } };
Der Kernel UpdateBatchOptionsAdam ist nach einem ähnlichen Schema aufgebaut, allerdings gibt es Unterschiede im Algorithmus der Optimierungsmethode. Der Kernel erhält in Parametern die Zeiger auf die gleichen Parameter- und Gradiententensoren und den Parameter der Optimierungsmethode.
Am Anfang des Kerns wird die Thread-Nummer definiert und die Verschiebung im Parameter-Tensor bestimmt.
Dann wird auf Basis der erhaltenen Daten das erste und zweite Moment berechnet. Die hier verwendeten Vektorberechnungen erlauben die Berechnung der Momente für zwei Parameter gleichzeitig.
Berechnen wir nun auf der Grundlage der erhaltenen Momente die Deltas und neue Parameterwerte. Die Berechnungsergebnisse werden in den entsprechenden Elementen des Tensors der Normalisierungsparameter gespeichert.
__kernel void UpdateBatchOptionsAdam(__global double *options, ///<[in,out] Options matrix m*9, where m - Number of neurons in previous layer __global double *matrix_g, ///<[in] Tensor of gradients at current layer const double l, ///< Learning rates const double b1, ///< First momentum multiplier const double b2 ///< Second momentum multiplier ) { const int n=get_global_id(0); const int shift=n*9; double grad=matrix_g[n]; //--- double2 mt=b1*(double2)(options[shift+5],options[shift+6])+(1-b1)*(double2)(grad*options[shift+2],grad); double2 vt=b2*(double2)(options[shift+5],options[shift+6])+(1-b2)*pow((double2)(grad*options[shift+2],grad),2); double2 delta=l*mt/sqrt(vt+1.0e-8); if(isnan(delta.s0) || isnan(delta.s1)) return; double2 weight=clamp((double2)(options[shift+3],options[shift+4])+delta,-MAX_WEIGHT,MAX_WEIGHT); //--- if(!isnan(weight.s0) && !isnan(weight.s1)) { options[shift+3]=weight.s0; options[shift+4]=weight.s1; options[shift+5]=mt.s0; options[shift+6]=mt.s1; options[shift+7]=vt.s0; options[shift+8]=vt.s1; } };
Um den Kernel aus dem Hauptprogramm zu starten, erstellen wir die Methode CNeuronBatchNormOCL::updateInputWeights. Die Methode erhält als Parameter einen Zeiger auf die vorherige Schicht des neuronalen Netzes. Eigentlich wird dieser Zeiger nicht im Methodenalgorithmus verwendet, sondern er wird für die Vererbung von Methoden aus der Elternklasse belassen.
Zu Beginn der Methode wird die Gültigkeit des empfangenen Zeigers und des Zeigers auf das OpenCL-Objekt überprüft. Wie bei der zuvor betrachteten Methode CNeuronBatchNormOCL::calcInputGradients prüfen wir die Stichprobe und die Gültigkeit des Parameterpuffers. Wir laden den Inhalt des Parameterpuffers in den Speicher der Grafikkarte. Die Anzahl der Threads wird auf gleich der Anzahl der Neuronen in der Schicht gesetzt.
Des Weiteren kann der Algorithmus je nach angegebener Optimierungsmethode zwei Optionen verfolgen. Wir übergeben die Anfangsparameter für den gewünschten Kernel und starten seine Ausführung neu.
Unabhängig von der Parameteroptimierungsmethode berechnen wir den aktualisierten Inhalt des Puffers für die Normalisierungsparameter und entfernen den Puffer aus dem Speicher der Videokarte.
bool CNeuronBatchNormOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- if(iBatchSize<=1) return (CheckPointer(PrevLayer)!=POINTER_INVALID); //--- if(CheckPointer(BatchOptions)==POINTER_INVALID || !BatchOptions.BufferCreate(OpenCL)) return false; uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=Neurons(); //--- if(optimization==SGD) { if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsMomentum,def_k_buom_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsMomentum,def_k_buom_matrix_g,Gradient.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsMomentum,def_k_buom_learning_rates,eta)) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsMomentum,def_k_buom_momentum,alpha)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_UpdateBatchOptionsMomentum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel UpdateBatchOptionsMomentum %d",GetLastError()); return false; } } else { if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsAdam,def_k_buoa_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsAdam,def_k_buoa_matrix_g,Gradient.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsAdam,def_k_buoa_l,lr)) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsAdam,def_k_buoa_b1,b1)) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsAdam,def_k_buoa_b2,b2)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_UpdateBatchOptionsAdam,1,global_work_offset,global_work_size)) { printf("Error of execution kernel UpdateBatchOptionsAdam %d",GetLastError()); return false; } } //--- if(!BatchOptions.BufferRead()) return false; BatchOptions.BufferFree(); //--- return true; }
Nach erfolgreicher Beendigung der Operationen verlassen wir die Methode mit dem Ergebnis true.
Die Methoden zum Ersetzen von Puffern wurden im vorigen Artikel ausführlich beschrieben und sollten daher meiner Meinung nach keine Schwierigkeiten bereiten. Dies betrifft auch Operationen mit Dateien (Speichern und Laden eines trainierten neuronalen Netzes).
Der gesamte Code aller Klassen und Methoden befindet sich in der Anlage.
2.4. Änderungen in den Basisklassen des neuronalen Netzwerks
Der gesamte Code aller Klassen und Methoden befindet sich im Anhang. Zunächst legen wir einen Bezeichner für die neue Klasse an.
#define defNeuronBatchNormOCL 0x7891 ///<Batchnorm neuron OpenCL \details Identified class #CNeuronBatchNormOCL
Als Nächstes definieren wir konstante Makro-Ersetzungen für die Arbeit mit neuen Kerneln.
#define def_k_BatchFeedForward 24 ///< Index of the kernel for Batch Normalization Feed Forward process (#CNeuronBathcNormOCL) #define def_k_bff_inputs 0 ///< Inputs data tensor #define def_k_bff_options 1 ///< Tensor of variables #define def_k_bff_output 2 ///< Tensor of output data #define def_k_bff_batch 3 ///< Batch size #define def_k_bff_optimization 4 ///< Optimization type #define def_k_bff_activation 5 ///< Activation type //--- #define def_k_CalcHiddenGradientBatch 25 ///< Index of the Kernel of the Batch neuron to transfer gradient to previous layer (#CNeuronBatchNormOCL) #define def_k_bchg_options 0 ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer #define def_k_bchg_matrix_g 1 ///<[in] Tensor of gradients at current layer #define def_k_bchg_matrix_i 2 ///<[in] Tensor of previous layer output #define def_k_bchg_matrix_ig 3 ///<[out] Tensor of gradients at previous layer #define def_k_bchg_activation 4 ///< Activation type (#ENUM_ACTIVATION) #define def_k_bchg_batch 5 ///< Batch size #define def_k_bchg_optimization 6 ///< Optimization type //--- #define def_k_UpdateBatchOptionsMomentum 26 ///< Index of the kernel for Describe the process of SGD optimization options for the Batch normalization Neuron (#CNeuronBatchNormOCL). #define def_k_buom_options 0 ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer #define def_k_buom_matrix_g 1 ///<[in] Tensor of gradients at current layer #define def_k_buom_learning_rates 2 ///< Learning rates #define def_k_buom_momentum 3 ///< Momentum multiplier //--- #define def_k_UpdateBatchOptionsAdam 27 ///< Index of the kernel for Describe the process of Adam optimization options for the Batch normalization Neuron (#CNeuronBatchNormOCL). #define def_k_buoa_options 0 ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer #define def_k_buoa_matrix_g 1 ///<[in] Tensor of gradients at current layer #define def_k_buoa_l 2 ///< Learning rates #define def_k_buoa_b1 3 ///< First momentum multiplier #define def_k_buoa_b2 4 ///< Second momentum multiplier
Im Konstruktor des neuronalen Netzes CNet::CNet fügen wir Blöcke hinzu, die neue Klassenobjekte erzeugen und die neuen Kernel initialisieren (die Änderungen sind im Code hervorgehoben).
CNet::CNet(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
//---
................
................
................
//---
for(int i=0; i<total; i++)
{
prev=desc;
desc=Description.At(i);
if((i+1)<total)
{
next=Description.At(i+1);
if(CheckPointer(next)==POINTER_INVALID)
return;
}
else
next=NULL;
int outputs=(next==NULL || (next.type!=defNeuron && next.type!=defNeuronBaseOCL) ? 0 : next.count);
temp=new CLayer(outputs);
int neurons=(desc.count+(desc.type==defNeuron || desc.type==defNeuronBaseOCL ? 1 : 0));
if(CheckPointer(opencl)!=POINTER_INVALID)
{
................
................
................
CNeuronBatchNormOCL *batch=NULL;
switch(desc.type)
{
................
................
................
................
//---
case defNeuronBatchNormOCL:
batch=new CNeuronBatchNormOCL();
if(CheckPointer(batch)==POINTER_INVALID)
{
delete temp;
return;
}
if(!batch.Init(outputs,0,opencl,desc.count,desc.window,desc.optimization))
{
delete batch;
delete temp;
return;
}
batch.SetActivationFunction(desc.activation);
if(!temp.Add(batch))
{
delete batch;
delete temp;
return;
}
batch=NULL;
break;
//---
default:
return;
break;
}
}
................
................
................
................
//---
if(CheckPointer(opencl)==POINTER_INVALID)
return;
//--- create kernels
opencl.SetKernelsCount(28);
................
................
................
................
opencl.KernelCreate(def_k_BatchFeedForward,"BatchFeedForward");
opencl.KernelCreate(def_k_CalcHiddenGradientBath,"CalcHiddenGradientBath");
opencl.KernelCreate(def_k_UpdateBatchOptionsMomentum,"UpdateBatchOptionsMomentum");
opencl.KernelCreate(def_k_UpdateBatchOptionsAdam,"UpdateBatchOptionsAdam");
//---
return;
}
In ähnlicher Weise initiieren wir neue Kernel, wenn wir ein vortrainiertes neuronales Netzwerk laden.
bool CNet::Load(string file_name,double &error,double &undefine,double &forecast,datetime &time,bool common=true) { if(MQLInfoInteger(MQL_OPTIMIZATION) || MQLInfoInteger(MQL_TESTER) || MQLInfoInteger(MQL_FORWARD) || MQLInfoInteger(MQL_OPTIMIZATION)) return false; //--- ................ ................ ................ //--- if(CheckPointer(opencl)==POINTER_INVALID) { opencl=new COpenCLMy(); if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true)) delete opencl; else { //--- create kernels opencl.SetKernelsCount(28); ................ ................ ................ opencl.KernelCreate(def_k_BatchFeedForward,"BatchFeedForward"); opencl.KernelCreate(def_k_CalcHiddenGradientBath,"CalcHiddenGradientBath"); opencl.KernelCreate(def_k_UpdateBatchOptionsMomentum,"UpdateBatchOptionsMomentum"); opencl.KernelCreate(def_k_UpdateBatchOptionsAdam,"UpdateBatchOptionsAdam"); } } ................ ................ ................ ................ ................ }
Fügen wir einen neuen Typ von Neuronen in die Methode ein, die das vortrainierte neuronale Netzwerk lädt.
bool CLayer::Load(const int file_handle) { iFileHandle=file_handle; if(!CArrayObj::Load(file_handle)) return false; if(CheckPointer(m_data[0])==POINTER_INVALID) return false; //--- CNeuronBaseOCL *ocl=NULL; CNeuronBase *cpu=NULL; switch(m_data[0].Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: case defNeuronBatchNormOCL: ocl=m_data[0]; iOutputs=ocl.getConnections(); break; default: cpu=m_data[0]; iOutputs=cpu.getConnections().Total(); break; } //--- return true; }
In ähnlicher Weise wird ein neuer Typ von Neuronen in die Dispatcher-Methoden der Basisklasse CNeuronBaseOCL aufgenommen.
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: case defNeuronBatchNormOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; } bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject) { if(CheckPointer(TargetObject)==POINTER_INVALID) return false; //--- ................ ................ ................ CNeuronBatchNormOCL *batch=NULL; switch(TargetObject.Type()) { ................ ................ ................ case defNeuronBatchNormOCL: batch=TargetObject; temp=GetPointer(this); return batch.calcInputGradients(temp); break; } //--- return false; } bool CNeuronBaseOCL::UpdateInputWeights(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: case defNeuronBatchNormOCL: temp=SourceObject; return updateInputWeights(temp); break; } //--- return false; }
Der vollständige Code aller Klassen und ihrer Methoden ist im Anhang verfügbar.
3. Tests
Wir fahren fort, neue Klassen in den zuvor erstellten Expert Advisors zu testen, was vergleichbare Daten für die Bewertung der Leistung einzelner Elemente liefert. Wir testen die Normalisierungsmethode auf der Basis des Expert Advisors aus dem Artikel 12, wobei wir Dropout durch die Stichprobe Normalisierung ersetzen. Die Struktur des neuronalen Netzes des neuen Expert Advisors ist unten dargestellt. Hier wurde die Lernrate von 0,000001 auf 0,001 erhöht.
//--- 0 CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBaseOCL; desc.optimization=ADAM; desc.activation=None; if(!Topology.Add(desc)) return INIT_FAILED; //--- 1 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBatchNormOCL; desc.window=100; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- 2 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronConvOCL; desc.window=12; desc.step=12; desc.window_out=24; desc.optimization=ADAM; desc.activation=None; if(!Topology.Add(desc)) return INIT_FAILED; //--- 3 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*24; desc.type=defNeuronBatchNormOCL; desc.window=100; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- 4 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronMLMHAttentionOCL; desc.window=24; desc.window_out=4; desc.step=8; //heads desc.layers=5; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- 5 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=None; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 6 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuronBatchNormOCL; desc.window=100; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- 7 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 8 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; desc.activation=SIGMOID; desc.optimization=ADAM;
Der Expert Advisor wurde mit EURUSD, Zeitrahmen H1, getestet. Die Daten der letzten 20 Kerzen wurden in das neuronale Netzwerk eingegeben, ähnlich wie bei den vorherigen Tests.
Das Diagramm des Vorhersagefehlers des neuronalen Netzwerks zeigt, dass der EA mit Stichprobe Normalisierung einen weniger geglätteten Graphen hat, was durch einen starken Anstieg der Lernrate verursacht werden kann. Der Vorhersagefehler ist jedoch fast während des gesamten Tests niedriger als bei den vorherigen Tests.
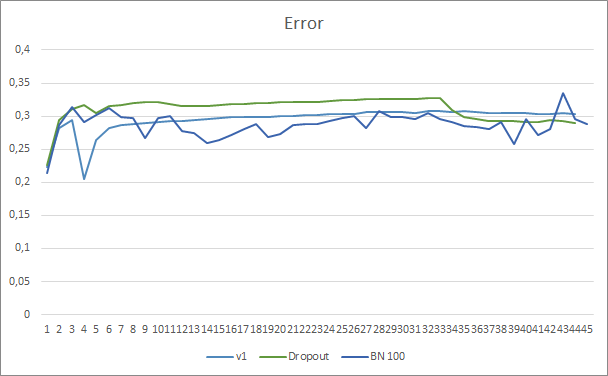
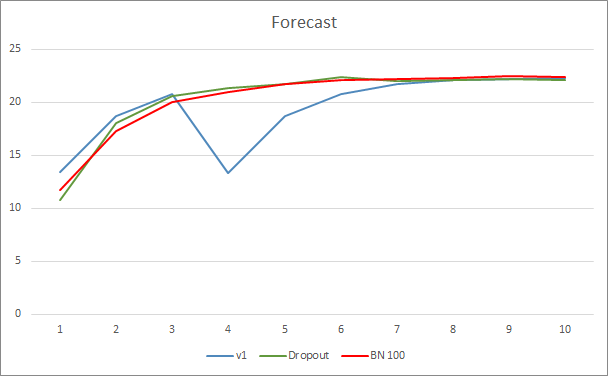
Die Vorhersagetreffergraphen aller drei Expert Advisors liegen recht nahe beieinander, so dass wir nicht schließen können, dass einer von ihnen definitiv besser ist.
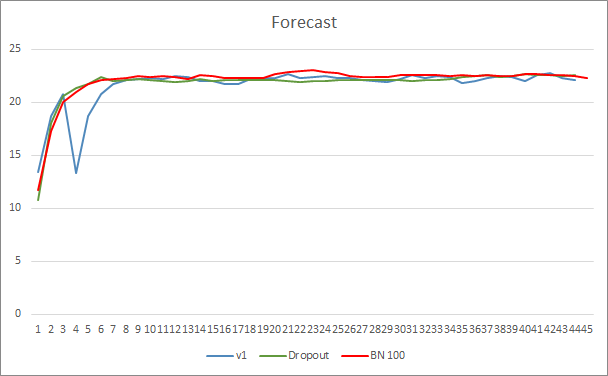
Schlussfolgerung
In diesem Artikel haben wir uns weiter mit Methoden beschäftigt, die darauf abzielen, die Konvergenz von neuronalen Netzwerken zu erhöhen, und haben unserer Bibliothek eine Klasse für Stichproben-Normalisierung hinzugefügt. Tests haben gezeigt, dass die Verwendung dieser Methode den Fehler des neuronalen Netzes reduzieren und die Lernrate erhöhen kann.
Referenzen
- Neuronale Netze leicht gemacht
- Neuronale Netze leicht gemacht (Teil 2): Netzwerktraining und Tests
- Neuronale Netze leicht gemacht (Teil 3): Convolutional Neurale Netzwerke
- Neuronale Netze leicht gemacht (Teil 4): Rekurrente Netze
- Neuronale Netze leicht gemacht (Teil 5): Parallele Berechnungen mit OpenCL
- Neuronale Netze leicht gemacht (Teil 6): Experimentieren mit der Lernrate des neuronalen Netzwerks
- Neuronale Netze leicht gemacht (Teil 7): Adaptive Optimierungsverfahren
- Neuronale Netze leicht gemacht (Teil 8): Attention-Mechanismen
- Neuronale Netze leicht gemacht (Teil 9): Dokumentation der Arbeit
- Neuronale Netze leicht gemacht (Teil 10): Multi-Head Attention
- Neuronale Netze leicht gemacht (Teil 11): Ein Blick auf GPT
- Neuronale Netze leicht gemacht (Teil 12): Dropout
- Stichproben-Normalisierung: Beschleunigung des Trainings von tiefen Netzwerken durch Reduzierung der internen Kovariatenverschiebung (in Englisch)
- Schicht-Normalisierung (in Englisch)
Die Programme dieses Artikels
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Fractal_OCL_AttentionMLMH_b.mq5 | Expert Advisor | Ein Expert Advisor mit dem neuronalen Klassifizierungsnetz (3 Neuronen in der Ausgabeschicht) unter Verwendung der GTP-Architektur, mit 5 Aufmerksamkeitsschichten + BatchNorm |
| 2 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek mit Klassen zum Erstellen eines neuronalen Netzwerks |
| 3 | NeuroNet.cl | Bibliothek | Die Bibliothek mit dem Programm-Code für OpenCL |
| 4 | NN.chm | HTML Hilfe | Eine kompilierte CHM-Hilfedatei |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/9207
 Brute-Force-Ansatz zur Mustersuche (Teil IV): Minimale Funktionalität
Brute-Force-Ansatz zur Mustersuche (Teil IV): Minimale Funktionalität
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.