Neuronale Netze leicht gemacht (Teil 6): Experimentieren mit der Lernrate des neuronalen Netzwerks

Inhalt

• Einführung
• 1. Das Problem
• 2. Experiment 1
• 3. Experiment 2
• 4. Experiment 3
• Schlussfolgerungen
• Referenzen
• Programme, die im diesem Artikel verwendet werden

Einführung

In früheren Artikeln haben wir uns mit den Funktionsprinzipien und Methoden zur Implementierung eines voll verbundenen Perzeptrons, von convolutionalen und rekurrenten Netzwerken beschäftigt. Zum Trainieren aller Netzwerke haben wir das Gradientenverfahren verwendet. Nach dieser Methode bestimmen wir den Vorhersagefehler des Netzwerks bei jedem Schritt und passen die Gewichte an, um den Fehler zu verringern. Wir eliminieren den Fehler jedoch nicht vollständig bei jedem Schritt, sondern passen nur die Gewichte an, um den Fehler zu reduzieren. Wir versuchen also, solche Gewichte zu finden, die das Trainingsset über seine gesamte Länge hinweg genau wiederholen. Die Lernrate ist für die Geschwindigkeit der Fehlerminimierung bei jedem Schritt verantwortlich.

1. Das Problem

Was ist das Problem bei der Auswahl der Lernrate? Lassen Sie uns die grundlegenden Fragen im Zusammenhang mit der Auswahl der Lernrate skizzieren.

1. Warum können wir nicht die Rate gleich "1" (oder einen nahen Wert) verwenden und den Fehler sofort kompensieren?
In diesem Fall hätten wir ein neuronales Netz, das für die letzte Situation übertrainiert wäre. Das Ergebnis ist, dass weitere Entscheidungen nur auf Basis der letzten Daten getroffen werden, während die Historie ignoriert wird.

2. Was ist das Problem mit einer wissentlich kleinen Rate, die eine Mittelung der Werte über die gesamte Stichprobe ermöglichen würde?
Das erste Problem bei diesem Ansatz ist die Trainingszeit des neuronalen Netzes. Wenn die Schritte zu klein sind, wird eine große Anzahl solcher Schritte benötigt. Dies erfordert Zeit und Ressourcen.

Das zweite Problem bei diesem Ansatz ist, dass der Weg zum Ziel nicht immer glatt ist. Er kann Täler und Hügel haben. Wenn wir uns in zu kleinen Schritten bewegen, können wir in einem dieser Werte stecken bleiben und ihn fälschlicherweise als globales Minimum bestimmen. In diesem Fall werden wir das Ziel nie erreichen. Dies kann teilweise durch die Verwendung eines Impulses in der Formel für die Gewichtsaktualisierung gelöst werden, aber das Problem besteht trotzdem.

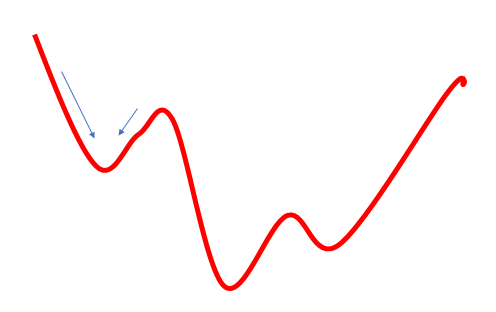
3. Wo liegt das Problem bei einer bewusst großen Rate, die eine Mittelung der Werte über eine bestimmte Strecke erlauben und lokale Minima vermeiden würde?
Der Versuch, das Problem des lokalen Minimums durch eine Erhöhung der Lernrate zu lösen, führt zu einem weiteren Problem: Die Verwendung einer großen Lernrate erlaubt es oft nicht, den Fehler zu minimieren, weil bei der nächsten Aktualisierung der Gewichte deren Änderung größer als die erforderliche ist, und als Folge davon werden wir über das globale Minimum springen. Wenn wir zu diesem wieder zurückkehren, wird die Situation ähnlich sein. Das Ergebnis ist, dass wir um das globale Minimum herum oszillieren werden.

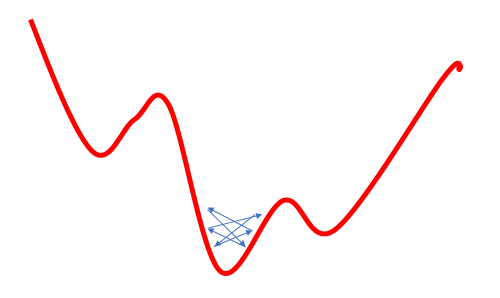
Diese Probleme sind bekannt und werden oft diskutiert, aber ich habe keine klaren Empfehlungen bezüglich der Auswahl der Lernrate gefunden. Alle schlagen die empirische Auswahl der Rate für jede spezifische Aufgabe vor. Einige andere Autoren schlagen die schrittweise Reduzierung der Rate während des Lernprozesses vor, um das oben beschriebene Risiko 3 zu minimieren.

In diesem Artikel schlage ich vor, einige Experimente durchzuführen, bei denen ein neuronales Netz mit verschiedenen Lernraten trainiert wird, um die Auswirkung dieses Parameters auf das Training des neuronalen Netzes als Ganzes zu sehen.    

2. Experiment 1

Der Einfachheit halber wollen wir die Variable eta aus der Klasse CNeuronBaseOCL zu einer globalen Variablen machen.

double   eta=0.01;
#include "NeuroNet.mqh"

und

class CNeuronBaseOCL    :  public CObject
  {
protected:
   ........
   ........
//---
   //const double      eta;

Erstellen Sie nun drei Kopien des Expert Advisors mit unterschiedlichen Lernratenparametern (0,1; 0,01; 0,001). Erstellen Sie außerdem den vierten EA, bei dem die anfängliche Lernrate auf 0,01 gesetzt ist und alle 10 Epochen um das Zehnfache reduziert wird. Fügen Sie dazu den folgenden Code in die Trainingsschleife der Funktion Train ein.

         if(discount>0)
            discount--;
         else
           {
            eta*=0.1;
            discount=10;
           }

Alle vier EAs wurden gleichzeitig in einem Terminal gestartet. In diesem Experiment habe ich Parameter aus früheren EA-Tests verwendet: Symbol EURUSD, Zeitrahmen H1, Daten von 20 aufeinanderfolgenden Kerzen werden in das Netzwerk eingespeist, und das Training wird anhand der Historie der letzten zwei Jahre durchgeführt. Die Trainingsstichprobe betrug etwa 12,4 Tausend Balken.

Alle EAs wurden mit zufälligen Gewichten im Bereich von -1 bis 1 initialisiert, wobei Nullwerte ausgeschlossen wurden.

Leider zeigte der EA mit der Lernrate gleich 0,1 einen Fehler nahe bei 1, und deshalb wird er in den Diagrammen nicht gezeigt. Die Lerndynamik der anderen EAs ist in den folgenden Diagrammen dargestellt.

Nach 5 Epochen erreichte der Fehler aller EAs das Niveau von 0,42, wo er für den Rest der Zeit weiter schwankte. Der Fehler des EAs mit der Lernrate gleich 0,001 war etwas geringer. Die Unterschiede traten in der dritten Nachkommastelle auf (0,420 gegenüber 0,422 der anderen beiden EAs).

Die Fehlertrajektorie des EAs mit variabler Lernrate folgt der Fehlerlinie des EAs mit einem Lernfaktor von 0,01. Dies ist in den ersten zehn Epochen durchaus zu erwarten, aber es gibt keine Abweichung, wenn die Rate abnimmt.

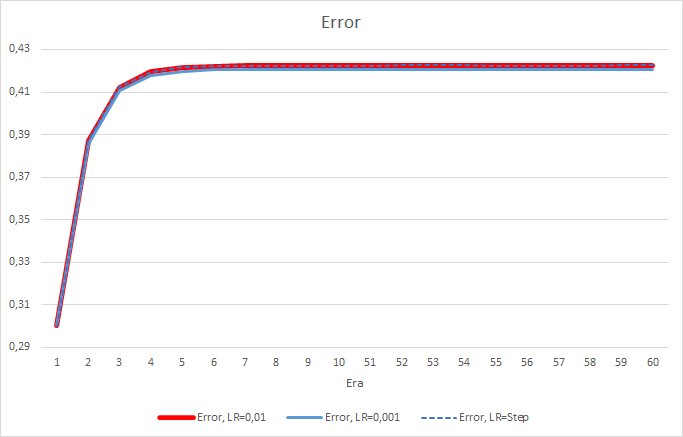
Schauen wir uns den Unterschied zwischen den Fehlern der oben genannten EAs genauer an. Fast während des gesamten Experiments schwankte die Differenz zwischen den Fehlern der EAs mit konstanten Lernraten von 0,01 und 0,001 um 0,0018. Außerdem hat eine Verringerung der Lernrate des EAs alle 10 Epochen fast keinen Effekt und die Abweichung vom EA mit einer Rate von 0,01 (gleich der anfänglichen Lernrate) schwankt um 0.

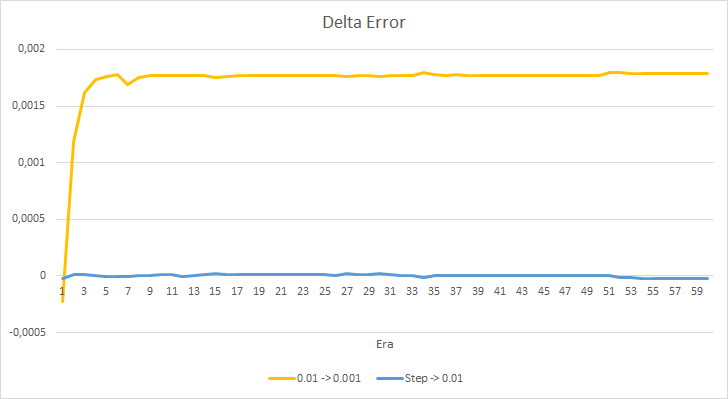
Die erhaltenen Fehlerwerte zeigen, dass die Lernrate von 0,1 in unserem Fall nicht anwendbar ist. Die Verwendung einer Lernrate von 0,01 und darunter führt zu ähnlichen Ergebnissen mit einem Fehler von ca. 42 %.

Der statistische Fehler des neuronalen Netzes ist recht deutlich. Wie wirkt sich dies auf die Leistung des EA aus? Lassen Sie uns die Anzahl der verpassten Fraktale überprüfen. Leider zeigten alle EAs während des Experiments schlechte Ergebnisse: sie verpassten alle fast 100 % der Fraktale. Darüber hinaus ermittelt ein EA mit der Lernrate von 0,01 etwa 2,5% Fraktale, während der EA mit der Rate von 0,001 100% der Fraktale überspringt. Nach der 52. Epoche zeigte der EA mit der Lernrate von 0,01 eine Tendenz zur Abnahme der Anzahl der übersprungenen Fraktale. Keine solche Tendenz zeigte der EA mit der variablen Rate. 

   

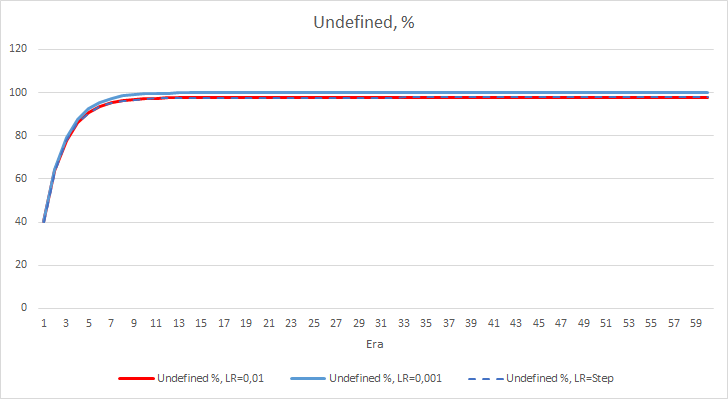
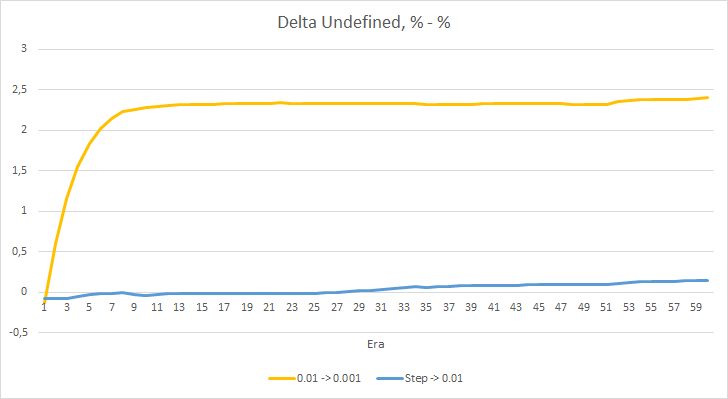
Das Diagramm der Deltas der fehlenden Fraktale in Prozent zeigt ebenfalls eine allmähliche Zunahme der Differenz zugunsten des EA mit einer Lernrate von 0,01.

Wir haben zwei Leistungsmetriken des neuronalen Netzwerks betrachtet, und bisher hat der EA mit einer niedrigeren Lernrate einen kleineren Fehler, aber er verpasst Fraktale. Nun wollen wir den dritten Wert prüfen: "hit" (Treffer) der vorhergesagten Fraktale.

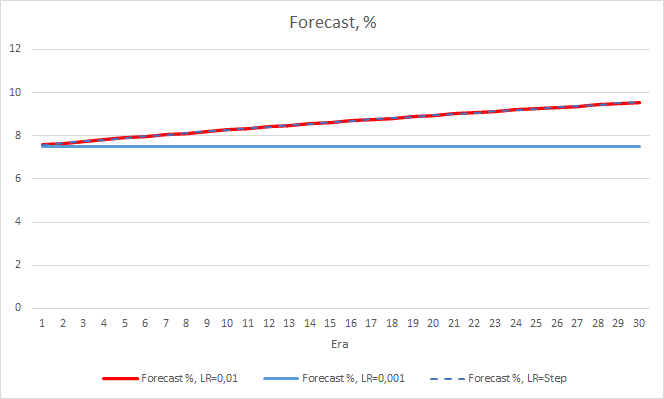
Die Diagramme unten zeigen das Wachstum des "Treffer"-Prozentsatzes beim Training von EAs mit einer Lernrate von 0,01 und mit einer dynamisch abnehmenden Rate. Die Wachstumsrate der Variablen nimmt mit einer Verringerung der Lernrate ab. Bei dem EA mit der Lernrate von 0,001 blieb der "Treffer"-Prozentsatz bei 0 hängen, was ganz natürlich ist, da er 100 % der Fraktale verfehlt. 

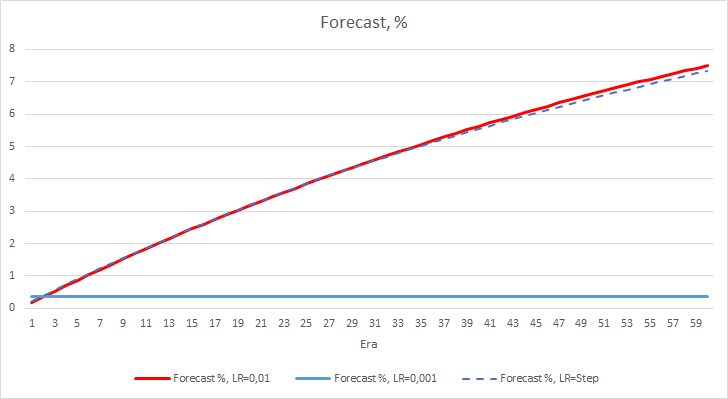
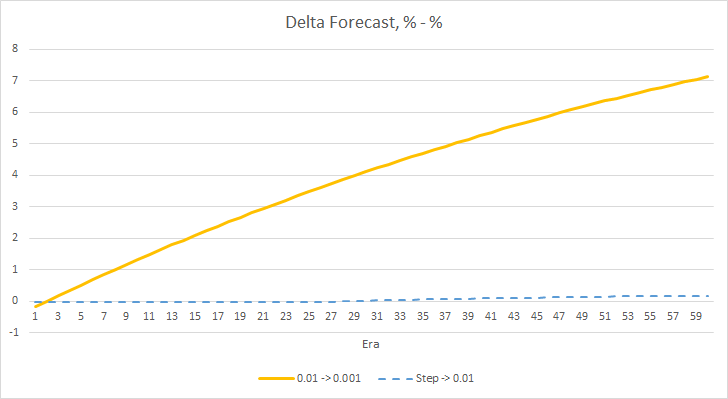
Das obige Experiment zeigt, dass die optimale Lernrate bzw. das Training eines neuronalen Netzwerks innerhalb unseres Problems nahe bei 0,01 liegt. Eine allmähliche Verringerung der Lernrate führte nicht zu einem positiven Ergebnis. Vielleicht ist der Effekt der Ratenverringerung ein anderer, wenn wir die Rate weniger oft als in 10 Epochen verringern. Vielleicht wären die Ergebnisse mit 100 oder 1000 Epochen besser. Dies muss jedoch noch experimentell überprüft werden.

3. Experiment 2

Im ersten Experiment wurden die Gewichtsmatrizen des neuronalen Netzes zufällig initialisiert. Daher hatten alle EAs unterschiedliche Anfangszustände. Um den Einfluss des Zufalls auf die Versuchsergebnisse zu eliminieren, laden Sie die aus dem vorherigen Experiment erhaltene Gewichtsmatrix mit dem EA, der eine Lernrate von 0,01 hat, in alle drei EAs und setzen das Training für weitere 30 Epochen fort.

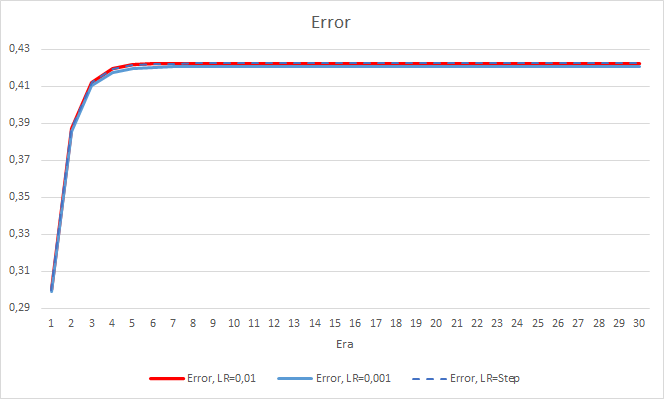
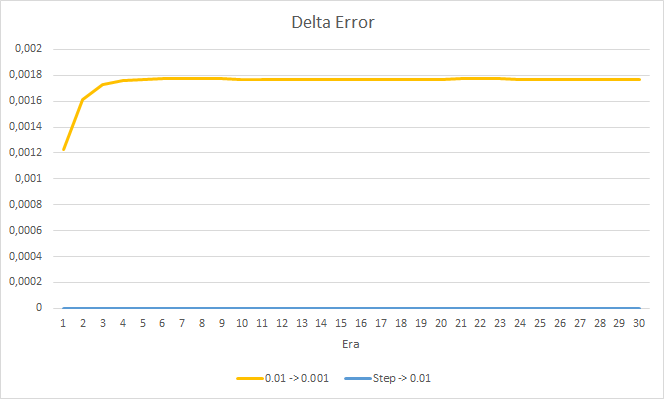
Das neue Training bestätigt die zuvor erhaltenen Ergebnisse. Wir sehen einen durchschnittlichen Fehler um 0,42 bei allen drei EAs. Der EA mit der niedrigsten Lernrate (0,001) hatte wieder einen etwas kleineren Fehler (mit der gleichen Differenz von 0,0018). Der Effekt einer schrittweisen Verringerung der Lernrate ist praktisch gleich 0.

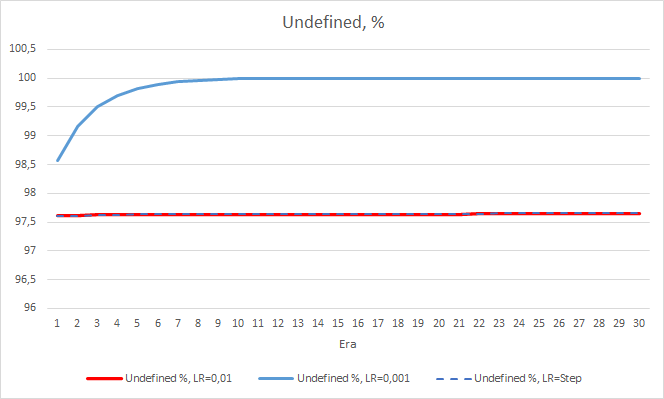
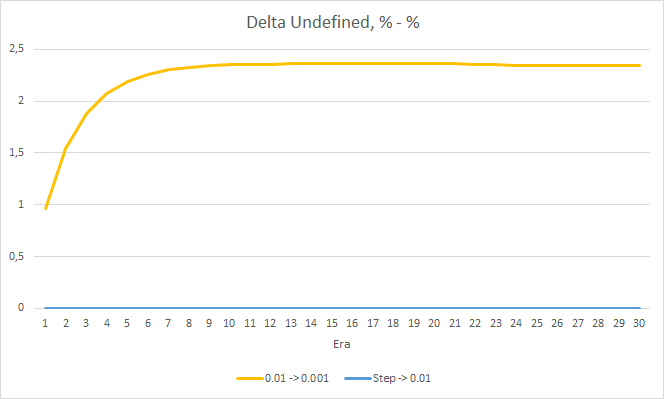
Was den Prozentsatz der verpassten Fraktale betrifft, so werden die früher erhaltenen Ergebnisse erneut bestätigt. Der EA mit einem niedrigeren Lernfaktor nähert sich in 10 Epochen 100 % der verpassten Fraktale, d. h. der EA ist nicht in der Lage, Fraktale anzuzeigen. Die anderen beiden EAs zeigen einen Wert von 97,6 %. Der Effekt einer schrittweisen Verringerung der Lernrate ist praktisch gleich 0.  

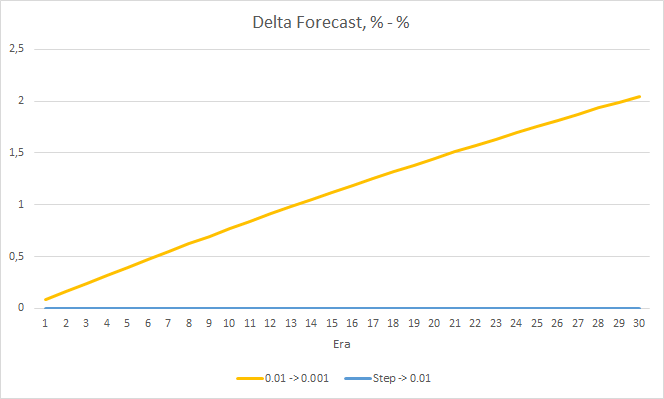
Der "Treffer"-Prozentsatz des EAs mit der Lernrate von 0,001 wächst allmählich weiter an. Eine allmähliche Verringerung der Lernrate hat keinen Einfluss auf diesen Wert. 

 

4. Experiment 3

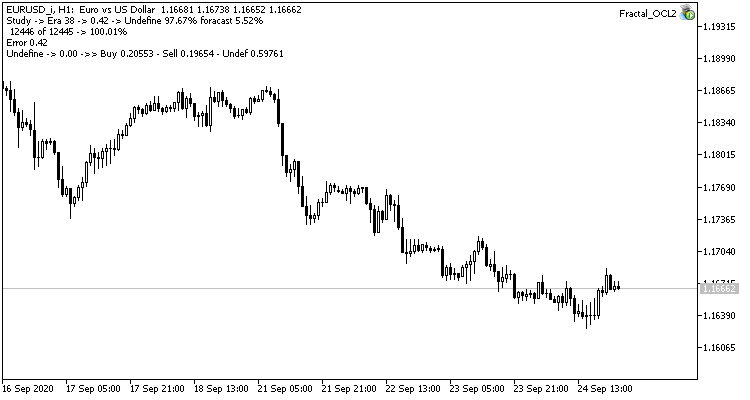
Das dritte Experiment ist eine leichte Abweichung vom Hauptthema des Artikels. Die Idee dazu entstand während der ersten beiden Experimente. Also beschloss ich, es mit Ihnen zu teilen. Bei der Beobachtung des Trainings des neuronalen Netzes ist mir aufgefallen, dass die Wahrscheinlichkeit des Ausbleibens eines Fraktals um 60-70 % schwankt und selten unter 50 % fällt. Die Wahrscheinlichkeit des Auftretens eines Fraktals, egal ob Kauf oder Verkauf, liegt bei etwa 20-30%. Das ist ganz natürlich, da es viel weniger Fraktale auf dem Chart gibt als Kerzen innerhalb von Trends. Unser neuronales Netzwerk ist also übertrainiert, und wir erhalten die oben genannten Ergebnisse. Fast 100 % der Fraktale werden übersehen, und nur seltene können erkannt werden.  

Um dieses Problem zu lösen, habe ich beschlossen, die Ungleichmäßigkeit der Stichprobe ein wenig zu kompensieren: Für das Fehlen eines Fraktals im Referenzwert habe ich beim Training des Netzes 0,5 statt 1 angegeben.

            TempData.Add((double)buy);
            TempData.Add((double)sell);
            TempData.Add((double)((!buy && !sell) ? 0.5 : 0));

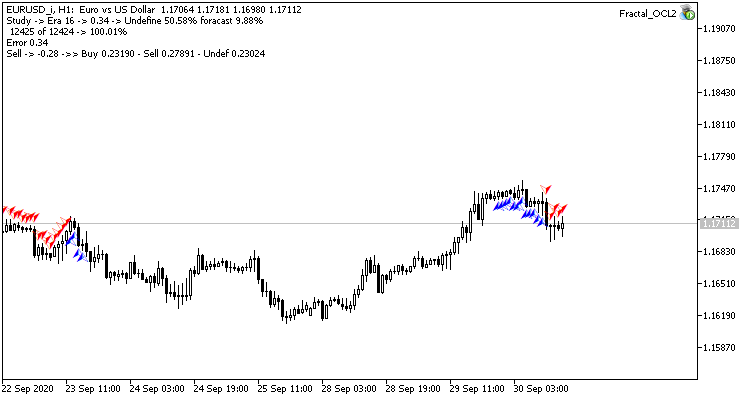
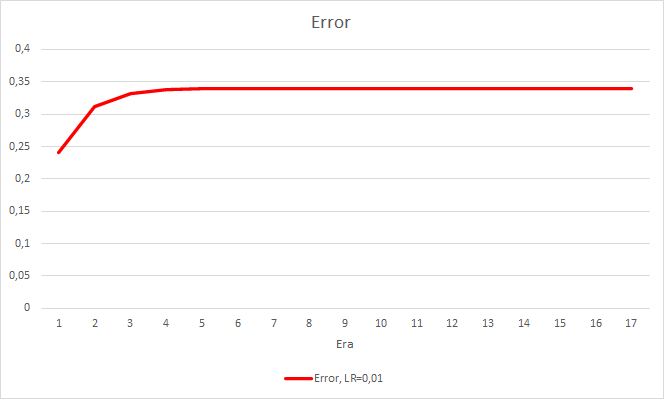
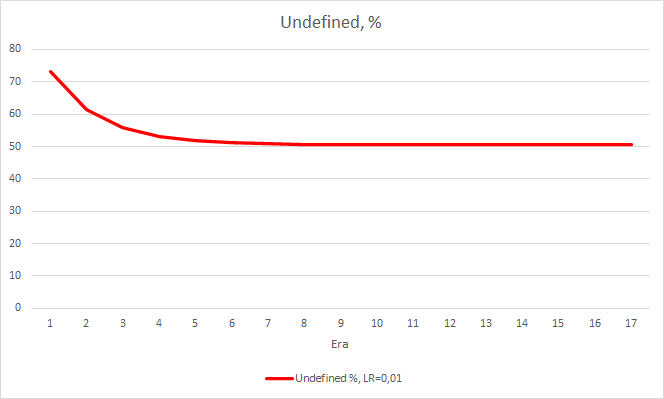
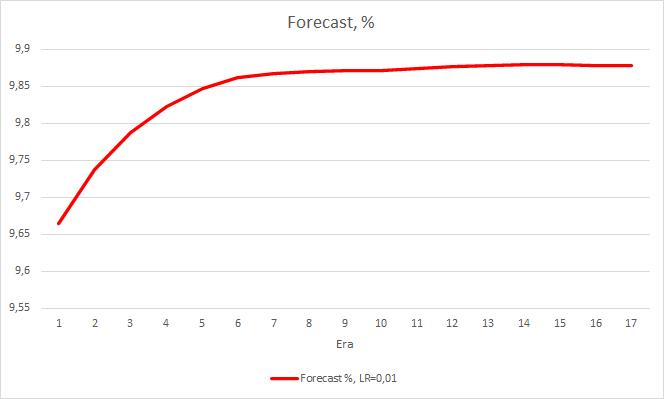
Dieser Schritt brachte einen guten Effekt. Der Expert Advisor, der mit einer Lernrate von 0,01 und einer aus früheren Experimenten gewonnenen Gewichtsmatrix läuft, zeigt nach 5 Trainingsepochen eine Fehlerstabilisierung von etwa 0,34. Der Anteil der verfehlten Fraktale sank auf 51 % und der Anteil der Treffer stieg auf 9,88 %. Sie können aus dem Diagramm erkennen, dass der EA Signale in Gruppen generiert und somit einige bestimmte Zonen aufweist. Offensichtlich erfordert die Idee weitere Entwicklung und Tests. Aber die Ergebnisse zeigen, dass dieser Ansatz recht vielversprechend ist. 

Schlussfolgerungen

Wir haben in diesem Artikel drei Experimente durchgeführt. Die ersten beiden Experimente haben gezeigt, wie wichtig die richtige Auswahl der Lernrate des neuronalen Netzes ist. Die Lernrate wirkt sich auf das gesamte Trainingsergebnis des neuronalen Netzes aus. Allerdings gibt es derzeit keine klare Regel für die Auswahl der Lernrate. Deshalb müssen Sie sie in der Praxis experimentell auswählen.

Das dritte Experiment hat gezeigt, dass ein Nicht-Standard-Ansatz zur Lösung eines Problems das Ergebnis verbessern kann. Die Anwendung der jeweiligen Lösung muss aber experimentell bestätigt werden.

Referenzen

1. Neuronale Netze leicht gemacht
2. Neuronale Netze leicht gemacht (Teil 2): Netzwerktraining und Tests
3. Neuronale Netze leicht gemacht (Teil 3): Convolutional Neurale Netzwerke
4. Neuronale Netze leicht gemacht (Teil 4): Rekurrente Netze
5. Neuronale Netze leicht gemacht (Teil 5): Parallele Berechnungen mit OpenCL

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Fractal_OCL1.mq5	Expert Advisor	Ein Expert Advisor mit dem klassifizierenden neuronalen Netz (3 Neuronen in der Ausgabeschicht) unter Verwendung der OpenCL-Technologie Lernrate = 0,1
2	Fractal_OCL2.mq5	Expert Advisor	Ein Expert Advisor mit dem klassifizierenden neuronalen Netz (3 Neuronen in der Ausgabeschicht) unter Verwendung der OpenCL-Technologie Lernrate = 0,01
3	Fractal_OCL3.mq5	Expert Advisor	Ein Expert Advisor mit dem klassifizierenden neuronalen Netz (3 Neuronen in der Ausgabeschicht) unter Verwendung der OpenCL-Technologie Lernrate = 0,001
4	Fractal_OCL_step.mq5	Expert Advisor	Ein Expert Advisor mit dem klassifizierenden neuronalen Netz (3 Neuronen in der Ausgabeschicht) unter Verwendung der OpenCL-Technologie Lernrate mit einer 10-fachen Verringerung von 0,01 alle 10 Epochen
5	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek mit Klassen zum Erstellen eines neuronalen Netzwerks
6	NeuroNet.cl	Bibliothek	Die Bibliothek mit dem Programm-Code für OpenCL