Neuronale Netze leicht gemacht (Teil 85): Multivariate Zeitreihenvorhersage

Einführung

Die Vorhersage von Zeitreihen ist eines der wichtigsten Elemente beim Aufbau einer effektiven Handelsstrategie. Wenn wir eine Handelsoperation in die eine oder andere Richtung durchführen, gehen wir von unserer eigenen Vorstellung (Prognose) von der bevorstehenden Preisbewegung aus. Jüngste Fortschritte bei Deep-Learning-Modellen, insbesondere architekturbasierte Transformer-Modelle, haben in diesem Bereich erhebliche Fortschritte gemacht und bieten ein großes Potenzial für die Lösung der vielschichtigen Probleme, die mit langfristigen Zeitreihenprognosen verbunden sind.

Es stellt sich jedoch die Frage nach der Effizienz der Verwendung der Architektur eines Transformers für Zwecke der Zeitreihenprognose. Die meisten der bisher betrachteten transformerbasierten Modelle verwenden den Mechanismus der Selbstbeobachtung, um langfristige Abhängigkeiten verschiedener Zeitschritte in der analysierten Sequenz zu erfassen. Einige Studien argumentieren jedoch, dass die meisten bestehenden Transformer-Modelle, die auf intertemporaler Aufmerksamkeit basieren, nicht in der Lage sind, intertemporale Abhängigkeiten angemessen zu untersuchen. Manchmal übertrifft ein einfaches lineares Modell einige Transformer-Modelle.

Die Autoren des Artikels „Client: Cross-variable Linear Integrated Enhanced Transformer for Multivariate Long-Term Time Series Forecasting“ hat sich diesem Thema auf recht konstruktive Weise genähert. Um das Ausmaß des Problems abzuschätzen, führten sie ein komplexes Experiment durch, bei dem sie Teile der historischen Reihen ausblendeten und einzelne Daten nach dem Zufallsprinzip durch „0“ ersetzten. Modelle, die empfindlicher auf die Zeitabhängigkeit reagieren, weisen ohne korrekte historische Daten eine starke Leistungsverschlechterung auf. Die Leistungsverschlechterung ist also ein Hinweis auf die Fähigkeit des Modells, zeitliche Muster zu erfassen. Das Experiment ergab, dass die Leistung der auf Cross-Attention basierenden Transformer-Modelle nicht signifikant abnimmt, wenn der Umfang der Datenmaskierung zunimmt. Einige dieser Modelle zeigen eine praktisch unveränderte Vorhersageleistung, selbst wenn bis zu 80 % der historischen Daten zufällig durch „0“ ersetzt werden. Dies könnte darauf hindeuten, dass die Vorhersageergebnisse solcher Modelle nicht auf Veränderungen in den analysierten Zeitreihen reagieren.

Meine persönliche Haltung zu den Ergebnissen der vorliegenden Analyse ist zwiespältig. Natürlich ist die mangelnde Empfindlichkeit gegenüber Veränderungen in den analysierten Zeitreihen, gelinde gesagt, alarmierend. Da das Modell als „Black Box“ betrachtet wird, ist es außerdem schwierig zu verstehen, welchen Teil der Daten das Modell berücksichtigt und welchen es ignoriert.

Andererseits enthalten die analysierten Zeitreihen im Umfeld stochastischer Finanzmärkte eine ganze Menge Rauschen, das vorzugsweise gefiltert werden sollte. In diesem Zusammenhang kann das Ignorieren kleiner Schwankungen oder Ausreißer, die nicht typisch für das betrachtete Umfeld sind, dazu beitragen, den wichtigsten Teil der analysierten Zeitreihe zu identifizieren.

Darüber hinaus stellten die Autoren des Papiers fest, dass in einigen multivariaten Zeitreihen verschiedene Variablen im Laufe der Zeit ähnliche Muster aufweisen. Dies legt die Möglichkeit nahe, Aufmerksamkeitsmechanismen zu nutzen, um Abhängigkeiten zwischen Variablen statt zwischen Zeitschritten zu lernen. Diese Annahme ermöglicht es, das Paradigma zu ändern, in dem der Mechanismus der Selbstaufmerksamkeit angewendet wird.

Obwohl der von den Autoren des Artikels vorgeschlagene Transformer die Nichtlinearität gut modelliert und die Abhängigkeiten zwischen den Variablen erfasst, funktioniert er bei der Extraktion von Trends aus den analysierten Reihen möglicherweise nicht gut. Diese Aufgabe wird von linearen Modellen gut erfüllt. Um das Beste aus beiden Welten zu vereinen, haben die Autoren des Artikels die Methode „Cross-variable Linear Integrated Enhanced Transformer - Client“ für multivariate langfristige Zeitreihenprognosen entwickelt. Der vorgeschlagene Algorithmus kombiniert die Fähigkeit linearer Modelle, Trends zu extrahieren, mit den Ausdrucksmöglichkeiten des erweiterten Transformers.

1. Der Algorithmus „Client“

Die Hauptidee von Client ist die Verlagerung der Aufmerksamkeit von der Zeit auf die Analyse der Abhängigkeiten zwischen den Variablen und die Integration eines linearen Moduls in das Modell, um die Abhängigkeiten zwischen den Variablen bzw. die Trendinformationen besser zu nutzen.

Die Autoren der Methode Client haben einen kreativen Ansatz zur Lösung des Problems der Zeitreihenprognose gewählt. Zum einen greift der vorgeschlagene Algorithmus auf bereits bekannte Ansätze zurück. Andererseits verwirft er einige bewährte Methoden. Die Aufnahme oder der Ausschluss jedes einzelnen Blocks in den Algorithmus wird von einer Reihe von Tests begleitet. Die Tests zeigen die Durchführbarkeit der getroffenen Entscheidung unter dem Gesichtspunkt der Wirksamkeit des Modells.

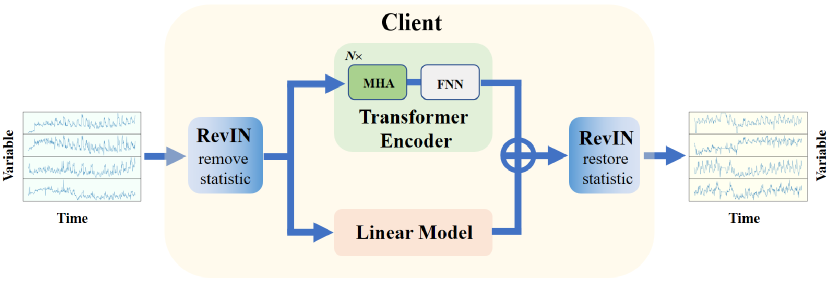
Um das Problem des Verteilungsbias zu lösen, verwenden die Autoren der Methode eine reversible Normalisierung mit einer symmetrischen Struktur (RevIN), die im vorherigen Artikel beschrieben wurde. RevIN wird zunächst verwendet, um statistische Informationen über die Zeitreihe aus den Originaldaten zu entfernen. Nachdem das Modell die Daten verarbeitet und Prognosewerte erzeugt hat, wird die statistische Information der ursprünglichen Zeitreihe in der Prognose wiederhergestellt, was im Allgemeinen die Stabilität der Modellschulung und die Qualität der Prognosewerte der Zeitreihe erhöht.

Um eine weitere Analyse in Form von Variablen und nicht in Form von Zeitschritten zu ermöglichen, schlagen die Autoren der Methode vor, die Ausgangsdaten zu transponieren.

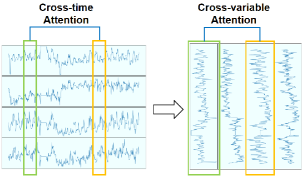
Die so aufbereiteten Daten werden in den Transformer-Encoder eingespeist, der aus mehreren Schichten von mehrköpfigen Self-Attention (MHA) und FeedForward (FFN)-Blöcken besteht.

Bitte beachten Sie, dass die Eingabe an den Encoder geleitet wird und die normalerweise vorhandene Einbettungsschicht umgangen wird. Die von den Autoren der Methode durchgeführten Tests haben gezeigt, dass ihre Anwendung unwirksam ist, da die zusätzliche Ebene der Datentransformation die Zeitinformationen verzerrt und zu einer Verringerung der Leistung des Modells führt. Außerdem entfällt der Block für die Positionskodierung, da es keine zeitliche Abfolge zwischen den verschiedenen Variablen gibt.

Nach der Merkmalsextraktion im Encoder wird die Zeitreihe an die Projektionsschicht weitergeleitet, die für jede Variable prognostizierte Werte erzeugt.

Die vorgeschlagene Projektionsschicht ersetzt den klassischen Transformer-Decoder. In ihrer Arbeit stellten die Autoren von Client fest, dass das Hinzufügen eines Decoders zu einem Rückgang der Gesamtleistung des Modells führte.

Parallel zum Aufmerksamkeitsblock enthält „Client“ ein integriertes, lineares Modul, das zur Untersuchung von Informationen über die Trends von Zeitreihen in unabhängigen Kanälen und einzelnen Variablen verwendet wird.

Die vorhergesagten Werte des Aufmerksamkeitsblocks und des linearen Moduls werden unter Berücksichtigung der erlernbaren Gewichte, die auf die Ergebnisse des linearen Moduls angewendet werden, summiert.

Am Ausgang des Modells werden die Ergebnisse erneut transponiert, um sie mit der Reihenfolge der ursprünglichen Daten in Einklang zu bringen. Die statistischen Informationen der Zeitreihe werden wiederhergestellt.

So verwendet die Methode Client das lineare Modul zur Erfassung von Trendinformationen und das erweiterte Modul des Transformers zur Erfassung nichtlinearer Informationen und Abhängigkeiten zwischen Variablen. Im Folgenden wird die Visualisierung der Methode durch den Autor vorgestellt.

2. Implementierung in MQL5

Nach der Betrachtung der theoretischen Aspekte der Methode Client, gehen wir zum praktischen Teil unseres Artikels über, in dem wir unsere Vision der vorgeschlagenen Ansätze mit MQL5 umsetzen.

2.1 Erstellen einer neuen neuronalen Schicht

Zunächst erstellen wir eine neue Klasse CNeuronClientOCL, die die meisten der vorgeschlagenen Ansätze kombiniert. Wir erstellen diese Klasse, wie die meisten anderen, die wir zuvor erstellt haben, indem wir von unserer Basisklasse für neuronale Schichten (CNeuronBaseOCL) erben.

class CNeuronClientOCL  :  public CNeuronBaseOCL
  {
protected:
   //--- Attention
   CNeuronMLMHAttentionOCL cTransformerEncoder;
   CNeuronConvOCL    cProjection;
   //--- Linear model
   CNeuronConvOCL    cLinearModel[];
   //---
   CNeuronBaseOCL    cInput;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);

public:
                     CNeuronClientOCL(void) {};
                    ~CNeuronClientOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint heads,
                          uint at_layers, uint count, uint &mlp[],
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronClientOCL;   }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual void      SetOpenCL(COpenCLMy *obj);
   virtual void      TrainMode(bool flag);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
  };

Der Aufmerksamkeitsblock wird aus 2 Objekten erstellt:

• cTransformerEncoder — das Objekt der Klasse CNeuronMLMHAttentionOCL, das es ermöglicht, den Encoder-Block des Mehrkopf-Transformers aus einer bestimmten Anzahl aufeinander folgender Schichten zu erstellen.
• cProjection — Projektionsschicht. Hier verwenden wir eine Faltungsschicht, um unabhängige Vorhersagen für einzelne Variablen zu treffen. Die Vorhersagetiefe bestimmt die Anzahl der Filter in der Schicht.

Um ein lineares Modul zu erstellen, werden wir ein dynamisches Array von Faltungsschichten cLinearModel[] erstellen, das es uns ermöglicht, unabhängige Prognosen für einzelne Variablen zu erstellen.

Beachten Sie, dass ich in dieser Implementierung beschlossen habe, die reversiblen Normalisierungs- und Datentranspositionsebenen außerhalb der Klasse zu platzieren. Der Grund dafür ist, dass der Client-Block in eine komplexere Architektur integriert werden kann. Daher können statistische Informationen weit entfernt von diesem Block gelöscht und wiederhergestellt werden.

Die Datenumsetzung kann auch in einem gewissen Abstand zum Client-Block erfolgen. Darüber hinaus ist es in einigen Fällen möglich, die erforderliche Reihenfolge der Quelldaten bereits in der Phase der Datenaufbereitung zu erstellen.

Der Methodensatz unserer neuen Klasse ist ziemlich standardisiert.

Wir deklarieren alle internen Objekte als statisch, was uns erlaubt, den Konstruktor und den Destruktor der Klasse leer zu lassen. Mit diesem Ansatz können wir uns weniger auf Probleme der Speicherbereinigung konzentrieren und diese Funktion an das System delegieren.

Die Initialisierung aller internen Objekte wird in der Methode Init durchgeführt. In den Parametern dieser Methode übergeben wir dem Klassenobjekt alle Informationen, die zur Organisation der gewünschten Architektur erforderlich sind.

An dieser Stelle sei angemerkt, dass wir im Klassenkörper 2 parallele Streams erzeugen:

• Der Transformer-Block
• Das lineare Modul

Beide Module haben komplexe und sehr unterschiedliche unabhängige Architekturen, obwohl sie mit demselben Datensatz arbeiten. Daher benötigen wir einen Mechanismus, um beide Module in das Architekturobjekt zu übertragen. Für den Transformer-Block werden wir den zuvor entwickelten Ansatz mit 5 Variablen verwenden:

• window: Größe des Vektors von 1 Element der Sequenz
• window_key: Größe des Vektors der internen Darstellung von 1 Element der Sequenz
• heads: Anzahl der Aufmerksamkeitsköpfe
• count: Anzahl der Elemente in der Sequenz
• at_layers: Anzahl der Ebenen im Encoder-Block

Um die Architektur des linearen Moduls zu beschreiben, verwenden wir ein numerisches Array mlp[]. Die Anzahl der Elemente in dem Array gibt die Anzahl der zu erstellenden Ebenen an. Der Wert der einzelnen Elemente gibt die Größe des Vektors an, der ein Element der Sequenz am Ausgang der Schicht beschreibt. Das lineare Modul arbeitet mit demselben Datensatz wie der Aufmerksamkeitsblock. Daher ist die Anzahl der Elemente in der Folge gleich.

Bitte beachten Sie, dass die Autoren der Client-Methode vorschlagen, die Abhängigkeiten zwischen den Variablen zu analysieren. Daher entspricht in diesem Fall die Größe des Vektors, der ein Element der Sequenz beschreibt, der Tiefe der analysierten Geschichte. Die Anzahl der Elemente in der Sequenz ist gleich der Anzahl der zu analysierenden Variablen. Die Eingabedaten müssen entsprechend umgewandelt werden, bevor sie in unser neues Klassenobjekt CNeuronClientOCL eingespeist werden.

Bei diesem Ansatz wird die Tiefe der Datenprognose im letzten Element des Arrays mlp[] angegeben.

Dies ist die Logik der Datenübertragung. Lassen Sie uns den vorgeschlagenen Ansatz in Code umsetzen. In den Parametern der Methode Init geben wir die oben vorgestellten Variablen an und ergänzen sie durch Elemente der Basisklasse.

bool CNeuronClientOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                            uint window, uint window_key, uint heads,
                            uint at_layers, uint count, uint &mlp[],
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   uint mlp_layers = mlp.Size();
   if(mlp_layers == 0)
      return false;

Im Hauptteil der Methode wird zunächst die Größe des linearen Modularchitektur-Beschreibungsarrays mlp[] überprüft. Sie muss mindestens ein Element enthalten, das die Tiefe der Datenprognose angibt. Wenn das Array leer ist, wird die Methode mit einem Ergebnis false beendet.

Im nächsten Schritt initialisieren wir die Klassenobjekte. Zunächst ändern wir das dynamische Feld des linearen Moduls.

   if(ArrayResize(cLinearModel, mlp_layers + 1) != (mlp_layers + 1))
      return false;

Bitte beachten Sie, dass die Arraygröße um 1 Element größer sein muss als die resultierende lineare Schichtenarchitektur. Auf die Gründe für diesen Schritt werden wir etwas später eingehen.

Als Nächstes rufen wir die gleiche Methode der übergeordneten Klasse auf, die alle geerbten Objekte initialisiert.

   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, mlp[mlp_layers - 1] * count, optimization_type, batch))
      return false;

Danach rufen wir die Initialisierungsmethode des Transformer-Encoders auf.

   if(!cTransformerEncoder.Init(0, 0, OpenCL, window, window_key, heads, count, at_layers, optimization, iBatch))
      return false;

Eine Hilfsebene zur vorübergehenden Speicherung der Eingabedaten.

   if(!cInput.Init(0, 1, open_cl, window * count, optimization_type, batch))
      return false;

Der nächste Schritt besteht darin, eine Schleife zu erstellen, in der wir die Schichten des linearen Moduls initialisieren.

   uint w = window;
   for(uint i = 0; i < mlp_layers; i++)
     {
      if(!cLinearModel[i].Init(0, i + 2, OpenCL, w, w, mlp[i], count, optimization, iBatch))
         return false;
      cLinearModel[i].SetActivationFunction(LReLU);
      w = mlp[i];
     }

Hier sei daran erinnert, dass die Autoren der Client-Methode vorschlagen, Lernkoeffizienten auf die Ergebnisse des linearen Moduls anzuwenden. Sie haben eine eher ungewöhnliche Methode gefunden, um lernfähige Multiplikatoren zu schaffen. Ich beschloss, sie durch eine Faltungsschicht zu ersetzen, wobei die Anzahl der Filter, die Fenstergröße und der Faltungsschritt gleich 1 sind. Wir fügen es dem letzten (von uns zuvor hinzugefügten) Element der linearen Modulanordnung hinzu.

   if(!cLinearModel[mlp_layers].Init(0, mlp_layers + 2, OpenCL, 1, 1, 1, w * count, optimization, iBatch))
      return false;

Es gibt noch eine weitere Sache hier. Bei der Normalisierung der Eingabedaten werden diese in einen Mittelwert von „0“ und eine Varianz von „1“ umgewandelt. Daher sollten auch die vorhergesagten Werte dieser Verteilung entsprechen. Um die vorhergesagten Werte einzuschränken, verwenden wir den hyperbolischen Tangens (tanh) als Aktivierungsfunktion.

Auf ähnliche Weise leiten wir die Projektionsschicht des Aufmerksamkeitsblocks ein.

   cLinearModel[mlp_layers].SetActivationFunction(TANH);
   if(!cProjection.Init(0, mlp_layers + 3, OpenCL, window, window, w, count, optimization, iBatch))
      return false;
   cProjection.SetActivationFunction(TANH);

Wie Sie sehen, werden beide Blöcke der Ausgangsdatenvorhersage durch die hyperbolische Tangente aktiviert. Um eine korrekte Übertragung des Fehlergradienten zu gewährleisten, legen wir eine ähnliche Aktivierungsfunktion für die gesamte Schicht fest.

   SetActivationFunction(TANH);

Da wir vorhaben, die Werte der beiden Module einfach zu addieren, können wir beim Rückwärtsdurchlauf den Fehlergradienten in vollem Umfang auf beide Module verteilen. Um unnötige Datenkopiervorgänge zu vermeiden, werden wir die Datenpuffer, in denen Fehlergradienten gespeichert sind, in den internen Schichten ersetzen.

   if(!SetGradient(cProjection.getGradient()))
      return false;
   if(!cLinearModel[mlp_layers].SetGradient(Gradient))
      return false;
//---
   return true;
  }

Vergessen Sie nicht, die Vorgänge in jeder Phase zu kontrollieren. Nach erfolgreicher Initialisierung aller verschachtelten Objekte geben wir das logische Ergebnis der Operationen an den Aufrufer zurück.

Nach der Initialisierung der verschachtelten Klassenobjekte geht es an die Organisation des Vorwärtsdurchgangs-Algorithmus in der Methode CNeuronClientOCL::feedForward. Wir haben die Grundprinzipien der Datenübertragung bei der Initialisierung von Objekten besprochen. Schauen wir uns nun die Umsetzung der vorgeschlagenen Ansätze an.

In den Parametern erhält die Methode einen Zeiger auf das Objekt der vorherigen neuronalen Schicht. Im Hauptteil der Methode rufen wir sofort die Vorwärts-Methode unseres mehrschichtigen Aufmerksamkeitsblocks auf.

bool CNeuronClientOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTransformerEncoder.FeedForward(NeuronOCL))
      return false;

Anschließend projizieren wir die Prognosewerte auf die erforderliche Planungstiefe.

   if(!cProjection.FeedForward(GetPointer(cTransformerEncoder)))
      return false;

Um zu vermeiden, dass das gesamte Volumen der Eingabedaten in die innere Schicht kopiert wird, kopieren wir nur den Zeiger auf den entsprechenden Datenpuffer.

   if(cInput.getOutputIndex() != NeuronOCL.getOutputIndex())
      cInput.getOutput().BufferSet(NeuronOCL.getOutputIndex());

Für das lineare Modul organisieren wir eine Vorwärtsschleife.

   uint total = cLinearModel.Size();
   CNeuronBaseOCL *neuron = NeuronOCL;
   for(uint i = 0; i < total; i++)
     {
      if(!cLinearModel[i].FeedForward(neuron))
         return false;
      neuron = GetPointer(cLinearModel[i]);
     }

In diesem Stadium liegen uns Projektionen der Prognosewerte für beide Module vor. Die linearen Modulprognosen wurden bereits um die Trainingskoeffizienten bereinigt. Jetzt müssen wir nur noch die Daten aus beiden Threads zusammenzählen.

   if(!SumAndNormilize(neuron.getOutput(), cProjection.getOutput(), Output, 1, false, 0, 0, 0, 
0.5 ))
      return false;
//---
   return true;
  }

In ähnlicher Weise, aber in umgekehrter Reihenfolge, führen wir eine Fehlergradientenfortpflanzung durch die verschachtelten Objekte bis zur vorherigen Schicht durch, entsprechend ihrem Einfluss auf das Endergebnis. Dies geschieht mit der Methode CNeuronClientOCL::calcInputGradients.

Da wir die Substitution von Datenpuffern verwenden, wird der Fehlergradient aus der nächsten Schicht direkt in die Objektpuffer beider Module geschrieben. Daher verzichten wir auf den unnötigen Vorgang der Verteilung des Fehlergradienten zwischen Transformer und einem linearen Modul. Wir gehen sofort zur Verteilung des Fehlergradienten durch die angegebenen Module über. Zunächst wird der Fehlergradient durch den Aufmerksamkeitsblock geleitet.

bool CNeuronClientOCL::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!cTransformerEncoder.calcHiddenGradients(cProjection.AsObject()))
      return false;
   if(!prevLayer.calcHiddenGradients(cTransformerEncoder.AsObject()))
      return false;

Dann leiten wir sie in der Backpropagation-Schleife durch das lineare Modul.

   CNeuronBaseOCL *neuron = NULL;
   int total = (int)cLinearModel.Size() - 1;
   for(int i = total; i >= 0; i--)
     {
      neuron = (i > 0 ? cLinearModel[i - 1] : cInput).AsObject();
      if(!neuron.calcHiddenGradients(cLinearModel[i].AsObject()))
         return false;
     }

Beachten Sie, dass Transformer den Fehlergradienten in den Puffer der vorherigen Schicht schreibt. Das lineare Modell schreibt es in den Puffer der inneren Schicht.

Bevor wir die Methode beenden, addieren wir die Fehlergradienten der beiden Ströme.

   if(!SumAndNormilize(neuron.getGradient(), prevLayer.getGradient(), prevLayer.getGradient(), 1, false))
      return false;
//---
   return true;
  }

Andere Methoden dieser Klasse sind in etwa gleich aufgebaut. Wir rufen die entsprechenden Methoden der internen Objekte nacheinander auf. Im Rahmen dieses Artikels werden wir nicht auf die Beschreibung ihres Algorithmus im Detail eingehen. Ich empfehle Ihnen, sich mit ihnen vertraut zu machen. Den vollständigen Code der Klasse und alle ihre Methoden finden Sie im Anhang. Der Anhang enthält auch den vollständigen Code aller im Artikel verwendeten Programme.

2.2 Modellarchitektur

Wir haben eine neue Klasse CNeuronClientOCL erstellt, die den Hauptteil der von den Autoren der Client-Methode vorgeschlagenen Ansätze implementiert. Einige Anforderungen der Methode müssen jedoch direkt in der Modellarchitektur umgesetzt werden.

Die Client-Methode wurde vorgeschlagen, um Probleme der Zeitreihenprognose zu lösen. Wir werden sie in unserem Encoder verwenden.

In der Struktur unserer Modelle wird der Encoder verwendet, um eine komprimierte Darstellung des Zustands der Umgebung zu erstellen. Das Akteursmodell verwendet diese Darstellung, um die optimale Aktion in einem bestimmten Zustand auf der Grundlage der erlernten Verhaltensregeln zu generieren. Um die bestmögliche Verhaltenspolitik zu erlernen, benötigen wir natürlich eine korrekte und informative Darstellung des Zustands der Umwelt.

Das Konzept der „korrekten und informativen verdichteten Darstellung des Zustands der Umwelt“ klingt recht abstrakt und vage. Es ist logisch anzunehmen, dass, da wir die Politik des Akteurs darauf trainieren, optimale Aktionen auszuführen, um den größtmöglichen Gewinn unter den Bedingungen der wahrscheinlichsten bevorstehenden Preisbewegung zu erzielen, die komprimierte Darstellung die größtmögliche Information über die wahrscheinlichste bevorstehende Preisbewegung enthalten sollte. Darüber hinaus müssen wir die Risiken und die Wahrscheinlichkeit einer gegenläufigen Kursentwicklung bewerten. Wir müssen auch das mögliche Ausmaß einer solchen Bewegung bewerten. In einem solchen Paradigma scheint es angemessen, den Encoder zu trainieren, um zukünftige Preisbewegungen vorherzusagen. Dann wird der verborgene Zustand des Encoders die größtmögliche Information über die bevorstehende Kursbewegung enthalten. Daher verwenden wir in der Architektur unseres Encoders die Ansätze der Client-Methode.

Die Architektur des Encoders wird in der Methode CreateEncoderDescriptions vorgestellt. In den Parametern erhält die Methode einen Zeiger auf ein dynamisches Array, in dem die Modellarchitektur gespeichert werden soll.

bool CreateEncoderDescriptions(CArrayObj *encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

Im Hauptteil der Methode wird der empfangene Zeiger überprüft und gegebenenfalls eine neue Instanz des dynamischen Array-Objekts erstellt.

Wie üblich füttern wir das Modell mit einer „rohen“ Beschreibung des Zustands der Umwelt. Um die Rohdaten zu erfassen, erstellen wir eine Basisschicht des neuronalen Netzes, die groß genug ist, um die Rohdaten aufzunehmen.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Auch hier wird die Schichtgröße durch das Produkt aus zwei Konstanten bestimmt:

• HistoryBars — die Tiefe der analysierten Geschichte der Zustände (Balken) der Umgebung
• BarDescr — die Größe des Vektors, der einen Balken des Umgebungszustands beschreibt

Aber es gibt eine Sache. Bisher haben wir das Modell bei jeder Iteration nur mit Informationen über den letzten geschlossenen Balken innerhalb der Kursbewegung gefüttert. Die gesamte erforderliche Tiefe der analysierten Geschichte wurde in Form von Einbettungen im Stapel der inneren Schicht unseres Modells akkumuliert. Die Autoren der Client-Methode gehen nun davon aus, dass die zusätzliche Einbettungsschicht die Zeitreiheninformationen verfälscht und empfehlen daher, sie zu eliminieren. Daher erweitern wir die Eingabedatenschicht des Modells, um es mit Daten zu füttern, die die gesamte Tiefe der zu analysierenden Geschichte abdecken.

Wir haben also den Wert der Konstante HistoryBars auf 120 erhöht. Damit können Sie die historischen Daten der letzten Woche im H1-Zeitrahmen analysieren.

#define        HistoryBars             120           //Depth of history

Die nächste Schicht ist wie zuvor eine Batch-Normalisierungsschicht, in der die Eingabedaten in eine vergleichbare Form gebracht werden, indem statistische Informationen aus den Zeitreihen entfernt werden.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Erinnern wir uns an den Identifikator dieser Ebene. Denn am Ausgang des Modells müssen wir die statistischen Informationen der Zeitreihen auf die Prognosewerte zurückführen.

Bei der Aufbereitung der Eingabedaten können wir diese als eine Folge von Daten einzelner Indikatoren (Variablen im Rahmen der Client-Methode) bilden. Optional können wir sie in Form einer Abfolge von Beschreibungen von Zeitschritten (Balken) zur Verfügung stellen, wie es zuvor getan wurde. Für die Zwecke dieses Artikels habe ich beschlossen, den Block zur Vorbereitung der Eingabedaten nicht zu ändern. So können wir bereits erstellte Umgebungsinteraktions-EAs mit minimalen Änderungen verwenden.

Eine solche Implementierung erfordert jedoch die Installation einer Datenumsetzungsschicht, die wir im nächsten Schritt hinzufügen werden.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   prev_count = descr.count = HistoryBars;
   int prev_wout = descr.window = BarDescr;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Nach der Transponierungsebene fügen wir eine Instanz unserer neuen Ebene hinzu - den Client-Block.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronClientOCL;
   descr.count = prev_wout;
   descr.window = prev_count;
   descr.step = 4;
   descr.window_out = EmbeddingSize;
   descr.layers = 5;
     {
      int temp[] = {1024, 1024, 1024, NForecast};
      ArrayCopy(descr.windows, temp);
     }
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Hier geben wir für die Größe der zu analysierenden Sequenz die Anzahl der zu analysierenden Variablen an (die Konstante BarDescr). Die Größe des Vektors, der ein Element der Sequenz beschreibt, ist gleich der Tiefe des zu analysierenden Verlaufs (die Konstante HistoryBars). Im Transformer-Block verwenden wir 4 Aufmerksamkeitsköpfe und erstellen 5 solcher Ebenen.

Wir werden ein lineares Modul aus 4 Schichten erstellen: 3 versteckte Schichten der Größe 1024 und die letzte Schicht gleich dem Planungshorizont (die NForecast-Konstante).

Als Nächstes führen wir die inverse Transposition der Daten durch.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   prev_count = descr.count = BarDescr;
   prev_wout = descr.window = NForecast;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Wir stellen darin statistische Informationen wieder her.

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   prev_count = descr.count = prev_count * prev_wout;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers = 1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Ich sollte ein paar Worte über die Architektur des Akteurs sagen. Er ist fast vollständig aus dem vorherigen Artikel übernommen. Es gibt jedoch ein Detail, das später erklärt wird. 

Die Architektur der Modelle Akteur (actor) und Kritiker (critic) wird in der Methode CreateDescriptions vorgestellt. In den Methodenparametern erhalten wir Zeiger auf 2 dynamische Arrays zur Erfassung der Modellarchitektur.

bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!critic)
     {
      critic = new CArrayObj();
      if(!critic)
         return false;
     }

Im Hauptteil der Methode werden die empfangenen Zeiger überprüft und gegebenenfalls neue Instanzen von dynamischen Array-Objekten erstellt.

Wie zuvor füttern wir das Akteursmodell mit einer Beschreibung des Standes der Leistungsbilanz und der offenen Positionen.

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = AccountDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Als Nächstes bilden wir die Einbettung des Kontostandes.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = EmbeddingSize;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Wir fügen 3 aufeinanderfolgende Schichten von Cross-Attention hinzu, in denen wir die Abhängigkeiten zwischen dem aktuellen Zustand des Kontos und der komprimierten Darstellung zukünftiger Zustände der Umgebung, die vom Encoder gebildet wird, analysieren.

//--- layer 2-4
   for(int i = 0; i < 3; i++)
     {
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronCrossAttenOCL;
        {
         int temp[] = {1, BarDescr};
         ArrayCopy(descr.units, temp);
        }
        {
         int temp[] = {EmbeddingSize, NForecast};
         ArrayCopy(descr.windows, temp);
        }
      descr.window_out = 16;
      descr.step = 4;
      descr.activation = None;
      descr.optimization = ADAM;
      if(!actor.Add(descr))
        {
         delete descr;
         return false;
        }
     }

Gemäß der Idee der Client-Methode verwenden wir für die Queranalyse die Daten aus dem verborgenen Zustand des Encoders, bevor wir die Daten neu transponieren. Auf diese Weise können wir die Abhängigkeiten der Leistungsbilanz mit den vorhergesagten Werten der einzelnen Variablen analysieren. Dies spiegelt sich in den neuen Werten der Arrays desc.units und descr.windows wider.

Als Nächstes folgt, wie zuvor, der Entscheidungsblock, wobei der Politik des Akteurs Stochastik hinzugefügt wird.

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 2 * NActions;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronVAEOCL;
   descr.count = NActions;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Ähnliche Änderungen betrafen das Modell Kritiker. Wie Sie sich erinnern, haben die Modelle Akteur und Kritiker eine ähnliche Architektur. Der Unterschied besteht darin, dass die Eingabe des Kritiker-Modells ein Aktionsvektor ist und nicht die Beschreibung des Kontostands. Am Ausgang des Modells wird der Aktionsvektor durch einen Belohnungsvektor ersetzt. Eine vollständige Beschreibung der architektonischen Lösungen aller verwendeten Modelle finden Sie in der Anlage. Der Anhang enthält auch den vollständigen Code aller im Artikel verwendeten Programme.

Zusätzlich haben wir den Wert des konstanten Zeigers auf die verborgene Schicht des Encoders für die Datenextraktion geändert.

#define        LatentLayer             3

Da wir viel Arbeit geleistet haben, um die architektonischen Lösungen der Modelle zu koordinieren und die verwendeten Konstanten zu ändern, können wir bereits erstellte EAs für die Interaktion mit der Umwelt praktisch ohne Änderungen verwenden. Wir müssen sie nur neu kompilieren und dabei die geänderten Konstanten und die Modellarchitektur berücksichtigen. Dies bezieht sich jedoch nicht auf den Trainings-EAs des Modells.

2.3 Trainings-EA des Vorhersagemodells

Das Modell für die Vorhersage der Umweltbedingungen wird mit dem EA „...\Experts\Client\StudyEncoder.mq5“ trainiert. Im Allgemeinen ist die Struktur des EA von früheren Arbeiten übernommen worden. Wir werden nicht auf alle Methoden im Detail eingehen. Betrachten wir nur die Phase der Modellschulung, die mit der Methode Train durchgeführt wird.

void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);
//---
   vector<float> result, target;
   bool Stop = false;
//---
   uint ticks = GetTickCount();

Im Hauptteil der Methode generieren wir zunächst einen Vektor von Wahrscheinlichkeiten für die Auswahl von Trajektorien aus dem Erfahrungswiedergabepuffer entsprechend ihrer tatsächlichen Rentabilität. Durchgänge mit Gewinn werden eher für den Lernprozess genutzt. So verlagern wir den Schwerpunkt des Training auf die Trajektorien mit der höchsten Rentabilität.

Nach den vorbereitenden Arbeiten organisieren wir die Modelltrainingsschleife. Im Gegensatz zu einigen neueren Arbeiten verwenden wir hier eine einfache Schleife und nicht das zuvor verwendete System der verschachtelten Schleifen. Dies ist möglich, weil wir in der Modellarchitektur keine wiederkehrenden Elemente (Stapel von Einbettungen) verwenden.

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++)
     {
      int tr = SampleTrajectory(probability);
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast));
      if(i <= 0)
        {
         iter--;
         continue;
        }

Im Hauptteil der Schleife werden die Trajektorie aus dem Erfahrungswiedergabepuffer und der Zustand der Umgebung erfasst.

Wir extrahieren die Beschreibung des abgetasteten Zustands der Umgebung aus dem Experimentwiedergabepuffer und übertragen die erhaltenen Werte in den Datenpuffer.

      bState.AssignArray(Buffer[tr].States[i].state);

Diese Informationen reichen aus, um einen Vorwärtsdurchgang des Encoders durchzuführen.

      //--- State Encoder
      if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Als Nächstes müssen wir einen Vektor von Zielwerten vorbereiten. Im Rahmen dieser Arbeit ist der Planungshorizont viel kleiner als die Tiefe der analysierten Geschichte. Dies vereinfacht unsere Aufgabe, Zielwerte zu erstellen, erheblich. Wir extrahieren einfach aus dem Erfahrungswiedergabepuffer eine Beschreibung des Umgebungszustands mit einer Einkerbung des Planungshorizonts. Wir nehmen auch die ersten Elemente des Tensors im gewünschten Volumen.

      //--- Collect target data
      if(!bState.AssignArray(Buffer[tr].States[i + NForecast].state))
         continue;
      if(!bState.Resize(BarDescr * NForecast))
         continue;

Wenn Sie einen Planungshorizont verwenden, der größer ist als die Tiefe der analysierten Historie, muss für die Erfassung der Zielwerte eine Schleife über die Zustände im Erfahrungswiedergabepuffer für den Planungshorizont erstellt werden.

Nach der Vorbereitung des Zielwerttensors führen wir den Rückwärtsdurchgang des Encoders durch, um die Parameter des trainierten Modells zu optimieren und den Datenvorhersagefehler zu minimieren.

      if(!Encoder.backProp(GetPointer(bState), (CBufferFloat*)NULL))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Schließlich informieren wir den Nutzer über den Trainingsfortschritt und gehen zur nächsten Trainingsiteration über.

      if(GetTickCount() - ticks > 500)
        {
         double percent = double(iter) * 100.0 / (Iterations);
         string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Encoder", percent, 
                                                                       Encoder.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }

Achten Sie darauf, dass Sie den Prozess der Durchführung von Vorgängen bei jedem Schritt kontrollieren. Nachdem alle Iterationen des Modelltrainings erfolgreich abgeschlossen wurden, wird das Kommentarfeld im Chart gelöscht.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Encoder", Encoder.getRecentAverageError());
   ExpertRemove();
//---
  }

Zeigen wir die Ergebnisse des Modelltrainings im Protokoll an. Initiieren der Beendigung des EA.

2.4 Akteurspolitischer Trainings-EA

Außerdem wurden einige Änderungen an dem EA „...\Experts\Client\Study.mq5“ für die Schulung zum Thema Akteurspolitik vorgenommen. Auch hier konzentrieren wir uns nur auf die Methode der Modellbildung.

void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);
//---
   vector<float> result, target;
   bool Stop = false;
//---
   uint ticks = GetTickCount();

Im Hauptteil der Methode wird zunächst ein Vektor der Auswahlwahrscheinlichkeiten der Trajektorien erzeugt und andere vorbereitende Arbeiten durchgeführt. In diesem Teil sehen wir eine exakte Wiederholung des Algorithmus des vorherigen EA.

Als Nächstes organisieren wir eine Modelltrainingsschleife, in der wir die Trajektorie aus dem Erfahrungswiedergabepuffer und den Zustand der Umgebung darauf abfragen.

Wir laden die ausgewählte Beschreibung des Umgebungszustands und führen einen Vorwärtsdurchgang des Encoders durch.

      bState.AssignArray(Buffer[tr].States[i].state);
      //--- State Encoder
      if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Damit ist das „Kopieren“ des Algorithmus des vorherigen EA abgeschlossen. Nachdem wir eine verdichtete Darstellung der Umgebung erstellt haben, optimieren wir zunächst die Parameter des Kritikers. Hier laden wir zunächst die Aktionen des Akteurs, die während der Interaktion mit der Umgebung im gegebenen Zustand ausgeführt wurden, und führen einen Vorwärtsdurchlauf des Kritikers aus.

      //--- Critic
      bActions.AssignArray(Buffer[tr].States[i].action);
      if(bActions.GetIndex() >= 0)
         bActions.BufferWrite();
      if(!Critic.feedForward((CBufferFloat*)GetPointer(bActions), 1, false, GetPointer(Encoder), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Wir extrahieren dann aus dem Erfahrungswiedergabepuffer die tatsächliche Belohnung, die der Akteur für seine Handlungen von der Umwelt erhält.

      result.Assign(Buffer[tr].States[i + 1].rewards);
      target.Assign(Buffer[tr].States[i + 2].rewards);
      result = result - target * DiscFactor;
      Result.AssignArray(result);

 Wir optimieren die Parameter des Kritikers, um den Fehler bei der Bewertung der Handlungen des Akteurs zu minimieren.

      Critic.TrainMode(true);
      if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Als Nächstes folgt der Block des zweistufigen Trainings der Politik des Akteurs. Hier extrahieren wir zunächst die Beschreibung des Kontostandes, die dem ausgewählten Umgebungszustand entspricht, und übertragen sie in den Datenpuffer.

      //--- Policy
      float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
      float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
      bAccount.Clear();
      bAccount.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance);
      bAccount.Add(Buffer[tr].States[i].account[1] / PrevBalance);
      bAccount.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity);
      bAccount.Add(Buffer[tr].States[i].account[2]);
      bAccount.Add(Buffer[tr].States[i].account[3]);
      bAccount.Add(Buffer[tr].States[i].account[4] / PrevBalance);
      bAccount.Add(Buffer[tr].States[i].account[5] / PrevBalance);
      bAccount.Add(Buffer[tr].States[i].account[6] / PrevBalance);

Danach fügen wir dem Puffer die Zeitstempel-Harmonien hinzu.

      double time = (double)Buffer[tr].States[i].account[7];
      double x = time / (double)(D'2024.01.01' - D'2023.01.01');
      bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_MN1);
      bAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_W1);
      bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_D1);
      bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      if(bAccount.GetIndex() >= 0)
         bAccount.BufferWrite();

Dann führen wir einen Vorwärtsdurchgang des Akteurs durch, um den Aktionsvektor zu erzeugen.

      //--- Actor
      if(!Actor.feedForward((CBufferFloat*)GetPointer(bAccount), 1, false, GetPointer(Encoder), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Wie oben erwähnt, wird die Politik des Akteurs in 2 Schritten trainiert. Zunächst passen wir die Politik des Akteurs so an, dass seine Aktionen innerhalb der Verteilung unserer Trainingsmenge bleiben. Um dies zu erreichen, minimieren wir den Fehler zwischen dem vom Akteur generierten Aktionsvektor und den tatsächlichen Aktionen aus dem Erfahrungswiedergabepuffer.

      if(!Actor.backProp(GetPointer(bActions), GetPointer(Encoder), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Im zweiten Schritt passen wir die Politik des Akteurs entsprechend der Bewertung der generierten Aktionen durch den Kritiker an. Hier müssen wir zunächst die Aktionen bewerten.

      if(!Critic.feedForward((CNet *)GetPointer(Actor), -1, (CNet*)GetPointer(Encoder), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Dann schalten wir den kritischen Lernmodus aus und propagieren durch ihn den Gradienten der Abweichung der Handlungsbewertung von dem, was in einem bestimmten Zustand tatsächlich möglich ist.

      Critic.TrainMode(false);
      if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder), LatentLayer) ||
         !Actor.backPropGradient((CNet *)GetPointer(Encoder), LatentLayer, -1, true))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Dabei gehen wir davon aus, dass sich die Politik des Akteurs im Laufe des Lernprozesses stets verbessern sollte. Die erhaltene Belohnung darf nicht schlechter sein als diejenige, die bei der Interaktion mit der Umwelt tatsächlich erhalten wurde.

Nach der Aktualisierung der Modellparameter informieren wir den Nutzer über den Fortschritt des Trainingsprozesses und fahren mit der nächsten Iteration der Schleife fort.

      if(GetTickCount() - ticks > 500)
        {
         double percent = double(iter) * 100.0 / (Iterations);
         string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent, 
                                                                       Actor.getRecentAverageError());
         str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Critic", percent, 
                                                                       Critic.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }

Vergessen Sie nicht, den Arbeitsablauf bei jedem Schritt zu kontrollieren.

Nachdem alle Iterationen des Modelltrainings erfolgreich abgeschlossen wurden, löschen wir das Kommentarfeld vom Chart.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic", Critic.getRecentAverageError());
   ExpertRemove();
//---
  }

Außerdem geben wir Informationen über die Trainingsergebnisse in das Terminalprotokoll ein und leiten die Beendigung von EA ein.

Auch hier finden Sie den vollständigen Code aller Programme im Anhang.

3. Tests

In diesem Artikel haben wir die Methode Client für multivariate Zeitreihenprognosen diskutiert und unsere Vision der vorgeschlagenen Ansätze in MQL5 umgesetzt. Nun kommen wir zur letzten Phase unserer Arbeit - dem Testen der Ergebnisse. In diesem Stadium werden wir die Modelle auf realen historischen Daten des Instruments EURUSD mit dem Zeitrahmen H1 für 2023 trainieren. Danach werden wir die Ergebnisse des trainierten Modells im MetaTrader 5 Strategy Tester mit historischen Daten vom Januar 2024 testen, wobei wir dasselbe Symbol und denselben Zeitrahmen verwenden, die wir zum Trainieren der Modelle nutzt haben.

Beachten Sie, dass die Eliminierung der Einbettungsschicht und die Erhöhung der Anzahl der Balken, die einen Zustand der Umgebung beschreiben, es uns nicht erlauben, den Trainingsdatensatz aus dem vorherigen Artikel zu verwenden. Deshalb müssen wir uns einen neuen Datensatz holen. Dieser Prozess wiederholt den im vorigen Artikel beschriebenen Algorithmus vollständig, sodass ich an dieser Stelle nicht auf die Einzelheiten eingehen werde.

Nach dem Sammeln der ersten Trainingsdaten trainieren wir zunächst das Zeitreihenvorhersagemodell. Hier kommt die erste unangenehme Überraschung: Die Qualität der Vorhersagen erwies sich als ziemlich niedrig. Wahrscheinlich haben das starke Rauschen in den Eingabedaten und die erhöhte Aufmerksamkeit des Modells für Zeitreihendetails das Ergebnis verschlechtert.

Aber wir geben nicht auf und setzen das Experiment fort. Mal sehen, ob sich das Akteursmodell an solche Prognosen anpassen kann. Wir führen mehrere Iterationen durch, um den Akteur zu trainieren und den Trainingsdatensatz zu aktualisieren. Aber leider. Wir konnten kein Modell trainieren, das in der Lage war, mit den Trainings- und natürlich auch den Testdatensätzen Gewinne zu erzielen. Die Saldenlinie bewegte sich nach unten. Der Wert des Gewinnfaktors lag bei etwa 0,5.

Vielleicht ist dieses Ergebnis nur für unsere Implementierung typisch. Aber es bleibt eine Tatsache. Das implementierte Modell ist nicht in der Lage, die gewünschte Qualität der Zeitreihenprognose in einem stark stochastischen Umfeld zu liefern.

Schlussfolgerung

In diesem Artikel haben wir einen recht interessanten und komplexen Algorithmus namens Client erörtert, der ein lineares Modell zur Untersuchung linearer Trends und ein Transformer-Modell mit der Analyse von Abhängigkeiten zwischen einzelnen Variablen zur Untersuchung nichtlinearer Informationen kombiniert. Die Autoren der Methode schließen in ihrem Modell die Aufmerksamkeit zwischen einzelnen, zeitlich getrennten Zuständen der Umwelt aus. Das vorgeschlagene verbesserte Transformer-Modell vereinfacht auch die Einbettungs- und Positionskodierungsebenen. Das Decodermodul wird durch eine Projektionsschicht ersetzt, was nach Ansicht der Autoren der Methode die Effizienz der Vorhersage deutlich erhöht. Darüber hinaus belegen die in der zitierten Arbeit vorgestellten experimentellen Ergebnisse, dass für Aufgaben der Zeitreihenprognose die Analyse von Abhängigkeiten zwischen Variablen in Transformer wichtiger ist als die Analyse von Abhängigkeiten zwischen einzelnen, zeitlich getrennten Zuständen der Umwelt.

Die Ergebnisse unserer Arbeit zeigen jedoch, dass die vorgeschlagenen Ansätze unter den hochgradig stochastischen Bedingungen der Finanzmärkte nicht wirksam sind.

Bitte beachten Sie, dass dieser Artikel die Ergebnisse von Tests unserer individuellen Implementierung der vorgeschlagenen Ansätze darstellt. Daher sind die erzielten Ergebnisse möglicherweise nur für diese Umsetzung relevant. Unter anderen Bedingungen ist es möglich, dass völlig entgegengesetzte Ergebnisse erzielt werden könnten.

Dieser Artikel soll lediglich dazu dienen, den Leser mit der Methode Client vertraut zu machen und eine der Möglichkeiten zur Umsetzung der vorgeschlagenen Ansätze aufzuzeigen. Wir bewerten den von den Autoren vorgeschlagenen Algorithmus in keiner Weise. Wir versuchen lediglich, die vorgeschlagenen Ansätze zur Lösung unserer Probleme anzuwenden.

Referenzen

Client: Cross-variable Linear Integrated Enhanced Transformer for Multivariate Long-Term Time Series Forecasting

Andere Artikel dieser Serie

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	EA	EA-Beispielsammlung
2	ResearchRealORL.mq5	EA	EA zum Sammeln von Beispielen mit der Real-ORL-Methode
3	Study.mq5	EA	Modelltrainings-EA
4	StudyEncoder.mq5	EA	Trainings-EA des Encoders
5	Test.mq5	EA	Modeltest-EA
6	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
7	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
8	NeuroNet.cl	Code Base	Die Bibliothek des Programmcodes von OpenCL