
Redes neuronales: así de sencillo (Parte 13): Normalización por lotes (Batch Normalization)
Contenido
- Introducción
- 1. Prerrequisitos teóricos de la normalización
- 2. Implementación
- 2.1. Creando una nueva clase para nuestro modelo
- 2.2. Propagación hacia delante
- 2.3. Propagación inversa
- 2.4. Cambios puntuales en las clases básicas de la red neronal
- 3. Simulación
- Conclusión
- Enlaces
- Programas utilizados en el artículo
Introducción
En el artículo anterior, comenzamos a analizar varios métodos para mejorar la convergencia de las redes neuronales durante el entrenamiento y nos familiarizamos con el Dropout, un método usado para reducir la adaptación conjunta de las características. En este artículo, continuaremos con el tema iniciado y nos familiarizaremos con los métodos de normalización.
1. Prerrequisitos teóricos de la normalización
En la práctica de uso de redes neuronales, se usan varios enfoques para la normalización de los datos, pero todos están orientados a mantener los datos de la muestra de entrenamiento y los datos de salida de las capas ocultas de la red neuronal en un intervalo dado y con ciertas características estadísticas de la muestra, como la varianza y la mediana. Esto es importante, porque las neuronas de la red usan transformaciones lineales que durante el entrenamiento desplazan la muestra hacia el antigradiente.
Vamos a analizar un perceptrón completamente conectado con 2 capas ocultas. Con la propagación hacia delante, cada capa genera algún conjunto de datos que sirve como una muestra de entrenamiento para la capa siguiente. El resultado de la capa de salida se compara con los datos de referencia y el gradiente de error de la capa de salida se distribuye en la propagación inversa a través de las capas ocultas hacia los datos iniciales. Tras recibir el gradiente de error en cada neurona, actualizaremos los coeficientes de peso, ajustando nuestra red neuronal para generar las muestras de la última propagación hacia delante. Aquí hay un conflicto: ajustamos la segunda capa oculta (H2 en la figura a continuación) para seleccionar los datos en la salida de la primera capa oculta (H1 en la figura), al tiempo que, modificando los parámetros de la primera capa oculta, cambiamos la matriz de datos. es decir, ajustamos la segunda capa oculta en función de la muestra de datos ya inexistente. Una situación similar sucede con la capa de salida, que ajustamos según la salida ya modificada de la segunda capa oculta. Y si además tenemos en cuenta la distorsión entre la primera y la segunda capas ocultas, las escalas de los errores aumentarán. Y cuanto más profunda sea la red neural, más intensamente se manifestará este efecto. Este fenómeno se llamaba desplazamiento interno de covarianza.
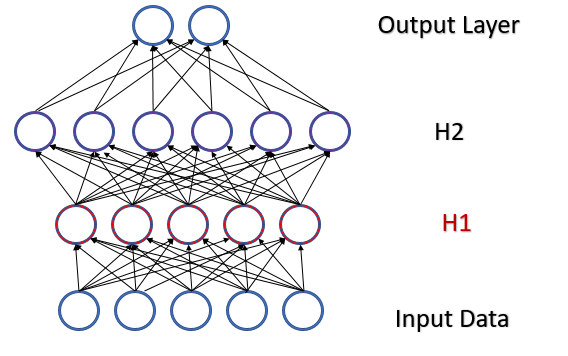
En las redes neuronales clásicas, el problema indicado se resolvía parcialmente disminuyendo el coeficiente de aprendizaje. Los pequeños cambios en los coeficientes de peso no modifican intensamente la distribución de la muestra en la salida de la capa neuronal. Pero este enfoque no resuelve el escalado del problema derivado del aumento en el número de capas de la red neuronal y reduce la velocidad de aprendizaje. Otro problema relacionado con un coeficiente de entrenamiento pequeño sería el atasco en el mínimo local; ya hemos hablado de ello en el artículo [6].
En febrero de 2015, Sergey Ioffe y Christian Szegedy propusieron un método de normalización por lotes de los datos (Batch Normalization) para resolver el problema del desplazamiento interno de covarianza [13]. La esencia del método consistía en normalizar cada neurona individual en un determinado intervalo temporal con un desplazamiento de la mediana de la muestra hacia cero y llevar la varianza de la muestra hacia 1.
El algoritmo de normalización es el siguiente. Al principio, se calcula el valor promedio según la muestra.
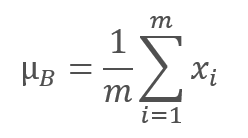
donde m es el tamaño de la muestra (batch).
Luego calculamos la varianza de la muestra original.
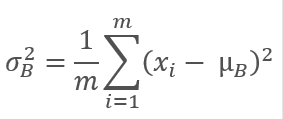
Los datos de la muestra se normalizan para llevar el lote a una media de cero y una varianza de 1.
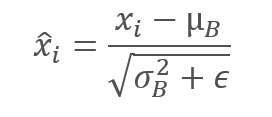
Tenga en cuenta que la constante ϵ, un pequeño número positivo, se añade a la varianza del lote en el denominador para evitar la división por cero.
Sin embargo, resultó que dicha normalización puede distorsionar la influencia de los datos originales. Por ello, los autores del método han añadido otro paso: el escalado y el desplazamiento. Han introducido dos variables γ y β, que se entrenan junto con la red neuronal mediante el método de descenso de gradiente.
![]()
La aplicación de este método permite obtener un lote de datos con la misma distribución en cada paso del entrenamiento, lo cual hace que el entrenamiento de la red neuronal sea más estable y permite aumentar la tasa de aprendizaje. En general, este método ayuda a mejorar la calidad del entrenamiento al tiempo que reduce el tiempo dedicado al entrenamiento de las redes neuronales.
No obstante, al mismo tiempo, los costes de almacenamiento de los coeficientes adicionales aumentarán. Además, los datos históricos de cada neurona para el tamaño completo del lote deberán almacenarse para calcular el valor promedio y la varianza. Y aquí podemos mirar hacia la media exponencial. La siguiente figura muestra los gráficos de la media móvil y la varianza móvil de 100 elementos en comparación con la media móvil exponencial y la varianza móvil exponencial de los mismos 100 elementos. El gráfico está construido para 1000 elementos aleatorios en el intervalo entre -1.0 y 1.0.
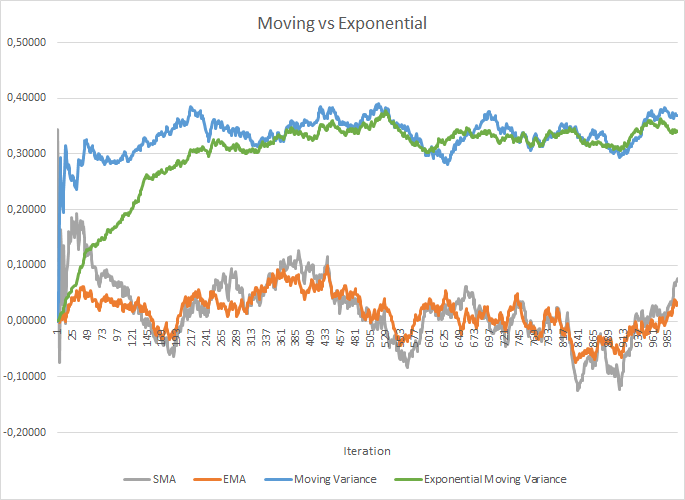
Como podemos ver en este gráfico, la media móvil y la media móvil exponencial se acercan la una a la otra después de 120-130 iteraciones y luego la desviación es mínima (por lo que se puede despreciar). Además, el gráfico de la media móvil exponencial tiene un aspecto más suave. La EMA se puede calcular conociendo el valor anterior de la función y el elemento actual de la secuencia. Veamos la fórmula de la media móvil exponencial.
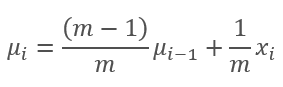 ,
,
donde
- m es el tamaño de la muestra (batch),
- i es la iteración.
Hemos necesitado algunas iteraciones más (310-320) para acercar los gráficos de varianza móvil y varianza móvil exponencial, pero el panorama general es similar. En el caso de la varianza, el uso del algoritmo exponencial no solo ahorra memoria, sino que también reduce significativamente el número de cálculos, ya que para la varianza móvil se calcularía la desviación del promedio para todo el lote.
Los experimentos realizados por los autores del método muestran que el uso del método Batch Normalization también sirve como regularizador. Esto reduce la necesidad de otros métodos de regularización, incluido el Dropout analizado anteriormente. Además, investigaciones posteriores muestran que el uso combinado del Dropout y la normalización por lotes tiene un efecto negativo en los resultados del aprendizaje de la red neuronal.
El algoritmo de normalización propuesto se puede encontrar en varias variaciones en las arquitecturas de redes neuronales modernas. Los autores sugieren usar la normalización por lotes inmediatamente antes de la no linealidad (fórmula de activación). El método de normalización de capas presentado en julio de 2016 puede considerarse una variación de este algoritmo. Ya hemos analizado este método al estudiar el mecanismo de atención [9].
2. Implementación
2.1 Creando una nueva clase para nuestro modelo
Ahora que hemos analizado los aspectos teóricos, vamos a ver cómo podemos implementar la clase en nuestra biblioteca. Creemos la nueva clase CNeuronBatchNormOCL para implementar el algoritmo.
class CNeuronBatchNormOCL : public CNeuronBaseOCL { protected: CNeuronBaseOCL *PrevLayer; ///< Pointer to the object of the previous layer uint iBatchSize; ///< Batch size CBufferDouble *BatchOptions; ///< Container of method parameters ///\ingroup neuron_base_ff virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); ///< \brief Feed Forward method of calling kernel ::BatchFeedForward().@param NeuronOCL Pointer to previos layer. ///\ingroup neuron_base_opt virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); ///< Method for updating weights.\details Calling one of kernels ::UpdateBatchOptionsMomentum() or ::UpdateBatchOptionsAdam() in depends of optimization type (#ENUM_OPTIMIZATION).@param NeuronOCL Pointer to previos layer. public: /** Constructor */CNeuronBatchNormOCL(void); /** Destructor */~CNeuronBatchNormOCL(void); //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, uint batchSize, ENUM_OPTIMIZATION optimization_type); ///< Method of initialization class.@param[in] numOutputs Number of connections to next layer.@param[in] myIndex Index of neuron in layer.@param[in] open_cl Pointer to #COpenCLMy object. #param[in] numNeurons Number of neurons in layer @param optimization_type Optimization type (#ENUM_OPTIMIZATION)@return Boolen result of operations. //--- virtual int getOutputIndex(void) { return (iBatchSize>1 ? Output.GetIndex() : PrevLayer.getOutputIndex()); } ///< Get index of output buffer @return Index virtual int getGradientIndex(void) { return (iBatchSize>1 ? Gradient.GetIndex() : PrevLayer.getGradientIndex()); } ///< Get index of gradient buffer @return Index //--- virtual int getOutputVal(double &values[]) { return (iBatchSize>1 ? Output.GetData(values) : PrevLayer.getOutputVal(values)); } ///< Get values of output buffer @param[out] values Array of data @return number of items virtual int getOutputVal(CArrayDouble *values) { return (iBatchSize>1 ? Output.GetData(values) : PrevLayer.getOutputVal(values)); } ///< Get values of output buffer @param[out] values Array of data @return number of items virtual int getGradient(double &values[]) { return (iBatchSize>1 ? Gradient.GetData(values) : PrevLayer.getGradient(values)); } ///< Get values of gradient buffer @param[out] values Array of data @return number of items virtual CBufferDouble *getOutput(void) { return (iBatchSize>1 ? Output : PrevLayer.getOutput()); } ///< Get pointer of output buffer @return Pointer to object virtual CBufferDouble *getGradient(void) { return (iBatchSize>1 ? Gradient : PrevLayer.getGradient()); } ///< Get pointer of gradient buffer @return Pointer to object //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); ///< Method to transfer gradient to previous layer by calling kernel ::CalcHiddenGradientBatch(). @param NeuronOCL Pointer to next layer. //--- virtual bool Save(int const file_handle);///< Save method @param[in] file_handle handle of file @return logical result of operation virtual bool Load(int const file_handle);///< Load method @param[in] file_handle handle of file @return logical result of operation //--- virtual int Type(void) const { return defNeuronBatchNormOCL; }///< Identificator of class.@return Type of class };
La nueva clase heredará de la clase básica CNeuronBaseOCL. Por analogía con la clase CNeuronDropoutOCL, añadiremos la variable PrevLayer. El método de sustitución de búferes de datos mostrado en el artículo anterior se aplicará al especificar un tamaño de lote inferior a "2", que se guardará en la variable iBatchSize.
El algoritmo Batch Normalization prevé el almacenamiento de una serie de parámetros que son individuales para cada neurona en la capa normalizada. Para no producir muchos búferes aparte para cada parámetro individual, crearemos un único búfer de parámetros BatchOptions con la siguiente estructura.

Como podemos ver en la estructura presentada, el tamaño del búfer de parámetros dependerá del método de optimización de parámetros utilizado y, por consiguiente, se creará en el método de inicialización de la clase.
El conjunto de métodos de la clase ya se ha convertido en un estándar; vamos a analizarlo por orden. En el constructor de la clase, ponemos a cero los punteros a los objetos y establecemos en uno el tamaño del lote, lo cual prácticamente excluirá la capa de la operación de la red hasta que se inicialice.
CNeuronBatchNormOCL::CNeuronBatchNormOCL(void) : iBatchSize(1) { PrevLayer=NULL; BatchOptions=NULL; }
En el destructor de clase, eliminamos el objeto del búfer de parámetros y ponemos a cero el puntero a la capa anterior. Debemos tener en cuenta que no estamos eliminando el objeto de la capa anterior, solo estamos poniendo a cero el puntero. El objeto se eliminará en el lugar donde se creó.
CNeuronBatchNormOCL::~CNeuronBatchNormOCL(void) { if(CheckPointer(PrevLayer)!=POINTER_INVALID) PrevLayer=NULL; if(CheckPointer(BatchOptions)!=POINTER_INVALID) delete BatchOptions; }
Ahora, vamos a analizar el método de inicialización de la clase CNeuronBatchNormOCL::Init. En los parámetros, transmitimos a la clase el número de neuronas de la siguiente capa, el índice para identificar la neurona, el puntero al objeto OpenCl, el número de neuronas en la capa de normalización, el tamaño del lote y el método de optimización de parámetros.
Al comienzo del método, llamamos al método homónimo de la clase padre, en el que se inicializarán las variables básicas y los búferes de datos. Luego, guardamos el tamaño del lote y establecemos la función de activación de la capa como None.
Aquí, debemos centrarnos en la función de activación. La inclusión de esta funcionalidad depende de la arquitectura de la red neuronal que estemos construyendo. Si la arquitectura de la red neuronal prevé la inclusión de la normalización antes de la función de activación, como recomiendan los autores del método, deberemos deshabilitar la función de activación en la capa anterior e indicar la función necesaria en la capa de normalización. Técnicamente, la función de activación se indica llamando al método SetActivationFunction de la clase padre después de inicializar la instancia de la clase. Si la arquitectura de la red prevé el uso de la normalización después de la función de activación, indicaremos el método de activación en la capa anterior, mientras que la capa de normalización permanecerá sin función de activación.
bool CNeuronBatchNormOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint numNeurons,uint batchSize,ENUM_OPTIMIZATION optimization_type) { if(!CNeuronBaseOCL::Init(numOutputs,myIndex,open_cl,numNeurons,optimization_type)) return false; activation=None; iBatchSize=batchSize; //--- if(CheckPointer(BatchOptions)!=POINTER_INVALID) delete BatchOptions; int count=(int)numNeurons*(optimization_type==SGD ? 7 : 9); BatchOptions=new CBufferDouble(); if(CheckPointer(BatchOptions)==POINTER_INVALID || !BatchOptions.BufferInit(count,0)) return false; //--- return true; }
Al final del método de inicialización, creamos un búfer de parámetros. Como ya hemos mencionado anteriormente, el tamaño del búfer dependerá del número de neuronas en la capa y del método de optimización de parámetros. Al usar SGD, reservamos 7 elementos para cada neurona, y cuando optimizamos utilizando el método de Adam, necesitamos 9 elementos de búfer para cada neurona. Después de crear con éxito el búfer, lo rellenamos con ceros y salimos del método con el resultado true.
Podrá familiarizarse con el código completo de todas las clases y sus métodos en los anexos.
2.2. Propagación hacia delante
Continuamos avanzando por el algoritmo y analizando el método de propagación hacia delante. Vamos a comenzar estudiando el kernel de propagación hacia delante BatchFeedForward. Ejecutamos el algoritmo del kernel para cada neurona individual.
En los parámetros, el núcleo obtiene los punteros a 3 búferes: el de datos iniciales, el búfer de parámetros y el búfer para escribir los resultados. Además, transmitiremos en los parámetros el tamaño del lote, el método de optimización y el algoritmo de activación neuronal.
Al inicio del kernel, verificamos el tamaño especificado de la ventana de normalización. Si la normalización se realiza en una neurona, saldremos del método sin realizar más operaciones.
Después realizar la verificación con éxito, obtendremos el identificador de hilo que indicará la posición del valor normalizado en el tensor de datos de entrada. Utilizándolo, determinamos el desplazamiento para el primer parámetro en el tensor de parámetros de normalización. En este paso, el método de optimización nos indicará la estructura del búfer de parámetros.
A continuación, calculamos la media exponencial y la varianza en este paso. Partiendo de ellos, calculamos el valor normalizado de nuestro elemento.
El siguiente paso en el algoritmo de normalización por lotes será el desplazamiento y el escalado. Recordemos que durante la inicialización hemos rellenado el búfer de parámetros con ceros, por lo que, si realizamos esta operación "en su forma pura", en el primer paso nos devolverá "0". Para evitar que esto ocurra, verificamos el valor actual del parámetro γ y, si es igual a "0", cambiaremos su valor a "1". El desplazamiento lo dejaremos como cero. Y de esta forma, realizaremos el desplazamiento y el escalado.
__kernel void BatchFeedForward(__global double *inputs, __global double *options, __global double *output, int batch int optimization, int activation) { if(batch<=1) return; int n=get_global_id(0); int shift=n*(optimization==0 ? 7 : 9); //--- for(int i=0;i<(optimization==0 ? 7 : 9);i++) if(isnan(options[shift+i])) options[shift+i]=0; //--- double mean=(options[shift]*((double)batch-1)+inputs[n])/((double)batch); double delt=inputs[n]-mean; double variance=options[shift+1]*((double)batch-1.0)+pow(delt,2); if(options[shift+1]>0) variance/=(double)batch; double nx=delt/sqrt(variance+1e-6); //--- if(options[shift+3]==0) options[shift+3]=1; //--- double res=options[shift+3]*nx+options[shift+4]; switch(activation) { case 0: res=tanh(clamp(res,-20.0,20.0)); break; case 1: res=1/(1+exp(-clamp(res,-20.0,20.0))); break; case 2: if(res<0) res*=0.01; break; default: break; } //--- options[shift]=mean; options[shift+1]=variance; options[shift+2]=nx; output[n]=res; }
Después de obtener el valor normalizado, verificamos la necesidad de ejecutar la función de activación en esta capa y realizamos las acciones necesarias.
Ahora, todo lo que nos queda es guardar los nuevos valores en los búferes de datos y salir del kernel.
Esperamos que el algoritmo para construir el kernel BatchFeedForward no genere ninguna pregunta. Vamos a proceder a crear un método para llamar al kernel desde el programa principal. Esta funcionalidad, como de costumbre, será ejecutada por el método CNeuronBatchNormOCL::feedForward. El algoritmo del método es similar a los métodos homónimos en otras clases. En los parámetros, el método obtiene el puntero a la capa anterior de la red neuronal.
Al inicio del método, verificamos la validez del puntero obtenido y el puntero al objeto OpenCL (no olvidemos que esta es una réplica de una clase de la biblioteca estándar para trabajar con el programa OpenCL).
En el siguiente paso, guardamos el puntero a la capa anterior de la red neuronal y verificamos el tamaño del lote. Si el tamaño de la ventana de normalización no es superior a "1", copiamos el tipo de función de activación de la capa anterior y salimos del método con el resultado true. De esta forma, proporcionaremos los datos necesarios para sustituir los búferes y excluiremos iteraciones innecesarias del algoritmo.
bool CNeuronBatchNormOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- PrevLayer=NeuronOCL; if(iBatchSize<=1) { activation=(ENUM_ACTIVATION)NeuronOCL.Activation(); return true; } //--- if(CheckPointer(BatchOptions)==POINTER_INVALID) { int count=Neurons()*(optimization==SGD ? 7 : 9); BatchOptions=new CBufferDouble(); if(!BatchOptions.BufferInit(count,0)) return false; } if(!BatchOptions.BufferCreate(OpenCL)) return false; //--- uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=Neurons(); if(!OpenCL.SetArgumentBuffer(def_k_BatchFeedForward,def_k_bff_inputs,NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_BatchFeedForward,def_k_bff_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_BatchFeedForward,def_k_bff_output,Output.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_BatchFeedForward,def_k_bff_batch,iBatchSize)) return false; if(!OpenCL.SetArgument(def_k_BatchFeedForward,def_k_bff_optimization,(int)optimization)) return false; if(!OpenCL.SetArgument(def_k_BatchFeedForward,def_k_bff_activation,(int)activation)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_BatchFeedForward,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Batch Feed Forward: %d",GetLastError()); return false; } if(!Output.BufferRead() || !BatchOptions.BufferRead()) return false; BatchOptions.BufferFree(); //--- return true; }
Si, tras todas las comprobaciones, hemos llegado al inicio del kernel de propagación hacia delante, prepararemos los datos iniciales para su inicio. Primero, verificamos la validez del puntero al búfer de parámetros del algoritmo de normalización. De ser necesario, crearemos e inicializaremos un nuevo búfer. A continuación, creamos un búfer en la memoria de la tarjeta gráfica y cargamos el contenido del búfer.
Después, establecemos un número de hilos iniciados igual al número de neuronas en la capa y transmitimos al kernel los punteros a los búferes de datos, junto con los parámetros requeridos.
Después de finalizar el trabajo preparatorio, enviamos el kernel para su ejecución y leemos los datos actualizados del búfer desde la memoria de la tarjeta gráfica. No olvidemos que hemos obtenido los datos de los 2 búferes de la tarjeta gráfica: la información de la salida del algoritmo y el búfer de parámetros en el que guardamos la media actualizada, la varianza y el valor normalizado. Necesitaremos estos datos en iteraciones posteriores.
Una vez haya finalizado el funcionamiento el algoritmo, eliminamos el búfer de parámetros de la memoria de la tarjeta gráfica, liberando así memoria para cargar los búferes de las capas posteriores de la red neuronal y salimos del método con el resultado true.
Podrá familiarizarse con el código completo de todas las clases de la biblioteca y sus métodos en los anexos.
2.3. Propagación inversa
La propagación inversa consta tradicionalmente de dos etapas: la propagación inversa del error y la actualización de los coeficientes de peso. Solo que, en lugar de los coeficientes de peso habituales, entrenaremos los parámetros γ y β de la función de escalado y desplazamiento.
Primero, vamos a ver la funcionalidad del descenso de gradiente. Para implementar su algoritmo, crearemos el kernel CalcHiddenGradientBatch. En los parámetros, el kernel obtiene los punteros a los tensores de los parámetros de normalización recibidos de la siguiente capa de gradientes, la salida de la capa anterior (obtenida durante la última propagación hacia adelante) y el tensor de gradiente de la capa anterior de la red neuronal, donde se escribirán los resultados del algoritmo. Además, en los parámetros, transmitiremos al kernel el tamaño del lote, el tipo de función de activación y el método para optimizar los parámetros.
Al igual que sucede con la propagación hacia delante, verificamos el tamaño del lote al inicio del kernel, y si es menor o igual a "1", salimos del kernel sin realizar otras iteraciones.
El siguiente paso consiste en obtener el número ordinal de nuestro hilo y determinar el desplazamiento en el tensor de parámetros. Estos pasos son similares a los descritos para la propagación hacia delante.
__kernel void CalcHiddenGradientBatch(__global double *options, ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer __global double *matrix_g, ///<[in] Tensor of gradients at current layer __global double *matrix_i, ///<[in] Tensor of previous layer output __global double *matrix_ig, ///<[out] Tensor of gradients at previous layer uint activation, ///< Activation type (#ENUM_ACTIVATION) int batch, ///< Batch size int optimization ///< Optimization type ) { if(batch<=1) return; //--- int n=get_global_id(0); int shift=n*(optimization==0 ? 7 : 9); //--- double inp=matrix_i[n]; double gnx=matrix_g[n]*options[shift+3]; double temp=1/sqrt(options[shift+1]+1e-6); double gmu=(-temp)*gnx; double gvar=(options[shift]*inp)/(2*pow(options[shift+1]+1.0e-6,3/2))*gnx; double gx=temp*gnx+gmu/batch+gvar*2*inp/batch*pow((double)(batch-1)/batch,2.0); //--- if(isnan(gx)) gx=0; switch(activation) { case 0: gx=clamp(gx+inp,-1.0,1.0)-inp; gx=gx*(1-pow(inp==1 || inp==-1 ? 0.99999999 : inp,2)); break; case 1: gx=clamp(gx+inp,0.0,1.0)-inp; gx=gx*(inp==0 || inp==1 ? 0.00000001 : (inp*(1-inp))); break; case 2: if(inp<0) gx*=0.01; break; default: break; } matrix_ig[n]=clamp(gx,-MAX_GRADIENT,MAX_GRADIENT); }
A continuación, calculamos secuencialmente los gradientes para todas las funciones del algoritmo.

Y finalmente, propagamos el gradiente a través de la función de activación de la capa anterior. Después, guardamos el valor obtenido en el tensor de gradiente de la capa anterior.
Tras el kernel CalcHiddenGradientBatсh, vamos a analizar el método CNeuronBatchNormOCL::calcInputGradients, que iniciará la ejecución del kernel desde el programa principal. Al igual que sucede en los métodos homónimos de las otras clases, en los parámetros este método obtenemos el puntero al objeto de la capa anterior de la red neuronal.
Al inicio del método, verificamos la validez del puntero obtenido y el puntero al objeto OpenCL. Después de ello, verificamos el tamaño del lote. Si es menor o igual a "1", salimos del método. El resultado retornado por el método dependerá de la validez del puntero a la capa anterior guardado durante la propagación hacia adelante.
Si avanzamos más en el algoritmo, podremos verificar la validez del búfer de parámetros. Si ocurre un error, salimos del método con el resultado false.
No olvidemos que el descenso de gradiente se refiere a la última propagación hacia delante. Por eso, en los dos últimos puntos de control, verificamos los objetos que participan en la propagación hacia delante.
bool CNeuronBatchNormOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- if(iBatchSize<=1) return (CheckPointer(PrevLayer)!=POINTER_INVALID); //--- if(CheckPointer(BatchOptions)==POINTER_INVALID || !BatchOptions.BufferCreate(OpenCL)) return false; //--- uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=Neurons(); if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_matrix_i,NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_matrix_g,Gradient.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_matrix_ig,NeuronOCL.getGradientIndex())) return false; if(!OpenCL.SetArgument(def_k_CalcHiddenGradientBatch,def_k_bchg_activation,NeuronOCL.Activation())) return false; if(!OpenCL.SetArgument(def_k_CalcHiddenGradientBatch,def_k_bchg_batch,iBatchSize)) return false; if(!OpenCL.SetArgument(def_k_CalcHiddenGradientBatch,def_k_bchg_optimization,(int)optimization)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_CalcHiddenGradientBatch,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Batch CalcHiddenGradient: %d",GetLastError()); return false; } if(!NeuronOCL.getGradient().BufferRead()) return false; BatchOptions.BufferFree(); //--- return true; }
Al igual que sucede con propagación hacia adelante, el número de hilos del kernel iniciados será igual al número de neuronas en la capa. Enviamos el contenido del búfer de parámetros de normalización a la memoria de la tarjeta gráfica y transmitimos al kernel los punteros a los tensores y parámetros requeridos.
Después de completar todas las operaciones anteriores, iniciamos el kernel para su ejecución y calculamos los gradientes obtenidos de la memoria de la tarjeta gráfica en el búfer correspondiente.
Al final del método, eliminamos el tensor de parámetros de normalización de la memoria de la tarjeta gráfica y salimos del método con el resultado true.
Después de transmitir el gradiente, es hora de actualizar los parámetros de desplazamiento y escalado. Para realizar estas iteraciones, crearemos 2 kernels según el número de métodos de optimización descritos anteriormente, UpdateBatchOptionsMomentum y UpdateBatchOptionsAdam.
Primero, echaremos un vistazo al método UpdateBatchOptionsMomentum. En los parámetros, el método recibe los punteros a 2 tensores: los parámetros de normalización y los gradientes. Además, en los parámetros del método, transmitimos las constantes del método de optimización: la tasa de aprendizaje y el impulso.
Al inicio del kernel, obtenemos el número de hilo y determinamos el desplazamiento en el tensor de los parámetros de normalización.
Basándonos en los datos iniciales, calculamos el tamaño de γ y β. Para efectuar esta operación, hemos utilizado cálculos vectoriales con un vector "double" de 2 elementos. Este método nos permite paralelizar los cálculos.
Corregimos los parámetros γ, β y guardemos los resultados en los elementos correspondientes del tensor de parámetros de normalización.
__kernel void UpdateBatchOptionsMomentum(__global double *options, ///<[in,out] Options matrix m*7, where m - Number of neurons in previous layer __global double *matrix_g, ///<[in] Tensor of gradients at current layer double learning_rates, ///< Learning rates double momentum ///< Momentum multiplier ) { const int n=get_global_id(0); const int shift=n*7; double grad=matrix_g[n]; //--- double2 delta=learning_rates*grad*(double2)(options[shift+2],1) + momentum*(double2)(options[shift+5],options[shift+6]); if(!isnan(delta.s0) && !isnan(delta.s1)) { options[shift+5]=delta.s0; options[shift+3]=clamp(options[shift+3]+delta.s0,-MAX_WEIGHT,MAX_WEIGHT); options[shift+6]=delta.s1; options[shift+4]=clamp(options[shift+4]+delta.s1,-MAX_WEIGHT,MAX_WEIGHT); } };
El kernel UpdateBatchOptionsAdam se ha diseñado según un esquema similar: las diferencias residen en el algoritmo del método de optimización en sí. En los parámetros, el kernel obtiene los punteros a los mismos tensores de parámetros y de gradiente. Además, obtiene los parámetros del método de optimización.
Al inicio del kernel, determinamos el número de hilo y determinamos el desplazamiento en el tensor de parámetros.
Usando los datos obtenidos, calculamos el primer y segundo momento. También usaremos cálculos vectoriales que nos permiten calcular los momentos para los 2 parámetros al mismo tiempo.
Teniendo en cuenta los momentos obtenidos, calculamos los deltas y los nuevos valores de los parámetros. Luego, guardamos los resultados del cálculo en los elementos correspondientes del tensor de parámetros de normalización.
__kernel void UpdateBatchOptionsAdam(__global double *options, ///<[in,out] Options matrix m*9, where m - Number of neurons in previous layer __global double *matrix_g, ///<[in] Tensor of gradients at current layer const double l, ///< Learning rates const double b1, ///< First momentum multiplier const double b2 ///< Second momentum multiplier ) { const int n=get_global_id(0); const int shift=n*9; double grad=matrix_g[n]; //--- double2 mt=b1*(double2)(options[shift+5],options[shift+6])+(1-b1)*(double2)(grad*options[shift+2],grad); double2 vt=b2*(double2)(options[shift+5],options[shift+6])+(1-b2)*pow((double2)(grad*options[shift+2],grad),2); double2 delta=l*mt/sqrt(vt+1.0e-8); if(isnan(delta.s0) || isnan(delta.s1)) return; double2 weight=clamp((double2)(options[shift+3],options[shift+4])+delta,-MAX_WEIGHT,MAX_WEIGHT); //--- if(!isnan(weight.s0) && !isnan(weight.s1)) { options[shift+3]=weight.s0; options[shift+4]=weight.s1; options[shift+5]=mt.s0; options[shift+6]=mt.s1; options[shift+7]=vt.s0; options[shift+8]=vt.s1; } };
Para ejecutar los kernels desde el programa principal, vamos a crear el método CNeuronBatchNormOCL::updateInputWeights. En los parámetros, el método obtiene el puntero a la capa anterior de la red neuronal. En esencia, este puntero no se usará en el algoritmo del método: lo dejaremos para la herencia desde los métodos de la clase principal.
Al inicio del método, verificamos la validez del puntero obtenido y el puntero al objeto OpenCL. Por analogía con el método CNeuronBatchNormOCL::calcInputGradients previamente analizado, verificamos el tamaño del lote y la validez del búfer de parámetros. Luego, cargamos el contenido del búfer de parámetros en la memoria de la tarjeta gráfica, y establezcamos un número de hilos igual al número de neuronas en la capa.
A continuación, viene la ramificación del algoritmo según el método de optimización especificado. Transmitimos los parámetros iniciales para el kernel necesario e iniciamos su ejecución.
Independientemente del método de optimización de los parámetros, calculamos el contenido actualizado del búfer de parámetros de normalización y eliminamos el búfer de la memoria de la tarjeta gráfica.
bool CNeuronBatchNormOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- if(iBatchSize<=1) return (CheckPointer(PrevLayer)!=POINTER_INVALID); //--- if(CheckPointer(BatchOptions)==POINTER_INVALID || !BatchOptions.BufferCreate(OpenCL)) return false; uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=Neurons(); //--- if(optimization==SGD) { if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsMomentum,def_k_buom_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsMomentum,def_k_buom_matrix_g,Gradient.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsMomentum,def_k_buom_learning_rates,eta)) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsMomentum,def_k_buom_momentum,alpha)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_UpdateBatchOptionsMomentum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel UpdateBatchOptionsMomentum %d",GetLastError()); return false; } } else { if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsAdam,def_k_buoa_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsAdam,def_k_buoa_matrix_g,Gradient.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsAdam,def_k_buoa_l,lr)) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsAdam,def_k_buoa_b1,b1)) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsAdam,def_k_buoa_b2,b2)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_UpdateBatchOptionsAdam,1,global_work_offset,global_work_size)) { printf("Error of execution kernel UpdateBatchOptionsAdam %d",GetLastError()); return false; } } //--- if(!BatchOptions.BufferRead()) return false; BatchOptions.BufferFree(); //--- return true; }
Después de ejecutar con éxito todas las operaciones del método, salimos con el resultado true.
Ya describimos con detalle en el artículo anterior los métodos para sustituir los búferes y, a nuestro juicio, no resultarán difíciles de comprender. Lo mismo sucede con los métodos para trabajar con archivos (guardar y cargar la red neuronal entrenada).
Podrá familiarizarse con el código completo de todas las clases y sus métodos en los anexos.
2.4. Cambios puntuales en las clases básicas de la red neronal
Bueno, siguiendo la tradición, tras crear una nueva clase, deberemos integrarla en la estructura general de nuestra red neuronal. Lo primero que debemos hacer es crear un identificador para nuestra clase.
#define defNeuronBatchNormOCL 0x7891 ///<Batchnorm neuron OpenCL \details Identified class #CNeuronBatchNormOCL
A continuación, definiremos las macrosustituciones de las constantes para trabajar con los nuevos kernels.
#define def_k_BatchFeedForward 24 ///< Index of the kernel for Batch Normalization Feed Forward process (#CNeuronBathcNormOCL) #define def_k_bff_inputs 0 ///< Inputs data tenzor #define def_k_bff_options 1 ///< Tenzor of variables #define def_k_bff_output 2 ///< Tenzor of output data #define def_k_bff_batch 3 ///< Batch size #define def_k_bff_optimization 4 ///< Optimization type #define def_k_bff_activation 5 ///< Activation type //--- #define def_k_CalcHiddenGradientBatch 25 ///< Index of the Kernel of the Batch neuron to transfer gradient to previous layer (#CNeuronBatchNormOCL) #define def_k_bchg_options 0 ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer #define def_k_bchg_matrix_g 1 ///<[in] Tensor of gradients at current layer #define def_k_bchg_matrix_i 2 ///<[in] Tensor of previous layer output #define def_k_bchg_matrix_ig 3 ///<[out] Tensor of gradients at previous layer #define def_k_bchg_activation 4 ///< Activation type (#ENUM_ACTIVATION) #define def_k_bchg_batch 5 ///< Batch size #define def_k_bchg_optimization 6 ///< Optimization type //--- #define def_k_UpdateBatchOptionsMomentum 26 ///< Index of the kernel for Describe the process of SGD optimization options for the Batch normalization Neuron (#CNeuronBatchNormOCL). #define def_k_buom_options 0 ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer #define def_k_buom_matrix_g 1 ///<[in] Tensor of gradients at current layer #define def_k_buom_learning_rates 2 ///< Learning rates #define def_k_buom_momentum 3 ///< Momentum multiplier //--- #define def_k_UpdateBatchOptionsAdam 27 ///< Index of the kernel for Describe the process of Adam optimization options for the Batch normalization Neuron (#CNeuronBatchNormOCL). #define def_k_buoa_options 0 ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer #define def_k_buoa_matrix_g 1 ///<[in] Tensor of gradients at current layer #define def_k_buoa_l 2 ///< Learning rates #define def_k_buoa_b1 3 ///< First momentum multiplier #define def_k_buoa_b2 4 ///< Second momentum multiplier
En el constructor de la red neuronal CNet::CNet, añadimos los bloques para crear los objetos de la nueva clase e inicializamos los nuevos kernels (hemos destacado los cambios).
CNet::CNet(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
//---
................
................
................
//---
for(int i=0; i<total; i++)
{
prev=desc;
desc=Description.At(i);
if((i+1)<total)
{
next=Description.At(i+1);
if(CheckPointer(next)==POINTER_INVALID)
return;
}
else
next=NULL;
int outputs=(next==NULL || (next.type!=defNeuron && next.type!=defNeuronBaseOCL) ? 0 : next.count);
temp=new CLayer(outputs);
int neurons=(desc.count+(desc.type==defNeuron || desc.type==defNeuronBaseOCL ? 1 : 0));
if(CheckPointer(opencl)!=POINTER_INVALID)
{
................
................
................
CNeuronBatchNormOCL *batch=NULL;
switch(desc.type)
{
................
................
................
................
//---
case defNeuronBatchNormOCL:
batch=new CNeuronBatchNormOCL();
if(CheckPointer(batch)==POINTER_INVALID)
{
delete temp;
return;
}
if(!batch.Init(outputs,0,opencl,desc.count,desc.window,desc.optimization))
{
delete batch;
delete temp;
return;
}
batch.SetActivationFunction(desc.activation);
if(!temp.Add(batch))
{
delete batch;
delete temp;
return;
}
batch=NULL;
break;
//---
default:
return;
break;
}
}
................
................
................
................
//---
if(CheckPointer(opencl)==POINTER_INVALID)
return;
//--- create kernels
opencl.SetKernelsCount(28);
................
................
................
................
opencl.KernelCreate(def_k_BatchFeedForward,"BatchFeedForward");
opencl.KernelCreate(def_k_CalcHiddenGradientBath,"CalcHiddenGradientBath");
opencl.KernelCreate(def_k_UpdateBatchOptionsMomentum,"UpdateBatchOptionsMomentum");
opencl.KernelCreate(def_k_UpdateBatchOptionsAdam,"UpdateBatchOptionsAdam");
//---
return;
}
De forma similar, iniciamos los nuevos kernels al cargar una red neuronal previamente entrenada.
bool CNet::Load(string file_name,double &error,double &undefine,double &forecast,datetime &time,bool common=true) { if(MQLInfoInteger(MQL_OPTIMIZATION) || MQLInfoInteger(MQL_TESTER) || MQLInfoInteger(MQL_FORWARD) || MQLInfoInteger(MQL_OPTIMIZATION)) return false; //--- ................ ................ ................ //--- if(CheckPointer(opencl)==POINTER_INVALID) { opencl=new COpenCLMy(); if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true)) delete opencl; else { //--- create kernels opencl.SetKernelsCount(28); ................ ................ ................ opencl.KernelCreate(def_k_BatchFeedForward,"BatchFeedForward"); opencl.KernelCreate(def_k_CalcHiddenGradientBath,"CalcHiddenGradientBath"); opencl.KernelCreate(def_k_UpdateBatchOptionsMomentum,"UpdateBatchOptionsMomentum"); opencl.KernelCreate(def_k_UpdateBatchOptionsAdam,"UpdateBatchOptionsAdam"); } } ................ ................ ................ ................ ................ }
Añadimos un nuevo tipo de neuronas al método de carga de la red neuronal preentrenada.
bool CLayer::Load(const int file_handle) { iFileHandle=file_handle; if(!CArrayObj::Load(file_handle)) return false; if(CheckPointer(m_data[0])==POINTER_INVALID) return false; //--- CNeuronBaseOCL *ocl=NULL; CNeuronBase *cpu=NULL; switch(m_data[0].Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: case defNeuronBatchNormOCL: ocl=m_data[0]; iOutputs=ocl.getConnections(); break; default: cpu=m_data[0]; iOutputs=cpu.getConnections().Total(); break; } //--- return true; }
De forma similar, añadimos un nuevo tipo de neuronas a los métodos de despacho de la clase básica CNeuronBaseOCL.
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: case defNeuronBatchNormOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; }
bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject) { if(CheckPointer(TargetObject)==POINTER_INVALID) return false; //--- ................ ................ ................ CNeuronBatchNormOCL *batch=NULL; switch(TargetObject.Type()) { ................ ................ ................ case defNeuronBatchNormOCL: batch=TargetObject; temp=GetPointer(this); return batch.calcInputGradients(temp); break; } //--- return false; }
bool CNeuronBaseOCL::UpdateInputWeights(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: case defNeuronBatchNormOCL: temp=SourceObject; return updateInputWeights(temp); break; } //--- return false; }
Podrá familiarizarse con el código completo de todas las clases y sus métodos en los anexos.
3. Simulación
Vamos a continuar poniendo a prueba las nuevas clases en los asesores expertos creados anteriormente. Esto nos ofrecerá datos comparables para valorar el funcionamiento de los elementos individuales. Probaremos el método de normalización basado en el asesor experto del artículo [12], en el que sustituiremos Dropout por Batch Normalization. La estructura de la red neuronal del nuevo asesor experto se presenta a continuación. Al mismo tiempo, la tasa de aprendizaje se ha incrementado de 0,000001 a 0,001.
//--- 0 CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBaseOCL; desc.optimization=ADAM; desc.activation=None; if(!Topology.Add(desc)) return INIT_FAILED; //--- 1 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBatchNormOCL; desc.window=100; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- 2 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronConvOCL; desc.window=12; desc.step=12; desc.window_out=24; desc.optimization=ADAM; desc.activation=None; if(!Topology.Add(desc)) return INIT_FAILED; //--- 3 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*24; desc.type=defNeuronBatchNormOCL; desc.window=100; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- 4 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronMLMHAttentionOCL; desc.window=24; desc.window_out=4; desc.step=8; //heads desc.layers=5; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- 5 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=None; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 6 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuronBatchNormOCL; desc.window=100; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- 7 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 8 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; desc.activation=SIGMOID; desc.optimization=ADAM;
Hemos puesto a prueba el asesor en EURUSD, con el marco temporal H1. A la entrada de la red neuronal, suministraremos los datos históricos de las últimas 20 velas, como en las pruebas anteriores.
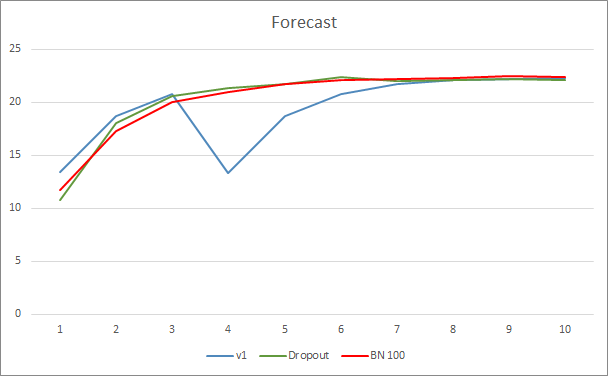
El gráfico de error de predicción de la red neuronal indica que el asesor normalizado muestra un gráfico menos suavizado, lo cual puede deberse a un fuerte aumento en la tasa de aprendizaje. Al mismo tiempo, el error de predicción en sí resulta menor que en las pruebas anteriores, además, durante casi toda la prueba.
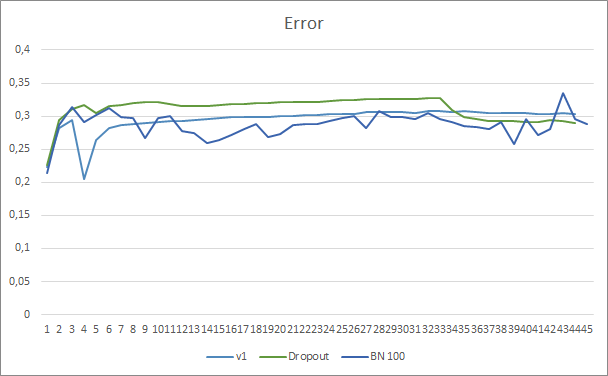
El gráfico de acierto de los patrones predichos para los tres asesores se encuentra bastente próximo y no nos permite sacar conclusiones sobre la superioridad de ninguno de los métodos.
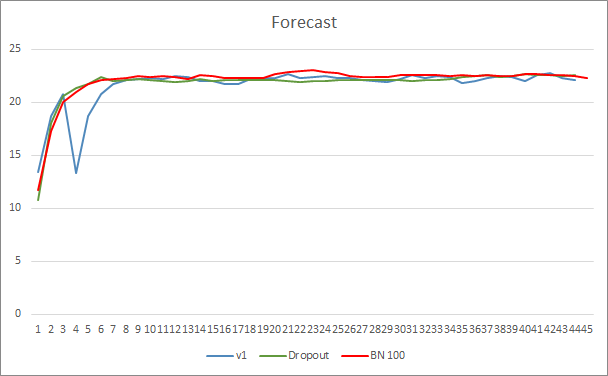
Conclusión
En este artículo, hemos seguido familiarizándonos con los métodos encargados de aumentar la convergencia de las redes neuronales, y también hemos añadido a nuestra biblioteca una clase para la normalización por lotes de los datos. Las pruebas han demostrado que el uso de este método permite reducir el error de la red neuronal y aumentar la tasa de aprendizaje.
Enlaces
- Redes neuronales: así de sencillo
- Redes neuronales: así de sencillo (Parte 2): Entrenamiento y prueba de la red
- Redes neuronales: así de sencillo (Parte 3): Redes convolucionales
- Redes neuronales: así de sencillo (Parte 4): Redes recurrentes
- Redes neuronales: así de sencillo (Parte 5): Cálculos multihilo en OpenCL
- Redes neuronales: así de sencillo (Parte 6): Experimentos con la tasa de aprendizaje de la red neuronal
- Redes neuronales: así de sencillo (Parte 7): Métodos de optimización adaptativos
- Redes neuronales: así de sencillo (Parte 8): Mecanismos de atención
- Redes neuronales: así de sencillo (Parte 9): Documentamos el trabajo realizado
- Redes neuronales: así de sencillo (Parte 10): Multi-Head Attention (atención multi-cabeza)
- Redes neuronales: así de sencillo (Parte 11): Variaciones de GTP
- Redes neuronales: así de sencillo (Parte 12): Dropout
- Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
- Layer Normalization
Programas utilizados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Fractal_OCL_AttentionMLMH_b.mq5 | Asesor | Asesor con la red neuronal de clasificación (3 neuronas en la capa de salida) con uso de la arquitectura GPT, 5 capas de atención + BatchNorm |
| 2 | NeuroNet.mqh | Biblioteca de clase | Biblioteca de clases para crear la red neuronal |
| 3 | NeuroNet.cl | Biblioteca | Biblioteca de código del programa OpenCL |
| 4 | NN.chm | Guía de ayuda de HTML | Archivo CHM compilado de ayuda sobre la biblioteca. |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/9207
 Plantilla para proyectar el MVC y posibilidades de uso
Plantilla para proyectar el MVC y posibilidades de uso
 Aproximación por fuerza bruta a la búsqueda de patrones (Parte IV): Funcionalidad mínima
Aproximación por fuerza bruta a la búsqueda de patrones (Parte IV): Funcionalidad mínima
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso