Neuronale Netze leicht gemacht (Teil 83): Der „Conformer“-Algorithmus für räumlich-zeitliche kontinuierliche Aufmerksamkeitstransformation
Einführung
Die Unvorhersehbarkeit des Verhaltens der Finanzmärkte kann wohl mit der Unbeständigkeit des Wetters verglichen werden. Allerdings hat die Menschheit auf dem Gebiet der Wettervorhersage schon eine Menge erreicht. Wir können den Wettervorhersagen der Meteorologen also durchaus vertrauen. Können wir ihre Entwicklungen nutzen, um das „Wetter“ auf den Finanzmärkten vorherzusagen? In diesem Artikel werden wir uns mit dem komplexen Algorithmus des „Conformer“ Spatio-Temporal Continuous Attention Transformer vertraut machen, der für die Zwecke der Wettervorhersage entwickelt wurde und in dem Artikel „Conformer: Embedding Continuous Attention in Vision Transformer for Weather Forecasting“. In ihrer Arbeit schlagen die Autoren der Methode den Algorithmus der kontinuierlichen Aufmerksamkeit (Continuous Attention) vor. Sie kombinieren sie mit denen, die wir in dem vorherigen Artikel über Neuronale ODE.
1. Der Algorithmus Conformer
Conformer wurde entwickelt, um kontinuierliche Wetterveränderungen im Laufe der Zeit zu untersuchen, indem Kontinuität in den Mehrkopf-Aufmerksamkeitsmechanismus implementiert wird. Der Aufmerksamkeitsmechanismus wird als differenzierbare Funktion in der Transformatorarchitektur kodiert, um komplexe Wetterdynamiken zu modellieren.
Ursprünglich standen die Autoren der Methode vor der Aufgabe, ein Modell zu erstellen, das Wetterdaten in der Form (XN*W*H, T) als Input erhält. Dabei ist N die Anzahl der Wettervariablen wie Temperatur, Windgeschwindigkeit, Luftdruck usw. W*H bezieht sich auf die räumliche Auflösung der Variablen. T ist die Zeit, in der sich das System entwickelt. Das Modell empfängt Wettervariablen über die Zeit t, untersucht die Entwicklung des räumlich-zeitlichen Systems und sagt das Wetter für den nächsten Zeitschritt t+1 voraus.
![]()
Da sich das Wetter im Laufe der Zeit ständig ändert, ist es auch wichtig, die kontinuierlichen Veränderungen innerhalb der bereitgestellten Daten für einen bestimmten Zeitraum zu erfassen. Die Idee ist, die kontinuierliche, latente Darstellung von Wetterdaten mit Hilfe von Differentialgleichungslösern (solver) zu erlernen. Das Modell sagt also nicht nur den Wert der Wettervariablen zum Zeitpunkt „T“ voraus, sondern das definite Integral untersucht auch die Veränderungen der Wettervariablen, z. B. der Temperatur, vom Anfangszeitpunkt bis zum Zeitpunkt „T“. Das System kann wie folgt dargestellt werden:
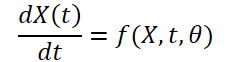
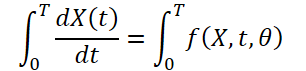
![]()
Wetterinformationen sind sehr variabel und sowohl zeitlich als auch räumlich schwer vorherzusagen. Zeitliche Ableitungen der einzelnen Wettervariablen werden berechnet, um die Wetterdynamik zu erhalten und eine bessere Extraktion von Merkmalen aus diskreten Daten zu ermöglichen. Die Autoren der Methode führen eine selektive Differenzierung auf Pixelebene durch, um kontinuierliche Veränderungen der Wetterphänomene im Laufe der Zeit zu erfassen.
Die Normalisierung von Ableitungen ist einer der wichtigsten Schritte, um die Verhaltensstabilität eines Deep-Learning-Modells zu gewährleisten. Die Autoren der Methode erweitern die Idee der Normalisierung als separate Elemente der Modellarchitektur. Sie untersuchen die Rolle der Normalisierung bei der direkten Anwendung auf Derivate. In diesem Beitrag werden die Auswirkungen der beiden gängigsten Normalisierungsmethoden und einer Vordifferenzierungsschicht auf die Leistung des Modells untersucht, um ihre Vorteile in kontinuierlichen Systemen zu demonstrieren.
Aufmerksamkeit ist eine der Schlüsselkomponenten der Transformer-Architektur. Es basiert auf der Idee, die wichtigsten Blöcke der Quelldaten im letzten Schritt der Prognose zu identifizieren. Trotz seines Erfolgs bei der Lösung verschiedener Probleme ist Transformer nach wie vor nur begrenzt in der Lage, die Einbettung von Informationen für hochdynamische Systeme wie die Wettervorhersage zu erlernen. Die Autoren der Conformer-Methode haben den Mechanismus der kontinuierlichen Aufmerksamkeit entwickelt, um kontinuierliche Veränderungen in den Wettervariablen zu modellieren. Erstens ersetzen sie die Analyse der Abhängigkeiten zwischen den Elementen des Ausgangszustands durch die Berücksichtigung der entsprechenden Parameter der verschiedenen Zustände der Umwelt. Dies ermöglicht die Berechnung des kontextuellen Einbettungsraums für jede zeitvariable Wettervariable. Dieser Schritt stellt sicher, dass das Modell dieselbe Variable in verschiedenen Zuständen in einem Stapel verarbeitet, anstatt auf Blöcke im selben Umgebungszustand zuzugreifen. Die Variablentransformation wird erlernt, indem jeder Variable eine eigene Abfrage, ein eigener Schlüssel und ein eigener Wert für jede Quelldatenprobe zugewiesen wird, ähnlich wie es in einem einzelnen Umgebungszustand gemacht wird. Der Aufmerksamkeitsmechanismus berechnet Abhängigkeitsschätzungen zwischen Variablen in verschiedenen Stichproben (an denselben Variablenpositionen). Ähnlich wie bei traditionellen Aufmerksamkeitsmechanismen können die für verschiedene Stapel erlernten Abhängigkeitsgewichte dazu verwendet werden, die mit diesen Variablen verbundenen Informationen zu aggregieren oder zu gewichten.
Diese Änderung ermöglicht es dem Modell, Beziehungen oder Abhängigkeiten zwischen denselben Wettervariablen in verschiedenen Umweltzuständen zu erfassen. Dies hat sich bei der Wettervorhersage als nützlich erwiesen, da das Modell in der Lage ist, die sich ständig weiterentwickelnden Eigenschaften der einzelnen Wettervariablen darzustellen. Um ein kontinuierliches Lernen zu gewährleisten, führen die Autoren der Methode Derivate in den Mechanismus der kontinuierlichen Aufmerksamkeit ein. Differentialgleichungen stellen die Dynamik eines physikalischen Systems im Zeitverlauf dar und berücksichtigen fehlende Datenwerte. Die Autoren der Methode kombinierten den Aufmerksamkeitsmechanismus mit dem Lernparadigma der Differentialgleichungen, um atmosphärische Veränderungen sowohl in räumlicher als auch in zeitlicher Hinsicht zu modellieren. Darüber hinaus beseitigt dieser Ansatz die Einschränkungen, die mit der Modellierung komplexer physikalischer Gleichungen in Modellen verbunden sind. Anstatt Vorhersagen nur für einen bestimmten Zeitpunkt zu machen, lernt der Conformer die Übergangsveränderungen von einem Zeitschritt zum nächsten, was wichtig ist, um noch nie dagewesene Wetterveränderungen zu erfassen.
Um die kontinuierliche Aufmerksamkeit zu berechnen, schlagen die Autoren der Methode vor, die Ableitungen der Ähnlichkeit für dieselben Variablen in jeder Datenstichprobe zu berechnen. Angenommen, wir haben 2 Eingabeproben der Größe (N*W*H). Bezeichnen wir sie als X0 and X1 zum Zeitpunkt t0 bzw. t1. Jede Variable hat in beiden Stichproben ihre eigenen Tensoren Q, K und V. Die kontinuierliche Aufmerksamkeit wird wie folgt berechnet:
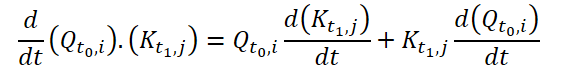
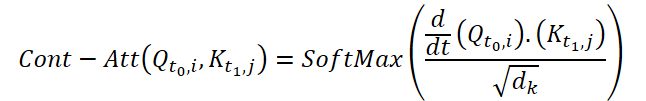
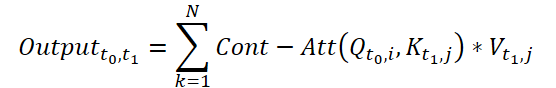
Das Ergebnis ist eine mit der Aufmerksamkeit gewichtete Summe der Werte ähnlicher Variablen in den Eingabedaten zu einem bestimmten Zeitpunkt t0 und t1. Das vorgestellte Verfahren berechnet die Aufmerksamkeit zwischen ähnlichen Variablen in den Eingabedaten über alle Zeitschritte hinweg, sodass das Modell Beziehungen oder Wechselwirkungen zwischen Variablen über die gesamte Abfolge von Eingabestichproben erfassen kann.
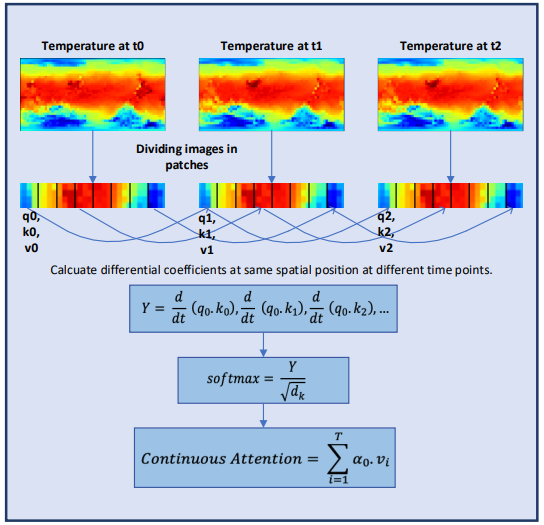
Um die kontinuierlichen Eigenschaften der meteorologischen Informationen weiter zu erforschen, fügen die Autoren von Conformer Schichten zum Modell Neuronalen ODE hinzu. Da die Löser mit adaptiver Größe eine höhere Genauigkeit aufweisen als die Löser mit fester Größe, wählten die Autoren der Methode die Dormand-Prince-Methode (Dopri5). Auf diese Weise lassen sich die kleinstmöglichen Veränderungen des Wetters im Laufe der Zeit untersuchen. Der vollständige Arbeitsablauf von Conformer und der Platzierung der neuronalen ODE-Schichten ist in der folgenden Visualisierung der Methode durch den Autor dargestellt.
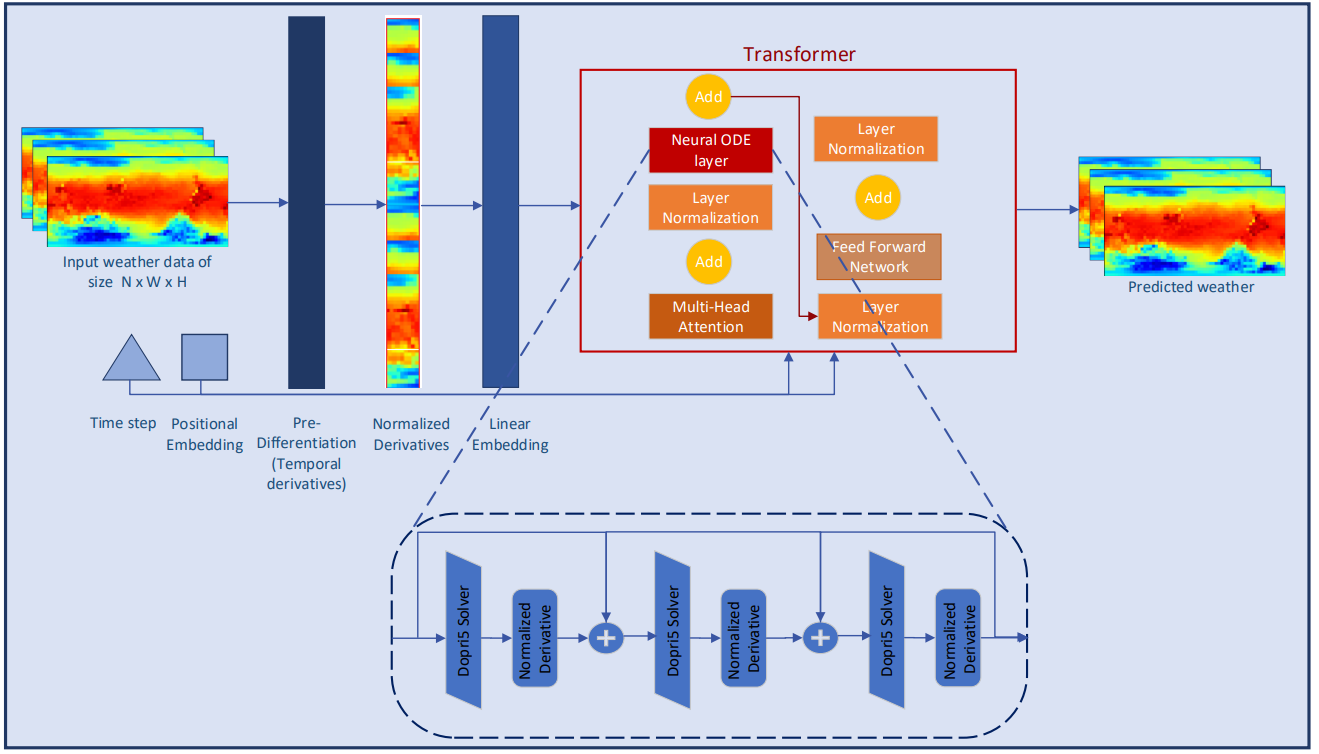
2. Implementierung in MQL5
Nachdem wir die theoretischen Aspekte der Conformer-Methoden besprochen haben, wenden wir uns nun der praktischen Umsetzung der vorgeschlagenen Ansätze mit MQL5 zu. Wir werden die Hauptfunktionalität in einer neuen Klasse CNeuronConformer implementieren, die von der Basisklasse CNeuronBaseOCL für neuronale Schichten abgeleitet ist.
2.1 Architektur der Klasse CNeuronConformer
In der Klassenstruktur CNeuronConformer sehen wir bereits bekannte Methoden, die in allen Klassen, die Aufmerksamkeitsmethoden implementieren, neu definiert werden. Allerdings unterscheidet sich die kontinuierliche Aufmerksamkeit (Continuous Attention) sehr von den bisher betrachteten Aufmerksamkeitsmethoden. Deshalb habe ich beschlossen, den Algorithmus von Grund auf neu zu implementieren. Dennoch werden bei dieser Umsetzung die Entwicklungen aus früheren Arbeiten genutzt.
Um die wichtigsten Parameter der Schichtenarchitektur zu schreiben, führen wir 5 Variablen ein:
- iWindow – die Größe des Vektors, der einen Parameter im Tensor der Ausgangsdaten beschreibt.
- iDimension – die Dimension des Vektors einer Entität aus Query, Key, Value (Abfrage, Schlüssel, Wert).
- iHeads – Anzahl der Aufmerksamkeitsköpfe.
- iVariables – die Anzahl der Parameter, die einen Zustand der Umgebung beschreiben.
- iCount – die Anzahl der analysierten Zustände der Umgebung (Länge der Sequenz der Ausgangsdaten).
Zur Erzeugung der Entitäten von Query-, Key- und Value verwenden wir, wie schon in ähnlichen Fällen, eine Faltungsschicht cQKV. Dieser Ansatz ermöglicht es uns, alle 3 Einheiten parallel zu implementieren. Wir werden die Ableitungen der Entitäten über die Zeit in die neuronale Basisschicht cdQKV schreiben.
Die Abhängigkeits-Koeffizienten werden, ähnlich wie beim nativen Transformer-Algorithmus, in der Matrix Score gespeichert. In dieser Implementierung werden wir jedoch keine Kopie der Matrix auf der Seite des Hauptprogramms erstellen. Wir werden nur einen Puffer im OpenCL-Kontext erstellen. In der lokalen Variable iScore der Klasse CNeuronConformer wird der Zeiger auf den Puffer gespeichert.
Die Ergebnisse der Multi-Head-Attention werden in den Puffern der neuronalen Basisschicht AttentionOut gespeichert. Wir werden die Dimensionalität der erhaltenen Daten mit Hilfe einer Faltungsschicht cW0 reduzieren.
Nach dem Conformer-Algorithmus folgt auf den Aufmerksamkeitsblock ein Block von neuronalen Schichten mit gewöhnlichen Differentialgleichungen. Für sie werden wir das Array cNODE erstellen. In ähnlicher Weise wird für den FeedForward-Block das cFF-Array erstellt.
class CNeuronConformer : public CNeuronBaseOCL { protected: //--- int iWindow; int iDimension; int iHeads; int iVariables; int iCount; //--- CNeuronConvOCL cQKV; CNeuronBaseOCL cdQKV; int iScore; CNeuronBaseOCL cAttentionOut; CNeuronConvOCL cW0; CNeuronNODEOCL cNODE[3]; CNeuronConvOCL cFF[2]; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool attentionOut(void); //--- virtual bool AttentionInsideGradients(void); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronConformer(void) {}; ~CNeuronConformer(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint variables, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); //--- virtual int Type(void) const { return defNeuronConformerOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual void SetOpenCL(COpenCLMy *obj); virtual CLayerDescription* GetLayerInfo(void); };
Alle internen Objekte der Klasse werden als statisch deklariert. So können wir den Konstruktor und den Destruktor der Klasse „leer“ lassen. Die Initialisierung des Klassenobjekts gemäß den Nutzeranforderungen wird in der Methode Init durchgeführt. In den Methodenparametern übergeben wir die Hauptparameter der Objektarchitektur.
bool CNeuronConformer::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint variables, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * variables * units_count, optimization_type, batch)) return false;
Im Hauptteil der Methode rufen wir die entsprechende Methode der übergeordneten Klasse auf, die die minimal notwendige Kontrolle der empfangenen Parameter und die Initialisierung der geerbten Objekte implementiert. Anhand des von der Methode zurückgegebenen logischen Ergebnisses können wir die Ergebnisse der Kontrollen und der Initialisierung überprüfen.
Als Nächstes initialisieren wir die innere Schicht cQKV, die dazu dient, die Entitäten Query, Key und Value zu erzeugen. Bitte beachten Sie, dass nach der Conformer-Methode Entitäten für jede einzelne Variable erstellt werden. Daher sind die Fenstergröße und der Faltungsschritt gleich der Länge des Einbettungsvektors einer Variablen. Die Anzahl der Faltungselemente ist gleich dem Produkt aus der Anzahl der Variablen, die einen Zustand der Umwelt beschreiben, und der Anzahl der zu analysierenden Zustände. Die Anzahl der Faltungsfilter entspricht den 3 Produkten aus der Länge einer Entität und der Anzahl der Aufmerksamkeitsköpfe.
if(!cQKV.Init(0, 0, OpenCL, window, window, 3 * window_key * heads, variables * units_count, optimization, iBatch)) return false;
Nach erfolgreichem Abschluss der 2 oben genannten Methoden speichern wir die erhaltenen Parameter in internen Variablen.
iWindow = int(fmax(window, 1)); iDimension = int(fmax(window_key, 1)); iHeads = int(fmax(heads, 1)); iVariables = int(fmax(variables, 1)); iCount = int(fmax(units_count, 1));
Wir initialisieren die innere Schicht, um partielle Ableitungen über die Zeit zu schreiben.
if(!cdQKV.Init(0, 1, OpenCL, 3 * iDimension * iHeads * iVariables * iCount, optimization, iBatch)) return false;
Wir erstellen einen Puffer von Aufmerksamkeitskoeffizienten.
iScore = OpenCL.AddBuffer(sizeof(float) * iCount * iHeads * iVariables * iCount, CL_MEM_READ_WRITE); if(iScore < 0) return false;
Mit der Initialisierung der internen Schichten AttentionOut und cW0 schließen wir die Vorbereitung der Objekte des Aufmerksamkeitsblocks ab.
if(!cAttentionOut.Init(0, 2, OpenCL, iDimension * iHeads * iVariables * iCount, optimization, iBatch)) return false; if(!cW0.Init(0, 3, OpenCL, iDimension * iHeads, iDimension * iHeads, iWindow, iVariables * iCount, optimization, iBatch)) return false;
Bitte beachten Sie, dass der Ausgang des Aufmerksamkeitsblocks eine Datendimension haben muss, die mit der Dimension der empfangenen Quelldaten übereinstimmt. Da der Conformer-Algorithmus außerdem die Analyse von Abhängigkeiten innerhalb einer Variablen, aber in verschiedenen Zuständen der Umgebung beinhaltet, führen wir auch eine Dimensionalitätsreduktion im Rahmen einzelner Variablen durch.
Alle verwendeten neuronalen Schichten für gewöhnliche Differentialgleichungen haben die gleiche Architektur. So können wir sie in einer Schleife initialisieren.
for(int i = 0; i < 3; i++) if(!cNODE[i].Init(0, 4 + i, OpenCL, iWindow, iVariables, iCount, optimization, iBatch)) return false;
Jetzt müssen wir nur noch die FeedForward-Blockobjekte initialisieren.
if(!cFF[0].Init(0, 7, OpenCL, iWindow, iWindow, 4 * iWindow, iVariables * iCount, optimization, iBatch)) return false; if(!cFF[1].Init(0, 8, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iVariables * iCount, optimization, iBatch)) return false;
Bevor die Methode abgeschlossen wird, organisieren wir die Ersetzung des Zeigers auf den Gradientenpuffer unserer Klasse durch den Gradientenpuffer der letzten Schicht des FeedForward-Blocks. Diese Technik ermöglicht es uns, unnötiges Kopieren von Daten zu vermeiden, und wir haben sie schon oft bei der Implementierung vieler anderer Methoden verwendet.
if(getGradientIndex() != cFF[1].getGradientIndex()) SetGradientIndex(cFF[1].getGradientIndex()); //--- return true; }
2.2 Implementierung des Feed-Forward-Passes
Nach der Initialisierung der Klasseninstanz fahren wir mit der Implementierung des Feed-Forward-Algorithmus fort. Schauen wir uns den Algorithmus der kontinuierlichen Aufmerksamkeit an, der von den Autoren der Conformer-Methode vorgeschlagen wurde. Sie verwendet partielle Ableitungen der Entitäten Query und Key über die Zeit.
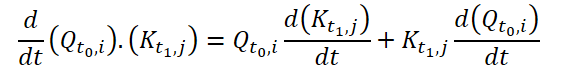
Es ist klar, dass wir in der Phase der Modelltraining nicht weiter als bis zur nächsten Annäherung an die Funktion der Abhängigkeit dieser Entitäten von der Zeit kommen. Daher werden wir die Frage der Definition von Ableitungen aus einem anderen Blickwinkel angehen. Erinnern wir uns zunächst an die geometrische Bedeutung der Ableitung einer Funktion. Sie besagt, dass die Ableitung einer Funktion in Bezug auf ein Argument in einem bestimmten Punkt der Neigungswinkel der Tangente an den Graphen der Funktion in diesem Punkt ist. Sie zeigt eine ungefähre (oder exakte für eine lineare Funktion) Änderung des Funktionswerts, wenn sich das Argument um 1 ändert.
In unseren Eingabedaten erhalten wir die Zustände der Umgebung mit einem festen Zeitschritt, der dem analysierten Zeitrahmen entspricht. Um unsere Implementierung zu vereinfachen, vernachlässigen wir den spezifischen Zeitrahmen und setzen den Zeitschritt zwischen 2 aufeinander folgenden Zuständen auf „1“. So können wir eine gewisse Annäherung an die Ableitung der Funktion analytisch erhalten, indem wir die durchschnittliche Änderung des Funktionswertes über zwei aufeinander folgende Übergänge zwischen den Zuständen vom vorherigen zum aktuellen und vom aktuellen zum nächsten nehmen.
Wir implementieren den vorgeschlagenen Mechanismus auf der OpenCL-Kontextseite im TimeDerivative-Kernel. In den Kernelparametern übergeben wir Zeiger auf 2 Puffer: Eingabedaten und Ergebnisse. Wir geben auch die Dimension einer Entität an.
__kernel void TimeDerivative(__global float *qkv, __global float *dqkv, int dimension) { const size_t pos = get_global_id(0); const size_t variable = get_global_id(1); const size_t head = get_global_id(2); const size_t total = get_global_size(0); const size_t variables = get_global_size(1); const size_t heads = get_global_size(2);
Wir planen, den Kernel in 3 Dimensionen zu starten:
- Anzahl der analysierten Umweltzustände,
- Anzahl der Variablen, die einen Zustand der Umwelt beschreiben,
- Anzahl der Aufmerksamkeitsköpfe.
Im Kernelkörper identifizieren wir sofort den aktuellen Thread in allen 3 Dimensionen. Danach bestimmen wir die Verschiebungen in den Puffern zu den zu bearbeitenden Entitäten. Der Einfachheit halber verwenden wir einen gleich großen Puffer für die Originaldaten und die Ergebnisse. Daher werden die Schichten identisch sein.
const int shift = 3 * heads * variables * dimension; const int shift_query = pos * shift + (3 * variable * heads + head) * dimension; const int shift_key = shift_query + heads * dimension;
Als Nächstes organisieren wir die Berechnung der Abweichungen in einer Schleife durch alle Elemente einer Entität. Zunächst bestimmen wir analytisch die Ableitung für Query.
for(int i = 0; i < dimension; i++) { //--- dQ/dt { int count = 0; float delta = 0; float value = qkv[shift_query + i]; if(pos > 0) { delta = value - qkv[shift_query + i - shift]; count++; } if(pos < (total - 1)) { delta += qkv[shift_query + i + shift] - value; count++; } if(count > 0) dqkv[shift_query + i] = delta / count; }
Dabei sind die Sonderfälle des ersten und letzten Elements der Folge zu beachten. In diesen Zuständen gibt es nur einen Übergang. Wir werden den Algorithmus nicht verkomplizieren und nur die verfügbaren Daten verwenden.
Auf ähnliche Weise berechnen wir die Ableitungen für Key.
//--- dK/dt { int count = 0; float delta = 0; float value = qkv[shift_key + i]; if(pos > 0) { delta = value - qkv[shift_key + i - shift]; count++; } if(pos < (total - 1)) { delta += qkv[shift_key + i + shift] - value; count++; } if(count > 0) dqkv[shift_key + i] = delta / count; } } }
Nachdem wir die partiellen Ableitungen nach der Zeit bestimmt haben, verfügen wir über alle notwendigen Daten für die Durchführung der kontinuierlichen Aufmerksamkeit. Auf der OpenCL-Kontextseite implementieren wir den vorgeschlagenen Algorithmus im FeedForwardContAtt-Kernel. In den Kernel-Parametern übergeben wir Zeiger auf 4 Datenpuffer: 2 Puffer für die Ausgangsdaten (Entitäten und ihre Ableitungen), einen Puffer für die Matrix der Abhängigkeitskoeffizienten und einen Puffer für die Ergebnisse der Mehrkopfaufmerksamkeit. Außerdem werden in den Kernel-Parametern 2 Konstanten angegeben: die Dimension des Vektors einer Entität und die Anzahl der Aufmerksamkeitsköpfe.
__kernel void FeedForwardContAtt(__global float *qkv, __global float *dqkv, __global float *score, __global float *out, int dimension, int heads) { const size_t query = get_global_id(0); const size_t key = get_global_id(1); const size_t variable = get_global_id(2); const size_t queris = get_global_size(0); const size_t keis = get_global_size(1); const size_t variables = get_global_size(2);
Im Kernelkörper identifizieren wir wie immer zuerst den aktuellen Thread in allen Dimensionen des Aufgabenraums. In diesem Fall verwenden wir einen 3-dimensionalen Aufgabenraum. Lokale Gruppen werden innerhalb einer Anfrage für eine Variable erstellt.
Hier deklarieren wir auch ein lokales Array für Zwischendaten.
const uint ls_score = min((uint)keis, (uint)LOCAL_ARRAY_SIZE); __local float local_score[LOCAL_ARRAY_SIZE];
Anschließend wird eine Schleife mit Iterationen entsprechend der Anzahl der Aufmerksamkeitsköpfe ausgeführt. Im Schleifenkörper wird die Datenanalyse nacheinander für alle Aufmerksamkeitsköpfe durchgeführt.
for(int head = 0; head < heads; head++) { const int shift = 3 * heads * variables * dimension; const int shift_query = query * shift + (3 * variable * heads + head) * dimension; const int shift_key = key * shift + (3 * variable * heads + heads + head) * dimension; const int shift_out = dimension * (heads * (query * variables + variable) + head); int shift_score = keis * (heads * (query * variables + variable) + head) + key;
Hier wird zunächst die Verschiebung in den Datenpuffern zu den benötigten Elementen ermittelt. Danach berechnen wir die Abhängigkeitskoeffizienten. Diese Koeffizienten werden in 3 Stufen ermittelt. Zunächst berechnen wir die Exponentialwerte d/dt(QK) und speichern sie im entsprechenden Element des Abhängigkeitskoeffizientenpuffers. Die Berechnungen werden in parallelen Threads einer Arbeitsgruppe durchgeführt.
//--- Score float scr = 0; for(int d = 0; d < dimension; d++) scr += qkv[shift_query + d] * dqkv[shift_key + d] + qkv[shift_key + d] * dqkv[shift_query + d]; scr = exp(min(scr / sqrt((float)dimension), 30.0f)); score[shift_score] = scr; barrier(CLK_LOCAL_MEM_FENCE);
Im zweiten Schritt wird die Summe aller erhaltenen Werte gebildet.
if(key < ls_score) { local_score[key] = scr; for(int k = ls_score + key; k < keis; k += ls_score) local_score[key] += score[shift_score + k]; } barrier(CLK_LOCAL_MEM_FENCE); //--- int count = ls_score; do { count = (count + 1) / 2; if(key < count) { if((key + count) < keis) { local_score[key] += local_score[key + count]; local_score[key + count] = 0; } } barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Im dritten Schritt normalisieren wir die Abhängigkeitskoeffizienten.
score[shift_score] /= local_score[0];
barrier(CLK_LOCAL_MEM_FENCE);
Am Ende der Iterationen der Schleife wird der Wert der Ergebnisse des Aufmerksamkeitsblocks gemäß den oben definierten Abhängigkeitskoeffizienten berechnet.
shift_score -= key; for(int d = key; d < dimension; d += keis) { float sum = 0; int shift_value = (3 * variable * heads + 2 * heads + head) * dimension + d; for(int v = 0; v < keis; v++) sum += qkv[shift_value + v * shift] * score[shift_score + v]; out[shift_out + d] = sum; } barrier(CLK_LOCAL_MEM_FENCE); } //--- }
Nachdem wir die Kernel für die Implementierung des Algorithmus der kontinuierlichen Aufruf (Continuous Attention) auf der Kontextseite von OpenCL erstellt haben, müssen wir den Aufruf der oben erstellten Kernel im Hauptprogramm implementieren. Dazu fügen wir die Methode attentionOut zu unserer CNeuronConformer-Klasse hinzu.
Wir teilen die Kernel-Aufrufe nicht in separate Methoden auf, da sie parallel aufgerufen werden. Allerdings haben wir den Algorithmus auf der Seite des OpenCL-Programms wegen der Unterschiede im Aufgabenbereich aufgeteilt.
Da diese Methode nur für den Aufruf innerhalb einer Klasse erstellt wird, basiert ihr Algorithmus vollständig auf der Verwendung von internen Objekten und Variablen. Dadurch konnten die Methodenparameter vollständig eliminiert werden.
bool CNeuronConformer::attentionOut(void) { if(!OpenCL) return false;
Im Methodenkörper wird die Relevanz des Zeigers auf den OpenCL-Kontext geprüft. Danach bereiten wir uns auf den Aufruf des ersten Kerns zur Definition abgeleiteter Entitäten vor.
Zunächst definieren wir den Aufgabenraum.
bool CNeuronConformer::attentionOut(void) { if(!OpenCL) return false; //--- Time Derivative { uint global_work_offset[3] = {0, 0, 0}; uint global_work_size[3] = {iCount, iVariables, iHeads};
Dann übergeben wir die Parameter an den Kernel.
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_TimeDerivative, def_k_tdqkv, cQKV.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_TimeDerivative, def_k_tddqkv, cdQKV.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_TimeDerivative, def_k_tddimension, int(iDimension))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Wir stellen den Kernel in die Ausführungswarteschlange.
if(!OpenCL.Execute(def_k_TimeDerivative, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } }
Der allgemeine Algorithmus zur Platzierung des zweiten Kernels in der Ausführungswarteschlange ist ähnlich. Diesmal fügen wir jedoch den Aufgabenbereich der Arbeitsgruppe hinzu.
//--- MH Attention Out { uint global_work_offset[3] = {0, 0, 0}; uint global_work_size[3] = {iCount, iCount, iVariables}; uint local_work_size[3] = {1, iCount, 1};
Außerdem steigt die Anzahl der übertragenen Parameter.
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardContAtt, def_k_caqkv, cQKV.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardContAtt, def_k_cadqkv, cdQKV.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardContAtt, def_k_cascore, iScore)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardContAtt, def_k_caout, cAttentionOut.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardContAtt, def_k_cadimension, int(iDimension))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardContAtt, def_k_caheads, int(iHeads))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Nach Abschluss der vorbereitenden Arbeiten stellen wir den Kernel in die Ausführungswarteschlange.
if(!OpenCL.Execute(def_k_FeedForwardContAtt, 3, global_work_offset, global_work_size, local_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } } //--- return true; }
Der Aufruf von 2 Kerneln implementiert jedoch nur einen Teil der vorgeschlagenen Conformer-Methode. Dies ist der wichtigste Teil der kontinuierlichen Aufmerksamkeit. Wir werden den vollständigen Algorithmus für den Feed-Forward-Durchgang unserer Klasse in der Methode CNeuronConformer::feedForward beschreiben. Ähnlich wie die entsprechenden Methoden der zuvor erstellten Klassen erhält die feedForward-Methode als Parameter einen Zeiger auf das Objekt der vorherigen Ebene, das die Eingabedaten für unsere Klasse enthält.
bool CNeuronConformer::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- Generate Query, Key, Value if(!cQKV.FeedForward(NeuronOCL)) return false;
Im Methodenkörper rufen wir zunächst die Feed-Forward-Methode der inneren Schicht cQKV auf, um die Entitätstensoren Query, Key und Value zu bilden. Danach rufen wir die oben erstellte Methode auf, um die Kernel des Continuous Attention Mechanismus aufzurufen.
//--- MH Continuas Attention if(!attentionOut()) return false;
Anschließend reduzieren wir die Dimensionalität der erhaltenen Ergebnisse der mehrköpfigen Aufmerksamkeit. Der resultierende Tensor wird zu den Eingabedaten hinzugefügt und innerhalb der einzelnen Variablen normalisiert.
if(!cW0.FeedForward(GetPointer(cAttentionOut))) return false; if(!SumAndNormilize(NeuronOCL.getOutput(), cW0.getOutput(), cW0.getOutput(), iDimension, true, 0, 0, 0, 1)) return false;
Auf den Block „Continuous Attention“ folgt nach dem Algorithmus „Conformer“ ein Block mit Lösern für gewöhnliche Differentialgleichungen. Wir implementieren ihre Aufrufe in einer Schleife. Danach summieren wir die Tensoren am Eingang und am Ausgang des Blocks und normalisieren das Ergebnis.
//--- Neural ODE CNeuronBaseOCL *prev = GetPointer(cW0); for(int i = 0; i < 3; i++) { if(!cNODE[i].FeedForward(prev)) return false; prev = GetPointer(cNODE[i]); } if(!SumAndNormilize(prev.getOutput(), cW0.getOutput(), prev.getOutput(), iDimension, true, 0, 0, 0, 1)) return false;
Am Ende der FeedForward-Methode führen wir einen FeedForward-Durchlauf des FeedForward-Blocks durch und summieren und normalisieren dann die Ergebnisse.
//--- Feed Forward for(int i = 0; i < 2; i++) { if(!cFF[i].FeedForward(prev)) return false; prev = GetPointer(cFF[i]); } if(!SumAndNormilize(prev.getOutput(), cNODE[2].getOutput(), getOutput(), iDimension, true, 0, 0, 0, 1)) return false; //--- return true; }
Damit ist unsere Arbeit an der Implementierung des Feed-Forward-Algorithmus abgeschlossen. Aber um die Modelle zu trainieren, müssen wir auch einen Backpropagation-Durchgang implementieren, der den Fehlergradienten auf alle Elemente entsprechend ihrem Einfluss auf das Endergebnis überträgt und die Modellparameter anpasst, um den Gesamtfehler des Modells zu reduzieren.
2.3 Organisation des Backpropagation-Passes
Um den Backpropagation-Algorithmus zu implementieren, müssen wir auch neue Kernel erstellen. Zunächst müssen wir einen Kernel erstellen, um Fehlergradienten durch den Block Continuous Attention - HiddenGradientContAtt zu propagieren. In den Kernelparametern übergeben wir Zeiger auf 6 Datenpuffer und 1 Konstante.
__kernel void HiddenGradientContAtt(__global float *qkv, __global float *qkv_g, __global float *dqkv, __global float *dqkv_g, __global float *score, __global float *out_g, int dimension) { const size_t pos = get_global_id(0); const size_t variable = get_global_id(1); const size_t head = get_global_id(2); const size_t total = get_global_size(0); const size_t variables = get_global_size(1); const size_t heads = get_global_size(2);
Ähnlich wie beim Feed-Forward-Kernel implementieren wir den Backpropagation-Durchlauf in einem 3-dimensionalen Aufgabenraum, jedoch ohne Gruppierung in Arbeitsgruppen. Im Kernelkörper identifizieren wir den Thread in allen Dimensionen des Aufgabenraums.
Der weitere Kernel-Algorithmus lässt sich je nach dem Objekt des Fehlergradienten in 3 Teile unterteilen. Im ersten Block verteilen wir den Fehlergradienten auf die Entität Value.
//--- Value gradient { const int shift_value = dimension * (heads * (3 * variables * pos + 3 * variable + 2) + head); const int shift_out = dimension * (head + variable * heads); const int shift_score = total * (variable * heads + head); const int step_out = variables * heads * dimension; const int step_score = variables * heads * total; //--- for(int d = 0; d < dimension; d++) { float sum = 0; for(int g = 0; g < total; g++) sum += out_g[shift_out + g * step_out + d] * score[shift_score + g * step_score]; qkv_g[shift_value + d] = sum; } }
Hier wird zunächst die Verschiebung in den Datenpuffern zu den benötigten Elementen ermittelt. Dann sammeln wir in einem Schleifensystem die Fehlergradienten in allen abhängigen Elementen und in allen Elementen des Entitätsvektors.
Im zweiten Block propagieren wir die Fehlergradienten bis zur Query. Allerdings ist der Algorithmus hier etwas komplizierter.
//--- Query gradient { const int shift_out = dimension * (heads * (pos * variables + variable) + head); const int step = 3 * variables * heads * dimension; const int shift_query = dimension * (3 * heads * variable + head) + pos * step; const int shift_key = dimension * (heads * (3 * variable + 1) + head); const int shift_value = dimension * (heads * (3 * variable + 2) + head); const int shift_score = total * (heads * (pos * variables + variable) + head);
Wie im ersten Block bestimmen wir zunächst die Verschiebung zu den zu analysierenden Elementen in den Datenpuffern. Danach müssen wir zunächst den Gradienten auf die Matrix der Abhängigkeitskoeffizienten verteilen und ihn an die Ableitung der SoftMax-Funktion anpassen.
//--- Score gradient for(int k = 0; k < total; k++) { float score_grad = 0; float scr = score[shift_score + k]; for(int v = 0; v < total; v++) { float grad = 0; for(int d = 0; d < dimension; d++) grad += qkv[shift_value + v * step + d] * out_g[shift_out + d]; score_grad += score[shift_score + v] * grad * ((float)(pos == v) - scr); } score_grad /= sqrt((float)dimension);
Erst dann können wir den Fehlergradienten an die Entität von Query weitergeben. Im Gegensatz zum nativen Transformer-Algorithmus propagieren wir in diesem Fall jedoch auch den Fehlergradienten auf die entsprechenden Ableitungen der Entität von Query nach der Zeit.
//--- Query gradient for(int d = 0; d < dimension; d++) { if(k == 0) { dqkv_g[shift_query + d] = score_grad * qkv[shift_key + k * step + d]; qkv_g[shift_query + d] = score_grad * dqkv[shift_key + k * step + d]; } else { dqkv_g[shift_query + d] += score_grad * qkv[shift_key + k * step + d]; qkv_g[shift_query + d] += score_grad * dqkv[shift_key + k * step + d]; } } } }
Die Weitergabe des Fehlergradienten an die Entität von Key und seine partielle Ableitung erfolgt auf ähnliche Weise. In der Matrix der Abhängigkeitskoeffizienten wird jedoch eine weitere Dimension berücksichtigt.
//--- Key gradient { const int shift_key = dimension * (heads * (3 * variables * pos + 3 * variable + 1) + head); const int shift_out = dimension * (heads * variable + head); const int step_out = variables * heads * dimension; const int step = 3 * variables * heads * dimension; const int shift_query = dimension * (3 * heads * variable + head); const int shift_value = dimension * (heads * (3 * variable + 2) + head) + pos * step; const int shift_score = total * (heads * variable + head); const int step_score = variables * heads * total; //--- Score gradient for(int q = 0; q < total; q++) { float score_grad = 0; float scr = score[shift_score + q * step_score]; for(int g = 0; g < total; g++) { float grad = 0; for(int d = 0; d < dimension; d++) grad += qkv[shift_value + d] * out_g[shift_out + d + g * step_out]; score_grad += score[shift_score + q * step_score + g] * grad * ((float)(q == pos) - scr); } score_grad /= sqrt((float)dimension); //--- Key gradient for(int d = 0; d < dimension; d++) { if(q == 0) { dqkv_g[shift_key + d] = score_grad * qkv[shift_query + q * step + d]; qkv_g[shift_key + d] = score_grad * dqkv[shift_query + q * step + d]; } else { qkv_g[shift_key + d] += score_grad * dqkv[shift_query + q * step + d]; dqkv_g[shift_key + d] += score_grad * qkv[shift_query + q * step + d]; } } } } }
Wie Sie sehen, haben wir im vorherigen Kernel den Fehlergradienten sowohl auf die Entitäten selbst als auch auf ihre Ableitungen übertragen. Ich möchte Sie daran erinnern, dass wir die partiellen Ableitungen nach der Zeit analytisch berechnet haben, und zwar auf der Grundlage der Werte der Entitäten selbst für verschiedene Zustände der Umwelt. Logischerweise können wir den Fehlergradienten auf ähnliche Weise fortschreiben. Wir implementieren einen solchen Algorithmus im Kernel HiddenGradientTimeDerivative.
__kernel void HiddenGradientTimeDerivative(__global float *qkv_g, __global float *dqkv_g, int dimension) { const size_t pos = get_global_id(0); const size_t variable = get_global_id(1); const size_t head = get_global_id(2); const size_t total = get_global_size(0); const size_t variables = get_global_size(1); const size_t heads = get_global_size(2);
Die Kernelparameter und der Aufgabenbereich sind ähnlich wie beim Feed-Forward-Durchlauf. Nur dass wir anstelle von Ergebnispuffern Fehlergradientenpuffer verwenden.
Im Hauptteil der Methode identifizieren wir den Thread in allen Dimensionen des verwendeten Aufgabenraums. Danach bestimmen wir die Verschiebung in den Datenpuffern.
const int shift = 3 * heads * variables * dimension; const int shift_query = pos * shift + (3 * variable * heads + head) * dimension; const int shift_key = shift_query + heads * dimension;
Ähnlich wie bei der Berechnung von Ableitungen setzen wir die Verteilung von Fehlergradienten um.
for(int i = 0; i < dimension; i++) { //--- dQ/dt { int count = 0; float grad = 0; float current = dqkv_g[shift_query + i]; if(pos > 0) { grad += current - dqkv_g[shift_query + i - shift]; count++; } if(pos < (total - 1)) { grad += dqkv_g[shift_query + i + shift] - current; count++; } if(count > 0) grad /= count; qkv_g[shift_query + i] += grad; }
//--- dK/dt { int count = 0; float grad = 0; float current = dqkv_g[shift_key + i]; if(pos > 0) { grad += current - dqkv_g[shift_key + i - shift]; count++; } if(pos < (total - 1)) { grad += dqkv_g[shift_key + i + shift] - current; count++; } if(count > 0) grad /= count; qkv_g[shift_key + i] += dqkv_g[shift_key + i] + grad; } } }
Der Aufruf dieser Kernel auf der Seite des Hauptprogramms erfolgt in der Methode CNeuronConformer::AttentionInsideGradients. Der Algorithmus für die Konstruktion dieser Methode ähnelt der entsprechenden Feedforward-Pass-Methode. Nur die Kernel werden in umgekehrter Reihenfolge aufgerufen. Zunächst wird die Ausführung des Kerns für die Gradientenausbreitung durch den Block „Continuous Attention“ in die Warteschlange gestellt.
bool CNeuronConformer::AttentionInsideGradients(void) { if(!OpenCL) return false; //--- MH Attention Out Gradient { uint global_work_offset[3] = {0, 0, 0}; uint global_work_size[3] = {iCount, iVariables, iHeads};
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientContAtt, def_k_hgcaqkv, cQKV.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientContAtt, def_k_hgcaqkv_g, cQKV.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientContAtt, def_k_hgcadqkv, cdQKV.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientContAtt, def_k_hgcadqkv_g, cdQKV.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientContAtt, def_k_hgcascore, iScore)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientContAtt, def_k_hgcaout_g, cAttentionOut.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_HiddenGradientContAtt, def_k_hgcadimension, int(iDimension))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.Execute(def_k_HiddenGradientContAtt, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } }
Dann addieren wir den Fehlergradienten aus den partiellen Ableitungen.
//--- Time Derivative Gradient { uint global_work_offset[3] = {0, 0, 0}; uint global_work_size[3] = {iCount, iVariables, iHeads};
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_HGTimeDerivative, def_k_tdqkv, cQKV.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HGTimeDerivative, def_k_tddqkv, cdQKV.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_HGTimeDerivative, def_k_tddimension, int(iDimension))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.Execute(def_k_HGTimeDerivative, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } } //--- return true; }
Nach Abschluss der vorbereitenden Arbeiten setzen wir den gesamten Algorithmus zur Verteilung der Fehlergradienten in der Methode CNeuronConformer::calcInputGradients zusammen. In seinen Parametern erhalten wir einen Zeiger auf das Objekt der vorherigen Ebene. Dies ist die Ebene, an die wir den Fehlergradienten weitergeben müssen.
bool CNeuronConformer::calcInputGradients(CNeuronBaseOCL *prevLayer) { //--- Feed Forward Gradient if(!cFF[1].calcInputGradients(GetPointer(cFF[0]))) return false; if(!cFF[0].calcInputGradients(GetPointer(cNODE[2]))) return false; if(!SumAndNormilize(Gradient, cNODE[2].getGradient(), cNODE[2].getGradient(), iDimension, false)) return false;
Dank der von uns veranlassten Vertauschung der Gradientenpuffer hat uns die nächste Schicht den Fehlergradienten direkt in den Puffer der letzten inneren Schicht im FeedForward-Block übergeben. Ohne unnötige Kopiervorgänge rufen wir nun nacheinander die Methoden des Backpropagation-Durchgangs der FeedForward-Blockobjekte auf.
Während des Feed-Forward-Durchlaufs haben wir die Werte der Puffer am Eingang und am Ausgang des FeedForward-Blocks addiert. Auf ähnliche Weise summieren wir die Fehlergradienten. Anschließend wird das erhaltene Ergebnis an den Ausgang des Blocks mit den Schichten der gewöhnlichen Differentialgleichungen weitergeleitet. Danach führen wir eine Umkehrschleife durch die internen Schichten des Neural ODE-Blocks durch und propagieren den Fehlergradienten in ihnen.
//--- Neural ODE Gradient CNeuronBaseOCL *prev = GetPointer(cNODE[1]); for(int i = 2; i > 0; i--) { if(!cNODE[i].calcInputGradients(prev)) return false; prev = GetPointer(cNODE[i - 1]); } if(!cNODE[0].calcInputGradients(GetPointer(cW0))) return false; if(!SumAndNormilize(cW0.getGradient(), cNODE[2].getGradient(), cW0.getGradient(), iDimension, false)) return false;
Auch hier summieren wir die Fehlergradienten am Eingang und am Ausgang des Blocks.
Der erste im Feed-Forward-Durchgang und der letzte im Backpropagation-Durchgang ist Continuous Attention. Zunächst verteilen wir den Fehlergradienten auf die Aufmerksamkeitsköpfe.
//--- MH Attention Gradient if(!cW0.calcInputGradients(GetPointer(cAttentionOut))) return false;
Dann verteilen wir den Fehlergradienten durch den Aufmerksamkeitsblock.
if(!AttentionInsideGradients()) return false;
Dann wird der Fehlergradient zurück auf die Ebene der vorherigen Schicht propagiert.
//--- Query, Key, Value Graddients if(!cQKV.calcInputGradients(prevLayer)) return false;
Am Ende der Methode wird der Fehlergradient am Eingang und am Ausgang des Aufmerksamkeitsblocks summiert.
if(!SumAndNormilize(cW0.getGradient(), prevLayer.getGradient(), prevLayer.getGradient(), iDimension, false)) return false; //--- return true; }
Nachdem wir den Fehlergradienten auf alle Objekte entsprechend ihrem Einfluss auf das Endergebnis verteilt haben, fahren wir mit der Optimierung der Parameter fort, um den Gesamtfehler der Modelle zu verringern.
Es sollte an dieser Stelle erwähnt werden, dass alle Lernparameter unserer Klasse CNeuronConformer in den inneren neuronalen Schichten enthalten sind. Um die Modellparameter zu aktualisieren, müssen wir daher nur die gleichnamigen Methoden der internen Objekte nacheinander aufrufen.
bool CNeuronConformer::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { //--- MH Attention if(!cQKV.UpdateInputWeights(NeuronOCL)) return false; if(!cW0.UpdateInputWeights(GetPointer(cAttentionOut))) return false;
//--- Neural ODE CNeuronBaseOCL *prev = GetPointer(cW0); for(int i = 0; i < 3; i++) { if(!cNODE[i].UpdateInputWeights(prev)) return false; prev = GetPointer(cNODE[i]); }
//--- Feed Forward for(int i = 0; i < 2; i++) { if(!cFF[i].UpdateInputWeights(prev)) return false; prev = GetPointer(cFF[i]); } //--- return true; }
Damit schließen wir unsere Ausführungen zu den neuen Methoden der Klasse CNeuronConformer ab, in denen wir die wichtigsten von den Autoren der Conformer-Methode vorgeschlagenen Ansätze implementiert haben. Leider erlaubt es das Format des Artikels nicht, näher auf die Hilfsmethoden der Klasse einzugehen. Sie können diese Methoden mit Hilfe der im Anhang beigefügten Dateien selbst untersuchen. Der Anhang enthält auch den vollständigen Code für alle im Artikel verwendeten Programme. Weiter geht's.
2.4 Modellarchitektur für das Training
Bevor wir uns der Architektur der trainierten Modelle zuwenden, möchte ich Sie daran erinnern, dass wir nach der Conformer-Methode die Analyse in Bezug auf einzelne Parameter der Umgebungsbeschreibung durchführen sollten. Daher müssen wir bei der anfänglichen Verarbeitung der Eingabedaten für jeden analysierten Parameter eine Einbettung erstellen.
Schauen wir uns zunächst die Struktur der zu analysierenden Daten an.
......... ......... sState.state[shift] = (float)(Rates[b].close - open); sState.state[shift + 1] = (float)(Rates[b].high - open); sState.state[shift + 2] = (float)(Rates[b].low - open); sState.state[shift + 3] = (float)(Rates[b].tick_volume / 1000.0f); sState.state[shift + 4] = rsi; sState.state[shift + 5] = cci; sState.state[shift + 6] = atr; sState.state[shift + 7] = macd; sState.state[shift + 8] = sign; ........ ........
In meiner Implementierung habe ich die Quelldaten wie folgt aufgeteilt:
- Beschreibung der letzten Kerze (4 Elemente)
- RSI (1 Element)
- CCI (1 Element)
- ATF (1 Element)
- MACD (2 Elemente)
Diese Aufteilung ist nur meine Vision. Sie können auch eine andere Einteilung wählen. Sie muss sich jedoch in der Architektur der trainierten Modelle widerspiegeln.
Die Architektur der trainierten Modelle wird in der Methode CreateDescriptions beschrieben. In den Parametern erhält die Methode 3 Zeiger auf dynamische Arrays, um die Architektur von 3 Modellen zu übertragen.
Im Hauptteil der Methode werden zunächst die empfangenen Zeiger überprüft und gegebenenfalls neue dynamische Array-Objekte erstellt.
bool CreateDescriptions(CArrayObj *encoder, CArrayObj *actor, CArrayObj *critic) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; }
Wir geben die unbearbeiteten Daten, die den aktuellen Zustand der Umgebung beschreiben, in das Encoder-Modell ein.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Die empfangenen Daten werden in der Batch-Normalisierungsschicht vorverarbeitet.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = MathMax(1000, GPTBars); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Danach erstellen wir Einbettungen der aktuellen Zustandsparameter entsprechend der oben dargestellten Struktur.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronEmbeddingOCL; { int temp[] = {4, 1, 1, 1, 2}; ArrayCopy(descr.windows, temp); }
Beachten Sie, dass wir in den zuvor besprochenen Einbettungsarchitekturen eine Fenstergröße festgelegt haben, die der Größe der Eingabedaten entspricht. Auf diese Weise haben wir eine Einbettung eines eigenen Zustands geschaffen. In diesem Fall gehen wir jedoch von der Analyse der Beschreibung des letzten Balkens aus und teilen die Parameter in die oben genannten Blöcke ein. Wenn Sie mehr als 1 Balken oder eine andere Datenkonfiguration analysieren, sollten Sie dies in der Größe der analysierten Datenfenster berücksichtigen.
prev_count = descr.count = GPTBars; int prev_wout = descr.window_out = EmbeddingSize / 2; if(!encoder.Add(descr)) { delete descr; return false; }
Die nachfolgende Faltungsschicht schließt den Prozess der Erzeugung von Einbettungen der Originaldaten ab.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = prev_count * 5; descr.step = descr.window = prev_wout; prev_wout = descr.window_out = EmbeddingSize; if(!encoder.Add(descr)) { delete descr; return false; }
Fügen wir den Einbettungen Positionskodierungsharmonien hinzu.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronPEOCL; descr.count = prev_count; descr.window = prev_wout * 5; if(!encoder.Add(descr)) { delete descr; return false; }
Am Ende des Encoder-Modells wird ein Block von 5 aufeinanderfolgenden Conformer-Schichten erstellt. Die Parameter der Schicht werden wie bei den anderen Aufmerksamkeitsschichten festgelegt. Die Anzahl der zu analysierenden Variablen ist in desc.layers angegeben.
for(int i = 0; i < 5; i++) { if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConformerOCL; descr.count = prev_count; descr.window = prev_wout; descr.step = 4; descr.window_out = EmbeddingSize; descr.layers = 5; if(!encoder.Add(descr)) { delete descr; return false; } }
Das Kernstück des Akteursmodells ist wie zuvor eine aufmerksamkeitsübergreifende Schicht, die Abhängigkeiten zwischen dem aktuellen Kontostand und der komprimierten Darstellung des aktuellen Umgebungszustands, die vom Encoder empfangen wird, schätzt.
Wir füttern das Modell zunächst mit einer Beschreibung des Kontostatus.
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = AccountDescr; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Wir konvertieren es zum Einbetten (embedding).
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = EmbeddingSize; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Wir fügen einen Block von 3 Cross-Attention-Schichten hinzu.
//--- layer 2-4 for(int i = 0; i < 3; i++) { if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronCrossAttenOCL; { int temp[] = {1, GPTBars * 5}; ArrayCopy(descr.units, temp); } { int temp[] = {EmbeddingSize, EmbeddingSize}; ArrayCopy(descr.windows, temp); } descr.window_out = 16; descr.step = 4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } }
Auf der Grundlage der Daten aus dem Cross-Attention-Block entwickeln wir die stochastische Politik des Akteurs.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 2 * NActions; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = NActions; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Das Kritiker-Modell basiert auf einer ähnlichen Struktur. Anstelle des Kontostatus werden jedoch die Aktionen des Akteurs mit dem Zustand der Umgebung verglichen.
Wir speisen die generierten Aktionen des Akteurs in das Modell ein.
//--- Critic critic.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = NActions; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Sie werden in eine Einbettung umgewandelt.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = EmbeddingSize; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Als Nächstes kommt der Querverbindungsblock aus 3 Schichten.
//--- layer 2-4 for(int i = 0; i < 3; i++) { if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronCrossAttenOCL; { int temp[] = {1, GPTBars * 5}; ArrayCopy(descr.units, temp); } { int temp[] = {EmbeddingSize, EmbeddingSize}; ArrayCopy(descr.windows, temp); } descr.window_out = 16; descr.step = 4; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } }
Die Aktionen werden im Perceptron-Block ausgewertet.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NRewards; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
2.5 Modelltraining
Die von uns vorgenommenen Änderungen hatten keinen Einfluss auf den Prozess der Interaktion mit der Umwelt. Daher können wir den EA „...\Conformer\Research.mq5“ ohne Änderung verwenden, um die anfänglichen Trainingsdaten zu sammeln und dann den Trainingsdatensatz zu aktualisieren. Darüber hinaus ist die Datenstruktur trotz der Änderungen in der Vorgehensweise bei der Analyse der Eingabedaten unverändert. Auf diese Weise können wir einen zuvor gesammelten Trainingsdatensatz verwenden, um das Modell zu trainieren.
Wir haben jedoch einige Änderungen am Modelltrainingsprozess innerhalb des Algorithmus der „...\Conformer\Study.mq5“ EA vorgenommen. In diesem Artikel betrachten wir nur die Modellbildungsmethode Train.
Wie zuvor erstellen wir zu Beginn der Methode einen Vektor von Wahrscheinlichkeiten für die Auswahl von Trajektorien in Abhängigkeit von ihrer Rentabilität. Die profitabelsten Pässe erhalten eine höhere Wahrscheinlichkeit, während des Modelltrainings ausgewählt zu werden.
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
Dann initialisieren wir die lokalen Variablen.
vector<float> result, target; bool Stop = false; //--- uint ticks = GetTickCount();
Wir erstellen ein System von verschachtelten Modell-Trainingsschleifen. Im Hauptteil der äußeren Schleife nehmen wir die Trajektorie aus dem Erfahrungswiedergabepuffer und den anfänglichen Trainingszustand auf.
int tr = SampleTrajectory(probability); int batch = GPTBars + 48; int state = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - PrecoderBars - batch)); if(state <= 0) { iter--; continue; }
Danach werden die rekurrenten Puffer des Encoders gelöscht und der endgültige Zustand des Trainingsdatensatzes bestimmt.
Encoder.Clear(); int end = MathMin(state + batch, Buffer[tr].Total - PrecoderBars);
Nach Abschluss der vorbereitenden Arbeiten organisieren wir eine verschachtelte Schleife durch die Trainingszustände.
for(int i = state; i < end; i++) { bState.AssignArray(Buffer[tr].States[i].state); //--- State Encoder if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Im Hauptteil der Schleife laden wir zunächst den Zustand der Umgebung aus dem Erfahrungswiedergabepuffer und analysieren ihn in unserem Encoder, indem wir die Feedforward-Methode aufrufen.
Als Nächstes laden wir die Aktionen des Akteurs aus dem Erfahrungswiedergabepuffer und bewerten sie mit unserem Kritiker.
//--- Critic bActions.AssignArray(Buffer[tr].States[i].action); if(bActions.GetIndex() >= 0) bActions.BufferWrite(); if(!Critic.feedForward((CBufferFloat*)GetPointer(bActions), 1, false, GetPointer(Encoder))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Dann passen wir die Bewertung des Kritikers an die tatsächliche Belohnung aus dem Erfahrungswiedergabepuffer an.
result.Assign(Buffer[tr].States[i + 1].rewards); target.Assign(Buffer[tr].States[i + 2].rewards); result = result - target * DiscFactor; Result.AssignArray(result); Critic.TrainMode(true); if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder)) || !Encoder.backPropGradient((CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Wir geben auch den Kritiker-Fehlergradienten an den Encoder weiter, um den Zustand der Umgebung zu analysieren.
Als Nächstes laden wir aus dem Erfahrungswiedergabepuffer eine Beschreibung des Kontostatus, die dem analysierten Zustand der Umgebung entspricht.
//--- Policy float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; bAccount.Clear(); bAccount.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[1] / PrevBalance); bAccount.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); bAccount.Add(Buffer[tr].States[i].account[2]); bAccount.Add(Buffer[tr].States[i].account[3]); bAccount.Add(Buffer[tr].States[i].account[4] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[5] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[6] / PrevBalance); double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); bAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(bAccount.GetIndex() >= 0) bAccount.BufferWrite();
Auf der Grundlage dieser Daten erstellen wir eine Akteur-Aktion in Übereinstimmung mit seiner aktuellen Politik.
//--- Actor if(!Actor.feedForward((CBufferFloat*)GetPointer(bAccount), 1, false, GetPointer(Encoder))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Dann bewerten wir die Aktionen mit unserem Kritiker.
if(!Critic.feedForward((CNet *)GetPointer(Actor), -1, (CNet*)GetPointer(Encoder))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Die Politik des Akteurs wird in 2 Schritten angepasst. Zunächst passen wir die Politik an, um die Abweichung von den tatsächlichen Handlungen des Agenten zu minimieren. Auf diese Weise können wir die Politik des Akteurs in der Verteilung nahe an unserem Trainingsset halten.
if(!Actor.backProp(GetPointer(bActions), GetPointer(Encoder)) || !Encoder.backPropGradient((CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Im zweiten Schritt passen wir die Politik des Akteurs entsprechend der Bewertung seiner Handlungen durch den Kritiker an. Zu diesem Zweck deaktivieren wir den Trainingsmodus des Kritikers und übertragen den Fehlergradienten durch ihn auf den Akteur. Danach passen wir die Politik an den erzielten Fehlergradienten an.
Critic.TrainMode(false); if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder)) || !Actor.backPropGradient((CNet *)GetPointer(Encoder), -1, -1, false) || !Encoder.backPropGradient((CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Beachten Sie, dass wir in beiden Fällen, in denen wir die Politik des Akteurs anpassen, den Fehlergradienten an unseren Encoder weitergeben und „seine Sicht“ auf die Umgebung anpassen. Auf diese Weise bemühen wir uns, die Aussagekraft der Umweltanalyse zu maximieren.
Nach der Aktualisierung der Parameter aller Modelle müssen wir den Nutzer nur noch über den Fortschritt des Trainingsprozesses informieren und zur nächsten Iteration des Schleifensystems übergehen.
if(GetTickCount() - ticks > 500) { double percent = (double(i - state) / ((end - state)) + iter) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent, Actor.getRecentAverageError()); str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Critic", percent, Critic.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } } }
Der Trainingsvorgang wird so lange wiederholt, bis alle Iterationen des Schleifensystems vollständig ausgeschöpft sind. Nach erfolgreichem Abschluss des Trainingsprozesses löschen wir das Kommentarfeld auf der Chart.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic", Critic.getRecentAverageError()); ExpertRemove(); //--- }
Wir geben die Ergebnisse des Modelltrainings in das Protokoll ein und initialisieren die Beendigung des Trainings EA.
Damit ist unsere Analyse der im Programmartikel verwendeten Algorithmen abgeschlossen. Den vollständigen Code finden Sie im Anhang.
3. Tests
In diesem Artikel haben wir die Conformer-Methode diskutiert und die vorgeschlagenen Ansätze mit MQL5 implementiert. Nun haben wir die Möglichkeit, das Modell mit der vorgeschlagenen Methode zu trainieren und es an realen Daten zu testen.
Wie üblich werden wir das Modell mit dem MetaTrader 5 Strategietester auf realen historischen EURUSD, H1 Daten trainieren und testen. Um die Modelle zu trainieren, verwenden wir historische Daten für die ersten 7 Monate des Jahres 2023. Anschließend wird das trainierte Modell mit historischen Daten vom August 2023 getestet.
Bei der Vorbereitung dieses Artikels habe ich das Modell mit der Stichprobe trainiert, die für das Training der Modelle in den vorangegangenen Artikeln dieser Reihe gesammelt wurde.
Ich muss sagen, dass eine Änderung der Architektur der Modelle und des Trainingsalgorithmus einen leichten Anstieg der Kosten pro Iteration verursacht hat. Die vorgeschlagenen Ansätze weisen jedoch eine Stabilität des Lernprozesses auf, was meines Erachtens die Anzahl der zum Trainieren des Modells erforderlichen Iterationen verringert.
Während des Trainingsprozesses erhielt ich ein Modell, das in der Lage war, sowohl mit Trainings- als auch mit Testdatensätzen Gewinne zu erzielen.
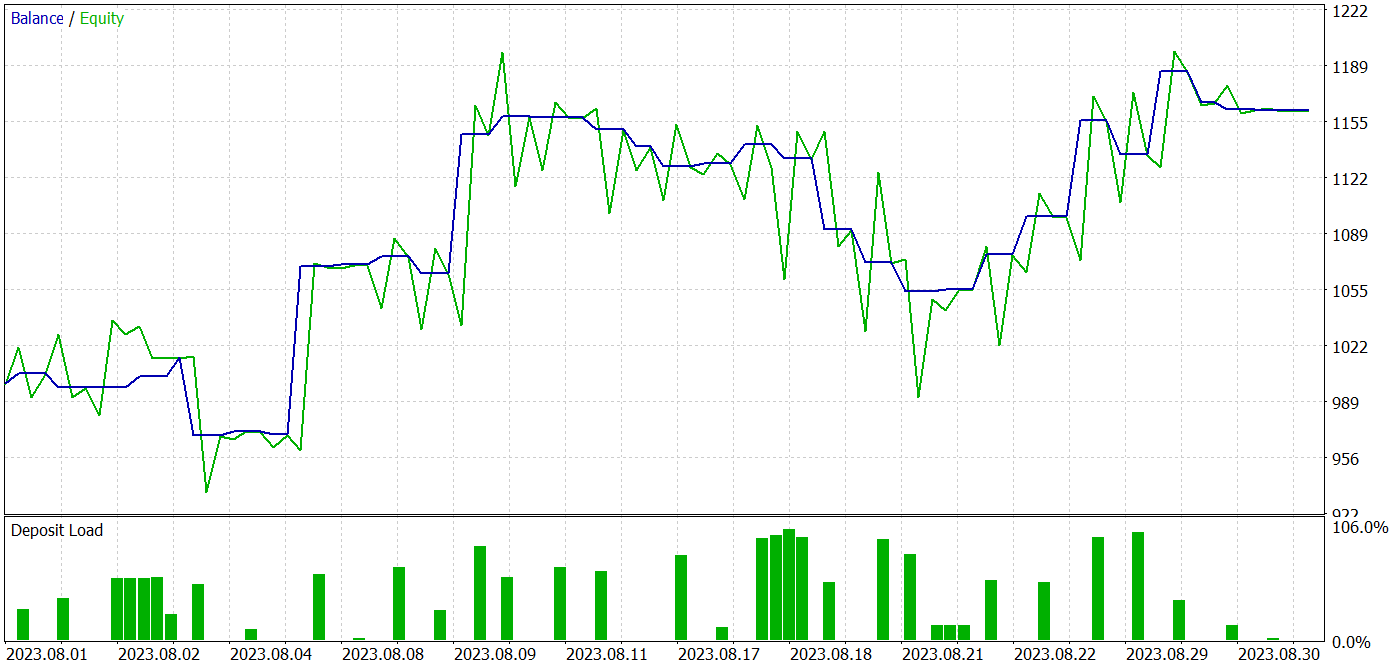
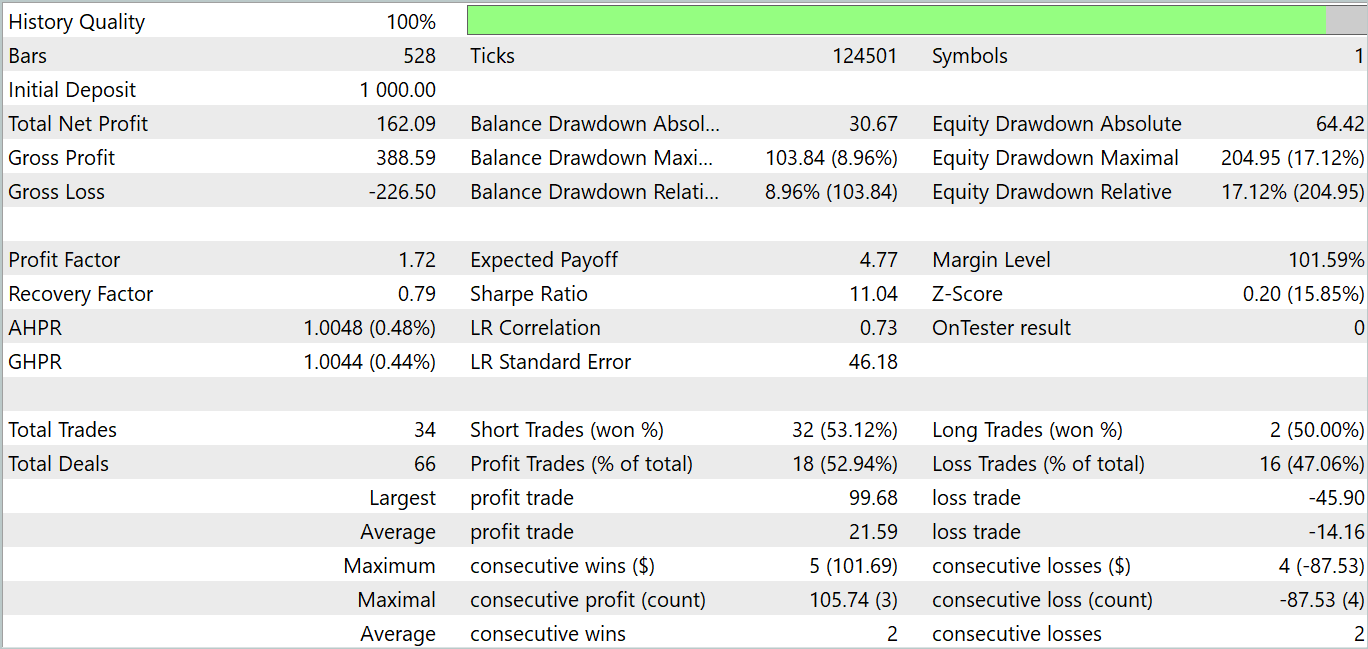
Während des Testzeitraums führte das Modell 34 Handelsgeschäfte aus, von denen 18 mit Gewinn abgeschlossen wurden. Dies entspricht 52,94 % der profitablen Geschäfte. Außerdem ist der durchschnittliche Gewinn um 52,47 % höher als der durchschnittliche Verlust. Der maximale Gewinn ist mehr als 2-mal höher als die gleiche Verlustvariable. Insgesamt ergab das Modell einen Gewinnfaktor von 1,72, und die Saldenkurve zeigt einen Aufwärtstrend. Der maximale Drawdown vom Kapital lag bei 17,12 % und der Drawdown des Saldos bei 8,96 %.
Schlussfolgerung
In diesem Artikel haben wir einen komplexen Algorithmus des Spatio-Temporal Constant Attention Transformer „Conformer“ kennengelernt, der für die Wettervorhersage entwickelt wurde und ursprünglich in dem Artikel „Conformer: Embedding Continuous Attention in Vision Transformer for Weather Forecasting“. Die Autoren der Methode schlagen den Algorithmus der Continuous Attention vor und kombinieren ihn mit der neuronalen ODE.
Im praktischen Teil unseres Artikels haben wir die vorgeschlagenen Ansätze in MQL5 implementiert. Wir haben die erstellten Modelle trainiert und getestet. Die Testergebnisse sind recht vielversprechend. Das Modell erzielte sowohl in den Trainings- als auch in den Testdatensätzen Gewinne.
Ich möchte Sie jedoch daran erinnern, dass alle in diesem Artikel vorgestellten Programme nur zu Informationszwecken dienen und die vorgeschlagenen Ansätze demonstrieren sollen.
Referenzen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | EA | EA-Beispielsammlung |
| 2 | ResearchRealORL.mq5 | EA | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | EA | Modelltraining EA |
| 4 | Test.mq5 | EA | Testmodel des EA |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Code Base | Die Bibliothek des Programmcodes von OpenCL |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/14615
 Entwicklung eines Expertenberaters für mehrere Währungen (Teil 8): Belastungstest und Handhabung eines neuen Balkens
Entwicklung eines Expertenberaters für mehrere Währungen (Teil 8): Belastungstest und Handhabung eines neuen Balkens
 Neuronale Netze leicht gemacht (Teil 82): Modelle für gewöhnliche Differentialgleichungen (NeuralODE)
Neuronale Netze leicht gemacht (Teil 82): Modelle für gewöhnliche Differentialgleichungen (NeuralODE)
 Brain Storm Optimierungsalgorithmus (Teil I): Clustering
Brain Storm Optimierungsalgorithmus (Teil I): Clustering
 Zeitreihen-Clustering für kausales Schlussfolgern
Zeitreihen-Clustering für kausales Schlussfolgern
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.