Zeitreihen-Clustering für kausales Schlussfolgern

Einführung

• Was ist Clustering?
• Anwendung des Clustering für kausales Schlussfolgern
• Abgleich durch Clustering
• Bestimmung des heterogenen Behandlungseffekts
• Definition der Marktarten

Clustering der Volatilität:

• Der Code
• Bewertung der Algorithmen
• Eingabeparameter des Modells

Abgleich der Handelsgeschäfte durch Clustering:

• Der Code
• Der Algorithmus
• Berücksichtigung der Heterogenität der Daten
• Ergebnisse
• Schlussfolgerung

Einführung

Clustering ist eine Technik des maschinellen Lernens, die einen Datensatz in Gruppen von Objekten (Cluster) aufteilt, sodass Objekte innerhalb desselben Clusters (Haufen) einander ähnlich sind und Objekte aus verschiedenen Clustern sich voneinander unterscheiden. Clustering kann dabei helfen, die Datenstruktur aufzudecken, verborgene Muster zu erkennen und Objekte auf der Grundlage ihrer Ähnlichkeit zu gruppieren.

Clustering kann für kausale Schlussfolgerungen verwendet werden. Eine Möglichkeit, Clustering in diesem Zusammenhang anzuwenden, besteht darin, Gruppen ähnlicher Objekte oder Ereignisse zu identifizieren, die mit einer bestimmten Ursache in Verbindung gebracht werden können. Sobald die Daten geclustert sind, können die Beziehungen zwischen Clustern und Ursachen analysiert werden, um potenzielle Ursache-Wirkungs-Beziehungen zu ermitteln.

Darüber hinaus kann das Clustering dazu beitragen, Gruppen von Objekten zu identifizieren, die möglicherweise denselben Auswirkungen unterliegen oder gemeinsame Ursachen haben, was auch bei der Analyse von Ursache-Wirkungs-Beziehungen nützlich sein kann.

Die Verwendung von Clustern bei kausalen Schlussfolgerungen kann besonders nützlich sein, um Daten zu analysieren und potenzielle Ursache-Wirkungs-Beziehungen zu ermitteln. In diesem Artikel werden wir untersuchen, wie Clustering in diesem Zusammenhang eingesetzt werden kann:

1. Identifizierung von Gruppen ähnlicher Objekte: Durch Clustering können Sie Gruppen von Objekten identifizieren, die ähnliche Merkmale oder ein ähnliches Verhalten aufweisen. Anschließend können Sie diese Gruppen analysieren und nach gemeinsamen Ursachen oder Faktoren suchen, die mit ihnen in Verbindung stehen könnten.
2. Ermittlung von Ursache-Wirkungs-Beziehungen: Sobald die Daten in Cluster eingeteilt sind, können die Beziehungen zwischen den Clustern untersucht und mögliche Ursache-Wirkungs-Beziehungen ermittelt werden. Wenn zum Beispiel eine bestimmte Gruppe von Objekten ein bestimmtes Verhalten oder bestimmte Merkmale aufweist, kann analysiert werden, welche Faktoren dafür verantwortlich sein könnten.
3. Verborgene Muster aufspüren: Clustering kann dazu beitragen, verborgene Muster in Daten aufzudecken, die mit Ursache-Wirkungs-Beziehungen in Zusammenhang stehen können. Durch die Analyse der Struktur von Clustern und die Identifizierung gemeinsamer Objektmerkmale innerhalb dieser Cluster können Faktoren entdeckt werden, die für das Auftreten bestimmter Phänomene eine Schlüsselrolle spielen können.
4. Vorhersage zukünftiger Ereignisse: Sobald Cluster und Ursache-Wirkungs-Beziehungen identifiziert wurden, können die gewonnenen Erkenntnisse zur Vorhersage künftiger Ereignisse oder Trends genutzt werden. Auf der Grundlage von Datenanalysen und erkannten Mustern können Sie Vermutungen darüber anstellen, welche Faktoren künftige Ereignisse beeinflussen können und welche Maßnahmen zu deren Bewältigung ergriffen werden können.

Clustering kann für den Abgleich (Matching) von kausalen Schlussfolgerungen verwendet werden. Für den Abgleich werden Objekte aus verschiedenen Datenbeständen auf der Grundlage ihrer Ähnlichkeit oder der Erfüllung bestimmter Kriterien abgeglichen. Im Zusammenhang mit Kausalschlüssen kann der Abgleich dazu verwendet werden, Beziehungen zwischen Ursachen und Wirkungen herzustellen und gemeinsame Merkmale oder Faktoren zu ermitteln, die für bestimmte Phänomene verantwortlich sein könnten.

Beim Abgleich kann das Clustering für Folgendes nützlich sein:

1. Gruppierung von Objekten: Clustering ermöglicht es Ihnen, einen Datensatz in Gruppen von Objekten zu unterteilen, die ähnliche Merkmale oder ein ähnliches Verhalten aufweisen. Danach können Sie innerhalb jedes Clusters einen Abgleich durchführen, um Übereinstimmungen zwischen Objekten zu finden und Verbindungen zwischen ihnen herzustellen.
2. Identifizierung der Ähnlichkeit: Sobald die Objekte in Cluster eingeteilt sind, können die Ähnlichkeiten zwischen den Objekten innerhalb jedes Clusters untersucht und für den Abgleich verwendet werden. Wenn beispielsweise eine bestimmte Gruppe von Objekten ein ähnliches Verhalten oder ähnliche Merkmale aufweist, kann ein Abgleich durchgeführt werden, um gemeinsame Faktoren zu finden, die mit diesen Objekten in Verbindung gebracht werden können.
3. Rauschreduktion: Clustering kann dazu beitragen, das Rauschen in den Daten zu reduzieren und größere Objektgruppen hervorzuheben, was den Abgleichprozess erleichtert. Durch die Aufteilung der Daten in Cluster können Sie sich auf die signifikantesten und ähnlichsten Objekte konzentrieren, was die Qualität des Abgleichs verbessert und es Ihnen ermöglicht, klarere Ursache-Wirkungs-Beziehungen zu erkennen.

Folglich kann das Clustering von Zeitreihen dazu beitragen, heterogene Behandlungseffekte zu ermitteln, d. h. Unterschiede in den Auswirkungen in verschiedenen Gruppen von Zeitreihen. Im Zusammenhang mit der Zeitreihenanalyse, bei der eine Klassifizierung oder Vorhersage durchgeführt wird, bedeutet der heterogene Behandlungseffekt, dass das Verhalten der Zeitreihe in Abhängigkeit von ihren Merkmalen oder anderen Faktoren variieren kann.

Durch das Clustern von Zeitreihen können also folgende Effekte erzielt werden:

1. Gruppierung von Zeitreihen: Durch Clustering können Zeitreihen auf der Grundlage ihrer Merkmale, Trends oder anderer Faktoren in Gruppen eingeteilt werden. Das Verhalten jeder Gruppe kann dann separat untersucht werden, um festzustellen, ob es Unterschiede bei der Vorhersage oder Klassifizierung zwischen verschiedenen Zeitreihenclustern gibt.
2. Identifizierung von Untergruppen mit unterschiedlichen Auswirkungen: Durch das Clustern von Zeitreihen können Untergruppen mit unterschiedlichen Verhaltensweisen oder Veränderungspfaden identifiziert werden. Auf diese Weise können Forscher feststellen, welche Merkmale oder Faktoren die Klassifizierungs- oder Vorhersageergebnisse beeinflussen können, und Teilmengen von Zeitreihen ermitteln, die möglicherweise unterschiedliche Analyseansätze erfordern.
3. Personalisierung der Modelle: Anhand von Clustering-Ergebnissen und identifizierten Untergruppen von Zeitreihen mit unterschiedlichem Verhalten können Sie Klassifizierungs- oder Prognosemodelle personalisieren und optimale Strategien für jede Gruppe auswählen. Dadurch können Sie die Vorhersage- und Klassifizierungsgenauigkeit verbessern und die Modelle an verschiedene Arten von Zeitreihen anpassen.

Die Clusterbildung kann auch unter dem Gesichtspunkt der Identifizierung von Marktregimen betrachtet werden, z. B. auf der Grundlage der Volatilität.

Die Analyse der Marktvolatilität ist ein wichtiges Instrument für Anleger und Händler, da sie es ihnen ermöglicht, die aktuelle Marktlage zu verstehen und fundierte Entscheidungen auf der Grundlage der erwarteten Kursbewegungen zu treffen. Im Zusammenhang mit der Finanzanalyse helfen volatilitätsbasierte Clustering-Algorithmen dabei, verschiedene „Markt-Regimes“ hervorzuheben, die auf unterschiedliche Trends, Konsolidierungsphasen oder Zeiten hoher Unsicherheit hinweisen können.

Wie funktioniert der Clustering-Algorithmus bei Problemen der Bestimmung von Marktregimen auf der Grundlage der Volatilität?

• Vorbereitung der Daten: Die rohen Preisvolatilitätszeitreihen für Vermögenswerte werden vorverarbeitet, einschließlich der Berechnung der Volatilität auf der Grundlage der Standardabweichung der Preise oder der Schwankungen in der Preisverteilung.
• Anwendung eines Clustering-Algorithmus: Der Clustering-Algorithmus wird dann auf die Volatilitätsdaten angewandt, um versteckte Strukturen und Gruppen von Marktregimen zu identifizieren. Als Clustering-Algorithmus können verschiedene Methoden verwendet werden, z. B. K-Means, DBSCAN, oder Algorithmen, die speziell für die Zeitreihenanalyse entwickelt wurden, z. B. Algorithmen, die zeitliche Abhängigkeiten berücksichtigen.
• Interpretation der Ergebnisse: Die sich daraus ergebenden Cluster stellen verschiedene Marktregime dar, die im Kontext von Handelsstrategien interpretiert werden können. So können beispielsweise Cluster mit geringer Volatilität Perioden eines Seitwärtstrends entsprechen, während Cluster mit hoher Volatilität Marktspitzen oder Trendwechsel anzeigen können.

Vorteile des Clustering-Algorithmus bei Problemen der Bestimmung von Marktregimen auf der Grundlage der Volatilität:

• Bestimmung der Marktstruktur: Clustering-Algorithmen ermöglichen es, die Marktstruktur zu beleuchten und verborgene Modi zu identifizieren, was Anlegern und Händlern hilft, den aktuellen Zustand des Marktes zu verstehen.
• Automatisierung der Analyse: Der Einsatz von Clustering-Algorithmen ermöglicht es, den Prozess der Analyse der Marktvolatilität und der Identifizierung der verschiedenen Modi zu automatisieren, was Zeit spart und die Wahrscheinlichkeit menschlicher Fehler verringert.
• Entscheidungshilfe: Das Erkennen von Marktmustern auf der Grundlage der Volatilität hilft bei der Vorhersage künftiger Kursbewegungen und ermöglicht fundierte Handels- und Investitionsentscheidungen.

Nachteile des Clustering-Algorithmus bei Problemen der Bestimmung von Marktregimen auf der Grundlage der Volatilität:

• Empfindlichkeit gegenüber der Parameterwahl: Die Clustering-Ergebnisse können von der Auswahl der Algorithmusparameter abhängen, z. B. von der Anzahl der Cluster oder der Abstandsmetrik, was eine sorgfältige Abstimmung erfordert.
• Beschränkungen der Algorithmen: Einige Clustering-Algorithmen sind bei der Verarbeitung großer Datenmengen möglicherweise nicht effizient oder berücksichtigen keine zeitlichen Abhängigkeiten.

Arten von Clustering-Algorithmen

Wir können verschiedene Clustering-Algorithmen für unsere Aufgaben verwenden. Die wichtigsten Arten des Clustering sind als fertige, in Python implementierte Bibliotheken verfügbar. Der beste Weg, mit dem Clustering zu experimentieren, ist also die Verwendung der Bibliotheken, da man nicht jeden Algorithmus von Grund auf neu implementieren muss. Dadurch wird der Aufbau und die Durchführung des Experiments erheblich beschleunigt.

Wir werden uns kurz mit den wichtigsten Clustering-Algorithmen befassen, die für uns von Nutzen sein können, und sie dann bei unseren Aufgaben anwenden.

• K-Means zeichnet sich durch seine Einfachheit und Effizienz aus, hat aber Einschränkungen wie die Abhängigkeit von den Anfangsbedingungen und die Notwendigkeit, die Anzahl der Cluster zu kennen.
• Bei der Affinitätsausbreitung muss die Anzahl der Cluster nicht im Voraus festgelegt werden, und sie funktioniert gut mit Daten unterschiedlicher Form, kann aber rechnerisch komplex sein.
• Mean Shift ist in der Lage, Cluster beliebiger Form zu erkennen und erfordert keine Angabe der Anzahl der Cluster. Bei der Arbeit mit großen Datenmengen kann dies sehr rechenintensiv sein.
• Spektrales Clustering eignet sich für Daten mit nichtlinearen Strukturen und ist universell einsetzbar. Es kann jedoch schwierig sein, die Parameter abzustimmen, und ist sehr rechenaufwändig.
• Das agglomerative Clustering erzeugt hierarchische Cluster und eignet sich für den Umgang mit einer unbekannten Anzahl von Clustern.
• GMM bietet einen probabilistischen Ansatz für das Clustering, der die Modellierung von Clustern mit unterschiedlichen Formen und Dichten ermöglicht.
• HDBSCAN und BIRCH bieten beide eine effiziente Handhabung großer Datenmengen und eine automatische Bestimmung der Anzahl von Clustern, haben aber auch ihre Nachteile, wie z. B. die Komplexität der Berechnungen und die Empfindlichkeit gegenüber Parametern.

Implementierung von Zeitreihenclustering (Volatilitätsclustering)

Wir interessieren uns für die Möglichkeit, Finanzzeitreihen zu clustern, sowohl um Marktregime zu bestimmen als auch um den heterogenen Behandlungseffekt anzupassen und zu bestimmen. Wir beginnen mit dem Versuch, die Marktregime zu gruppieren.

Der folgende Code trainiert das Meta-Learning-Modell und trainiert dann das endgültige Modell und Meta-Modell auf der Grundlage der Ergebnisse des Clustering, das auf der Volatilität der Finanzdaten basiert:

def meta_learner(models_number: int, 
                 iterations: int, 
                 depth: int, 
                 bad_samples_fraction: float, 
                 n_clusters: int, 
                 algorithm: int) -> pd.DataFrame:
    
    dataset = get_labels(get_prices())
    data = dataset[(dataset.index < FORWARD) & (dataset.index > BACKWARD)].copy()
    X = data[data.columns[1:-2]]
    X = X.loc[:, ~X.columns.str.contains('std')]
    meta_X = data.loc[:, data.columns.str.contains('std')]
    y = data['labels']

    B_S_B = pd.DatetimeIndex([])
    for i in range(models_number):
        X_train, X_val, y_train, y_val = train_test_split(
            X, y, train_size = 0.5, test_size = 0.5, shuffle = True)
        
        # learn debias model with train and validation subsets
        meta_m = CatBoostClassifier(iterations = iterations,
                                depth = depth,
                                custom_loss = ['Accuracy'],
                                eval_metric = 'Accuracy',
                                verbose = False,
                                use_best_model = True)
        
        meta_m.fit(X_train, y_train, eval_set = (X_val, y_val), plot = False)
        
        coreset = X.copy()
        coreset['labels'] = y
        coreset['labels_pred'] = meta_m.predict_proba(X)[:, 1]
        coreset['labels_pred'] = coreset['labels_pred'].apply(lambda x: 0 if x < 0.5 else 1)
        
        # add bad samples of this iteration (bad labels indices)
        diff_negatives = coreset['labels'] != coreset['labels_pred']
        B_S_B = B_S_B.append(diff_negatives[diff_negatives == True].index)

    to_mark = B_S_B.value_counts()
    marked_idx = to_mark[to_mark > to_mark.mean() * bad_samples_fraction].index
    data.loc[data.index.isin(marked_idx), 'meta_labels'] = 0.0


    if algorithm==0:
        data['clusters'] = KMeans(n_clusters=n_clusters).fit(meta_X).labels_
    elif algorithm==1:
        data['clusters'] = AffinityPropagation().fit(meta_X).predict(meta_X)
    elif algorithm==2:
        data['clusters'] = SpectralClustering(n_clusters=n_clusters, assign_labels='discretize', random_state=0).fit_predict(meta_X)
    elif algorithm==3:
        data['clusters'] = MeanShift().fit_predict(meta_X)
    elif algorithm==4:
        data['clusters'] = AgglomerativeClustering(n_clusters=n_clusters).fit_predict(meta_X)
    elif algorithm==5:
        data['clusters'] = mixture.GaussianMixture(n_components=n_clusters, covariance_type='full').fit(meta_X).predict(meta_X)
    elif algorithm==6:
        data['clusters'] = HDBSCAN(min_cluster_size=150).fit_predict(meta_X)
    elif algorithm==7:
        data['clusters'] = Birch(threshold=0.01, n_clusters=n_clusters).fit_predict(meta_X)
    return data[data.columns[1:]]

Beschreibung der Funktion:

Die Funktion meta_learner dient dem Meta-Training eines Klassifikationsmodells, um falsch beschriftete Proben in einem Datensatz zu identifizieren und zu korrigieren. Es verwendet ein Ensemble von CatBoostClassifier-Modellen, um solche Proben zu identifizieren, und wendet Clustering-Algorithmen zur weiteren Verarbeitung der Daten an. Hier finden Sie eine genauere Beschreibung des Prozesses:

1. Aufbereitung der Daten: Die Funktion beginnt mit dem Abrufen eines Datensatzes, der nach Zeitstempeln gefiltert ist (wobei Daten aus bestimmten Zeiträumen ausgeschlossen werden). Anschließend werden die Daten in Merkmale (X), Metamerkmale (meta_X) auf der Grundlage von Standardabweichungen und Zielkennzeichnung (y) unterteilt.

2. Initialisierung der Variablen: Ein leerer Datumsindex B_S_B wird erstellt, um Indizes von falsch gekennzeichneten Proben zu speichern.

3. Training von Modellen und Identifizierung falscher Kennzeichnungen: Für jedes der Modelle models_number werden die Daten in Trainings- und Validierungssätze aufgeteilt. Dann wird das Modell CatBoostClassifier mit den angegebenen Parametern trainiert. Nach dem Training wird das Modell zur Vorhersage von Bezeichnungen für den gesamten Satz von Merkmalen X verwendet. Durch den Vergleich der vorhergesagten Bezeichnungen mit den ursprünglichen Bezeichnungen identifiziert die Funktion falsch bezeichnete Proben und fügt ihre Indizes zu B_S_B hinzu.

4. Kennzeichnung schlechter Proben: Nach dem Training aller Modelle analysiert die Funktion die Indizes der schlechten Proben, die in B_S_B gespeichert sind, und markiert diejenigen, die häufiger vorkommen als durch bad_samples_fraction bestimmt, mit 0,0 in der Spalte meta_labels in den Quelldaten.

5. Clustering: Je nach Wert des Parameters „Algorithmus“ wendet die Funktion einen der Clustering-Algorithmen auf Meta-Merkmale (meta_X) an und fügt die daraus resultierenden Kennzeichen (label) der Cluster zu den Quelldaten hinzu.

6. Rückgabe eines Ergebnisses: Die Funktion gibt einen aktualisierten Datensatz mit Kennzeichnung und zugewiesenen Clustern zurück.

Mit diesem Ansatz lassen sich nicht nur Fehler in den Datenkennzeichnung erkennen und korrigieren, sondern auch Daten für die weitere Analyse oder das Modelltraining gruppieren, was besonders bei Problemen mit einer großen Anzahl falsch gekennzeichneter Proben nützlich sein kann.

Die Trainingsfunktion für die endgültigen Modelle sieht folgendermaßen aus:

def fit_final_models(dataset) -> list:
    # features for model\meta models. We learn main model only on filtered labels 
    X, X_meta = dataset[dataset['meta_labels']==1], dataset[dataset.columns[:-3]]
    X = X[X.columns[:-3]]
    X = X.loc[:, ~X.columns.str.contains('std')]
    X_meta = X_meta.loc[:, X_meta.columns.str.contains('std')]
    
    # labels for model\meta models
    y, y_meta = dataset[dataset['meta_labels']==1], dataset[dataset.columns[-1]]
    y = y[y.columns[-3]]
    
    y = y.astype('int16')
    y_meta = y_meta.astype('int16')

    # train\test split
    train_X, test_X, train_y, test_y = train_test_split(
        X, y, train_size=0.8, test_size=0.2, shuffle=True)
    
    train_X_m, test_X_m, train_y_m, test_y_m = train_test_split(
        X_meta, y_meta, train_size=0.8, test_size=0.2, shuffle=True)

    # learn main model with train and validation subsets
    model = CatBoostClassifier(iterations=200,
                               custom_loss=['Accuracy'],
                               eval_metric='Accuracy',
                               verbose=False,
                               use_best_model=True,
                               task_type='CPU')
    model.fit(train_X, train_y, eval_set=(test_X, test_y),
              early_stopping_rounds=25, plot=False)
    
    # learn meta model with train and validation subsets
    meta_model = CatBoostClassifier(iterations=100,
                                    custom_loss=['F1'],
                                    eval_metric='F1',
                                    verbose=False,
                                    use_best_model=True,
                                    task_type='CPU')
    meta_model.fit(train_X_m, train_y_m, eval_set=(test_X_m, test_y_m),
              early_stopping_rounds=15, plot=False)
    
    R2 = test_model([model, meta_model])
    if math.isnan(R2):
        R2 = -1.0
        print('R2 is fixed to -1.0')
    print('R2: ' + str(R2))
    return [R2, model, meta_model]

Die Funktion fit_final_models dient dem Training der Haupt- und Metamodelle auf dem bereitgestellten Datensatz. Hier finden Sie eine detaillierte Beschreibung der Funktionsweise:

1. Aufbereitung der Daten:

• Die Funktion wählt aus dem Datensatz die Zeilen aus, in denen meta_labels gleich 1 ist, um das Hauptmodell (X, y) zu trainieren.
• Alle Zeilen des Datensatzes (X_meta, y_meta) werden für das Training des Metamodells verwendet.
• Spalten, die „std“ im Namen enthalten, sowie die letzten drei Spalten werden von den Merkmalen für das Training des Hauptmodells ausgeschlossen.
• Für das Metamodell verwendet die Funktion nur die Merkmale, die „std“ im Namen enthalten.
• Die Zielvariable (y) für das Hauptmodell wird der dritten Spalte von hinten entnommen und in den Typ int16 umgewandelt.
• Die Zielvariable für das Metamodell (y_meta) wird der letzten Spalte entnommen und ebenfalls in int16 umgewandelt.

2. Aufteilung der Daten in Trainings- und Testproben:

• Für das Hauptmodell und das Metamodell werden die Daten in einem Verhältnis von 80 % zu 20 % in Trainings- und Testproben aufgeteilt.

3. Grundlegendes Modelltraining:

• Wir verwenden den CatBoostClassifier-Klassifikator mit 200 Iterationen, die Verlustfunktion „Accuracy“ und die Bewertungsmetrik „Accuracy“. Es werden keine Informationen über den Trainingsfortschritt ausgegeben, das beste Modell wird ausgewählt und der Aufgabentyp wird auf „CPU“ gesetzt.
• Das Modell wird mit dem Trainingsdatensatz trainiert. Außerdem ist eine vorzeitige Abschaltung nach 25 Schuss vorgesehen, wenn sich die Messwerte nicht verbessern.

4. Metamodelltraining:

• Ähnlich wie das Hauptmodell, jedoch mit 100 Iterationen, Verlustfunktion „F1“, Bewertungsmetrik „F1“ und vorzeitigem Abbruch nach 15 Runden.

5. Modeltests:

• Die trainierten Modelle werden mit der Funktion test_model getestet, die den Wert der R2-Metrik liefert.
• Wenn der resultierende R2-Wert NaN ist, wird er durch -1,0 ersetzt und eine entsprechende Meldung ausgegeben.

6. Die Rückgabewerte sind:

• Die Funktion gibt eine Liste zurück, die den R2-Wert, das Hauptmodell und das Metamodell enthält.

Dieses Merkmal ist Teil eines maschinellen Lernprozesses, bei dem das Hauptmodell auf gefilterten Daten trainiert wird (bei denen davon ausgegangen wird, dass die Kennzeichnungen validiert oder angepasst wurden) und das Metamodell trainiert wird, um ausgewählte Volatilitätscluster vorherzusagen.

Der gesamte Algorithmus wird in einer Schleife trainiert:

Diese Funktion trainiert ein Modell und ein Metamodell auf der Grundlage des Eingabedatensatzes. Sie gibt dann eine Liste mit dem R2-Wert, dem Hauptmodell und dem Metamodell zurück.

# LEARNING LOOP
models = []
for i in range(1):
    data = meta_learner(5, 25, 2, 0.9, n_clusters=N_CLUSTERS, algorithm=6)
    for clust in data['clusters'].unique():
        print(f'Iteration: {i}, Cluster: {clust}')
        filtered_data = data.copy()
        filtered_data['clusters'] = filtered_data['clusters'].apply(lambda x: 1 if x == clust else 0)
        models.append(fit_final_models(filtered_data))

Bei diesem Code handelt es sich um eine Trainingsschleife, die die Funktion meta_learner für das Meta-Training des Modells verwendet und dann die endgültigen Modelle auf der Grundlage der resultierenden Cluster trainiert. Hier finden Sie eine genauere Beschreibung des Prozesses:

1. Initialisierung der Modellliste: Es wird eine leere Liste „Modelle“ erstellt, in der die trainierten endgültigen Modelle gespeichert werden.

2. Laufen der Trainingsschleife: Die „for-Schleife“ ist für eine Iteration konfiguriert (range(1)), d.h. der gesamte Prozess wird einmal ausgeführt. Dies geschieht zu Demonstrations- oder Testzwecken, da diese Schleifen aufgrund der Randomisierung der Lernalgorithmen in der Regel mehr Iterationen benötigen.

3. Meta-Lernen mit meta_learner: Die Funktion meta_learner wird mit den angegebenen Parametern aufgerufen:

• models_number=5: Wir verwenden 5 Grundmodelle für das Meta-Lernen.
• iterations=25: jedes Basismodell wird mit 25 Iterationen trainiert.
• depth=2: Die Tiefe des Klassifikatorbaums für die Basismodelle wird auf 2 gesetzt.
• bad_samples_fraction=0.9: Der Anteil der falsch gekennzeichneten Proben beträgt 90%.
• n_clusters=N_CLUSTERS: die Anzahl der Cluster für den Clustering-Algorithmus, wobei N_CLUSTERS im Voraus festgelegt werden muss.
• Algorithmus=6: Es wird der HDBSCAN-Clusteralgorithmus verwendet.

Die Funktion meta_learner gibt einen aktualisierten Datensatz mit Beschriftungen und zugeordneten Clustern zurück.

4. Wir iterieren über eindeutige Cluster: Für jedes einzelne Cluster im Datensatz wird eine Meldung mit der Iterations- und Clusternummer angezeigt. Die Daten werden dann so gefiltert, dass alle Datensätze, die zum aktuellen Cluster gehören, mit 1 und alle anderen mit 0 gekennzeichnet werden. Auf diese Weise wird für jeden Cluster eine binäre Klassifizierung erstellt.

5. Training der endgültigen Modelle: Für jeden Cluster wird die Funktion fit_final_models aufgerufen, die ein Modell auf der Grundlage der gefilterten Daten trainiert und zurückgibt. Die trainierten Modelle werden der Liste „Modelle“ hinzugefügt.

Mit diesem Ansatz können Sie eine Reihe spezialisierter Modelle trainieren, die sich jeweils auf ein bestimmtes Datencluster konzentrieren, was die Gesamtmodellierungsleistung verbessern kann, da die Merkmale verschiedener Datengruppen genauer berücksichtigt werden.

Alle vorgeschlagenen Clustering-Algorithmen wurden analysiert, um Marktregime zu bestimmen. Einige Algorithmen schnitten gut ab, während andere schlecht abschnitten.

Nachfolgend sind die Trainingsergebnisse mit verschiedenen Clustering-Algorithmen aufgeführt:

In erster Linie interessierte mich die Geschwindigkeit des Clustering. Die Algorithmen Affinity Propagation, Spectral Clustering, Agglomerative Clustering und Mean Shift erwiesen sich als sehr langsam, weshalb sie alle am Ende der Rangliste stehen. Da ich mit den Standardeinstellungen keine Clustering-Ergebnisse erzielen konnte, werden die Ergebnisse für diese Algorithmen nicht angezeigt.

Ich habe im Internet eine Bestätigung dafür gefunden:

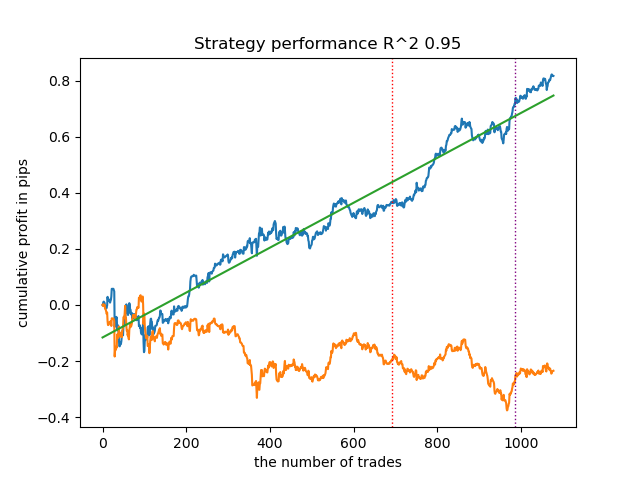
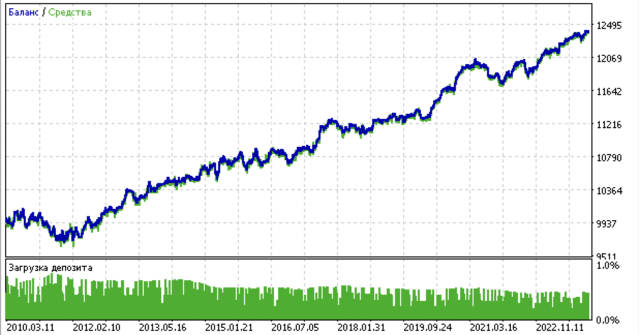
Ich habe 10 Iterationen des gesamten Trainingsprozesses durchgeführt, um aussagekräftigere Ergebnisse zu erhalten, da die Ergebnisse bei den verschiedenen Trainingsiterationen aufgrund der Randomisierung innerhalb der Algorithmen unterschiedlich sind.

• Blaue Linie zeigt ein Saldenkurve an.
• Die orangefarbene Linie ist das Chart des Finanzinstruments (in diesem Fall EURUSD).

1. Unter den vier verbleibenden Algorithmen habe ich mich entschieden, HDBSCAN an die Spitze der Bewertung zu setzen. Es trennt die Daten gut und erfordert keine Festlegung der Anzahl der Cluster.

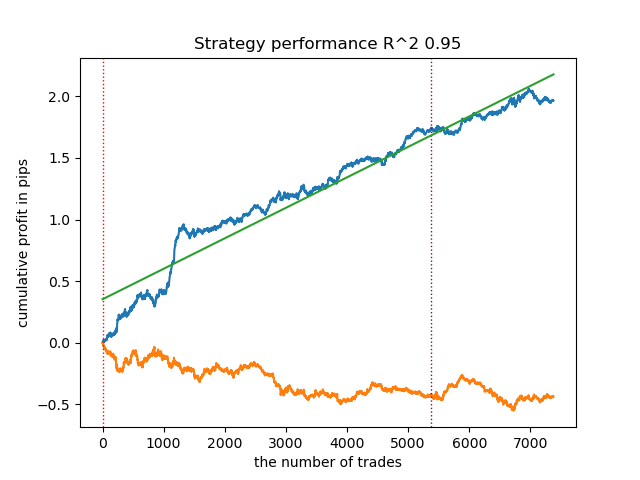
2. K-means zeigt eine gute Leistung und recht gute Testergebnisse. Der Nachteil ist die Empfindlichkeit gegenüber der Anzahl der Cluster, in diesem Fall sind es zehn.

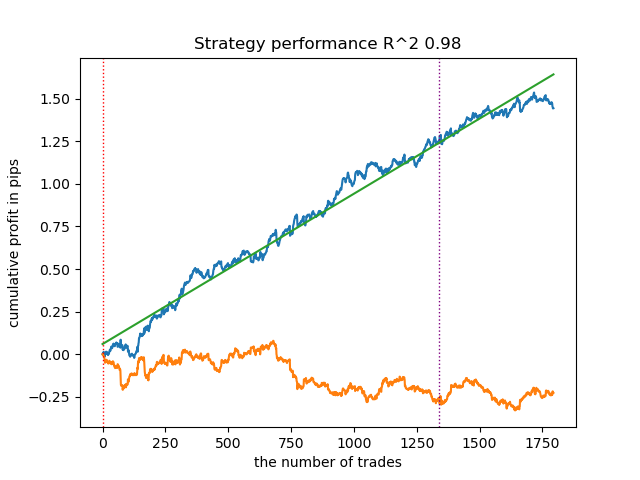
3. BIRCH zeigt gute Ergebnisse, rechnet aber etwas langsamer als frühere Algorithmen. Auch gibt es keine Vorschrift für eine anfängliche Anzahl von Clustern.

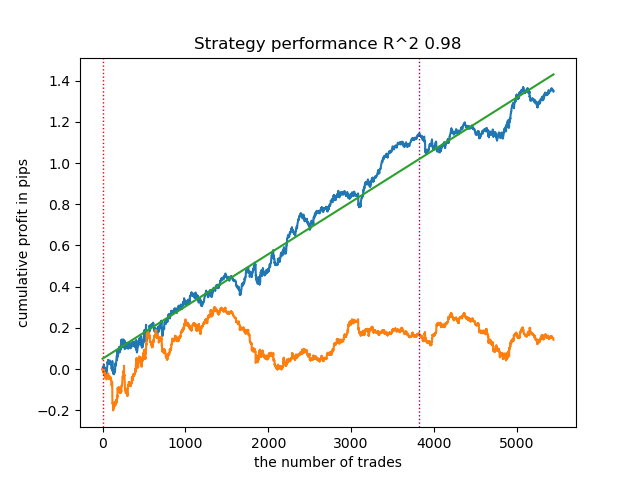
4. Die „Gaussian Mixture“ vervollständigt diese Bewertung. Die Testergebnisse schienen mir schlechter zu sein als bei der Verwendung anderer Clustering-Algorithmen. Optisch drückt sich dies in einer Saldenkurve mit „mehr Rauschen“ aus. Wie bei K-means haben wir 10 Cluster definiert.

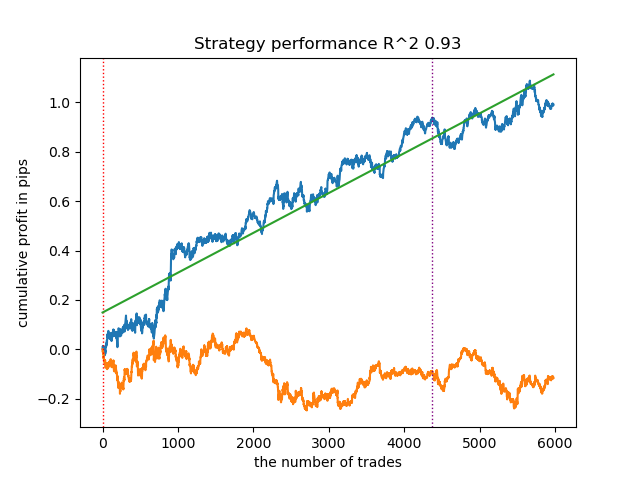
So können wir je nach dem gewählten Marktregime verschiedene Handelssysteme erhalten. Während des Trainingsprozesses werden die Ergebnisse der Modelltests in jedem Regime auf der Grundlage einer bestimmten Anzahl von Clustern angezeigt.

Die Qualität des Clustering wird durch die Eingabeparameter beeinflusst. Im Folgenden sind die verwendeten Parameter aufgeführt:

• Währungspaar
• Zeitrahmen
• Anfangs- und Enddatum des Trainings
• Anzahl der Merkmale für das Hauptmodell
• Anzahl der Merkmale für das Metamodell (Volatilität)
• Anzahl von Clustern n_clusters
• Parameter „min“ und „max“ der Funktion get_labels(min, max)

Hier ist zum Beispiel ein weiterer Satz von Clustering-Ergebnissen mit den folgenden Parametern:

SYMBOL = 'EURUSD'
MARKUP = 0.00010
PERIODS = [i for i in range(10, 100, 10)]
PERIODS_META = [20]
BACKWARD = datetime(2019, 1, 1)
FORWARD = datetime(2023, 1, 1)
n_clusters = 40

def get_labels(dataset, min = 5, max = 5)

Timeframe = H1

Da der Algorithmus für die Clustersuche ebenfalls nach dem Zufallsprinzip arbeitet, empfiehlt es sich, ihn mehrmals auszuführen.

Abgleich der Handelsgeschäfte durch Clustering

Kommen wir nun zum letzten Teil, der eigentlich der Hauptteil des Artikels ist. Ich wollte das Verständnis des Kausalschlusses vertiefen, indem ich ihn um ein Clusterelement ergänzte. In diesem Artikel wird erklärt, was kausale Inferenz ist, und ein weiterer Artikel behandelt den Abgleich durch Propensity Score. Ersetzen wir nun den Abgleich durch den Propensity Score (Neigungsrate) durch unseren eigenen Ansatz, d. h. den Abgleich durch Clustering. Für diese Zwecke werden wir den Algorithmus aus dem ersten Artikel verwenden und ihn abändern.

def meta_learners(models_number: int, iterations: int, depth: int, bad_samples_fraction: float, n_clusters: int):
    dataset = get_labels(get_prices())
    data = dataset[(dataset.index < FORWARD) & (dataset.index > BACKWARD)].copy()

    X = data[data.columns[1:-2]]
    y = data['labels']
    clusters = KMeans(n_clusters=n_clusters).fit(X[X.columns[0:1]]).labels_

    BAD_CLUSTERS = []
    for _ in range(n_clusters):
        sublist =  [pd.DatetimeIndex([]), pd.DatetimeIndex([])]
        BAD_CLUSTERS.append(sublist)

    for i in range(models_number):
        X_train, X_val, y_train, y_val = train_test_split(
            X, y, train_size = 0.5, test_size = 0.5, shuffle = True)
        
        # learn debias model with train and validation subsets
        meta_m = CatBoostClassifier(iterations = iterations,
                                depth = depth,
                                custom_loss = ['Accuracy'],
                                eval_metric = 'Accuracy',
                                verbose = False,
                                use_best_model = True)
        
        meta_m.fit(X_train, y_train, eval_set = (X_val, y_val), plot = False)
        
        coreset = X.copy()
        coreset['labels'] = y
        coreset['labels_pred'] = meta_m.predict_proba(X)[:, 1]
        coreset['labels_pred'] = coreset['labels_pred'].apply(lambda x: 0 if x < 0.5 else 1)
        coreset['clusters'] = clusters
        
        # add bad samples of this iteration (bad labels indices)
        coreset_b = coreset[coreset['labels']==0]
        coreset_s = coreset[coreset['labels']==1]

        for clust in range(n_clusters):
            diff_negatives_b = (coreset_b['labels'] != coreset_b['labels_pred']) & (coreset['clusters'] == clust)
            diff_negatives_s = (coreset_s['labels'] != coreset_s['labels_pred']) & (coreset['clusters'] == clust)
            BAD_CLUSTERS[clust][0] = BAD_CLUSTERS[clust][0].append(diff_negatives_b[diff_negatives_b == True].index)
            BAD_CLUSTERS[clust][1] = BAD_CLUSTERS[clust][
        1].append(diff_negatives_s[diff_negatives_s == True].index)

    for clust in range(n_clusters):
        to_mark_b = BAD_CLUSTERS[clust][0].value_counts()
        to_mark_s = BAD_CLUSTERS[clust][1].value_counts()
        marked_idx_b = to_mark_b[to_mark_b > to_mark_b.mean() * bad_samples_fraction].index
        marked_idx_s = to_mark_s[to_mark_s > to_mark_s.mean() * bad_samples_fraction].index
        data.loc[data.index.isin(marked_idx_b), 'meta_labels'] = 0.0
        data.loc[data.index.isin(marked_idx_s), 'meta_labels'] = 0.0

    return data[data.columns[1:]]

Für diejenigen, die meine früheren Artikel nicht gelesen haben, werde ich eine kurze Beschreibung des Algorithmus geben:

• Datenverarbeitung:
• Zu Beginn verwenden wir die Funktionen get_prices() und get_labels(), um den Datensatz zu erhalten. Diese Funktionen liefern Preisinformationen bzw. Klassenbezeichnungen.
• get_labels() assoziiert Preisdaten mit Labels, was eine häufige Aufgabe bei ML im Zusammenhang mit Finanzdaten ist.
• Die Daten werden dann nach Zeitintervallen gefiltert, die durch die Konstanten FORWARD und BACKWARD definiert sind.
• Aufbereitung der Daten:
• Die Daten werden in Merkmale (X) und Bezeichnungen (y) unterteilt.
• Dann verwenden wir den KMeans-Clusteralgorithmus, um Datencluster zu erstellen.
• Modelltraining:
• In einer for-Schleife ermitteln wir die Anzahl der Modelle (models_number). In jeder Iteration wird das Modell auf der Hälfte des Datensatzes trainiert (train_size = 0,5) und auf der zweiten Hälfte validiert (Validierungsset).
• Wir verwenden das CatBoostClassifier-Modell mit bestimmten Parametern. Diese Gradient-Boosting-Methode ist speziell für die Arbeit mit kategorialen Merkmalen konzipiert.
• Bitte beachten Sie, dass der Algorithmus die nutzerdefinierte Verlustfunktion „Accuracy“ und die Bewertungsmetrik „Accuracy“ verwendet. Dies zeigt, dass wir uns auf die Vorhersagegenauigkeit konzentrieren.
• Das Metamodell wird dann angewendet, um die Vorhersagen der primären Modelle zu bewerten und anzupassen. Dadurch können wir mögliche Verzerrungen oder Fehler in den primären Modellen berücksichtigen.
• Identifizierung schlechter Proben:
• Der Algorithmus erstellt Listen mit „BAD_CLUSTERS“, die Informationen über die schlechten Proben in jedem Cluster enthalten. Schlechte Stichproben werden als solche definiert, bei denen das Modell eine signifikante Anzahl von Fehlern aufweist.
• Bei jeder Trainingsiteration identifiziert der Algorithmus schlechte Proben und speichert ihre Indizes in der entsprechenden Liste.
• Meta-Analyse und Korrektur:
• Die Indizes der im vorangegangenen Schritt ermittelten schlechten Proben werden aggregiert und dann zur Kennzeichnung der entsprechenden Proben in den Stammdaten verwendet.
• Dies soll dazu beitragen, die Qualität der Modelltraining zu verbessern, indem schlechte Stichproben eliminiert oder korrigiert werden.
• Daten zurücksenden:
• Die Funktion gibt die vorbereiteten Daten ohne die erste Spalte zurück, die Zeitstempel enthält.

Dieser Algorithmus zielt darauf ab, die Qualität von Modellen des maschinellen Lernens zu verbessern, indem er schlechte Proben erkennt und korrigiert und ein Metamodell verwendet, um Fehler in den primären Modellen zu berücksichtigen. Es ist komplex und erfordert eine sorgfältige Abstimmung der Parameter, um effektiv zu arbeiten.

In dem vorgestellten Code hilft die Clusterung, die Heterogenität der Daten auf verschiedene Weise zu berücksichtigen:

• Identifizierung von Datenclustern:
• Mit Hilfe des KMeans-Clusteralgorithmus können wir Daten in Gruppen ähnlicher Objekte unterteilen. Jeder Cluster enthält Daten mit ähnlichen Merkmalen. Dies ist vor allem bei heterogenen Daten nützlich, bei denen die Objekte verschiedenen Kategorien angehören oder unterschiedliche Strukturen aufweisen können.
• Separate Analyse und Bearbeitung von Clustern:
• Jedes Cluster wird getrennt von den anderen bearbeitet, sodass die Datenmerkmale und die Struktur innerhalb jeder Gruppe berücksichtigt werden können. Dies hilft dabei, die Heterogenität der Daten zu verstehen und die Lernalgorithmen an die spezifischen Bedingungen in jedem Cluster anzupassen.
• Fehlerkorrektur innerhalb von Clustern:
• Nach dem Training der Modelle werden in einer Schleife schlechte Proben für jeden Cluster analysiert. Dies sind die Stichproben, bei denen das Modell eine erhebliche Anzahl von Fehlern aufweist. Auf diese Weise können Sie die Fehlerkorrektur innerhalb jedes Clusters separat lokalisieren und fokussieren, was effektiver sein kann als die Anwendung der gleichen Korrekturen auf alle Daten als Ganzes.
• Berücksichtigung von Datenmerkmalen bei dem Training von Metamodellen:
• Clustering wird auch verwendet, um Unterschiede zwischen Clustern beim Training eines Metamodells zu berücksichtigen. Auf diese Weise kann sich das Metamodell besser an die Heterogenität der Daten anpassen, da es Informationen über die Struktur der Daten in den einzelnen Clustern enthält.

Das Clustering spielt also eine Schlüsselrolle bei der Berücksichtigung der Heterogenität der Daten, sodass sich der Algorithmus besser an die Vielfalt der Objekte und Datenstrukturen anpassen kann.

Die Ergebnisse der Modelltraining sind unten dargestellt. Sie können sehen, dass das Modell mit neuen Daten stabiler geworden ist.

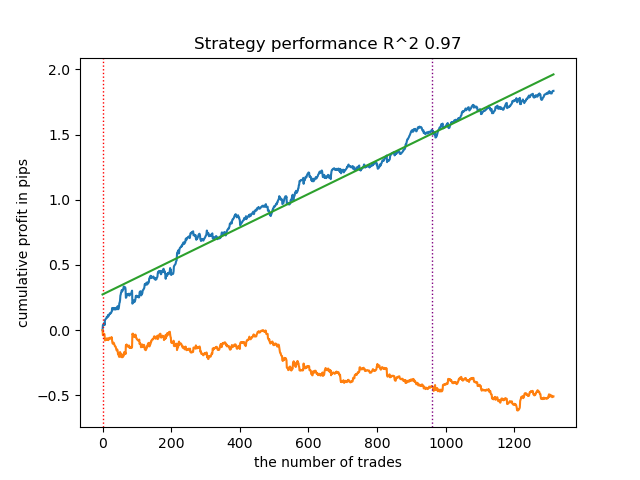
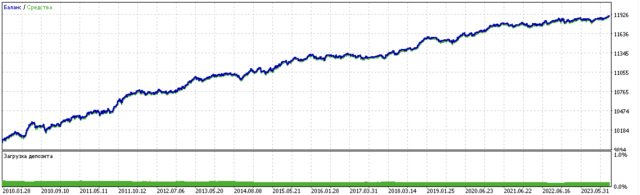
Dieses Modell kann in das ONNX-Format exportiert werden und ist vollständig kompatibel mit dem EA ONNX Trader.

Schlussfolgerung

In diesem Artikel haben wir den ursprünglichen Ansatz des Autors für das Clustering von Zeitreihen diskutiert. Ich habe verschiedene Algorithmen zur Clusterung von Marktregimen nach Volatilität getestet. Ich habe festgestellt, dass komplexe Algorithmen nicht immer die Erwartungen erfüllen: Manchmal leisten einfache und schnelle Clustering-Algorithmen wie K-means bessere Arbeit. Gleichzeitig hat mir der HDBSCAN-Algorithmus sehr gut gefallen.

Im zweiten Teil wurde das Clustering eingesetzt, um den heterogenen Behandlungseffekt zu ermitteln. Experimente haben gezeigt, dass die Berücksichtigung schlechter Geschäfte durch Clustering die Wertespanne verringert (die Saldenkurve wird glatter) und die Fähigkeit des Modells zur Vorhersage auf neuen Daten verbessert. Im Allgemeinen handelt es sich hierbei um ein recht komplexes und tiefgründiges Thema, das die Konfiguration von Hyperparametern zur Feinabstimmung des Algorithmus erfordert.