Die Kreuzvalidierung und die Grundlagen der kausalen Inferenz in CatBoost-Modellen, Export ins ONNX-Format

Einführung

In den vorangegangenen Artikeln habe ich verschiedene Möglichkeiten beschrieben, Algorithmen des maschinellen Lernens zur Erstellung von Handelssystemen zu nutzen. Einige erwiesen sich als recht erfolgreich, andere (meist aus frühen Veröffentlichungen) waren stark übertrainiert. Die Abfolge meiner Artikel spiegelt also die Entwicklung des Verständnisses wider, wozu maschinelles Lernen tatsächlich in der Lage ist. Wir sprechen hier natürlich von der Klassifizierung von Zeitreihen.

Im vorangegangenen Artikel „Metamodelle im maschinellen Lernen“ wurde zum Beispiel der Algorithmus zum Auffinden von Mustern durch die Interaktion von zwei Klassifikatoren betrachtet. Diese nicht triviale Methode wurde gewählt, weil ML-Algorithmen zwar gut verallgemeinern und vorhersagen können, aber bei der Suche nach Ursache-Wirkungs-Beziehungen „faul“ sind. Mit anderen Worten, sie verallgemeinern Trainingsbeispiele, in denen bereits eine Ursache-Wirkungs-Beziehung hergestellt werden kann, die auch bei neuen Daten bestehen bleibt, aber diese Verbindung kann sich auch als assoziativ, d. h. vorübergehend und unzuverlässig erweisen. 

Das Modell versteht nicht, mit welchen Zusammenhängen es zu tun hat. Es nimmt alle Trainingsdaten als solche wahr - als Trainingsdaten. Dies ist ein großes Problem für Anfänger, die versuchen, ihm beizubringen, wie man mit neuen Daten gewinnbringend handelt. Deshalb wurde im letzten Artikel versucht, dem Algorithmus beizubringen, seine eigenen Fehler zu analysieren, um statistisch signifikante Vorhersagen von zufälligen zu trennen.

Der aktuelle Artikel ist eine Weiterentwicklung des vorherigen Themas und der nächste Schritt auf dem Weg zur Entwicklung eines selbstlernenden Algorithmus, der in der Lage ist, nach Mustern in den Daten zu suchen und gleichzeitig die Überanpassung zu minimieren. Schließlich wollen wir durch den Einsatz des maschinellen Lernens einen echten Effekt erzielen, sodass es nicht nur Trainingsbeispiele verallgemeinert, sondern auch das Vorhandensein von Ursache-Wirkungs-Beziehungen in ihnen feststellt.

YIN (Theorie)

Dieser Abschnitt wird ein gewisses Maß an subjektiver Argumentation enthalten, die auf einer gewissen Erfahrung beruht, die ich bei Versuchen zur Schaffung einer „künstlichen Intelligenz“ im Forex-Bereich gesammelt habe. Denn es ist noch keine Liebe, aber es ist eine Erfahrung. 

Genauso wie unsere Schlussfolgerungen oft falsch sind und überprüft werden müssen, sollten auch die Ergebnisse der Vorhersagen von Modellen des maschinellen Lernens doppelt überprüft werden. Wenn wir den Prozess der doppelten Kontrolle auf uns selbst anwenden, erhalten wir Selbstkontrolle. Die Selbstkontrolle eines maschinellen Lernmodells besteht darin, seine Vorhersagen in verschiedenen, aber ähnlichen Situationen mehrmals auf Fehler zu überprüfen. Wenn das Modell im Durchschnitt nur wenige Fehler macht, bedeutet dies, dass es nicht übertrainiert ist, aber wenn es häufig Fehler macht, dann stimmt etwas nicht.

Wenn wir das Modell einmal mit ausgewählten Daten trainieren, kann es keine Selbstkontrolle durchführen. Wenn wir ein Modell viele Male auf zufälligen Teilstichproben trainieren und dann die Qualität der Vorhersage auf jeder Teilstichprobe überprüfen und alle Fehler addieren, erhalten wir ein relativ zuverlässiges Bild von den Fällen, in denen es sich tatsächlich als falsch erweist, und den Fällen, in denen es häufig richtig liegt. Diese Fälle können in zwei Gruppen unterteilt und voneinander getrennt werden. Dies ist vergleichbar mit der Durchführung einer Walk-Forward-Validierung oder Kreuzvalidierung, jedoch mit zusätzlichen Elementen. Nur so lässt sich Selbstkontrolle erreichen und ein robusteres Modell erstellen.

Daher ist es notwendig, eine Kreuzvalidierung des Trainingsdatensatzes durchzuführen, die Modellvorhersagen mit den Trainingsmarkierungen zu vergleichen und die Ergebnisse über alle Faltungen (folds) zu mitteln. Die Beispiele, die im Durchschnitt falsch vorhergesagt wurden, sollten als fehlerhaft aus der endgültigen Trainingsmenge entfernt werden. Wir sollten auch ein zweites Modell mit allen Daten trainieren, das gut vorhersagbare Fälle von schlecht vorhersagbaren unterscheidet und es uns ermöglicht, alle möglichen Ergebnisse vollständiger zu erfassen. 

Wenn schlechte Trainingsbeispiele entfernt werden, hat das Hauptmodell einen kleinen Klassifizierungsfehler, schneidet aber bei der Vorhersage der Fälle, die entfernt wurden, schlecht ab. Sie hat eine hohe Genauigkeit, aber einen geringen Wiedererkennungswert. Wenn wir nun einen zweiten Klassifikator hinzufügen und ihm beibringen, das erste Modell nur in den Fällen handeln zu lassen, in denen das erste Modell gelernt hat, gut zu klassifizieren, dann sollte er die Ergebnisse des gesamten TS verbessern, da er eine geringere Genauigkeit, aber eine höhere Wiedererkennung hat.

Es stellt sich heraus, dass die Fehler des ersten Modells auf den zweiten Klassifikator übertragen werden, aber nirgendwo verschwinden, sodass dieser nun häufiger falsche Vorhersagen macht. Da aber die Richtung der Transaktion nicht direkt vorhergesagt werden kann und die Datenabdeckung größer ist, sind solche Vorhersagen dennoch wertvoll.

Wir gehen davon aus, dass zwei Modelle ausreichen, um Trainingsfehler durch ihre positiven Ergebnisse zu kompensieren.

Indem wir also schlechte Trainingsbeispiele eliminieren, suchen wir nach Situationen, die im Durchschnitt einen Gewinn bringen. Und wir werden versuchen, nicht an Orten zu handeln, die im Durchschnitt Verluste verursachen.

Algorithmus-Kern

Die Funktion „meta learner“ ist das Herzstück des Algorithmus und übernimmt alle oben genannten Aufgaben, weshalb sie genauer analysiert werden sollte. Die übrigen Funktionen sind Hilfsfunktionen.

def meta_learner(folds_number: int, iter: int, depth: int, l_rate: float) -> pd.DataFrame:
    dataset = get_labels(get_prices())
    data = dataset[(dataset.index < FORWARD) & (dataset.index > BACKWARD)].copy()

    X = data[data.columns[1:-2]]
    y = data['labels']

    B_S_B = pd.DatetimeIndex([])

    # learn meta model with CV method
    meta_model = CatBoostClassifier(iterations = iter,
                                max_depth = depth,
                                learning_rate=l_rate,
                                verbose = False)
    
    predicted = cross_val_predict(meta_model, X, y, method='predict_proba', cv=folds_number)
    
    coreset = X.copy()
    coreset['labels'] = y
    coreset['labels_pred'] = [x[0] < 0.5 for x in predicted]
    coreset['labels_pred'] = coreset['labels_pred'].apply(lambda x: 0 if x < 0.5 else 1)
    
    # select bad samples (bad labels indices)
    diff_negatives = coreset['labels'] != coreset['labels_pred']
    B_S_B = B_S_B.append(diff_negatives[diff_negatives == True].index)
    to_mark = B_S_B.value_counts()
    marked_idx = to_mark.index
    data.loc[data.index.isin(marked_idx), 'meta_labels'] = 0.0
    return data[data.columns[1:]]

Sie akzeptiert:

• Anzahl der Faltungen für die Kreuzvalidierung
• Die Anzahl der Trainingswiederholungen für das Basis-Lernen
• Die Tiefe des Basis-Lernbaums
• Die Schrittweite des Gradienten

Diese Parameter beeinflussen das Endergebnis und sollten empirisch oder mit Hilfe eines Rasters ausgewählt werden. 

Die Funktion cross_val_predict des Paketes scikit learn gibt die Ergebnisse der Kreuzvalidierung für jedes Trainingsbeispiel zurück und vergleicht diese Ergebnisse dann mit den ursprünglichen Bezeichnungen. Wenn die Vorhersagen falsch sind, werden sie in das Buch der schlechten Beispiele eingetragen, auf dessen Grundlage dann „Meta-Labels“ für den zweiten Klassifikator erstellt werden.

Die Funktion gibt den an sie übergebenen Datenrahmen mit zusätzlichen „Meta-Labels“ zurück. Dieser Datenrahmen wird dann zum Trainieren der endgültigen Modelle verwendet, wie in der Auflistung gezeigt.

# features for model\meta models. We learn main model only on filtered labels 
    X, X_meta = dataset[dataset['meta_labels']==1], dataset[dataset.columns[:-2]]
    X = X[X.columns[:-2]]
    
    # labels for model\meta models
    y, y_meta = dataset[dataset['meta_labels']==1], dataset[dataset.columns[-1]]
    y = y[y.columns[-2]]

Im obigen Code ist vermerkt, dass das erste Modell nur mit den Zeilen trainiert wird, deren Meta-Labels der Zahl 1 entsprechen, d. h. sie werden als gute Trainingsbeispiele markiert. Der zweite Klassifikator wird mit dem gesamten Datensatz trainiert.

Dann werden einfach zwei Klassifikatoren trainiert. Die eine sagt die Wahrscheinlichkeiten von Käufen und Verkäufen voraus, während die zweite bestimmt, ob sich der Handel lohnt oder nicht.

Auch hier hat jedes Modell seine eigenen Trainingsparameter, die nicht in den Hyperparametern enthalten sind. Diese können separat konfiguriert werden, aber ich habe absichtlich eine kleine Anzahl von Iterationen von 100 gewählt, damit die Modelle in dieser letzten Phase nicht übertrainiert werden. Wir können die relative Größe der Zug- und der Teststichprobe ändern, was sich ebenfalls leicht auf die Endergebnisse auswirkt. Im Allgemeinen ist das erste Modell recht einfach zu trainieren, da es nur auf Beispielen trainiert wird, die gut klassifiziert sind. Eine hohe Komplexität des Modells ist nicht erforderlich. Das zweite Modell hat eine komplexere Aufgabe, sodass die Komplexität des Modells erhöht werden kann.

# train\test split
    train_X, test_X, train_y, test_y = train_test_split(
        X, y, train_size=0.5, test_size=0.5, shuffle=True)
    
    train_X_m, test_X_m, train_y_m, test_y_m = train_test_split(
        X_meta, y_meta, train_size=0.5, test_size=0.5, shuffle=True)

    # learn main model with train and validation subsets
    model = CatBoostClassifier(iterations=100,
                               custom_loss=['Accuracy'],
                               eval_metric='Accuracy',
                               verbose=False,
                               use_best_model=True,
                               task_type='CPU')
    model.fit(train_X, train_y, eval_set=(test_X, test_y),
              early_stopping_rounds=15, plot=False)
    
    # learn meta model with train and validation subsets
    meta_model = CatBoostClassifier(iterations=100,
                                    custom_loss=['Accuracy'],
                                    eval_metric='Accuracy',
                                    verbose=False,
                                    use_best_model=True,
                                    task_type='CPU')
    meta_model.fit(train_X_m, train_y_m, eval_set=(test_X_m, test_y_m),
              early_stopping_rounds=15, plot=False)

Hyperparameter des Algorithmus

Bevor wir mit dem Training beginnen, sollten wir alle Eingabeparameter, die auch das Endergebnis beeinflussen, korrekt konfigurieren.

export_path = '/Users/dmitrievsky/Library/Application Support/MetaTrader 5/\
Bottles/metatrader5/drive_c/Program Files/MetaTrader 5/MQL5/Include/'

# GLOBALS
SYMBOL = 'EURUSD'
MARKUP = 0.00015
PERIODS = [i for i in range(10, 50, 10)]
BACKWARD = datetime(2015, 1, 1)
FORWARD = datetime(2022, 1, 1)

• Pfad zum Include-Terminal-Ordner zum Speichern trainierter Modelle
• Symbol Ticker
• Durchschnittlicher Aufschlag in Punkten für Spread, Provisionen und Slippages
• Periodenlänge des Gleitende Durchschnitts, die zur Berechnung von Preisschritten verwendet werden. Dies sind Attribute für das Training des Modells.
• Datumsbereich für die Schulung. Links und rechts von diesem Bereich befindet sich der Verlauf ohne Training (OOS) für Tests mit neuen Daten.

def get_labels(dataset, min= 3, max= 25) -> pd.DataFrame:

Diese Funktion hat die Argumente „min“ und „max“, um eine Zufallsstichprobe von Handelsgeschäften zu erstellen. Jedes neue Handelsgeschäft hat eine zufällige Dauer in Balken. Wenn wir die gleichen Werte festlegen, haben alle Handelsgeschäfte eine feste Laufzeit. 

Hilfsfunktionen und Bibliotheken

Bevor wir beginnen, stellen Sie sicher, dass alle erforderlichen Pakete installiert und importiert sind

import numpy as np
import pandas as pd
import random
import math
from datetime import datetime
import matplotlib.pyplot as put
from catboost import CatBoostClassifier
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_predict

Als Nächstes sollten wir die Kurse aus dem MetaTrader 5-Terminal exportieren. Wir wählen das gewünschte Symbol, den Zeitrahmen und den Umfang der Historien aus und speichern alles im Unterverzeichnis /files unseres Python-Projekts.

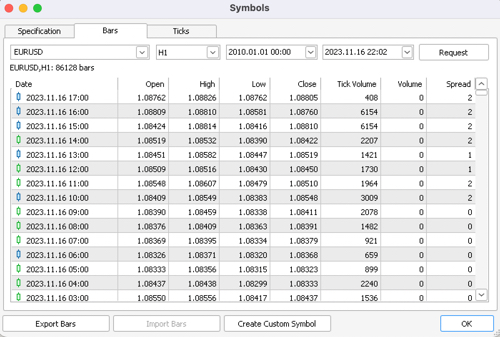
def get_prices() -> pd.DataFrame:
    p = pd.read_csv('files/EURUSD_H1.csv', delim_whitespace=True)
    pFixed = pd.DataFrame(columns=['time', 'close'])
    pFixed['time'] = p['<DATE>'] + ' ' + p['<TIME>']
    pFixed['time'] = pd.to_datetime(pFixed['time'], format='mixed')
    pFixed['close'] = p['<CLOSE>']
    pFixed.set_index('time', inplace=True)
    pFixed.index = pd.to_datetime(pFixed.index, unit='s')
    pFixed = pFixed.dropna()
    pFixedC = pFixed.copy()

    count = 0
    for i in PERIODS:
        pFixed[str(count)] = pFixedC.rolling(i).mean() - pFixedC
        count += 1

    return pFixed.dropna()

Der hervorgehobene Code zeigt, woher der Bot die Kurse bezieht und wie er Attribute erstellt - durch Subtraktion der Schlusskurse vom gleitenden Durchschnitt, der in der Liste PERIODS als Hyperparameter angegeben ist.

Danach wird der erzeugte Datensatz an die nächste Funktion zur Markierung von Etiketten (oder Zielen) weitergegeben.

def get_labels(dataset, min= 3, max= 25) -> pd.DataFrame:
    labels = []
    meta_labels = []
    for i in range(dataset.shape[0]-max):
        rand = random.randint(min, max)
        curr_pr = dataset['close'][i]
        future_pr = dataset['close'][i + rand]

        if future_pr < curr_pr:
            labels.append(1.0)
            if future_pr + MARKUP < curr_pr:
                meta_labels.append(1.0)
            else:
                meta_labels.append(0.0)
        elif future_pr > curr_pr:
            labels.append(0.0)
            if future_pr - MARKUP > curr_pr:
                meta_labels.append(1.0)
            else:
                meta_labels.append(0.0)
        else:
            labels.append(2.0)
            meta_labels.append(0.0)
        
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset['meta_labels'] = meta_labels
    dataset = dataset.dropna()
    dataset = dataset.drop(
        dataset[dataset.labels == 2.0].index)
    
    return dataset

Diese Funktion gibt denselben Datenrahmen zurück, jedoch mit zusätzlichen Spalten „labels“ und „meta labels“.

Die Funktion des Testers wurde erheblich beschleunigt. Jetzt können wir große Datensätze laden und müssen uns keine Sorgen machen, dass die Tests zu lange dauern:

def tester(dataset: pd.DataFrame, plot= False):
    last_deal = int(2)
    last_price = 0.0
    report = [0.0]
    chart = [0.0]
    line = 0
    line2 = 0

    indexes = pd.DatetimeIndex(dataset.index)
    labels = dataset['labels'].to_numpy()
    metalabels = dataset['meta_labels'].to_numpy()
    close = dataset['close'].to_numpy()

    for i in range(dataset.shape[0]):
        if indexes[i] <= FORWARD:
            line = len(report)
        if indexes[i] <= BACKWARD:
            line2 = len(report)

        pred = labels[i]
        pr = close[i]
        pred_meta = metalabels[i] # 1 = allow trades

        if last_deal == 2 and pred_meta==1:
            last_price = pr
            last_deal = 0 if pred <= 0.5 else 1
            continue

        if last_deal == 0 and pred > 0.5 and pred_meta == 1:
            last_deal = 2
            report.append(report[-1] - MARKUP + (pr - last_price))
            chart.append(chart[-1] + (pr - last_price))
            continue

        if last_deal == 1 and pred < 0.5 and pred_meta==1:
            last_deal = 2
            report.append(report[-1] - MARKUP + (last_price - pr))
            chart.append(chart[-1] + (pr - last_price))

    y = np.array(report).reshape(-1, 1)
    X = np.arange(len(report)).reshape(-1, 1)
    lr = LinearRegression()
    lr.fit(X, y)

    l = lr.coef_
    if l >= 0:
        l = 1
    else:
        l = -1

    if(plot):
        plt.plot(report)
        plt.plot(chart)
        plt.axvline(x = line, color='purple', ls=':', lw=1, label='OOS')
        plt.axvline(x = line2, color='red', ls=':', lw=1, label='OOS2')
        plt.plot(lr.predict(X))
        plt.title("Strategy performance R^2 " + str(format(lr.score(X, y) * l,".2f")))
        plt.xlabel("the number of trades")
        plt.ylabel("cumulative profit in pips")
        plt.show()

    return lr.score(X, y) * l

Die Hilfsfunktion zum Testen bereits trainierter Modelle hat nun ein übersichtlicheres Aussehen. Es nimmt eine Liste von Modellen als Eingabe, berechnet Klassenwahrscheinlichkeiten und gibt sie an den Tester weiter, als ob es sich um einen vorgefertigten Datenrahmen mit Merkmalen und Bezeichnungen zum Testen handeln würde. Das Prüfgerät selbst arbeitet daher sowohl mit den ursprünglichen Trainingsdaten als auch mit den Daten, die durch den Erhalt von Prognosen aus bereits trainierten Modellen erzeugt wurden.

def test_model(result: list, plt= False):
    pr_tst = get_prices()
    X = pr_tst[pr_tst.columns[1:]]
    pr_tst['labels'] = result[0].predict_proba(X)[:,1]
    pr_tst['meta_labels'] = result[1].predict_proba(X)[:,1]
    pr_tst['labels'] = pr_tst['labels'].apply(lambda x: 0.0 if x < 0.5 else 1.0)
    pr_tst['meta_labels'] = pr_tst['meta_labels'].apply(lambda x: 0.0 if x < 0.5 else 1.0)

    return tester(pr_tst, plot=plt)

YANG (Praxis)

Nach der Festlegung der Hyperparameter gehen wir direkt zum Training der Modelle über, das in einer Schleife durchgeführt wird.

options = []
for i in range(25):
    print('Learn ' + str(i) + ' model')
    options.append(learn_final_models(meta_learner(folds_number= 5, iter= 150, depth= 5, l_rate= 0.01)))

options.sort(key=lambda x: x[0])
test_model(options[-1][1:], plt=True)

Hier werden wir 25 Modelle trainieren, sie anschließend testen und in das MetaTrader 5-Terminal exportieren.

Die Trainingsergebnisse werden am stärksten von den gewählten Parametern, dem Datumsbereich für Training und Test sowie der Dauer der Transaktionen beeinflusst. Wir sollten mit diesen Einstellungen experimentieren.

Schauen wir uns die 5 besten Modelle nach R^2 unter Berücksichtigung der neuen Daten an. Die horizontalen Linien in den Diagrammen zeigen die OOS auf der linken und rechten Seite.

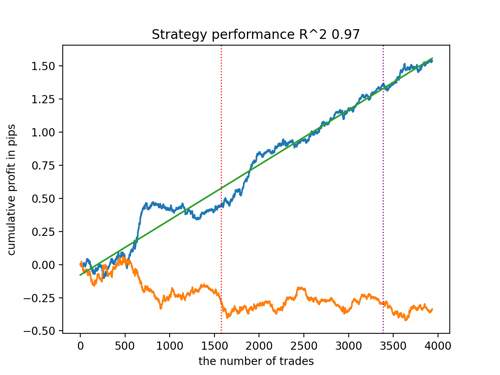
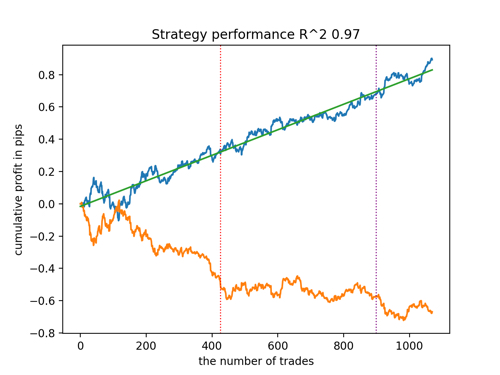
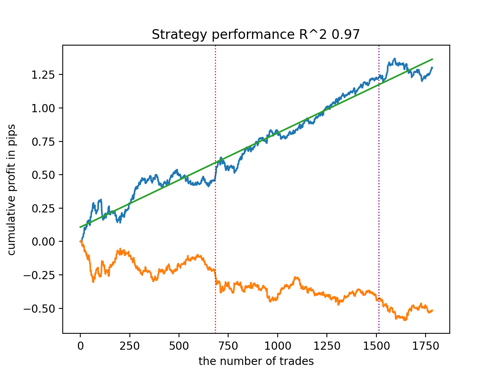
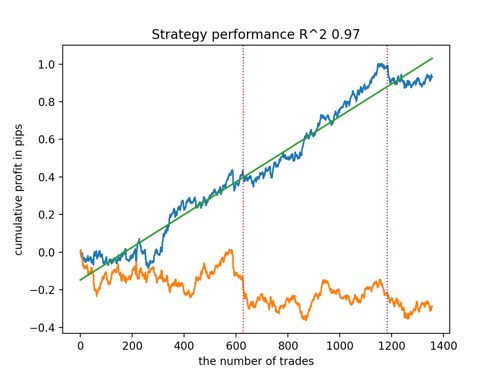
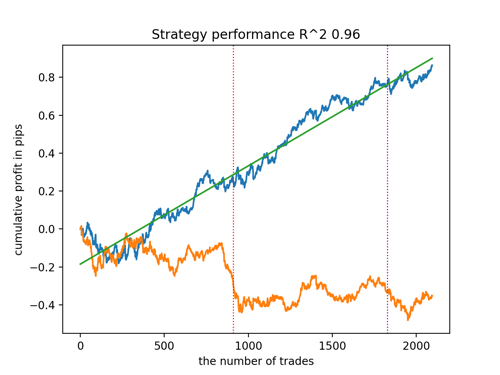
Die Saldenkurve ist blau und das Kursentwicklung orange dargestellt. Wir können sehen, dass sich alle Modelle voneinander unterscheiden. Dies ist auf die Zufallsstichprobe von Transaktionen sowie auf die in jedes Modell integrierte Zufallssteuerung zurückzuführen. Diese Modelle sehen jedoch nicht mehr wie Gralstests aus und funktionieren recht zuverlässig in OOS. Darüber hinaus können wir die Anzahl der Transaktionen, den Gewinn in Punkten und das allgemeine Aussehen der Kurven vergleichen. Natürlich sind das erste und das zweite Modell vergleichsweise günstig, sodass wir sie in das Terminal exportieren.

Es ist zu bedenken, dass wir durch Änderung der Trainingsparameter und mehrere Neustarts ein einzigartiges Verhalten erhalten. Die Diagramme werden fast nie identisch sein, aber ein bedeutender Teil von ihnen (der wichtig ist) wird auf dem OOS gut zu sehen sein.

Exportieren des Modells in das ONNX-Format

In früheren Artikeln habe ich Parsing-Modelle von cpp zu MQL verwendet. Derzeit unterstützt das MetaTrader 5-Terminal den Import von Modellen im ONNX-Format. Dies ist sehr praktisch, da Sie weniger Code schreiben und fast jedes in Python trainierte Modell übertragen können.

Der CatBoost-Algorithmus hat seine eigene Methoden für den Export von Modellen im ONNX-Format. Schauen wir uns den Exportvorgang genauer an.

Am Ausgang haben wir zwei CatBoost-Modelle und eine Funktion, die Merkmale in Form von Inkrementen erzeugt. Da die Funktion recht einfach ist, werden wir sie einfach in den Bot-Code übertragen, während die Modelle in ONNX-Dateien exportiert werden.

def export_model_to_ONNX(model, model_number):
    model[1].save_model(
    export_path +'catmodel' + str(model_number) +'.onnx',
    format="onnx",
    export_parameters={
        'onnx_domain': 'ai.catboost',
        'onnx_model_version': 1,
        'onnx_doc_string': 'test model for BinaryClassification',
        'onnx_graph_name': 'CatBoostModel_for_BinaryClassification'
    },
    pool=None)

    model[2].save_model(
    export_path + 'catmodel_m' + str(model_number) +'.onnx',
    format="onnx",
    export_parameters={
        'onnx_domain': 'ai.catboost',
        'onnx_model_version': 1,
        'onnx_doc_string': 'test model for BinaryClassification',
        'onnx_graph_name': 'CatBoostModel_for_BinaryClassification'
    },
    pool=None)
    
    code = '#include <Math\Stat\Math.mqh>'
    code += '\n'
    code += '#resource "catmodel'+str(model_number)+'.onnx" as uchar ExtModel[]'
    code += '\n'
    code += '#resource "catmodel_m'+str(model_number)+'.onnx" as uchar ExtModel2[]'
    code += '\n'
    code += 'int Periods' + '[' + str(len(PERIODS)) + \
        '] = {' + ','.join(map(str, PERIODS)) + '};'
    code += '\n\n'

    # get features
    code += 'void fill_arays' + '( double &features[]) {\n'
    code += '   double pr[], ret[];\n'
    code += '   ArrayResize(ret, 1);\n'
    code += '   for(int i=ArraySize(Periods'')-1; i>=0; i--) {\n'
    code += '       CopyClose(NULL,PERIOD_H1,1,Periods''[i],pr);\n'
    code += '       ret[0] = MathMean(pr) - pr[Periods[i]-1];\n'
    code += '       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n'
    code += '   ArraySetAsSeries(features, true);\n'
    code += '}\n\n'

    file = open(export_path + str(SYMBOL) + ' ONNX include' + str(model_number) + '.mqh', "w")
    file.write(code)

    file.close()
    print('The file ' + 'ONNX include' + '.mqh ' + 'has been written to disk')

Die Exportfunktion erhält eine Liste von Modellen. Jede von ihnen wird in ONNX mit optionalen Exportparametern gespeichert. Der gesamte Code speichert die Modelle im Include-Ordner des Terminals und erzeugt außerdem eine .mqh-Datei, die etwa so aussieht:

#resource "catmodel.onnx" as uchar ExtModel[]
#resource "catmodel_m.onnx" as uchar ExtModel2[]

#include <Math\Stat\Math.mqh>
int Periods[4] = {10,20,30,40};

void fill_arays( double &features[]) {
   double pr[], ret[];
   ArrayResize(ret, 1);
   for(int i=ArraySize(Periods)-1; i>=0; i--) {
       CopyClose(NULL,PERIOD_H1,1,Periods[i],pr);
       ret[0] = MathMean(pr) - pr[Periods[i]-1];
       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }
   ArraySetAsSeries(features, true);
}

Als Nächstes müssen wir ihn mit dem Bot verbinden. Jede Datei hat einen eindeutigen Namen, der durch das Tickersymbol und die Seriennummer des Modells am Ende angegeben wird. Daher können wir eine Sammlung solcher trainierten Modelle auf der Festplatte speichern oder mehrere Modelle gleichzeitig mit dem Bot verbinden. Ich werde mich zu Demonstrationszwecken auf eine Datei beschränken.

#include <EURUSD ONNX include1.mqh>

In der Funktion müssen wir die Modelle wie unten gezeigt korrekt initialisieren.  Das Wichtigste ist, die Dimensionen der Eingabe- und Ausgabedaten richtig einzustellen. Unsere Modelle haben einen Merkmalsvektor mit variabler Länge, die von der Anzahl der Merkmale abhängt, die in der PERIODS-Liste oder dem exportierten Array angegeben sind, daher definieren wir die Dimension des Eingabevektors wie unten dargestellt. Beide Modelle nehmen die gleiche Anzahl von Merkmalen als Eingabe.

Die Dimension des Ausgangsvektors kann zu Verwirrung führen. 

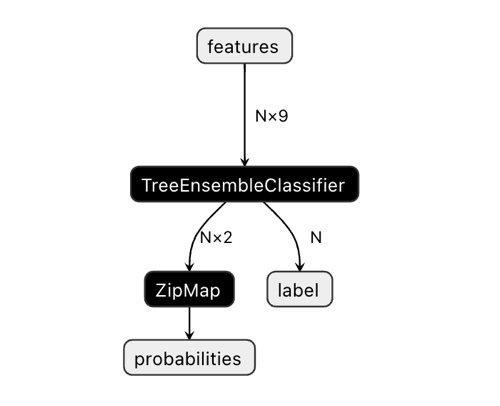
In der Netron-Anwendung können wir sehen, dass das Modell zwei Ausgaben hat. Der erste ist ein Einheitstensor mit Klassenbeschriftungen, die später im Code als Nullausgabe oder Nullindexausgabe definiert werden. Sie kann jedoch nicht für Vorhersagen verwendet werden, da es bekannte Probleme gibt, die in der Dokumentation von CatBoost beschrieben sind:

„Bei der binären Klassifizierung wird das Label falsch abgeleitet. Dies ist ein bekannter Fehler in der Implementierung von onnxruntime. Ignorieren Sie den Wert dieses Parameters im Falle einer binären Klassifizierung.“

Dementsprechend sollten wir den zweiten Ausgang „Wahrscheinlichkeiten“ verwenden, aber ich konnte ihn im MQL-Code nicht richtig einstellen, also habe ich ihn einfach nicht definiert. Sie wurde jedoch eigenständig definiert und alles funktioniert. Ich habe keine Ahnung, warum.

Daher wird die zweite Ausgabe verwendet, um Klassenwahrscheinlichkeiten im Bot zu erhalten.

const long  ExtInputShape [] = {1, ArraySize(Periods)};

int OnInit() {
   ExtHandle = OnnxCreateFromBuffer(ExtModel, ONNX_DEFAULT);
   ExtHandle2 = OnnxCreateFromBuffer(ExtModel2, ONNX_DEFAULT);

   if(ExtHandle == INVALID_HANDLE || ExtHandle2 == INVALID_HANDLE) {
      Print("OnnxCreateFromBuffer error ", GetLastError());
      return(INIT_FAILED);
   }

   if(!OnnxSetInputShape(ExtHandle, 0, ExtInputShape)) {
      Print("OnnxSetInputShape failed, error ", GetLastError());
      OnnxRelease(ExtHandle);
      return(-1);
   }

   if(!OnnxSetInputShape(ExtHandle2, 0, ExtInputShape)) {
      Print("OnnxSetInputShape failed, error ", GetLastError());
      OnnxRelease(ExtHandle2);
      return(-1);
   }

   const long output_shape[] = {1};
   if(!OnnxSetOutputShape(ExtHandle, 0, output_shape)) {
      Print("OnnxSetOutputShape error ", GetLastError());
      return(INIT_FAILED);
   }
   if(!OnnxSetOutputShape(ExtHandle2, 0, output_shape)) {
      Print("OnnxSetOutputShape error ", GetLastError());
      return(INIT_FAILED);
   }

   return(INIT_SUCCEEDED);
}

Der Empfang von Modellsignalen wird auf diese Weise realisiert. Hier deklarieren wir ein Array von Merkmalen und füllen es mit der Funktion fill_arrays(), die sich in der exportierten .mqh-Datei befindet.

Als Nächstes habe ich ein weiteres Array f deklariert, um die Reihenfolge der Werte des Features-Arrays umzukehren, und es an Onnx Runtime zur Ausführung übergeben. Die erste Ausgabe als Vektor muss nur übergeben werden, aber wir werden sie nicht verwenden. Das Array der Strukturen wird als zweite Ausgabe übergeben.

Die Modelle (main und meta) werden ausgeführt und geben vorhergesagte Werte an das Tensor-Array zurück. Ich entnehme ihr Wahrscheinlichkeiten zweiter Klasse.

void OnTick() {
   if(!isNewBar())
      return;

   double features[];
   fill_arays(features);

   double f[ArraySize(Periods)];

   int k = ArraySize(Periods) - 1;
   for(int i = 0; i < ArraySize(Periods); i++) {
      f[i] = features[i];
      k--;
   }

   static vector out(1), out_meta(1);

   struct output {
      long           label[];
      float          tensor[];
   };

   output out2[], out2_meta[];

   OnnxRun(ExtHandle, ONNX_DEBUG_LOGS, f, out, out2);
   OnnxRun(ExtHandle2, ONNX_DEBUG_LOGS, f, out_meta, out2_meta);

   double sig = out2[0].tensor[1];
   double meta_sig = out2_meta[0].tensor[1];

Der Rest des Bot-Codes sollte Ihnen aus dem vorherigen Artikel bekannt sein. Wir prüfen das Freigabesignal meta_sig. Ist es größer als 0,5, so sind die Handelstätigkeiten von Eröffnen und Schließen in Abhängigkeit von der durch das Signal Sig des ersten Modells festgelegten Richtung zulässig.

if(meta_sig > 0.5)
      if(count_market_orders(0) || count_market_orders(1))
         for(int b = OrdersTotal() - 1; b >= 0; b--)
            if(OrderSelect(b, SELECT_BY_POS) == true) {
               if(OrderType() == 0 && OrderSymbol() == _Symbol && OrderMagicNumber() == OrderMagic && sig > 0.5)
                  if(SymbolInfoInteger(_Symbol, SYMBOL_TRADE_FREEZE_LEVEL) < MathAbs(Bid - OrderOpenPrice())) {
                     int res = -1;
                     do {
                        res = OrderClose(OrderTicket(), OrderLots(), OrderClosePrice(), 0, Red);
                        Sleep(50);
                     } while (res == -1);
                  }
               if(OrderType() == 1 && OrderSymbol() == _Symbol && OrderMagicNumber() == OrderMagic && sig < 0.5)
                  if(SymbolInfoInteger(_Symbol, SYMBOL_TRADE_FREEZE_LEVEL) < MathAbs(Bid - OrderOpenPrice())) {
                     int res = -1;
                     do {
                        res = OrderClose(OrderTicket(), OrderLots(), OrderClosePrice(), 0, Red);
                        Sleep(50);
                     } while (res == -1);
                  }
            }


   if(meta_sig > 0.5)
      if(countOrders() < max_orders && CheckMoneyForTrade(_Symbol, LotsOptimized(meta_sig), ORDER_TYPE_BUY)) {
         double l = LotsOptimized(meta_sig);
         if(sig < 0.5) {
            int res = -1;
            do {
               double stop = Bid - stoploss * _Point;
               double take = Ask + takeprofit * _Point;
               res = OrderSend(Symbol(), OP_BUY, l, Ask, 0, stop, take, comment, OrderMagic);
               Sleep(50);
            } while (res == -1);
         } else {
            if(sig > 0.5) {
               int res = -1;
               do {
                  double stop = Ask + stoploss * _Point;
                  double take = Bid - takeprofit * _Point;
                  res = OrderSend(Symbol(), OP_SELL, l, Bid, 0, stop, take, comment, OrderMagic);
                  Sleep(50);
               } while (res == -1);
            }
         }
      }

Abschließende Tests

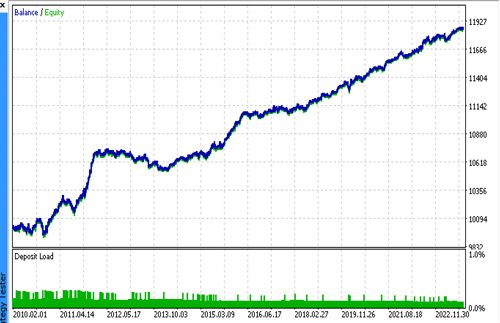
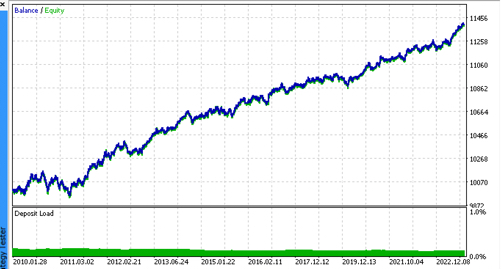
Wir verbinden nacheinander 2 Dateien mit den von uns gewünschten Modellen und stellen sicher, dass die Ergebnisse des nutzerdefinierten Testers vollständig mit den Ergebnissen des MetaTrader 5-Testers übereinstimmen.

Darüber hinaus können wir die Bots mit echten Ticks testen, Stop-Loss und Take-Profit optimieren, die Losgröße auswählen und weitere Deals im MetaTrader 5 Optimizer hinzufügen.

Schlusswort

Ich weiß nicht, ob es eine wissenschaftliche Grundlage für diesen Ansatz zur Klassifizierung von Zeitreihen für Handelsaufgaben gibt. Es wurde durch Versuch und Irrtum erfunden und schien mir recht interessant und vielversprechend zu sein.

Mit dieser kleinen Studie wollte ich aufzeigen, dass Modelle für maschinelles Lernen manchmal anders trainiert werden sollten, als es offensichtlich ist. Neben einer spezifischen Architektur ist auch die Art und Weise, wie diese Modelle angewandt werden, von großer Bedeutung. Gleichzeitig rückt ein statistischer Ansatz zur Analyse von Trainingsergebnissen in den Vordergrund, sei es der in diesem Artikel vorgestellte vollautomatische Ansatz von „Händler und Forscher“ oder einfachere Algorithmen, die das fachkundige Eingreifen eines „Lehrers“ erfordern.