Кластеризация временных рядов в причинно-следственном выводе

Введение:

• Что такое кластеризация
• Применение кластеризации в причинно-следственном выводе
• Матчинг при помощи кластеризации
• Определение гетерогенного тритмент эффекта
• Определение режимов рынка

Кластеризация волатильности:

• Код
• Рейтинг алгоритмов
• Входные параметры моделей

Матчинг сделок при помощи кластеризации:

• Код
• Описание алгоритма
• Учет гетерогенности данных
• Результаты
• Заключение

Введение

Кластеризация — это метод машинного обучения, который используется для разделения набора данных на группы объектов (кластеры) таким образом, чтобы объекты внутри одного кластера были похожи друг на друга, а объекты из разных кластеров были различны. Кластеризация позволяет выявить структуру данных, выделить скрытые закономерности и группировать объекты на основе их сходства.

Кластеризация может быть использована в причинно-следственном выводе. Одним из способов применения кластеризации в этом контексте является выявление групп схожих объектов или событий, которые могут быть связаны с определенной причиной. После кластеризации данных можно анализировать связи между кластерами и причинами, чтобы выявить потенциальные причинно-следственные связи.

Кроме того, кластеризация может помочь в выделении групп объектов, которые могут быть подвержены одному и тому же воздействию или иметь общие причины, что также может быть полезно при анализе причинно-следственных связей.

Применение кластеризации в причинно-следственном выводе может быть очень полезным для анализа данных и выявления потенциальных причинно-следственных связей. Ниже рассмотрим несколько способов, как кластеризация может быть использована в этом контексте:

1. Выявление групп схожих объектов: кластеризация позволяет выделить группы объектов, которые имеют схожие характеристики или поведение. После этого можно анализировать эти группы и искать общие причины или факторы, которые могут быть связаны с ними.
2. Определение причинно-следственных связей: после того, как данные были разделены на кластеры, можно исследовать взаимосвязи между кластерами и выявить потенциальные причинно-следственные связи. Например, если определенный кластер объектов демонстрирует определенное поведение или характеристики, можно провести анализ, чтобы выяснить, какие факторы могут быть ответственны за это.
3. Поиск скрытых закономерностей: кластеризация может помочь выявить скрытые закономерности в данных, которые могут быть связаны с причинно-следственными связями. Путем анализа структуры кластеров и выделения общих характеристик объектов внутри них можно обнаружить факторы, которые могут играть ключевую роль в возникновении определенных явлений.
4. Прогнозирование будущих событий: после того, как были выделены кластеры и выявлены причинно-следственные связи, можно использовать полученные знания для прогнозирования будущих событий или тенденций. На основе анализа данных и выявленных закономерностей можно делать предположения о том, какие факторы могут повлиять на будущие события и какие меры можно предпринять для управления ими.

Кластеризация может быть применена для матчинга в причинно-следственном выводе. Матчинг — это процесс сопоставления объектов из разных наборов данных на основе их сходства или соответствия определенным критериям. В контексте причинно-следственного вывода матчинг может использоваться для установления связей между причинами и следствиями, а также для выявления общих характеристик или факторов, которые могут быть ответственны за определенные явления.

Кластеризация может помочь в процессе матчинга следующим образом:

1. Группировка объектов: кластеризация позволяет разделить набор данных на группы объектов, которые имеют схожие характеристики или поведение. После этого можно провести матчинг внутри каждого кластера, чтобы найти соответствия между объектами и установить связи между ними.
2. Идентификация сходств: после того, как объекты были разделены на кластеры, можно исследовать сходства между объектами внутри каждого кластера и использовать их для матчинга. Например, если определенный кластер объектов демонстрирует похожее поведение или характеристики, можно провести матчинг, чтобы найти общие факторы, которые могут быть связаны с этими объектами.
3. Уменьшение шума: кластеризация может помочь уменьшить шум в данных и выделить основные группы объектов, что упрощает процесс матчинга. Путем разделения данных на кластеры можно сосредоточиться на наиболее значимых и сходных объектах, что улучшает качество матчинга и позволяет выявить более четкие причинно-следственные связи.

Отсюда вытекает, что кластеризация временных рядов может помочь выявить гетерогенный тритмент эффект, то есть различия в эффектах в разных группах временных рядов. В контексте анализа временных рядов, где проводится классификация или прогнозирование, гетерогенный тритмент эффект означает, что поведение временных рядов может различаться в зависимости от их характеристик или других факторов.

Таким образом, проводя кластеризацию временных рядов, можно добиться следующих эффектов:

1. Группировка временных рядов: кластеризация позволяет разделить временные ряды на группы на основе их характеристик, динамики изменений или других факторов. Затем можно изучить поведение каждой группы отдельно, чтобы определить, есть ли различия в прогнозах или классификации между разными кластерами временных рядов.
2. Идентификация подгрупп с разным эффектом: проведя кластеризацию временных рядов, можно выявить подгруппы с разным поведением или траекториями изменений. Это позволяет исследователям определить, какие характеристики или факторы могут влиять на результаты классификации или прогнозирования и выделить подгруппы временных рядов, которые могут требовать различных подходов к анализу.
3. Персонализация моделей: используя результаты кластеризации и выявленные подгруппы временных рядов с разным поведением, можно персонализировать модели классификации или прогнозирования и выбирать оптимальные стратегии для каждой группы. Это позволяет улучшить точность прогнозов и классификации и адаптировать модели к различным типам временных рядов.

Также можно рассматривать кластеризацию с точки зрения определения рыночных режимов, например на основе волатильности.

Анализ волатильности рынка является ключевым инструментом для инвесторов и трейдеров, поскольку он позволяет понять текущее состояние рынка и принимать обоснованные решения на основе ожидаемых колебаний цен. В контексте финансового анализа алгоритмы кластеризации на основе волатильности помогают выделить различные "режимы" рынка, которые могут указывать на различные тренды, фазы консолидации или периоды высокой неопределенности.

Как работает алгоритм кластеризации в задачах определения режимов рынка на основании волатильности:

• Подготовка данных: исходные временные ряды ценовой волатильности для активов подвергаются предварительной обработке, включая вычисление волатильности на основе стандартного отклонения цен или вариаций в распределении цен.
• Применение алгоритма кластеризации: затем применяется алгоритм кластеризации к данным о волатильности, чтобы выявить скрытые структуры и группы режимов рынка. В качестве алгоритма кластеризации могут использоваться различные методы, такие как K-Means, DBSCAN или алгоритмы, специально разработанные для анализа временных рядов, например, алгоритмы, учитывающие временные зависимости.
• Интерпретация результатов: полученные кластеры представляют различные режимы рынка, которые могут быть интерпретированы в контексте торговых стратегий. Например, кластеры с низкой волатильностью могут соответствовать периодам бокового тренда, тогда как кластеры с высокой волатильностью могут указывать на рыночные всплески или изменения тренда.

Плюсы алгоритма кластеризации в задачах определения режимов рынка на основании волатильности:

• Выделение структуры рынка: алгоритмы кластеризации позволяют выделить структуру рынка и выявить скрытые режимы, что помогает инвесторам и трейдерам понимать текущее состояние рынка.
• Автоматизация анализа: использование алгоритмов кластеризации позволяет автоматизировать процесс анализа волатильности рынка и выделения различных режимов, что экономит время и снижает вероятность человеческих ошибок.
• Поддержка принятия решений: выделение режимов рынка на основе волатильности помогает прогнозировать будущее движение цен и принимать обоснованные решения о торговле и инвестировании.

Минусы алгоритма кластеризации в задачах определения режимов рынка на основании волатильности:

• Чувствительность к выбору параметров: результаты кластеризации могут зависеть от выбора параметров алгоритма, таких как количество кластеров или метрика расстояния, что требует тщательной настройки.
• Ограничения алгоритмов: некоторые алгоритмы кластеризации могут быть неэффективны при обработке больших объемов данных или не учитывать временные зависимости.

Виды алгоритмов кластеризации

Мы можем использовать разные алгоритмы кластеризации для своих задач. Ситуация улучшается тем, что есть специализированные библиотеки на языке Python, в которых уже реализованы основные виды кластеризации. Это самый оптимальный путь для того, чтобы начать экспериментировать с ними, поскольку не придется реализовывать каждый алгоритм c нуля. То есть мы максимально ускорим процесс постановки и проведения эксперимента.

Здесь мы вкратце рассмотрим основные алгоритмы кластеризации, которые могут нам пригодиться. А затем применим их в своих задачах.

• K-Means выделяется своей простотой и эффективностью, но имеет ограничения, такие как зависимость от начальных условий и необходимость знать количество кластеров.
• Affinity Propagation не требует предварительного определения числа кластеров и хорошо работает с данными различной формы, но может быть вычислительно сложным.
• Mean shift способен обнаруживать кластеры произвольной формы и не требует задания числа кластеров. Является вычислительно затратным при работе с большими объемами данных.
• Spectral Clustering подходит для данных с нелинейными структурами и является универсальным. Однако может оказаться сложным в настройке параметров и вычислительно затратным.
• Agglomerative Clustering создает иерархические кластеры и подходит для работы с неизвестным числом кластеров.
• GMM предлагает вероятностный подход к кластеризации, позволяя моделировать кластеры с различными формами и плотностями.
• HDBSCAN и BIRCH оба обеспечивают эффективную работу с большими объемами данных и автоматическое определение числа кластеров, но тоже имеют свои недостатки, такие как вычислительная сложность и чувствительность к параметрам.

Реализация кластеризации временных рядов (кластеризация волатильности)

Нас интересует возможность кластеризации финансовых временных рядов как с точки зрения определения рыночных режимов, так и с точки зрения матчинга и определения гетерогенного тритмент эффекта. Начнем с попытки кластеризации рыночных режимов.

Следующий код выполняет обучение модели мета-обучения и последующее обучение финальной модели и мета-модели на основе результатов кластеризации, которая основана на волатильности финансовых данных:

def meta_learner(models_number: int, 
                 iterations: int, 
                 depth: int, 
                 bad_samples_fraction: float, 
                 n_clusters: int, 
                 algorithm: int) -> pd.DataFrame:
    
    dataset = get_labels(get_prices())
    data = dataset[(dataset.index < FORWARD) & (dataset.index > BACKWARD)].copy()
    X = data[data.columns[1:-2]]
    X = X.loc[:, ~X.columns.str.contains('std')]
    meta_X = data.loc[:, data.columns.str.contains('std')]
    y = data['labels']

    B_S_B = pd.DatetimeIndex([])
    for i in range(models_number):
        X_train, X_val, y_train, y_val = train_test_split(
            X, y, train_size = 0.5, test_size = 0.5, shuffle = True)
        
        # learn debias model with train and validation subsets
        meta_m = CatBoostClassifier(iterations = iterations,
                                depth = depth,
                                custom_loss = ['Accuracy'],
                                eval_metric = 'Accuracy',
                                verbose = False,
                                use_best_model = True)
        
        meta_m.fit(X_train, y_train, eval_set = (X_val, y_val), plot = False)
        
        coreset = X.copy()
        coreset['labels'] = y
        coreset['labels_pred'] = meta_m.predict_proba(X)[:, 1]
        coreset['labels_pred'] = coreset['labels_pred'].apply(lambda x: 0 if x < 0.5 else 1)
        
        # add bad samples of this iteration (bad labels indices)
        diff_negatives = coreset['labels'] != coreset['labels_pred']
        B_S_B = B_S_B.append(diff_negatives[diff_negatives == True].index)

    to_mark = B_S_B.value_counts()
    marked_idx = to_mark[to_mark > to_mark.mean() * bad_samples_fraction].index
    data.loc[data.index.isin(marked_idx), 'meta_labels'] = 0.0


    if algorithm==0:
        data['clusters'] = KMeans(n_clusters=n_clusters).fit(meta_X).labels_
    elif algorithm==1:
        data['clusters'] = AffinityPropagation().fit(meta_X).predict(meta_X)
    elif algorithm==2:
        data['clusters'] = SpectralClustering(n_clusters=n_clusters, assign_labels='discretize', random_state=0).fit_predict(meta_X)
    elif algorithm==3:
        data['clusters'] = MeanShift().fit_predict(meta_X)
    elif algorithm==4:
        data['clusters'] = AgglomerativeClustering(n_clusters=n_clusters).fit_predict(meta_X)
    elif algorithm==5:
        data['clusters'] = mixture.GaussianMixture(n_components=n_clusters, covariance_type='full').fit(meta_X).predict(meta_X)
    elif algorithm==6:
        data['clusters'] = HDBSCAN(min_cluster_size=150).fit_predict(meta_X)
    elif algorithm==7:
        data['clusters'] = Birch(threshold=0.01, n_clusters=n_clusters).fit_predict(meta_X)
    return data[data.columns[1:]]

Описание функции:

Функция `meta_learner` предназначена для метаобучения модели классификации с целью выявления и коррекции неправильно помеченных образцов в наборе данных. Она использует ансамбль моделей `CatBoostClassifier` для определения таких образцов и применяет алгоритмы кластеризации для дальнейшей обработки данных. Вот более подробное описание процесса:

1. Подготовка данных: функция начинается с получения набора данных, который фильтруется по временным меткам (исключая данные за определенные периоды). Далее, данные разделяются на признаки (`X`), мета-признаки (`meta_X`), основанные на стандартных отклонениях, и целевые метки (`y`).

2. Инициализация переменных: создается пустой индекс даты `B_S_B` для хранения индексов неправильно помеченных образцов.

3. Обучение моделей и выявление неправильных меток: для каждой из `models_number` моделей данные разделяются на обучающую и валидационную выборки. Затем обучается модель `CatBoostClassifier` с заданными параметрами. После обучения модель используется для предсказания меток на всем наборе признаков `X`. Сравнивая предсказанные метки с исходными, функция определяет неправильно помеченные образцы и добавляет их индексы в `B_S_B`.

4. Маркировка неправильных образцов: после обучения всех моделей функция анализирует индексы неправильно помеченных образцов, хранящиеся в `B_S_B`, и маркирует те из них, которые встречаются чаще, чем это определено долей `bad_samples_fraction`, помечая их в исходных данных как `0.0` в столбце `meta_labels`.

5. Кластеризация: в зависимости от значения параметра `algorithm`, функция применяет один из алгоритмов кластеризации к мета-признакам (`meta_X`) и добавляет полученные метки кластеров в исходные данные.

6. Возвращение результата: функция возвращает обновленный набор данных с метками и присвоенными кластерами.

Этот подход позволяет не только выявить и исправить ошибки в метках данных, но и группировать данные для дальнейшего анализа или обучения моделей, что может быть особенно полезно в задачах, где присутствует значительное количество неправильно помеченных образцов.

Функция обучения финальных моделей выглядит следующим образом:

def fit_final_models(dataset) -> list:
    # features for model\meta models. We learn main model only on filtered labels 
    X, X_meta = dataset[dataset['meta_labels']==1], dataset[dataset.columns[:-3]]
    X = X[X.columns[:-3]]
    X = X.loc[:, ~X.columns.str.contains('std')]
    X_meta = X_meta.loc[:, X_meta.columns.str.contains('std')]
    
    # labels for model\meta models
    y, y_meta = dataset[dataset['meta_labels']==1], dataset[dataset.columns[-1]]
    y = y[y.columns[-3]]
    
    y = y.astype('int16')
    y_meta = y_meta.astype('int16')

    # train\test split
    train_X, test_X, train_y, test_y = train_test_split(
        X, y, train_size=0.8, test_size=0.2, shuffle=True)
    
    train_X_m, test_X_m, train_y_m, test_y_m = train_test_split(
        X_meta, y_meta, train_size=0.8, test_size=0.2, shuffle=True)

    # learn main model with train and validation subsets
    model = CatBoostClassifier(iterations=200,
                               custom_loss=['Accuracy'],
                               eval_metric='Accuracy',
                               verbose=False,
                               use_best_model=True,
                               task_type='CPU')
    model.fit(train_X, train_y, eval_set=(test_X, test_y),
              early_stopping_rounds=25, plot=False)
    
    # learn meta model with train and validation subsets
    meta_model = CatBoostClassifier(iterations=100,
                                    custom_loss=['F1'],
                                    eval_metric='F1',
                                    verbose=False,
                                    use_best_model=True,
                                    task_type='CPU')
    meta_model.fit(train_X_m, train_y_m, eval_set=(test_X_m, test_y_m),
              early_stopping_rounds=15, plot=False)
    
    R2 = test_model([model, meta_model])
    if math.isnan(R2):
        R2 = -1.0
        print('R2 is fixed to -1.0')
    print('R2: ' + str(R2))
    return [R2, model, meta_model]

Функция `fit_final_models` предназначена для обучения основной и мета-модели на предоставленном наборе данных. Вот подробное описание её работы:

1. Подготовка данных:

• Из набора данных выбираются строки, где `meta_labels` равно 1, для обучения основной модели (`X`, `y`).
• Для обучения мета-модели используются все строки набора данных (`X_meta`, `y_meta`).
• Из признаков для обучения основной модели исключаются столбцы, содержащие в названии 'std', а также последние три столбца.
• Для мета-модели используются только те признаки, которые содержат в названии 'std'.
• Целевая переменная (`y`) для основной модели берётся из третьего с конца столбца и приводится к типу `int16`.
• Целевая переменная для мета-модели (`y_meta`) берётся из последнего столбца и также приводится к типу `int16`.

2.  Разделение данных на обучающую и тестовую выборки:

• Для основной модели и мета-модели данные разделяются на обучающую и тестовую выборки в соотношении 80% на 20%.

3. Обучение основной модели:

• Используется классификатор `CatBoostClassifier` с 200 итерациями, функцией потерь 'Accuracy', метрикой оценки 'Accuracy', без вывода информации о ходе обучения, с выбором лучшей модели и заданием типа задачи как 'CPU'.
• Модель обучается на обучающей выборке с ранней остановкой через 25 раундов, если метрика не улучшается.

4. Обучение мета-модели:

• Аналогично основной модели, но с 100 итерациями, функцией потерь 'F1', метрикой оценки 'F1' и ранней остановкой через 15 раундов.

5. Тестирование моделей:

• Проводится тестирование обученных моделей с помощью функции `test_model`, которая возвращает значение метрики R2.
• Если полученное значение R2 является `NaN`, оно заменяется на -1.0, и выводится соответствующее сообщение.

6. Возвращаемые значения:

• Функция возвращает список, содержащий значение R2, основную модель и мета-модель.

Эта функция представляет собой часть процесса машинного обучения, где основная модель обучается на отфильтрованных данных (где предполагается, что метки были проверены или скорректированы), а мета-модель обучается предсказывать выбранных кластер волатильности.

Обучение всего алгоритма происходит в цикле:

Эта функция обучает модель и мета-модель на основе входного набора данных. Возвращает список, содержащий значение R2, основную модель и мета-модель.

# LEARNING LOOP
models = []
for i in range(1):
    data = meta_learner(5, 25, 2, 0.9, n_clusters=N_CLUSTERS, algorithm=6)
    for clust in data['clusters'].unique():
        print(f'Iteration: {i}, Cluster: {clust}')
        filtered_data = data.copy()
        filtered_data['clusters'] = filtered_data['clusters'].apply(lambda x: 1 if x == clust else 0)
        models.append(fit_final_models(filtered_data))

Этот код представляет собой обучающий цикл, в котором используется функция `meta_learner` для метаобучения модели и последующего обучения конечных моделей на основе полученных кластеров. Вот более подробное описание процесса:

1. Инициализация списка моделей: создается пустой список `models`, который будет использоваться для хранения обученных конечных моделей.

2. Запуск обучающего цикла: цикл `for` настроен на одну итерацию (`range(1)`), что означает, что весь процесс будет выполнен один раз. Это сделано для демонстрации или тестирования, поскольку обычно в таких циклах используется большее количество итераций ввиду рандомизации алгоритмов обучения.

3. Метаобучение с помощью `meta_learner`: Вызывается функция `meta_learner` с заданными параметрами:

• `models_number=5`: используется 5 базовых моделей для метаобучения.
• `iterations=25`: каждая базовая модель обучается с 25 итерациями.
• `depth=2`: глубина дерева классификатора для базовых моделей установлена в 2.
• `bad_samples_fraction=0.9`: доля ошибочно помеченных образцов, которые будут помечены, составляет 90%.
• `n_clusters=N_CLUSTERS`: количество кластеров для алгоритма кластеризации, где `N_CLUSTERS` должно быть определено заранее.
• `algorithm=6`: используется алгоритм кластеризации HDBSCAN.

Функция `meta_learner` возвращает обновленный набор данных с пометками и присвоенными кластерами.

4. Итерация по уникальным кластерам: для каждого уникального кластера в наборе данных выводится сообщение с номером итерации и кластера. Затем данные фильтруются таким образом, чтобы все записи, принадлежащие текущему кластеру, помечались как `1`, а все остальные - как `0`. Это создает двоичную классификацию для каждого кластера.

5. Обучение конечных моделей: для каждого кластера вызывается функция `fit_final_models`, которая, обучает и возвращает модель на основе фильтрованных данных. Обученные модели добавляются в список `models`.

Этот подход позволяет обучить ряд специализированных моделей, каждая из которых фокусируется на определенном кластере данных, что может улучшить общую производительность моделирования за счет более точного учета особенностей различных групп данных.

Были проанализированы все предложенные алгоритмы кластеризации на предмет определения рыночных режимов. Некоторые алгоритмы показали себя хорошо, тогда как работа остальных оказалась неудовлетворительной.

Ниже представлены результаты обучения с использованием разных алгоритмов кластеризации:

Прежде всего, меня интересовала скорость кластеризации. Было обнаружено, что алгоритмы Affinity propagation, Spectral clustering, Agglomerative clustering и Mean shift оказались очень медленными, поэтому все они находятся в конце рейтинга. Мне не удалось дождаться результатов кластеризации при использовании стандартных настроек, поэтому результаты для этих алгоритмов не приведены.

Я нашел подтверждение в интернете:

Я запустил 10 повторений всего процесса обучения для более информативных результатов, потому что результаты отличаются от обучения к обучению ввиду рандомизации внутри алгоритмов.

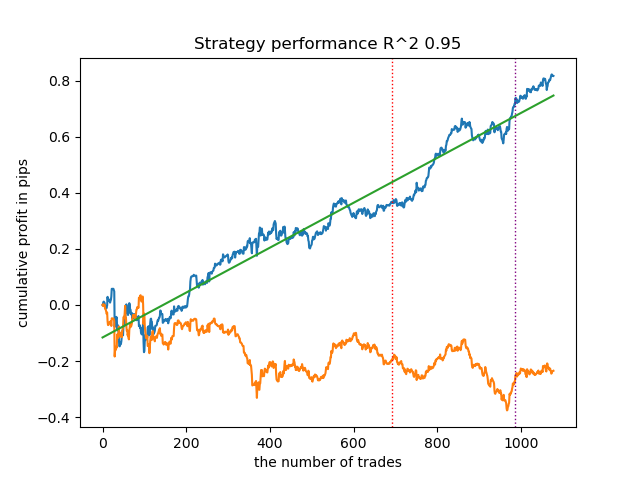
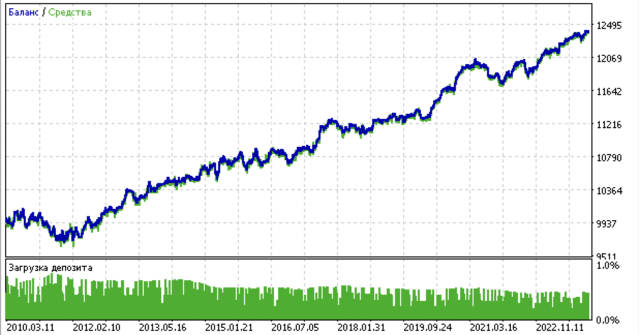
• Синяя линяя отображает график баланса,
• Оранжевая линия - график финансового инструмента (в данном случае EURUSD).

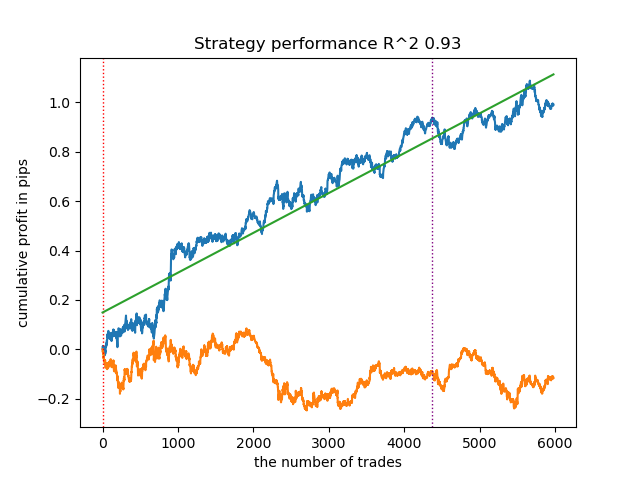
1. HDBSCAN я решил вынести в топ рейтинга из четырех оставшихся алгоритмов. Он хорошо разделяет данные и не требует задания количества кластеров.

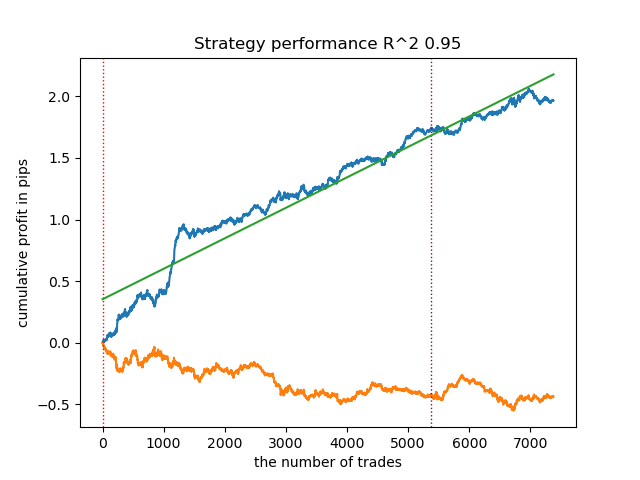
2. K-means показывает хорошую производительность и достаточно неплохие результаты тестирования. Минусом является чувствительность к количеству кластеров, в данном случае оно равно десяти.

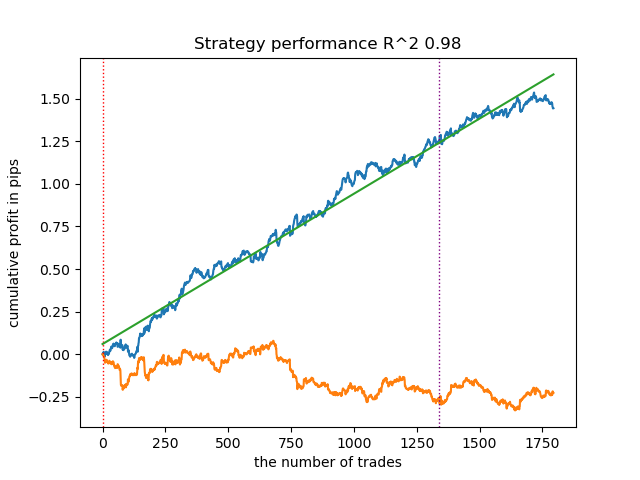
3. BIRCH демонстрирует неплохие результаты, однако считает несколько медленнее предыдущих алгоритмов. Здесь также не требуется начальное количество кластеров.

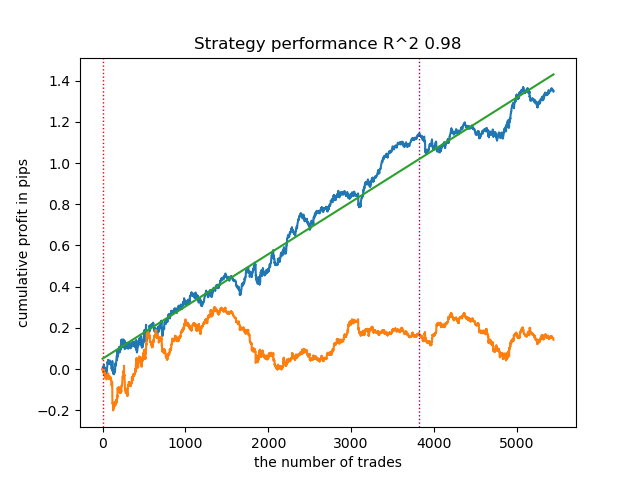
4. Gaussian mixture завершает данный рейтинг. Результаты тестирования показались мне хуже, чем при использовании остальных алгоритмов кластеризации. Визуально это выражается в более "шумном" графике баланса. Как и в случае K-means, было задано 10 кластеров.

Таким образом, можно получать различные торговые системы, в зависимости от выбранного режима рынка. В процессе обучения выводятся результаты тестирования моделей для каждого из режимов, на основании заданного количества кластеров.

Поскольку на качество кластеризации влияет набор входных параметров, следует их перечислить:

• Валютная пара
• Таймфрейм
• Начальная и конечная даты обучения
• Количество признаков для основной модели
• Количество признаков для мета модели (волатильность)
• Количество кластеров n_clusters
• Параметры min и max функции get_labels(min, max)

Например, вот еще один из результатов кластеризации с приведенными ниже параметрами:

SYMBOL = 'EURUSD'
MARKUP = 0.00010
PERIODS = [i for i in range(10, 100, 10)]
PERIODS_META = [20]
BACKWARD = datetime(2019, 1, 1)
FORWARD = datetime(2023, 1, 1)
n_clusters = 40

def get_labels(dataset, min = 5, max = 5)

Timeframe = H1

Поскольку алгоритм поиска кластеров также рандомизирован, хорошей практикой является несколько перезапусков.

Матчинг сделок при помощи кластеризации

Переходим к финальной части, ради которой задумывалась вся эта статья. Я хотел углубить понимание причинно-следственного вывода, добавив в него элемент кластеризации. Соответственно, в этой статье вы узнаете что такое причинно-следственный вывод, а в этой статье узнаете о матчинге посредством propensity score (показателя склонности). Теперь заменим матчинг через показатель склонности своим авторским подходом - матчингом посредством кластеризации. Для этого возьмем алгоритм из первой статьи и модифицируем его.

def meta_learners(models_number: int, iterations: int, depth: int, bad_samples_fraction: float, n_clusters: int):
    dataset = get_labels(get_prices())
    data = dataset[(dataset.index < FORWARD) & (dataset.index > BACKWARD)].copy()

    X = data[data.columns[1:-2]]
    y = data['labels']
    clusters = KMeans(n_clusters=n_clusters).fit(X[X.columns[0:1]]).labels_

    BAD_CLUSTERS = []
    for _ in range(n_clusters):
        sublist =  [pd.DatetimeIndex([]), pd.DatetimeIndex([])]
        BAD_CLUSTERS.append(sublist)

    for i in range(models_number):
        X_train, X_val, y_train, y_val = train_test_split(
            X, y, train_size = 0.5, test_size = 0.5, shuffle = True)
        
        # learn debias model with train and validation subsets
        meta_m = CatBoostClassifier(iterations = iterations,
                                depth = depth,
                                custom_loss = ['Accuracy'],
                                eval_metric = 'Accuracy',
                                verbose = False,
                                use_best_model = True)
        
        meta_m.fit(X_train, y_train, eval_set = (X_val, y_val), plot = False)
        
        coreset = X.copy()
        coreset['labels'] = y
        coreset['labels_pred'] = meta_m.predict_proba(X)[:, 1]
        coreset['labels_pred'] = coreset['labels_pred'].apply(lambda x: 0 if x < 0.5 else 1)
        coreset['clusters'] = clusters
        
        # add bad samples of this iteration (bad labels indices)
        coreset_b = coreset[coreset['labels']==0]
        coreset_s = coreset[coreset['labels']==1]

        for clust in range(n_clusters):
            diff_negatives_b = (coreset_b['labels'] != coreset_b['labels_pred']) & (coreset['clusters'] == clust)
            diff_negatives_s = (coreset_s['labels'] != coreset_s['labels_pred']) & (coreset['clusters'] == clust)
            BAD_CLUSTERS[clust][0] = BAD_CLUSTERS[clust][0].append(diff_negatives_b[diff_negatives_b == True].index)
            BAD_CLUSTERS[clust][1] = BAD_CLUSTERS[clust][
        1].append(diff_negatives_s[diff_negatives_s == True].index)

    for clust in range(n_clusters):
        to_mark_b = BAD_CLUSTERS[clust][0].value_counts()
        to_mark_s = BAD_CLUSTERS[clust][1].value_counts()
        marked_idx_b = to_mark_b[to_mark_b > to_mark_b.mean() * bad_samples_fraction].index
        marked_idx_s = to_mark_s[to_mark_s > to_mark_s.mean() * bad_samples_fraction].index
        data.loc[data.index.isin(marked_idx_b), 'meta_labels'] = 0.0
        data.loc[data.index.isin(marked_idx_s), 'meta_labels'] = 0.0

    return data[data.columns[1:]]

Для тех, кто не читал мои предыдущие статьи, сделаю краткое описание алгоритма:

• Обработка данных:
• Начало функции предполагает использование функций get_prices() и get_labels(), чтобы получить набор данных. Эти функции, возвращают ценовую информацию и метки классов соответственно.
• get_labels() ассоциирует ценовые данные с метками, что является общей задачей в машинном обучении финансовых данных.
• Данные затем фильтруются по временным интервалам, определяемым константами FORWARD и BACKWARD.
• Подготовка данных:
• Данные разделяются на признаки (X) и метки (y).
• Применяется алгоритм кластеризации KMeans для создания кластеров данных.
• Обучение моделей:
• В цикле for, определяется количество моделей models_number. В каждой итерации модель обучается на половине данных (train_size = 0.5) и оценивается на второй половине (validation set).
• Используется модель CatBoostClassifier с определенными параметрами. Это градиентный бустинговый метод, специально разработанный для работы с категориальными признаками.
• Важно отметить, что в этом алгоритме используется кастомная функция потерь 'Accuracy' и метрика оценки 'Accuracy'. Это указывает на то, что основное внимание уделяется точности предсказания.
• Затем применяется мета-модель для оценки и корректировки прогнозов первичных моделей. Это позволяет учесть возможные смещения или ошибки первичных моделей.
• Определение плохих образцов:
• Создаются списки BAD_CLUSTERS, которые содержат информацию о плохих образцах в каждом кластере. Плохие образцы определяются как те, для которых модель допускает значительное количество ошибок.
• Для каждой итерации обучения определяются плохие образцы, их индексы сохраняются в соответствующем списке.
• Мета-анализ и коррекция:
• Индексы плохих образцов, выявленных в предыдущем этапе, агрегируются и затем используются для пометки соответствующих образцов в основных данных.
• Предполагается, что это помогает улучшить качество обучения моделей, исключая или корректируя плохие образцы.
• Возврат данных:
• Функция возвращает подготовленные данные без первого столбца, который, содержит временные метки.

Этот алгоритм стремится к улучшению качества моделей машинного обучения путем обнаружения и коррекции плохих образцов, а также использования мета-модели для учета ошибок первичных моделей. Он является сложным и требует внимательной настройки параметров для эффективной работы.

В представленном коде кластеризация помогает учесть гетерогенность в данных несколькими способами:

• Идентификация кластеров данных:
• Применение алгоритма кластеризации KMeans позволяет разделить данные на группы схожих объектов. Каждый кластер содержит данные с похожими характеристиками. Это особенно полезно в случае гетерогенных данных, где объекты могут принадлежать разным категориям или иметь различные структуры.
• Анализ и обработка кластеров по отдельности:
• Каждый кластер обрабатывается отдельно от других, что позволяет учитывать особенности и структуру данных внутри каждой группы. Это помогает лучше понять гетерогенность данных и адаптировать алгоритмы обучения под конкретные условия в каждом кластере.
• Коррекция ошибок внутри кластеров:
• После обучения моделей в цикле для каждого кластера происходит анализ плохих образцов, то есть тех, для которых модель допускает значительное количество ошибок. Это позволяет локализовать и сконцентрироваться на коррекции ошибок внутри каждого кластера отдельно, что может быть более эффективным, чем применение одинаковых коррекций ко всем данным в целом.
• Учет особенностей данных в обучении мета-модели:
• Кластеризация также используется для того, чтобы учесть различия между кластерами при обучении мета-модели. Это позволяет мета-модели лучше адаптироваться к гетерогенности данных, за счет включения информации о структуре данных внутри каждого кластера.

Таким образом, кластеризация играет ключевую роль в учете гетерогенности данных, позволяя алгоритму более эффективно адаптироваться к разнообразию объектов и структур данных.

Результат обучения такой модели представлен ниже. Видно, что модель стала более устойчивой на новых данных.

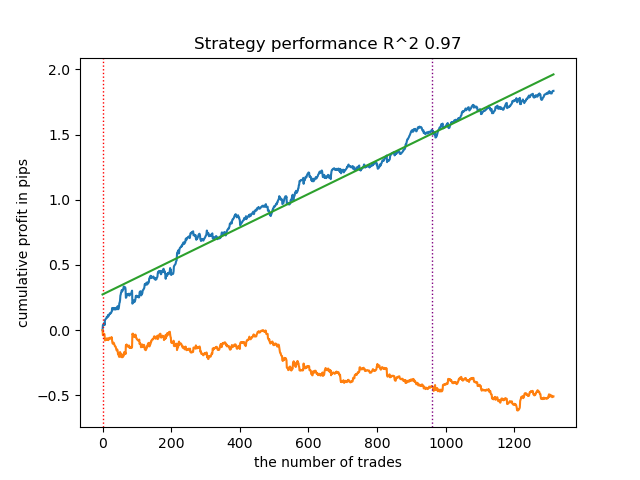
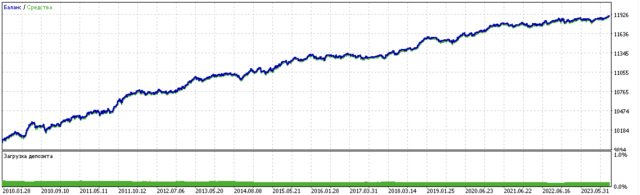
Данная модель экспортируется в формат ONNX и полностью совместима с советником ONNX Trader.

Заключение

В данной статье был рассмотрен авторский подход к кластеризации временных рядов. Я провел тестирование различных алгоритмов кластеризации рыночных режимов по волатильности. Было обнаружено, что сложные алгоритмы не всегда соответствуют ожиданиям: иногда простые и быстрые алгоритмы кластеризации вроде K-means справляются с задачей лучше. В то же время, очень понравился алгоритм HDBSCAN.

Во второй части кластеризация была задействована для определения гетерогенного тритмент эффекта. Эксперименты показали, что учет плохих сделок с применением кластеризации, снижает разброс значений (кривая баланса становится более гладкой) и улучшает предсказание модели на новых данных. В целом, это достаточно сложная и глубокая тема, которая требует перебора гиперпараметров для тонкой настройки алгоритма.