Agrupamento de séries temporais na inferência causal

Introdução:

• O que é agrupamento
• Aplicando agrupamento na inferência causal
• Correspondência por meio de agrupamento
• Determinação do efeito de tratamento heterogêneo
• Identificação dos regimes de mercado

Agrupamento da volatilidade:

• Código
• Classificação de algoritmos
• Parâmetros de entrada dos modelos

Correspondência de negociações por meio de agrupamento:

• Código
• Descrição do algoritmo
• Consideração da heterogeneidade dos dados
• Resultados
• Considerações finais

Introdução

O agrupamento é um método de aprendizado de máquina que é usado para dividir um conjunto de dados em grupos de objetos (clusters) de tal forma que os objetos dentro de um mesmo cluster sejam semelhantes entre si, enquanto os objetos de clusters diferentes sejam distintos. O agrupamento permite revelar a estrutura dos dados, destacar padrões ocultos e reunir objetos com base em suas semelhanças.

O agrupamento pode ser usado na inferência causal. Uma das maneiras de aplicar o agrupamento nesse contexto é identificar grupos de objetos ou eventos semelhantes que podem estar relacionados a uma determinada causa. Após o agrupamento dos dados, é possível analisar as conexões entre os clusters e as causas para identificar potenciais relações de causa e efeito.

Além disso, o agrupamento ajuda a destacar grupos de objetos que podem estar sujeitos à mesma influência ou ter causas comuns, o que também pode ser útil ao analisar as relações de causa e efeito.

A aplicação do agrupamento na inferência causal pode ser muito útil para a análise de dados e para identificar potenciais relações de causa e efeito. A seguir, vamos examinar algumas maneiras de como o agrupamento pode ser usado nesse contexto:

1. Identificação de grupos de objetos semelhantes: o agrupamento permite destacar grupos de objetos que têm características ou comportamentos semelhantes. Após isso, esses grupos podem ser analisados para buscar causas ou fatores comuns que possam estar relacionados a eles.
2. Determinação de relações de causa e efeito: depois que os dados foram divididos em clusters, é possível investigar as interrelações entre os clusters e identificar potenciais relações de causa e efeito. Por exemplo, se um determinado cluster de objetos demonstra um comportamento ou características específicas, pode-se realizar uma análise para descobrir quais fatores podem ser responsáveis por isso.
3. Busca de padrões ocultos: o agrupamento pode ajudar a identificar padrões ocultos nos dados que podem estar relacionados a relações de causa e efeito. Analisando a estrutura dos clusters e destacando as características comuns dos objetos dentro deles, é possível descobrir fatores que podem desempenhar um papel importante no surgimento de determinados fenômenos.
4. Previsão de eventos futuros: após a identificação dos clusters e das relações de causa e efeito, os conhecimentos adquiridos podem ser utilizados para prever eventos ou tendências futuras. Com base na análise dos dados e nas regularidades identificadas, é possível fazer suposições sobre quais fatores podem influenciar eventos futuros e quais medidas podem ser tomadas para geri-los.

O agrupamento pode ser usado para fazer correspondências ao implementar inferência causal. Esse processo consiste em comparar objetos de diferentes conjuntos de dados com base em sua semelhança ou em critérios específicos. Na inferência causal, a correspondência ajuda a estabelecer ligações entre causas e efeitos, além de identificar características ou fatores comuns que possam estar ligados a certos fenômenos.

O agrupamento pode ajudar ao fazer correspondências da seguinte maneira:

1. Agrupamento de objetos: elepermite dividir um conjunto de dados em grupos de objetos que têm características ou comportamentos semelhantes. Depois disso, pode-se encontrar correspondências entre os objetos e estabelecer conexões entre eles dentro de cada cluster.
2. Identificação de semelhanças: após os objetos serem divididos em clusters, é possível explorar as semelhanças entre os objetos dentro de cada cluster e usá-las para estabelecer correspondências. Por exemplo, se um determinado cluster de objetos demonstrar comportamento ou características semelhantes, pode-se realizar correspondências para encontrar fatores comuns que possam estar relacionados a esses objetos.
3. Redução de ruído: o agrupamento pode ajudar a reduzir o ruído nos dados e destacar os principais grupos de objetos, o que simplifica o processo de encontrar correspondências. Ao dividir os dados em clusters, é possível focar nos objetos mais significativos e semelhantes, melhorando a qualidade da correspondências e permitindo identificar relações de causa e efeito mais claras.

Daqui resulta que o agrupamento de séries temporais pode ajudar a identificar o efeito de tratamento heterogêneo, ou seja, as diferenças nos efeitos em diferentes grupos de séries temporais. No contexto da análise de séries temporais, onde se realiza classificação ou previsão, o efeito de tratamento heterogêneo significa que o comportamento das séries temporais pode variar dependendo de suas características ou de outros fatores.

Assim, realizando o agrupamento de séries temporais, é possível alcançar os seguintes efeitos:

1. Agrupamento de séries temporais: ele permite dividir as séries temporais em grupos com base em suas características, dinâmica de mudanças ou outros fatores. Em seguida, pode-se estudar o comportamento de cada grupo separadamente para determinar se há diferenças nas previsões ou na classificação entre os diferentes clusters de séries temporais.
2. Identificação de subgrupos com efeitos diferentes: ao realizar o agrupamento de séries temporais, é possível identificar subgrupos com comportamentos ou trajetórias de mudança diferentes. Isso permite que os pesquisadores determinem quais características ou fatores podem influenciar os resultados da classificação ou previsão e destaquem subgrupos de séries temporais que podem exigir abordagens diferentes para análise.
3. Personalização de modelos: usando os resultados do agrupamento e os subgrupos de séries temporais identificados com comportamentos diferentes, é possível personalizar modelos de classificação ou previsão e escolher as estratégias ótimas para cada grupo. Isso permite melhorar a precisão das previsões e da classificação, além de adaptar os modelos a diferentes tipos de séries temporais.

Também é possível considerar o agrupamento do ponto de vista da definição de regimes de mercado, como, por exemplo, com base na volatilidade.

A análise da volatilidade do mercado é uma ferramenta crucial para investidores e traders, por permitir compreender o estado atual do mercado e tomar decisões fundamentadas com base nas flutuações de preços esperadas. No contexto da análise financeira, os algoritmos de agrupamento baseados na volatilidade ajudam a destacar diferentes "regimes" de mercado, que podem indicar diversas tendências, fases de consolidação ou períodos de alta incerteza.

Como funciona o algoritmo de agrupamento nas tarefas de definição de regimes de mercado com base na volatilidade:

• Preparação dos dados: as séries temporais originais de volatilidade de preços dos ativos passam por um pré-processamento, incluindo o cálculo da volatilidade com base no desvio padrão dos preços ou nas variações na distribuição dos preços.
• Aplicação do algoritmo de agrupamento: em seguida, aplica-se o algoritmo de agrupamento aos dados de volatilidade para identificar estruturas ocultas e grupos de regimes de mercado. Podem ser usados diversos métodos de agrupamento, como K-Means, DBSCAN ou algoritmos especificamente desenvolvidos para análise de séries temporais, como aqueles que consideram dependências temporais.
• Interpretação dos resultados: os clusters obtidos representam diferentes regimes de mercado, que podem ser interpretados no contexto de estratégias de negociação. Por exemplo, clusters com baixa volatilidade podem corresponder a períodos de tendência lateral, enquanto clusters com alta volatilidade podem indicar picos de mercado ou mudanças de tendência.

Vantagens do algoritmo de agrupamento nas tarefas de definição de regimes de mercado com base na volatilidade:

• Destacar a estrutura do mercado: os algoritmos de agrupamento permitem destacar a estrutura do mercado e identificar regimes ocultos, ajudando investidores e traders a entenderem o estado atual do mercado.
• Automatização da análise: o uso de algoritmos de agrupamento permite automatizar o processo de análise da volatilidade do mercado e a identificação de diferentes regimes, economizando tempo e reduzindo a probabilidade de erros humanos.
• Suporte à tomada de decisões: a identificação de regimes de mercado com base na volatilidade ajuda a prever movimentos futuros dos preços e a tomar decisões informadas sobre negociação e investimento.

Desvantagens do algoritmo de agrupamento nas tarefas de definição de regimes de mercado com base na volatilidade:

• Sensibilidade à escolha dos parâmetros: os resultados do agrupamento podem depender da escolha dos parâmetros do algoritmo, como o número de clusters ou a métrica de distância, exigindo uma configuração cuidadosa.
• Limitações dos algoritmos: alguns algoritmos de agrupamento podem ser ineficazes ao lidar com grandes volumes de dados ou ao não considerar dependências temporais.

Tipos de algoritmos de agrupamento

Podemos utilizar diferentes algoritmos de agrupamento para nossas tarefas. A situação é favorecida pelo fato de existirem bibliotecas especializadas em Python, nas quais os principais tipos de agrupamento já estão implementados. Este é o caminho mais otimizado para começar a experimentá-los, pois não será necessário implementar cada algoritmo do zero. Isso acelera ao máximo o processo de configuração e execução dos experimentos.

Aqui, faremos uma breve revisão dos principais algoritmos de agrupamento que podem ser úteis para nós. Em seguida, aplicaremos esses algoritmos em nossas tarefas.

• K-Means destaca-se por sua simplicidade e eficiência, mas tem limitações, como a dependência das condições iniciais e a necessidade de conhecer o número de clusters.
• Affinity Propagation não requer a definição prévia do número de clusters e funciona bem com dados de diferentes formas, mas pode ser computacionalmente complexo.
• Mean Shift pode detectar clusters de forma arbitrária e não exige a definição do número de clusters. No entanto, é computacionalmente intensivo ao lidar com grandes volumes de dados.
• Spectral Clustering é adequado para dados com estruturas não lineares, sendo considerado universal. No entanto, pode ser difícil de configurar os parâmetros e é computacionalmente exigente.
• Agglomerative Clustering cria clusters hierárquicos, sendo adequado para trabalhar com um número desconhecido de clusters.
• GMM (Gaussian Mixture Model) oferece uma abordagem probabilística para o agrupamento, permitindo modelar clusters com diferentes formas e densidades.
• HDBSCAN e BIRCH ambos garantem um desempenho eficiente com grandes volumes de dados e a definição automática do número de clusters, mas também têm suas desvantagens, como complexidade computacional e sensibilidade aos parâmetros.

Implementação de agrupamento de séries temporais (agrupamento de volatilidade)

Estamos interessados na possibilidade de clusterizar séries temporais financeiras, tanto do ponto de vista da definição de regimes de mercado quanto do ponto de vista de correspondência e identificação do efeito de tratamento heterogêneo. Começamos com a tentativa de clusterizar regimes de mercado.

O código a seguir realiza o treinamento de um modelo de meta-aprendizado e o subsequente treinamento do modelo final e da meta-modelo com base nos resultados do agrupamento, que é baseada na volatilidade dos dados financeiros:

def meta_learner(models_number: int, 
                 iterations: int, 
                 depth: int, 
                 bad_samples_fraction: float, 
                 n_clusters: int, 
                 algorithm: int) -> pd.DataFrame:
    
    dataset = get_labels(get_prices())
    data = dataset[(dataset.index < FORWARD) & (dataset.index > BACKWARD)].copy()
    X = data[data.columns[1:-2]]
    X = X.loc[:, ~X.columns.str.contains('std')]
    meta_X = data.loc[:, data.columns.str.contains('std')]
    y = data['labels']

    B_S_B = pd.DatetimeIndex([])
    for i in range(models_number):
        X_train, X_val, y_train, y_val = train_test_split(
            X, y, train_size = 0.5, test_size = 0.5, shuffle = True)
        
        # learn debias model with train and validation subsets
        meta_m = CatBoostClassifier(iterations = iterations,
                                depth = depth,
                                custom_loss = ['Accuracy'],
                                eval_metric = 'Accuracy',
                                verbose = False,
                                use_best_model = True)
        
        meta_m.fit(X_train, y_train, eval_set = (X_val, y_val), plot = False)
        
        coreset = X.copy()
        coreset['labels'] = y
        coreset['labels_pred'] = meta_m.predict_proba(X)[:, 1]
        coreset['labels_pred'] = coreset['labels_pred'].apply(lambda x: 0 if x < 0.5 else 1)
        
        # add bad samples of this iteration (bad labels indices)
        diff_negatives = coreset['labels'] != coreset['labels_pred']
        B_S_B = B_S_B.append(diff_negatives[diff_negatives == True].index)

    to_mark = B_S_B.value_counts()
    marked_idx = to_mark[to_mark > to_mark.mean() * bad_samples_fraction].index
    data.loc[data.index.isin(marked_idx), 'meta_labels'] = 0.0


    if algorithm==0:
        data['clusters'] = KMeans(n_clusters=n_clusters).fit(meta_X).labels_
    elif algorithm==1:
        data['clusters'] = AffinityPropagation().fit(meta_X).predict(meta_X)
    elif algorithm==2:
        data['clusters'] = SpectralClustering(n_clusters=n_clusters, assign_labels='discretize', random_state=0).fit_predict(meta_X)
    elif algorithm==3:
        data['clusters'] = MeanShift().fit_predict(meta_X)
    elif algorithm==4:
        data['clusters'] = AgglomerativeClustering(n_clusters=n_clusters).fit_predict(meta_X)
    elif algorithm==5:
        data['clusters'] = mixture.GaussianMixture(n_components=n_clusters, covariance_type='full').fit(meta_X).predict(meta_X)
    elif algorithm==6:
        data['clusters'] = HDBSCAN(min_cluster_size=150).fit_predict(meta_X)
    elif algorithm==7:
        data['clusters'] = Birch(threshold=0.01, n_clusters=n_clusters).fit_predict(meta_X)
    return data[data.columns[1:]]

Descrição da função:

A função `meta_learner` é projetada para o meta-aprendizado de um modelo de classificação visando identificar e corrigir amostras rotuladas incorretamente no conjunto de dados. Ela usa um ensemble de modelos `CatBoostClassifier` para identificar tais amostras e aplica algoritmos de agrupamento para o processamento posterior dos dados. Aqui está uma descrição mais detalhada do processo:

1. Preparação dos dados: a função começa obtendo um conjunto de dados, filtrado por carimbos de tempo (excluindo dados de certos períodos). Em seguida, os dados são divididos em características (`X`), meta-características (`meta_X`), baseadas em desvios padrão, e rótulos-alvo (`y`).

2. Inicialização de variáveis: é criado um índice de data vazio `B_S_B` para armazenar os índices de amostras rotuladas incorretamente.

3. Treinamento de modelos e identificação de rótulos incorretos: para cada um dos `models_number` modelos, os dados são divididos em conjuntos de treinamento e validação. Em seguida, é treinado o modelo `CatBoostClassifier` com os parâmetros definidos. Após o treinamento, o modelo é utilizado para prever os rótulos em todo o conjunto de características `X`. Comparando os rótulos previstos com os rótulos originais, a função identifica as amostras rotuladas incorretamente e adiciona seus índices ao `B_S_B`.

4. Marcação de amostras incorretas: após o treinamento de todos os modelos, a função analisa os índices das amostras rotuladas incorretamente, armazenados em `B_S_B`, e marca aquelas que aparecem com mais frequência do que o determinado pela fração `bad_samples_fraction`, rotulando-as nos dados originais como `0.0` na coluna `meta_labels`.

5. Agrupamento: dependendo do valor do parâmetro `algorithm`, a função aplica um dos algoritmos de agrupamento às meta-características (`meta_X`) e adiciona os rótulos dos clusters obtidos aos dados originais.

6. Retorno do resultado: a função retorna o conjunto de dados atualizado com os rótulos e clusters atribuídos.

Essa abordagem permite não apenas identificar e corrigir erros nos rótulos dos dados, mas também agrupar os dados para análises futuras ou para o treinamento de modelos, o que pode ser especialmente útil em tarefas onde há uma quantidade significativa de amostras rotuladas incorretamente.

A função de treinamento dos modelos finais é a seguinte:

def fit_final_models(dataset) -> list:
    # features for model\meta models. We learn main model only on filtered labels 
    X, X_meta = dataset[dataset['meta_labels']==1], dataset[dataset.columns[:-3]]
    X = X[X.columns[:-3]]
    X = X.loc[:, ~X.columns.str.contains('std')]
    X_meta = X_meta.loc[:, X_meta.columns.str.contains('std')]
    
    # labels for model\meta models
    y, y_meta = dataset[dataset['meta_labels']==1], dataset[dataset.columns[-1]]
    y = y[y.columns[-3]]
    
    y = y.astype('int16')
    y_meta = y_meta.astype('int16')

    # train\test split
    train_X, test_X, train_y, test_y = train_test_split(
        X, y, train_size=0.8, test_size=0.2, shuffle=True)
    
    train_X_m, test_X_m, train_y_m, test_y_m = train_test_split(
        X_meta, y_meta, train_size=0.8, test_size=0.2, shuffle=True)

    # learn main model with train and validation subsets
    model = CatBoostClassifier(iterations=200,
                               custom_loss=['Accuracy'],
                               eval_metric='Accuracy',
                               verbose=False,
                               use_best_model=True,
                               task_type='CPU')
    model.fit(train_X, train_y, eval_set=(test_X, test_y),
              early_stopping_rounds=25, plot=False)
    
    # learn meta model with train and validation subsets
    meta_model = CatBoostClassifier(iterations=100,
                                    custom_loss=['F1'],
                                    eval_metric='F1',
                                    verbose=False,
                                    use_best_model=True,
                                    task_type='CPU')
    meta_model.fit(train_X_m, train_y_m, eval_set=(test_X_m, test_y_m),
              early_stopping_rounds=15, plot=False)
    
    R2 = test_model([model, meta_model])
    if math.isnan(R2):
        R2 = -1.0
        print('R2 is fixed to -1.0')
    print('R2: ' + str(R2))
    return [R2, model, meta_model]

A função `fit_final_models` é projetada para treinar o modelo principal e a meta-modelo no conjunto de dados fornecido. Aqui está uma descrição detalhada de seu funcionamento:

1. Preparação dos dados:

• Do conjunto de dados, são selecionadas as linhas onde `meta_labels` é igual a 1 para o treinamento do modelo principal (`X`, `y`).
• Para o treinamento da meta-modelo, são utilizadas todas as linhas do conjunto de dados (`X_meta`, `y_meta`).
• Das características para o treinamento do modelo principal, são excluídas as colunas que contêm 'std' no nome, bem como as três últimas colunas.
• Para a meta-modelo, são utilizadas apenas as características que contêm 'std' no nome.
• A variável alvo (`y`) para o modelo principal é retirada da terceira coluna a partir do final e convertida para o tipo `int16`.
• A variável alvo para a meta-modelo (`y_meta`) é retirada da última coluna e também convertida para o tipo `int16`.

2.  Divisão dos dados em conjuntos de treino e teste:

• Para o modelo principal e a meta-modelo, os dados são divididos em conjuntos de treino e teste na proporção de 80% para treino e 20% para teste.

3. Treinamento do modelo principal:

• Utiliza-se o classificador `CatBoostClassifier` com 200 iterações, função de perda 'Accuracy', métrica de avaliação 'Accuracy', sem exibição de informações sobre o progresso do treinamento, com seleção do melhor modelo e definição do tipo de tarefa como 'CPU'.
• O modelo é treinado no conjunto de treino com parada antecipada após 25 rodadas, caso a métrica não melhore.

4. Treinamento da meta-modelo:

• Similar ao modelo principal, mas com 100 iterações, função de perda 'F1', métrica de avaliação 'F1' e parada antecipada após 15 rodadas.

5. Teste dos modelos:

• É realizado o teste dos modelos treinados utilizando a função `test_model`, que retorna o valor da métrica R2.
• Se o valor de R2 for `NaN`, ele é substituído por -1.0, e uma mensagem correspondente é exibida.

6. Valores retornados:

• A função retorna uma lista contendo o valor de R2, o modelo principal e a meta-modelo.

Essa função é parte de um processo de aprendizado de máquina, onde o modelo principal é treinado em dados filtrados (onde se presume que os rótulos foram verificados ou corrigidos), e a meta-modelo é treinada para prever o cluster de volatilidade selecionado.

O treinamento de todo o algoritmo ocorre em um ciclo:

Essa função treina o modelo e a meta-modelo com base no conjunto de dados de entrada. Ela retorna uma lista contendo o valor de R2, o modelo principal e a meta-modelo.

# LEARNING LOOP
models = []
for i in range(1):
    data = meta_learner(5, 25, 2, 0.9, n_clusters=N_CLUSTERS, algorithm=6)
    for clust in data['clusters'].unique():
        print(f'Iteration: {i}, Cluster: {clust}')
        filtered_data = data.copy()
        filtered_data['clusters'] = filtered_data['clusters'].apply(lambda x: 1 if x == clust else 0)
        models.append(fit_final_models(filtered_data))

Este código representa um ciclo de treinamento, no qual a função `meta_learner` é usada para o meta-aprendizado do modelo e o subsequente treinamento dos modelos finais com base nos clusters obtidos. Aqui está uma descrição mais detalhada do processo:

1. Inicialização da lista de modelos: é criada uma lista vazia `models`, que será usada para armazenar os modelos finais treinados.

2. Início do ciclo de treinamento: o loop `for` é configurado para uma iteração (`range(1)`), o que significa que todo o processo será executado uma vez. Isso é feito para demonstração ou teste, pois normalmente em tais ciclos, um número maior de iterações é utilizado devido à aleatoriedade dos algoritmos de treinamento.

3. Meta-aprendizado com a função `meta_learner`: A função `meta_learner` é chamada com os seguintes parâmetros:

• `models_number=5`: são usados 5 modelos básicos para o meta-aprendizado.
• `iterations=25`: cada modelo básico é treinado com 25 iterações.
• `depth=2`: a profundidade da árvore do classificador para os modelos básicos é definida como 2.
• `bad_samples_fraction=0.9`: a fração de amostras rotuladas incorretamente, que serão marcadas, é de 90%.
• `n_clusters=N_CLUSTERS`: o número de clusters para o algoritmo de agrupamento, onde `N_CLUSTERS` deve ser definido previamente.
• `algorithm=6`: o algoritmo de agrupamento HDBSCAN é utilizado.

A função `meta_learner` retorna o conjunto de dados atualizado com rótulos e clusters atribuídos.

4. Iteração sobre clusters únicos: para cada cluster único no conjunto de dados, é exibida uma mensagem com o número da iteração e o cluster. Em seguida, os dados são filtrados de modo que todos os registros pertencentes ao cluster atual sejam rotulados como `1`, enquanto todos os outros são rotulados como `0`. Isso cria uma classificação binária para cada cluster.

5. Treinamento dos modelos finais: para cada cluster, é chamada a função `fit_final_models`, que treina e retorna um modelo com base nos dados filtrados. Os modelos treinados são adicionados à lista `models`.

Esse enfoque permite treinar uma série de modelos especializados, cada um focado em um cluster específico de dados, o que pode melhorar o desempenho geral da modelagem ao considerar de forma mais precisa as características de diferentes grupos de dados.

Foram analisados todos os algoritmos de agrupamento propostos para a definição de regimes de mercado. Alguns algoritmos apresentaram um bom desempenho, enquanto o desempenho dos outros foi insatisfatório.

Abaixo são apresentados os resultados do treinamento com o uso de diferentes algoritmos de agrupamento:

Primeiramente, me interessei pela velocidade de agrupamento. Foi observado que os algoritmos Affinity Propagation, Spectral Clustering, Agglomerative Clustering e Mean Shift foram muito lentos, por isso todos eles estão no final do ranking. Não consegui aguardar os resultados do agrupamento ao usar as configurações padrão, por isso os resultados desses algoritmos não foram apresentados.

Encontrei confirmação na internet:

Executei 10 repetições de todo o processo de treinamento para obter resultados mais informativos, pois os resultados variam de um treinamento para outro devido à aleatoriedade dentro dos algoritmos.

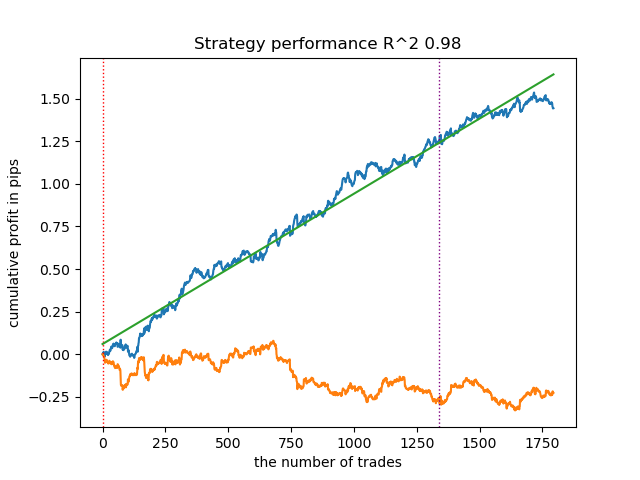
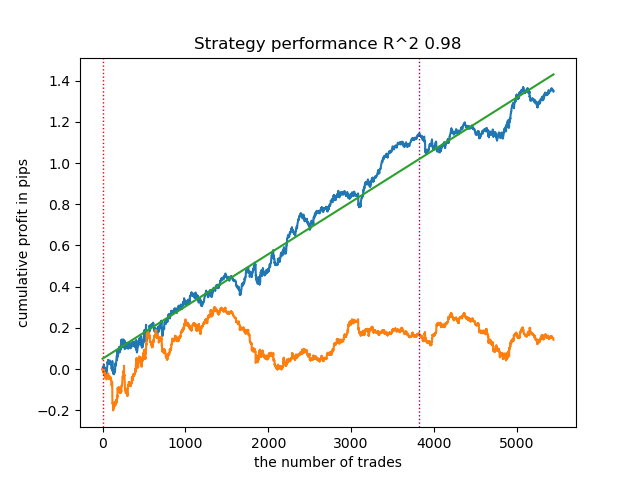
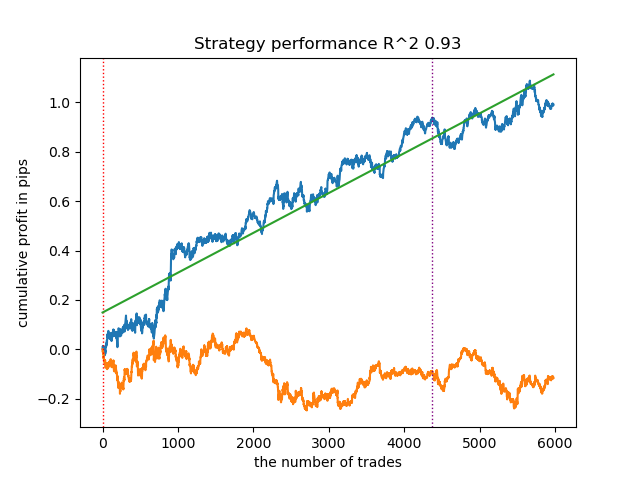
• A linha azul mostra o gráfico do saldo,
• A linha laranja representa o gráfico do instrumento financeiro (neste caso, EURUSD).

1. HDBSCAN: decidi colocá-lo no topo do ranking dos quatro algoritmos restantes. Ele divide os dados de maneira eficaz e não requer a definição do número de clusters.

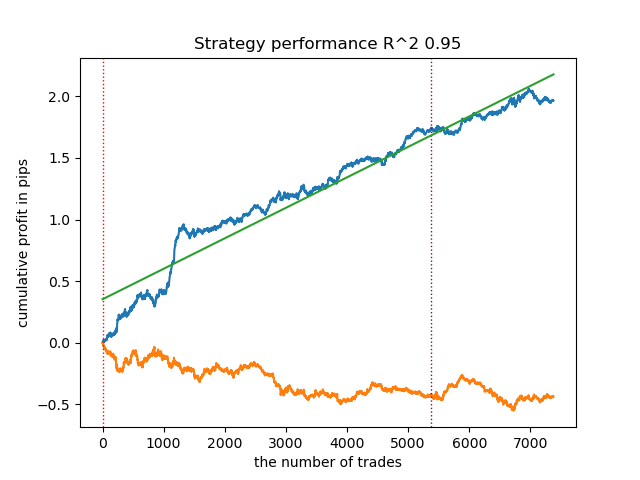
2. K-means: apresenta bom desempenho e resultados de teste razoavelmente bons. A desvantagem é a sensibilidade ao número de clusters; neste caso, foram definidos dez.

3. BIRCH: demonstra resultados satisfatórios, mas processa um pouco mais lentamente do que os algoritmos anteriores. Aqui também não é necessário definir o número de clusters inicialmente.

4. Gaussian Mixture: finaliza este ranking. Os resultados dos testes pareceram-me inferiores aos dos outros algoritmos de agrupamento. Visualmente, isso se reflete em um gráfico de saldo mais "ruidoso". Como o K-means, foram definidos 10 clusters.

Assim, é possível obter diferentes sistemas de negociação, dependendo do regime de mercado escolhido. Durante o processo de treinamento, são exibidos os resultados dos testes dos modelos para cada um dos regimes, com base no número de clusters definido.

Como a qualidade do agrupamento é influenciada pelo conjunto de parâmetros de entrada, eles devem ser listados:

• Par de moedas
• Timeframe
• Datas de início e término do treinamento
• Número de características para o modelo principal
• Número de características para a meta-modelo (volatilidade)
• Número de clusters n_clusters
• Parâmetros min e max da função get_labels(min, max)

Por exemplo, aqui está outro resultado do agrupamento com os parâmetros listados abaixo:

SYMBOL = 'EURUSD'
MARKUP = 0.00010
PERIODS = [i for i in range(10, 100, 10)]
PERIODS_META = [20]
BACKWARD = datetime(2019, 1, 1)
FORWARD = datetime(2023, 1, 1)
n_clusters = 40

def get_labels(dataset, min = 5, max = 5)

Timeframe = H1

Como o algoritmo de busca de clusters também é randomizado, é uma boa prática realizar várias reinicializações.

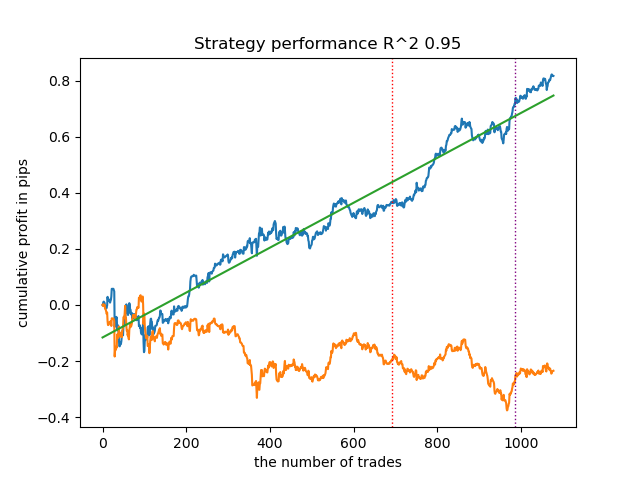
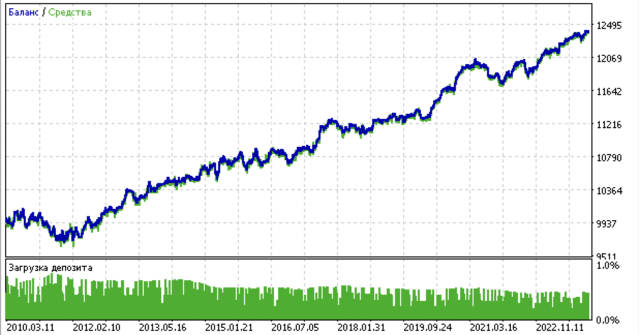
Encontrando correspondências de negociações por meio de agrupamento

Chegamos à parte final do nosso artigo, que é o objetivo principal deste texto. Vamos explorar a inferência causal com um foco especial no elemento de agrupamento. Assim, neste artigo você aprenderá o que é inferência causal, e neste artigo aprenderá sobre encontrar correspondências por meio do *propensity score* (pontuação de propensão). Agora, ao invés de usar a correspondência baseada na pontuação de propensão, vamos adotar a nossa abordagem exclusiva: a correspondência por meio de agrupamento. Para isso, pegaremos o algoritmo do primeiro artigo e o modificaremos.

def meta_learners(models_number: int, iterations: int, depth: int, bad_samples_fraction: float, n_clusters: int):
    dataset = get_labels(get_prices())
    data = dataset[(dataset.index < FORWARD) & (dataset.index > BACKWARD)].copy()

    X = data[data.columns[1:-2]]
    y = data['labels']
    clusters = KMeans(n_clusters=n_clusters).fit(X[X.columns[0:1]]).labels_

    BAD_CLUSTERS = []
    for _ in range(n_clusters):
        sublist =  [pd.DatetimeIndex([]), pd.DatetimeIndex([])]
        BAD_CLUSTERS.append(sublist)

    for i in range(models_number):
        X_train, X_val, y_train, y_val = train_test_split(
            X, y, train_size = 0.5, test_size = 0.5, shuffle = True)
        
        # learn debias model with train and validation subsets
        meta_m = CatBoostClassifier(iterations = iterations,
                                depth = depth,
                                custom_loss = ['Accuracy'],
                                eval_metric = 'Accuracy',
                                verbose = False,
                                use_best_model = True)
        
        meta_m.fit(X_train, y_train, eval_set = (X_val, y_val), plot = False)
        
        coreset = X.copy()
        coreset['labels'] = y
        coreset['labels_pred'] = meta_m.predict_proba(X)[:, 1]
        coreset['labels_pred'] = coreset['labels_pred'].apply(lambda x: 0 if x < 0.5 else 1)
        coreset['clusters'] = clusters
        
        # add bad samples of this iteration (bad labels indices)
        coreset_b = coreset[coreset['labels']==0]
        coreset_s = coreset[coreset['labels']==1]

        for clust in range(n_clusters):
            diff_negatives_b = (coreset_b['labels'] != coreset_b['labels_pred']) & (coreset['clusters'] == clust)
            diff_negatives_s = (coreset_s['labels'] != coreset_s['labels_pred']) & (coreset['clusters'] == clust)
            BAD_CLUSTERS[clust][0] = BAD_CLUSTERS[clust][0].append(diff_negatives_b[diff_negatives_b == True].index)
            BAD_CLUSTERS[clust][1] = BAD_CLUSTERS[clust][
        1].append(diff_negatives_s[diff_negatives_s == True].index)

    for clust in range(n_clusters):
        to_mark_b = BAD_CLUSTERS[clust][0].value_counts()
        to_mark_s = BAD_CLUSTERS[clust][1].value_counts()
        marked_idx_b = to_mark_b[to_mark_b > to_mark_b.mean() * bad_samples_fraction].index
        marked_idx_s = to_mark_s[to_mark_s > to_mark_s.mean() * bad_samples_fraction].index
        data.loc[data.index.isin(marked_idx_b), 'meta_labels'] = 0.0
        data.loc[data.index.isin(marked_idx_s), 'meta_labels'] = 0.0

    return data[data.columns[1:]]

Para aqueles que não leram meus artigos anteriores, farei uma breve descrição do algoritmo:

• Processamento de dados:
• O início da função pressupõe o uso das funções get_prices() e get_labels() para obter o conjunto de dados. Essas funções retornam as informações de preços e os rótulos das classes, respectivamente.
• get_labels() associa os dados de preços com rótulos, o que é uma tarefa comum no aprendizado de máquina aplicado a dados financeiros.
• Os dados são então filtrados por intervalos de tempo, definidos pelas constantes FORWARD e BACKWARD.
• Preparação dos dados:
• Os dados são divididos em características (X) e rótulos (y).
• Aplica-se o algoritmo de agrupamento KMeans para criar clusters nos dados.
• Treinamento de modelos:
• No ciclo for, define-se o número de modelos models_number. Em cada iteração, o modelo é treinado em metade dos dados (train_size = 0.5) e avaliado na outra metade (conjunto de validação).
• Utiliza-se o modelo CatBoostClassifier com parâmetros definidos. Este é um método de gradient boosting, especialmente projetado para trabalhar com características categóricas.
• É importante notar que este algoritmo utiliza uma função de perda customizada 'Accuracy' e a métrica de avaliação 'Accuracy'. Isso indica que o foco principal é a precisão da previsão.
• Em seguida, aplica-se uma meta-modelo para avaliar e corrigir as previsões dos modelos primários. Isso permite considerar possíveis vieses ou erros dos modelos primários.
• Identificação de amostras ruins:
• São criadas listas BAD_CLUSTERS, que contêm informações sobre as amostras ruins em cada cluster. Amostras ruins são aquelas para as quais o modelo comete uma quantidade significativa de erros.
• Para cada iteração de treinamento, as amostras ruins são identificadas, e seus índices são armazenados na lista correspondente.
• Meta-análise e correção:
• Os índices das amostras ruins, identificadas na etapa anterior, são agregados e então usados para marcar as amostras correspondentes nos dados principais.
• Presume-se que isso ajude a melhorar a qualidade do treinamento dos modelos, excluindo ou corrigindo as amostras ruins.
• Retorno dos dados:
• A função retorna os dados preparados sem a primeira coluna, que contém os carimbos de tempo.

Este algoritmo visa melhorar a qualidade dos modelos de aprendizado de máquina, detectando e corrigindo amostras ruins, além de utilizar uma meta-modelo para considerar erros dos modelos primários. Ele é complexo e requer ajuste cuidadoso dos parâmetros para funcionar de maneira eficaz.

No código apresentado, o agrupamento ajuda a considerar a heterogeneidade dos dados de várias maneiras:

• Identificação de clusters de dados:
• A aplicação do algoritmo de agrupamento KMeans permite dividir os dados em grupos de objetos semelhantes. Cada cluster contém dados com características parecidas. Isso é especialmente útil em casos de dados heterogêneos, onde os objetos podem pertencer a diferentes categorias ou ter diferentes estruturas.
• Análise e processamento de clusters separadamente:
• Cada cluster é processado separadamente dos outros, o que permite considerar as características e a estrutura dos dados dentro de cada grupo. Isso ajuda a entender melhor a heterogeneidade dos dados e a adaptar os algoritmos de aprendizado às condições específicas de cada cluster.
• Correção de erros dentro dos clusters:
• Após o treinamento dos modelos no ciclo, para cada cluster ocorre a análise das amostras ruins, ou seja, aquelas para as quais o modelo comete uma quantidade significativa de erros. Isso permite localizar e focar na correção de erros dentro de cada cluster separadamente, o que pode ser mais eficaz do que aplicar as mesmas correções a todos os dados em geral.
• Consideração das características dos dados no treinamento da meta-modelo:
• O agrupamento também é utilizado para considerar as diferenças entre os clusters durante o treinamento da meta-modelo. Isso permite que a meta-modelo se adapte melhor à heterogeneidade dos dados, incorporando informações sobre a estrutura dos dados dentro de cada cluster.

Assim, o agrupamento desempenha um papel fundamental na consideração da heterogeneidade dos dados, permitindo que o algoritmo se adapte de maneira mais eficaz à diversidade de objetos e estruturas de dados.

O resultado do treinamento desse modelo é apresentado abaixo. Observa-se que o modelo tornou-se mais robusto em novos dados.

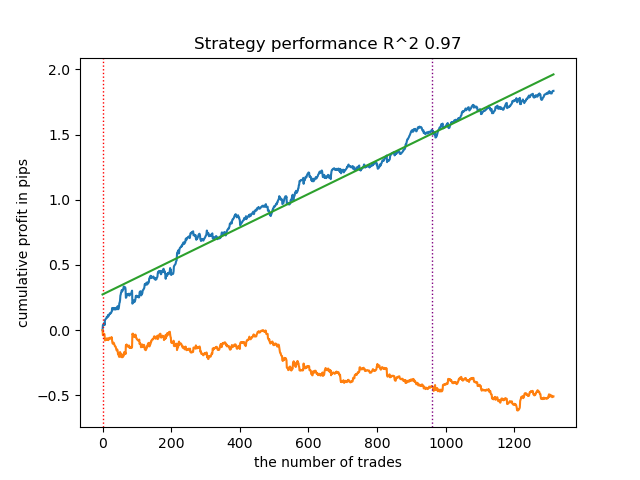
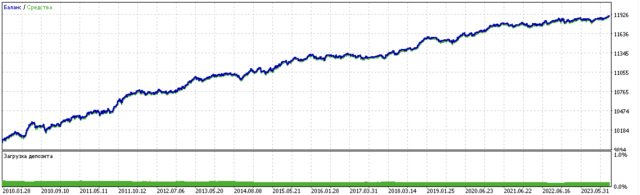
Este modelo é exportado no formato ONNX e é totalmente compatível com o EA ONNX Trader.

Considerações finais

Neste artigo, foi apresentada uma abordagem autoral para o agrupamento de séries temporais. Realizei testes com diversos algoritmos de agrupamento de regimes de mercado baseados na volatilidade. Descobri que algoritmos complexos nem sempre correspondem às expectativas: às vezes, algoritmos de agrupamento simples e rápidos, como o K-means, realizam a tarefa de forma mais eficaz. Por outro lado, gostei muito do algoritmo HDBSCAN.

Na segunda parte, o agrupamento foi utilizado para identificar o efeito de tratamento heterogêneo. Os experimentos mostraram que considerar operações ruins com o uso de agrupamento reduz a dispersão dos valores (a curva de saldo torna-se mais suave) e melhora a previsão do modelo em novos dados. Em geral, este é um tema bastante complexo e profundo, que requer a seleção cuidadosa de hiperparâmetros para o ajuste fino do algoritmo.