MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 51): Verstärkungslernen mit SAC

Einführung

Soft Actor Critic (SAC) ist ein weiterer Verstärkungslernalgorithmus, den wir in Betracht ziehen, nachdem wir bereits einige Algorithmen wie Proximal Policy Optimization, Deep-Q-Netze, SARSA und andere untersucht haben. Dieser Algorithmus verwendet jedoch, wie einige andere, die wir bereits untersucht haben, neuronale Netze, allerdings mit einigen wichtigen Einschränkungen. Insgesamt werden drei Netze verwendet, und zwar folgende: 2 Kritikernetze und ein Akteursnetz. Die beiden Netzwerte der Kritiker (Critic) machen Belohnungsvorhersagen (Q-Werte), wenn ihnen eine Aktion und ein Umgebungszustand eingegeben werden, und das Minimum der Ausgaben dieser beiden Netze wird zur Modulation der Verlustfunktion verwendet, die für das Training des Netzes des Akteurs (Actor) verwendet wird.

Die Eingaben für das Akteursnetz sind die Koordinaten des Umgebungszustands, die Ausgaben sind 2-fach. Einen Mittelwertvektor und einen Vektor der logarithmischen Standardabweichung. Mit Hilfe der Dichtefunktion wird aus diesen beiden Vektoren eine Wahrscheinlichkeitsverteilung für die möglichen Handlungen abgeleitet, die dem Akteur offen stehen. Während die beiden Kritikernetze auf herkömmliche Weise trainiert werden können, ist das Akteursnetz eine ganz andere Sache. Es gibt hier eine ganze Menge zu erklären, also lassen Sie uns zunächst die Grundlagen wiederholen, bevor wir weitermachen. Die beiden Kritikernetze für die Eingabe nehmen den aktuellen Zustand der Umgebung und eine Aktion. Ihr Ergebnis ist eine Schätzung des erwarteten Ertrags (Q-Wert) für die Durchführung dieser Aktion in diesem Zustand. Die Verwendung von zwei Kritikern trägt dazu bei, die Überschätzung zu reduzieren, ein häufiges Problem beim Q-Learning.

Das Akteursnetz hat den aktuellen Zustand der Umgebung als Input. Das Ergebnis ist eine Wahrscheinlichkeitsverteilung über mögliche Aktionen, wobei diese Verteilung stochastisch ist, um die Erkundung zu fördern. Ich verwende den Ausdruck „effektiv“, weil die tatsächlichen Ausgaben des Akteursnetzes zwei Vektoren sind, die mit einer Gaußschen Wahrscheinlichkeitsverteilung gefüttert werden müssen, um die Gewichte der einzelnen Aktionen zu erhalten. In MQL5 erreichen wir dies wie folgt:

//+------------------------------------------------------------------+
// Function to compute the Gaussian probability distribution and log
// probabilities
//+------------------------------------------------------------------+
vectorf CSignalSAC::LogProbabilities(vectorf &Mean, vectorf &Log_STD)
{  vectorf _log_probs;
   // Compute standard deviations from log_std
   vectorf _std = exp(Log_STD);
   // Sample actions and compute log probabilities
   float _z = float(rand() % USHORT_MAX / USHORT_MAX); // Generate N(0, 1) sample
   // Sample action using reparameterization trick: action = mean + std * N(0, 1)
   vectorf _actions = Mean + (_std * _z);
   // Compute log probability of the sampled action
   vectorf _variance = _std * _std;
   vectorf _diff = _actions - Mean;
   _log_probs = -0.5f * (log(2.0f * M_PI * _variance) + (_diff * _diff) / _variance);
   return(_log_probs);
}

Wie SAC funktioniert

SAC funktioniert wie die meisten Algorithmen des verstärkten Lernens. Zunächst erfolgt eine Aktionsauswahl, bei der der Akteur eine Aktion aus der Wahrscheinlichkeitsverteilung der Ausgaben des Akteursnetzwerks auswählt. Darauf folgt die „Umweltinteraktion“, bei der der Agent die gesampelte Aktion in der Umwelt ausführt und seinen nächsten Zustand und seine Belohnung beobachtet. Anschließend erfolgt die Aktualisierung der Kritik, bei der die beiden kritischen Netze durch eine Verlustfunktion aktualisiert werden, die einen Vergleich zwischen den vorhergesagten Q-Werten und den Ziel-Q-Werten verwendet. Wie bereits erwähnt, stellt die Aktualisierung des Akteursnetzwerks jedoch insofern eine Neuheit dar, als sie mit Hilfe eines Policy-Gradienten aktualisiert wird, der darauf abzielt, den erwarteten Ertrag zu maximieren, indem die Entropie der Policy-Verteilung berücksichtigt wird. Dies soll die Erkundung fördern und eine vorzeitige Konvergenz zu suboptimalen Lösungen verhindern.

Die Entropie der Politikverteilung im SAC misst die Zufälligkeit oder Unsicherheit. Im SAC entspricht eine höhere Entropie mehr Erkundungsaktionen, während eine niedrigere Entropie deterministische Entscheidungen betonen soll. Die Ergebnisse für das Akteursnetzwerk in SAC sind von Natur aus eine stochastische Politik, die durch eine Wahrscheinlichkeitsverteilung parametrisiert ist, die in unserem Fall (für diesen Artikel) die Dichtefunktion ist. Die Entropie dieser Verteilung zeichnet ein Bild der Aktionen, die ein Agent ausführen könnte, wenn ihm ein bestimmter Zustand (die Eingaben) präsentiert wird.

Damit soll die Erkundung durch die Agenten gefördert werden, wie es bei den meisten Algorithmen des Verstärkungslernens üblich ist, um das Risiko einer vorzeitigen Konvergenz zu suboptimalen Strategien zu verringern. So entsteht ein Gleichgewicht zwischen Erkundung und Nutzung. SAC integriert einen Entropie-Term in sein Optimierungsziel, um sowohl die erwarteten Belohnungen als auch die Entropie zu maximieren. Die Zielgleichung lautet wie folgt:

wobei:

• α: Entropie-Temperatur, Ausgleich zwischen Belohnungsmaximierung und Erkundung.
• logπ(a∣s): Logarithmische Wahrscheinlichkeit der Aktion (die Ausgabe unserer Funktion, deren Code oben geteilt wird), die sowohl von μ als auch von log(σ) abhängt.
• Q(s,a): ist der minimale Q-Wert der beiden Ausgänge der kritischen Netze.

Eine höhere Entropie führt in der Regel zu einer robusteren Entscheidungsfindung in Umgebungen mit unvollständigen Informationen, da sie eine Überanpassung an bestimmte Szenarien verhindert. Die Maximierung der Entropie ist also eine gute Sache im SAC. Neben einer verbesserten Erkundung, da der Agent ermutigt wird, eine größere Bandbreite an Aktionen auszuprobieren, oder der Vermeidung von suboptimalen Strategien, die verhindern, dass er in lokalen Optima stecken bleibt, dient es inhärent als eine Form der Regularisierung, indem es übermäßig deterministische Strategien verhindert, die in unvorhergesehenen Szenarien versagen könnten. Außerdem führen allmähliche Entropieanpassungen oft zu sanfteren Aktualisierungen der Strategien, was eine stabile Ausbildung und Konvergenz gewährleistet.

Der Temperatursteuerungsparameter ist sehr empfindlich gegenüber der Entropie und dem Lernprozess des Akteursnetzes, weshalb es erwähnenswert ist. Für unsere Zwecke legen wir diesen Wert auf 0,5 fest, wie in der Funktion Logarithmuswahrscheinlichkeiten zu sehen ist, deren MQL5-Code oben gemeinsam genutzt wird. Der Temperaturparameter alpha bestimmt jedoch, wie viel Gewicht der Energie im Ziel gegeben wird. Ein höherer Alphawert fördert die Erkundung, während ein niedrigerer Wert deterministische Strategien oder Ausbeutung fördert. Der Wert von 0,5 für unsere Zwecke ist also eine Art Gleichgewicht.

Es ist jedoch häufig der Fall, dass SAC einen automatischen Mechanismus zur Entropie-Abstimmung verwendet, der Alpha dynamisch anpasst, um ein Ziel-Entropieniveau aufrechtzuerhalten und ein Gleichgewicht zwischen Exploration und Ausbeutung herzustellen. In der Praxis bedeutet dies: robustes Lernen über verschiedene Aufgaben hinweg; Schaffung von Generalisierungsstrategien, die mit unvollständigen Informationen umgehen können (stochastische Strategien); und die Schaffung einer Grundlage für kontinuierliches Lernen. Dies birgt vor allem zwei potenzielle Nachteile. Zu viel Erkundung und Rechenaufwand.

Eine übermäßige Entropie kann zu ineffizientem Lernen führen, da der Schwerpunkt auf explorativen Aktionen liegt und bekannte Strategien mit hohen Gewinnen nicht genutzt werden. Dies ist immer mit der Berechnung und Optimierung von Entropie-Termen verbunden, die im Vergleich zu Algorithmen, die sich nur auf die Maximierung der Belohnung konzentrieren, einen zusätzlichen Rechenaufwand bedeuten. Das Akteursnetzwerk gibt, wie oben erwähnt, zwei Vektoren MU und Log-STD aus, wie wirken sich diese auf die Entropie aus?

MU stellt die zentrale Tendenz der Aktionsverteilung der Politik dar. Sie wirkt sich nicht direkt auf die Entropie aus, definiert aber in gewisser Weise das mittlere Verhalten der Politik. Die Log-STD hingegen steuert die Streuung oder Unsicherheit der Aktionsverteilung und beeinflusst direkt die Entropie. Ein höherer Log-STD-Wert bedeutet eine breitere, unsicherere Handlungsverteilung, während ein niedrigerer Log-STD-Wert auf das Gegenteil hindeutet. Was hat dann die Größe einer bestimmten Aktion in der Log-STD mit der Wahrscheinlichkeit der Auswahl zu tun?

Die Besonderheiten werden, wie bereits erwähnt, durch den Gauß-Prozess bestimmt. Ein niedriger Log-STD bedeutet jedoch oft, dass das Akteursnetzwerk von der optimalen Aktion überzeugt ist, MU. Dies impliziert häufig eine geringere Variabilität der beprobten Maßnahmen. Die in die Stichprobe einbezogenen Aktionen werden sich stärker auf den entsprechenden MU-Wert dieser Aktion konzentrieren, der einen niedrigen Log-STD-Wert aufweist, was eine stärkere Nutzung von Maßnahmen im Umfeld dieser Aktion fördern würde. Niedrige Log-STD-Werte machen eine Aktion zwar nicht direkt wahrscheinlicher, aber sie schränken die Bandbreite möglicher Aktionen ein und erhöhen so die Wahrscheinlichkeit, dass Aktionen gewählt werden, die nahe an MU liegen.

Es gibt auch einige praktische Anpassungen, die häufig auf die Entropie angewandt werden. Erstens: Da Log-STD direkt die Entropie bestimmt, begrenzt SAC bei stabilem Training log(σ) in der Regel innerhalb eines Bereichs, um eine extrem hohe oder niedrige Entropie zu vermeiden. Dies geschieht mit dem Parameter 'z', der in unserer obigen Funktion Log Probabilities gezeigt wird. Zweitens ist die Einstellung von Alpha (das wir in unserer Funktion Log Probabilities auf 0,5f gesetzt haben) von entscheidender Bedeutung, um das erwähnte Gleichgewicht zwischen Erkunden und Ausnutzen zu erreichen. Zu diesem Zweck wird häufig die automatische Alpha-Anpassung als Mittel zur dynamischen Herstellung eines Gleichgewichts zwischen Ausbeutung und Erkundung eingesetzt.

Dies wird durch die Verwendung eines Entropieziels H erreicht. Die folgende Gleichung definiert dies:

wobei:

• alpha (α t ): Ist die aktuelle Temperatur, die das Gewicht des Entropie-Terms im Ziel steuert, wobei höhere Werte die Erkundung fördern, während kleinere Werte zur Nutzung tendieren.

• alpha (αt+1 ): Ist der aktualisierte Temperaturparameter, nachdem die Rückmeldung der aktuellen Entropie im Verhältnis zum Zielwert berücksichtigt wurde.

• lambda (λ): Ist eine Lernrate für den Alpha-Anpassungsprozess, die steuert, wie schnell sich Alpha an Abweichungen vom Entropieziel H anpasst.

• E (E a~π ): Ist die Erwartung, die sich aus den Maßnahmen ergibt, die im Rahmen des aktuellen Strategieplans ausgewählt wurden.

• Log(a|s): Ist die logarithmische Wahrscheinlichkeit für die Aktion-a im Zustand-s bei der aktuellen Politik. Sie quantifiziert die Unsicherheit bei der Auswahl der Maßnahmen.

• H target : Dient als Zielwert für die Entropie der Richtlinie. Sie wird häufig auf der Grundlage der Dimensionalität des Aktionsraums (Anzahl und Umfang der verfügbaren Aktionen) zugewiesen, wenn die Aktionen diskret sind, wie z. B. bei den bisher betrachteten Implementierungen (Kaufen, Verkaufen, Halten); sie kann auch skaliert werden, wenn die Aktionen kontinuierlich sind (z. B. wenn wir zwei dimensionierte Marktaufträge haben, die beide von 0,01 bis 0,10 skaliert sind, um die Positionsgröße von zwei gleichzeitig zu kaufenden Wertpapieren zu bestimmen, wobei die Werte ein Prozentsatz der freien Marge sind).

Die Verwendung einer automatischen Alpha-Anpassung, auch wenn sie in unserer Implementierung für diesen Artikel nicht untersucht wurde, stellt sicher, dass sich der Agent dynamisch an Veränderungen in der Umgebung anpasst, macht eine manuelle Alpha-Einstellung überflüssig und fördert effizientes Lernen durch die Beibehaltung eines voreingestellten Kompromisses zwischen Erkundung und Ausbeutung.

Vergleich zwischen SAC und DQN

Wir haben bisher einen anderen Algorithmus des verstärkenden Lernens betrachtet, der ein einziges neuronales Netz verwendet, nämlich das Deep-Q-Networks (DQN). Welche Vorteile, wenn überhaupt, zeichnen sich also für die Verwendung von SAC mit seinen mehreren Netzen ab? Um die Vorteile von SAC zu verdeutlichen, betrachten wir ein Anwendungsszenario für eine Robotermanipulationsaufgabe. Hier also die Aufgabe: Ein Roboterarm soll Objekte halten und zu bestimmten Zielorten bewegen. Den Gelenken seiner Arme würden kontinuierliche Aktionsräume zugewiesen, die die erforderlichen Drehmoment- und Winkeleinstellungen usw. quantifizieren.

Die Herausforderung bei der Verwendung eines DQN in diesem Fall besteht darin, dass sich das DQN am besten für diskrete Aktionsräume eignet. Der Versuch, es auf einen kontinuierlichen Raum auszudehnen, würde zu einem exponentiellen Wachstum der Anzahl verfügbarer diskreter Aktionen für höherdimensionale Aktionsräume führen, was das Training zu teuer und ineffizient macht. DQNs verlassen sich auch auf Epsilon-Greedy-Strategien, um ein Gleichgewicht zwischen Erkundung und Ausbeutung herzustellen, und diese können in den diskretisierten Räumen höherer Dimensionen nur schwer effizient arbeiten. Schließlich ist DQN anfällig für Überschätzungsfehler, was zu einer gewissen Instabilität beim Training führen könnte, insbesondere in komplexen Umgebungen mit hoher Variabilität der Belohnung.

SAC wäre in diesem Fall besser geeignet, vor allem wegen seiner kontinuierlichen Aktionsraumunterstützung. Dies zeigt sich in der Art und Weise, wie SAC die stochastische Politik über kontinuierliche Handlungsräume optimiert, wodurch die Notwendigkeit einer Handlungsdiskretisierung (oder Klassifizierung) entfällt. Dies führt zu einer reibungslosen und präzisen Steuerung des Roboterarms. Die drei Netze im SAC arbeiten synergetisch zusammen, wobei das Akteursnetz eine stochastische Politik zur Festlegung der Verteilung (probabilistische Gewichtung) der kontinuierlichen Aktionen entwickelt. Dies fördert die Effizienz und vermeidet gleichzeitig eine vorzeitige Erkundung.

Die kritischen Netzwerke ihrerseits verwenden eine Methode zur Schätzung des doppelten Q-Wertes, die dazu beiträgt, den Fehler der Überschätzung zu vermeiden, indem sie den Mindestwert an das Akteursnetzwerk weiterleitet. Dies stabilisiert das Training und sorgt für genauere Ergebnisse. Zusammenfassend lässt sich sagen, dass die entropieerhöhte Zielsetzung, die zu mehr Exploration ermutigt (insbesondere in Verbindung mit der automatischen Temperaturanpassung, wie oben bei alpha argumentiert), sowie die Robustheit und Stabilität, die durch die Fähigkeit von SAC, mit hochdimensionalen Aktionsräumen umzugehen, gewährleistet werden, es eindeutig über das DQN stellen. Zu diesem Zweck zeigen die veröffentlichten Leistungsbeispiele des Gyms von Open AI die Aufgaben von Reacher und Fetch deutlich, dass DQN aufgrund seiner diskretisierten Aktionsausgaben und der schlechten Exploration Schwierigkeiten hat, glatte Armbewegungen zu erzeugen, wobei die Strategien oft zu suboptimalen Strategien konvergieren. Andererseits erzeugt SAC reibungslose, präzise Aktionen mit einer stochastischen Strategie, die zu einer schnelleren Aufgabenerfüllung, weniger Kollisionen und einer besseren Anpassung an sich ändernde Objektpositionen oder Zielorte führt, wiederum dank des stochastischen Strategieansatzes.

Python und TensorFlow

Im Gegensatz zu den vergangenen Artikeln über maschinelles Lernen tauchen wir in diesem Artikel in Pythons TensorFlow ein. MQL5, die Muttersprache von MetaQuotes, bleibt natürlich weiterhin relevant, da die mit dem Assistenten zusammengestellten Expert Advisors auf dieser Sprache basieren. Für neue Leser gibt es hier und hier Anleitungen, wie man den am Ende dieses Artikels beigefügten Code verwendet, um einen Expert Advisor zusammenzustellen. Python ist jedoch dabei, die Bedeutung und Dominanz von MQL5 als bevorzugte Programmiersprache für die Entwicklung von Finanzmodellen zu überholen. Eine schnelle Erkundung könnte darauf hindeuten, dass MetaQuotes einfach mehr Bibliotheken auf Python herausbringen muss, um mit der Innovation Schritt zu halten und seine Dominanz weiter zu behaupten. 

Ich bin jedoch alt genug, um mich an die Einführung von MetaTrader 5 im Jahr 09(?) zu erinnern. Und die mühsam errungene Akzeptanz bei den Kunden, trotz aller Vorteile, die es bot. Ich kann daher nachvollziehen, warum sie zögern, aktive Bibliotheken auf Python auszurollen und zu pflegen. Abgesehen davon kommen die Innovationen, die hier vorgestellt werden, größtenteils von den „Kunden“ (d.h. der Python-Gemeinschaft) und nicht von MetaQuotes, wie es beim MetaTrader 5 der Fall war, wo Positionen im Gegensatz zu Aufträgen eingeführt wurden. Vielleicht müssen sie dies also dringend beachten? Die Zeit wird es zeigen, aber in der Zwischenzeit sind die Effizienzvorteile, die die Verwendung von TensorFlow und sogar PyTorch nicht nur bei der Entwicklung, sondern vor allem beim Training von Netzwerken mit sich bringt, wirklich gigantisch!

Meiner Meinung nach kann MetaQuotes das Sponsoring durch Unternehmen prüfen, einen Beitrag leisten oder sogar Fork-Projekte für die wichtigen Python-Bibliotheken Pandas, NumPy und Sci-Kit erstellen; und unter anderem das Lesen der hochkomprimierten Dateiformate *.*hcc und *.*tkc ermöglichen. Aber das sind allgemeine Gedanken. Um auf TensorFlow zurückzukommen: Es bietet fortgeschrittene Deep-Learning-Fähigkeiten, die in erster Linie zweierlei sind. An der Softwarefront und auf der GPU-/Hardware-Seite.  

MQL5 unterstützt OpenCL, sodass man argumentieren könnte, die beiden Sprachen könnten sich auf Augenhöhe begegnen. Das Gleiche kann man jedoch sicherlich nicht über die fortschrittlichen Bibliotheken und Tools von Python zum Erstellen, Trainieren und Optimieren von Deep-Learning-Modellen sagen. Diese Bibliotheken bieten Unterstützung für komplexe Architekturen wie SAC über TensorFlow Agents.

Es bietet auch ein reichhaltiges Ökosystem mit vorgefertigten Werkzeugen wie z.B. Stable-Baseline für die Förderung von Reinforcement Learning (neben Tensor-Agenten); es ermöglicht Flexibilität und Experimentieren, da man schnell Prototypen erstellen und eine Vielzahl von Modellimplementierungen testen kann; es ist in hohem Maße reproduzierbar und leicht zu debuggen (insbesondere wenn man Werkzeuge wie Tensor-Board für die Visualisierung und das Training von Matrizen/Kernen einsetzt); es bietet Interoperabilität mit exportierbaren Formaten wie ONNX; und es hat eine sehr große und wachsende Community-Unterstützung sowie regelmäßige Updates.

SAC kann in Python auf sehr unterschiedliche Weise implementiert werden. Zur Veranschaulichung der Grundprinzipien wollen wir uns auf zwei Ansätze beschränken. In der ersten werden die drei Hauptnetze des SAC manuell definiert und mit Hilfe von for-Schleifen-Iterationen das SAC-Modell trainiert und getestet. Die zweite verwendet die bereits erwähnten Tensor-Agenten, die in der Python-Bibliothek enthalten sind und speziell für die Unterstützung des Reinforcement Learning gedacht sind.

Die Schritte des manuellen iterativen Ansatzes sind: Entwurf der SAC-Komponenten in TensorFlow/Keras, wobei für das Akteursnetzwerk ein neuronales Netzwerk definiert werden muss, das eine stochastische Politik für Gaussian Sampling ausgibt; für die kritischen Netzwerke bedeutet dies die Konstruktion von 2 Q-Wert-Netzwerken für Twin-Q-Learning, um die Überschätzungsverzerrung zu bewältigen; und die Definition eines n-Entropie-Regularisierungsregimes für effiziente Exploration. Wie bereits erwähnt, verwenden wir für unsere Entropie einen festen Wert von Alpha von 0,5. Die erste Quelle, die diese Themen behandelt, lautet wie folgt:

import numpy as np
import pandas as pd

from sklearn.model_selection import train_test_split

import tensorflow as tf

print("Num GPUs Available: ", len(tf.config.list_physical_devices('GPU')))

from tensorflow.keras import optimizers
from tensorflow.keras.layers import Input
from tensorflow.keras import layers
from tensorflow import keras
import tf2onnx
import onnx

import os

# Define the actor network
def ActorNetwork(state_dim, action_dim, hidden_units=256):
    """
    Creates a simple SAC actor network.
    
    :param state_dim: The dimension of the state space.
    :param action_dim: The dimension of the action space.
    :param hidden_units: The number of hidden units in each layer.
    :return: A Keras model representing the actor network.
    """
    # Input layer
    state_input = layers.Input(shape=(state_dim, ))
    
    # Hidden layers (Dense layers with ReLU activation)
    x = layers.Dense(hidden_units, activation='relu')(state_input)
    x = layers.Dense(hidden_units, activation='relu')(x)
    
    # Output layer: output means (mu) and log standard deviation (log_std) for Gaussian distribution
    
    output_size = action_dim + action_dim
    stacked_mean_logs = layers.Dense(output_size)(x)
    
    # Create the model

    actor_model = tf.keras.Model(inputs=state_input, outputs=stacked_mean_logs)
    
    return actor_model

# Define the critic network
def CriticNetwork(state_dim, action_dim, hidden_units=256):
    """
    Creates a simple SAC critic network (Q-value approximation).
    
    :param state_dim: The dimension of the state space.
    :param action_dim: The dimension of the action space.
    :param hidden_units: The number of hidden units in each layer.
    :return: A Keras model representing the critic network.
    """
    
    input_size = state_dim + action_dim
    state_action_inputs = layers.Input(shape=(None, input_size, 1))  # Concatenate state and action
    
    # Hidden layers (Dense layers with ReLU activation)
    x = layers.Dense(hidden_units, activation='relu')(state_action_inputs)
    x = layers.Dense(hidden_units, activation='relu')(x)
    
    # Output layer: Q-value for the given state-action pair
    q_value_output = layers.Dense(1)(x)  # Single output for Q-value
    
    # Create the model 
    critic_model = tf.keras.Model(inputs=state_action_inputs, outputs=q_value_output)
    
    return critic_model

Danach müssten wir das SAC-Modell in TensorFlow/Keras trainieren. Dies würde in der Regel die Verwendung einer alten MetaTrader 5-Bibliothek beinhalten, um MetaTrader 5-Daten aus dem MetaTrader-Terminal zu importieren und diese Daten dann in Test- und Trainingsdaten aufzuteilen. Wir verwenden ein Zwei-Drittel-Trainingsverhältnis, sodass ein Drittel für Tests übrig bleibt. Wir simulieren das Handels-Setup von MetaTrader 5 in einer langwierigen und höchst ineffizienten for-Schleife, die erwartungsgemäß auf eine Anzahl von Epochen und die Größe der Trainingsdaten ausgelegt ist. Außerdem versuchen wir, die Netzwerke der Akteure und Kritiker mit der SAC-Zielfunktion zu optimieren, einschließlich des Entropie-Terms. Der damit verbundene Code wird im Folgenden vorgestellt:

# Filter the DataFrame to keep only the '<state>' column
df = pd.read_csv(name_csv)

states = df.filter(['<STATE>']).astype(int).values
# Extract the '<state>' column as an integer array
rewards = df.filter(['<REWARD>']).values

states_size = int(len(states)*(2.0/3.0))
actor_x_train = states[0:states_size,:]
actor_x_test = states[states_size:,:1]
rewards_size = int(len(rewards)*(2.0/3.0))
critic_y_train = rewards[0:rewards_size,:]
critic_y_test = rewards[rewards_size:,:1]

# Initialize networks and optimizers
input_dim = 1  # 2 states, of 3 gradations are flattened into a single index
output_dim = 3  # possible actions buy, sell, hold
actor = ActorNetwork(input_dim, output_dim)
critic1 = CriticNetwork(input_dim, output_dim)  # Input paired with action
critic2 = CriticNetwork(input_dim, output_dim)  # Input paired with action

critic_optimizer_1 = tf.keras.optimizers.Adam(learning_rate=0.001)
critic_optimizer_2 = tf.keras.optimizers.Adam(learning_rate=0.001)
actor_optimizer = tf.keras.optimizers.Adam(learning_rate=0.001)

# Training loop
for e in range(epoch_size):
    train_critic_loss1 = 0
    train_critic_loss2 = 0
    train_actor_loss = 0
    
    for i in range(actor_x_train.shape[0]):
        input_state = tf.expand_dims(actor_x_train[i], axis=0)  # Select a single sample and maintain batch dim
        target_q = tf.expand_dims(critic_y_train[i], axis=0)

        # Actor forward pass and sampling
        with tf.GradientTape(persistent=True) as tape:

            actor_output = actor(input_state)
            # Split the vector into mean and log_std
            mu = actor_output[:, :output_dim]     # First 3 values
            log_std = actor_output[:, output_dim:]  # Last 3 values
            std = tf.exp(log_std)
            sampled_action = tf.random.normal(shape=mu.shape, mean=mu, stddev=std)  # Sample action from Gaussian

            # Concatenate the state and action tensors
            in_state = tf.convert_to_tensor(tf.cast(input_state, dtype=tf.float32), dtype=tf.float32)  # Ensure it's a tensor
            in_action = tf.convert_to_tensor(tf.cast(sampled_action, dtype=tf.float32), dtype=tf.float32)
            
            # Concatenate along the last axis
            critic_raw_input = tf.concat([in_state, in_action], axis=-1)  # Ensure correct axis
            critic_input = tf.reshape(critic_raw_input, [-1, 1, 4, 1])  # -1 infers the batch size dynamically

            q_value1 = critic1(critic_input)
            q_value2 = critic2(critic_input)

            # Critic loss (mean squared error)
            critic_loss1 = tf.reduce_mean((tf.cast(q_value1, tf.float32) - tf.cast(target_q, tf.float32)) ** 2)
            critic_loss2 = tf.reduce_mean((tf.cast(q_value2, tf.float32) - tf.cast(target_q, tf.float32)) ** 2)

            # Actor loss (maximize expected Q-value based on minimum critic output)
            min_q_value = tf.minimum(q_value1, q_value2)  # Take the minimum Q-value
            actor_loss = tf.reduce_mean(min_q_value)  # Maximize expected Q-value (negative for minimization)

        # Backpropagation
        critic_gradients1 = tape.gradient(critic_loss1, critic1.trainable_variables)
        critic_gradients2 = tape.gradient(critic_loss2, critic2.trainable_variables)
        actor_gradients = [-grad for grad in tape.gradient(actor_loss, actor.trainable_variables)]

        del tape  # Free up resources from persistent GradientTape
        
        critic_optimizer_1.apply_gradients(zip(critic_gradients1, critic1.trainable_variables))
        critic_optimizer_2.apply_gradients(zip(critic_gradients2, critic2.trainable_variables))
        actor_optimizer.apply_gradients(zip(actor_gradients, actor.trainable_variables))
        
        # Accumulate losses for epoch summary
        train_critic_loss1 += critic_loss1.numpy()
        train_critic_loss2 += critic_loss2.numpy()
        train_actor_loss += actor_loss.numpy()

    print(f"  Epoch {e + 1}/{epoch_size}:")
    print(f"  Train Critic Loss 1: {train_critic_loss1 / actor_x_train.shape[0]:.4f}")
    print(f"  Train Critic Loss 2: {train_critic_loss2 / actor_x_train.shape[0]:.4f}")
    print(f"  Train Actor Loss: {train_actor_loss / actor_x_train.shape[0]:.4f}")
    print("-" * 40)

critic2.summary()
critic1.summary()
actor.summary()

Nach dem Training wären wir bereit, unser Modell, das aus drei Netzen besteht, in ONNX zu exportieren. ONNX, die Abkürzung für Open Neural Network Exchange, ist ein offener Standard für die Interoperabilität des maschinellen Lernens, bei dem Modelle, die in Python mit verschiedenen Bibliotheken wie PyTorch oder SciKit-Learn trainiert wurden, in dieses Format exportiert werden können, um sie auf einer Vielzahl von Plattformen und Programmiersprachen zu verwenden, darunter auch MQL5. Durch diese Kompatibilität entfällt die Notwendigkeit, komplexe Logik des maschinellen Lernens zu replizieren, was Zeit spart und Fehler reduziert.

Der Import von ONNX als Ressource ermöglicht die Kompilierung einer einzigen ex5-Datei, die das ONNX-Modell für maschinelles Lernen und die MQL5-Handelsausführungslogik enthält, sodass Händler sich nicht mit mehreren Dateien auseinandersetzen müssen. Damit ist der Exportprozess von Python nach ONNX abgeschlossen. Mehrere Optionen, eine davon ist tf2onnx, aber das ist nicht die einzige, denn es gibt auch onnxmltools, skl2onnx, transformers.onnx (für „Hugging Face“) und mxnet.contrib.onnx.  In der Exportphase muss jedoch sichergestellt werden, dass die Formen der Eingangs- und Ausgangsschichten jedes Netzes ordnungsgemäß protokolliert und aufgezeichnet werden, da diese Informationen in MQL5 für die genaue Initialisierung der jeweiligen ONNX-Handles für jedes Netz entscheidend sind. Wir gehen dabei wie folgt vor:

# Check input and output layer shapes for importing ONNX
import onnxruntime as ort

session_critic2 = ort.InferenceSession(path_critic2_onnx)
session_critic1 = ort.InferenceSession(path_critic1_onnx)
session_actor = ort.InferenceSession(path_actor_onnx)

for i in session_critic2.get_inputs():
    print(f"in critic2 Name: {i.name}, Shape: {i.shape}, Type: {i.type}")

for i in session_critic1.get_inputs():
    print(f"in critic1 Name: {i.name}, Shape: {i.shape}, Type: {i.type}")

for i in session_actor.get_inputs():
    print(f"in actor Name: {i.name}, Shape: {i.shape}, Type: {i.type}")
    

for o in session_critic2.get_outputs():
    print(f"out critic2 Name: {o.name}, Shape: {o.shape}, Type: {o.type}")

for o in session_critic1.get_outputs():
    print(f"out critic1 Name: {o.name}, Shape: {o.shape}, Type: {o.type}")

for o in session_actor.get_outputs():
    print(f"out actor Name: {o.name}, Shape: {o.shape}, Type: {o.type}")

Die Leistung des Python-Codes mit dieser Implementierung, die wie oben angegeben for-Schleifen verwendet, ist bei weitem nicht effizient, sondern ähnelt sehr stark der von MQL5, da die Verwendung von Tensoren/Graphen nicht richtig genutzt wird. Es ist jedoch notwendig, da die Fitness-Funktion von TensorFlow, die oft verwendet wird, um die Trainingseffizienz von TensorFlow zu nutzen, in diesem Fall nicht anwendbar gewesen wäre, da bei der Backpropagation die Ausgaben der beiden kritischen Netzwerke (die Q-Werte) verwendet werden, um das Akteursnetzwerk zu trainieren. Das Akteursnetzwerk hat keine Zielvektoren oder Zieldatensätze wie die kritischen Netzwerke oder die meisten typischen neuronalen Netzwerke.

Der zweite Ansatz zur Implementierung verwendet Tensor-Agenten, die eingebaute Bibliotheken für die Handhabung von Verstärkung in TensorFlow und Python sind. Wir werden uns in den nächsten Artikeln eingehend damit befassen, aber es genügt zu sagen, dass die Initialisierung nicht nur die konstituierenden Netzwerke umfasst, sondern auch die Umgebung und die Agenten berücksichtigt. Entscheidende Aspekte des Reinforcement Learning, die übersehen werden könnten, wenn man sich zu sehr auf die Effizienz des Netzwerktrainings konzentriert.

Kombinieren mit MQL5

Wir importieren unsere exportierten ONNX-Modelle in die MQL5-Ressourcen, wodurch wir die folgende Kopfzeile für unsere nutzerdefinierte Signalklassendatei erhalten.

//+------------------------------------------------------------------+
//|                                                    SignalSAC.mqh |
//|                   Copyright 2009-2017, MetaQuotes Software Corp. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#include <Expert\ExpertSignal.mqh>
#include <My\Cql.mqh>
#resource "Python/EURUSD_H1_D1_critic2.onnx" as uchar __CRITIC_2[]
#resource "Python/EURUSD_H1_D1_critic1.onnx" as uchar __CRITIC_1[]
#resource "Python/EURUSD_H1_D1_actor.onnx" as uchar __ACTOR[]
#define  __ACTIONS 3
#define  __ENVIONMENTS 3

Die Daten, die wir in Python exportiert haben, waren für das Symbol EURUSD auf dem 1-Stunden-Zeitrahmen vom 2023.12.12 bis 2024.12.12. Das Training verwendete zwei Drittel der Zeit, also acht Monate, das heißt, wir haben vom 2023.12.12 bis zum 2024.08.12 trainiert. Daher können wir ab 2024.08.12 Tests in der Zukunft durchführen. Das ergibt einen Zeitraum von knapp über 4 Monaten, was eigentlich nicht so lang ist, aber da wir den 1-Stunden-Zeitrahmen wiederverwenden, könnte er signifikant sein.

Da die Rückwärtspropagation bereits in Python erfolgt, werden keine speziellen Eingabeparameter für die Optimierung dieses Vorwärtslaufs verwendet. Unsere Klassenschnittstelle sieht daher wie folgt aus:

//+------------------------------------------------------------------+
//| SACs CSignalSAC.                                                 |
//| Purpose: Soft Actor Critic for Reinforcement-Learning.           |
//|            Derives from class CExpertSignal.                     |
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalSAC   : public CExpertSignal
{
protected:

   long                          m_critic_2_handle;
   long                          m_critic_1_handle;
   long                          m_actor_handle;

public:
   void                          CSignalSAC(void);
   void                          ~CSignalSAC(void);

   //--- methods of setting adjustable parameters

   //--- method of verification of arch
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);

protected:
   vectorf           GetOutput();
   vectorf           LogProbabilities(vectorf &Mean, vectorf &Log_STD);
};

Wir initialisieren und validieren die Größen der Eingabe- und Ausgabeschichten der einzelnen ONNX-Modelle wie folgt:

//+------------------------------------------------------------------+
//| Validation arch protected data.                                  |
//+------------------------------------------------------------------+
bool CSignalSAC::ValidationSettings(void)
{  if(!CExpertSignal::ValidationSettings())
      return(false);
//--- initial data checks
   if(m_period > PERIOD_H1)
   {  Print(" time frame too large ");
      return(false);
   }
   ResetLastError();
   if(m_critic_2_handle == INVALID_HANDLE)
   {  Print("Crit 2 OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   if(m_critic_1_handle == INVALID_HANDLE)
   {  Print("Crit 1 OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   if(m_actor_handle == INVALID_HANDLE)
   {  Print("Actor OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   // Set input shapes
   const long _critic_in_shape[] = {1, 4, 1};
   const long _actor_in_shape[] = {1};
   // Set output shapes
   const long _critic_out_shape[] = {1, 4, 1, 1};
   const long _actor_out_shape[] = {1, 6};
   if(!OnnxSetInputShape(m_critic_2_handle, ONNX_DEFAULT, _critic_in_shape))
   {  Print("Crit 2  OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_critic_2_handle, 0, _critic_out_shape))
   {  Print("Crit 2  OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetInputShape(m_critic_1_handle, ONNX_DEFAULT, _critic_in_shape))
   {  Print("Crit 1 OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_critic_1_handle, 0, _critic_out_shape))
   {  Print("Crit 1 OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetInputShape(m_actor_handle, ONNX_DEFAULT, _actor_in_shape))
   {  Print("Actor OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_actor_handle, 0, _actor_out_shape))
   {  Print("Actor OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
//read best weights
//--- ok
   return(true);
}

Bei den Ebenenformen ist es bemerkenswert, dass wir Änderungen vornehmen mussten, die unseren Export nach ONNX erleichterten, obwohl sie gegen die Grundlogik von SAC verstießen. Zunächst soll das Akteursnetzwerk 2 Vektoren der Mittelwerte und einen Vektor der logarithmischen Standardabweichung exportieren. Diese in der ONNX-Schichtform zu definieren, wäre zu fehleranfällig gewesen, daher haben wir sie in Python zu einem einzigen Vektor zusammengefasst, wie im obigen for-loop-Code angegeben. Auch die Eingaben für die kritischen Netze sind zweifach, der Zustand der Umgebung und die Verteilung der Handlungswahrscheinlichkeit, wie sie vom Akteursnetz bereitgestellt wird. Auch dieser kann typischerweise durch 2 Tensoren definiert werden, der Einfachheit halber haben wir diese jedoch wieder zu einem einzigen Vektor von 4 Größen zusammengefasst. Unsere Get-Output-Funktion lautet wie folgt:

//+------------------------------------------------------------------+
//| This function calculates the next actions to be selected from    |
//| the Reinforcement Learning Cycle.                                |
//+------------------------------------------------------------------+
vectorf CSignalSAC::GetOutput()
{  vectorf _out;
   int _load = 1;
   static vectorf _x_states(1);
   _out.Init(__ACTIONS);
   _out.Fill(0.0);
   vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(_load) &&
      _in_row.CopyRates(m_symbol.Name(), PERIOD_H1, 8, 0, _load) &&
      _in_row.Size() == _load
      &&
      _in_row_old.Init(_load) &&
      _in_row_old.CopyRates(m_symbol.Name(), PERIOD_H1, 8, 1, _load) &&
      _in_row_old.Size() == _load
      &&
      _in_col.Init(_load) &&
      _in_col.CopyRates(m_symbol.Name(), PERIOD_D1, 8, 0, _load) &&
      _in_col.Size() == _load
      &&
      _in_col_old.Init(_load) &&
      _in_col_old.CopyRates(m_symbol.Name(), PERIOD_D1, 8, 1, _load) &&
      _in_col_old.Size() == _load
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      Cql *QL;
      Sql _RL;
      _RL.actions  = __ACTIONS;//buy, sell, do nothing
      _RL.environments = __ENVIONMENTS;//bullish, bearish, flat
      QL = new Cql(_RL);
      vector _e(_load);
      QL.Environment(_in_row, _in_col, _e);
      delete QL;
      _x_states[0] = float(_e[0]);
      static matrixf _y_mu_logstd(6, 1);
//--- run the inference
      ResetLastError();
      if(!OnnxRun(m_actor_handle, ONNX_NO_CONVERSION, _x_states, _y_mu_logstd))
      {  Print("Actor OnnxConversion error ", GetLastError());
         return(_out);
      }
      else
      {  vectorf _mu(__ACTIONS), _logstd(__ACTIONS);
         _mu.Fill(0.0); _logstd.Fill(0.0);
         for(int i=0;i<__ACTIONS;i++)
         {  _mu[i] = _y_mu_logstd[i][0];
            _logstd[i] = _y_mu_logstd[i+__ACTIONS][0];
         }
         _out = LogProbabilities(_mu, _logstd);
      }
   }
   return(_out);
}

Wir bleiben bei dem bisher verwendeten Modell mit 9 Umweltzuständen und 3 möglichen Aktionen. Um die Wahrscheinlichkeitsverteilung der Aktionen zu verarbeiten, benötigen wir die Funktion „log probabilities“, deren Code zu Beginn dieses Beitrags vorgestellt wurde.  Nach der Kompilierung mit dem Assistenten und der Durchführung eines Testlaufs für die verbleibenden 4 Monate des Datenfensters erhalten wir den folgenden Bericht:

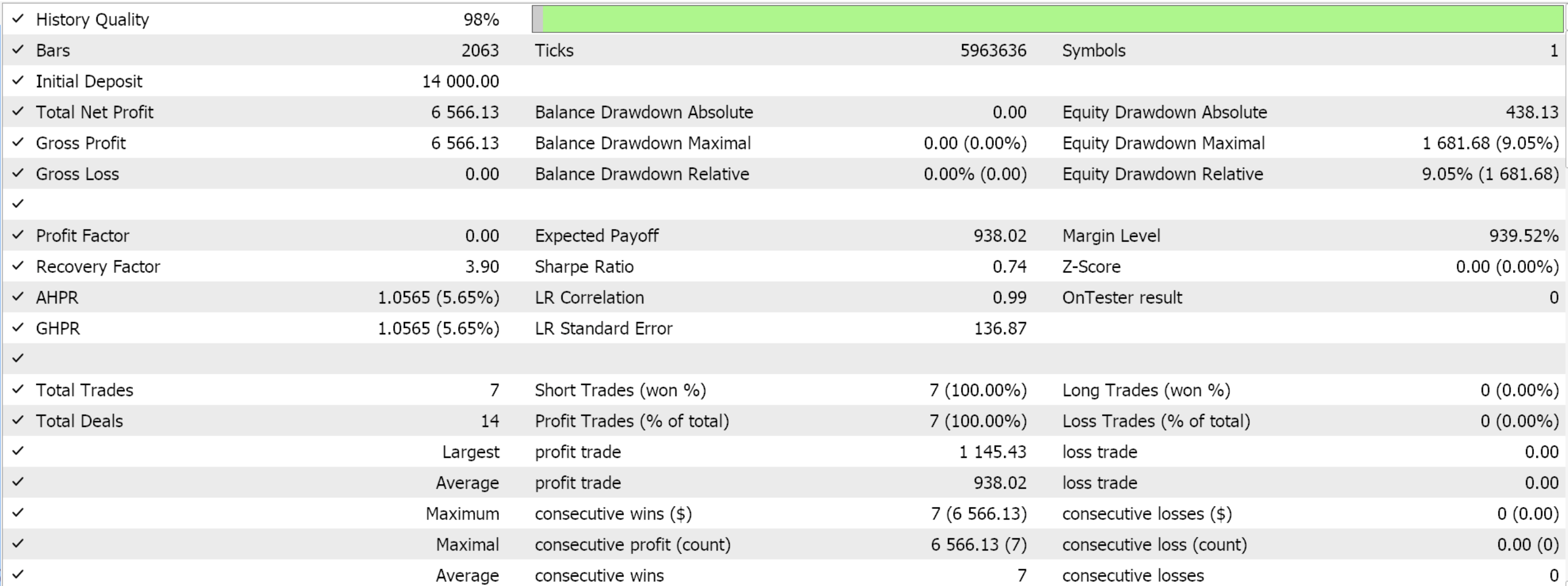
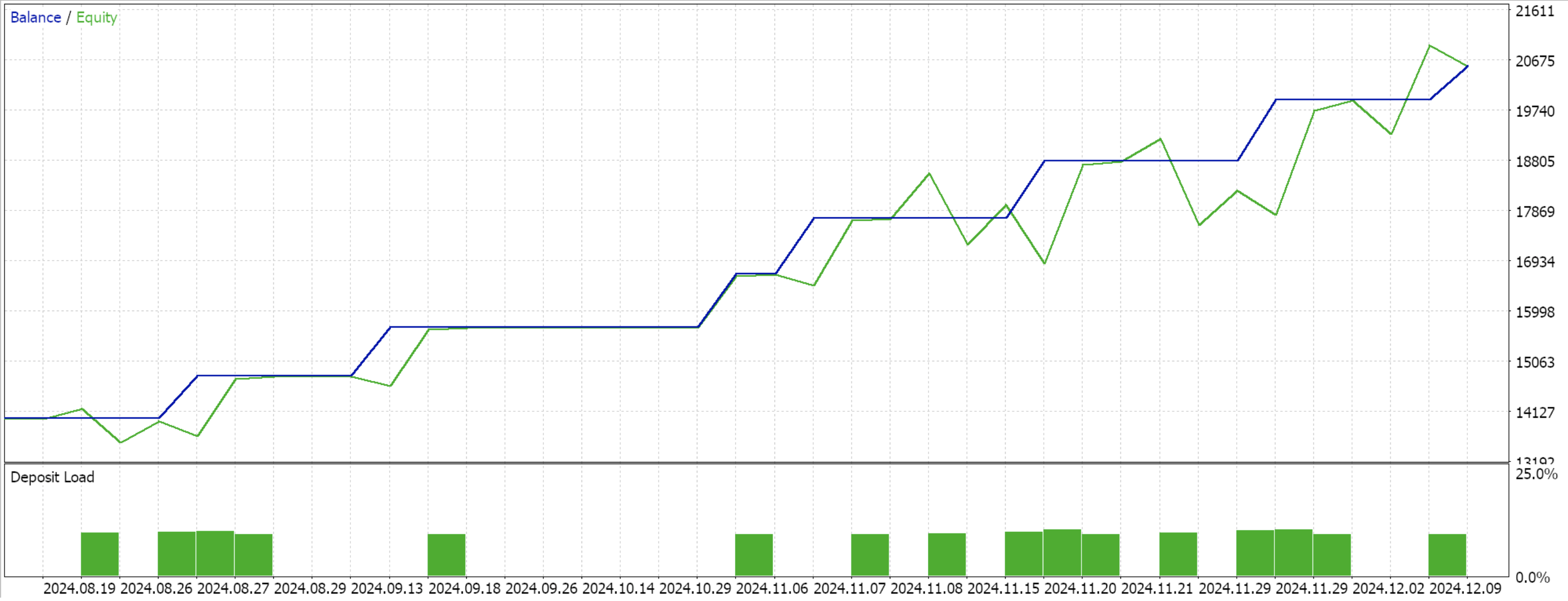
Schlussfolgerung

Wir haben uns ein sehr einfaches Implementierungsszenario von Reinforcement Learnings SAC in Python angesehen, bei dem die Tensor-Agent-Bibliothek nicht verwendet wurde und somit auch nicht die Effizienz, die sie mit sich bringt. Dieser Ansatz legt die SAC-Grundlagen dar und verdeutlicht, warum die Backpropagation etwas langwierig ist, da mehrere Netze gepaart werden müssen und eines dieser Netze keinen typischen Trainingsdatensatz hat. SAC soll im Prinzip auf sichere Weise mehr Exploration durch Entropie fördern, die durch den Alpha-Parameter moduliert wird (den wir bei der Gauß-Verteilung angewendet haben). Der Leser ist daher eingeladen, dies näher zu untersuchen, indem er ein nicht festes Alpha, wie die automatische Anpassung mit einem Ziel-Entropiewert, in Betracht zieht. In künftigen Artikeln werden wir auch auf diese Beispiele eingehen.

Datei Name	Beschreibung
WZ_51.mq5	Mit dem Assistenten erstellter Expert Advisor, dessen Kopfzeile dazu dient, die verwendeten Dateien anzuzeigen
SignalWZ_51.mqh	Nutzerdefinierte Signalklassendatei
EURUSD_H1_D1_critic2.onnx	Kritiker 2 ONNX-Netzwerk
EURUSD_H1_D1_critic1.onnx	Kritiker 1 ONNX-Netzwerk
EURUSD_H1_D1_actor.onnx	Akteursnetzwerk