Técnicas do MQL5 Wizard que você deve conhecer (Parte 15): Máquinas de Vetores de Suporte com o Polinômio de Newton

Introdução

Máquinas de Vetores de Suporte (SVM) é um algoritmo de classificação de aprendizado de máquina. A classificação é diferente da clusterização, que consideramos em artigos anteriores aqui e aqui, sendo que a principal diferença entre os dois é que a classificação separa dados em conjuntos predefinidos, com supervisão, enquanto a clusterização busca determinar quais e quantos são esses conjuntos, sem supervisão.

Em resumo, o SVM classifica dados considerando a relação que cada ponto de dados terá com todos os outros, se uma dimensão fosse adicionada aos dados. A classificação é alcançada se um hiperplano puder ser definido, separando claramente os conjuntos de dados predefinidos.

Frequentemente, os conjuntos de dados considerados têm múltiplas dimensões, e é essa característica que torna o SVM uma ferramenta muito poderosa para classificar esses conjuntos de dados, especialmente se os números em cada conjunto forem pequenos ou se a proporção relativa dos conjuntos de dados for distorcida. O código-fonte de implementação para SVMs que têm mais de 2 dimensões é muito complexo, e os casos de uso em Python ou C# geralmente utilizam bibliotecas, deixando ao usuário um mínimo de entrada de código para obter um resultado.

Dados de alta dimensão tendem a ajustar excessivamente os dados de treinamento, o que os torna menos confiáveis em dados fora da amostra, e esta é uma das principais desvantagens do SVM. Dados de menor dimensão, por outro lado, se validam cruzadamente de forma muito melhor e têm casos de uso mais comuns.

Para este artigo, consideraremos um caso muito básico de SVM que lida com dados bidimensionais (também conhecido como SVM linear), pois o código-fonte completo da implementação será compartilhado sem referência a bibliotecas de terceiros. Normalmente, o hiperplano separador é derivado de um dos dois métodos: um kernel polinomial ou um kernel radial. Este último é mais complexo e não será discutido aqui, pois lidaremos apenas com o primeiro, o kernel polinomial.

Tipicamente, ao usar o kernel polinomial, que é formalmente definido pela equação abaixo,

determinar os valores ideais de c e d, que definem a equação do hiperplano, é um processo iterativo que visa afastar o máximo possível os vetores de suporte, uma vez que eles medem a lacuna entre os dois conjuntos de dados.

Para este artigo, como indicado no título, usaremos o Polinômio de Newton para derivar a equação do hiperplano em conjuntos de dados bidimensionais. Nós já examinamos o Polinômio de Newton em um artigo recente, então algumas de suas implementações serão brevemente abordadas.

Implementamos o Polinômio de Newton (NP) em três cenários. Primeiro, interpolamos pontos médios entre dois conjuntos de dados predefinidos para obter um conjunto de pontos de limite e esses pontos são usados para derivar uma equação de linha/curva que define nosso hiperplano. Com esse hiperplano definido, tratamos ele como um classificador ao executar decisões de negociação para uma classe de sinal especialista de teste, a ser usada. No segundo cenário, adicionamos uma função de regressão para que a classe de sinal especialista não forneça saídas apenas de valores 0 ou 100 (como no primeiro) mas também valores dentro da faixa. Calculamos o valor da regressão a partir da proximidade do vetor não classificado em relação aos pontos vetoriais conhecidos. Por fim, construímos sobre o segundo cenário, interpolando apenas um pequeno número de pontos ao definir o hiperplano. O pequeno número de pontos, também conhecidos como vetores de suporte, sendo aqueles mais próximos do outro conjunto de dados, assim 'refinando' a equação do hiperplano enquanto mantemos todo o resto.

Antecedentes sobre o Kernel Polinomial

Para este artigo, estamos considerando SVMs lineares, dado que a implementação completa do código-fonte será compartilhada, e queremos evitar o uso de bibliotecas, oferecendo total transparência em todo o código-fonte. Nas aplicações do mundo real de SVM, no entanto, os tipos não lineares são muito utilizados, dada a complexidade inerente e a multidimensionalidade de muitos conjuntos de dados. Lidar com esses desafios em SVMs tem se mostrado gerenciável graças ao truque do kernel. Este é um método que permite que um conjunto de dados seja estudado em uma dimensão superior, mantendo sua estrutura original. O truque do kernel usa o produto escalar de vetores para preservar os valores vetoriais de menor dimensão. Ao apontar o conjunto de dados para dimensões superiores, a separação dos conjuntos de dados é facilmente alcançada, e isso é feito com menos recursos computacionais também.

Como indicado acima, nossa função de kernel é formalmente definida como:

com x e y servindo como pontos de dados em qualquer dois pontos de dados comparados em cada conjunto, c sendo uma constante (cujo valor geralmente é definido como 1 inicialmente) e d sendo o grau do polinômio. À medida que d aumenta, uma equação de hiperplano mais precisa pode ser definida, mas isso tende a levar ao overfitting, e é necessário estabelecer um equilíbrio. Os pontos de dados x e y estão, em muitos casos, em formato vetorial ou até mesmo matricial, por isso o expoente T representa a transposição de x.

Implementar um kernel polinomial em MQL5, para fins ilustrativos, poderia ter a seguinte forma.

//+------------------------------------------------------------------+
//| Define a data point structure                                    |
//+------------------------------------------------------------------+
struct Sdatapoint
{  double      features[2];
   int               label;
                     Sdatapoint()
   {                 ArrayInitialize(features, 0.0);
      label = 0;
   };
                    ~Sdatapoint() {};

};

//+------------------------------------------------------------------+
//| Function to calculate the polynomial kernel value                |
//+------------------------------------------------------------------+
double PolynomialKernel(Sdatapoint &A, Sdatapoint &B, double Constant, int Degree)
{  double _kernel_sum = 0.0;
   for (int i = 0; i < 2; i++)
   {  _kernel_sum += (A.features[i] * B.features[i]);
   }
   _kernel_sum += Constant; // Add constant term
   return(pow(_kernel_sum, Degree));
}

Os pesos de relacionamento entre pontos de dados que estão em conjuntos separados são calculados e armazenados em uma matriz de kernel. Essa matriz de kernel quantifica o espaçamento dos pontos de dados e, portanto, filtra os vetores de suporte, que são os pontos de dados na borda de cada conjunto de dados e que estão mais próximos do conjunto vizinho.

source

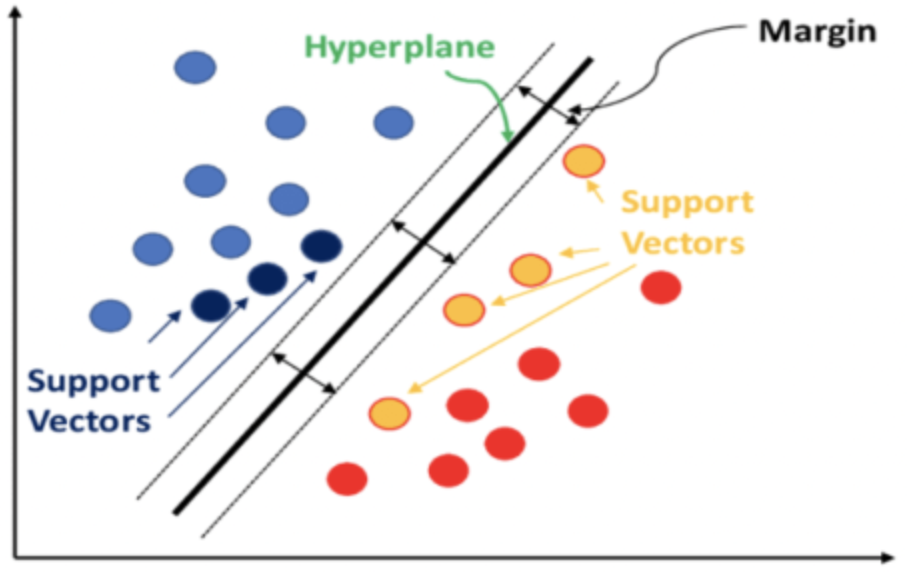
Esses vetores de suporte então servem como entrada para o cálculo da equação do hiperplano. Tudo isso é tratado em funções de bibliotecas como: PyLIBSVM ou Shogun para Python; ou Kernlab ou SVMlight em R. São essas funções de bibliotecas, dadas a complexidade de derivar a equação do hiperplano, que computam e geram o hiperplano.

Ao determinar a matriz de kernel, vários valores constantes e graus polinomiais podem ser considerados para chegar a uma solução ideal. No entanto, isso torna o processo já complexo de derivar um hiperplano a partir de uma única matriz ainda mais complicado ao fazê-lo em várias matrizes. Por isso, é mais prudente sempre selecionar um valor constante definitivo (ou subótimo com base no conhecimento) e o grau polinomial logo no início e usá-los para chegar ao hiperplano. Nesse sentido, o valor constante também é frequentemente definido como 1. E como se poderia esperar, quanto maior o grau polinomial, melhor a classificação, mas isso envolve os riscos de overfitting já mencionados.

Além disso, graus polinomiais mais altos tendem a ser mais intensivos computacionalmente, então um valor intuitivo que não seja muito alto precisa ser estabelecido desde o início.

Os kernels polinomiais que são considerados aqui são relativamente fáceis de entender, mas não são o kernel mais usado ou preferido em muitas implementações de SVM, pois esse título vai para o kernel de função de base radial.

O kernel de função de base radial (RBF) é mais comumente escolhido porque a vantagem do SVM está em lidar com dados multidimensionais, e o kernel RBF se destaca nisso melhor do que o kernel polinomial. Uma vez escolhido um kernel, o problema de otimização dual, onde, como mencionado acima, os conjuntos de dados são mapeados para um espaço de dimensão superior, seria realizado e, graças às regras do produto escalar capturadas no que é referido como o truque do kernel, essa otimização (ida e volta) pode ser feita de maneira mais eficiente, além de ser expressa de forma mais clara. A natureza complexa das equações de hiperplano para conjuntos de dados com mais de 2 dimensões torna isso indispensável. Quando tudo estiver dito e feito, a equação do hiperplano assume a seguinte forma:

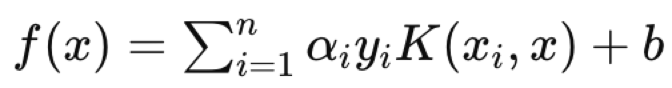
onde:

• f(x) é a função de decisão.
• αi são os coeficientes obtidos do processo de otimização.
• yi são as etiquetas de classe.
• K(xi,x) é a função kernel.
• b é o termo de viés.

A equação do hiperplano define como os dois conjuntos de dados são separados pela função de decisão, atribuindo uma etiqueta de classe que define de qual lado qualquer ponto de consulta pertence. Então, um ponto de dados de consulta seria o x na equação, com xi e yi sendo os dados de treinamento e seus classificadores, respectivamente.

Como observação, as aplicações do SVM são vastas, podendo variar de: filtragem de spam, se você conseguir incorporar cabeçalhos de e-mails e conteúdo em um formato estruturado; triagem de candidatos a empréstimos contra inadimplência; etc. O que tornaria o SVM ideal em comparação com outras alternativas de aprendizado de máquina é a robustez para desenvolver modelos a partir de conjuntos de dados pequenos ou muito distorcidos.

Implementação no MQL5

A estrutura do modelo que usamos para armazenar os valores de x e y é muito semelhante às nossas implementações recentes, com a diferença aqui sendo a adição de um contador para cada tipo de classificador. O SVM é inerentemente um classificador, e veremos exemplos disso em ação onde esses contadores serão úteis.

Então, os valores do vetor x são 2 em cada índice, já que estamos restringindo a multidimensionalidade de nossos conjuntos de dados para 2, para poder usar o Polinômio de Newton. Aumentar a dimensionalidade também corre o risco de overfitting. A primeira dimensão ou valor de x são as mudanças no buffer de preços altos, enquanto a segunda será as mudanças no buffer de preços baixos, como seria de se esperar. A escolha dos dados de entrada é agora um aspecto crucial no aprendizado de máquina. Embora transformers, CNNs e RNNs sejam muito úteis, a decisão sobre os dados de entrada e como você os incorpora ou normaliza pode ser mais crítica.

Escolhemos um conjunto de dados muito simples, mas o leitor deve estar ciente de que sua escolha de dados de entrada não se limita a dados de preços brutos ou até mesmo valores de indicadores, mas pode incluir valores de indicadores econômicos de notícias. E, novamente, como você escolhe normalizar isso pode fazer toda a diferença.

//+------------------------------------------------------------------+
//| Function to get and prepare data.                                |
//+------------------------------------------------------------------+
double CSignalSVM::GetOutput(int Index)
{  double _get = 0.0;
   

        ....
        ....

   int _x = StartIndex() + Index;
   for(int i = 0; i < m_length; i++)
   {  for(int ii = 0; ii < Dimensions(); ii++)
      {  if(ii == 0) //dim-1
         {  m_model.x[i][ii] = m_high.GetData(StartIndex() + i + _x) - m_high.GetData(StartIndex() + i + _x + 1);
         }
         else if(ii == 1) //dim-2
         {  m_model.x[i][ii] = m_low.GetData(StartIndex() + i + _x) - m_low.GetData(StartIndex() + i + _x + 1);
         }
      }
      if(i > 0) //assign classifier
      {  if(m_close.GetData(StartIndex() + i + _x - 1) - m_close.GetData(StartIndex() + i + _x) > 0.0)
         {  m_model.y[i - 1] = 1;
            m_model.y1s++;
         }
         else if(m_close.GetData(StartIndex() + i + _x - 1) - m_close.GetData(StartIndex() + i + _x) < 0.0)
         {  m_model.y[i - 1] = 0;
            m_model.y0s++;
         }
      }
   }
//
   _get = SetOutput();
   return(_get);
}

Nosso conjunto de dados y será formado por mudanças antecipadas no preço de fechamento, como foi o caso anteriormente. Introduzimos contadores para as duas classes, que são rotuladas como ‘y0’ e ‘y1’. Esses contadores simplesmente registram, para cada barra processada cujos dois valores de x são estabelecidos, se a mudança subsequente no preço de fechamento foi de alta (neste caso, um 0 é registrado) ou se foi de baixa (onde um 1 seria registrado).

Como y é um vetor, poderíamos, como uma observação lateral, recuperar essas contagens de 0 e 1 comparando seus valores atuais com vetores preenchidos com 0s e vetores preenchidos com 1s, já que os valores retornados seriam efetivamente uma contagem de 0s e 1s presentes no vetor y, respectivamente.

A função ‘set-output’ é outra adição às funções que já temos para processar as informações do nosso modelo. Ela recebe os valores do vetor x para cada classe e interpola um ponto médio entre os dois conjuntos que poderia servir como um hiperplano dos dois conjuntos. Isso não é a abordagem do SVM, como já mencionado, mas o que isso faz por nós, já que queremos definir um hiperplano usando o Polinômio de Newton, é nos dar um conjunto de pontos com os quais podemos trabalhar para derivar uma equação de hiperplano.

//+------------------------------------------------------------------+
//| Function to set and train data                                   |
//+------------------------------------------------------------------+
double CSignalSVM::SetOutput(void)
{  double _set = 0.0;
   matrix _a,_b;
   Classifier(_a,_b);
   if(_a.Rows() * _b.Rows() > 0)
   {  matrix _interpolate;
      _interpolate.Init(_a.Rows() * _b.Rows(), Dimensions());
      for(int i = 0; i < int(_a.Rows()); i++)
      {  for(int ii = 0; ii < int(_b.Rows()); ii++)
         {  _interpolate[(i*_b.Rows())+ii][0] = 0.5 * (_a[i][0] + _b[ii][0]);
            _interpolate[(i*_b.Rows())+ii][1] = 0.5 * (_a[i][1] + _b[ii][1]);
         }
      }
      vector _w;
      vector _x = _interpolate.Col(0);
      vector _y = _interpolate.Col(1);
      _w.Init(m_model.y0s * m_model.y1s);
      _w[0] = _y[0];
      m_newton.Set(_w, _x, _y);
      double _xx = m_model.x[0][0], _yy = m_model.x[0][1], _zz = 0.0;
      m_newton.Get(_w, _xx, _zz);
      if(_yy < _zz)
      {  _set = 100.0;
      }
      else if(_yy > _zz)
      {  _set = -100.0;
      }
      _set *= Regressor(_x, _y, _xx, _yy);
   }
   return(_set);
}

Estamos considerando três abordagens para derivar o hiperplano dentro deste método. A primeira abordagem considera todos os pontos em cada conjunto ao propor os pontos do hiperplano, interpolando a média de cada ponto em um conjunto para cada ponto no conjunto alternativo. Isso claramente não considera vetores de suporte, mas é apresentado aqui para fins de estudo e comparação com as outras abordagens.

O segundo método é semelhante ao primeiro, com a única diferença sendo que o valor de previsão de y é regredido, ou seja, em vez de ser 0 ou 1, usamos uma função ‘reguladora’ para transformar ou normalizar as previsões de saída como um valor de ponto flutuante na faixa de 0,0 a 1,0. Isso efetivamente produz um sistema que, em princípio, está ainda mais distante dos SVMs, mas ainda usa um hiperplano para diferenciar pontos de dados bidimensionais.

//+------------------------------------------------------------------+
//| Regressor for the model                                          |
//+------------------------------------------------------------------+
double CSignalSVM::Regressor(vector &X, vector &Y, double XX, double YY)
{  double _x_max = fmax(X.Max(), XX);
   double _x_min = fmin(X.Min(), XX);
   double _y_max = fmax(Y.Max(), YY);
   double _y_min = fmin(Y.Min(), YY);
   return(0.5 * ((1.0 - ((_x_max - XX) / fmax(m_symbol.Point(), _x_max - _x_min))) + (1.0 - ((_y_max - YY) / fmax(m_symbol.Point(), _y_max - _y_min)))));
}

Podemos obter um valor regressivo proxy comparando o valor previsto com o valor máximo e mínimo em seu conjunto, de modo que, se ele corresponder ao mínimo, 0 é retornado, enquanto 1 seria retornado se corresponder ao valor máximo.

Por fim, melhoramos o método na parte 2, adicionando uma função ‘classificadora’ que filtra os pontos em cada um dos conjuntos que são usados na derivação do hiperplano. Ao considerar pontos que estão mais distantes do centroide do seu próprio conjunto, enquanto estão mais próximos do centroide do conjunto oposto, chegamos a dois subconjuntos de pontos, um de cada classe, que podem ser usados para interpolar a fronteira do hiperplano entre os dois conjuntos.

//+------------------------------------------------------------------+
//| 'Classifier' for the model that identifies Support Vector points |
//|  for each set.                                                   |
//+------------------------------------------------------------------+
void CSignalSVM::Classifier(matrix &A, matrix &B)
{  if(m_model.y0s * m_model.y1s > 0)
   {  matrix _a_centroid, _b_centroid;
      _a_centroid.Init(1, Dimensions());
      _b_centroid.Init(1, Dimensions());
      for(int i = 0; i < m_length; i++)
      {  if(m_model.y[i] == 0)
         {  _a_centroid[0][0] += m_model.x[i][0];
            _a_centroid[0][1] += m_model.x[i][1];
         }
         else if(m_model.y[i] == 1)
         {  _b_centroid[0][0] += m_model.x[i][0];
            _b_centroid[0][1] += m_model.x[i][1];
         }
      }
      _a_centroid[0][0] /= m_model.y0s;
      _a_centroid[0][1] /= m_model.y0s;
      _b_centroid[0][0] /= m_model.y1s;
      _b_centroid[0][1] /= m_model.y1s;
      double _a_sd = 0.0, _b_sd = 0.0;
      double _ab_sd = 0.0, _ba_sd = 0.0;
      for(int i = 0; i < m_length; i++)
      {  if(m_model.y[i] == 0)
         {  double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            _a_sd += sqrt(_0);
            double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            _ab_sd += sqrt(_1);
         }
         else if(m_model.y[i] == 1)
         {  double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            _b_sd += sqrt(_1);
            double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            _ba_sd += sqrt(_0);
         }
      }
      _a_sd /= m_model.y0s;
      _ab_sd /= m_model.y0s;
      _b_sd /= m_model.y1s;
      _ba_sd /= m_model.y1s;
      for(int i = 0; i < m_length; i++)
      {  if(m_model.y[i] == 0)
         {  double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            if(sqrt(_0) >= _a_sd && _ab_sd <= sqrt(_1))
            {  A.Resize(A.Rows()+1,Dimensions());
               A[A.Rows()-1][0] = m_model.x[i][0];
               A[A.Rows()-1][1] = m_model.x[i][1];
            }
         }
         else if(m_model.y[i] == 1)
         {  double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            if(sqrt(_1) >= _b_sd && _ba_sd <= sqrt(_0))
            {  B.Resize(B.Rows()+1,Dimensions());
               B[B.Rows()-1][0] = m_model.x[i][0];
               B[B.Rows()-1][1] = m_model.x[i][1];
            }
         }
      }
   }
}

O código compartilhado acima que faz isso é um pouco extenso, e tenho certeza de que implementações mais eficientes podem ser feitas, especialmente se alguém utilizar as funções embutidas dos tipos de dados de vetor e matriz que foram recentemente introduzidos no MQL5. Mas o que estamos fazendo é primeiro encontrar o centroide (ou média) de cada conjunto de dados. Uma vez que isso esteja definido, procedemos a calcular o desvio padrão de cada conjunto de dados, obtido pelas variáveis que têm o sufixo ‘_sd’. Uma vez armados com as coordenadas do centroide e a magnitude do desvio padrão, podemos medir e comparar, para cada ponto, quão distante ele está de seu centroide, bem como quão distante está do centroide do conjunto de dados oposto, com os desvios padrões calculados servindo como um limite para estar muito longe ou muito próximo.

Pontos interpolados são tudo o que precisamos para definir uma equação com o Polinômio de Newton. Como vimos aqui, quanto mais pontos forem fornecidos, maior será o expoente da equação. O número máximo de pontos interpolados que podemos usar com o Polinômio de Newton é controlado pelo tamanho dos conjuntos de dados, e isso é diretamente proporcional ao parâmetro ‘m_length’, uma variável que define quantos pontos de dados na história precisamos observar ao definir os dois conjuntos de dados no modelo.

Dos três métodos usados para derivar um hiperplano, apenas o último guarda alguma semelhança com os métodos típicos de SVM. Ao selecionar pontos dentro de cada conjunto que estão mais próximos da fronteira do conjunto e, portanto, são mais relevantes para o hiperplano, estamos definindo os vetores de suporte. Esses pontos de vetor de suporte, então, servem como entrada para nossa classe Polinômio de Newton na derivação da equação do hiperplano. Em contraste, se fôssemos fazer um SVM estrito, adicionaríamos uma dimensão extra aos nossos pontos de dados para uma diferenciação adicional, enquanto iteramos pelos constantes na equação do kernel polinomial, que permite isso. Mesmo com dados bidimensionais, isso é claramente uma ordem de magnitude mais complexa, sem mencionar os recursos computacionais envolvidos. Na verdade, para simplicidade ou melhor prática, uma dessas constantes (o c) é sempre assumida como 1, enquanto apenas a variável do grau polinomial (o d nas equações acima) é otimizada. E, como você pode imaginar, com conjuntos de dados que têm mais de 2 dimensões, isso claramente necessitaria de uma biblioteca de terceiros, porque, se nada mais, a equação de expoente 4, 5 ou n que se busca será algumas ordens de magnitude mais complexa.

A implementação do Polinômio de Newton é muito semelhante ao que abordamos no artigo relacionado anterior, exceto por algumas correções na função ‘Get’, que executa a equação construída para determinar o próximo valor de y. Isso está anexado abaixo.

Resultados do Testador

Os 3 arquivos de classe de sinal anexados no final deste artigo podem ser montados em um expert advisor através do MQL5 wizard. Exemplos de como isso é feito estão disponíveis em artigos aqui e aqui.

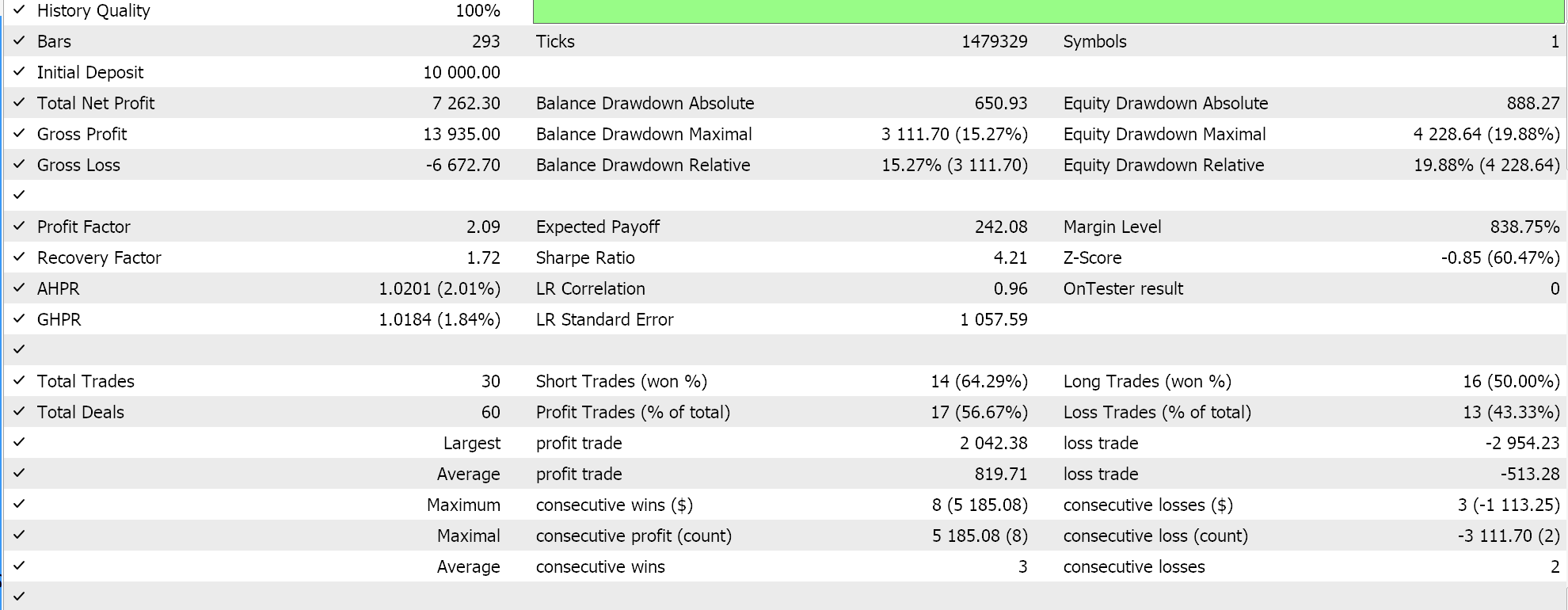
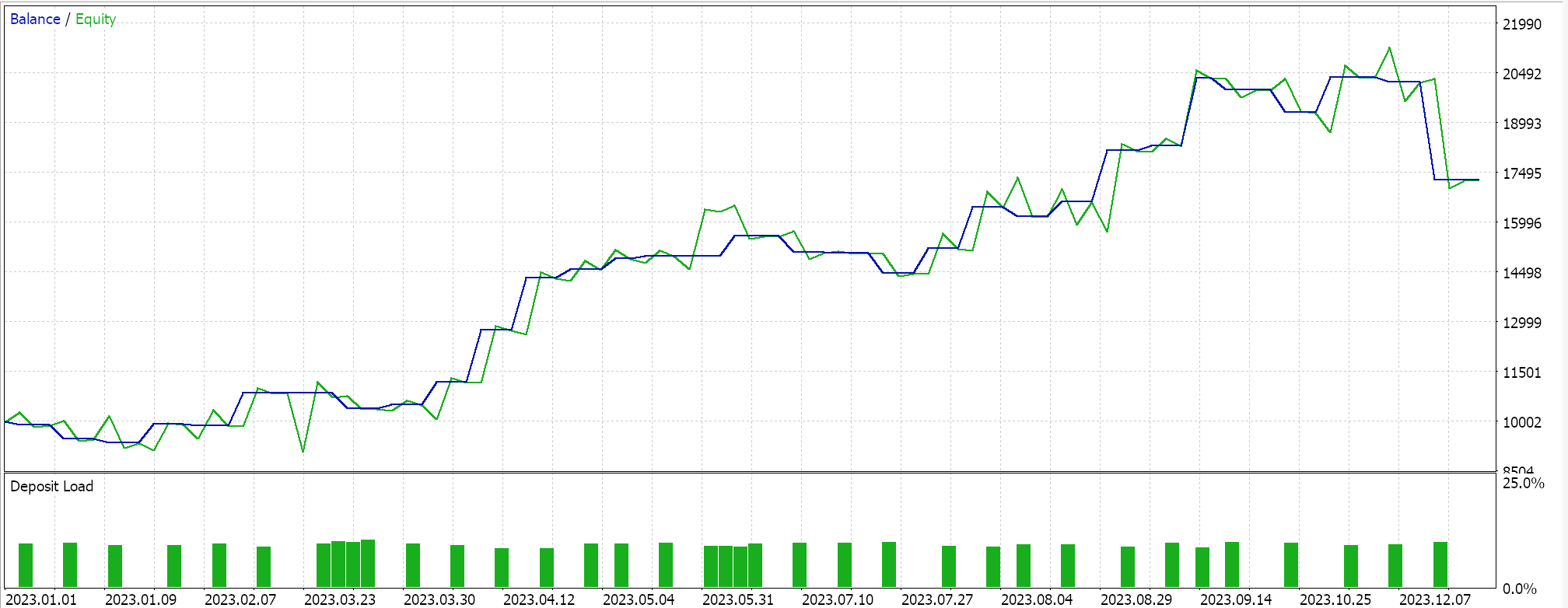
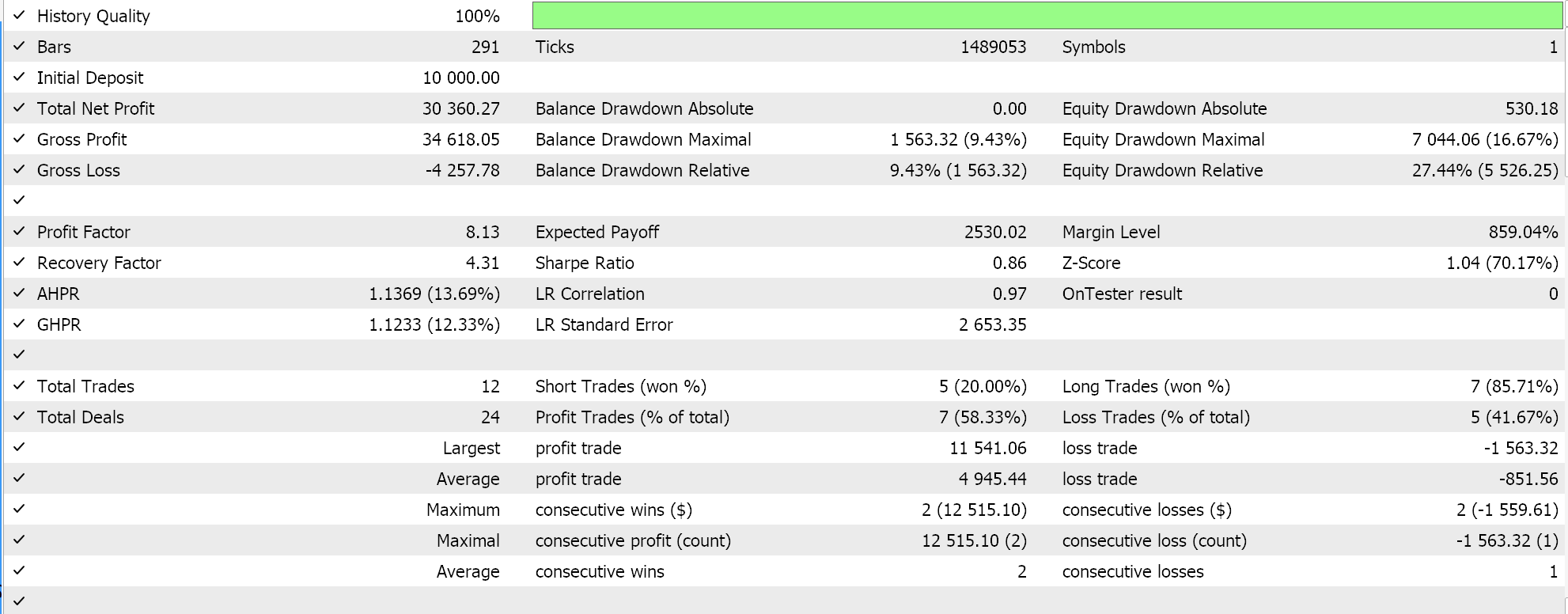
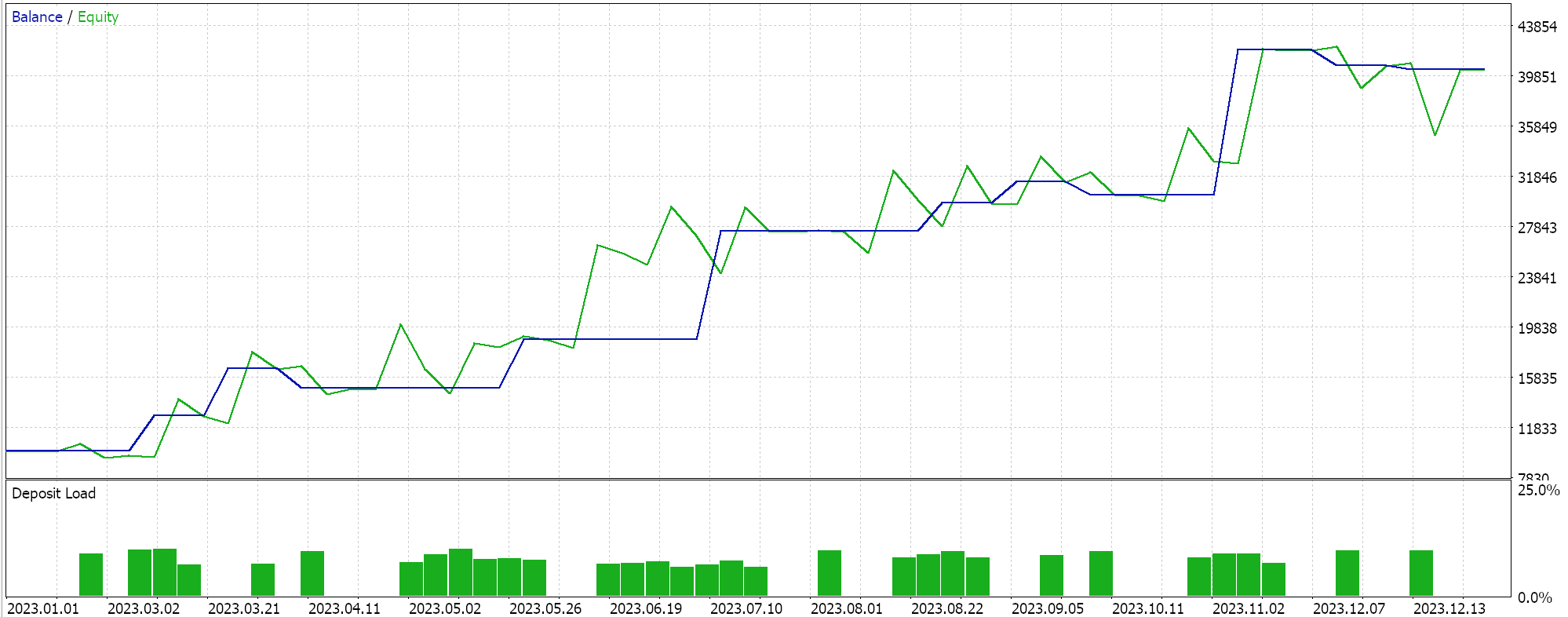
Então, ao executar testes para a primeira implementação, onde o hiperplano é obtido interpolando todos os pontos em qualquer conjunto sem selecionar vetores de suporte, obtemos os seguintes resultados:

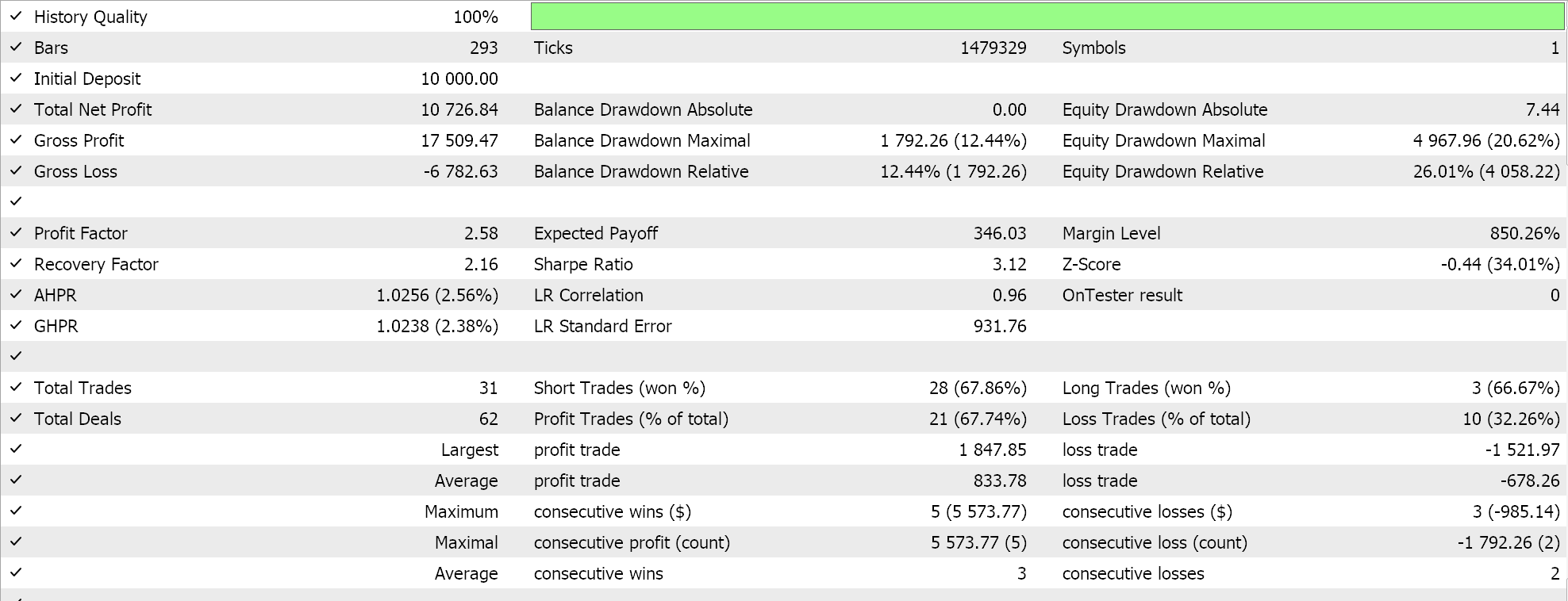
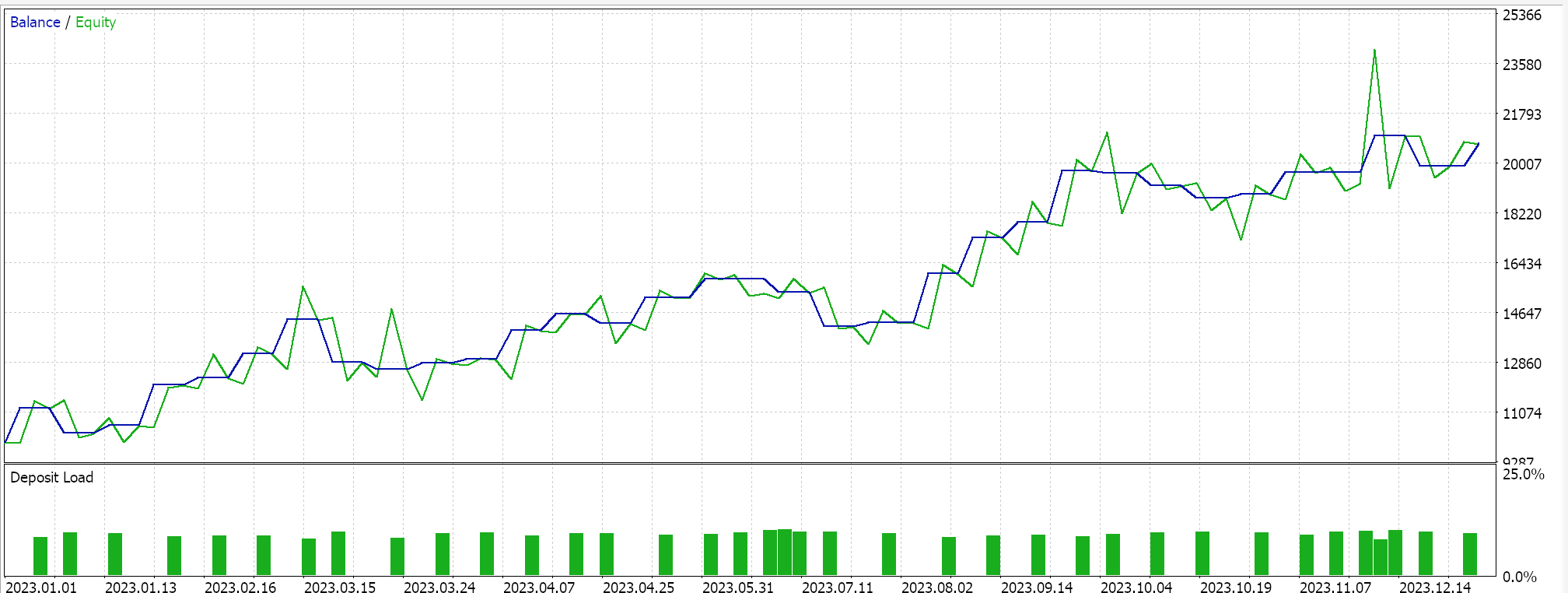
Se fizermos testes semelhantes aos acima, onde nosso símbolo de teste é EURJPY no timeframe diário para o ano de 2023, para o segundo método, que apenas adiciona regressão ao método acima, temos os seguintes resultados:

Por fim, a abordagem mais semelhante ao SVM, que seleciona pontos do conjunto de dados de vetores de suporte antes de derivar seu hiperplano, quando testada, nos dá os seguintes resultados:

A partir dos nossos relatórios acima, pode-se, a partir de uma rápida análise, concluir que o método que usa vetores de suporte é o mais promissor, e isso provavelmente não deve ser uma surpresa, dado o ajuste fino adicional (mesmo que o número de parâmetros seja idêntico em todos os três métodos) envolvido.

Como observação lateral, esse teste é realizado com ticks reais, com ordens limitadas e sem metas de lucro ou stop losses. Como sempre, mais testes são necessários antes de tirar conclusões mais significativas. No entanto, é interessante notar que, com o mesmo número de parâmetros de entrada, o método de vetor de suporte teve um desempenho melhor. Ele fez menos negociações, e isso resultou em um desempenho drasticamente melhor do que as outras duas abordagens.

Adicionar regressão na segunda abordagem melhorou marginalmente o desempenho, como pode ser visto nos resultados. O número de negociações também foi quase o mesmo; no entanto, pré-selecionar os pontos do conjunto de dados para vetores de suporte antes de definir o hiperplano foi claramente um divisor de águas. Os relatórios do MetaTrader são muito subjetivos, com muitos discutindo qual seria a estatística mais crítica para confiar como um indicador de se o sistema de negociação pode avançar, e eu também não tenho uma resposta definitiva sobre esse tópico. No entanto, acho que uma comparação entre o lucro médio e a perda média (por negociação), ao mesmo tempo em que se observa a razão entre vitórias consecutivas médias e perdas consecutivas médias, pode ser esclarecedora. Todos esses valores são frequentemente combinados no cálculo de uma relação referida como a expectativa. Isso é muito diferente do payoff esperado, que é simplesmente o lucro dividido por todas as negociações. Se compararmos a expectativa de todos os relatórios, então o método que usou vetores de suporte é melhor por uma magnitude de quase 10 em comparação com as outras 2 abordagens.

Conclusão

Para resumir, examinamos outro exemplo de desenvolvimento rápido e teste de uma possível ideia de negociação para avaliar se é uma melhoria ou se se encaixa em uma estratégia existente.

SVM é um algoritmo bastante complicado que raramente, se é que alguma vez, é implementado sem a ajuda de uma biblioteca de terceiros, seja PyLIBSVM para Python ou SVMlight para R, e mais do que isso, um dos parâmetros otimizáveis ​​é frequentemente tomado como sendo igual a 1 para simplificar esse processo. Para recapitular, nesse processo, uma cópia de um conjunto de dados em estudo tem suas dimensões aumentadas via uma fórmula reversível específica chamada de kernel polinomial. É a simplicidade e reversibilidade relativa desse kernel polinomial que lhe dá o nome de ‘truque do kernel’. Essa simplicidade e reversibilidade, que é possível graças aos produtos escalares, é muito necessária em casos onde o conjunto de dados tem mais de 2 dimensões, porque, como se pode imaginar, em casos de conjuntos de dados com dimensionalidade muito alta, a equação do hiperplano que classifica adequadamente esses conjuntos de dados tende a ser muito complexa.

Então, ao introduzir uma maneira alternativa de derivar o hiperplano via Polinômio de Newton, que primeiro não é tão intenso computacionalmente, mas também é muito melhor para entender e apresentar; implementações variantes de SVM podem não apenas ser testadas, mas também consideradas como alternativas para uma estratégia existente ou como acréscimos. O IDE MQL5 permite ambos os cenários, onde no primeiro você desenvolveria um sistema de negociação inteiramente novo com base no código de classe de sinal compartilhado aqui. Mas talvez o que muitas vezes é negligenciado é o potencial adicional apresentado pelo assistente MQL5 que permite a montagem e o teste de várias estratégias simultaneamente. Isso também pode ser feito rapidamente e com o mínimo de codificação ao examinar ideias e estratégias na fase preliminar. E, como sempre, além de olhar para a classe de sinal das classes montadas pelo assistente, as classes de trailing e de gerenciamento de dinheiro também podem ser exploradas.