知っておくべきMQL5ウィザードのテクニック（第15回）：ニュートンの多項式を用いたサポートベクトルマシン

はじめに

サポートベクトルマシン(SVM)は機械学習の分類アルゴリズムです。分類は、こちらとこちらで以前の記事で検討したクラスタリングとは異なります。両者の主な違いは、SVMが教師あり学習で,分類がデータをあらかじめ定義されたセットに分ける一方、クラスタリングは教師なし学習でこれらのセットがどのようなもので、いくつあるかを決定しようとすることです。

一言で言えば、SVMは、データに次元が追加された場合、各データ点が他のすべてのデータ点とどのような関係を持つかを考慮することによってデータを分類します。分類は、あらかじめ定義されたデータセットをきれいに分離する超平面が定義できれば達成されます。

多くの場合、対象となるデータセットは多次元であり、特に各セットの数が少なかったり、データセットの相対的な割合が偏っていたりする場合に、SVMがそのようなデータセットの分類において非常に強力なツールとなるのは、まさにこの属性によるものです。2次元を超えるSVMの実装ソースコードは非常に複雑ですが、多くの場合、pythonやC#のユースケースは常にライブラリを使用するため、ユーザーは最小限のコードしか入力せずに結果を得ることができます。

高次元のデータは訓練データを曲線あてはめさせる傾向があり、サンプル外のデータでは信頼性が低くなります。これがSVMの主な欠点の1つです。一方、低次元のデータでは交差検証をよりうまくおこなうことができ、これはより一般的に使用されています。

この記事では、完全な実装ソースコードがサードパーティライブラリを参照せずに共有されるため、2次元データを処理する非常に基本的なSVM（線形SVMとも呼ばれる）について検討します。通常、分離超平面は、多項式カーネル（英語）または放射状カーネルの2つの方法のどちらか一方から導かれます。ここでは前者の多項式カーネルのみを扱います。後者はより複雑であり、ここでは説明しません。

通常、多項式カーネルを使用する場合は、以下の式で正式に定義されます。

超平面の方程式を設定する理想的な c 値と d 値を決定することは、2 つのデータ セット間のギャップを測定するため、サポート ベクトルをできるだけ遠く離すことを目的とした反復プロセスです（分離超平面定理）。

ただし、この記事では、題名にあるように、2次元データセットの超平面の方程式を導くためにニュートンの多項式を使用します。ニュートンの多項式については最近の記事で見ましたが、その実装の一部をざっと見ておきます。

ニュートンの多項式(NP)を3つのシナリオで実装します。まず、あらかじめ定義された2つのデータセットの中間点を補間して境界点を求め、これらの点を用いて超平面を定義する直線/曲線の方程式を導出します。この超平面が定義されたら、これをテストのExpertSignalクラスで取引決定を実行する際の分類器として扱い、使用します。2番目のシナリオでは、ExpertSignalクラスが（1番目のように）0か100の値しか出力しないのではなく、その中間の値も出力するように、回帰関数を追加します。未分類のベクトルが既知のベクトル点にどれだけ近いかから回帰値を計算します。第3に、2番目のシナリオを足場として、超平面を定義する際に少数の点のみを補間します。少数の点（別名、サポートベクトル）は他のデータセットに近い点であるため、他のすべてを採用しながら超平面方程式を「洗練」します。

多項式カーネルの背景

ここでは、完全なソースコード実装が共有されることを前提に線形SVMを考えています。ライブラリの使用を避けて、すべてのソースコードに完全な透明性を提供します。SVMの実世界での応用では、多くのデータセットに内在する複雑さと多次元性を考慮して、非線形型が多く使用されます。SVMにおけるこれらの課題は、カーネル法のおかげで対処できることがわかっています。これは、データセットを元の構造を維持したまま、より高い次元で研究することを可能にする手法です。カーネル法は、低次元のベクトル値を保持するためにベクトルのドット積を使用します。データセットをより高い次元に向けることで、データセットの分離は容易に達成され、これはより少ない計算リソースでおこなわれます。

上に示したように、私たちのカーネル関数は正式に次のように定義されます。

ここで、xとyは各セット内の任意の2つの比較されたデータ点間のデータ点として機能し、cは定数（その値はしばしば最初に1に設定される）であり、dは多項式の次数です。dが大きくなるにつれて、より正確な超平面方程式を定義することができますが、これは過剰適合につながる傾向があるので、バランスをとる必要があります。xとyのデータ点は多くの場合ベクトル、あるいは行列形式であり、そのため冪乗Tはxの転置を表します。

説明のためにMQL5で多項式カーネルを実装すると、次のような形になります。

//+------------------------------------------------------------------+
//| Define a data point structure                                    |
//+------------------------------------------------------------------+
struct Sdatapoint
{  double      features[2];
   int               label;
                     Sdatapoint()
   {                 ArrayInitialize(features, 0.0);
      label = 0;
   };
                    ~Sdatapoint() {};

};

//+------------------------------------------------------------------+
//| Function to calculate the polynomial kernel value                |
//+------------------------------------------------------------------+
double PolynomialKernel(Sdatapoint &A, Sdatapoint &B, double Constant, int Degree)
{  double _kernel_sum = 0.0;
   for (int i = 0; i < 2; i++)
   {  _kernel_sum += (A.features[i] * B.features[i]);
   }
   _kernel_sum += Constant; // Add constant term
   return(pow(_kernel_sum, Degree));
}

別々のセットに含まれるデータ点間の関係重みが計算され、カーネル行列に格納されます。このカーネル行列はデータ点の間隔を定量化するため、各データセットの端にあり、隣接するデータセットに近いデータ点をサポートベクトルから除外します。

ソース

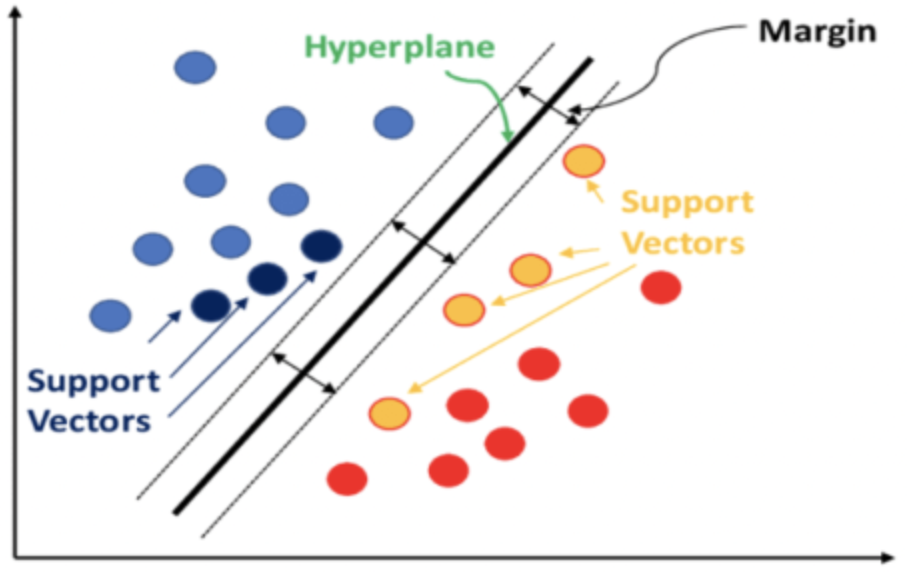
これらのサポートベクトルは、超平面方程式を計算する入力となります。これらはすべて、次のようなライブラリ関数で処理されます。超平面方程式を導出するという複雑な性質を考慮すると、超平面を計算して出力するのは、PyLIBSVM、またはPythonのshogun、RのkernlabまたはSVMlightのようなライブラリ関数です。

カーネル行列を決定する際、最適解を得るために様々な定数や多項式の次数値を考慮することができます。ただでさえ複雑な超平面を1つの行列から導き出す作業を複数の行列にわたっておこなうことでさらに複雑にしてしまうため、まず必ず定数と多項式次数を一度だけ（あるいはノウハウから最適でないものを）決めておき、それを使って超平面を導き出す方が賢明です。このため、定数値も1として設定されます。そして予想されるように、次数の高い多項式ほど良い分類ができますが、これにはすでに述べたような過剰適合のリスクがあります。

また、多項式の次数が高いほど計算量が多くなる傾向があるため、高すぎない直感的な値を最初に設定する必要があります。

ここで検討する多項式カーネルは比較的理解しやすいものですが、多くのSVM実装で最も使用されたり好まれたりするカーネルではありません。それを自慢できる権利は放射基底関数カーネルにあります。

放射基底関数(RBF)カーネルがより一般的に選択されるのは、SVMの長所が多次元データの処理にあり、RBFカーネルが多項式カーネルよりもこれを得意とするからです。カーネルが選択されると、前述したように、データセットが高次元空間にマッピングされる二重最適化問題が開始されます。 カーネル法と呼ばれるもので取り込まれたドット積ルールのおかげで、この最適化 (前後) をより効率的に実行できると同時に、よりわかりやすく表現することができます。2次元を超えるデータセットに対する超平面方程式は複雑な性質を持っているため、これは不可欠です。すべてが終わると、超平面方程式は次のような形になります。

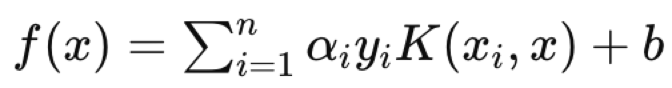
ここで

• f(x)：決定関数
• αi​ ：最適化プロセスで得られた係数
• yi​ ：クラスラベル
• K(xi​x)：カーネル関数
• b：バイアス項

超平面方程式は、任意のクエリ点がどちらに属するかを定義するクラスラベルを割り当てる決定関数によって、2つのデータセットがどのように分離されるかを定義します。つまり、クエリデータ点は式中のxとなり、xiとyiはそれぞれ訓練データとその分類子となります。

余談ですが、SVMの応用範囲は広く、例えば、電子メールのヘッダーとコンテンツを構造化されたフォーマットに埋め込むことができれば、スパムフィルタリングができます。SVMが他の機械学習と違って理想的なのは、小さなデータセットや非常に歪んだデータセットからモデルを開発するのに頑健だからです。

MQL5での実装

xとyの値を格納するために使用するモデル構造体は、最近の実装と非常によく似ていますが、ここでの違いは、分類器タイプごとにカウンタを追加していることです。SVMは本質的に分類器です。これらのカウンタが役に立つ実例を見てみましょう。

つまり、ニュートンの多項式を使用できるようにデータセットの多次元性を2に制限しているので、xベクトルの値は各インデックスで2です。次元が高くなると、過剰適合の危険性もあります。xの最初の次元または値は、高価格バッファの変化であり、2番目の次元または値は、予想通り低価格バッファの変化です。入力データの選択は、今や機械学習において極めて重要な要素となっています。Transformer、CNN、RNNは非常に機知に富んでいますが、入力データの決定や、それらをどのように埋め込んだり正規化したりするかがより重要になります。

ここでは非常に単純なデータセットを選択しましたが、入力データの選択が生の価格データや指標値に限定されるものではなく、ニュース経済指標値も含まれることにご留意ください。そしてまた、これをどのように正常化するかによって、すべての違いが出てきます。

//+------------------------------------------------------------------+
//| Function to get and prepare data.                                |
//+------------------------------------------------------------------+
double CSignalSVM::GetOutput(int Index)
{  double _get = 0.0;
   

        ....
        ....

   int _x = StartIndex() + Index;
   for(int i = 0; i < m_length; i++)
   {  for(int ii = 0; ii < Dimensions(); ii++)
      {  if(ii == 0) //dim-1
         {  m_model.x[i][ii] = m_high.GetData(StartIndex() + i + _x) - m_high.GetData(StartIndex() + i + _x + 1);
         }
         else if(ii == 1) //dim-2
         {  m_model.x[i][ii] = m_low.GetData(StartIndex() + i + _x) - m_low.GetData(StartIndex() + i + _x + 1);
         }
      }
      if(i > 0) //assign classifier
      {  if(m_close.GetData(StartIndex() + i + _x - 1) - m_close.GetData(StartIndex() + i + _x) > 0.0)
         {  m_model.y[i - 1] = 1;
            m_model.y1s++;
         }
         else if(m_close.GetData(StartIndex() + i + _x - 1) - m_close.GetData(StartIndex() + i + _x) < 0.0)
         {  m_model.y[i - 1] = 0;
            m_model.y0s++;
         }
      }
   }
//
   _get = SetOutput();
   return(_get);
}

Yのデータセットは、これまでと同様、終値の変化を前方ラグしたものとなります。y0とy1とラベル付けされた2つのクラスにカウンタを導入します。これらは単純に、2つのxの値が確立された処理された各バーについて、その後の終値の変化が強気であったか（この場合、0が記録される）、弱気であったか（この場合、1が記録される）を記録します。

yはベクトルなので、補足として、現在の値を0で満たされたベクトルおよび1で満たされたベクトルと比較することによって、これらの0と1のカウントを取得することができます。返される値が実質的にyベクトルにそれぞれ0と1が存在するカウントになるためです。

set-output関数は、モデル情報を処理する上で、これまでの関数に追加されたものです。これは各クラスのxベクトル値を取り、2つのセットの超平面として機能する2つのセットの中間点を補間します。これはすでに述べたSVMアプローチではありませんが、ニュートン多項式によって超平面を定義したいので、これがおこなうことは、超平面方程式を導出するために使用できる点のセットを与えることです。

//+------------------------------------------------------------------+
//| Function to set and train data                                   |
//+------------------------------------------------------------------+
double CSignalSVM::SetOutput(void)
{  double _set = 0.0;
   matrix _a,_b;
   Classifier(_a,_b);
   if(_a.Rows() * _b.Rows() > 0)
   {  matrix _interpolate;
      _interpolate.Init(_a.Rows() * _b.Rows(), Dimensions());
      for(int i = 0; i < int(_a.Rows()); i++)
      {  for(int ii = 0; ii < int(_b.Rows()); ii++)
         {  _interpolate[(i*_b.Rows())+ii][0] = 0.5 * (_a[i][0] + _b[ii][0]);
            _interpolate[(i*_b.Rows())+ii][1] = 0.5 * (_a[i][1] + _b[ii][1]);
         }
      }
      vector _w;
      vector _x = _interpolate.Col(0);
      vector _y = _interpolate.Col(1);
      _w.Init(m_model.y0s * m_model.y1s);
      _w[0] = _y[0];
      m_newton.Set(_w, _x, _y);
      double _xx = m_model.x[0][0], _yy = m_model.x[0][1], _zz = 0.0;
      m_newton.Get(_w, _xx, _zz);
      if(_yy < _zz)
      {  _set = 100.0;
      }
      else if(_yy > _zz)
      {  _set = -100.0;
      }
      _set *= Regressor(_x, _y, _xx, _yy);
   }
   return(_set);
}

私この方法の中で超平面を導き出すアプローチを3つ考えています。最初のアプローチは、セット内の各点の平均を代替セット内の各点に補間することで、超平面点を導き出す際に各セット内のすべての点を考慮します。これは明らかにサポートベクトルを考慮していませんが、他のアプローチとの研究および比較の目的でここに示しました。

2つ目の方法は1つ目の方法と似ていますが、唯一の違いは、予測y値が回帰されることです。つまり、0または1としてではなく、「正則化」関数を使用して、出力予測を0.0～1.0の範囲の浮動小数点値として変換または正規化します。これは、原理的にはSVMからさらに進んだシステムですが、2次元のデータ点を区別するために超平面を使用します。

//+------------------------------------------------------------------+
//| Regressor for the model                                          |
//+------------------------------------------------------------------+
double CSignalSVM::Regressor(vector &X, vector &Y, double XX, double YY)
{  double _x_max = fmax(X.Max(), XX);
   double _x_min = fmin(X.Min(), XX);
   double _y_max = fmax(Y.Max(), YY);
   double _y_min = fmin(Y.Min(), YY);
   return(0.5 * ((1.0 - ((_x_max - XX) / fmax(m_symbol.Point(), _x_max - _x_min))) + (1.0 - ((_y_max - YY) / fmax(m_symbol.Point(), _y_max - _y_min)))));
}

予測値をそのセットの最大値および最小値と比較することで、最大値と一致する場合は1が返されるのに対し、最小値と一致する場合は0が返されるように、代理回帰値を得ることができます。

第3そして最後に、超平面の導出に使用される各セットの点をフィルタリングする「分類器」関数を追加することによって、第2部の方法を改善します。自分のセットの重心から最も遠く、反対側のセットの重心に最も近い点を考慮することで、2つのセットの間の超平面境界を補間するために使用できる、各クラスから1つずつ、2つの点のサブセットが得られます。

//+------------------------------------------------------------------+
//| 'Classifier' for the model that identifies Support Vector points |
//|  for each set.                                                   |
//+------------------------------------------------------------------+
void CSignalSVM::Classifier(matrix &A, matrix &B)
{  if(m_model.y0s * m_model.y1s > 0)
   {  matrix _a_centroid, _b_centroid;
      _a_centroid.Init(1, Dimensions());
      _b_centroid.Init(1, Dimensions());
      for(int i = 0; i < m_length; i++)
      {  if(m_model.y[i] == 0)
         {  _a_centroid[0][0] += m_model.x[i][0];
            _a_centroid[0][1] += m_model.x[i][1];
         }
         else if(m_model.y[i] == 1)
         {  _b_centroid[0][0] += m_model.x[i][0];
            _b_centroid[0][1] += m_model.x[i][1];
         }
      }
      _a_centroid[0][0] /= m_model.y0s;
      _a_centroid[0][1] /= m_model.y0s;
      _b_centroid[0][0] /= m_model.y1s;
      _b_centroid[0][1] /= m_model.y1s;
      double _a_sd = 0.0, _b_sd = 0.0;
      double _ab_sd = 0.0, _ba_sd = 0.0;
      for(int i = 0; i < m_length; i++)
      {  if(m_model.y[i] == 0)
         {  double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            _a_sd += sqrt(_0);
            double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            _ab_sd += sqrt(_1);
         }
         else if(m_model.y[i] == 1)
         {  double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            _b_sd += sqrt(_1);
            double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            _ba_sd += sqrt(_0);
         }
      }
      _a_sd /= m_model.y0s;
      _ab_sd /= m_model.y0s;
      _b_sd /= m_model.y1s;
      _ba_sd /= m_model.y1s;
      for(int i = 0; i < m_length; i++)
      {  if(m_model.y[i] == 0)
         {  double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            if(sqrt(_0) >= _a_sd && _ab_sd <= sqrt(_1))
            {  A.Resize(A.Rows()+1,Dimensions());
               A[A.Rows()-1][0] = m_model.x[i][0];
               A[A.Rows()-1][1] = m_model.x[i][1];
            }
         }
         else if(m_model.y[i] == 1)
         {  double _1 = 0.0;
            _1 += pow(_b_centroid[0][0] - m_model.x[i][0], 2.0);
            _1 += pow(_b_centroid[0][1] - m_model.x[i][1], 2.0);
            double _0 = 0.0;
            _0 += pow(_a_centroid[0][0] - m_model.x[i][0], 2.0);
            _0 += pow(_a_centroid[0][1] - m_model.x[i][1], 2.0);
            if(sqrt(_1) >= _b_sd && _ba_sd <= sqrt(_0))
            {  B.Resize(B.Rows()+1,Dimensions());
               B[B.Rows()-1][0] = m_model.x[i][0];
               B[B.Rows()-1][1] = m_model.x[i][1];
            }
         }
      }
   }
}

これをおこなう上で共有されたコードは少し長いですが、特に最近MQL5で導入されたベクトルデータ型と行列データ型の組み込み関数を使用した場合、より効率的な実装が可能であると確信しています。ただし、まずやるのは、各データセットの重心（または平均）を見つけることです。これが定義されたら、各データセットの標準偏差を計算します。これは、接尾辞「_sd」の付いた変数によって取得されます。重心座標と標準偏差の大きさを準備したら、計算された標準偏差を遠すぎる、または近すぎる閾値として使用して、各点がその重心からどのくらい離れているか、また反対側のデータセットの重心からどのくらい離れているかを測定して比較できます。

補間された点は、ニュートンの多項式で方程式を定義するのに必要なすべてです。こちらで見たように、より多くの点を提供すればするほど、方程式の指数は高くなります。ニュートンの多項式で使用できる補間点の最大数はデータセットのサイズによって制御され、これはm_lengthパラメータに正比例します。これは、モデル内の2つのデータセットを定義するときに、履歴内で遡る必要があるデータ 点の数を設定する変数です。

超平面を導き出すために使用される3つの方法のうち、最後の方法だけが典型的なSVMの方法と似ています。各セット内で、セットの境界に最も近く、したがって超平面に関連性の高い点をスクリーニングすることで、サポートベクトルを定義しています。これらのサポートベクトル点は、超平面方程式を導出する際に、ニュートン多項式クラスの入力となります。対照的に、もし厳密なSVMをおこなうのであれば、これを可能にする多項式カーネル方程式の定数を繰り返しながら、微分のためにデータ点に余分な次元を追加することになります。たった2次元のデータであっても、計算リソースが必要なことは言うまでもありませんが、明らかに桁違いに複雑です。実際、簡潔化のためあるいはベストプラクティスのため、これらの定数のうちの1つ(c)は常に1と仮定され、多項式の次数変数（上式のd）のみが最適化されます。また、2次元を超えるデータセットでは、サードパーティのライブラリが必要になることは想像に難くありません。なぜなら、4、5、またはn番目の指数方程式を求めると、何倍も複雑になるからです。

ニュートン多項式の実装は、次のy値を決定するためにビルドされた方程式を実行するGet関数のデバッグを除いては、前の関連記事で取り上げたものと非常によく似ています。以下に添付します。

テスター結果

この記事の最後に添付した3つのシグナルクラスファイルは、それぞれMQL5ウィザードを使ってEAに組み立てることができます。その方法については、こちらとこちらの記事で紹介しています。

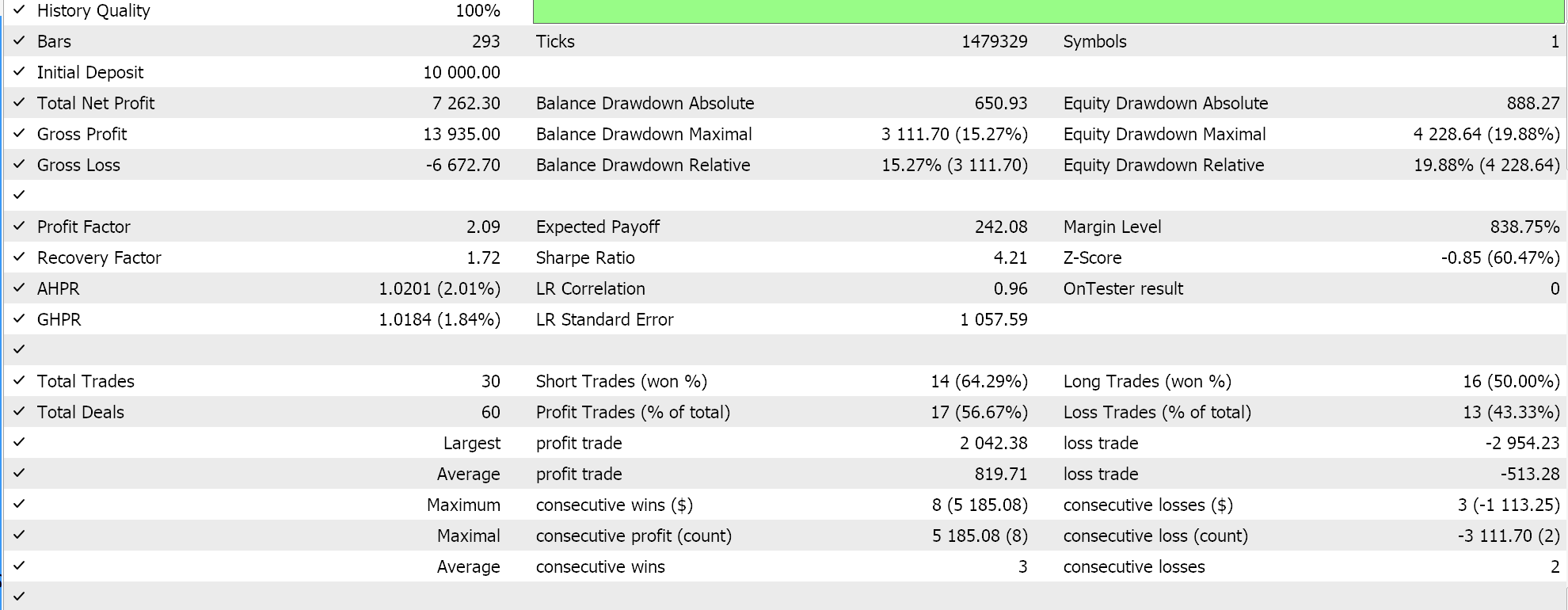
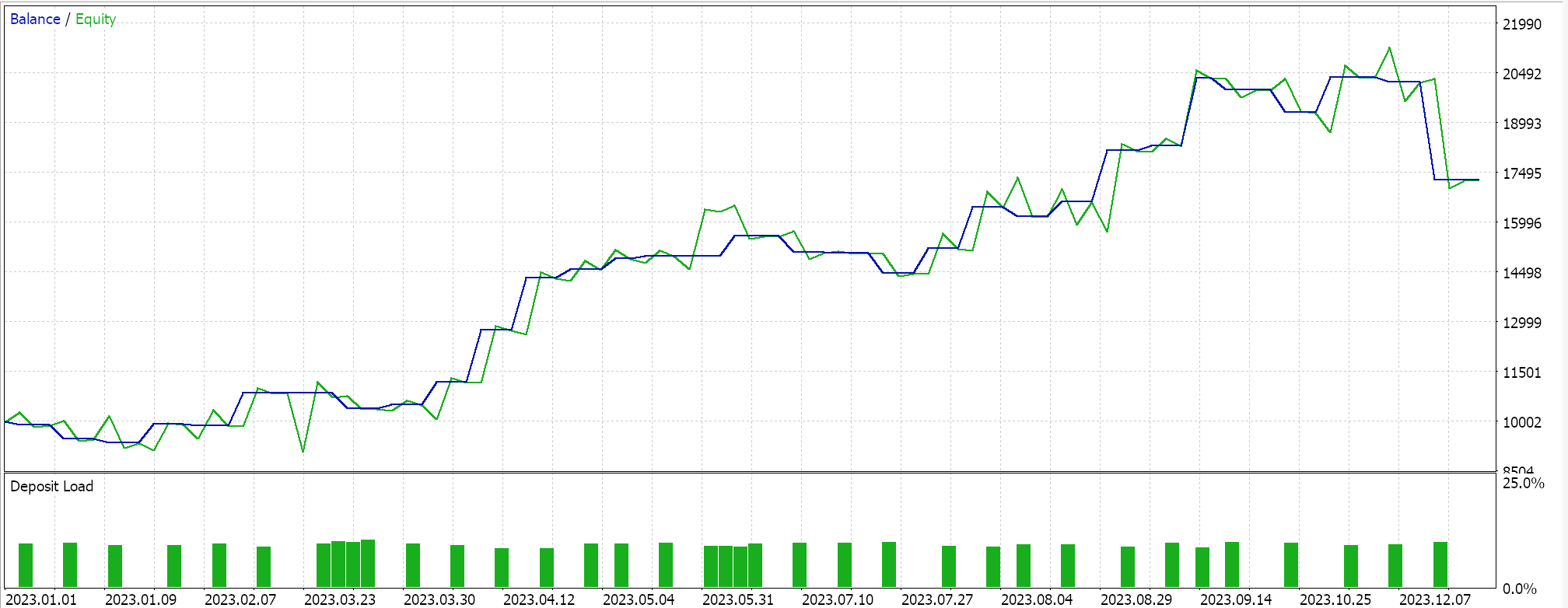
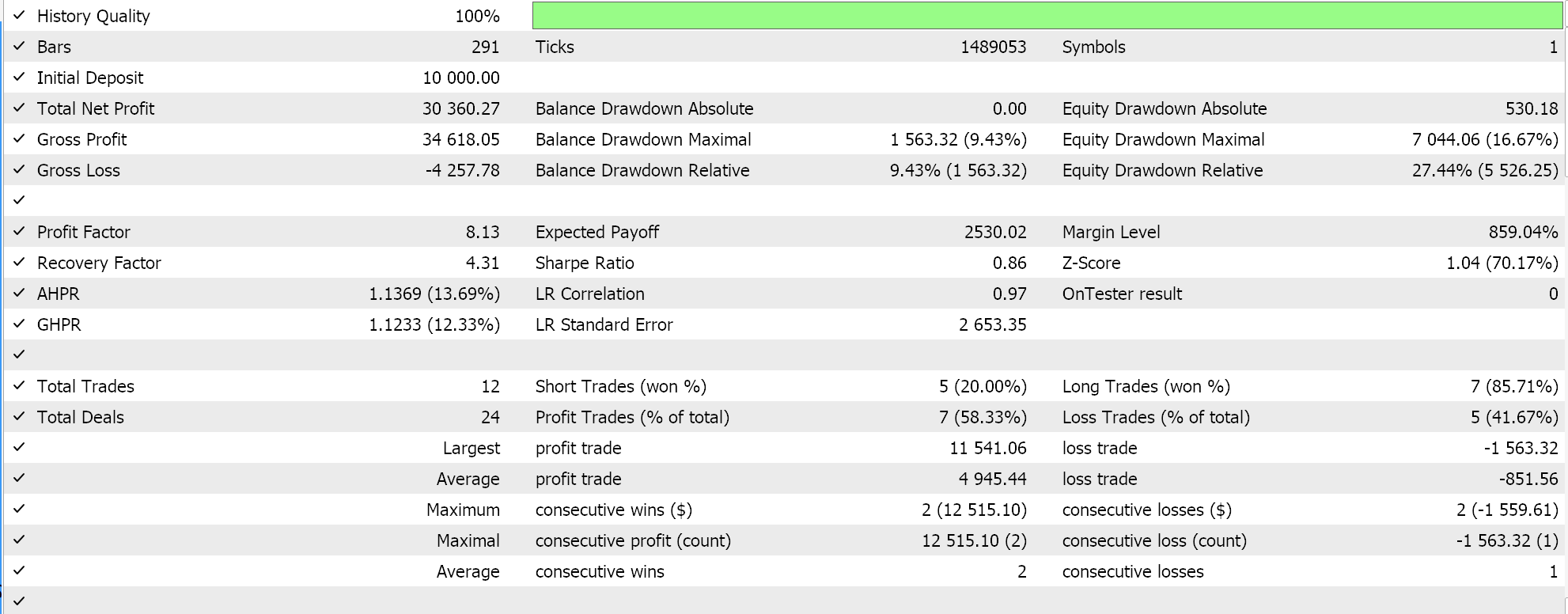
そこで、サポートベクトルをスクリーニングすることなく、どちらかのセットのすべての点を補間して超平面を得るという最初の実装のテストを実行したところ、次のような結果が得られました。

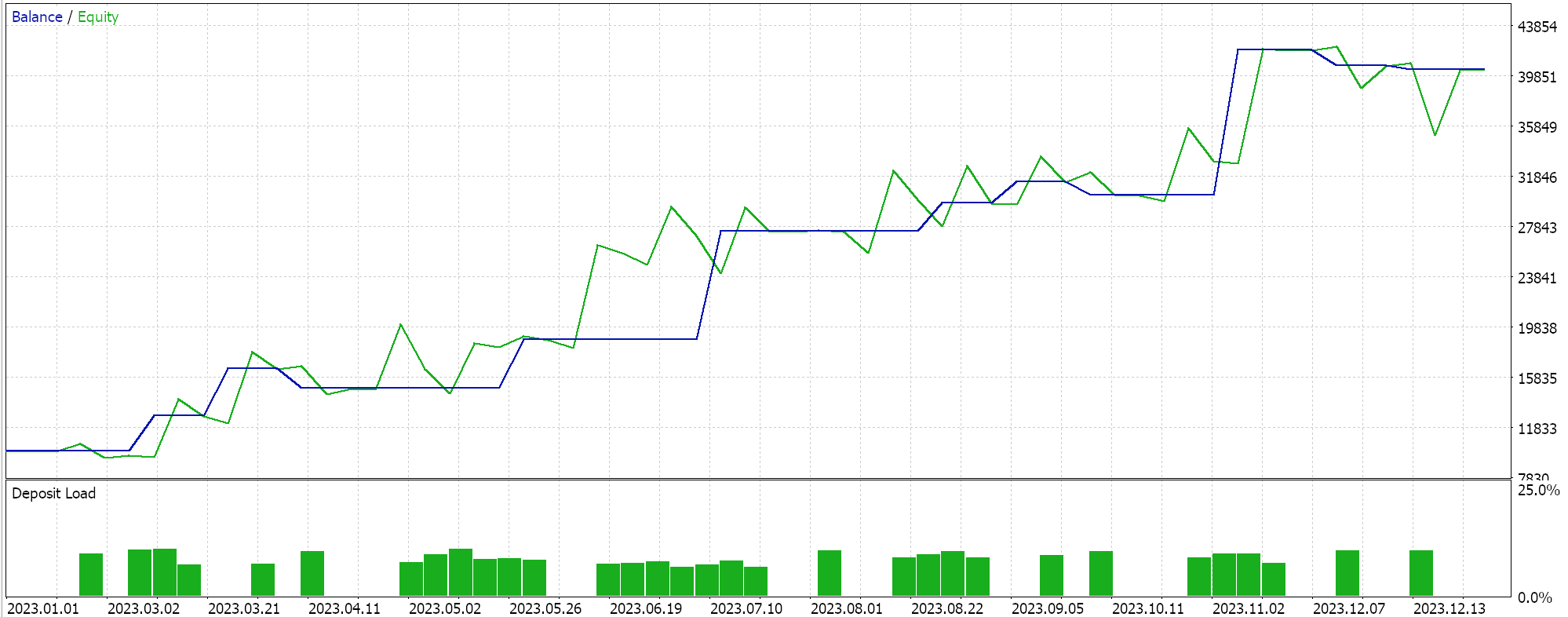
テスト銘柄が2023年の日足でEURJPYである場合、上記と同様のテスト実行をおこなうと、上記の方法に回帰を追加しただけの2番目の方法では、以下のようになります。

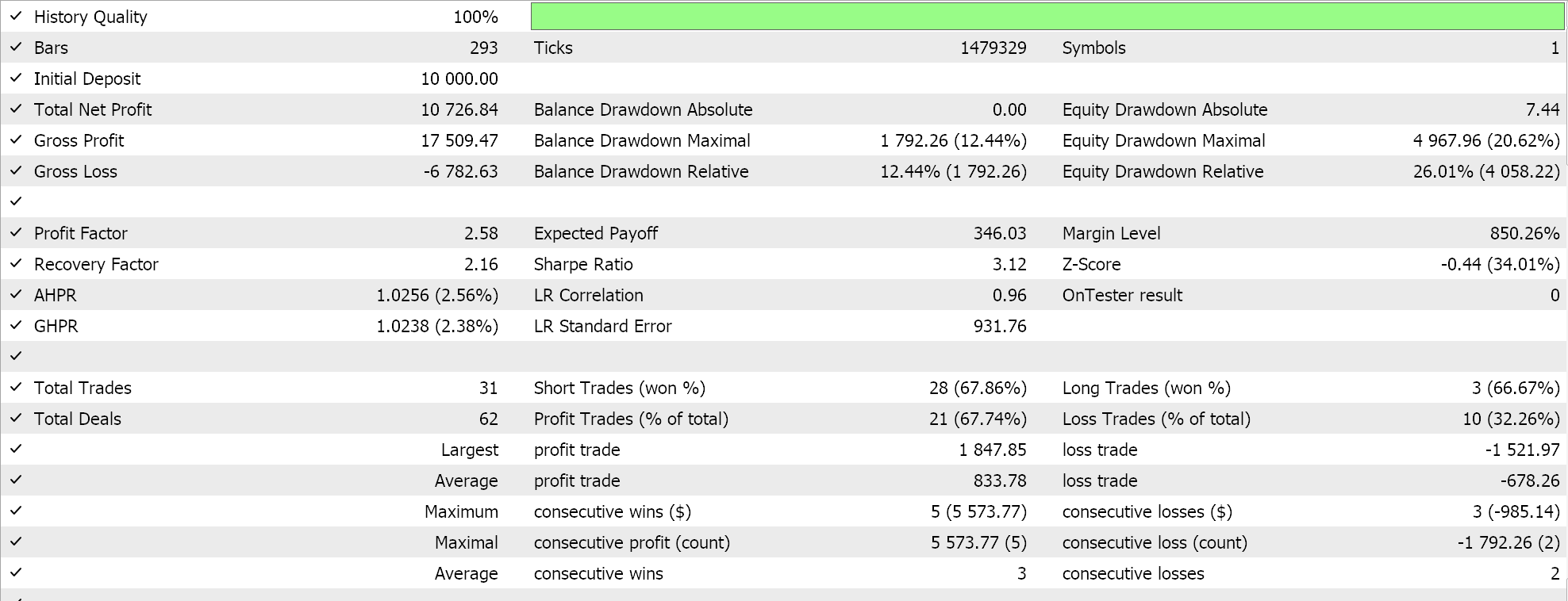
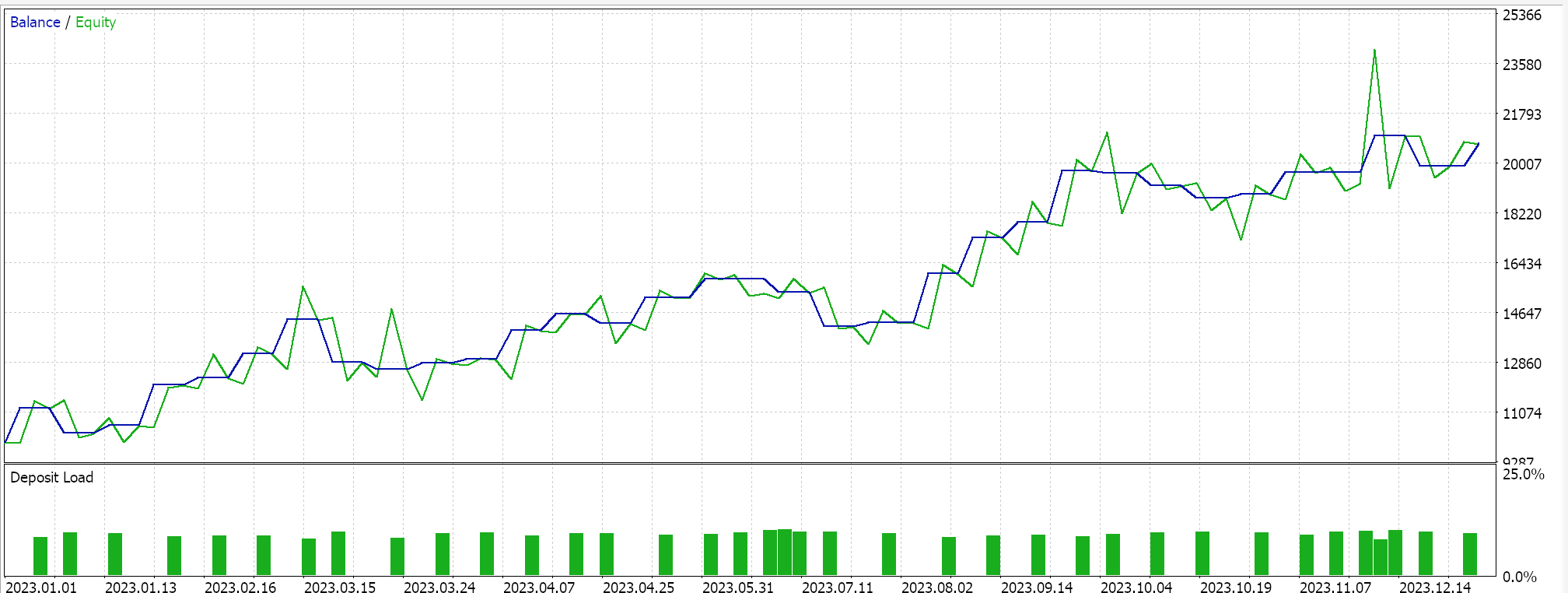
最後に、超平面を導出する前にサポートベクトル点を探すためにいずれかのデータセットをスクリーニングする、SVMに最も類似したアプローチをテストしたところ、次のような結果が得られました。

上記の報告から、ざっと見たところ、サポートベクトルを使用する方法が最も有望であると推測されますが、（パラメータの数は3つの方法とも同じであるにもかかわらず）余分な微調整が必要であることを考えれば、これは驚くべきことではないでしょう。

余談ですが、このテストは指値注文で実際のティックでおこなわれ、テイクプロフィットやストップロスは使用されていません。いつものことですが、より意味のある結論を導き出すには、より多くのテストが必要です。ただし、興味深いことに、同じ数の入力パラメータでは、サポートベクトル法の方が良い結果を出しています。取引回数は少なく、他の2つのアプローチよりも劇的に優れたパフォーマンスを示しました。

2つ目のアプローチで回帰を加えても、結果からわかるように、パフォーマンスはわずかにしか向上しませんでした。取引回数もほぼ同じでしたが、超平面を定義する前にサポートベクトルについてデータセット点を事前にスクリーニングしたことは、明らかにゲームチェンジャーとなりました。MetaTraderのレポートは非常に主観的なもので、取引システムが前進できるかどうかの指標として最も重要な統計は何かという議論が多いです。私もそのトピックについて明確な答えを持っていません。しかし、平均連勝率と平均連敗率を気にしながら、（1取引あたりの）平均利益と平均損失を比較することは、洞察に役立つと思います。これらの値はすべて、期待値と呼ばれる比率を計算する際に組み合わされることが多いです。これは、単純に利益を全取引で割った期待ペイオフとは大きく異なります。すべてのレポートの期待値を比較すると、サポートベクトルを使用した方法は、他の2つのアプローチと比較して、ほぼ10倍優れています。

結論

最後に、可能性のある取引のアイデアを素早く開発し、テストすることで、それが改善策となるか、あるいは既存の戦略に適合するかを評価する、もう1つの例を見てきました。

SVMはかなり複雑なアルゴリズムで、PythonのPyLIBSVMやRのSVMlightなどのサードパーティライブラリの助けを借りずに実装されることはほとんどありません。それに、このプロセスを簡素化するために、最適化可能なパラメータの1つが1であるとみなされることがよくあります。要約すると、このプロセスでは、研究対象のデータセットのコピーの次元が、多項式カーネルと呼ばれる特定の可逆式によって増やされます。この多項式カーネルが比較的単純で可逆的であることから、「カーネル法」と呼ばれています。ドット積のおかげで可能になったこの単純さと可逆性は、データセットが2次元以上の場合に大いに必要とされます。なぜなら、非常に高次元のデータセットの場合、そのようなデータセットを適切に分類する超平面方程式は非常に複雑になることが想像できるからです。

そのため、ニュートン多項式を介して超平面を導出する別の方法を導入することで、まず、計算量がそれほど多くなく、理解と提示がはるかに容易になります。SVMのさまざまな実装はテストできるだけでなく、既存の戦略の代替として、または追加として検討することもできます。MQL5 IDEではどちらのシナリオも可能ですが、前者の場合は、ここで共有したシグナルクラスのコードに基づいて、まったく新しい取引システムを開発することになります。ただし、おそらく見落とされがちなのは、複数のストラテジーを同時に組み立ててテストできるMQL5ウィザードがもたらす付加的な可能性でしょう。これも、予備段階でアイデアや戦略をスクリーニングする際に、最小限のコーディングで素早くおこなうことができます。そしていつものように、ウィザードが組み立てたクラスのシグナルクラスを見るだけでなく、トレーリングクラスやマネーマネージメントクラスも調べることができます。